Riemann Problem for the Isentropic Euler Equations of Mixed Type in the Dark Energy Fluid
Abstract
1. Introduction
2. Preliminaries
3. Shock Waves
3.1. Discontinuity Curves
3.2. Admissible Criterion
3.3. Admissible Shock Waves
4. Rarefaction Waves
5. Riemann Solutions
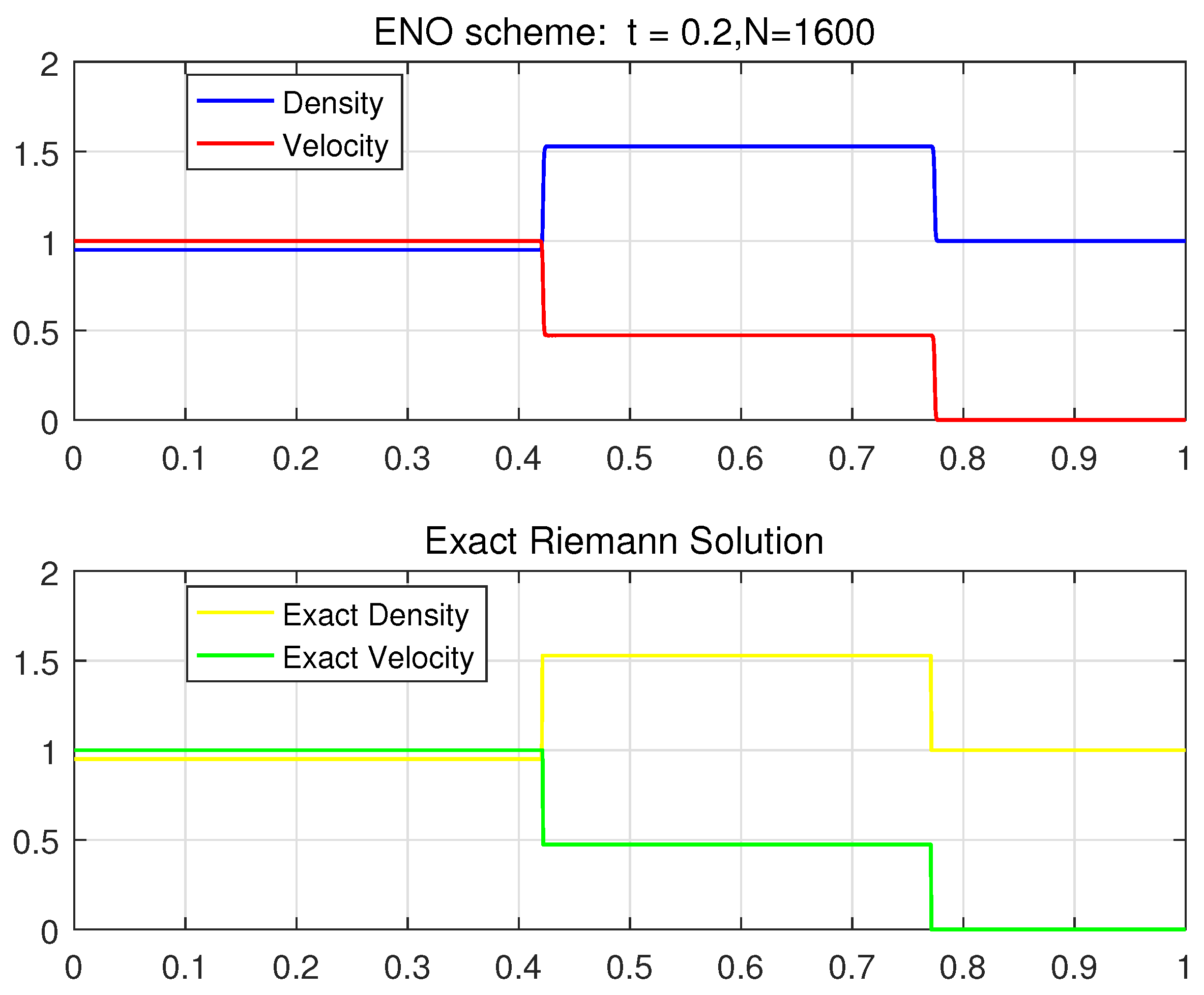
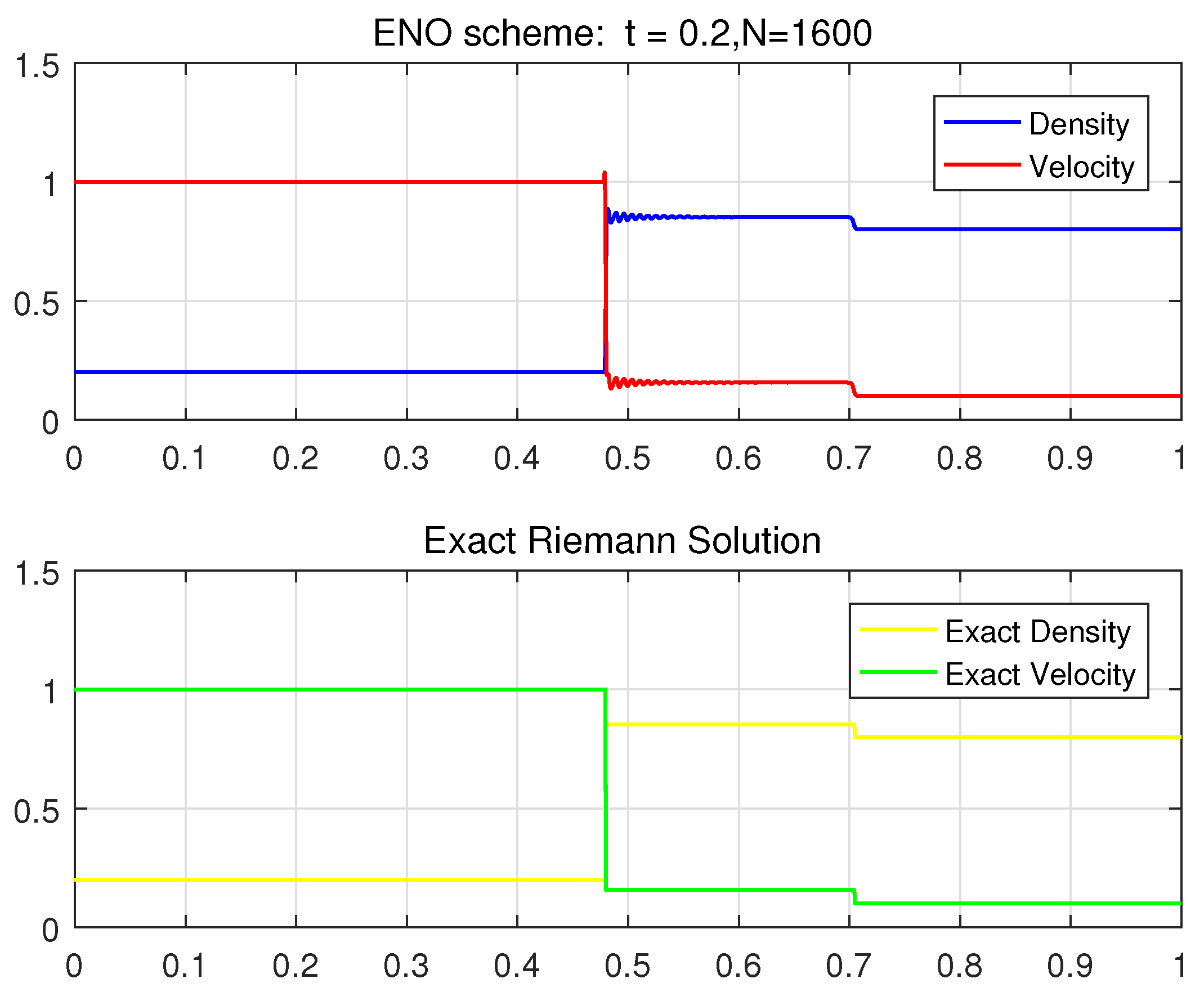
6. Numerical Tests
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Diperna, R. Convergence of viscosity method for isentropic gas dynamics. Commun. Math. Phys. 1983, 91, 1–30. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Generalized Logarithmic equation of state in classical and loop quantum cosmology dark energy-dark matter coupled systems. Ann. Phys. 2019, 409, 167934. [Google Scholar] [CrossRef]
- Pan, S.; Yang, W.; Di Valentino, E.; Saridakis, E.N.; Chakraborty, S. Interacting scenarios with dynamical dark energy: Observational constraints and alleviation of the H0 tension. Phys. Rev. D 2019, 100, 103520. [Google Scholar] [CrossRef]
- Mayer, B.; Anton, H.; Bott, E.; Methfessel, M.; Sticht, J.; Harris, J.; Schmidt, P.C. Ab-initio calculation of the elastic constants and thermal expansion coefficients of Laves phases. Intermetallics 2003, 11, 23–32. [Google Scholar] [CrossRef]
- Chen, G.Q. The Theory of Compensated Compactness and the System of Isentropic Gas Dynamics; Math Sciences Research Institute: Berkeley, CA, USA, 1990; Preprint 00527-91. [Google Scholar]
- Chen, G.Q.; Le Floch, P. Compressible Euler equations with general pressure law. Arch. Ration. Mech. Anal. 2000, 153, 221–259. [Google Scholar] [CrossRef]
- Chen, G.Q.; Huang, F.M.; Wang, T.Y. Isothermal limit of entropy solutions of the Euler equations for isentropic gas dynamics. SIAM J. Math. Anal. 2024, 56, 1300–1320. [Google Scholar] [CrossRef]
- Ding, X.Q.; Chen, G.Q.; Luo, P.Z. Convergence of the Lax-Friedrichs scheme for isentropic gas dynamics (I). Acta Math. Sci. (Engl. Ed.) 1985, 5, 415–432. [Google Scholar] [CrossRef]
- Ding, X.Q.; Chen, G.Q.; Luo, P.Z. Convergence of the Lax-Friedrichs scheme for isentropic gas dynamics (II). Acta Math. Sci. (Engl. Ed.) 1985, 5, 433–472. [Google Scholar] [CrossRef]
- Huang, F.M.; Wang, Z. Convergence of viscosity solutions for isothermal gas dynamics. SIAM J. Math. Anal. 2002, 34, 595–610. [Google Scholar] [CrossRef]
- Lions, P.L.; Perthame, B.; Tadmor, E. Kinetic formulation of the isentropic gas dynamics and p-systems. Commun. Math. Phys. 1994, 163, 169–172. [Google Scholar] [CrossRef]
- Lions, P.L.; Perthame, B.; Souganidis, P. Existence and stability of entropy solutions for the hyperbolic systems of isentropic gas dynamics in Eulerian and Lagrangian coordinates. Commun. Pure Appl. Math. 1996, 49, 599–638. [Google Scholar] [CrossRef]
- Lu, Y.G. Existence of global entropy solutions to a nonstrictly hyperbolic system. Arch. Ration. Mech. Anal. 2005, 178, 287–299. [Google Scholar] [CrossRef]
- Shah, S.; Singh, R.; Jena, J. Steepened wave in two-phase Chaplygin flows comprising a source term. Appl. Math. Comput. 2022, 413, 126656. [Google Scholar] [CrossRef]
- Brenier, Y. Solutions with concentration to the Riemann problem for the one-dimensional Chaplygin gas equations. J. Math. Fluid Mech. 2005, 7, S326–S331. [Google Scholar] [CrossRef]
- Sun, M. Concentration and cavitation phenomena of Riemann solutions for the isentropic Euler system with the logarithmic equation of state. Nonlinear Anal. Real World Appl. 2020, 53, 103068. [Google Scholar] [CrossRef]
- Chavanis, P.H. The Logotropic dark fluid as a unification of dark matter and dark energy. Phys. Lett. B 2016, 758, 59–66. [Google Scholar] [CrossRef]
- Evans, L.C. Partial Differential Equations, 2nd ed.; American Mathematical Society: Providence, RI, USA, 2010; pp. xxii+749. [Google Scholar]
- Mercier, J.M.; Piccoli, B. Admissible Riemann solvers for genuinely nonlinear p-systems of mixed type. J. Differ. Equ. 2002, 80, 395–426. [Google Scholar] [CrossRef]
- Fan, H.; Slemrod, M. The Riemann problem for systems of conservation laws of mixed type. In Shock Induced Transitions and Phase Structures in General Media; The IMA Volumes in Mathematics and its Applications; Springer: New York, NY, USA, 1993; Volume 52, pp. 61–69. [Google Scholar]
- Slemrod, M. Admissibility criteria for propagating phase boundaries in a van der Waals fluid. Arch. Rational Mech. Anal. 1983, 81, 301–315. [Google Scholar] [CrossRef]
- Shearer, M. The Riemann problem for a class of conservation laws of mixed type. J. Differ. Equ. 1982, 46, 426–443. [Google Scholar] [CrossRef]
- Thanh, M.D.; Vinh, D.X. The Riemann problem for van der Waals fluids with nonclassical phase transitions. Hokkaido Math. J. 2021, 50, 263–295. [Google Scholar] [CrossRef]
- Lax, P.D. Hyperbolic systems of conservation laws. Commun. Pure Appl. Math. 1957, 10, 537–566. [Google Scholar] [CrossRef]
- Liu, T.P. The Riemann problem for general system of conservation laws. J. Differ. Equ. 1975, 18, 218–234. [Google Scholar] [CrossRef]
- Azevedo, A.V.; Marchesin, D. Multiple viscous profile Riemann solutions in mixed elliptic-hyperbolic models for flow in porous media. In Nonlinear Evolution Equations that Change Type; The IMA Volumes in Mathematics and its Applications; Springer: New York, NY, USA, 1990; Volume 27, pp. 1–17. [Google Scholar]
- Azevedo, A.V.; Marchesin, D.; Plohr, B.; Zumbrun, K. Capillary instability in models for three-phase flow. Z. Angew. Math. Phys. 2002, 53, 713–746. [Google Scholar] [CrossRef]
- Chalons, C.; Coquel, F.; Engel, P.; Rohde, C. Fast relaxation solvers for hyperbolic-elliptic phase transition problems. SIAM J. Sci. Comput. 2012, 34, A1753–A1776. [Google Scholar] [CrossRef][Green Version]
- He, F.; Wang, Z.; Chen, T. The Shock Waves for a Mixed-Type System from Chemotaxis. Acta Math. Sci. Ser. B (Engl. Ed.) 2023, 43, 1717–1734. [Google Scholar] [CrossRef]
- Holden, H. On the Riemann problem for a prototype of a mixed type conservation law. Commun. Pure Appl. Math. 1987, 40, 229–264. [Google Scholar] [CrossRef]
- Hsiao, L.; De Mottoni, P. Existence and uniqueness of the Riemann problem for a nonlinear system of conservation laws of mixed type. Trans. Am. Math. Soc. 1990, 322, 121–158. [Google Scholar] [CrossRef]
- Keyfitz, B.L.; Sanders, R.; Sever, M. Lack of hyperbolicity in the two-fluid model for two-phase incompressible flow. Discret. Contin. Dyn. Syst. Ser. B 2003, 3, 541–563. [Google Scholar] [CrossRef]
- Li, T.; Liu, H.; Wang, L. Oscillatory traveling wave solutions to an attractive chemotaxis system. J. Differ. Equ. 2016, 261, 7080–7098. [Google Scholar] [CrossRef]
- Li, T.; Mathur, N. Riemann problem for a non-srtrictly hyperbolic system in chemotaxis. Discret. Contin. Dyn. Syst. Ser. B 2022, 27, 2173–2187. [Google Scholar] [CrossRef]
- Mailybaev, A.A.; Marchesin, D. Lax shocks in mixed-type systems of conservation laws. J. Hyperbolic Differ. Equ. 2008, 5, 295–315. [Google Scholar] [CrossRef]
- Medeiros, H.B. Stable hyperbolic singularities for three-phase flow models in oil reservoir simulation. Acta Appl. Math. 1992, 28, 135–159. [Google Scholar] [CrossRef]
- Smoller, J. Shock Waves and Reaction-Diffusion Equations, 2nd ed.; Springer: New York, NY, USA, 1994. [Google Scholar]
- Gottlieb, D.; Shu, C.W. On the Gibbs phenomenon and its resolution. SIAM Rev. 1997, 39, 644–668. [Google Scholar] [CrossRef]
- Hsiao, L. Uniqueness of admissibel solutions of Riemann problem of systems of conservation laws of mixed type. J. Differ. Equ. 1990, 86, 197–233. [Google Scholar] [CrossRef]
- Jiang, G.S.; Shu, C.W. Efficient implementation of weighted ENO schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Shearer, M. Nonuniqueness of admissible solutions of Riemann initial value problems for a system of conservation laws of mixed type. Arch. Ration. Mech. Anal. 1986, 93, 45–59. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Jiang, W.; Li, T.; Wang, Z.; Lin, J. Riemann Problem for the Isentropic Euler Equations of Mixed Type in the Dark Energy Fluid. Mathematics 2024, 12, 2444. https://doi.org/10.3390/math12162444
Chen T, Jiang W, Li T, Wang Z, Lin J. Riemann Problem for the Isentropic Euler Equations of Mixed Type in the Dark Energy Fluid. Mathematics. 2024; 12(16):2444. https://doi.org/10.3390/math12162444
Chicago/Turabian StyleChen, Tingting, Weifeng Jiang, Tong Li, Zhen Wang, and Junhao Lin. 2024. "Riemann Problem for the Isentropic Euler Equations of Mixed Type in the Dark Energy Fluid" Mathematics 12, no. 16: 2444. https://doi.org/10.3390/math12162444
APA StyleChen, T., Jiang, W., Li, T., Wang, Z., & Lin, J. (2024). Riemann Problem for the Isentropic Euler Equations of Mixed Type in the Dark Energy Fluid. Mathematics, 12(16), 2444. https://doi.org/10.3390/math12162444