Abstract
As the transmission component in mechanical systems, hydrodynamic journal bearing is widely used in large electromechanical equipment. The instability of the hydrodynamic journal bearing often results in mechanical wear and damage, which may cause maintenance shutdowns and significant financial losses. Accordingly, assessing the hydrodynamic journal bearing online is a highly effective approach to guaranteeing reliability. To analyze oil film thickness distribution under various assembly characteristics, this paper proposes a Fluid–Solid coupling analysis method based on hydrodynamic lubrication theory and Hertzian elastic deformation theory. The novelty is that the difference between the oil film thicknesses at the same measuring angle within the two opposing faces of the bearing shell is taken as the assessment parameter, which can directly indicate the deviation degree of the stator axis. Comparison of simulation and experimental results validated that the proposed method exhibits exceptional accuracy in practical applications.
Keywords:
hydrodynamic journal bearing; oil film thickness; assembly characteristics; Fluid–Solid coupling analysis; state assessment MSC:
76-10
1. Introduction
The rapid advancement of modern industry has imposed higher demands on rotating machinery, which means increased rotation speed, heavier workloads, and enhanced operational stability are necessary [1,2,3]. As crucial supporting components in rotating machinery, hydrodynamic journal bearing (HJB) has gained widespread use due to its notable advantages, including high load-bearing capacity, extended lifespan, and robust operational stability [4,5,6,7].
Under the conditions of liquid lubrication, the shaft journal and bearing shell are effectively isolated by lubricating oil to minimize surface wear and ensure optimal operational efficiency and safety performance of the entire mechanical system [8,9,10]. However, variations in assembly characteristics can cause misalignment between the stator axis and the ideal position, resulting in friction between the shaft journal and the bearing shell during normal operation. These lead to instability in the oil film, abrasion of the bearing shell, fatigue breakage, and other issues [11,12,13,14,15]. Real-time assessment is crucial for extending the service life of the HJB [16,17,18,19].
In the Rotor-Bearing system, the assembly error is a primary factor contributing to misalignment, which subsequently triggers detrimental dynamic effects on the HJB, such as oil film shock, instability, and wear damage. For years, a comprehensive theoretical framework has been established to study the oil film characteristics of the HJB. The Reynolds equation proposed by O. Reynolds in 1886 laid a solid foundation for hydrodynamic lubrication research [20]. To efficiently obtain numerical solutions to the Reynolds equation, researchers worldwide have continuously improved numerical analysis methods and fluid simulation techniques [21].
To calculate the oil film pressure distribution of the HJB, Wei et al. [22] effectively combined the double conjugate gradient stability algorithm with Reynolds boundary conditions to enhance the solving efficiency of the Reynolds equation in steady-state and dynamic analysis. Cam et al. [23] proposed a novel numerical solution for simulating the two-dimensional hydrodynamic lubrication process by considering slip avoidance and eliminating air pockets. Lv et al. [24] introduced a simulation method for analyzing unsteady mixed lubricity bearings and utilized the transient generalized Reynolds equation to examine liquid film behavior in hydrodynamic lubrication regions, particularly focusing on local turbulence effects. Mao et al. [25] developed a turbulent lubrication model to investigate the performance of dynamic pressure radial plain bearings under actual operating conditions, studying variations in parameters such as Reynolds number, oil film thickness, oil film pressure, bearing capacity, attitude angle, and discharge rate.
Extensive research and experimental verification have been conducted by scholars both domestically and internationally to comprehend the impact of assembly errors on the oil film characteristics and wear mechanism of dynamic pressure radial plain bearings. Du et al. [26] conducted a comprehensive investigation into the wear mechanism, classification of wear experiments, test bench for wear testing, and predictive model for bearing wear in journal bearings. Zhang et al. [27] examined the influence of axial displacement on the failure limit of journal bearings through experimental studies under various operating speeds with occlusal load as a research parameter. Abdou et al. [28], who aimed to study the dynamic response of oil film in journal bearings during rotor instability, solved nonlinear dynamic equations based on specific directions and degrees of displacement to verify critical stability limits at different eccentricities. Jeon et al. [29], to enhance lubrication performance in journal bearings, designed a flexible structure for reducing the impact of assembly errors. They evaluated and analyzed lubrication performance using minimum oil film thickness as an evaluation index.
Additionally, Sysaykeo et al. [30] designed a bionic bearing to extend its service life and conducted simulation and experimental verification on its working contact pressure and eccentric load, whose results indicate superior performance compared to traditional bearings.
The aforementioned research focuses on the numerical analysis and simulation method of hydrodynamic lubrication, as well as its application in studying the influence of assembly errors on the performance of the HJB. Meanwhile, Joon et al. [31] provided an extensive review of the literature concerning the misalignment in journal bearings and elucidated the foundational theories and empirical outcomes associated with such misalignments to delineate the overarching tendencies that arise from such deviations. However, there has been no research conducted on constructing oil film mathematical models suitable for different assembly characteristics of the HJB. Additionally, the elastic deformation of the shaft journal and bearing shell under eccentric loads is rarely taken into account.
According to the oil film characteristic changes under various assembly conditions, a new state assessment method for hydrodynamic journal bearing is studied in this research. The novelties of this study are as follows. (1) The Fluid–Solid coupling model is established to solve oil film characteristics such as oil film pressure distribution and oil film thickness distribution under various assembly characteristics; (2) The difference between the oil film thicknesses at the same measuring angle within the two opposing faces of the bearing shell is taken as the assessment parameter, which can directly indicate the deviation degree of the stator axis.
The remainder of this paper is organized as follows: Section 2 introduces the Fluid–Solid coupling analysis method for the HJB. Section 3 defines multiple assembly characteristics, such as stator axis translation, stator axis rotation, and stator axis misalignment. Section 4 introduces the process used to solve oil film characteristics. Section 5 shows simulation processes and experimental results. Finally, Section 6 presents conclusions along with prospects for future work.
2. Fluid–Solid Coupling Analysis of the HJB
2.1. Analysis of Oil Film Lubricating Properties
The bearing shell of the HJB is securely fixed onto the bearing housing, and there will be a specific gap maintained between the bearing shell and the shaft journal when the shaft journal rotates.
When the shaft journal is rotating, lubricating oil is drawn into the gap, which results in a certain dynamic pressure generated within the oil film. In the meantime, the oil volume in the wedge void will increase as the speed of the shaft journal increases. Once the speed of the shaft journal stabilizes, a stable oil film will completely separate the shaft journal from the bearing shell, which may eliminate mechanical contact and reduce surface wear. Figure 1a shows the usage examples of the HJB, and Figure 1b shows the general structure of the HJB. Ideal and non-ideal assembly states are shown in Figure 1c and Figure 1d, respectively.
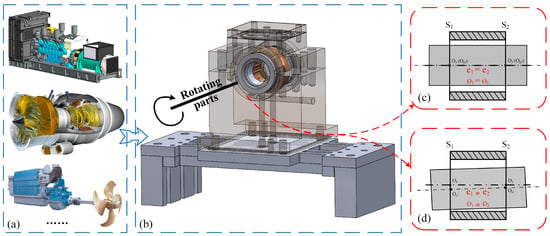
Figure 1.
The general structure of the HJB. (a) The mechanical system using the HJB. (b) Structures of the HJB. (c) Ideal assembly state of the HJB. (d) Non-ideal assembly state of the HJB.
2.1.1. Solution of Oil Film Thickness Distribution
The dynamic oil film is mathematically modeled to accurately reflect the complex structure and real working conditions of the HJB, thereby enhancing the effectiveness and precision of assessing the bearing state.
The capacity of the lubricating oil film to bear loads is determined by two critical parameters. One is the ratio of the width and diameter of the HJB, and the other one is the eccentricity ratio of the HJB. The bearing capacity coefficient is ascertained through numerical integration methodologies, which are complemented by pertinent line graphs or tabular data for utilization in design applications [32]. The bearing capacity coefficient can be expressed as Equation (1).
where represents the external load, represents the clearance ratio (the ratio of radial clearance to shaft journal radius) of the HJB, represents the dynamic viscosity of the lubricating oil at the operating temperature, represents the width of bearing shell, and represent angular velocity and diameter of the shaft journal respectively.
The bearing capacity coefficient is a function that characterizes the relative position of the shaft journal and the central axis of the HJB under the specified boundary conditions.
Based on the aforementioned research, the eccentricity can be determined by consulting the corresponding table, and a mathematical model for the oil film thickness at each point in the HJB is constructed, as illustrated in Figure 2.
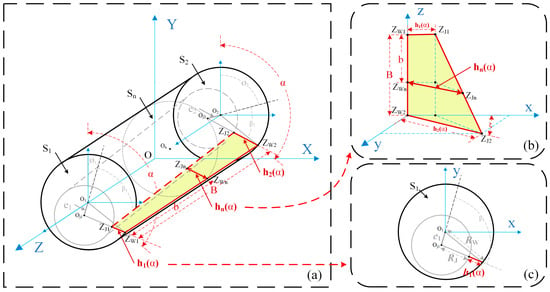
Figure 2.
The mathematical model of oil film thickness. (a) Assembly parameters of the HJB. (b) Oil film thickness at any given angle (). (c) Geometric parameters in the section ().
In the - coordinate system, the origin is located at the midpoint of the axis of the bearing shell, while the axis of the bearing shell simultaneously aligns with the -axis. and denote the two opposing faces of the bearing shell while and represent the centers of and respectively.
Similarly, within the two designated cross-sections (, ), and represent centers of shaft journal respectively, and represent attitude angles of shaft journal, respectively, and represent eccentric distances of shaft journal respectively, and are points located on circles of the bearing shell at any given angle (), while oil film thicknesses at points (, ) are represented by and , respectively.
As , indicating that the eccentric distance is significantly less than half the diameter of the bearing shell, the negligible effects of and can be disregarded.
The attitude angle of the shaft journal varies across different sections, as depicted in Figure 2a. The parameter is introduced to denote the difference between any given angle () and the attitude angle (), as shown in Equation (2).
Oil film thicknesses at any given angle () can be calculated [32] based on Equation (3).
The radial clearance, denoted as , signifies the difference between the radius of the bearing shell () and that of the shaft journal (), as illustrated in Figure 2c.
To determine the oil film thickness at the point () for any given cross-section () and any given Angle (), the coordinate system () is constructed with as the origin, while the line () coincides with the -axis, as illustrated in Figure 2b. The angle between and can be expressed as the Equation (4).
where parameters (, ) used in calculating are shown in Equation (5).
where and represent the radius of the bearing shell and the shaft journal, respectively.
The oil film thickness () at the point () can be calculated based on the mathematical model of oil film thickness, as demonstrated in Equation (6).
where parameters (, , ) used in calculating are shown in Equation (7).
where the variable represents the distance between two cross-sections (, ), while is parallel to .
2.1.2. Reynolds Equations and Assumptions
The fundamental equation of hydrodynamic lubrication theory is the differential equation governing the pressure distribution in a fluid film, which is derived from the basic equation of viscous fluid dynamics under certain assumptions [33]. Considering the structural parameters and lubrication characteristics of the HJB, the following assumptions are made:
- (1)
- For the purpose of simplifying the calculation of shear stress, the lubricating oil under consideration is assumed to behave as a Newtonian fluid. According to Newton’s law of viscosity, shear stress within a fluid is directly proportional to the velocity gradient perpendicular to the direction of flow.
- (2)
- Due to the extremely small thickness of the oil film, the effect of fluid flow in the direction perpendicular to the film thickness is disregarded.
- (3)
- To streamline the continuity equation, the fluid is assumed to be incompressible, meaning that changes in volume due to pressure variations are considered negligible compared to those resulting from velocity gradients.
- (4)
- To simplify the modeling of fluid flow behavior, the analysis excludes considerations of fluid particle rotation or deformation, focusing solely on the translational characteristics of fluid particles.
- (5)
- To simplify the velocity field near the solid boundary, a no-slip condition is assumed between the fluid and solid surfaces, meaning the velocities of both are equal at the boundary.
- (6)
- To simplify the calculation of pressure distribution within the oil film, the effect of pressure variation in the direction perpendicular to the oil film thickness is neglected.
- (7)
- To simplify the momentum balance equation, the influences of inertial forces and gravitational effects on the oil film particles are neglected.
These assumptions collectively streamline the mathematical modeling of fluid flow, facilitating the solution of differential equations that describe the behavior of the oil film under defined conditions. A set of four-member differential equations comprising the Navier–Stokes equation and the Continuity equation are derived to analyze the oil film pressure distribution. The two-dimensional Reynolds equation can be expressed as Equation (8).
where represents the oil film thickness, represents the oil film pressure, represents the linear velocity of the shaft journal, while -axis and -axis are Cartesian axes.
The dimensionless Reynolds equation is employed to analyze the dynamic characteristics of the HJB based on the hydrodynamic lubrication theory, aiming to elucidate the action mechanism of various factors and ensure that each variable remains within a reasonable range, as demonstrated in Equation (9).
where represents the dimensionless oil film thickness, represents the dimensionless oil film pressure, while -axis and -axis are dimensionless Cartesian axes.
The Reynolds equation is solved with Reynolds boundary conditions to ensure the fulfillment of fluid continuity and positive pressure requirements.
2.1.3. Solution of Oil Film Pressure Distribution
To simplify the calculation process, the partial differential equations are transformed into algebraic equations. The finite difference method is employed to discretize the oil film into grids, while the partial derivative term in the Reynolds equation is approximated by utilizing various orders of difference quotients formed by the pressure values on grid nodes. By solving for the pressure values at each node within the grid, we can obtain a comprehensive oil film pressure distribution [34,35], as demonstrated in Equation (10).
where , , , , , are coefficient matrixes, as shown in the Equation (11).
where and represent node numbers in directions of and respectively, while and represent different steps in directions of and respectively.
The initial pressure distribution is established by assigning values to each boundary node based on the boundary condition and setting the pressure value of other points as zero. Subsequently, an iterative calculation process is employed to obtain a more accurate approximation of the pressure distribution step by step.
The iteration results can be evaluated for their ideal accuracy based on the criterion of relative convergence, as depicted in Equation (12).
The relative error value can be taken as to ensure the accuracy of model solving.
2.2. Analysis of Elastic Deformation
The lubricating oil directly contacts both the shaft journal and bearing shell in the HJB, allowing the oil film to support the solid surfaces of the shaft journal and bearing shell directly. By treating the oil film pressure as the contact pressure applied to the shaft journal and the bearing shell [36], the radial deformations occurring on the two cylinders are considered as elastic deformations in accordance with Hertzian contact theory [37,38]. The variable denotes the aggregate of these deformations, and the corresponding expression is given by Equation (13).
where parameters (, , ) used in calculating are shown in the Equation (14).
where and represent Poisson’s ratio of the bearing shell and the shaft journal, respectively, while and represent the Elastic Modulus of the bearing shell and the shaft journal, respectively.
3. Definition of Assembly Characteristics
3.1. Stator Axis Translation
Variations in the following assembly characteristics will cause the actual position of the stator axis to be different from the ideal position––the coaxiality of the bearing shell and the shaft journal will exceed the allowable range. Under stable working conditions, the actual stator axis remains parallel to the ideal stator axis even if the relative translation occurs, as shown in Figure 3.
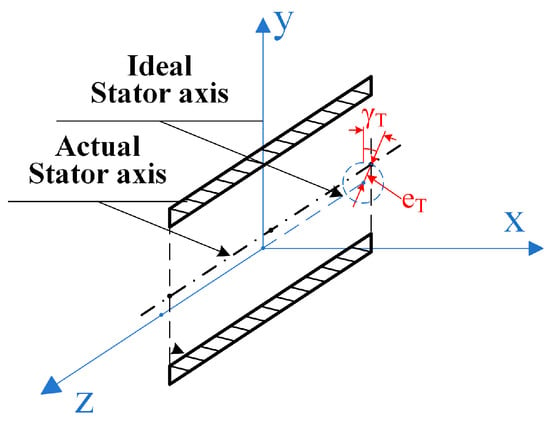
Figure 3.
The diagram of stator axis translation.
The coordinate system is established with the origin located at the central point of the ideal stator axis that coincides with the -axis.
In the operational state of stator axis translation, eccentric distances (, ) of shaft journal within the two designated cross-sections (, ) can be determined according to Equations (15) and (16).
Similarly, in the stator axis translation scenario, and represent angular displacement and linear distance within the cross-section (), respectively, that determine the positional correlation between the actual stator axis and the ideal stator axis. Attitude angles (, ) of shaft journal within the two designated cross-sections (, ) can be determined according to Equations (17) and (18).
where parameters represent variations in attitude angles under the condition of stator axis translation, as demonstrated in Equation (19).
3.2. Stator Axis Rotation
Variations in the following assembly characteristics will cause the actual position of the stator axis to be different from the ideal position––the coaxiality of the bearing shell and the shaft journal will exceed the allowable range. Under stable working conditions, the midpoint of the actual stator axis remains aligned with the midpoint of the ideal stator axis even if the relative rotation occurs, as shown in Figure 4.
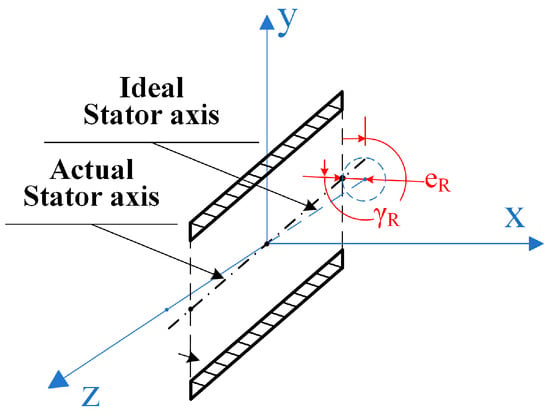
Figure 4.
The diagram of stator axis rotation.
The coordinate system is established with the origin located at the central point of the ideal stator axis that coincides with the -axis.
In the operational state of stator axis rotation, eccentric distances (, ) of shaft journal within the two designated cross-sections (, ) can be determined according to Equations (20) and (21).
Similarly, in the stator axis rotation scenario, and represent angular displacement and linear distance within the cross-section (), respectively, that determine the positional correlation between the actual stator axis and the ideal stator axis. Attitude angles (, ) of shaft journal within the two designated cross-sections (, ) can be determined according to Equations (22) and (23).
where parameters represent variations in attitude angles under the condition of stator axis rotation, as demonstrated in Equation (24).
3.3. Stator Axis Misalignment
Variations in the following assembly characteristics will cause the actual position of the stator axis to be different from the ideal position––the coaxiality of the bearing shell and the shaft journal will exceed the allowable range. There is a special condition called stator axis misalignment, which can be interpreted as the combined effect of stator axis translation and stator axis rotation. For example, the actual stator axis rotates around the point (), as shown in Figure 5.
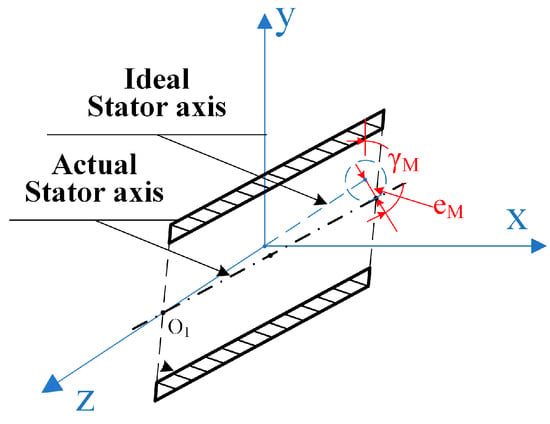
Figure 5.
The diagram of stator axis misalignment.
The coordinate system is established with the origin located at the central point of the ideal stator axis that coincides with the -axis.
In the operational state of stator axis misalignment, eccentric distances (, ) of shaft journal within the two designated cross-sections (, ) can be determined according to Equations (25) and (26).
Similarly, in the stator axis misalignment scenario, and represent angular displacement and linear distance within the cross-section (), respectively, that determine the positional correlation between the actual stator axis and the ideal stator axis. Attitude angles (, ) of shaft journal within the two designated cross-sections (, ) can be determined according to Equations (27) and (28).
where parameter represents variations in attitude angle under the condition of stator axis misalignment, as demonstrated in Equation (29).
4. Solving Procedure
In this section, an iterative solution method is proposed for addressing the problem of Fluid–Solid coupling analysis with various assembly characteristics, such as stator axis translation, stator axis rotation, and stator axis misalignment, based on hydrodynamic lubrication theory and Hertzian deformation theory. Figure 6 illustrates the process of solving the Fluid–Solid coupling model of the HJB.
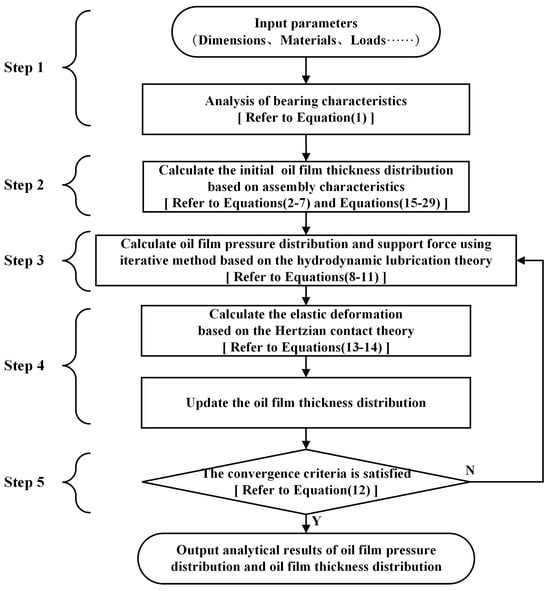
Figure 6.
The process of solving the Fluid–Solid coupling model of the HJB.
Step 1: Analyze the bearing characteristics of the HJB based on parameters such as boundary dimensions, material characteristics, external loads, and other relevant factors.
Step 2: Taking into account the influence of various assembly characteristics such as stator axis translation, stator axis rotation, and stator axis misalignment on attitude angles and eccentric distance, the initial oil film thickness distribution can be determined based on the aforementioned mathematical model of oil film thickness.
Step 3: The finite difference method is employed to calculate the pressure values at each node of the oil film grid, which forms an approximate expression of the oil film pressure distribution. Afterwards, the supporting force of oil film in various directions can be analyzed based on the numerical integration method.
Step 4: In accordance with the Hertzian contact theory, the elastic deformation occurring on cylinders, including shaft journal and bearing shell, can be resolved and incorporated into the oil film thickness distribution.
Step 5: The compensated oil film thickness distribution is brought back into the Reynolds equation system for solving to obtain the updated oil film pressure distribution. The last two analytical results of oil film pressure distribution can serve as a foundation for assessing the fulfillment of convergence criteria.
If the analysis results fail to meet the convergence criteria, it will become necessary to transfer the oil film thickness distribution from Step 4 to Step 3 and proceed with subsequent steps until the convergence criteria are satisfied. Finally, analysis results of oil film pressure distribution and oil film thickness distribution are generated as output.
5. Results and Discussion
5.1. Simulation
To verify the analytical efficiency and accuracy of the Fluid–Solid coupling model with various assembly characteristics, such as stator axis translation, stator axis rotation, and stator axis misalignment, this section will take a specific HJB as the analytic target. Specifically, the bearing shell material is tin bronze, and the shaft journal material is alloy steel, with detailed parameters provided in Table 1.

Table 1.
Key parameters of the HJB.
The rotational speed of the shaft journal in the simulation experiment ranges from 1000 rpm to 6000 rpm to maintain consistency with actual working conditions as much as possible. Across all three scenarios, including stator axis translation, stator axis rotation, and stator axis misalignment, the maximum linear distance (, , ) within the cross-section () is defined as half of the radial clearance (), while the angular displacement (, , ) within the cross-section () ranges from 0 to 360 degrees.
The difference between the oil film thicknesses (DBOFT) at the same measuring angle within two cross-sections (S1, S2) is considered to be the evaluation parameter. A larger DBOFT means that the stator axis exhibits a higher degree of deviation, which supports the state assessment of the HJB.
In the stator axis translation scenario, the simulation of the DBOFT is carried out while the measuring angles are set to 150 degrees and 210 degrees, respectively. Figure 7 illustrates the simulation results.
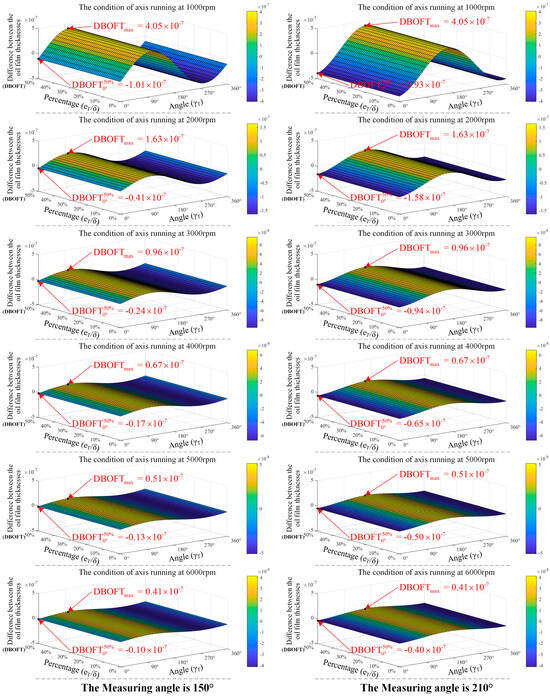
Figure 7.
The simulation results of the DBOFT in the stator axis translation scenario.
In the stator axis rotation scenario, the simulation of the DBOFT is carried out while the measuring angles are set to 150 degrees and 210 degrees, respectively. Figure 8 illustrates the simulation results.
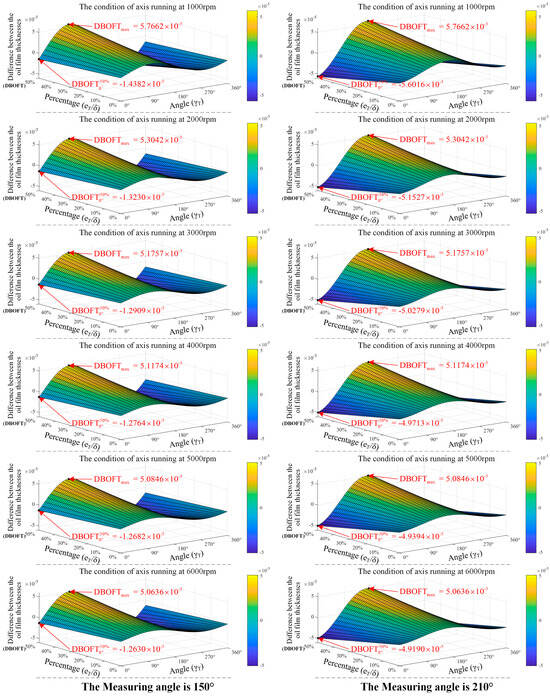
Figure 8.
The simulation results of the DBOFT in the stator axis rotation scenario.
In the stator axis misalignment scenario, the simulation of the DBOFT is carried out while the measuring angles are set to 150 degrees and 210 degrees, respectively. Figure 9 illustrates the simulation results.
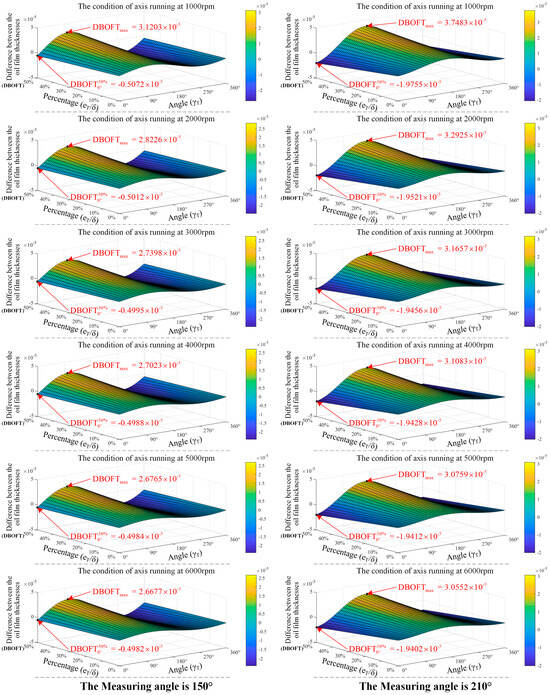
Figure 9.
The simulation results of the DBOFT in the stator axis misalignment scenario.
The following conclusions can be derived through simulation and analysis in the stator axis translation scenario:
- (1)
- The DBOFT is expressed in nanometer scales.
- (2)
- Through the horizontal comparison of Figure 7, the maximum DBOFT remains unaffected by different measuring angles.
- (3)
- Through the longitudinal comparison of Figure 7, the absolute value of the DBOFT decreases as the rotational speed increases gradually, indicating a tendency towards stable operation of the Rotor-Bearing system.
- (4)
- According to the subgraphs in Figure 7, the DBOFT remains unaffected by varying linear distance () when the angular displacement () is constant.
- (5)
- The variation range of the DBOFT is significantly influenced by the rotational speed when the linear distance () and the angular displacement () are constant. There is a specific scenario where and . When the range of rotational speed is , the variation range of the DBOFT is at a measuring angle of 150 degrees and at a measuring angle of 210 degrees, with the DBOFT decreasing by 90.1 percent and 89.8 percent, respectively.
The following conclusions can be derived through simulation and analysis in the stator axis rotation scenario:
- (1)
- Similar to the radial clearance, the magnitude order of the DBOFT is micron. Therefore, the rotation scenario can be effectively distinguished from the translation scenario.
- (2)
- Through the horizontal comparison of Figure 8, the maximum DBOFT remains unaffected by different measuring angles, which is analogous to the translation scenario.
- (3)
- Through the longitudinal comparison of Figure 8, the absolute value of the DBOFT decreases as the rotational speed increases gradually, which is analogous to the translation scenario, indicating a tendency toward stable operation of the Rotor-Bearing system.
- (4)
- The variation range of the DBOFT is less influenced by the rotational speed when the linear distance () and the angular displacement () are constant. There is a specific scenario where and . When the range of rotational speed is , the variation range of the DBOFT is at a measuring angle of 150 degrees and at a measuring angle of 210 degrees, both of which exhibit a decrease of 12.2 percent.
The following conclusions can be derived through simulation and analysis in the stator axis misalignment scenario:
- (1)
- Similar to the radial clearance, the magnitude order of the DBOFT is micron. Therefore, the misalignment scenario can be effectively distinguished from the translation scenario.
- (2)
- Through the horizontal comparison of Figure 9, the maximum DBOFT varies with different measuring angles. Therefore, the misalignment scenario can be effectively distinguished from the translation scenario and the rotation scenario.
- (3)
- Through the longitudinal comparison of Figure 9, the absolute value of the DBOFT decreases as the rotational speed increases gradually, which is analogous to the translation scenario and the rotation scenario, indicating a tendency toward stable operation of the Rotor-Bearing system.
- (4)
- The variation range of the DBOFT is subtly influenced by the rotational speed when the linear distance () and the angular displacement () are constant. There is a specific scenario where and . When the range of rotational speed is , the variation range of the DBOFT is at a measuring angle of 150 degrees and at a measuring angle of 210 degrees, both of which exhibit a decrease of 1.8 percent.
5.2. Experiments
The exact and real-time measurement of oil film thickness can provide a mass of data that supports the state assessment of the HJB. The application of the eddy current displacement sensor (ECDS) in measuring oil film thickness offers significant advantages, including higher sensitivity, higher sampling frequency, stronger reliability, and a non-destructive property [39,40,41,42].
The Rotor-Bearing system and experimental setup are depicted in Figure 10. The shaft journal is supported by two HJBs spaced 220 mm apart. The elastic coupling establishes a connection between the shaft journal and the driving motor, enabling precise regulation of the rotational speed of the shaft journal. At the same time, the data acquisition system (DAQ) is composed of NI equipment, ECDSs, and a set of self-developed data acquisition procedures.
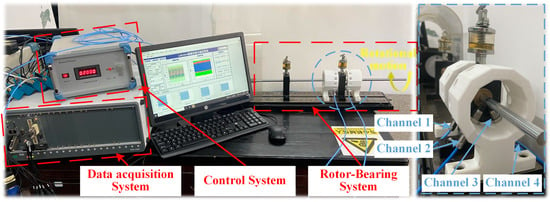
Figure 10.
Diagram of the Rotor-Bearing system and experimental setup.
To verify the accuracy of the Fluid–Solid coupling analysis method proposed in this paper, four ECDSs are arranged at both ends of the bearing shell to monitor the oil film thicknesses at measuring angles of 150 degrees and 210 degrees. Multiple rotational speeds of the shaft journal are set to 1000 rpm, 2000 rpm, 3000 rpm, 4000 rpm, 5000 rpm, and 6000 rpm. The sampling frequency and the sampling period are set to 1000 Hz and 10 s, respectively.
The relative error (acc) between the simulated value and the measured value is taken as the criteria for state assessment, as shown in Equation (30).
where represent the simulated value and the measured value, respectively.
In the specific stator axis translation scenario where the angular displacement is 0 and the linear distance is 0.02 mm, the data sets collected at various rotational speeds are statistically analyzed, as shown in Table 2.

Table 2.
Experimental results under the condition of stator axis translation.
The variation range of the DBOFT is at measuring angle of 150 degrees and at measuring angle of 210 degrees when the range of rotational speed is , with the DBOFT decreasing by 90.2 percent and 89.9 percent, respectively. The simulation results are consistent with the measured results.
In the specific stator axis rotation scenario where the angular displacement is 0 and the linear distance is 0.02 mm, the data sets collected at various rotational speeds are statistically analyzed, as shown in Table 3.

Table 3.
Experimental results under the condition of stator axis rotation.
The variation range of the DBOFT is at measuring angle of 150 degrees and at measuring angle of 210 degrees when the range of rotational speed is , with the DBOFT decreasing by 13.0 percent and 13.2 percent, respectively. The simulation results are consistent with the measured results.
In the specific stator axis misalignment scenario where the angular displacement is 0 and the linear distance is 0.02 mm, the data sets collected at various rotational speeds are statistically analyzed, as shown in Table 4.

Table 4.
Experimental results under the condition of stator axis misalignment.
The variation range of the DBOFT is at measuring angle of 150 degrees and at measuring angle of 210 degrees when the range of rotational speed is , with the DBOFT decreasing by 1.9 percent and 2.0 percent, respectively. The simulation results are consistent with the measured results.
5.3. Discussion
In the process of researching the state assessment method for the HJB under different assembly characteristics, the DBOFT is used as a quantitative assessment index. Figure 11 presents the comparison between simulation results and measured results.
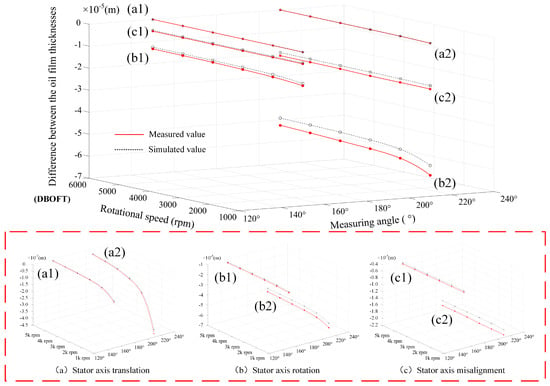
In the simulation experiments, according to the magnitude order of the DBOFT, the translation scenario can be effectively distinguished from the rotation scenario and the misalignment scenario. Similarly, according to the difference between maximum DBOFTs with different measuring angles, the misalignment scenario can be effectively distinguished from the translation scenario and the rotation scenario.
6. Conclusions and Future Work
There are some problems in the process of researching the state assessment method for the HJB. At first, the mathematical model for determining the oil film thickness distribution with various assembly characteristics is lacking. Secondly, the omission of elastic deformations occurring on cylinders, including shaft journal and bearing shell, often impacts the analysis results of oil film characteristics. Thirdly, the coupling relationship between mechanics and hydrodynamics of the HJB remains ambiguous.
In this paper, a Fluid–Solid coupling analysis method is proposed to take the elastic deformation of the shaft journal and the bearing shell into account, thereby effectively improving the numerical accuracy of oil film characteristics and providing a practical method for industrial applications. It is a simple and efficient method to use the DBOFT as a quantitative assessment index, and the coupling mechanism of the HJB is successfully revealed by the Fluid–Solid coupling analysis method. Experimental and simulation results verified the effectiveness and superiority of the proposed model, and the comparison results show that accuracies are all above 89.47 percent.
In future work, larger-diameter hydrodynamic journal bearings will be the focus of the study, encompassing the impact of different loads on bearing characteristics. We will comprehensively consider factors such as oil film viscosity, flow state, and boundary conditions to strengthen the performance of the assessment model.
Author Contributions
Conceptualization, H.L.; methodology, J.D., Q.L. and J.M.; software, J.H.; validation, J.D.; formal analysis, J.D.; investigation, J.M.; resources, H.L.; data curation, J.D. and J.H.; writing—original draft preparation, J.D.; writing—review and editing, H.L. and Q.L.; supervision, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China [grant number 52275505] and the Fundamental Research Funds for the Central Universities [grant number WUT 104972024RSCbs0027].
Data Availability Statement
Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclatures
The following nomenclatures are used in this manuscript:
| The bearing capacity coefficient | |
| The external load | |
| The clearance ratio | |
| The dynamic viscosity of the lubricating oil | |
| The angular velocity of the shaft journal | |
| The width of the bearing shell | |
| The diameter of the bearing shell | |
| The diameter of the shaft journal | |
| The given angle | |
| The attitude angle of the shaft journal | |
| The difference between any given angle and the attitude angle | |
| The radial clearance | |
| , | The two opposing faces of the bearing shell |
| , | The centers of and |
| , | The centers of the shaft journal within , |
| , | The attitude angles of the shaft journal within , |
| , | The eccentric distances of shaft journal within , |
| , | Points located on circles of the bearing shell at within , |
| , | Points located on circles of the shaft journal at within , |
| , | Oil film thicknesses at the two points (, ) |
| The angle between and | |
| , | The radius of the bearing shell and the shaft journal |
| b | The distance between the two cross-sections (, ) |
| The point located on the circle of the bearing shell at within | |
| The oil film thickness at the point () | |
| , | Parameters used in calculating |
| , , | Parameters used in calculating |
| H | The oil film thickness |
| P | The oil film pressure |
| The linear velocity of the shaft journal | |
| x, y, z | Cartesian axes |
| The dimensionless oil film thickness | |
| The dimensionless oil film pressure | |
| , | Dimensionless Cartesian axes |
| , , , , , | Coefficient matrixes |
| The relative error value | |
| The aggregate of radial deformations occurring on the two cylinders | |
| , , | Parameters used in calculating |
| , | Poisson’s ratio of the bearing shell and the shaft journal |
| , | Elastic Modulus of the bearing shell and the shaft journal |
| , | Angular displacement and linear distance within the cross-section () in the stator axis translation scenario |
| , | The eccentric distances of the shaft journal within the two designated cross-sections (, ) in the stator axis translation scenario |
| , | The attitude angles of the shaft journal within the two designated cross-sections (, ) in the stator axis translation scenario |
| , | Variations in attitude angles under the condition of stator axis translation |
| , | Angular displacement and linear distance within the cross-section () in the stator axis rotation scenario |
| , | The eccentric distances of the shaft journal within the two designated cross-sections (, ) in the stator axis rotation scenario |
| , | The attitude angles of the shaft journal within the two designated cross-sections (, ) in the stator axis rotation scenario |
| , | Variations in attitude angles under the condition of stator axis rotation |
| , | Angular displacement and linear distance within the cross-section () in the stator axis misalignment scenario |
| , | The eccentric distances of the shaft journal within the two designated cross-sections (, ) in the stator axis misalignment scenario |
| , | The attitude angle of the shaft journal within the two designated cross-sections (, ) in the stator axis misalignment scenario |
| Variations in attitude angle under the condition of stator axis misalignment |
References
- Gui, W.; Chen, X.; Zhou, H.; Yang, S.; Lu, G. Transient running stability assessment of industrial rotating machinery based on bag of correlated vibration feature representation. Meas. Sci. Technol. 2023, 34, 015110. [Google Scholar] [CrossRef]
- Zheng, H.; Qiao, X. Reliability Analysis Method of Rotating Machinery Based on Conditional Random Field. Comput. Intell. Neurosci. 2022, 2022, 7326730. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, E.A.; Alves, D.S.; Cavalca, K.L.; Bavastri, C.A. Stability analysis and optimization of a hybrid rotating machinery support combining journal bearings with viscoelastic supports. Mech. Mach. Theory 2021, 156, 104166. [Google Scholar] [CrossRef]
- da Silva, D.A.; Daniel, G.B.; Cavalca, K.L. Development of a Robust Test Rig for Tilting Pad Journal Bearing Validation. Machines 2022, 10, 189. [Google Scholar] [CrossRef]
- Yan, K.; Huang, D. Investigation on static and dynamic characteristics of high-speed and heavy-load tilting pad journal bearings. Ind. Lubr. Tribol. 2022, 74, 1063–1073. [Google Scholar] [CrossRef]
- Visnadi, L.B.; de Castro, H.F. Influence of bearing clearance and oil temperature uncertainties on the stability threshold of cylindrical journal bearings. Mech. Mach. Theory 2019, 134, 57–73. [Google Scholar] [CrossRef]
- Pérez, N.; Rodríguez, C. Vertical rotor model with hydrodynamic journal bearings. Eng. Fail. Anal. 2021, 119, 104964. [Google Scholar] [CrossRef]
- Sadiq, M.; Ghopa, W.; Nuawi, M.; Rasani, M.; Khamis, N.; Mansor, M. Investigation of stiffness and damping coefficients in fluid film bearing with bio-oils and mineral-based oil. Energy Rep. 2022, 8, 419–429. [Google Scholar] [CrossRef]
- Sadiq, M.I.; Ghopa, W.A.W.; Nuawi, M.Z.; Rasani, M.R.; Sabri, M.A.M. Experimental and Numerical Investigation of Static and Dynamic Characteristics of Bio-Oils and SAE40 in Fluid Film Journal Bearing. Materials 2022, 15, 3595. [Google Scholar] [CrossRef]
- Tofighi-Niaki, E.; Safizadeh, M.S. Dynamic of a Flexible Rotor-Bearing System Supported by Worn Tilting Journal Bearings Experiencing Rub-Impact. Lubricants 2023, 11, 212. [Google Scholar] [CrossRef]
- Erkaya, S.; Doğan, S.; Ulus, Ş. Effects of joint clearance on the dynamics of a partly compliant mechanism: Numerical and experimental studies. Mech. Mach. Theory 2015, 88, 125–140. [Google Scholar] [CrossRef]
- Xu, F.; Ding, N.; Li, N.; Liu, L.; Hou, N.; Xu, N.; Guo, W.; Tian, L.; Xu, H.; Lawrence, W.C.; et al. A review of bearing failure Modes, mechanisms and causes. Eng. Fail. Anal. 2023, 152, 107518. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, C.; Bao, M.; Gu, L.; Wang, L.; Wei, X.; Li, W. Scratch damage on guiding surfaces of high-speed bearings under oil cut-off condition. Eng. Fail. Anal. 2022, 140, 106624. [Google Scholar] [CrossRef]
- Xiong, G.; Mao, Z.; Zhang, J.; Wang, Z.; Wang, H.; Jiang, Z. Coupled effects of misalignment and viscoelastic deformation on dynamically loaded journal bearings. Int. J. Mech. Sci. 2023, 251, 108347. [Google Scholar] [CrossRef]
- Zeng, W.; Lu, W.; Xu, F. Model-based low-speed rotation error prediction for the rigid shaft-bearing system considering the assembly deviation. Mech. Mach. Theory 2023, 184, 105294. [Google Scholar] [CrossRef]
- Zhou, H.; Huang, X.; Wen, G.; Lei, Z.; Dong, S.; Zhang, P.; Chen, X. Construction of health indicators for condition monitoring of rotating machinery: A review of the research. Expert Syst. Appl. 2022, 203, 117297. [Google Scholar] [CrossRef]
- Ma, J.; Fu, C.; Zhang, H.; Chu, F.; Shi, Z.; Gu, F.; Ball, A.D. Modelling non-Gaussian surfaces and misalignment for condition monitoring of journal bearings. Measurement 2021, 174, 108983. [Google Scholar] [CrossRef]
- Wei, S.; Wang, J.; Cui, J.; Song, S.; Li, H.; Fu, J. Online monitoring of oil film thickness of journal bearing in aviation fuel gear pump. Measurement 2022, 204, 112050. [Google Scholar] [CrossRef]
- Ding, N.; Li, H.; Yin, Z.; Jiang, F. A novel method for journal bearing degradation evaluation and remaining useful life prediction under different working conditions. Measurement 2021, 177, 109273. [Google Scholar] [CrossRef]
- Reynolds, O. On the Theory of Lubrication and Its Application to Mr. Beauchamp Tower’s Experiments, including an experimental determination of the viscosity of olive oil. Proc. R. Soc. Lond. 1886, 177, 157–234. [Google Scholar]
- Lin, L.; He, M.; Ma, W.; Wang, Q.; Zhai, H.; Deng, C. Dynamic Characteristic Analysis of the Multi-Stage Centrifugal Pump Rotor System with Uncertain Sliding Bearing Structural Parameters. Machines 2022, 10, 473. [Google Scholar] [CrossRef]
- Wei, B.; Jiao, Y.; Wu, X. Numerical Calculation of Fluid Film Force on Journal Bearings Based on a Biconjugate Gradient-Stabilized Algorithm. J. Tribol. 2022, 144, 114502. [Google Scholar] [CrossRef]
- Çam, M.Y.; Giacopini, M.; Dini, D.; Biancofiore, L. A numerical algorithm to model wall slip and cavitation in two-dimensional hydrodynamically lubricated contacts. Tribol. Int. 2023, 184, 108444. [Google Scholar] [CrossRef]
- Lv, F.; Zhang, X.; Ji, C.; Rao, Z. Theoretical and experimental investigation on local turbulence effect on mixed-lubrication journal bearing during speeding up. Phys. Fluids 2022, 34, 113104. [Google Scholar] [CrossRef]
- Mao, Y.; Li, L.; Li, D.; Zheng, J. Analysis of the Turbulent Lubrication of a Textured Hydrodynamic Journal Bearing. Lubricants 2023, 11, 362. [Google Scholar] [CrossRef]
- Du, F.; Li, D.; Sa, X.; Li, C.; Yu, Y.; Li, C.; Wang, J.; Wang, W. Overview of Friction and Wear Performance of Sliding Bearings. Coatings 2022, 12, 1303. [Google Scholar] [CrossRef]
- Zhang, X.; Yin, Z.; Dong, Q. An experimental study of axial misalignment effect on seizure load of journal bearings. Tribol. Int. 2019, 131, 476–487. [Google Scholar] [CrossRef]
- Abdou, K.M.; Saber, E. Effect of rotor misalignment on stability of journal bearings with finite width. Alex. Eng. J. 2020, 59, 3407–3417. [Google Scholar] [CrossRef]
- Jeon, W.J.; Hong, S.H. A New Type of Misaligned Journal Bearing with Flexible Structure. Lubricants 2023, 11, 256. [Google Scholar] [CrossRef]
- Sysaykeo, D.; Linares, J.M.; Mermoz, E. Wear Behavior of a Bio-inspired Bearing for off-center Loads. J. Bionic Eng. 2020, 17, 1251–1262. [Google Scholar] [CrossRef]
- Jang, J.Y.; Khonsari, M.M. On the characteristics of misaligned journal bearings. Lubricants 2015, 3, 27–53. [Google Scholar] [CrossRef]
- Guoan, Y. Practical Techniques for Diagnosing Sliding Bearing Failures, 1st ed.; China Petrochemical Press: Beijing, China, 2012; pp. 14–23. [Google Scholar]
- Zhang, J.; Dong, Q. Lubrication performance analysis of crankshaft bush in compressor. Eng. Fail. Anal. 2018, 90, 277–289. [Google Scholar] [CrossRef]
- Du, F.; Chen, C.; Zhang, K. Fluid Characteristics Analysis of the Lubricating Oil Film and the Wear Experiment Investigation of the Sliding Bearing. Coatings 2022, 12, 67. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, M.; Qin, D.; Yan, Z. Performance of high-speed hydrodynamic sliding bearings with lubricating oils combining laminar and turbulent flows. Adv. Mech. Eng. 2020, 12, 1–13. [Google Scholar] [CrossRef]
- Reis, V.L.; Daniel, G.B.; Cavalca, K.L. Dynamic analysis of a lubricated planar slider-crank mechanism considering friction and Hertz contact effects. Mech. Mach. Theory 2014, 74, 257–273. [Google Scholar] [CrossRef]
- Goldsmith, W.; Frasier, J.T. Impact: The Theory and Physical Behavior of Colliding Solids. J. Appl. Mech. 1961, 28, 639. [Google Scholar] [CrossRef]
- Dubowsky, S.; Freudenstein, F. Dynamic analysis of mechanical systems with clearances—Part 1: Formation of dynamic response. J. Manuf. Sci. Eng. Trans. ASME 1971, 93, 305–309. [Google Scholar] [CrossRef]
- Wang, S.C.; Xie, B.R.; Huang, S.M. Design and Analysis of Small Size Eddy Current Displacement Sensor. Sensors 2022, 22, 7444. [Google Scholar] [CrossRef] [PubMed]
- Tiainen, T.; Viitala, R.; Holopainen, T.P.; Hemming, B. Analysis of total rotor runout components with multi-probe roundness measurement method. Measurement 2021, 179, 109422. [Google Scholar] [CrossRef]
- Li, W.; Hu, J.; Su, Z.; Wang, D. Analysis and design of axial inductive displacement sensor. Measurement 2022, 187, 110159. [Google Scholar] [CrossRef]
- Talantsev, A.; Paz, E.; Böhnert, T.; Araújo, A.; Ferreira, R. Magnetic tunnel junction platforms for linear positioning and nanoscale displacement sensing. Measurement 2023, 223, 113663. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).