Global Exponential Stability of Impulsive Delayed Neural Networks with Parameter Uncertainties and Reaction–Diffusion Terms
Abstract
1. Introduction
2. Model Description and Some Preliminaries
- (1)
- is a piecewise continuous function with the first kind of discontinuity point at for all and is right-continuous at each discontinuity point ;
- (2)
- satisfies system (1) for all , and ;
3. Global Exponential Stability Criteria
- (C1)
- There exist a vector and a constant such thatwhere with , , , diag, diag, and E is a n-dimensional identity matrix.
- (C2)
- There is a positive number such thatwhere .
- (D1)
- There exist a vector and a constant such thatwhere , , , , , diag, and diag;
- (D2)
- There is a positive number such thatwhere .
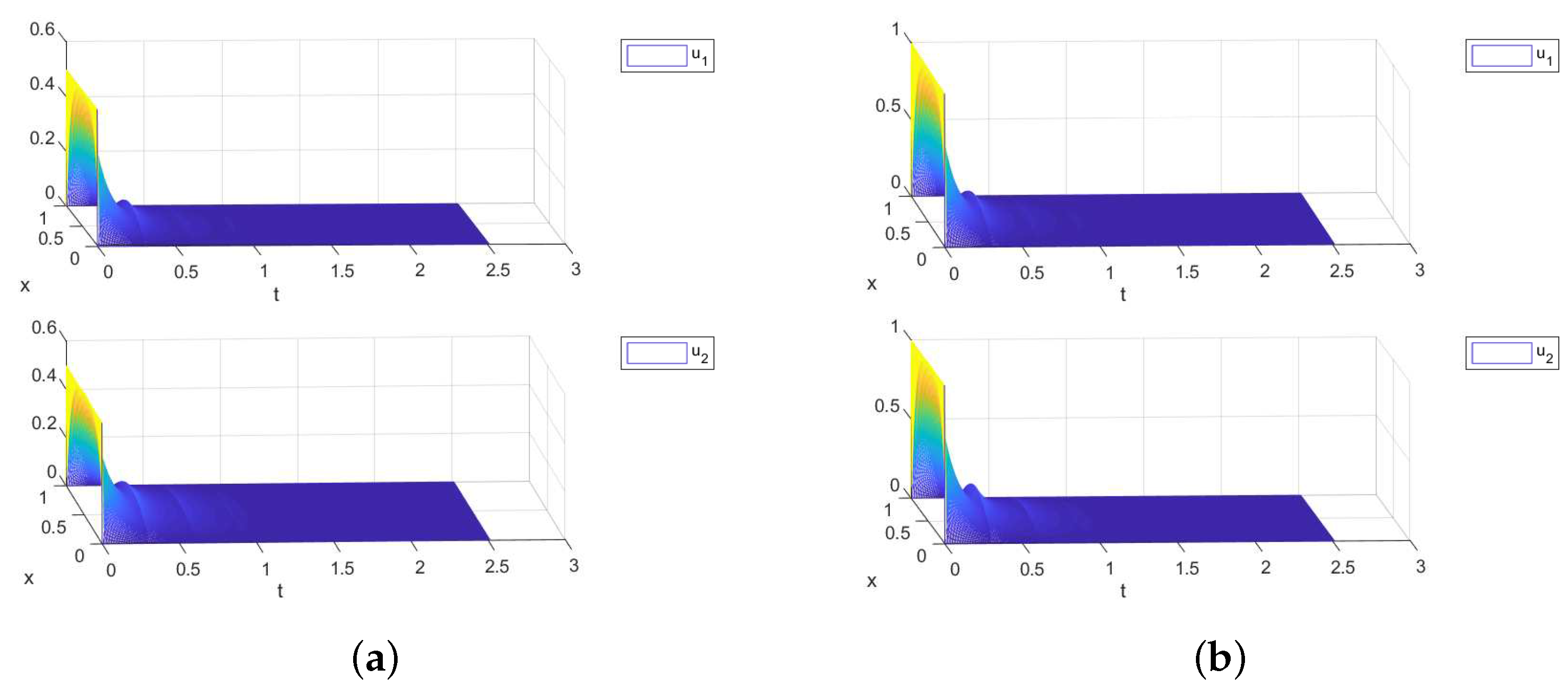
4. Illustrative Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chua, L.O.; Yang, L. Cellular neural networks: Theory. IEEE Trans. Circuits Syst. 1998, 35, 1257–1272. [Google Scholar] [CrossRef]
- Chen, W.; Zheng, W. Improved delay-dependent asymptotic stability criteria for delayed neural networks. IEEE Trans. Neural Netw. 2008, 19, 2154–2161. [Google Scholar] [CrossRef] [PubMed]
- Hua, C.; Yang, X.; Yan, J.; Guan, X. New exponential stability criteria for neural networks with time-varying delay. IEEE Trans. Circuits Syst. II Exp. Briefs 2011, 58, 931–935. [Google Scholar] [CrossRef]
- Liu, X.; Tang, M.; Wang, F. Improved exponential stability criterion for neural networks with time-varying delay. Neurocomputing 2017, 234, 154–163. [Google Scholar] [CrossRef]
- Ji, M.; He, Y.; Zhang, C.; Wu, M. Novel stability criteria for recurrent neural networks with time-varying delay. Neurocomputing 2014, 38, 383–391. [Google Scholar] [CrossRef]
- Cheng, J.; Park, J.H.; Wu, Z. Finite-time control of Markov jump Lur’e systems with singular perturbations. IEEE Trans. Autom. Control 2023, 68, 6804–6811. [Google Scholar] [CrossRef]
- Xue, Y.; Liu, C.; Zhang, X. State bounding description and reachable set estimation for discrete-time genetic regulatory networks with time-varying delays and bounded disturbances. IEEE Trans. Syst. Man. Cybernet. Syst. 2022, 52, 6652–6661. [Google Scholar] [CrossRef]
- Zhang, X.; Han, Y.; Wu, L.; Wang, Y. State estimation for delayed genetic regulatory networks with reaction–diffusion terms. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 299–309. [Google Scholar] [CrossRef]
- Zhang, Y. Robust exponential stability of uncertain impulsiv eneural networks with time-varying delays and delayed impulses. Neurocomputing 2011, 74, 3268–3276. [Google Scholar] [CrossRef]
- Meng, F.; Li, K.; Zhao, Z.; Song, Q.; Liu, Y.; Alsaadi, F.E. Periodicity of impulsive Cohen–Grossberg–type fuzzy neural networks with hybrid delays. Neurocomputing 2019, 368, 153–162. [Google Scholar] [CrossRef]
- Meng, F.; Li, K.; Song, Q.; Liu, Y.; Alsaadi, F.E. Periodicity of Cohen–Grossberg–type fuzzy neural networks with impulses and time varying delays. Neurocomputing 2019, 325, 254–259. [Google Scholar] [CrossRef]
- Hu, W.; Li, K. Global exponential stability and periodicity of nonautonomous impulsive neural networks with time-varying delays and reaction-diffusion terms. Complexity 2021, 2021, 3495545. [Google Scholar] [CrossRef]
- Xu, C.; Liao, M.; Li, P.; Liu, Z.; Yuan, S. New results on pseudo almost periodic solutions of quaternion–valued fuzzy cellular neural networks with delays. Fuzzy Set. Syst. 2021, 411, 25–47. [Google Scholar] [CrossRef]
- Stamov, G.; Stamova, I.; Martynyuk, A.; Stamov, T. Almost periodic dynamics in a new class of impulsive reaction-diffusion neural networks with fractional-like derivatives. Chaos Solitons Fractals 2021, 143, 110647. [Google Scholar] [CrossRef]
- Cong, E.; Han, X.; Zhang, X. Global exponential stabolity analysis of discrete-time BAM neural networks with delays: A mathematical induction approach. Neurcomputing 2020, 379, 227–235. [Google Scholar] [CrossRef]
- Li, W.; Zhang, X.; Liu, C.; Yang, X. Global Exponential Stability Conditions for Discrete-Time BAM Neural Networks Affected by Impulses and Time-Varying Delays. Circuits Syst. Signal Process. 2024, 43, 4850–4868. [Google Scholar] [CrossRef]
- Rajchakit, G.; Sriraman, R.; Vignesh, P.; Lim, C.P. Impulsive effects on Clifford-valued neural networks with time-varying delays: An asymptotic stability analysis. Appl. Math. Comput. 2021, 407, 126309. [Google Scholar] [CrossRef]
- Dong, Z.; Zhang, X.; Wang, X. Global exponential stability of discrete-time higher-order Cohen-Grossberg neural networks with time-varying delays connection weights and impulses. J. Franklin Inst. 2021, 358, 5931–5950. [Google Scholar] [CrossRef]
- Sergey, D.; Michael, K.; Andrii, M.; Lars, N. Stability of interconnected impulsive systems with and without time delays, using Lyapunov methods. Nonlinear Anal. Hybrid Syst. 2012, 6, 899–915. [Google Scholar]
- Liang, J.; Cao, J. Global exponential stability of reaction-diffusion recurrent neural networks with time-varying delays. Phys. Lett. A 2003, 314, 434–442. [Google Scholar] [CrossRef]
- Wang, L.; Gao, Y. Global exponential robust stability of reaction-diffusion interval neural networks with time-varying delays. Phys. Lett. A 2006, 350, 342–348. [Google Scholar] [CrossRef]
- Huang, T. Exponential stability of delayed fuzzy cellular neural networks with diffusion. Chaos Solitons Fractals 2007, 31, 658–664. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, Y.; Huang, Y. Global exponential stability of interval general BAM neural networks with reaction-diffusion terms and multiple time-varying delays. Neural Netw. 2011, 24, 457–465. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, H. Global asymptotic stability of reaction-diffusion Cohen-Grossberg neural networks with continuously distributed delays. IEEE Trans. Neural Netw. 2010, 21, 39–49. [Google Scholar] [CrossRef] [PubMed]
- Lu, J. Robust global exponential stability for interval reaction-diffusion hopfield neural networks with distributed delays. IEEE Trans. Circuits Syst. II Exp. Briefs 2007, 54, 1115–1119. [Google Scholar]
- Lu, J. Global exponential stability and periodicity of reaction-diffusion delayed recurrent neural networks with dirichlet boundary conditions. Chaos Solitons Fractals 2008, 35, 116–125. [Google Scholar] [CrossRef]
- Lu, X.; Chen, W.; Ruan, Z.; Huang, T. A new method for global stability analysis of delayed reaction-diffusion neural networks. Neurocomputing 2018, 317, 127–136. [Google Scholar] [CrossRef]
- Zhang, H.; Zeng, Z. stability and synchronization of nonautonomous reaction-diffusion neural networks with general time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 5804–5817. [Google Scholar] [CrossRef]
- Pan, J.; Zhong, S. Novel criteria on global robust exponential stability to a class of reaction-diffusion neural networks with delays. Discrete Dyn. Nat. Soc. 2009, 2009, 291594. [Google Scholar] [CrossRef]
- Rao, R. Delay-dependent exponential stability for nonlinear reaction-diffusion uncertain Cohen-Grossberg neural networks with partially known transition rates via Hardy-Poincar’e inequality. Chin. Ann. Math. Ser. B 2014, 35, 575–598. [Google Scholar] [CrossRef]
- Balasubramaniam, P.; Syed Ali, M. Robust stability of uncertain fuzzy cellular neural networks with time-varying delays and reaction diffusion terms. Neurocomputing 2010, 73, 439–446. [Google Scholar] [CrossRef]
- Wang, J.; Lu, J. Global exponential stability of fuzzy cellular neural networks with delays and reaction-diffusion terms. Chaos Solitons Fractals 2008, 38, 878–885. [Google Scholar] [CrossRef]
- Gokulakrishnan, V.; Srinivasan, R. Event-Triggered controller on practically exponential input-to-state stabilization of stochastic reaction–diffusion Cohen–Grossberg neural networks and its application to image encryption. Neural Process Lett. 2023, 55, 11147–11171. [Google Scholar] [CrossRef]
- Shanmugam, S.; Narayanan, G.; Rajagopal, K.; Syed Ali, M. Finite-time synchronization of complex-valued neural networks with reaction-diffusion terms: An adaptive intermittent control approach. Neural Comput. Appl. 2024, 36, 7389–7404. [Google Scholar] [CrossRef]
- Chen, Y.; Bi, W. New robust exponential stability analysis for uncertain neural networks with time-varying delay. Int. J. Autom. and Comput. 2008, 5, 395–400. [Google Scholar] [CrossRef]
- Gau, R.S.; Lien, C.H.; Hsieh, J.G. Global exponential stability for uncertain cellular neural networks with multiple time-varying delays via LMI approach. Chaos Solitons Fractals 2007, 32, 1258–1267. [Google Scholar] [CrossRef]
- Hua, M.; Liu, X.; Deng, F.; Fei, J. New results on robust exponential stability of uncertain stochastic neural networks with mixed time-varying delays. Neural Process. Lett. 2010, 32, 219–233. [Google Scholar] [CrossRef]
- Balasubramaniam, P.; Syed Ali, M. Robust exponential stability of uncertain fuzzy Cohen-Grossberg neural networks with time-varying delays. Fuzzy Set. Syst. 2010, 161, 608–618. [Google Scholar] [CrossRef]
- Cheng, C. Robust control of a class of neural networks with bounded uncertainties and time-varying delays. Comput. Math. Appl. 2008, 56, 1245–1254. [Google Scholar] [CrossRef][Green Version]
- Li, K. Stability analysis for impulsive Cohen–Grossberg neural networks with time-varying delays and distributed delays. Nonlinear Anal. Real World Appl. 2009, 10, 2784–2798. [Google Scholar] [CrossRef]
- Li, Z.; Li, K. Stability analysis of impulsive Cohen–Grossberg neural networks with distributed delays and reaction–diffusion terms. Appl. Math. Model 2009, 33, 1337–1348. [Google Scholar] [CrossRef]
- Berman, A.; Plemmons, R.J. Nonnegative Matrices in the Mathematical Science; Academic Press: Cambridge, MA, USA, 1979. [Google Scholar]
- Yang, Z.; Xu, D. Impulsive effects on stability of Cohen–Grossberg neural networks with variable delays. Appl. Math. Comput. 2008, 177, 63–78. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, F.; Hu, W.; Wu, E.; Yuan, X. Global Exponential Stability of Impulsive Delayed Neural Networks with Parameter Uncertainties and Reaction–Diffusion Terms. Mathematics 2024, 12, 2395. https://doi.org/10.3390/math12152395
Luo F, Hu W, Wu E, Yuan X. Global Exponential Stability of Impulsive Delayed Neural Networks with Parameter Uncertainties and Reaction–Diffusion Terms. Mathematics. 2024; 12(15):2395. https://doi.org/10.3390/math12152395
Chicago/Turabian StyleLuo, Fei, Weiyi Hu, Enli Wu, and Xiufang Yuan. 2024. "Global Exponential Stability of Impulsive Delayed Neural Networks with Parameter Uncertainties and Reaction–Diffusion Terms" Mathematics 12, no. 15: 2395. https://doi.org/10.3390/math12152395
APA StyleLuo, F., Hu, W., Wu, E., & Yuan, X. (2024). Global Exponential Stability of Impulsive Delayed Neural Networks with Parameter Uncertainties and Reaction–Diffusion Terms. Mathematics, 12(15), 2395. https://doi.org/10.3390/math12152395




