Fractional Dynamics of Cassava Mosaic Disease Model with Recovery Rate Using New Proposed Numerical Scheme
Abstract
1. Introduction
2. Basic Model Structure
- Only healthy cuttings are selected for propagation.
- Diseased cassava plants may be substantially less vigorous than healthy ones, as evidenced by a consistent loss rate due to disease. Any roguing procedures are also considered to increase the loss rate of unhealthy plants.
- The replanting rate for the cassava plant is higher than that for the harvest and roguing rates.
- The propagation rate of whiteflies is higher than the death rate.
- Once a cassava plant gets infected, it remains infectious until recovered or harvested.
- The rate at which the whiteflies vector gets infected from the infected cassava plants and the rate at which the virus acquisition by non-infective vectors is equal.
- Once whiteflies get infected, they remain infectious for life, but their offspring are not infective.
3. Fractional Operators
4. CMD Model with Caputo–Fabrizio Derivative
4.1. Existence and Uniqueness of CMD Model
4.2. Stability Analysis
5. Numerical Results
5.1. Numerical Method
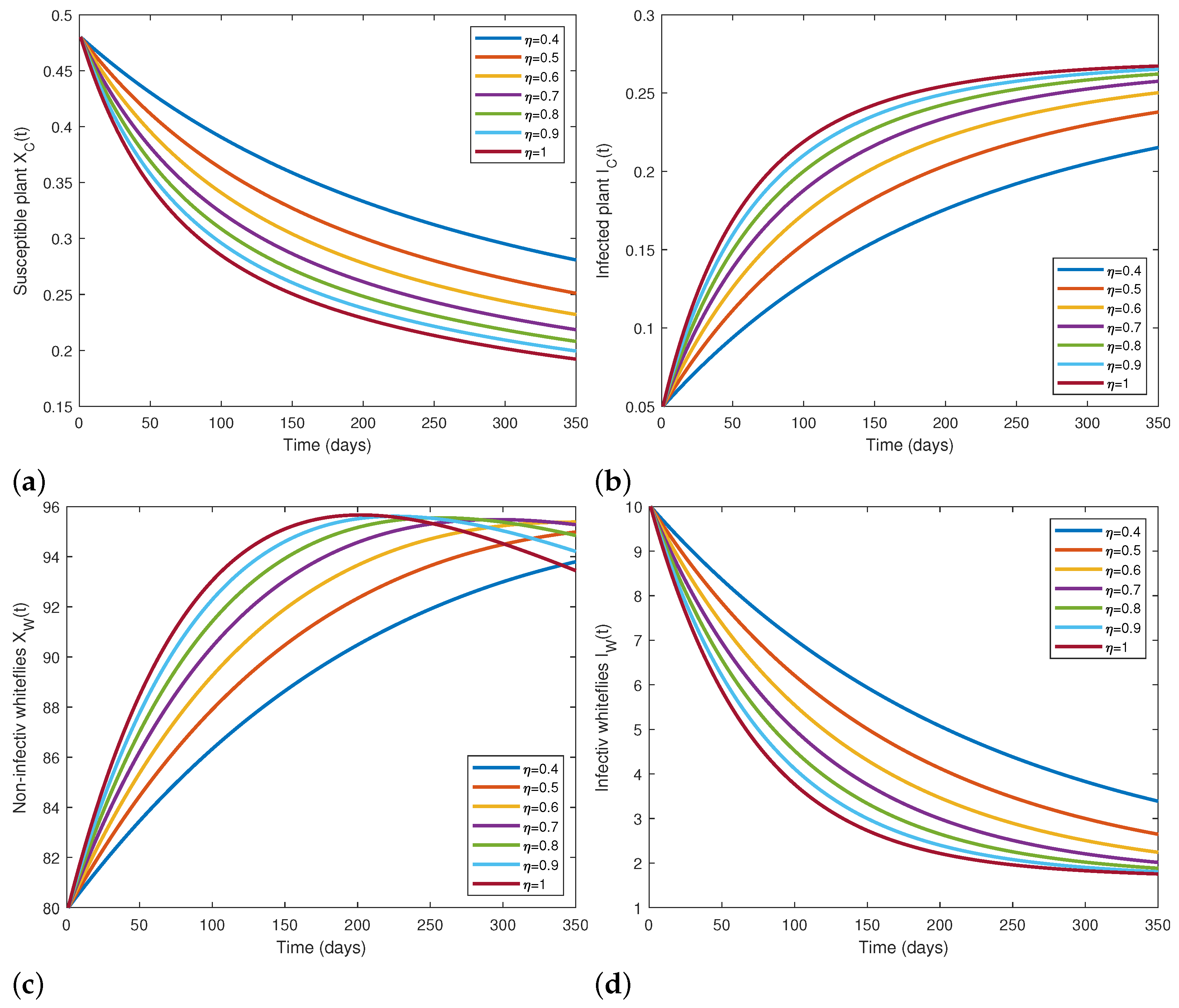
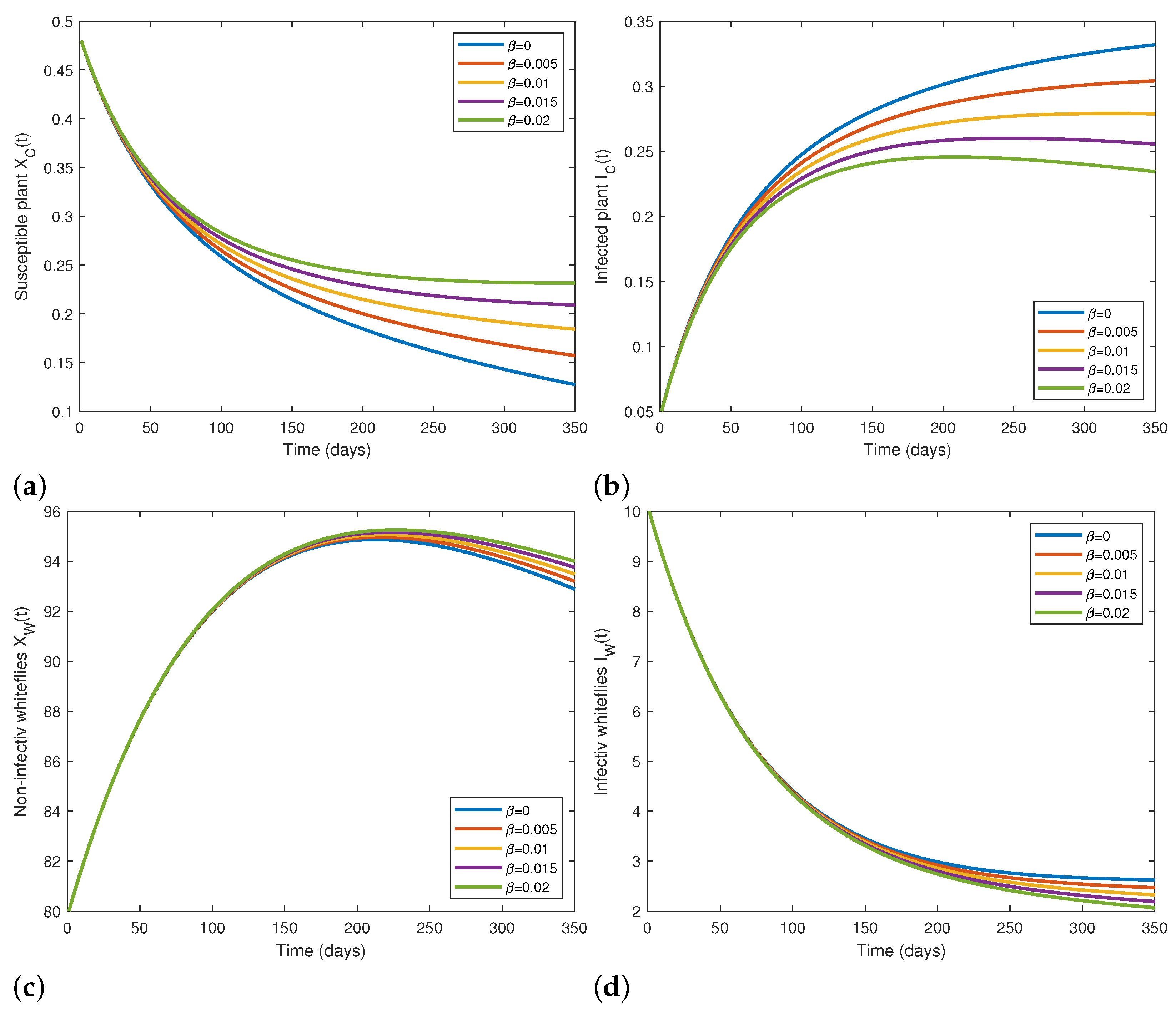
5.2. Numerical Simulations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rey, C.; Vanderschuren, H. Cassava mosaic and brown streak diseases: Current perspectives and beyond. Annu. Rev. Virol. 2017, 4, 429–452. [Google Scholar] [CrossRef]
- Byju, G.; Suja, G. Mineral nutrition of cassava. Adv. Agron. 2020, 159, 169–235. [Google Scholar]
- FAOSTAT FAO Statistics. Food and Agriculture Organization of the United Nations 2018. 2020. Available online: http://www.fao.org/faostat/en/ (accessed on 1 June 2018).
- Tafesse, A.; Mena, B.; Belay, A.; Aynekulu, E.; Recha, J.W.; Osano, P.M.; Darr, D.; Demissie, T.D.; Endalamaw, T.B.; Solomon, D. Cassava production efficiency in southern Ethiopia: The parametric model analysis. Front. Sustain. Food Syst. 2021, 5, 758951. [Google Scholar] [CrossRef]
- Legg, J.; Winter, S. Cassava mosaic viruses (Geminiviridae). In Reference Module in Life Sciences; Elsevier: Amsterdam, The Netherlands, 2020; Volume 2020, pp. 1–12. [Google Scholar]
- Al-Basir, F.; Banerjee, A.; Ray, S. Role of farming awareness in crop pest management—A mathematical model. J. Theor. Biol. 2019, 461, 59–67. [Google Scholar] [CrossRef]
- Chowdhury, J.; Al-Basir, F.; Takeuchi, Y.; Ghosh, M.; Roy, P.K. A mathematical model for pest management in Jatropha curcas with integrated pesticides-An optimal control approach. Ecol. Complex. 2019, 37, 24–31. [Google Scholar] [CrossRef]
- Melese, A.S.; Makinde, O.D.; Obsu, L.L. Mathematical modelling and analysis of coffee berry disease dynamics on a coffee farm. Math. Biosci. Eng. 2022, 19, 7349–7373. [Google Scholar] [CrossRef]
- Tabonglek, S.; Humphries, U.W.; Khan, A. Mathematical Model for Rice Blast Disease Caused by Spore Dispersion Affected from Climate Factors. Symmetry 2022, 14, 1131. [Google Scholar] [CrossRef]
- Blyuss, K.B.; Al-Basir, F.; Tsygankova, V.A.; Biliavska, L.O.; Iutynska, G.O.; Kyrychko, S.N.; Dziuba, S.V.; Tsyliuryk, O.I.; Izhboldin, O. Control of mosaic disease using microbial biostimulants: Insights from mathematical modelling. Ric. Mat. 2020, 69, 437–455. [Google Scholar] [CrossRef]
- Atanasov, A.; Georgiev, S.; Vulkov, L. Numerical Analysis of the Transfer Dynamics of Heavy Metals from Soil to Plant and Application to Contamination of Honey. Symmetry 2024, 16, 110. [Google Scholar] [CrossRef]
- Al-Basir, F.; Ray, S. Impact of farming awareness based roguing, insecticide spraying and optimal control on the dynamics of mosaic disease. Ric. Mat. 2020, 69, 393–412. [Google Scholar] [CrossRef]
- Al-Basir, F.; Roy, P.K. Dynamics of mosaic disease with roguing and delay in Jatropha curcas plantations. J. Appl. Math. Comput. 2018, 58, 1–31. [Google Scholar] [CrossRef]
- Rakshit, N.; Al-Basir, F.; Banerjee, A.; Ray, S. Dynamics of plant mosaic disease propagation and the usefulness of roguing as an alternative biological control. Ecol. Complex. 2019, 38, 15–23. [Google Scholar] [CrossRef]
- Al-Basir, F.; Kyrychko, Y.N.; Blyuss, K.B.; Ray, S. Effects of vector maturation time on the dynamics of cassava mosaic disease. Bull. Math. Biol. 2021, 83, 1–21. [Google Scholar] [CrossRef]
- Maity, S.; Mandal, P.S. A comparison of deterministic and stochastic plant-vector-virus models based on probability of disease extinction and outbreak. Bull. Math. Biol. 2022, 84, 1–41. [Google Scholar] [CrossRef] [PubMed]
- Jittamai, P.; Chanlawong, N.; Atisattapong, W.; Anlamlert, W.; Buensanteai, N. Reproduction number and sensitivity analysis of cassava mosaic disease spread for policy design. Math. Biosci. Eng. 2021, 18, 5069–5093. [Google Scholar] [CrossRef]
- Ahmed, I.; Kiataramkul, C.; Muhammad, M.; Tariboon, J. Existence and Sensitivity Analysis of a Caputo Fractional-Order Diphtheria Epidemic Model. Mathematics 2024, 12, 2033. [Google Scholar] [CrossRef]
- Subramanian, S.; Kumaran, A.; Ravichandran, S.; Venugopal, P.; Dhahri, S.; Ramasamy, K. Fuzzy Fractional Caputo Derivative of Susceptible-Infectious-Removed Epidemic Model for Childhood Diseases. Mathematics 2024, 12, 466. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Alsaedi, A. Analysis of time-fractional Hunter-Saxton equation: A model of neumatic liquid crystal. Open Phys. 2016, 14, 145–149. [Google Scholar] [CrossRef]
- Fahad, A.; Boulaaras, S.M.; Rehman, H.U.R.; Iqbal, I.; Saleem, M.S.; Chou, D. Analysing soliton dynamics and a comparative study of fractional derivatives in the nonlinear fractional Kudryashov’s equation. Results Phys. 2023, 55, 107114. [Google Scholar] [CrossRef]
- Li, J.F.; Ahmad, I.; Ahmad, G.; Shah, D.; Chu, U.M.; Thounthong, P.; Ayaz, M. Numerical solution of two-term time-fractional PDE models arising in mathematical physics using local meshless method. Open Phys. 2020, 18, 1063–1072. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. Caputo-Fabrizio derivative applied to groundwater flow within confined aquifer. J. Eng. Mech. 2017, 143, D4016005. [Google Scholar] [CrossRef]
- Khan, A.; Abdeljawad, T.; Gomez-Aguilar, J.F.; Khan, H. Dynamical study of fractional order mutualism parasitism food web module. Chaos Solit. Fractals 2020, 134, 109685. [Google Scholar] [CrossRef]
- Khan, A.; Gomez-Aguilar, J.F.; Abdeljawad, T.; Khan, H. Stability and numerical simulation of a fractional order plant-nectar-pollinator model. Alex. Eng. J. 2020, 59, 49–59. [Google Scholar] [CrossRef]
- Hussain, S.; Madi, E.N.; Iqbal, N.; Botmart, T.; Karaca, Y.; Mohammed, W.W. Fractional dynamics of vector-borne infection with sexual transmission rate and vaccination. Mathematics 2021, 9, 3118. [Google Scholar] [CrossRef]
- Cao, X.; Ghosh, S.; Rana, S.; Bose, H.; Roy, P.K. Application of an Optimal Control Therapeutic Approach for the Memory-Regulated Infection Mechanism of Leprosy through Caputo-Fabrizio Fractional Derivative. Mathematics 2023, 11, 3630. [Google Scholar] [CrossRef]
- Thabet, S.T.M.; Abdo, M.S.; Shah, K.; Abdeljawad, T. Study of transmission dynamics of COVID-19 mathematical model under ABC fractional order derivative. Results Phys. 2020, 19, 103507. [Google Scholar] [CrossRef] [PubMed]
- Begum, R.; Tunç, O.; Khan, H.; Gulzar, H.; Khan, A. A fractional order Zika virus model with Mittag-Leffler kernel. Chaos Solit. Fractals 2021, 146, 110898. [Google Scholar] [CrossRef]
- Shah, N.; Nor, H.; Jan, R.; Ahmad, H.; Razak, N.N.A.; Ahmad, I.; Ahmad, H. Enhancing public health strategies for tungiasis: A mathematical approach with fractional derivative. AIMS Bioeng. 2023, 10, 384–405. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Micula, S.; Nieto, J.J. A novel technique to control the accuracy of a nonlinear fractional order model of COVID-19: Application of the CESTAC method and the CADNA library. Mathematics 2021, 9, 1321. [Google Scholar] [CrossRef]
- Tomasiello, S.; Macías-Díaz, J.E. A Mini-Review on Recent Fractional Models for Agri-Food Problems. Mathematics 2023, 11, 2316. [Google Scholar] [CrossRef]
- Abdullah, T.Q.S.; Huang, G.; Al-Sadi, W. A curative and preventive treatment fractional model for plant disease in Atangana-Baleanu derivative through Lagrange interpolation. Int. J. Biomath. 2022, 15, 2250052. [Google Scholar] [CrossRef]
- Guo, W.; Campanella, O.H. A relaxation model based on the application of fractional calculus for describing the viscoelastic behavior of potato tubers. Trans. ASABE 2017, 60, 259–264. [Google Scholar]
- Achar, S.J.; Baishya, C.; Veeresha, P.; Akinyemi, L. Dynamics of fractional model of biological pest control in tea plants with Beddington–DeAngelis functional response. Fractal Fract. 2021, 6, 1. [Google Scholar] [CrossRef]
- Liu, S.; Huang, M.; Wang, J. Bifurcation control of a delayed fractional Mosaic disease model for Jatropha curcas with farming awareness. J. Complex. 2020, 2020, 2380451. [Google Scholar] [CrossRef]
- Kumar, P.; Erturk, V.S.; Almusawa, H. Mathematical structure of mosaic disease using microbial biostimulants via Caputo and Atangana-Baleanu derivatives. Results Phys. 2021, 24, 104186. [Google Scholar] [CrossRef]
- Kumar, P.; Erturk, V.S.; Almusawa, H. Dynamic analysis and bifurcation control of a fractional-order cassava mosaic disease model. J. Appl. Math. Comput. 2023, 69, 1705–1730. [Google Scholar]
- Achar, S.J.K.; Geetha, N. Dynamics of fractional plant virus propagation model with influence of seasonality and intraspecific competition. Math. Methods Appl. Sci. 2024, 47, 6415–6430. [Google Scholar] [CrossRef]
- Ghalib, M.M.; Zafar, A.A.; Hammouch, Z.; Riaz, M.B.; Shabbir, K. Analytical results on the unsteady rotational flow of fractional-order non-newtonian fluids with shear stress on the boundary. Discret. Contin. Dyn. Syst.-S 2020, 13, 683. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Losada, J.; Nieto, J.J. Properties of a new fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Wang, J.; Zhou, Y.; Medved, M. Picard and weakly Picard operators technique for nonlinear differential equations in Banach spaces. J. Math. Anal. Appl. 2012, 389, 261–274. [Google Scholar] [CrossRef]
- Baleanu, D.; Mohammadi, H.; Rezapour, S. A fractional differential equation model for the COVID-19 transmission by using the Caputo-Fabrizio derivative. Adv. Differ. Equ. 2020, 2020, 299. [Google Scholar] [CrossRef] [PubMed]
- Mahatekar, Y.; Scindia, P.S.; Kumar, P. A new numerical method to solve fractional differential equations in terms of Caputo-Fabrizio derivatives. Phys. Scr. 2023, 98, 024001. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Jafari, H. An iterative method for solving nonlinear functional equations. J. Math. Anal. Appl. 2006, 316, 753–763. [Google Scholar] [CrossRef]
- Holt, J.; Jeger, M.J.; Thresh, J.M.; Otim-Nape, G.W. An epidemilogical model incorporating vector population dynamics applied to African cassava mosaic virus disease. J. Appl. Ecol. 1997, 34, 793–806. [Google Scholar] [CrossRef]
- Santra, N.; Sahoo, D.; Mondal, S.; Samanta, G. An epidemiological multi-delay model on cassava mosaic disease with delay-dependent parameters. Filomat 2023, 37, 2887–2921. [Google Scholar] [CrossRef]
- Caspary, R.; Wosula, E.N.; Issa, K.A.; Amour, M.; Legg, J.P. Cutting dipping application of Flupyradifurone against cassava whiteflies Bemisia tabaci and impact on its parasitism in cassava. Insects 2023, 14, 796. [Google Scholar] [CrossRef] [PubMed]
- Kalyebi, A.; Macfadyen, S.; Hulthen, A.; Ocitti, P.; Jacomb, F.; Tay, W.T.; Colvin, J.; De Barro, P. Within-season changes in land-use impact pest abundance in smallholder African cassava production systems. Insects 2021, 12, 269. [Google Scholar] [CrossRef]
- Macfadyen, S.; Tay, W.K.; Hulthen, A.D.; Paull, C.; Kalyebi, A.; Jacomb, F.; Parry, H.; Sseruwagi, P.; Seguni, Z.; Omongo, C.A.; et al. Landscape factors and how they influence whitefly pests in cassava fields across East Africa. J. Landsc. Ecol. 2021, 36, 45–67. [Google Scholar] [CrossRef]

| Parameter | Description | Value |
|---|---|---|
| a | The maximum replanting rate | 0.05 day−1 |
| k | The maximum abundance of cassava plant | 0.5 m−2 |
| The recovery rate of cassava plant | 0.003 day−1 | |
| r | Infection rate | 0.008 vector−1 day−1 |
| The harvesting rate of cassava plant | 0.003 day−1 | |
| g | Roguing/removed plant rate | 0.003 day−1 |
| b | The growth rate of whitefly vectors | 0.2 day−1 |
| The external sources of infections | 1 vector−1 day−1 | |
| The maximum abundance of vectors | 500 plant−1 | |
| m | The rate of virus acquisition by non-infective vectors | 0.008 plant−1 day−1 |
| Death rate of whitefly vectors | 0.12 day−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdullah, T.Q.S.; Huang, G.; Al-Sadi, W.; Aboelmagd, Y.; Mobarak, W. Fractional Dynamics of Cassava Mosaic Disease Model with Recovery Rate Using New Proposed Numerical Scheme. Mathematics 2024, 12, 2386. https://doi.org/10.3390/math12152386
Abdullah TQS, Huang G, Al-Sadi W, Aboelmagd Y, Mobarak W. Fractional Dynamics of Cassava Mosaic Disease Model with Recovery Rate Using New Proposed Numerical Scheme. Mathematics. 2024; 12(15):2386. https://doi.org/10.3390/math12152386
Chicago/Turabian StyleAbdullah, Tariq Q. S., Gang Huang, Wadhah Al-Sadi, Yasser Aboelmagd, and Wael Mobarak. 2024. "Fractional Dynamics of Cassava Mosaic Disease Model with Recovery Rate Using New Proposed Numerical Scheme" Mathematics 12, no. 15: 2386. https://doi.org/10.3390/math12152386
APA StyleAbdullah, T. Q. S., Huang, G., Al-Sadi, W., Aboelmagd, Y., & Mobarak, W. (2024). Fractional Dynamics of Cassava Mosaic Disease Model with Recovery Rate Using New Proposed Numerical Scheme. Mathematics, 12(15), 2386. https://doi.org/10.3390/math12152386






