On the Asymptotic Network Indices of Weighted Three-Layered Structures with Multi-Fan Composed Subgraphs
Abstract
1. Introduction
- I
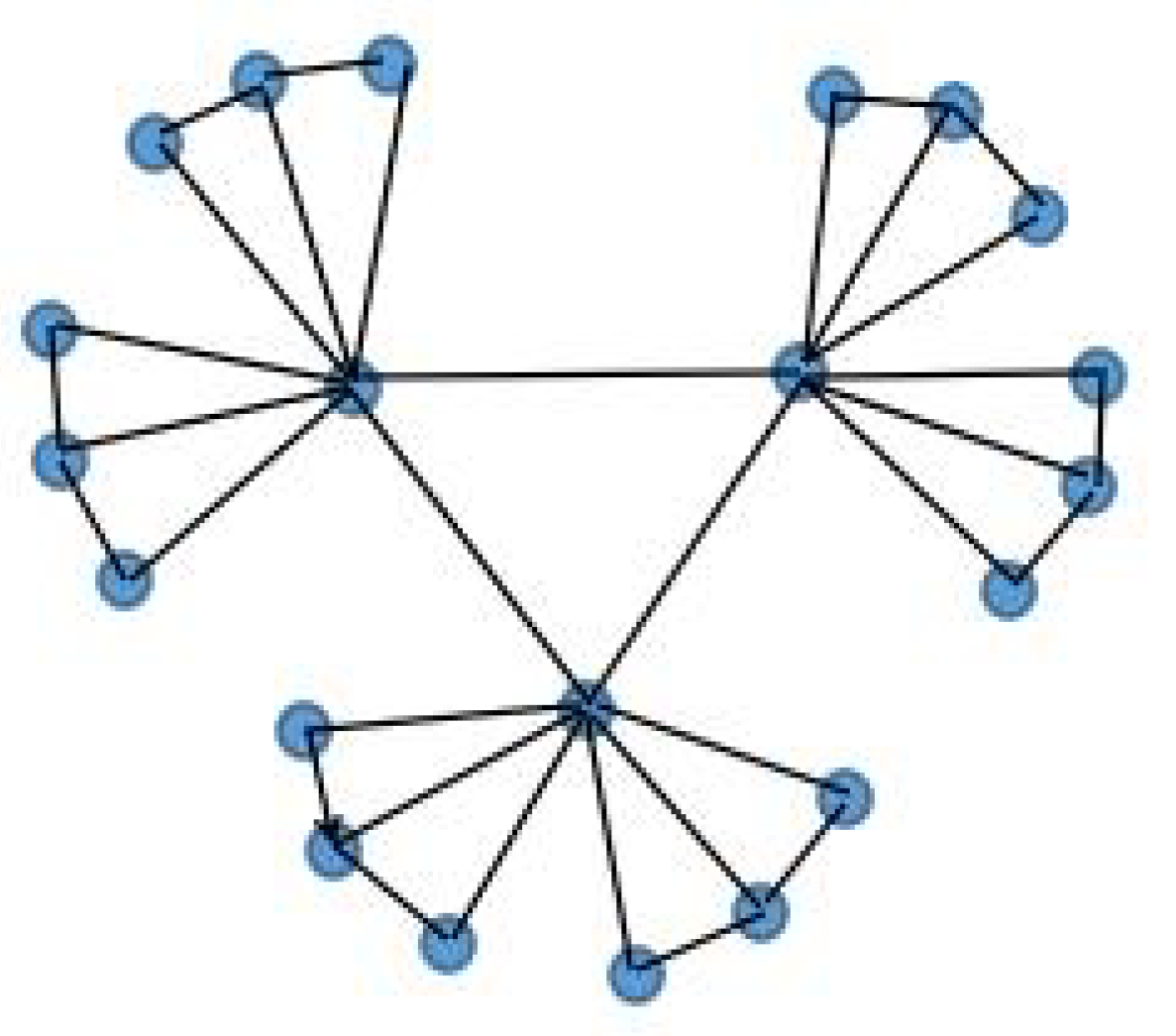
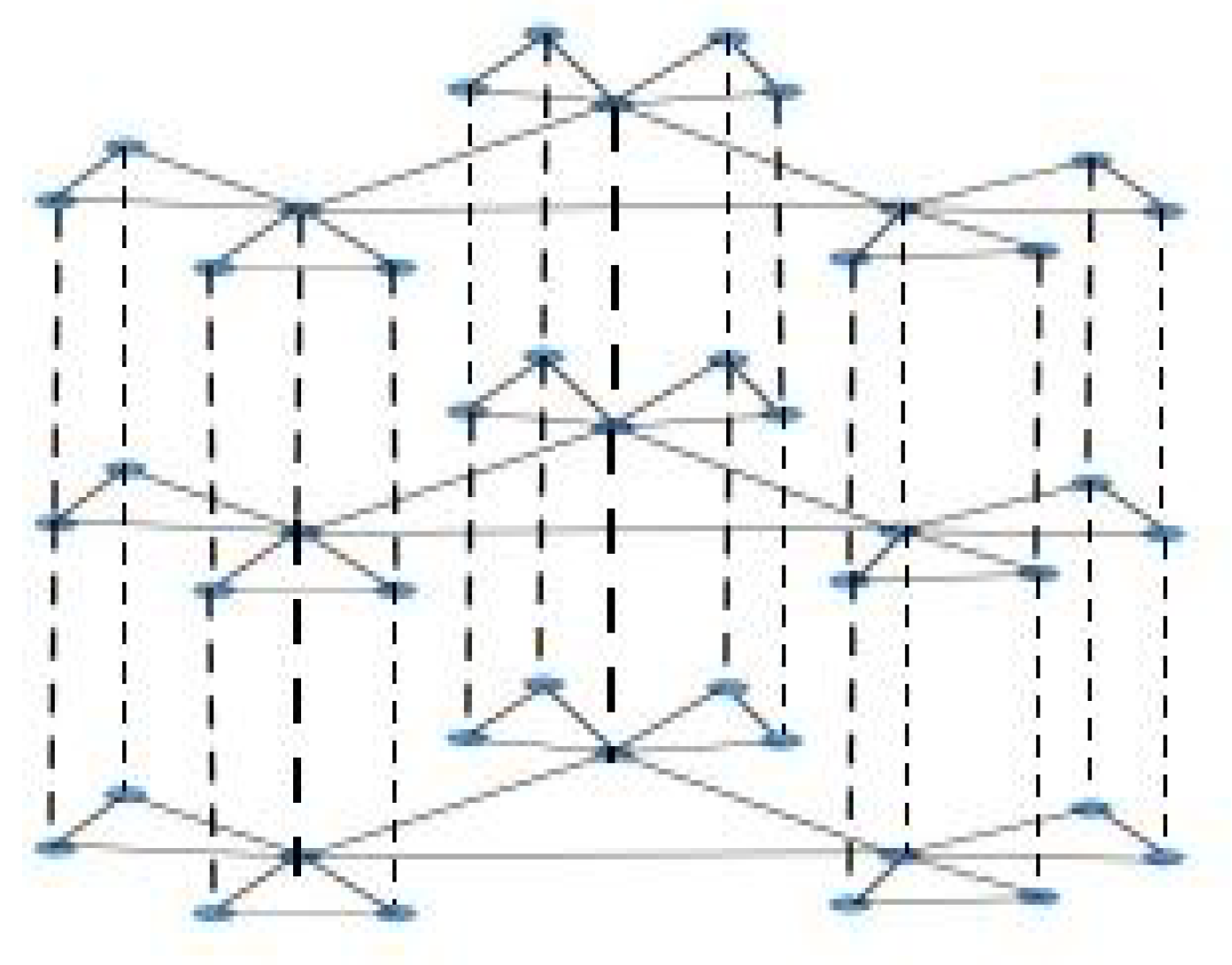
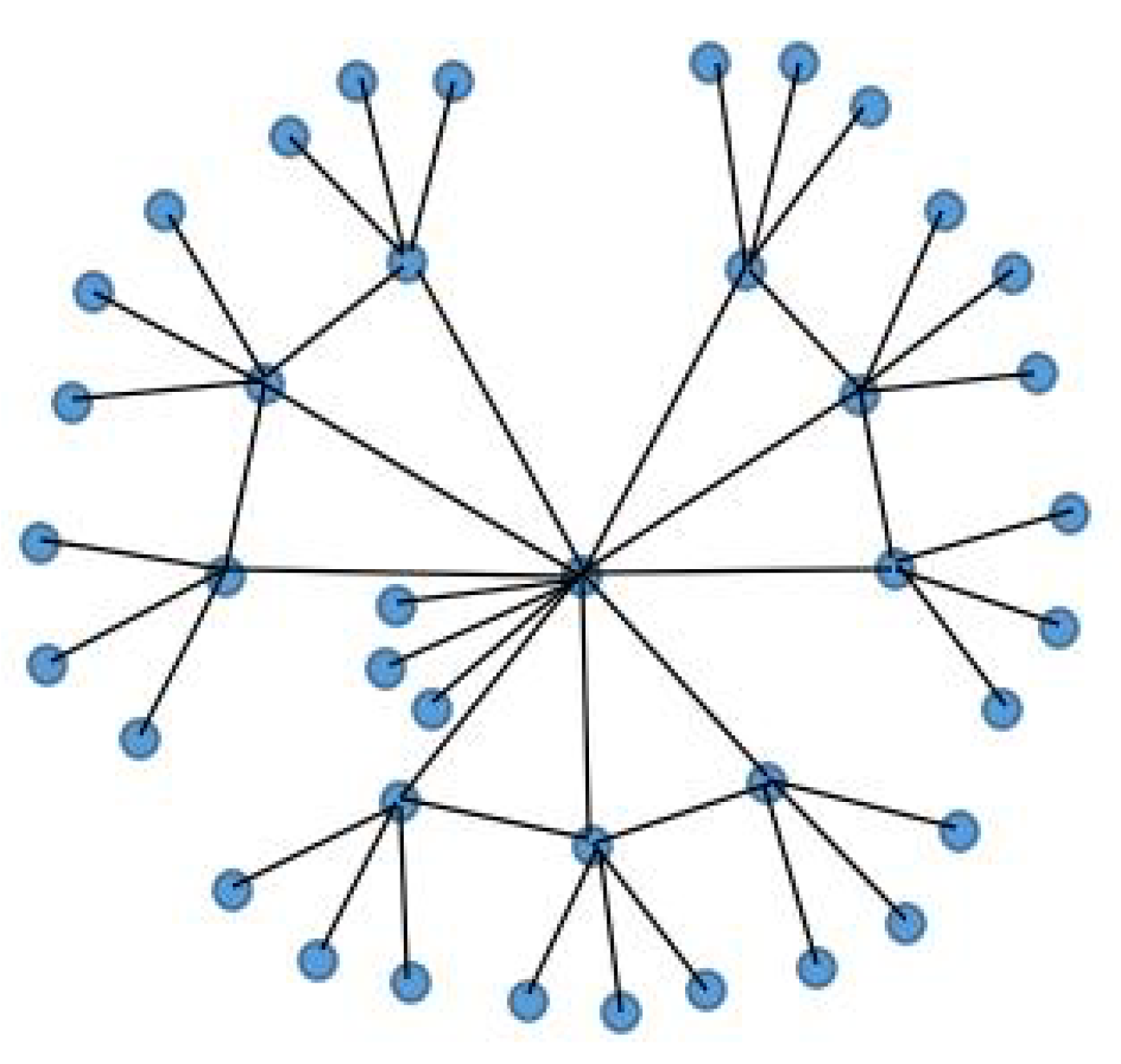
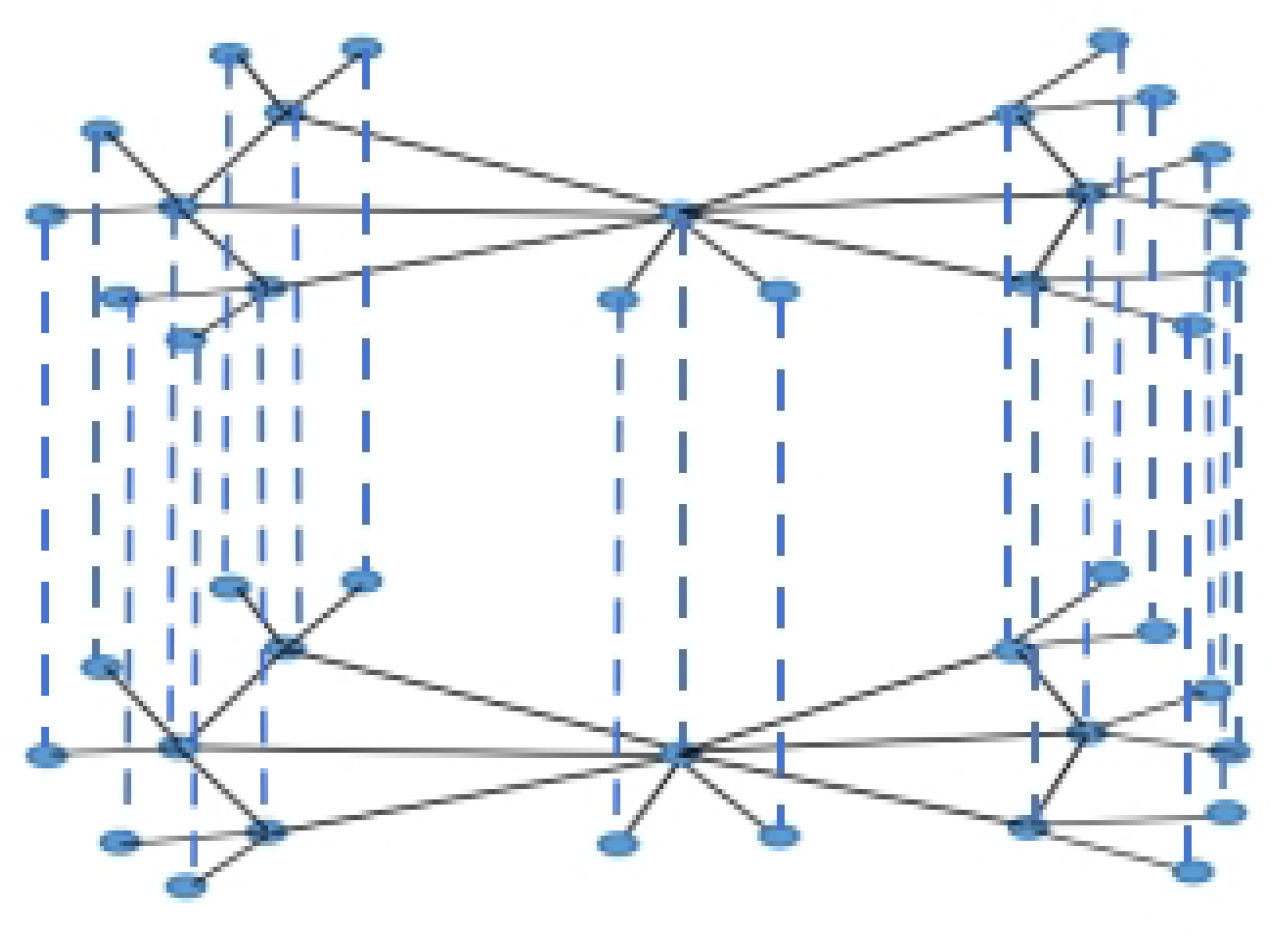
- Two novel non-isomorphic weighted three-layered multi-fan composed networks are constructed by graph operation.
- II
- Novel results of expression for the three sorts of network indices of the considered weighted graphs are given, and an analysis approach with multiple variables is utilized to calculate the asymptotic properties.
- III
- We find that if the cardinalities of the vertices on a sector-edge-link tend to infinity, the asymptotic properties of indices of FONC and EMFPT are irrelevant with the number of copies of the fan-substructure based on this paper’s topological framework.
2. Preliminaries
Basic Notations
3. Main Results
3.1. The Performance Indices for Network
3.2. The Performance Indices for
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saber, O.; Murray, R. Consensus problems in Networks of Agents with Switching Topology and Time-Delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Ren, W. On consensus algorithms for double-integrator dynamics. IEEE Trans. Autom. Control 2008, 53, 1503–1509. [Google Scholar] [CrossRef]
- Yu, W.; Chen, G.; Cao, M.; Kurths, J. Second-order consensus for multiagent systems with directed topologies and nonlinear dynamics. IEEE Trans. Syst. Man Cybern. Part Cybern. 2010, 40, 881–891. [Google Scholar]
- Wen, G.; Duan, Z.; Yu, W.; Chen, G. Consensus of second-order multi-agent systems with delayed nonlinear dynamics and intermittent communications. Int. J. Control 2013, 86, 322–331. [Google Scholar] [CrossRef]
- Yu, Z.; Jiang, H.; Hu, C.; Yu, J. Leader-following consensus of fractional-order multi-agent systems via adaptive pinning control. Int. J. Control 2015, 88, 1746–1756. [Google Scholar] [CrossRef]
- Sun, J.; Guo, C.; Liu, L.; Shan, Q. Adaptive consensus control of second-order nonlinear multi-agent systems with event-dependent intermittent communications. J. Frankl. Inst. 2023, 360, 2289–2306. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, G.; Rahmani, A.; Peng, Z.; Hu, W. Cluster consensus of multi-agent systems with general linear and nonlinear dynamics via intermittent adaptive pinning control. Trans. Inst. Meas. Control 2021, 43, 1337–1346. [Google Scholar] [CrossRef]
- Yu, Z.; Yu, S.; Jiang, H.; Mei, X. Distributed fixed-time optimization for multi-agent systems over a directed network. Nonlinear Dyn. 2021, 103, 775–789. [Google Scholar] [CrossRef]
- Li, X.; Yu, Z.; Jiang, H. Event-triggered fixed-time integral sliding mode control for nonlinear multi-agent systems with disturbances. Entropy 2021, 23, 1412. [Google Scholar] [CrossRef]
- Young, G.; Scardovi, L.; Leonard, N. Robustness of Noisy Consensus Dynamics with Directed Communication. In Proceedings of the American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 6312–6317. [Google Scholar]
- Bamieh, B.; Jovanovi, M.R.; Mitra, P.; Patterson, S. Coherence in large-scale networks: Dimension-dependent limitations of local feedback. IEEE Trans. Autom. Control 2012, 57, 2235–2249. [Google Scholar] [CrossRef]
- Patterson, S.; Bamieh, B. Consensus and Coherence in Fractal Networks. IEEE Trans. Control Netw. Syst. 2014, 1, 338–348. [Google Scholar] [CrossRef]
- Patterson, S.; Yi, Y.; Zhang, Z. A Resistance-Distance-Based Approach for Optimal Leader Selection in Noisy Consensus Networks. IEEE Trans. Control Netw. Syst. 2018, 6, 191–201. [Google Scholar] [CrossRef]
- Yi, Y.; Zhang, Z.; Shan, L.; Chen, G. Robustness of First-and Second-Order Consensus Algorithms for a Noisy Scale-Free Small-World Koch Network. IEEE Trans. Control Syst. Technol. 2016, 25, 342–350. [Google Scholar] [CrossRef]
- Sun, W.; Hong, M.; Liu, S.; Fan, K. Leader-follower coherence in noisy ring-trees networks. Nonlinear Dyn. 2020, 102, 1657–1665. [Google Scholar] [CrossRef]
- Liu, J.; Bao, Y.; Zheng, W.; Hayat, S. Network coherence analysis on a family of nested weighted n-polygon networks. Fractals 2021, 29, 2150260. [Google Scholar] [CrossRef]
- Liu, J.; Wang, X.; Cao, J. The Coherence and Properties Analysis of Balanced 2p-Ary Tree Networks. IEEE Trans. Netw. Sci. Eng. 2024. early access. [Google Scholar] [CrossRef]
- Wan, Y.; Namuduri, K.; Akula, S.; Varanasi, M. The impact of multi-group multi-layer network structure on the performance of distributed consensus building strategies. Int. Robust. Nonlinear Control 2012, 23, 653–662. [Google Scholar] [CrossRef]
- Drauschke, F.; Sawicki, J.; Berner, R.; Omelchenko, I.; Schöll, E. Effect of topology upon relay synchronization in triplex neuronal networks. Chaos 2020, 30, 051104. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Jia, Z.; Deng, Y. Eigenvalue Spectrum and Synchronizability of Two Types of Double-Layer Star-Ring Networks with Hybrid Directional Coupling. Discret. Dyn. Nat. Soc. 2021, 2021, 6623648. [Google Scholar] [CrossRef]
- Zhu, J.; Huang, D.; Gao, H.; Li, X. The Laplacian spectrum of weighted composite networks and the applications. Aip Adv. 2024, 14, 035229. [Google Scholar] [CrossRef]
- Xu, M.M.; Lu, J.A.; Zhou, J. Synchronizability and eigenvalues of two-layer star networks. Acta Phys. Sin. 2016, 65, 028902. [Google Scholar]
- Kenyeres, M.; Kenyeres, J. Distributed Mechanism for Detecting Average Consensus with Maximum-Degree Weights in Bipartite Regular Graphs. Mathematics 2021, 9, 3020. [Google Scholar] [CrossRef]
- He, W.; Chen, G.; Han, Q.-L.; Du, W.; Cao, J.; Qian, F. Multiagent Systems on Multilayer Networks: Synchronization Analysis and Network Design. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1655–1667. [Google Scholar] [CrossRef]
- Hu, C.; He, H.; Jiang, H. Edge-Based Adaptive Distributed Method for Synchronization of Intermittently Coupled Spatiotemporal Networks. IEEE Trans. Autom. Control 2022, 67, 2597–2604. [Google Scholar] [CrossRef]
- Hu, C.; He, H.; Jiang, H. Synchronization of complex-valued dynamic networks with intermittently adaptive coupling: A direct error method. Automatica 2020, 112, 108675. [Google Scholar] [CrossRef]
- Yang, Y.; Klein, D.J. Comparison theorems on the resistance distances and Kirchhoff indices of S,T-isomers. Discret. Appl. Math. 2014, 175, 87–93. [Google Scholar] [CrossRef]
- Yang, Y.; Yu, Y. Resistance Distances and Kirchhoff indices under graph operations. IEEE Access 2020, 8, 95650–95656. [Google Scholar] [CrossRef]
- Wang, X.; Dai, M.; Chen, Y. Determining entire mean first-passage time for Cayley networks. Int. J. Mod. Phys. C 2018, 29, 1850009. [Google Scholar] [CrossRef]
- Kivela, M.; Arenas, A.; Barthelemy, M.; Gleeson, J.P.; Moreno, Y.; Porter, M.A. Multilayer Networks. J. Complex Netw. 2014, 2, 203. [Google Scholar] [CrossRef]
- Wang, Z.; Xia, C.; Chen, Z.; Chen, G. Epidemic Propagation with Positive and Negative Preventive Information in Multiplex Networks. IEEE Trans. Cybern. 2021, 51, 1454–1462. [Google Scholar] [CrossRef]
- Cvetkovic, D.; Rowlinson, P.; Simic, S. An Introduction to the Theory of Graph Spectra; Cambridge University Press: Cambridge, UK; London, UK, 2010. [Google Scholar]
- Barik, S.; Pati, S.; Sarma, B. The Spectrum of The Corona of Two Graphs. SIAM J. Discret. Math. 2007, 21, 47–56. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, Y.; Li, C. Kirchhoff index of composite graphs. Discret. Appl. Math. 2009, 157, 2918–2927. [Google Scholar] [CrossRef]
- Wang, X.; Hao, Y.; Wang, Q. On the controllability of Corona product network. J. Frankl. Inst. 2020, 357, 6228–6240. [Google Scholar] [CrossRef]
- Khalifeh, M.H.; Yousefi-Azari, H.; Ashrafi, A.R. The hyper-Wiener index of graph operations. Comput. Math. Appl. 2008, 56, 1402–1407. [Google Scholar] [CrossRef]
- Hammack, R.; Imrich, W.; Klavzar, S. Hand Book of Product Graphs; Taylor& Francis Group: London, UK; CRC Press: London, UK, 2011. [Google Scholar]
- Chen, X.; Liu, J.; Meng, J. The restricted arc connectivity of Cartesian product digraphs. Inf. Process. Lett. 2009, 109, 1202–1205. [Google Scholar] [CrossRef]
- Liu, J.; Pan, X. A unified approach to the asymptotic topological indices of various lattices. Appl. Math. Comput. 2015, 270, 62–73. [Google Scholar] [CrossRef]
- Han, D.; Zhou, H.; Weng, T.-H.; Wu, Z.; Han, B.; Li, K.-C.; Pathan, A.-S.K. LMCA: A lightweight anomaly network traffic detection model integrating adjusted mobilenet and coordinate attention mechanism for IoT. Telecommun. Syst. 2023, 84, 549–564. [Google Scholar] [CrossRef]
- Shi, S.; Han, D.; Cui, M. A multimodal hybrid parallel network intrusion detection model. Connect. Sci. 2023, 35, 2227780. [Google Scholar] [CrossRef]
- Chen, C.; Han, D.; Shen, X. CLVIN: Complete language-vision interaction network for visual question answering. Knowl. Based Syst. 2023, 275, 110706. [Google Scholar] [CrossRef]
- Xie, G.; Fu, B.; Li, H.; Du, W.; Zhong, Y.; Wang, L.; Geng, H.; Zhang, J.; Si, L. A gradient-enhanced physics-informed neural networks method for the wave equation. Eng. Anal. Bound. Elem. 2024, 166, 105802. [Google Scholar] [CrossRef]
- Wang, S.; Lu, T.; Hao, R.; Li, J.; Guo, Y.; He, X.; Han, X. An Identification Method for Anomaly Types of Active Distribution Network Based on Data Mining. IEEE Trans. Power Syst. 2024, 39, 5548–5560. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, S.; Yang, Q.; Liew, S.C. Account Service Network: A Unified Decentralized Web 3.0 Portal with Credible Anonymity. IEEE Netw. 2023, 37, 101–108. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, J.; Huang, D.; Zhu, J.; Chen, X. On the Asymptotic Network Indices of Weighted Three-Layered Structures with Multi-Fan Composed Subgraphs. Mathematics 2024, 12, 2359. https://doi.org/10.3390/math12152359
Bian J, Huang D, Zhu J, Chen X. On the Asymptotic Network Indices of Weighted Three-Layered Structures with Multi-Fan Composed Subgraphs. Mathematics. 2024; 12(15):2359. https://doi.org/10.3390/math12152359
Chicago/Turabian StyleBian, Jicheng, Da Huang, Jian Zhu, and Xing Chen. 2024. "On the Asymptotic Network Indices of Weighted Three-Layered Structures with Multi-Fan Composed Subgraphs" Mathematics 12, no. 15: 2359. https://doi.org/10.3390/math12152359
APA StyleBian, J., Huang, D., Zhu, J., & Chen, X. (2024). On the Asymptotic Network Indices of Weighted Three-Layered Structures with Multi-Fan Composed Subgraphs. Mathematics, 12(15), 2359. https://doi.org/10.3390/math12152359





