Abstract
In scientific and engineering disciplines, vectorial problems involving systems of equations or functions with multiple variables frequently arise, often defying analytical solutions and necessitating numerical techniques. This research introduces an efficient numerical scheme capable of simultaneously approximating all roots of nonlinear equations with a convergence order of ten, specifically designed for vectorial problems. Random initial vectors are employed to assess the global convergence behavior of the proposed scheme. The newly developed method surpasses methods in the existing literature in terms of accuracy, consistency, computational CPU time, residual error, and stability. This superiority is demonstrated through numerical experiments tackling engineering problems and solving heat equations under various diffusibility parameters and boundary conditions. The findings underscore the efficacy of the proposed approach in addressing complex nonlinear systems encountered in diverse applied scenarios.
Keywords:
vectorial problems; global convergence; residual error; percentage efficiency; computational convergence order MSC:
65H04; 65H05; 65H10; 65H17
1. Introduction
Scalar nonlinear equations of a single variable ,
play a pivotal role in advancing scientific understanding and engineering [1,2]. Various scientific disciplines, including physics, chemistry, biology, and economics, utilize nonlinear equations to describe complex correlations and interactions between variables. These equations enable scientists to more accurately characterize chaotic systems, fluid dynamics, and population dynamics compared to linear models. In engineering, nonlinear equations are crucial in areas such as control systems [3], structural analysis [4], and electrical circuits [5]. Engineers use these equations to model and predict real-world behaviors by accounting for nonlinearities in materials and systems. Nonlinear optimization techniques are essential for solving engineering problems including parameter estimation [6], optimal control [7], and system design [8]. The significance of nonlinear equations extends to emerging fields like artificial intelligence and machine learning [9], where they are used for complex data processing and pattern recognition [10]. Overall, nonlinear equations and their associated systems are indispensable tools for scientists and engineers striving to understand and manage complex systems, thereby fostering the advancement of knowledge and technology.
Solving nonlinear equations analytically can be challenging, and often impossible, due to the intrinsic complexity of nonlinear interactions. Nonlinear equations include terms that are not simply proportional to the variable of interest, and their solutions may not be expressible in closed-form expressions or simple algebraic equations [11,12,13,14]. Therefore, we turn to numerical iterative schemes. Iterative numerical methods are effective in solving nonlinear equations and systems, making them invaluable tools for researchers across various fields [15,16,17,18]. These numerical iterative techniques are classified into three types: single root-finding schemes with local convergence behavior, simultaneous methods for finding all roots of (1) with global convergence behavior, and schemes that find all solutions to nonlinear systems of equations (i.e., vectorial problems). Iterative techniques for solving nonlinear systems of equations, such as gradient descent [19] or evolutionary algorithms that search for roots simultaneously across multiple dimensions in the solution space [20], exhibit local convergence behavior.
The simplest and most efficient method is the classical Newton’s method [21] for solving (1), given by
The method (2) exhibits local quadratic convergence. To reduce the computational cost of (2), Steffensen [22] proposed the following modified version:
where , and is the first-order forward difference on , i.e., [23]. In high-precision computing, the divided difference is replaced with a first-order central difference on as follows:
where and is the first-order central difference operator. The two-step modified Newton’s method [24] of the third-order convergence has the form
where
Higher-order schemes offer considerable advantages over lower-order schemes for solving nonlinear equations due to improved accuracy and efficiency. They achieve higher accuracy per iteration step, reducing truncation errors and requiring fewer iterations to obtain the desired precision. The order of convergence can increase up to three, four, and so on, such as the well-known Ostrowski’s method [25].
Similarly, Kou et al. [26] developed sixth-order methods using the weight function technique, written as
Liu et al. [27] presented the following eighth-order methods using the weight function technique:
where
Numerous single- and multi-step methods exist for solving (1), and some of these methods can be applied to solving systems of nonlinear equations with local convergence behavior [28]. Noot et al. [29], Darvishi et al. [30], Babajee et al. [31], Ortega et al. [32], and others (see e.g., [33,34] and references therein) have employed (2) as a predictor step to construct multi-step approaches to solving nonlinear equation systems. Iterative methods for finding a single root of nonlinear equations, though widely used, have certain inherent limitations that researchers must consider. One primary concern is convergence; these methods may fail to find a solution if the initial guess is not close enough to a root or if the function has abrupt changes. The dependence on initial guesses poses a significant challenge, as inaccurate or poorly chosen starting points can result in a slow convergence or divergence [35,36]. Furthermore, iterative methods usually provide only local solutions, with no guarantee of accurately identifying all roots, particularly multiple roots. The computational cost can be significant, especially for complex functions or high-dimensional systems, and ill-conditioned problems can lead to numerical instability. Additionally, these methods generally provide root values without information about their multiplicity, and their applicability may be limited in the presence of discontinuities or non-smooth features [37]. Due to these limitations, when using iterative methods, we may need to investigate alternative approaches based on the specific characteristics of the nonlinear equations under investigation. Therefore, we turn to simultaneous methods, which are more stable, consistent, and reliable, and can also be applied to parallel computing (see e.g., [38,39]).
In 1891, Weierstrass [40] introduced the generalized form of (2) by incorporating the Weierstrass correction, which was later explored by Presic [41], Durand [42], Dochev [43], and Kerner [44]. In 2015, Proinov et al. [45] proposed the local convergence theorem for the double Weierstrass technique. In 2016, Nedzibove created a modified version of the Weierstrass technique [46] and presented its local convergence [47] in 2018. In 1973, Aberth [48] developed a third-order convergent simultaneous method with derivatives, which was then accelerated by Nourein [49] to the fourth order in 1977, by Petković [50] to the sixth order in 2020, and by Mir et al. [51] to the tenth order using various single root-finding methods as corrections. Cholakov [52,53] and Marcheva et al. [54] proposed the local convergence of multi-step simultaneous methods for determining all roots of (1). In 2023, Shams et al. [55,56] described the global convergence behavior of simultaneous algorithms using random initial gauge values, along with contributions from many others.
Among derivative-free simultaneous methods, the Weierstrass–Dochive method [57] (abbreviated as BM) is the most attractive. It is given by
where
is the Weierstrass correction. The method (10) has local quadratic convergence.
In 1977, Ehrlich [58] presented the following convergent simultaneous method (abbreviated as EM) of the third order:
where is used as a correction. Petkovic et al. [59] accelerated the convergence order of (11) from three to six:
where and
Petkovic et al. [60] accelerated the convergence order of (11) from three to ten, as shown in the following method (abbreviated as PMϵ):
where ,
Shams et al. [61] proposed a three-step simultaneous scheme for finding all polynomial roots (abbreviated as MMϵ):
where and ; The numerical scheme (14) exhibits a convergence order of twelve.
A review of the existing literature reveals the following:
- Most iterative methods used for solving nonlinear equations and systems are highly effective at converging to solutions when the initial guess is close to a root.
- These iterative techniques are particularly sensitive to initial guesses and may fail to converge if the initial values are not chosen precisely.
- Local convergence algorithms may lack stability and consistency in many cases.
- Iterative methods are susceptible to rounding errors and may fail to converge when the problem is poorly conditioned.
- Nonlinear equations and systems can have multiple solutions, and achieving convergence to the desired solution based on initial estimates can be challenging.
Hirstov et al. [62] proposed the generalized Weierstrass method for solving systems of nonlinear equations (abbreviated as BMϵ):
Chinesta et al. [63] proposed the generalized method (11) for nonlinear systems (abbreviated as EMϵ):
where , and The order of convergence of EMϵ is 2. Motivated by prior work, the main objective of this study is to develop a novel family of efficient, higher-order simultaneous schemes. These schemes aim not only to compute all roots of nonlinear equations simultaneously but also to solve nonlinear systems of equations comprehensively, thereby addressing the limitations outlined earlier. The structure of the paper is as follows: after the introduction, Section 2 introduces and analyzes a new family of two-step vectorial simultaneous algorithms. Section 3 is dedicated to discussing computational efficiencies, while in Section 4, we present and discuss the numerical results obtained from our proposed schemes. Finally, the concluding section summarizes the key findings, contributions of this research, and directions for future work.
2. Constructing a Family of Simultaneous Methods for Distinct Roots
Consider the two-step Newton’s method [64] for finding the simple root of (1):
The methods in (17) exhibit third-order convergence if is a simple root of (1), , and the error equation is described by
or
Suppose (1) has m distinct roots. Then, and can be approximated as
This implies that
By using (22) in (11), we developed a new simultaneous scheme (abbreviated as BDϵ):
where with and where and The method (23) for multiple roots can also be expressed as (abbreviated as BMϵ)
where To develop a derivative-free approach, we replace with the central difference operator , resulting in (abbreviated as DFϵ)
where , and
Assume the system
has m solutions for , where is defined over an open convex domain . The primary goal of this research study is to develop a numerical scheme that can find all solutions of the nonlinear system of equations (26) simultaneously. To find all solutions, we assume a set of m initial guesses for , and define [65],
where
and
Using (27) and (28) in (25), we develop a new simultaneous scheme (abbreviated as DSϵ) as follows:
where , and is the first-central forward difference on .
The theoretical order of convergence of the parallel scheme BDϵ − BMϵ for approximating the roots of nonlinear equations is demonstrated in Theorem 1. For the case of multiplicity unity, we observe the convergence of BDϵ.
Theorem 1.
Let be simple roots of (1) with multiplicity ℘. If the initial guesses are sufficiently close to the actual roots, then the BMϵ method has a convergence order of ten.
Proof.
Let , and represent the errors in and , respectively. Considering the first step of BMϵ, we have
where For distinct roots, we have
For multiple roots, the BDϵ method can be expressed as
where as per [24]. Using Equation (37) and , we obtain
Assuming , from Equation (38), we have
Now, consider the second step of BMϵ:
Using Equation (44) and the definition of , we have
Assuming , from Equation (45), we obtain
Hence, the theorem is proved. □
The theoretical order of convergence of the derivative-free parallel scheme DFϵ to approximate all the roots of nonlinear equations is demonstrated in Theorem 2.
Theorem 2.
Let be the simple roots of Equation (1). If the initial guesses are sufficiently close to these roots, then the DFϵ scheme achieves eighth-order convergence.
Proof.
Let , , and be the errors in , , and , respectively. Expanding using the Taylor series around , we have
where for . Thus,
Considering the first step of DFϵ, we have
Now, considering the second step of DFϵ, we have
Since (as shown in [66]), then , and
Hence, the theorem is proved. □
The theoretical order of convergence of the derivative-free parallel scheme DSϵ to approximate all solutions of the vectorial problems simultaneously is demonstrated in Theorem 3.
Theorem 3.
Consider a sufficiently differentiable function defined on a convex neighborhood of denoted by , satisfying , for . If , then there exists close enough to , such that the iterative sequence DSϵ converges to the exact solution of (26) with order-eight convergence.
Proof.
Let
and be the errors in the estimates , and, respectively. Consider where and the coordinate of is . Using Taylor series expansion around , we have
where for all and . The residual term contains the higher-order terms of the Taylor series, where the sum of exponents of for satisfies . We have
Then
for and . Therefore, is replaced by and by . Now, expanding , and around , we have
Therefore,
where Considering the first step of DSϵ, we have
Now, considering the second step of DSϵ, we have
As [67], we have , and
Hence the theorem is proved. □
3. Computational Analysis of Simultaneous Methods
The computational efficiency of iterative methods for finding all roots of nonlinear equations is a topic of significant importance in numerical analysis. Iterative methods, both sequential and parallel numerical schemes, often demonstrate favorable computational efficiency due to their ability to iteratively refine estimates for each root. The iterative process of root-finding methods allows them to adapt effectively to complex and nonlinear functions. However, their efficiency can be influenced by factors such as the choice of initial guesses, the characteristics of the function being solved, and potential convergence issues. In cases of rapid convergence, iterative methods offer a computationally efficient approach to simultaneously find all roots. Conversely, slow convergence, particularly with high-degree polynomials or ill-conditioned problems, can negatively impact computational efficiency. Evaluating the computational efficiency of iterative methods involves assessing their convergence rates, sensitivity to initial conditions, and suitability for various types of nonlinear equations, contributing to a nuanced understanding of their performance across different scenarios. For further details on computational efficiency, refer to [68].
Figure 1a–d presents the percentage computational efficiency ratios of MMϵ, with respect to PMϵ, BDϵand, respectively. Meanwhile, Figure 2a–e illustrate the computational efficiency of MMϵ, BDϵ, EMϵ, BMϵ, and DFϵ relative to the PMϵ technique. The computational efficiency curves clearly demonstrate that the newly developed method is more efficient and consistent than the PMϵ method.
where and and represent the number of arithmetic operations of addition and subtraction, and multiplications and division, respectively [69]. Using the data provided in Table 1, we have
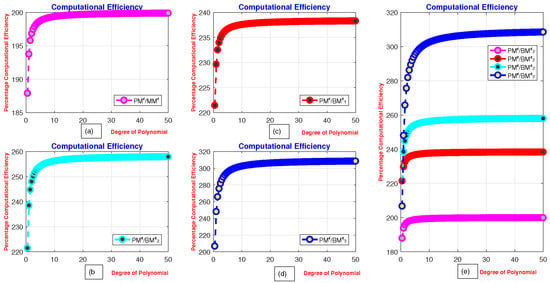
Figure 1.
(a–e) Computational efficiency of MMϵ compared to PMϵ and DBϵ − DFϵ. In Figure 1, (a) shows the computational efficiency of MMϵ with respect to PMϵ, (b) with respect to DBϵ, (c) with respect to DFϵ, (d) with respect to EMϵ, and (e) with respect to BMϵ4.
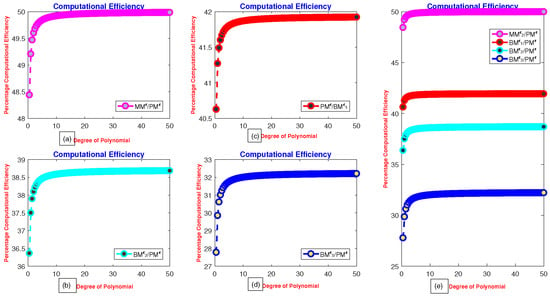
Figure 2.
(a–e) Computational efficiency of MMϵ1 BMϵ1 − BMϵ4 with respect to PMϵ1.

Table 1.
Computational cost and basic operations for simultaneous schemes.
4. Numerical Outcomes
To evaluate the performance and efficiency of the newly designed vectorial scheme, we solved nonlinear vectorial problems arising in science and engineering. We terminated the computer program using the following criteria:
where represents the absolute error using the Euclidean norm-2, i.e., [70,71]. In the numerical calculations, we utilized vectors v1–v3 from Appendix A Table A1, Table A2 and Table A3 for (29) and abbreviated as , , and , respectively. The numerical outcomes considered the following points to analyze the simultaneous schemes PMϵ, MMϵ, BDϵ, BMϵ, DFϵ, and DSϵ:
- Computational CPU time (CPU-time);
- Residual error computed for all roots using Algorithms 1–3;
- Efficiency of the simultaneous schemes PMϵ, MMϵ, BDϵ, BMϵ, DFϵ, and DSϵ;
- Consistency and stability analysis;
| Algorithm 1: Method for finding all distinct and multiple roots of (1). |
| Algorithm 2: Derivative-free method for finding all roots of (1). |
| Algorithm 3: For finding all solution of (26). |
Example 1: Quarter car suspension model
The shock absorber in the suspension system regulates the transient behavior of both the vehicle and suspension mass [72,73]. The nonlinear behavior of the suspension system makes it one of its most complex components. Nonetheless, the damping force of the dampers is characterized by an asymmetric nonlinear hysteresis loop. Automobile engineers utilize a quarter car suspension model, which is a simplified representation, to examine the vertical dynamics of a vehicle’s single wheel and its interaction with the road. This model is a component of the broader field of vehicle dynamics and suspension design. The quarter car model divides the vehicle into two primary parts: the sprung mass and the unsprung mass.
Automobile Structure Sprung Weight: The vehicle body mass includes the chassis, occupants, and other components directly supported by the suspension. The majority of the sprung mass is typically concentrated around the vehicle’s center of gravity.
The Unsprung Weight and Suspension of the Wheels: The unsprung mass includes the wheel, tire, and any suspension components directly linked to the wheel. These components are not supported by the suspension springs.
The suspension system, comprising a spring and a damper, regulates the interaction between sprung and unsprung masses. The spring represents the suspension’s elasticity, while the damper simulates the shock absorber’s damping effect. Using the quarter car suspension model, engineers can analyze how a vehicle responds to potholes and other road irregularities. This model allows for the calculation of dynamic quantities such as suspension deflection, wheel displacement, and vehicle body forces. Understanding these fundamental dynamics and characteristics of suspension systems aids in designing and optimizing suspension systems for improved ride comfort, handling, and stability. Despite the availability of more advanced models, such as half-car or full-car models, the quarter car model remains a critical tool in vehicle dynamics studies. The equations for mass motion are as follows:
where represents the mass above the spring, denotes the mass below the spring, signifies the displacement of the sprung mass, indicates the displacement of the unsprung mass, represents disturbances from road bumps, corresponds to the spring stiffness, and pertains to the tire stiffness. To accurately model the damper force F, one can use the polynomial presented by Barethiye [74] in Equation (64):
The exact roots of Equation (65) are
Initial guesses: The numerical outcomes for the initial guesses, which are sufficiently close to the exact values, are presented in Table 2.

Table 2.
Residual error with initial values near exact root.
The results of Table 2 clearly show that BFϵ and BDϵ are superior to PMϵ, MMϵ, BM, and EM in terms of computational order of convergence, CPU-time, residual error, and error iteration (Error it) for solving (85).
The initial vectors provided in Table A1 [75] are used to verify the global convergence of PMϵ, MMϵ, BM, EM, DFϵ, and BDϵ.
The numerical outcomes of the simultaneous vectorial method for solving (85) in terms of residual error, CPU time, local computational order of convergence, and iterations are shown in Table 3, Table 4 and Table 5 and Figure 3. Table 3, Table 4 and Table 5 clearly illustrate that DFϵ outperforms MMϵ, BM, EM, PMϵ, and BDϵ in terms of global convergence, as it converges faster and utilizes less CPU time and fewer iterations than the other methods.

Table 3.
Residual error using a random set of initial-guess vectors.

Table 4.
CPU time using a random set of starting vectors v1–v3 taken from Appendix A Table A1.

Table 5.
Iterations using random initial guess vectors v1–v3 from Appendix A Table A1.
The numerical results from iterative methods using random initial vectors, as presented in Table 3, Table 4, Table 5 and Table 6, demonstrate that the newly developed schemes BDϵ and DFϵ outperform existing methods such as PMϵ, MMϵ, BM, and EM, achieving a significantly higher accuracy with maximum errors of 0.11 × 10−57, 0.98 × 10−54, and 7.98 × 10−54 for the three sets of initial vectors v1–v3 (see Table 3 and Figure 3). These techniques also exhibit superior performance compared to DM, DM1, and DM3 in terms of average CPU time (Avg-CPU) and average number of iterations (Avg-Iterations). Table 6 provides an overall assessment of the simultaneous schemes, confirming that DFϵ shows greater stability and consistency compared to MMϵ, BDϵ, BMϵ, PMϵ, and DSϵ, respectively.

Table 6.
Consistency of the numerical scheme for solving (85).
Example 2: Solving a non-differentiable system [76]
Consider the non-differentiable system:
The exact solutions to are , and the trivial solution is . We chose the following initial guesses: and . The numerical results are presented in Table 7.

Table 7.
Simultaneous determination of of (86) using parallel schemes.
The results of Table 7 clearly demonstrate that outperforms − , MMϵ, EMϵ, and BM in terms of computational order of convergence, CPU-time, and residual error for solving (86).
To check the global convergence behavior, we utilized the following starting set of vectors presented in Appendix A Table A2.
In terms of residual error, CPU time, local computational order of convergence, and iterations, the numerical results of the simultaneous vectorial method for solving (86) are presented in Table 8, Table 9 and Table 10 and Figure 4. These tables clearly illustrate that outperforms − , MMϵ, EMϵ, and BMϵ in terms of global convergence, converging faster, and utilizing less CPU time and fewer iterations than other methods.

Table 8.
Residual error using a random set of initial-guess vectors.

Table 9.
CPU time using a random set of starting vectors v1–v3 from Appendix A Table A2.

Table 10.
Iterations using a random set of starting vectors v1–v3 from Appendix A Table A2.
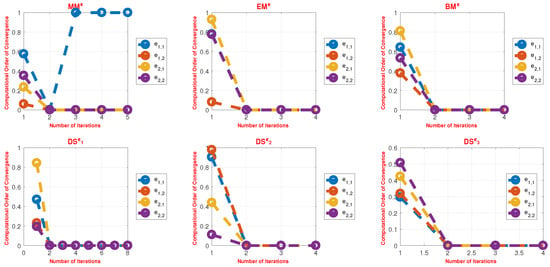
Figure 4.
Computational local order of convergence of simultaneous schemes MMϵ, EMϵ, BMϵ, DSϵ1 − DSϵ3, using a random initial vector array (Appendix A Table A2) to solve (86).
The numerical results of the iterative method using random initial vectors presented in Table 8, Table 9 and Table 10 show that the newly developed scheme − is more efficient than existing methods MMϵ, EMϵ, BMϵ because it achieves a much higher accuracy, with errors of 4.8756 × 10−18, 7.651 × 10−29, and 7.654 × 10−29 for the three sets of initial vectors v1–v3, respectively. Additionally, it consumes less CPU time and requires fewer iterations. Table 11 depicts the overall behavior of the simultaneous schemes and demonstrates that is more stable and consistent than − , MMϵ, EMϵ, and BMϵ.

Table 11.
Consistency of the numerical scheme for solving (86) using vectors v1–v3 taken from Appendix A Table A2.
Example 3: Computing the steady state of the epidemic model [77]
Consider the following system of nonlinear equations:
where , and , although different values of R may be considered. The exact solutions of are and . We choose the initial guesses as and . The numerical results are presented in Table 12.

Table 12.
Simultaneous finding of s of (87) using parallel schemes.
The results of Table 12 clearly show that outperforms − , MMϵ, EMϵ, and BMϵ in terms of computational order of convergence, CPU-time, and residual error for solving (87).
To evaluate the global convergence behavior, we utilize the initial vector set presented in Appendix A Table A3.
In terms of residual error, CPU time, local computational order of convergence, and iterations, the numerical outcomes of the simultaneous vectorial method for solving (87) are shown in Table 13, Table 14 and Table 15 and Figure 5. Table 13, Table 14 and Table 15 clearly illustrate that outperforms − , MMϵ, EMϵ, and BM in terms of global convergence, converging faster and consuming less CPU time, and requiring fewer iterations than other methods.

Table 13.
Residual error using a random set of starting vectors.

Table 14.
CPU time using a random set of starting vectors v1–v3 taken from Appendix A Table A3.

Table 15.
Iterations using a random set of starting vectors v1–v3 from Appendix A Table A3.
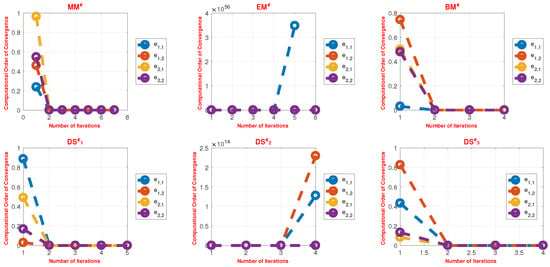
Figure 5.
Computational local order of convergence of simultaneous schemes MMϵ, EMϵ, BMϵ, − , using a random initial vector array (Appendix A Table A3) to solve (87).
With errors of 8.75 × 10−18, 1.124 × 10−24, and 1.121 × 10−24 for the three sets of initial vectors v1–v3, the newly developed scheme − achieved a significantly higher accuracy compared to the existing methods MMϵ, EMϵ, and BMϵ. It also consumed less CPU time and required fewer iterations, as evidenced by the numerical results of the iterative method using random initial vectors presented in Table 3, Table 4, Table 5 and Table 6. Table 16 depicts the overall behavior of the simultaneous schemes and demonstrates that DS is more stable and consistent than − , MMϵ, EMϵ, and BMϵ.

Table 16.
Consistency of the numerical scheme for solving (87) using vectors v1–v3 from Appendix A Table A3.
Example 4: Searching for the equilibrium point of the N-Body system [78]
Consider the nonlinear system of equations describing how to find the equilibrium solution in an N-body system as
The nonlinear system of equations Ņ has more than one solution depending on the parameter values. For instance, if we choose and , Ņ has five solutions. Initial starting values are chosen as and . The numerical outcomes are presented in Table 7.
The results in Table 17 clearly demonstrate that outperforms − , MMϵ, EMϵ, and BMϵ in terms of computational order of convergence, CPU-time, and residual error for solving (88).

Table 17.
Determination of of (88) using parallel schemes.
To assess the global convergence behavior, we utilize the following initial set of vectors presented in Appendix A Table A4.
In terms of residual error, CPU time, local computational order of convergence, and iterations, the numerical outcomes of the simultaneous vectorial method for solving (88) are shown in Table 18, Table 19 and Table 20 and Figure 6. These tables clearly illustrate that outperforms − , MMϵ, EMϵ, and BMϵ in terms of global convergence, again converging faster and requiring less CPU time and iterations than other methods.

Table 18.
Residual errors using a random set of starting vectors.

Table 19.
CPU time using a random set of starting vectors v1–v3 taken from Appendix A Table A4.

Table 20.
Iterations using a random set of starting vectors v1–v3 taken from Appendix A Table A4.
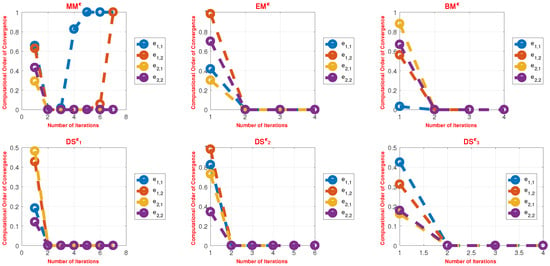
Figure 6.
Computational local order of convergence of simultaneous schemes MMϵ, EMϵ, BMϵ, DSϵ1 − DSϵ3, using a random initial vector array (Appendix A Table A4) to solve (88).
The newly developed schemes − achieved a substantially higher accuracy than the existing methods, with errors of 4.876 × 10−18, 4.875 × 10−18, and 4.34 × 10−18 for the three sets of initial vectors v1–v3. The numerical results of the iterative method using random initial vectors reported in Table 18, Table 19 and Table 20 also indicate that − required less CPU time and fewer iterations Table 21 presents the overall behavior of the simultaneous schemes and demonstrates that is more stable and consistent than − , MMϵ, EMϵ, and BMϵ.

Example 5: Solving the diffusion equation [79]
Consider the heat diffusion equation with various boundary conditions as follows:
To find the solution of (89), we set the diffusivity parameter as and ensure the stability of the implicit finite difference scheme with :
Applying approximations to (89), we derive the tridiagonal system of equations:
For different initial and boundary conditions, we obtain an additional set of partial differential equations:
Using (90) in (92), we derive a nonlinear system of equations similar to (91) after incorporating the initial and boundary conditions. The exact and approximate solutions obtained by BDSϵ1 − DSϵ3, MMϵ, EMϵ, and BM are presented in Figure 7.
Using (90) in (93), we obtain another nonlinear system of equations similar to (91) after incorporating the respective initial and boundary conditions. The exact and approximate solutions obtained by DSϵ1 − DSϵ3, MMϵ, EMϵ, and BM are presented in Figure 8.
Using a random set of initial vectors from Appendix A Table A5, the numerical results from Table 22, Table 23 and Table 24 and Figure 7, Figure 8 and Figure 9 clearly show that the scheme DSϵ3 is more stable and consistent than DSϵ1 − DSϵ2, MMϵ, EMϵ, and BM when solving (89) with different boundary and initial conditions.
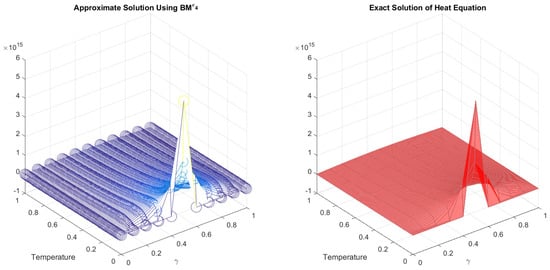
Figure 7.
Approximate and exact solutions to the heat Equation (92).
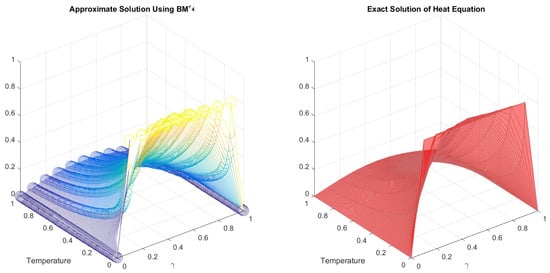
Figure 8.
Approximate and exact solutions to the heat Equation (93).

Table 22.
Numerical results of iterative techniques for solving (92).

Table 23.
Numerical results of iterative techniques for solving (93).

Table 24.
Numerical results of iterative techniques for solving (94).
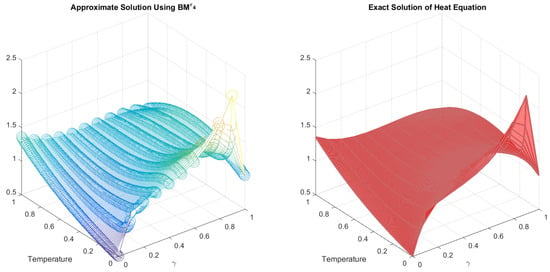
Figure 9.
Approximate and exact solutions to the heat Equation (94).
The scheme DSϵ1 − DSϵ3 outperformed the MMϵ, EMϵ, and BMϵ. It also required less CPU time and fewer iterations, as evidenced by the numerical results of the iterative technique under various initial conditions shown in Table 22, Table 23 and Table 24. These tables depict the overall behavior of the simultaneous schemes and demonstrate that DSϵ3 is more stable and consistent than DSϵ1 − DSϵ2, MMϵ, EMϵ, and BMϵ.
5. Conclusions
In this study, novel parallel numerical schemes are developed for solving nonlinear equations and their systems, including vectorial problems. A convergence analysis reveals that these parallel vertorial schemes achieve a high order of convergence, up to 10. Engineering applications using various random initial approximations were employed to assess the efficiency of MMϵ, PMϵ, BDϵ, BMϵ, DFϵ, and DSϵ. Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14, Table 15, Table 16, Table 17, Table 18, Table 19, Table 20, Table 21, Table 22, Table 23 and Table 24 and Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 present the numerical outcomes from these experiments. The results clearly demonstrate that the newly developed schemes exhibit greater stability and consistency with global convergence compared to previous methods documented in the literature. Table 2, Table 7, Table 12, Table 18 and Table 22 illustrate that utilizing initial approximations close to exact solutions enhances the convergence rate of DSϵ1 − DSϵ3, MMϵ, EMϵ, and BM. Future research will focus on developing similar higher-order simultaneous iterative methods to tackle more intricate engineering challenges involving nonlinear equations and associated systems [80,81].
Author Contributions
Conceptualization, M.S. and B.C.; methodology, M.S.; software, M.S.; validation, M.S.; formal analysis, B.C.; investigation, M.S.; resources, B.C.; writing—original draft preparation, M.S. and B.C.; writing—review and editing, B.C.; visualization, M.S. and B.C.; supervision, B.C.; project administration, B.C.; funding acquisition, B.C. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by Provincia autonoma di Bolzano/Alto Adigeâ euro Ripartizione Innovazione, Ricerca, Universitá e Musei (contract nr. 19/34). Bruno Carpentieri is a member of the Gruppo Nazionale per it Calcolo Scientifico (GNCS) of the Istituto Nazionale di Alta Matematia (INdAM), and this work was partially supported by INdAM-GNCS under Progetti di Ricerca 2022.
Data Availability Statement
Data will be made available on request.
Acknowledgments
The work was supported by the Free University of Bozen-Bolzano (IN200Z SmartPrint). Bruno Carpentieri is a member of the Gruppo Nazionale per il Calcolo Scientifico (GNCS) of the Istituto Nazionale di Alta Matematica (INdAM), and this work was partially supported by INdAM-GNCS under Progetti di Ricerca 2024.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this article.
Abbreviations
In this study’s article, the following abbreviations are used:
| BDϵ, BMϵ, DFϵ | Newly developed Schemes |
| Error it | Iterations |
| CPU time | Computational Time in Seconds |
| e- | |
| Computational local convergence order | |
| Parameters | |
| Computational local convergence order |
Appendix A. Random Set of Initial Vectors Used in Numerical Experiments

Table A1.
Random set of initial vectors used in Example 2 for solving nonlinear systems of equations.
Table A1.
Random set of initial vectors used in Example 2 for solving nonlinear systems of equations.
| v | ||||
| v1 = | ||||
| v2 = | ||||
| v3 = | ||||
| ⋮ | ⋮, | ⋮, | ⋮, | ⋮ |

Table A2.
Random set of initial vectors used in Example 3 for solving nonlinear systems of equations.
Table A2.
Random set of initial vectors used in Example 3 for solving nonlinear systems of equations.
| v | ||||
| v1 = | ||||
| v2 = | ||||
| v3 = | ||||
| ⋮ | ⋮, | ⋮, | ⋮, | ⋮ |

Table A3.
Random set of initial vectors used in Example 4 for solving nonlinear systems of equations.
Table A3.
Random set of initial vectors used in Example 4 for solving nonlinear systems of equations.
| v | ||||
| v1 = | ||||
| v2 = | ||||
| v3 = | ||||
| ⋮ | ⋮, | ⋮, | ⋮, | ⋮ |

Table A4.
Random set of initial vectors used in Example 5 for solving nonlinear systems of equations.
Table A4.
Random set of initial vectors used in Example 5 for solving nonlinear systems of equations.
| v | ||||
| v1 = | ||||
| v2 = | ||||
| v3 = | ||||
| ⋮ | [, | ⋮, | ⋮, |

Table A5.
Random set of initial vectors used in Example 6 for solving nonlinear systems of equations.
Table A5.
Random set of initial vectors used in Example 6 for solving nonlinear systems of equations.
| ⋯ | ||||||
|---|---|---|---|---|---|---|
| v | ⋯ | |||||
| v1 = | ⋯ | |||||
| v2 = | ⋯ | |||||
| v3 = | ⋯ | |||||
| ⋮ | ⋮, | ⋮, | ⋮, | ⋮ | ⋮, | ⋮ |
References
- Bielik, T.; Fonio, E.; Feinerman, O.; Duncan, R.G.; Levy, S.T. Working together: Integrating computational modeling approaches to investigate complex phenomena. J. Sci. Educ. Technol. 2021, 30, 40–57. [Google Scholar] [CrossRef]
- Chen, L.; He, A.; Zhao, J.; Kang, Q.; Li, Z.Y.; Carmeliet, J.; Tao, W.Q. Pore-scale modeling of complex transport phenomena in porous media. Prog. Energy Combust. Sci. 2022, 88, 100968. [Google Scholar] [CrossRef]
- Kumar, A. Control of Nonlinear Differential Algebraic Equation Systems with Applications to Chemical Processes; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar]
- Chichurin, A.; Filipuk, G. The properties of certain linear and nonlinear differential equations of the fourth order arising in beam models. J. Phys. Conf. Ser. 2019, 1425, 012107. [Google Scholar] [CrossRef]
- Zein, D.A. Solution of a set of nonlinear algebraic equations for general-purpose CAD programs. IEEE Circuits Devices Mag. 1985, 1, 7–20. [Google Scholar] [CrossRef]
- Moles, C.G.; Mendes, P.; Banga, J.R. Parameter estimation in biochemical pathways: A comparison of global optimization methods. Genome Res. 2003, 13, 2467–2474. [Google Scholar] [CrossRef] [PubMed]
- Andersson, J.A.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi: A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Ni, P.; Li, J.; Hao, H.; Yan, W.; Du, X.; Zhou, H. Reliability analysis and design optimization of nonlinear structures. Reliab. Eng. Syst. Saf. 2020, 198, 106860. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Khan, J.A.; Chaudhary, N.I.; Shivanian, E. Reliable numerical treatment of nonlinear singular Flierl–Petviashivili equations for unbounded domain using ANN, GAs, and SQP. Appl. Soft. Comp. 2016, 38, 617–636. [Google Scholar] [CrossRef]
- Jeswal, S.K.; Chakraverty, S. Solving transcendental equation using artificial neural network. Appl. Soft. Comp. 2018, 73, 562–571. [Google Scholar] [CrossRef]
- Lai, Y.C. Finding nonlinear system equations and complex network structures from data: A sparse optimization approach. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 1–10. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method: A new nonlinear analytical technique. Appl. Math. Comp. 2003, 135, 73–79. [Google Scholar] [CrossRef]
- Liao, S. On the homotopy analysis method for nonlinear problems. Appl. Math. Comp. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Berger, M.S. Nonlinearity and Functional Analysis: Lectures on Nonlinear Problems in Mathematical Analysis; Academic Press: Cambridge, MA, USA, 1977; Volume 74. [Google Scholar]
- Liu, C.S.; Atluri, S.N. A novel time integration method for solving a large system of non-linear algebraic equations. CMES Comp. Model. Eng. Sci. 2008, 31, 71–83. [Google Scholar]
- Dennis, J.E., Jr.; Schnabel, R.B. Numerical methods for unconstrained optimization and nonlinear equations. SAIM 1996, 1, 1–10. [Google Scholar]
- Eichfelder, G.; Jahn, J. Vector optimization problems and their solution concepts. In Recent Developments in Vector Optimization; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1–27. [Google Scholar]
- Budzko, D.; Cordero, A.; Torregrosa, J.R. A new family of iterative methods widening areas of convergence. Appl. Math. Comput. 2015, 252, 405–417. [Google Scholar] [CrossRef]
- Drummond, L.G.; Iusem, A.N. A projected gradient method for vector optimization problems. Comput. Optimiz. Appl. 2004, 28, 5–29. [Google Scholar] [CrossRef]
- Yun, B.I. A non-iterative method for solving non-linear equations. Appl. Math. Comput. 2008, 198, 691–699. [Google Scholar]
- Kelley, C.T. Solving nonlinear equations with Newton’s method. SIAM 2003, 1, 1–12. [Google Scholar]
- Ortega, J.M.; Rheinbolt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Wang, X.; Fan, X. Two Efficient Derivative-Free Iterative Methods for Solving Nonlinear Systems. Algorithms 2016, 9, 14. [Google Scholar] [CrossRef]
- Amat, S.; Busquier, S.; Gutiérrez, J.M. Third-order iterative methods with applications to Hammerstein equations: A unified approach. J. Comput. Appl. Math. 2011, 235, 2936–2943. [Google Scholar] [CrossRef]
- Ostrowski, A.M. Solution of equations in Euclidean and Banach spaces. SIAM Rev. 1974, 16, 1–25. [Google Scholar]
- Kou, J.; Li, Y.; Wang, X. Some variants of Ostrowski’s method with seventh-order convergence. J. Computat. Appl. Math. 2007, 209, 153–159. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X. Eighth-order methods with high efficiency index for solving nonlinear equations. Appl. Math. Comput. 2010, 215, 3449–3454. [Google Scholar] [CrossRef]
- Liu, T.; Qin, X.; Wang, P. Local convergence of a family of iterative methods with sixth and seventh order convergence under weak conditions. Inter. J. Comput. Meth. 2019, 16, 1850120. [Google Scholar] [CrossRef]
- Noor, M.A.; Waseem, M. Some iterative methods for solving a system of nonlinear equations. Comput. Math. Appl. 2009, 57, 101–106. [Google Scholar] [CrossRef]
- Darvishi, M.T.; Barati, A. Super cubic iterative methods to solve systems of nonlinear equations. Appl. Math. Comput. 2007, 188, 1678–1685. [Google Scholar] [CrossRef]
- Golbabai, A.; Javidi, M. A new family of iterative methods for solving system of nonlinear algebric equations. Appl. Math. Comput. 2007, 190, 1717–1722. [Google Scholar] [CrossRef]
- Ortega, J.M. Matrix Theory: A Second Course; Springer Science & Business: Berlin, Germany, 2013. [Google Scholar]
- Shah, F.A.; Noor, M.A.; Batool, M. Derivative-free iterative methods for solving nonlinear equations. Appl. Math. Inf. Sci. 2014, 8, 2189. [Google Scholar] [CrossRef]
- Thangkhenpau, G.; Panday, S.; Panday, B.; Stoenoiu, C.E.; Jäntschi, L. Generalized high-order iterative methods for solutions of nonlinear systems and their applications. AIMS Math. 2024, 9, 6161–6182. [Google Scholar] [CrossRef]
- Heath, M.T.; Ng, E.; Peyton, B.W. Parallel algorithms for sparse linear systems. SIAM Rev. 1991, 33, 420–460. [Google Scholar] [CrossRef]
- Pelinovsky, D.E.; Stepanyants, Y.A. Convergence of Petviashvili’s iteration method for numerical approximation of stationary solutions of nonlinear wave equations. SIAM J. Numer. Anal. 2004, 42, 1110–1127. [Google Scholar] [CrossRef]
- Varona, J.L. Graphic and numerical comparison between iterative methods. Math. Intell. 2002, 24, 37–47. [Google Scholar] [CrossRef]
- Werner, W. On the simultaneous determination of polynomial roots. In Iterative Solution of Nonlinear Systems of Equations: Proceedings of a Meeting Held at Oberwolfach, Germany; Springer: Berlin/Heidelberg, Germany, 1982; Volume 5, pp. 188–202. [Google Scholar]
- Batiha, B. Innovative Solutions for the Kadomtsev–Petviashvili Equation via the New Iterative Method. Math. Probl. Eng. 2024, 1, 5541845. [Google Scholar] [CrossRef]
- Falcão, M.I.; Miranda, F.; Severino, R.; Soares, M.J. Weierstrass method for quaternionic polynomial root-finding. Math. Methods Appl. Sci. 2018, 41, 423–437. [Google Scholar] [CrossRef]
- Presic, S. Un procédé itératif pour la factorisation des polynômes. CR Acad. Sci. Paris 1966, 262, 862–863. [Google Scholar]
- Terui, A.; Sasaki, T. Durand-Kerner method for the real roots. Jpn. J. Ind. Appl. Math. 2002, 19, 19–38. [Google Scholar] [CrossRef]
- Dochev, K. Modified Newton methodfor the simultaneous computation of all roots of a givenalgebraic equation. Bulg. Phys. Math. J. Bulg. Acad. Sci. 1962, 5, 136–139. [Google Scholar]
- Kerner, I.O. Ein gesamtschrittverfahren zur berechnung der nullstellen von polynomen. Numer. Math. 1966, 8, 290–294. [Google Scholar] [CrossRef]
- Proinov, P.D.; Cholakov, S.I. Semilocal convergence of Chebyshev-like root-finding method for simultaneous approximation of polynomial zeros. Appl. Math. Comput. 2014, 236, 669–682. [Google Scholar] [CrossRef]
- Nedzhibov, G.H. Convergence of the modified inverse Weierstrass method for simultaneous approximation of polynomial zeros. Commun. Numer. Anal. 2016, 16, 74–80. [Google Scholar] [CrossRef]
- Nedzhibov, G.H. Improved local convergence analysis of the Inverse Weierstrass method for simultaneous approximation of polynomial zeros. In Proceedings of the MATTEX 2018 Conference, Targovishte, Bulgaria, 16–17 November 2018; Volume 1, pp. 66–73. [Google Scholar]
- Aberth, O. Iteration methods for finding all zeros of a polynomial simultaneously. Math. Comput. 1973, 27, 339–344. [Google Scholar] [CrossRef]
- Nourein, A.W.M. An improvement on two iteration methods for simultaneous determination of the zeros of a polynomial. Int. J. Comp. Math. 1977, 6, 241–252. [Google Scholar] [CrossRef]
- Petković, M.S. On a general class of multipoint root-finding methods of high computational efficiency. SIAM J. Numer. Anal. 2010, 47, 4402–4414. [Google Scholar] [CrossRef]
- Mir, N.A.; Shams, M.; Rafiq, N.; Akram, S.; Rizwan, M. Derivative free iterative simultaneous method for finding distinct roots of polynomial equation. Alex. Eng. J. 2020, 59, 1629–1636. [Google Scholar] [CrossRef]
- Cholakov, S.I.; Vasileva, M.T. A convergence analysis of a fourth-order method for computing all zeros of a polynomial simultaneously. J.Comput. Appl. Math. 2017, 321, 270–283. [Google Scholar] [CrossRef]
- Cholakov, S.I. Local and semilocal convergence of Wang-Zheng’s method for simultaneous finding polynomial zeros. Symmetry 2019, 11, 736. [Google Scholar] [CrossRef]
- Marcheva, P.I.; Ivanov, S.I. Convergence analysis of a modified Weierstrass method for the simultaneous determination of polynomial zeros. Symmetry 2020, 12, 1408. [Google Scholar] [CrossRef]
- Shams, M.; Carpentieri, B. On highly efficient fractional numerical method for solving nonlinear engineering models. Mathematics 2023, 11, 4914. [Google Scholar] [CrossRef]
- Shams, M.; Carpentieri, B. Efficient inverse fractional neural network-based simultaneous schemes for nonlinear engineering applications. Fractal Fract. 2023, 7, 849. [Google Scholar] [CrossRef]
- Weierstraß, K. Neuer beweis des satzes, dass jede ganze rationale funktion einer veranderlichen dargestellt werden kann als ein product aus linearen funktionen derstelben veranderlichen. Ges. Werke 1903, 3, 251–269. [Google Scholar]
- Neves Machado, R.; Lopes, L.G. Ehrlich-type methods with King’s correction for the simultaneous approximation of polynomial complex zeros. Math. Statist. 2019, 7, 129–134. [Google Scholar] [CrossRef]
- Petković, M.S.; Petković, L.D.; Džunić, J. Accelerating generators of iterative methods for finding multiple roots of nonlinear equations. Comput. Math. Appl. 2010, 59, 2784–2793. [Google Scholar] [CrossRef]
- Petković, M.S.; Petković, L.D.; Džunić, J. On an efficient simultaneous method for finding polynomial zeros. Appl. Math. Lett. 2014, 28, 60–65. [Google Scholar] [CrossRef]
- Shams, M.; Rafiq, N.; Kausar, N.; Agarwal, P.; Park, C.; Mir, N.A. On highly efficient derivative-free family of numerical methods for solving polynomial equation simultaneously. Adv. Differ. Equ. 2021, 2021, 1–10. [Google Scholar] [CrossRef]
- Hristov, V.H.; Kyurkchiev, N.V.; Iliev, A.I. On the Solutions of Polynomial Systems Obtained by Weierstrass Method. Comptes Rendus l’Acad. Bulg. Sci. 2009, 62, 1–9. [Google Scholar]
- Chinesta, F.; Cordero, A.; Garrido, N.; Torregrosa, J.R.; Triguero-Navarro, P. Simultaneous roots for vectorial problems. Comput. Appl. Math. 2023, 42, 227. [Google Scholar] [CrossRef]
- Argyros, I.K. Computational theory of iterative methods, series. Stud. Comput. Math. 2017, 15, 1–19. [Google Scholar]
- Triguero-Navarro, P.; Cordero, A.; Torregrosa, J.R. CMMSE: Jacobian-free vectorial iterative scheme to find several solutions simultaneously. Authorea Preprints 2023. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, Q.; Zhao, P. A variant of Steffensen’s method of fourth-order convergence and its applications. Appl. Math. Comput. 2010, 216, 1978–1983. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, T. A family of steffensen type methods with seventh-order convergence. Numer. Algor. 2013, 62, 429–444. [Google Scholar] [CrossRef]
- Mir, N.A.; Shams, M.; Rafiq, N.; Rizwan, M.; Akram, S. Derivative free iterative simultaneous method for finding distinct roots of non-linear equation. PONTE Int. Sci. Res. J. 2019, 75, 1–9. [Google Scholar] [CrossRef]
- Akram, S.; Shams, M.; Rafiq, N.; Mir, N.A. On the stability of Weierstrass type method with King’s correction for finding all roots of non-linear function with engineering application. Appl. Math. Sci. 2020, 14, 461–473. [Google Scholar] [CrossRef]
- Rafiq, N.; Shams, M.; Mir, N.A.; Gaba, Y.U. A highly efficient computer method for solving polynomial equations appearing in engineering problems. Math. Prob. Eng. 2021, 1, 9826693. [Google Scholar] [CrossRef]
- Shams, M.; Rafiq, N.; Carpentieri, B.; Ahmad Mir, N. A New Approach to Multiroot Vectorial Problems: Highly Efficient Parallel Computing Schemes. Fractal Fract. 2024, 8, 162. [Google Scholar] [CrossRef]
- Chapra, S.C. Numerical Methods for Engineers; Mcgraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Kiusalaas, J. Numerical Methods in Engineering with Python 3; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Acary, V.; Brogliato, B. Numerical Methods for Nonsmooth Dynamical Systems: Applications in Mechanics and Electronics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Shams, M.; Carpentieri, B. Q-Analogues of Parallel Numerical Scheme Based on Neural Networks and Their Engineering Applications. Appl. Sci. 2024, 14, 1540. [Google Scholar] [CrossRef]
- Xavier, A.E.; Xavier, V.L. Flying elephants: A general method for solving non-differentiable problems. J. Heuristics 2016, 22, 649–664. [Google Scholar] [CrossRef]
- Budzko, D.A.; Hueso, J.L.; Martinez, E.; Teruel, C. Dynamical study while searching equilibrium solutions in N-body problem. J. Comput. Appl. Math. 2016, 297, 26–40. [Google Scholar] [CrossRef]
- Grosan, C.; Abraham, A. Multiple solutions for a system of nonlinear equations. Int. J. Innov. Comput. Inf. Control 2008, 4, 2161–2170. [Google Scholar]
- Özışık, M.N. Boundary Value Problems of Heat Conduction; Courier Corporation: Chelmsford, MA, USA, 1989. [Google Scholar]
- Pavkov, T.M.; Kabadzhov, V.G.; Ivanov, I.K.; Ivanov, S.I. Local convergence analysis of a one parameter family of simultaneous methods with applications to real-world problems. Algorithms 2023, 16, 103. [Google Scholar] [CrossRef]
- Corr, R.B.; Jennings, A. A simultaneous iteration algorithm for symmetric eigenvalue problems. Int. J. Numer. Methods Eng. 1976, 10, 647–663. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).