Exploring Wave Interactions and Conserved Quantities of KdV–Caudrey–Dodd–Gibbon Equation Using Lie Theory
Abstract
1. Introduction
2. Preliminaries
The Idea of the Proposed Method
- Type 1: When ,
- Type 2: When , ,
- Type 3: When , ,
- Type 4: When , ,
- Type 5: When , ,
- Type 6: When , ,
- Type 7: When ,
- Type 8: When , ,
- Type 9: When ,
3. Symmetry Analysis of Equation (1)
4. Traveling Waves of Equation (1) by Abelian Algebra
- For Family 1: When ,
- For Family 2: When , ,
- For Family 3: When , ,
- For Family 4: When , ,
- For Family 5: When , ,
- For Family 6: When , ,
- For Family 7: When ,
- For Family 8: When and
- For Family 9: When ,
- For Family 10: When , ,
5. Graphical Representations
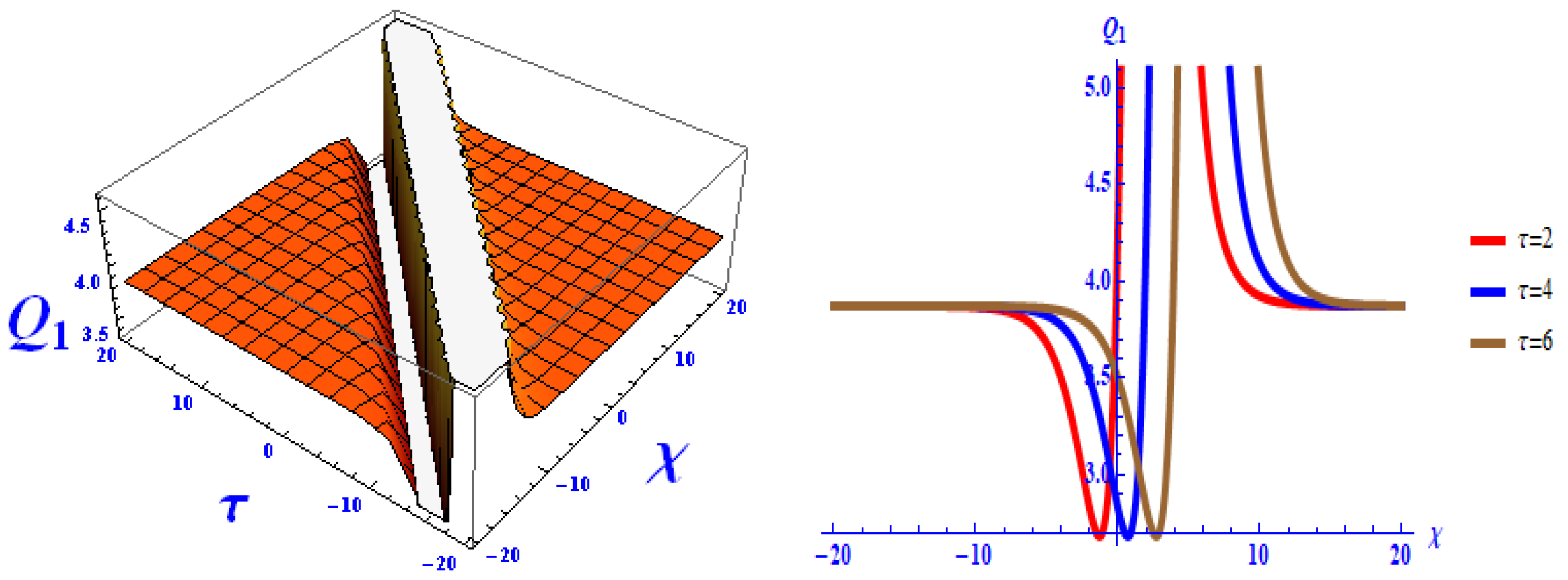
- Figure 1 demonstrates the 3D and 2D versions of for , , , , , and .
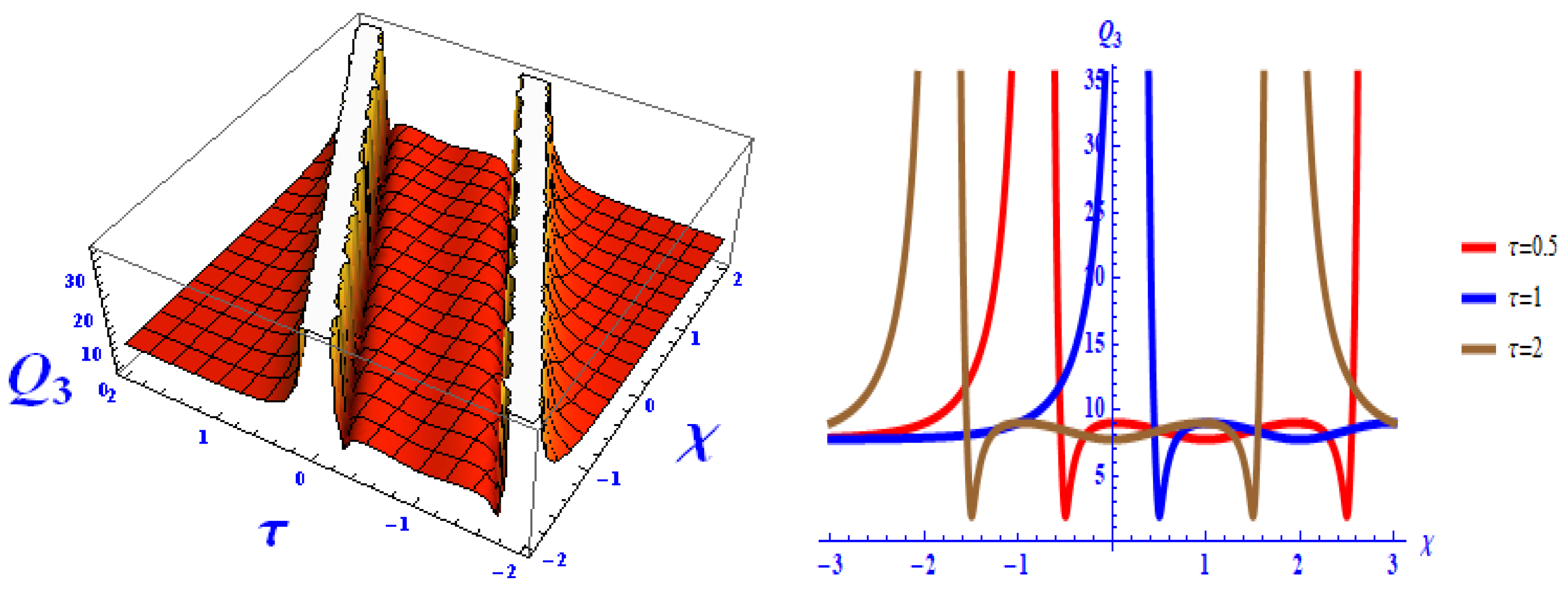
- The plotted curves of can be seen for , , , , , and . Their corresponding values are shown in Figure 2.
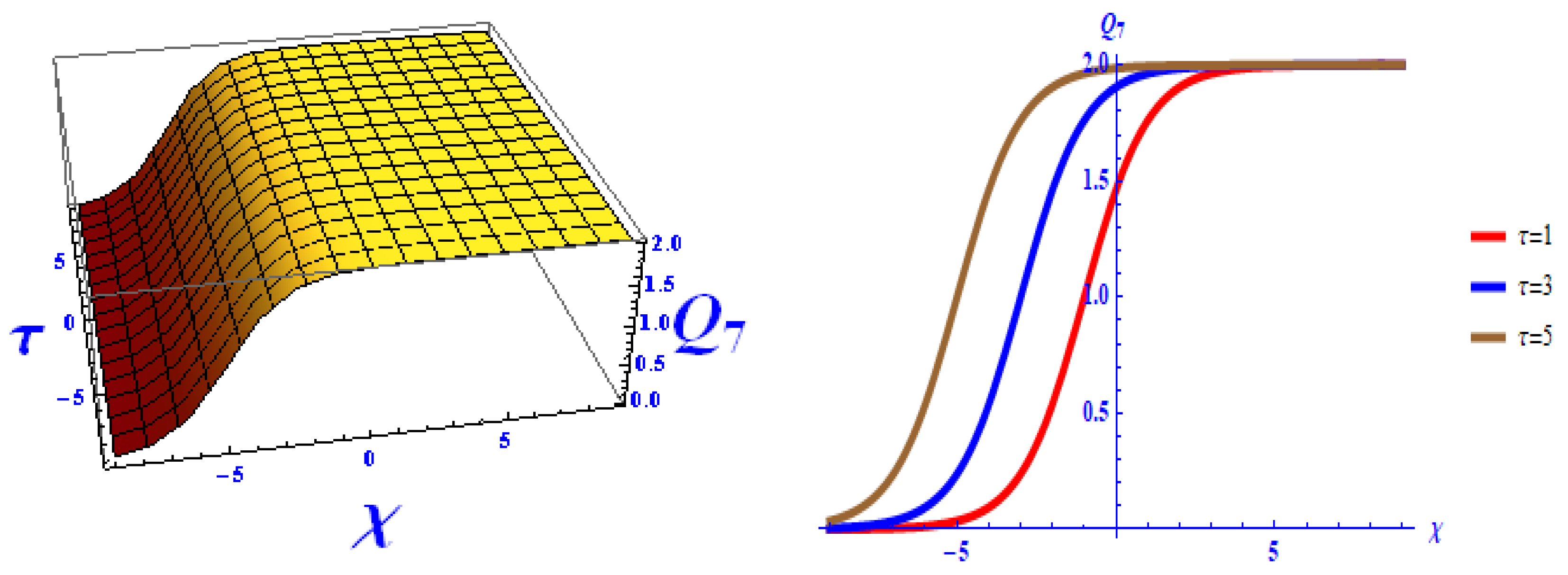
- The graphics of for , , , , and are shown in Figure 3. It shows the effect of the velocity of the soliton.
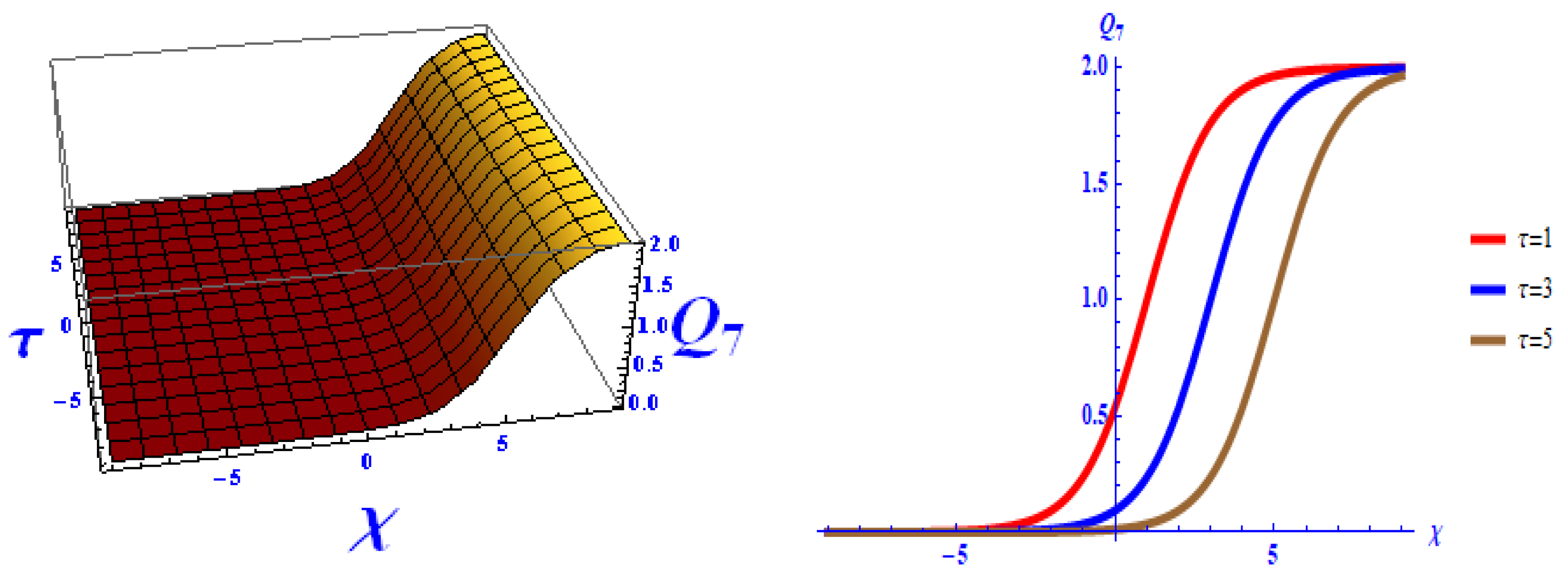
- Furthermore, Figure 4 shows the 3D and 2D graph of for , , , , , and .
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Qi, J.M.; Tang, X.H.; Gu, Y.Y. Further Results about traveling wave exact solutions of the (2+1)-dimensional modified KdV equation. Adv. Math. Phys. 2019, 2019, 3053275. [Google Scholar] [CrossRef]
- Ilie, M.; Biazar, J.; Ayati, Z. The first integral method for solving some conformable fractional differential equations. Opt. Quantum Electron. 2018, 50, 55. [Google Scholar] [CrossRef]
- Akbar, M.A.; Ali, N.H.M.; Islam, M.T. Multiple closed-form solutions to some fractional order nonlinear evolution equations in physics and plasma physics. AIMS Math. 2019, 4, 397–411. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, Y.; Triki, H.; Mirzazadeh, M.; Ekici, M.; Zhou, Q.; Biswas, A.; Belic, M. Interaction properties of solitonic in inhomogeneous optical fibers. Nonlinear Dyn. 2019, 95, 557–563. [Google Scholar] [CrossRef]
- Abdelrahman, M.; Zahran, E.H.M.; Khater, M.M.A. The exp(−ϕ(ξ))-expansion method and its application for solving nonlinear evolution equations. Int. J. Mod. Nonlinear Theory Appl. 2015, 4, 37–47. [Google Scholar] [CrossRef]
- Noor, N.F.M.; Haq, R.U.; Abbasbandy, S.; Hashim, I. Heat flux performance in a porous medium embedded Maxwell fluid flow over a vertically stretched plate due to heat absorption. J. Nonlinear Sci. Appl. 2016, 9, 2986–3001. [Google Scholar] [CrossRef]
- Ilhan, O.A.; Manafian, J.; Shahriari, M. Lump wave solutions and the interaction phenomenon for a variable-coefficient Kadomtsev-Petviashvili equation, Comput. Math. Appl. 2019, 78, 2429–2448. [Google Scholar]
- Manafian, J.; Ilhan, O.A.; Alizadeh, A. Periodic wave solutions and stability analysis for the KP-BBM equation with abundant novel interaction solutions. Phys. Scr. 2020, 95, 065203. [Google Scholar] [CrossRef]
- Akbar, M.A.; Ali, N.H.M. The improved F-expansion method with Riccati equation and its applications in mathematical physics. Cogent Math. 2017, 4, 1282577. [Google Scholar] [CrossRef]
- Zhang, S.; Li, J.; Zhang, L. A direct algorithm of exp-function method for non-linear evolution equations in fluids. Therm. Sci. 2016, 20, 881–884. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H.; Sulaiman, T.A. New complex hyperbolic structures to the Lonngren wave equation by using sine-Gordon expansion method. Appl. Math. Nonlinear Sci. 2019, 4, 129–138. [Google Scholar] [CrossRef]
- El-Sayed, M.F.; Moatimid, G.M.; Moussa, M.H.M.; El-Shiekh, R.M.; Khawlani, M.A. New exact solutions for coupled equal width wave equation and (2+1)-dimensional Nizhnik-Novikov-Veselov system using modified Kudryashov method. Int. J. Adv. Appl. Math. Mech. 2014, 2, 19–25. [Google Scholar]
- Akbar, M.A.; Ali, N.H.M.; Hussain, J. Optical soliton solutions to the (2+1)-dimensional Chaffee-Infante equation and the dimensionless form of the Zakharov equation. Adv. Differ. Equ. 2019, 2019, 446. [Google Scholar] [CrossRef]
- Jafari, M.; Mahdion, S.; Akgül, A.; Eldin, S.M. New conservation laws of the Boussinesq and generalized Kadomtsev—Petviashvili equations via homotopy operator. Results Phys. 2023, 1, 106369. [Google Scholar] [CrossRef]
- Osman, M.S.; Rezazadeh, H.; Eslami, M. Traveling wave solutions for (3+1) dimensional conformable fractional Zakharov-Kuznetsov equation with power law nonlinearity. Nonlinear Eng. 2019, 8, 559–567. [Google Scholar] [CrossRef]
- Osman, M.S. New analytical study of water waves described by coupled fractional variant Boussinesq equation in fluid dynamics. Pramana J. Phys. 2019, 93, 26. [Google Scholar] [CrossRef]
- Hu, W.P.; Deng, Z.C.; Han, S.M.; Fa, W. Multi-symplectic Runge-Kutta methods for Landau Ginzburg-Higgs equation. Appl. Math. Mech. 2009, 30, 1027–1034. [Google Scholar] [CrossRef]
- Osman, M.S. One-soliton shaping and inelastic collision between double solitons in the fifth-order variable-coefficient Sawada-Kotera equation. Nonlinear Dyn. 2019, 96, 1491–1496. [Google Scholar] [CrossRef]
- Javid, A.; Raza, N.; Osman, M.S. Multi-solitons of thermophoretic motion equation depicting the wrinkle propagation in substrate-supported graphene sheets. Commun. Theor. Phys. 2019, 71, 362–366. [Google Scholar] [CrossRef]
- Almusawa, H.; Jhangeer, A. Soliton solutions, Lie symmetry analysis and conservation laws of ionic waves traveling through microtubules in live cells. Results Phys. 2022, 43, 106028. [Google Scholar] [CrossRef]
- Jhangeer, A.; Hussain, A.; Junaid-U-Rehman, M.; Baleanu, D.; Riaz, M.B. Quasi-periodic, chaotic and traveling wave structures of modified Gardner equation. Chaos Solitons Fractals 2021, 143, 110578. [Google Scholar] [CrossRef]
- Hussain, A.; Jhangeer, A.; Abbas, N.; Khan, I. ESM Sherif Optical solitons of fractional complex Ginzburg–Landau equation with conformable, beta, and M-truncated derivatives: A comparative study. Adv. Differ. Equ. 2020, 1, 1–19. [Google Scholar]
- Jhangeer, A. Beenish, Study of magnetic fields using dynamical patterns and sensitivity analysis. Chaos Solitons Fractals 2024, 182, 114827. [Google Scholar] [CrossRef]
- Almusawa, H.; Alam, N.; Fayz-Al-Asad, M.; Osman, M.S. New soliton configurations for two different models related to the nonlinear Schrödinger equation through a graded-index waveguide. Aip. Adv. 2021, 11, 065320. [Google Scholar] [CrossRef]
- Malik, S.; Almusawa, H.; Kumar, S.; Wazwaz, A.M.; Osman, M.S. A (2+1)-dimensional Kadomtsev-Petviashvili equation with competing dispersion effect: Painlevé analysis, dynamical behavior and invariant solutions. Results Phys. 2021, 23, 104043. [Google Scholar] [CrossRef]
- Kumar, S.; Almusawa, H.; Kumar, A. Some more closed-form invariant solutions and dynamical behavior of multiple solitons for the (2+1)-dimensional rdDym equation using the Lie symmetry approach. Results Phys. 2021, 24, 104201. [Google Scholar] [CrossRef]
- Kumar, S.; Almusawa, H.; Hamid, I.; Abdou, M.A. Abundant closed-form solutions and solitonic structures to an integrable fifth-order generalized nonlinear evolution equation in plasma physics. Results Phys. 2021, 26, 104453. [Google Scholar] [CrossRef]
- Raslan, K.R.; Ali, K.K.; Shallal, M.A. The modified extended tanh method with the Riccati equation for solving the space-time fractional EW and MEW equations. Chaos Solitons Fractals 2017, 103, 404–409. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Osman, M.S.; Eslami, M.; Mirzazadeh, M.; Zhou, Q.; Badri, S.A.; Korkmaz, A. Hyperbolic rational solutions to a variety of conformable fractional Boussinesqlike equations. Nonlinear Eng. 2019, 8, 224–230. [Google Scholar] [CrossRef]
- Islam, R.; Khan, K.; Akbar, M.A.; Islam, M.E.; Ahmed, M.T. Traveling wave solutions of some nonlinear evolution equations. Alex. Eng. J. 2015, 54, 263–269. [Google Scholar]
- Ghanbari, B.; Osman, M.S.; Baleanu, D. Generalized exponential rational function method for extended Zakharov Kuznetsov equation with conformable derivative. Mod. Phys. Lett. A 2019, 34, 1950155. [Google Scholar] [CrossRef]
- Ansari, A.R.; Jhangeer, A.; Imran, M.; Beenish; Inc, M. A study of self-adjointness, Lie analysis, wave structures, and conservation laws of the completely generalized shallow water equation. Eur. Phys. J. Plus 2024, 139, 489. [Google Scholar] [CrossRef]
- Riaz, M.B.; Awrejcewicz, J.; Jhangeer, A.; Junaid-U-Rehman, M. A Variety of New Traveling Wave Packets and Conservation Laws to the Nonlinear Low-Pass Electrical Transmission Lines via Lie Analysis. Fractal Fract. 2021, 5, 170. [Google Scholar] [CrossRef]
- Jhangeer, A.; Hussain, A.; Junaid-U-Rehman, M.; Khan, I.; Baleanu, D.; Nisar, K.S. Lie analysis, conservation laws and traveling wave structures of nonlinear Bogoyavlenskii–Kadomtsev–Petviashvili equation. Results Phys. 2020, 19, 103492. [Google Scholar] [CrossRef]
- Kurkcu, H.; Riaz, M.B.; Imran, M.; Jhangeer, A. Lie analysis and nonlinear propagating waves of the (3+1)-dimensional generalized Boiti–Leon–Manna–Pempinelli equation. Alex. Eng. J. 2023, 80, 475. [Google Scholar]
- Akbar, M.A.; Ali, N.H.M.; Tanjim, T. Adequate soliton solutions to the perturbed Boussinesq equation and the KdV-Caudrey-Dodd-Gibbon equation. J. King Saud Univ. Sci. 2020, 32, 2777–2785. [Google Scholar] [CrossRef]
- Asjad, M.I.; Ur Rehman, H.; Ishfaq, Z.; Awrejcewicz, J.; Akgül, A.; Riaz, M.B. On Soliton Solutions of Perturbed Boussinesq and KdV-Caudery-Dodd-Gibbon Equations. Coatings 2021, 11, 1429. [Google Scholar] [CrossRef]
- Tu, J.M.; Tian, S.F.; Xu, M.J.; Zhang, T.T. Quasi-periodic waves and solitary waves to a generalized KdV-Caudrey-Dodd-Gibbon equation from fluid dynamics. Taiwanese J. Math. 2016, 20, 823–848. [Google Scholar] [CrossRef]
- Dehghan, M.; Manafian, J.; Saadatmandi, A. Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer. Methods Partial. Diff. Equ. 2010, 26, 448–479. [Google Scholar] [CrossRef]
- Ma, W.X.; Yo, Y. Solving the Korteweg-de Vries equation by its bilinear form: Wronskian solutions. Trans. Am. Math. Soc. 2005, 57, 1753–1778. [Google Scholar] [CrossRef]
- Rogers, C.; Carillo, S. On reciprocal properties of the Caudrey-Dodd-Gibbon and Kaup-Kupershmidt hierarchies. Phys. Scr. 1987, 36, 865. [Google Scholar] [CrossRef]
- Biswas, A.; Ebadi, G.; Triki, H.; Yildirim, A.; Yousefzadeh, N. Topological soliton and other exact solutions to KdV–Caudrey–Dodd–Gibbon equation. Results Math. 2013, 63, 687–703. [Google Scholar] [CrossRef]
- Akbulut, A.; Kaplan, M. Auxiliary equation method for time-fractional differential equations with conformable derivative. Comput. Math. Appl. 2018, 75, 876–882. [Google Scholar] [CrossRef]
- Bluman, G.W.; Peter, J. Olver, Applications of Lie Groups to Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Bluman, G.W. Applications of Symmetry Methods to Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Kour, B.; Kumar, S. Space time fractional Drinfel’d-Sokolov-Wilson system with time-dependent variable coefficients: Symmetry analysis, power series solutions and conservation laws. Eur. Phys. J. Plus 2019, 134, 467. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Lavrova, S.F.; Nifontov, D.R. Bifurcations of Phase Portraits, Exact Solutions and Conservation Laws of the Generalized Gerdjikov–Ivanov Model. Mathematics 2023, 11, 4760. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almusawa, H.; Jhangeer, A. Exploring Wave Interactions and Conserved Quantities of KdV–Caudrey–Dodd–Gibbon Equation Using Lie Theory. Mathematics 2024, 12, 2242. https://doi.org/10.3390/math12142242
Almusawa H, Jhangeer A. Exploring Wave Interactions and Conserved Quantities of KdV–Caudrey–Dodd–Gibbon Equation Using Lie Theory. Mathematics. 2024; 12(14):2242. https://doi.org/10.3390/math12142242
Chicago/Turabian StyleAlmusawa, Hassan, and Adil Jhangeer. 2024. "Exploring Wave Interactions and Conserved Quantities of KdV–Caudrey–Dodd–Gibbon Equation Using Lie Theory" Mathematics 12, no. 14: 2242. https://doi.org/10.3390/math12142242
APA StyleAlmusawa, H., & Jhangeer, A. (2024). Exploring Wave Interactions and Conserved Quantities of KdV–Caudrey–Dodd–Gibbon Equation Using Lie Theory. Mathematics, 12(14), 2242. https://doi.org/10.3390/math12142242




