Abstract
This work investigates the stability conditions for linear systems with time-varying delays via an augmented Lyapunov–Krasovskii functional (LKF). Two types of augmented LKFs with cross terms in integrals are suggested to improve the stability conditions for interval time-varying linear systems. In this work, the compositions of the LKFs are considered to enhance the feasible region of the stability criterion for linear systems. Mathematical tools such as Wirtinger-based integral inequality (WBII), zero equalities, reciprocally convex approach, and Finsler’s lemma are utilized to solve the problem of stability criteria. Two sufficient conditions are derived to guarantee the asymptotic stability of the systems using linear matrix inequality (LMI). First, asymptotic stability criteria are induced by constructing the new augmented LKFs in Theorem 1. Then, simplified LKFs in Corollary 1 are proposed to show the effectiveness of Theorem 1. Second, asymmetric LKFs are shown to reduce the conservatism and the number of decision variables in Theorem 2. Finally, the advantages of the proposed criteria are verified by comparing maximum delay bounds in four examples. Four numerical examples show that the proposed Theorems 1 and 2 obtain less conservative results than existing outcomes. Particularly, Example 2 shows that the asymmetric LKF methods of Theorem 2 can provide larger delay bounds and fewer decision variables than Theorem 1 in some specific systems.
Keywords:
augmented approaches; linear system; Lyapunov–Krasovskii functional; stability analysis; time delay MSC:
34K20; 34K25
1. Introduction
It is well-known that time delays in system operations create unexpected dynamic situations such as quality degradation, vibration, and instability [1,2]. This is why time delays have received a lot of attention in many fields, such as aircraft, biological systems, chemical processes, networked control systems, neural networks, fuzzy systems, and so on. One of the crucial concerns in studying time-delay systems is the development of stability conditions while increasing the upper bounds of the time delay compared with others. On the other hand, the stability analysis of time-delay systems can be classified into two broad categories: delay-independent and delay-dependent. In the general case, the delay-dependent case is known to be less conservative than the delay-independent one when the size of the time delay is small [3]. Therefore, research on delay-dependent systems has been more actively conducted.
For the past decades, lots of stability criteria have been suggested based on the Lyapunov stability theorem [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. Here, two methods are available for deriving enhanced stability conditions for linear systems with interval time-varying delays. One approach involves determining the Lyapunov–Krasovskii functional (LKF) to derive less conservative stability conditions for the system [8]. Another method utilizes mathematical tools to handle issues such as quadratic terms, non-LMI forms, and so on [9,10]. Indicators evaluating these methods include the maximum delay upper bound and the number of decision variables [11].
It is well recognized that finding new LKFs is also an important and significant job [12]. The conservatism of the stability results is determined by how the LKFs are constructed. A notable trend is to design them as complex integrals, including double and triple integrals and even augmented forms, within LKFs to include more information on system dynamics and delay properties. In [13,14], the integral term was integrated into the form in the design of LKFs, with [14] further enhancing this approach by incorporating delay terms. Moreover, refs. [15,16] expanded LKFs by proposing augmented quadratic forms for single and double integral terms, resulting in more conservative results. Refs. [3,17] improved LKFs by introducing an additional integral term for interval time-varying delays. And some researchers obtained conservative results by proposing various triple integral terms [18].
When extracting stability conditions based on LKFs, the quadratic terms within the integral term derived from the derivative of the double integral are of interest. To solve the quadratic terms within the integral, numerous integral inequalities offering the lower bound of integral terms have been proposed for decades. Many researchers have suggested various methods to reduce the conservatism of the LMI and computational burdens. The Jensen integral inequality was first used by Gu [19] to improve the stability conditions of time-delay systems. The Wirtinger-based integral inequality (WBII) [20] was introduced to obtain a tighter lower bound for the quadratic form in the integral term than that provided by Jensen’s inequality [21]. Park [22] presented the Wirtinger-based double integral inequality for the quadratic double integral form in the stability of time-delay systems. Moreover, generalized versions of the WBII were introduced using an auxiliary function in [23], while recent works in [9,24,25] have presented further generalized integral inequalities. Another mathematical technique is the reciprocally convex approach, which provides the lower bound of integral terms [26]. Since then, some improved versions have been introduced [27,28,29]. Zhang et al. [27] proposed delay-dependent matrix-based reciprocally convex inequality and estimation approaches for stability analysis with time-varying delays of linear systems. In addition to the methods mentioned so far, other techniques have been proposed to improve the stability conditions of systems. By adding a cross term to the time derivative LKF term, ref. [30] suggested several zero equations and ultimately yielded improved results. Generalized zero equality techniques that exploit the relationships among the integral terms have been introduced for linear systems with interval time-varying delays [31]. The work [32] applied the augmented zero equality method derived from Finsler Lemma and zero equalities to obtain improved results and proposed an approach to mitigate computational complexity. Numerous authors [33,34,35] adopted various functions to reduce the conservatism of stability conditions for time-delay systems. And ref. [36] proposed asymmetric LKF in which not all the involved matrix variables are required to be positive definite.
In this paper, the stability criteria for the linear systems with interval time-varying delays are studied. Two types of augmented LKFs with cross terms in integrals are suggested to improve the stability conditions for interval time-varying linear systems. To solve the problem of stability criteria, generalized integral inequality [9], zero equalities, reciprocally convex approach [26], and Finsler’s lemma [37] are utilized. In Theorem 1, stability criteria are derived by constructing augmented LKFs and employing zero equalities and WBII. In Theorem 2, asymmetric LKFs are constructed to reduce the number of decision variables. Finally, four numerical examples show that the proposed Theorems 1 and 2 obtain less conservative results than existing outcomes.
Notations.
, , and () denote n-vectors, matrices, and symmetric (positive) matrix, respectively. denotes an identity matrix. denotes a zero matrix. and denote and the column vector. ∗ is used to represent symmetric terms as needed. ⊙ denotes the quadratic form of the matrix. denotes a basis for the null space of X. is a matrix with respect to , i.e., .
2. Problem Statement
In this paper, we consider the following linear systems with time-varying delays:
where represents the state vector, is the initial condition, are constant matrices. is a time-varying delay satisfying a continuous function with and , where and are known positive scalars and is any constant one.
The purpose of this paper is to derive the stability criteria for linear systems (1) with interval time-varying delays. The following lemmas are used to derive the main results.
Lemma 1
([9]). For scalars , a vector , and a matrix , the following inequality holds:
where , and
Lemma 2
([26]). For a scalar , vectors , matrices , , and , the following inequality holds: , with .
Lemma 3
([37]). Let , , . The following formulas are equivalent:
3. Main Results
This section presents the stability criteria for system (1). At first, a stability criterion is obtained by utilizing an augmented LKF and Lemmas 1–3. Following this, the stability criteria are improved through an asymmetric LKF. To simplify the expression of LMIs, an augmented vector is defined as
where
Here, means and means .
And the block entry matrices , are utilized, e.g., . Also, the following notations are defined:
Theorem 1.
For given scalars and satisfying and , system (1) is asymptotically stable if there exist matrices and satisfying the following LMIs:
Proof of Theorem 1.
Consider the LKF candidate given by
where
where .
The time derivative of Lyapunov–Krasovskii functionals can be represented as
Let us introduce zero equalities for symmetric matrices inspired by the work [30].
And, adding (12) and (13) to (11), the following equality can be obtained:
Moreover, by employing Lemma 1 (N = 1), the upper bounds of integral terms in (14) can be obtained as follows:
By using Lemma 2,
Based on the relationships between the elements of the augmented vector, the following equality is derived:
Also, by Lemma 1 (N = 1), the Lyapunov functional is induced:
Thus, is
Regarding system (1), a stability condition can be expressed as
Considering parts (i) and (iii) of Lemma 3, condition (24) is equivalent to
Remark 1.
In ref. [3], the augmented vector for the single integral term includes only , , and . However, in of Theorem 1, double integral terms are considered such as , and in and , additional single integral terms, such as , are considered. Accordingly, the augmented vector is further considered as , and stability conditions are derived using zero equality (20). In the next section, it is shown that Theorem 1 can provide larger delay bounds than those of [3].
To show the effectiveness of LKFs (7), let us consider LKFs as . The LKFs are simplified by removing double integral terms in the LKFs of Theorem 1. An augmented vector for Corollary 1 is defined as follows:
and the block entry matrices are utilized. Also, the following notations are defined:
Corollary 1.
For given scalars and satisfying and , system (1) is asymptotically stable if there exist matrices and satisfying the following LMIs:
Proof of Corollary 1.
Consider the LKF candidate given by
where
In the above results, LKFs are typically expected to be symmetric. However, the LKF in Theorem 2 is asymmetric. Then, the following theorem is introduced as the result with the asymmetric functionals. The augmented vector of Theorem 2 is presented as follows:
And the block entry matrices are utilized. Also, the following notations are defined:
Theorem 2.
For given scalars and satisfying and , system (1) is asymptotically stable if there exist matrices with and , and satisfying the following LMIs:
Proof of Theorem 2.
Consider the LKF candidate given by
where
Since the sum of LKFs must be positive in an asymmetric LKF method, it must be guaranteed that is positive if of and W of are positive.
By using Lemma 1 (N = 0), can be bounded as
By adding the lower bound of to , the following can be obtained.
Then, the lower bound of (38) can be bounded as follows by using Lemma 1 (N = 0), since , :
As a result, it is proven that is positive and (32) is obtained.
The time derivative of is induced as follows:
Since the subsequent process is similar to Theorem 1, the proof of Theorem 2 is complete. □
Remark 2.
Asymmetric LKFs are proposed in [36], and asymmetric LKFs are also used in Theorems 2, but in [36], it is applied to part , whereas in Theorem 2, it is applied to part because there is to . In Section 4, Theorem 2 can provide larger delay bounds than [3,14,38] by comparing maximum delay bounds. Furthermore, Theorem 2 shows slightly larger delay bounds than Theorem 1 in Example 2, while the number of decision variables in Theorem 2 is used less than that of Theorem 1.
Remark 3.
If the information of the time derivative is unavailable ( is unknown), one can set or in Theorems 1 and 2 and Corollary 1 to obtain a delay-dependent stability criterion.
4. Examples
In this section, the effectiveness and superiority of the proposed stability criteria are demonstrated through four examples.
Example 1.
Consider system (1) based on [3,14,38]:
Table 1 and Table 2 list the maximum delay bounds for various s as determined by Theorems 1 and 2 and Corollary 1, as well as those of [3,14,38], when is 0.1 and 0.5, respectively. It is listed in Table 1 that Theorems 1 and 2 provide larger delay bounds than those of [3,14,38]. Additionally, Theorem 1 yields slightly larger delay bounds compared to Corollary 1. Table 2 also shows the superiority of Theorems 1 and 2 when . As a result, it can be confirmed that improved results can be obtained from the suggested Theorems 1 and 2. Figure 1 shows that the state responses of system (1) converge to zero as time goes to infinity.

Table 1.
Maximum delay bound for various s with (Example 1).

Table 2.
Maximum delay bound for various s with (Example 1).
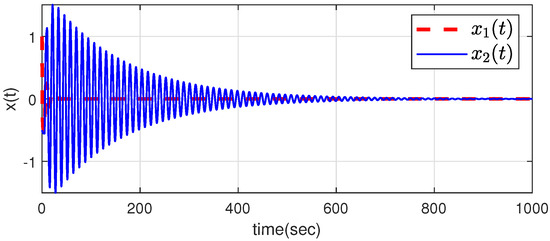
Figure 1.
The state responses of system (1) (Example 1).
Example 2.
Consider the water pollution control problem based on [39]; the dynamical behavior is as follows:
Table 3 lists the maximum delay bounds for various s at , comparing the results of Theorems 1 and 2, Corollary 1, and [3]. And it can also be shown that Theorem 2 provides larger delay bounds than Theorem 1. Table 4 also shows the effectiveness and superiority of Theorem 2 because the number of decision variables(NoDVs) used is smaller than that of Theorem 1. Finally, it can be seen that the state responses of system (1) in Figure 2 converge to zero.

Table 3.
Maximum delay bound for various s with (Example 2).

Table 4.
Number of decision variables.
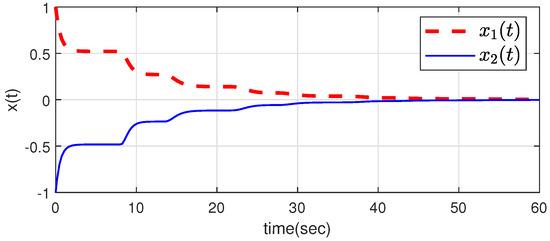
Figure 2.
The state responses of system (1) (Example 2).
Remark 4.
By Example 1, Theorems 1 and 2 show the effectiveness of the proposed criteria compared with [3,14,38] based on maximum delay bound. By Example 2, the asymmetric LKFs method of Theorem 2 can provide larger delay bounds than Theorem 1 and reduce decision variables in some specific systems. This supports the fact that the considered LKFs in Theorem 2 are effective in enhancing the feasible region compared to Theorem 1.
Example 3.
Consider the inverted pendulum problem based on [40]:
In Table 5, the maximum delay bounds for various s and s are shown using Theorems 1 and 2, and these are compared with [3]. To confirm the effectiveness of the proposed results, Figure 3 and Figure 4 show the system’s state trajectories for , , and with the initial condition . Figure 3 shows that the system is unstable when . In contrast, Figure 4 demonstrate that the system is asymptotically stable within the maximum delay bound obtained using Theorems 1 and 2.

Table 5.
Maximum delay bound for various s and s (Example 3).
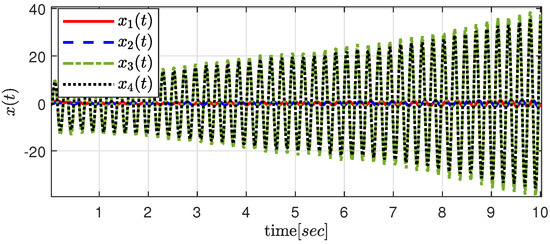
Figure 3.
The state responses of system (1) with (Example 3).
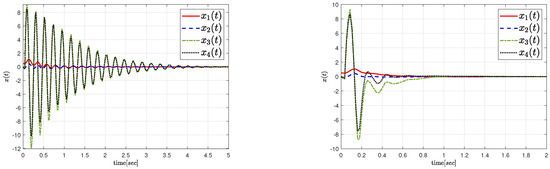
Figure 4.
The state responses of system (1) with (left) and (right) (Example 3).
Example 4.
Consider system (1) based on [41,42,43,44]:
Table 6 lists the maximum delay bounds for various s, as determined by Theorems 1 and 2 and Corollary 1 as well as those of [41,42,43,44] when is unknown. It is listed in Table 6 that Theorems 1 and 2 provide larger delay bounds than those of [41,42,43,44]. To confirm the effectiveness of the proposed results, Figure 5 shows the system’s state trajectories for with the initial condition . Figure 5 shows that the state responses of the system (1) converge to zero as time goes to infinity.

Table 6.
Maximum delay bound for various s with unknown s (Example 4).
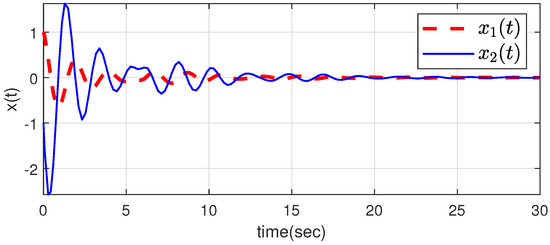
Figure 5.
The state responses of system (1) (Example 4).
5. Conclusions
The stability problem of linear systems with interval time-varying delays is studied in this paper. The compositions of the LKFs are considered to improve the feasible region of stability criteria for linear systems through this work. In Theorem 1, the asymptotic stability criteria of the systems are derived by constructing the augmented LKFs. Then, simplified LKFs in Corollary 1 are proposed to show the effectiveness of Theorem 1. In Theorem 2, asymmetric LKFs are presented to reduce the conservatism and the number of decision variables. Four numerical examples are given to show the effectiveness and superiority of the proposed criteria. Based on this research, the method can be applied to T-S fuzzy systems or neural network systems with interval time-varying delays.
Author Contributions
Conceptualization, O.-M.K.; methodology, O.-M.K. and S.-H.L.; software, D.-H.L., Y.-J.K. and S.-H.L.; validation, D.-H.L., Y.-J.K. and S.-H.L.; formal analysis, D.-H.L. and S.-H.L.; investigation, D.-H.L.; resources, O.-M.K.; data curation, D.-H.L. and Y.-J.K.; writing—original draft preparation, D.-H.L. and Y.-J.K.; writing—review and editing, D.-H.L. and Y.-J.K.; visualization, D.-H.L. and Y.-J.K.; supervision, S.-H.L.; project administration, O.-M.K.; funding acquisition, O.-M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education under Grant NRF-2020R1A6A1A12047945 and in part by Innovative Human Resource Development for Local Intellectualization program through the Institute of Information & Communications Technology Planning & Evaluation (IITP) grant funded by the Korean government (MSIT) (IITP-2024-2020-0-01462, 50%).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LKF | Lyapunov–Krasovskii functional |
| WBII | Wirtinger-based integral inequality |
| LMI | Linear matrix inequality |
| BOD | biochemical oxygen demand |
| DO | dissolved oxygen |
| NoDVs | number of decision variables |
References
- Niculescu, S.I. Delay Effects on Stability: A Robust Control Approach; Springer Science+Business Media: London, UK, 2001; Volume 269. [Google Scholar]
- Richard, J.P. Time-delay systems: An overview of some recent advances and open problems. Automatica 2003, 39, 1667–1694. [Google Scholar] [CrossRef]
- Kwon, O.M.; Park, M.J.; Park, J.H.; Lee, S.M. Enhancement on stability criteria for linear systems with interval time-varying delays. Int. J. Control Autom. Syst. 2016, 14, 12–20. [Google Scholar] [CrossRef]
- Barbashin, E.A. Introduction of the Theory of Stability; Wolters-Noordhoff: Groningen, The Netherlands, 1970. [Google Scholar]
- Gu, K.Q.; Chen, J.; Kharitonov, V.L. Stability of Time-Delay Systems; Springer Science & Business Media: Birkhäuser Boston, MA, USA, 2003. [Google Scholar]
- Merkin, D.R. Introduction of the Theory of Stability; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Medvedeva, I.V.; Zhabko, A.P. Synthesis of Razumikhin and Lyapunov–Krasovskii approaches to stability analysis of time-delay systems. Automatica 2015, 51, 372–377. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Seuret, A.; Gouaisbaut, F.; He, Y. Overview of recent advances in stability of linear systems with time-varying delays. IET Control Theory Appl. 2019, 13, 1–16. [Google Scholar] [CrossRef]
- Park, M.J.; Kwon, O.M.; Ryu, J.H. Generalized integral inequality: Application to time-delay systems. Appl. Math. Lett. 2018, 77, 6–12. [Google Scholar] [CrossRef]
- Zeng, H.B.; Lin, H.C.; He, Y.; Teo, K.L.; Wang, W. Hierarchical stability conditions for time-varying delay systems via an extended reciprocally convex quadratic inequality. J. Frankl. Inst. Eng. Appl. Math. 2020, 357, 9930–9941. [Google Scholar] [CrossRef]
- Xu, S.Y.; Lam, J. A survey of linear matrix inequality techniques in stability analysis of delay systems. Int. J. Syst. Sci. 2008, 39, 1095–1113. [Google Scholar] [CrossRef]
- Zhang, C.K.; He, Y.; Jiang, L.; Wu, M.; Zeng, H.B. Stability analysis of systems with time-varying delay via relaxed integral inequalities. Syst. Control Lett. 2016, 92, 52–61. [Google Scholar] [CrossRef]
- He, Y.; Wang, Q.G.; Lin, C.; Wu, M. Augmented Lyapunov functional and delay-dependent stability criteria for neutral systems. Int. J. Robust Nonlinear Control 2005, 15, 923–933. [Google Scholar] [CrossRef]
- Sun, J.; Liu, G.P.; Chen, J.; Rees, D. Improved delay-range-dependent stability criteria for linear systems with time-varying delays. Automatica 2016, 92, 52–61. [Google Scholar] [CrossRef]
- Kwon, O.M.; Park, M.J.; Park, J.H.; Lee, S.M.; Cha, E.J. Improved results on stability of linear systems with time-varying delays via wirtinger-based integral inequality. J. Frankl. Inst. Eng. Appl. Math. 2014, 351, 5386–5398. [Google Scholar] [CrossRef]
- Qian, W.; Li, T.; Cong, S.; Fei, S.M. Stability analysis for interval time-varying delay systems based on time-varying bound integral method. J. Frankl. Inst. Eng. Appl. Math. 2014, 351, 4892–4903. [Google Scholar] [CrossRef]
- Lee, S.H.; Park, M.J.; Kwon, O.M.; Choi, S.G. Less conservative stability criteria for general neural networks through novel delay-dependent functional. Appl. Math. Comput. 2022, 420, 126886. [Google Scholar] [CrossRef]
- Zhao, X.; Lin, C.; Chen, B.; Wang, Q.G. Stability analysis for linear time-delay systems using new inequality based on the second-order derivative. J. Frankl. Inst. Eng. Appl. Math. 2019, 356, 8770–8784. [Google Scholar] [CrossRef]
- Gu, K.Q. An integral inequality in the stability problem of time-delay systems. In Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, Australia, 12–15 December 2000; pp. 2805–2810. [Google Scholar]
- Seuret, A.; Gouaisbaut, F. Wirtinger-based integral inequality: Application to time-delay systems. Automatica 2013, 49, 2860–2866. [Google Scholar] [CrossRef]
- Gu, K.Q. A further refinement of discretized Lyapunov functional method for the stability of time-delay systems. Int. J. Control 2001, 74, 967–976. [Google Scholar] [CrossRef]
- Park, M.J.; Kwon, O.M.; Park, J.H.; Lee, S.M.; Cha, E.J. Stability of time-delay systems via Wirtinger-based double integral inequality. Automatica 2015, 55, 204–208. [Google Scholar] [CrossRef]
- Park, P.G.; Lee, W.I.; Lee, S.Y. Auxiliary function-based integral inequalities for quadratic functions and their applications to time-delay systems. J. Frankl. Inst. Eng. Appl. Math. 2015, 352, 1378–1396. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Stability of linear systems with time-varying delays using bessel-legendre inequalities. IEEE Trans. Autom. Control 2018, 63, 225–232. [Google Scholar] [CrossRef]
- Zeng, H.B.; Liu, X.G.; Wang, W. A generalized free-matrix-based integral inequality for stability analysis of time-varying delay systems. Appl. Math. Comput. 2019, 354, 1–8. [Google Scholar] [CrossRef]
- Park, P.G.; Ko, J.W.; Jeong, C. Reciprocally convex approach to stability of systems with time-varying delays. Automatica 2011, 47, 235–238. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Seuret, A.; Gouaisbaut, F. An improved reciprocally convex inequality and an augmented Lyapunov-Krasovskii functional for stability of linear systems with time-varying delay. Automatica 2017, 84, 221–226. [Google Scholar] [CrossRef]
- Seuret, A.; Liu, K.; Gouaisbaut, F. Generalized reciprocally convex combination lemmas and its application to time-delay systems. Automatica 2017, 84, 221–226. [Google Scholar] [CrossRef]
- Zhang, R.M.; Zeng, D.Q.; Park, J.H.; Zhong, S.M.; Liu, Y.J.; Zhou, X. New approaches to stability analysis for time-varying delay systems. J. Frankl. Inst. Eng. Appl. Math. 2019, 356, 4174–4189. [Google Scholar] [CrossRef]
- Kim, S.H.; Park, P.; Jeong, C. Robust h stabilisation of networked control systems with packet analyser. IET Control Theory Appl. 2019, 356, 4174–4189. [Google Scholar] [CrossRef]
- Lee, S.Y.; Lee, W.I.; Park, P. Improved stability criteria for linear systems with interval time-varying delays: Generalized zero equalities approach. Appl. Math. Comput. 2017, 292, 336–348. [Google Scholar] [CrossRef]
- Kwon, O.M.; Lee, S.H.; Park, M.J.; Lee, S.M. Augmented zero equality approach to stability for linear systems with time-varying delay. Appl. Math. Comput. 2020, 381, 125329. [Google Scholar] [CrossRef]
- Li, Z.C.; Yan, H.C.; Zhang, H.; Zhan, X.S.; Huang, C.Z. Improved inequality-based functions approach for stability analysis of time delay system. Automatica 2019, 108, 108416. [Google Scholar] [CrossRef]
- Li, Z.C.; Yan, H.C.; Zhang, H.; Peng, Y.; Park, J.H.; He, Y. Stability analysis of linear systems with time-varying delay via intermediate polynomial-based functions. Automatica 2020, 113, 108756. [Google Scholar] [CrossRef]
- Zhang, C.K.; Long, F.; He, Y.; Yao, W.; Jiang, L.; Wu, M. A relaxed quadratic function negative-determination lemma and its application to time-delay systems. Automatica 2020, 113, 108764. [Google Scholar] [CrossRef]
- Sheng, Z.L.; Lin, C.; Chen, B.; Wang, Q.G. Asymmetric Lyapunov-Krasovskii functional method on stability of time-delay systems. Int. J. Robust Nonlinear Control 2021, 31, 2847–2854. [Google Scholar] [CrossRef]
- De Oliveira, M.C.; Skelton, R.E. Stability tests for constrained linear systems. In Perspectives in Robust Control; Springer: London, UK, 2007; pp. 1–10. [Google Scholar]
- Liu, Y.; Hu, L.S.; Shi, P. A novel approach on stabilization for linear systems with time-varying input delay. Appl. Math. Comput. 2012, 218, 5937–5947. [Google Scholar] [CrossRef]
- Lee, C.S.; Leitmann, G. Continuous feedback guaranteeing uniform ultimate boundedness for uncertain linear delay systems—An application to river pollution-control. Comput. Math. Appl. 1988, 16, 929–938. [Google Scholar] [CrossRef]
- Aranda-Escolástico, E.; Guinaldo, M.; Gordillo, F.; Dormido, S. A novel approach to periodic event-triggered control: Design and application to the inverted pendulum. ISA Trans. 2016, 65, 327–338. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Seuret, A.; Xia, Y. Stability analysis of systems with time-varying delays via the second-order bessel-legendre inequality. Automatica 2017, 76, 138–142. [Google Scholar] [CrossRef]
- Ren, Z.; Tian, J.K. Stability Analysis of Systems with Interval Time-Varying Delays via a New Integral Inequality. Complexity 2020, 2020, 2854293. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, J.H.; Park, P.G. A generalized multiple-integral inequality based on free matrices: Application to stability analysis of time-varying delay systems. Appl. Math. Comput. 2022, 430, 127288. [Google Scholar] [CrossRef]
- Zhai, Z.; Yan, H.; Chen, S.; Li, Z.; Wang, M. Hierarchical stability conditions for linear systems with interval time-varying delay. J. Frankl. Inst. 2024, 361, 1403–1415. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).