Target Damage Calculation Method of Nash Equilibrium Solution Based on Particle Swarm between Projectile and Target Confrontation Game
Abstract
1. Introduction
1.1. Research Background and Significance
1.2. Related Work
1.3. The Work and Highlights of This Thesis
- (1)
- Based on the basic model of a zero-sum game, this paper regards the projectile and the target as the participants in the model, regards the fragments formed by the explosion of the projectile as the incomes of the projectile in the strategy under the condition of effectively hitting the target, and regards the damage area by the projectile fragments as the target loss, forming a new game model of projectile and target confrontation, which is a highlight and innovation of this paper.
- (2)
- On the premise of the hit and defense strategy of the projectile and the target encounter, we established the target damage strategy model of the projectile–target encounter game and studied the game Nash equilibrium composed of the income-loss function in the game model. According to the definition of the possibility degree of the interval number in the uncertain multi-attribute decision-making, this paper proposed a method for solving the Nash equilibrium value of the payoff matrix of the two sides of the game by using the interval possibility degree.
- (3)
- According to the payoff matrix of the two sides of the interval possibility game, we proposed a method for solving the Nash equilibrium value of the game target damage based on a particle swarm optimization algorithm. This method is mainly to initialize the particle swarm by using the randomly generated position and velocity in the whole search space. By sorting each current particle and its corresponding individual optimal particle, a new individual optimal particle is obtained, and all the individual optimal particles are sorted to obtain a new global optimal particle so as to judge whether the iterative termination condition is satisfied, and the global optimal particle is output so as to obtain the Nash equilibrium value of the game target damage.
- (4)
- Through the quantitative calculation of typical cases, the feasibility and scientificity of the calculation model and the Nash equilibrium solution of the game are verified.
- (1)
- We establish the target damage model of projectile–target encounter game and give the calculation method of target damage evaluation.
- (2)
- We propose a method for solving the Nash equilibrium value of the payoff matrix of the two sides of the game by using the interval possibility degree.
2. Target Damage Mechanism of the Intersection between Projectile and Target Game
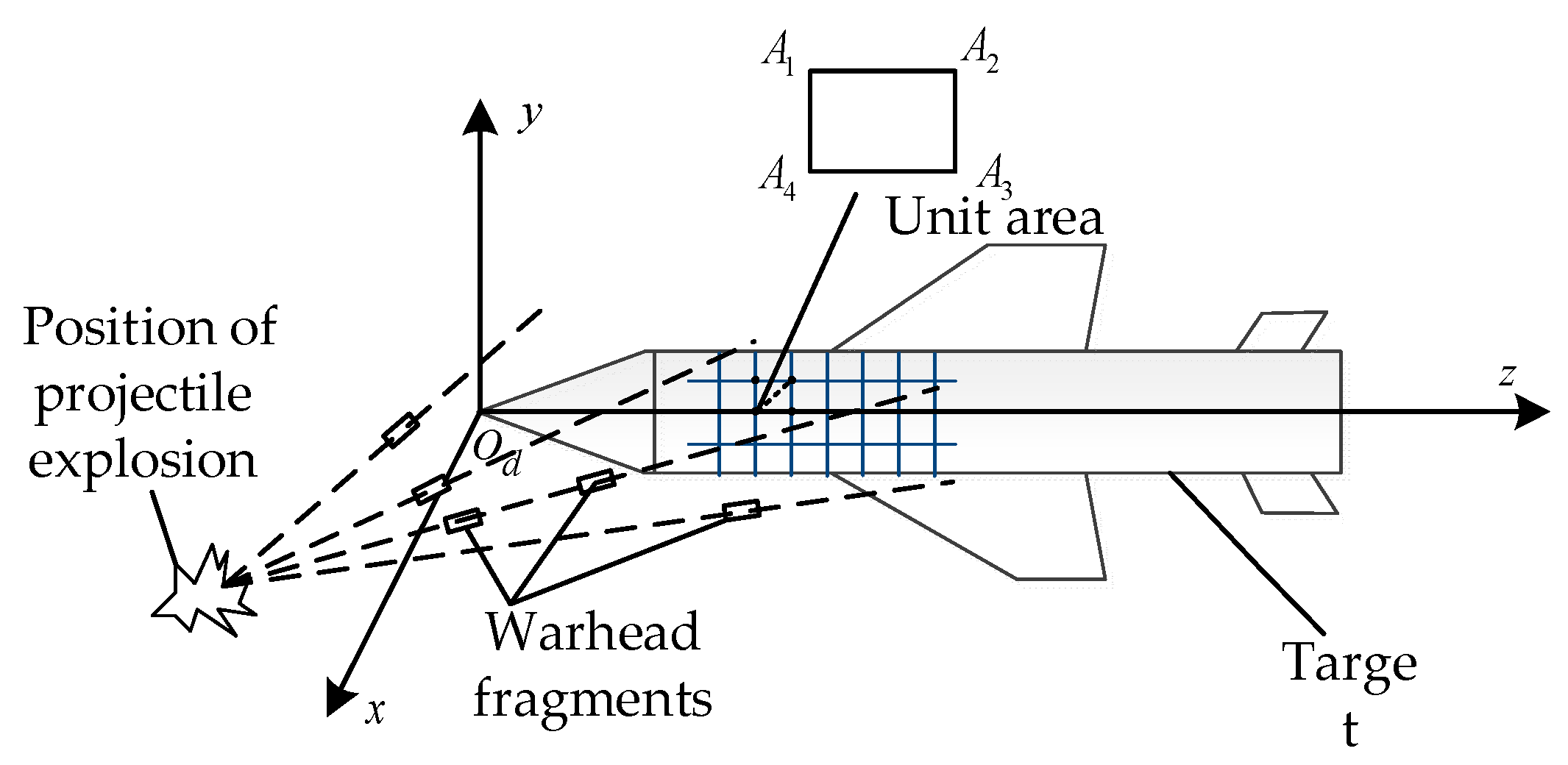
2.1. The Intersection between Projectile and Target Game Model
2.2. Target Damage Probability Calculation Model
3. Establishment of Target Damage Payoff Function in the Game of Projectile and Target with Uncertain Information
4. Nash Equilibrium Solution of Offensive and Defensive Game Based on Uncertain Information
- (1)
- Assuming that the individual optimal particle of the previous generation is , the optimal particle of the current individual is , and the newly generated particle is . If , then , where represents the fitness function.
- (2)
- If , then .
5. Case Calculation and Analysis
5.1. Calculation and Analysis of Game Strategy under Different Fragment Postures
5.2. Damage Probability and Fitness Calculation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, S.; Zhang, H.; Xu, X. Echo Characteristic of Planar Target in Pulsed Laser Fuze Detection. Army J. 2018, 39, 1095–1102. [Google Scholar]
- Wang, H.; Chen, Z.; Feng, X.; Di, X.; Liu, D.; Zhao, J.; Sui, X. Research on network security situation assessment and quantification method based on analytic hierarchy process. Wirel. Pers. Commun. 2018, 102, 1401–1420. [Google Scholar] [CrossRef]
- Chen, R.; Chen, D.; Ji, B.; Ni, J. Inversion method of the key structure parameters of light screen array measurement system using genetic algorithm. Optik 2020, 206, 164064. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X. Three-dimensional coordinates test method with uncertain projectile proximity explosion position based on dynamic seven photoelectric detection screen. Def. Technol. 2022, 18, 1643–1652. [Google Scholar] [CrossRef]
- Chen, R.; Ni, J. Optimization Method of Light-screen-array Structure Parameters of Photoelectric Target Based on Orthogonal Test. J. Ordnance Eng. 2017, 38, 2234–2239. [Google Scholar]
- Ma, W.; Dong, T.; Tian, H.; Ni, J. Line-scan CCD camera calibration in 2D coordinate measurement. Optik 2014, 125, 4795–4798. [Google Scholar] [CrossRef]
- Cui, Q.; Park, J.; Smith, R.T.; Gao, L. Snapshot hyperspectral light field imaging using image mapping spectrometry. Opt. Lett. 2020, 45, 772–775. [Google Scholar] [CrossRef]
- Liu, C.; Qiu, J.; Jiang, M. Light field reconstruction from projection modeling of focal stack. Opt. Express 2017, 25, 11377–11388. [Google Scholar] [CrossRef]
- Huijbregts, M.A.J.; Hellweg, S.; Hertwich, E. Average damage functions are not emission-rated distance to targets. Environ. Sci. Technol. 2012, 46, 569–572. [Google Scholar] [CrossRef]
- Fu, C.; Huang, K.; Tong, L.; Zhao, Y. Assess damage effectiveness for warhead to complex targets. J. Syst. Simul. 2009, 21, 5971–5976. [Google Scholar]
- Zhang, Z.; Zhang, L.; Xie, C.; Zhang, B.; Yang, B. Battle damage effect assessment based on improved GA-BP neural Network. Fire Control. Command. Control. 2021, 46, 42–48. [Google Scholar]
- Yu, B.; Li, X.; Lu, F. Fast analysis method for vulnerability of single fragment damage to missile cabin. Acta Ordnance Equip. Eng. 2020, 41, 82–86. [Google Scholar]
- Li, X.; Liu, Y.; Zhao, H.; Wang, G. Reduced-order vulnerability analysis and evaluation simulation of main battle tank weapon system. Technol. Bull. 2015, 33, 89–93. [Google Scholar]
- Fu, Z.; Fan, W.; Li, R.; Yang, L.; Wang, Y.; Chen, Y. Study on the damage effect of prefabricated fragments on human targets with two postures. Accord. J. Weapon Equip. Eng. 2024, 45, 62–69. [Google Scholar]
- Zhang, C.; Shu, J.; Wu, J.; Su, G. Current Status and Development of Target Damage Effect Evaluation Technology. Aviat. Proj. 2017, 45, 68–72. [Google Scholar]
- Liu, H.; Shi, X. Damage effectiveness calculation of hitting targets with ammunition based on bayesian multinomial distribution. Symmetry 2022, 14, 892. [Google Scholar] [CrossRef]
- Zhai, C.; Chen, X. Probability damage calculation of building targets under the projectile warhead strike. Reliab. Eng. Syst. Saf. 2020, 202, 107030. [Google Scholar] [CrossRef]
- Li, H.; Li, Y. Multi-burst location optical testing method and target damage efficiency assessment arithmetic. IEEE Sens. J. 2015, 15, 240–247. [Google Scholar]
- Chen, J.; Gao, X.; Ding, L. Design and operation strategies of the system for destroying time-sensitive target based on system effectiveness. J. Syst. Eng. Electron. 2008, 19, 1151–1156. [Google Scholar]
- Zhang, Y. Research on Damage Assessment Strategy of Projectile-Target Intersection Target. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2021. [Google Scholar]
- Orphal, D.L.; Anderson, C.E. Target damage from highly oblique hypervelocities impacts of steel spheres thin laminated targets. Int. J. Impact Eng. 2001, 26, 567–578. [Google Scholar] [CrossRef]
- Xu, Z.; Xue, J.; Liu, T.; Zhang, P.; Xie, X. Equivalent damage study of projectile due to energetic fragment warhead. Nanjing Univ. Technol. 2020, 44, 348–353. [Google Scholar]
- Lin, D.; Zhu, Y.; Yang, J. A Weapon-Target Assignment Method for Dynamic Damage Probability and Target Value. Fire Command Control 2024, 49, 138–143. [Google Scholar]
- Lu, D.; Chen, X.; Du, Z.; Pan, L. Simulation Research on Damage Probability of Distributed MEFP Warheads Hitting Air Target. J. Ballist. 2015, 27, 46–52. [Google Scholar]
- Fu, J.; Guo, G.; Feng, S.; Cehn, Z.; Zhao, T.; Hou, X. Damage Assessment Method and Application of Blast-fragmentation Warhead Ground Target. J. Ordnance Eng. 2016, 37, 7–12. [Google Scholar]
- Wang, Z.; Hu, J.; Zhu, X.; Zhang, Y. Damage effect evaluation of multiple missiles irregular surface targets under unascertained conditions. J. Natl. Univ. Def. Technol. 2024, 46, 213–221. [Google Scholar]
- Peng, Y.; Lu, F.; Li, X. Damage effectiveness evaluation method for penetrator. J. Weapon Equip. Eng. 2024, 45, 159–165. [Google Scholar]
- Qu, W. Research on Single Target Damage Effect Evaluation Model. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2023. [Google Scholar]
- Li, H.; Lei, Z. Measurement of spatial burst point position of projectile based on camera method. Opt. Precis. Eng. 2012, 20, 329–336. [Google Scholar]
- Li, H.; Lei, Z. Multi-screen optical method to measure the coordinates of projectile burst point and error analysis. Opt. J. 2012, 32, 136–142. [Google Scholar]









| Tactical Factors | Degree of Income | |||
|---|---|---|---|---|
| Smaller | Moderate | Larger | ||
| Number of fragment hits | 100 | 0.1 | 0.2 | 0.4 |
| 200 | 0.2 | 0.3 | 0.5 | |
| 300 | 0.4 | 0.6 | 0.8 | |
| Tactical Factors | Degree of Income | |||
|---|---|---|---|---|
| Smaller | Moderate | Larger | ||
| Fragment velocities (m/s) | 1000 | 0.1 | 0.2 | 0.3 |
| 1500 | 0.2 | 0.4 | 0.5 | |
| 2000 | 0.3 | 0.5 | 0.7 | |
| Tactical Factors | Degree of Income | |||
|---|---|---|---|---|
| Smaller | Moderate | Larger | ||
| The intersection angle(/°) | 15 | 0.7 | 0.8 | 0.9 |
| 30 | 0.4 | 0.5 | 0.7 | |
| 45 | 0.3 | 0.4 | 0.6 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, Y.; Li, H. Target Damage Calculation Method of Nash Equilibrium Solution Based on Particle Swarm between Projectile and Target Confrontation Game. Mathematics 2024, 12, 2166. https://doi.org/10.3390/math12142166
Hao Y, Li H. Target Damage Calculation Method of Nash Equilibrium Solution Based on Particle Swarm between Projectile and Target Confrontation Game. Mathematics. 2024; 12(14):2166. https://doi.org/10.3390/math12142166
Chicago/Turabian StyleHao, Yun, and Hanshan Li. 2024. "Target Damage Calculation Method of Nash Equilibrium Solution Based on Particle Swarm between Projectile and Target Confrontation Game" Mathematics 12, no. 14: 2166. https://doi.org/10.3390/math12142166
APA StyleHao, Y., & Li, H. (2024). Target Damage Calculation Method of Nash Equilibrium Solution Based on Particle Swarm between Projectile and Target Confrontation Game. Mathematics, 12(14), 2166. https://doi.org/10.3390/math12142166






