Abstract
In order to scientifically evaluate the target damage effect of uncertain intersection between projectile and target confrontation game, this paper establishes a basic model of target damage in the intersection between projectile and target game, which is through the spatial relationship between the explosive position of the projectile and the target position and gives a calculation method of target damage evaluation. The study applies Nash equilibrium theory to analyze income-loss functions in an adversarial game model. According to the definition of the possibility degree of interval number in uncertain multi-attribute decision-making, we proposed a method of solving the Nash equilibrium value of the income matrix of both sides of the game, which is using the interval possibility degree. We used quantitative calculations to analyze game strategies and changes in target damage under different states, such as fragment numbers, velocities, and angles of hit in the confrontation game between projectile and target. Based on the Nash equilibrium value solution method of the particle swarm optimization algorithm, we quantitatively calculated the fitness change relationship between the projectile and the target under different strategy sets. Based on the actual projectile confrontation game test, we analyze the damage probability effects of two projectiles at different explosion positions and different rendezvous angle angles on the three cabins. The results show that in the same area, the intersection angle is smaller, the probability of target damage is greater, and the intersection distance is farther, the damage probability is smaller.
Keywords:
the intersection between projectile and target; game; target damage; Nash equilibrium; fragments MSC:
91A05; 91A10; 91-04
1. Introduction
1.1. Research Background and Significance
The damage effect of the explosion of the projectile proximity fuze on the target is closely related to the relative spatial position of the target intersection. That said, the effectiveness of the projectile proximity effect depends on the relative spatial position between the projectile and the target, and the detonation in the effective spatial range may produce a damaging effect on the target. The mechanism of projectile fuze detonation is that its internal device obtains the energy reflected back by the target and starts the detonation control mechanism [1,2,3]. It constitutes an adversarial damage relationship with the hit target. Therefore, studying the damage effectiveness of the projectile proximity to the target can be mapped to the confrontation game correlation system, which is between the position of the projectile proximity action and the target damage. When the target intersects the flight trajectory of the projectile with different attitudes, it will form a variety of uncertain damage effects. How to effectively improve the effective damage effect of projectile proximity on the target is a current research hotspot to the current miss distance parameters of various types of projectile fuze. It is also one of the effective guarantees for the study of the target damage mechanism of new high-efficiency intelligent ammunition. At the same time, the spatial position of the explosion of the proximity fuze relative to the target is an important basis, which is for analyzing the damage efficiency of the projectile fragment to the target and the improvement of the fuze. For the measurement of the burst point position of the proximity fuze, the commonly used methods are the multi-screen target method, the high-velocity photography method, and the acoustic method [4,5,6]. The multi-screen target intersection measurement method can construct the two-dimensional coordinate parameters of the projectile front approaching the target and can also obtain parameters such as the flight angle before the projectile is detonated. The acoustic method uses the acoustic principle to establish the spatial geometric structure model of the projectile passing through the acoustic array sensor to obtain the parameters, but this method cannot obtain the spatial three-dimensional coordinate parameters of the projectile’s proximity. The above method provides a theoretical model and calculation basis for an in-depth study of the damage effect evaluation of projectile proximity to the target, and it can also effectively improve the combat capability of the projectile fuze.
The evaluation of target damage effectiveness under space confrontation is not an evaluation system determined by a single parameter but a combination of multiple parameters of projectile proximity explosion and multiple vulnerability parameters of the target. The projectile proximity explosion uses the echo energy characteristics, which are provided by the control body of the projectile fuze and the target in the spatial position state, to control the detonation. According to the timely detonation attitude, the relative flight attitude of the target and the vulnerability distribution characteristics of the target, we can obtain the best effective damage efficiency state or the ideal damage efficiency state within a certain range [7,8]. Through the game relationship between the near-blast space of the projectile and the effective damage mechanism of the target, the near-blast and damage correlation parameter model and the damage efficiency strategy under the equilibrium game is established, and the scientific evaluation mechanism under the space confrontation on the battlefield is established for the optimal damage, which has high research significance.
The target damage of the projectile–target encounter proximity fuze is based on the fact that when the projectile approaches the target, the projectile uses the echo information reflected by the target to produce an explosion. Therefore, the damage of the fragment formed by the projectile to the target is based on the fact that the projectile can produce an explosion. Therefore, there is a certain distance between the projectile and the target when the projectile explodes. This distance is generally called the miss distance of the projectile fuze near an explosion. Based on these background requirements of the near-blast target damage of the projectile, it can be found that there are two characteristics of the fragments formed by the projectile explosion in this target damage state. First, the number of fragments is generally relatively small, usually 100 to 300 fragments, and some types of near-blast projectiles. The fragments formed may be more. At the same time, the cone-shaped distribution area of the fragments formed when the projectile explodes is relatively large. Under the premise of the standard near-blast miss distance of the projectile, the dispersion angle formed by the projectile reaches 45°. If the projectile is in the range of 4 m to 6 m, the area covered by it is 50.23–113.04 m2. This area is much larger than the volume of the projectile target itself; the second damaged target is generally relatively small in size. The target belongs to a small projectile. Its length is generally 4.65 m, and its diameter is 380 mm. As a result, only a small number of fragments of the projectile explosion can intersect with the damaged target. Based on these two factors, only a small number of fragments hit the projectile target in the process of projectile–target encounter.
In addition, another important factor in evaluating the damage effect of projectile–target encounters on the target is the dynamic process of projectile–target encounter damage, which belongs to a dynamic confrontation game. This dynamic game needs to be analyzed and evaluated from the damage strategy of both the projectile side and the target side. This game strategy is uncertain, which is embodied in the intersection state of the projectile and the projectile target. Therefore, the dynamic confrontation game is a balanced strategy with certain conditions. Therefore, this paper studies the effect of projectile near explosion on target damage under the exploration of the game confrontation mechanism of projectile–target encounter, establishes the target damage strategy model of projectile–target encounter, and uses particle swarm to solve the Nash equilibrium of damage strategy.
1.2. Related Work
The research on the theory and method of target damage power test and damage assessment has always been a research hotspot and difficult problem at home and abroad, especially in the aspect of damage effectiveness evaluation of space air defense interception targets. It is related to the parameters of air defense proximity elements. In the actual space projectile–target intersection penetration damage, it is very difficult to obtain accurate target damage information. The information can be expressed as uncertain, incomplete, or fuzzy decisions in mathematics. In addition, the uncertainty of the vulnerability of the target itself makes it more difficult to establish a scientific theoretical model and evaluation system, which is for the damage assessment of air defense proximity targets. In particular, the projectile and the target are capable of intelligent control and confrontation. The target damage of the intersection between the projectile and target confrontation game is one of the key contents of the current target damage test. This paper considers the damage caused to the target under different game confrontation strategies and establishes the target damage game model based on game confrontation theory so as to obtain the damage assessment method formed by the equilibrium confrontation between the projectile and the target with game confrontation nature, which is different from other existing literature.
For the calculation of target damage assessment, the U.S. military took the lead in applying Bayesian network theory to the field of target damage assessment and proposed a Bayesian network decision model for target damage assessment [9]. Fu et al. [10] summarized the general methods and key technologies of related research by establishing the research content system framework of quantitative evaluation of damage effectiveness and analyzing the four aspects of target vulnerability analysis and calculation, warhead power analysis and calculation, damage effect test and calculation, and comprehensive evaluation of damage effectiveness. Taking the penetration warhead against building targets as an example, the quantitative evaluation model of missile damage effectiveness is given. Wang et al. [11] established the evaluation model of surface target damage effect under given parameters by Monte Carlo method. In order to evaluate the uncertainty of the problem, this paper used the reliability distribution function. The evaluation results show that the uncertainty of the damage effect is high. The simulation results show that the unascertained range of the effective damage rate of the surface target is significantly reduced. This study can effectively guide the evaluation of the damage effect and reduce the uncertainty. Yu et al. [12] used the plane triangular element method to describe the surface of the component and calculated the target vulnerable area and damage probability. Li et al. [13] proposed a method for evaluating the damage power of blasting ammunition hitting targets in actual combat under the condition of damage conditions, determined the damage efficiency of blasting ammunition targets, established different damage law models, and obtained the damage law model of fragment group to the vulnerable parts of armored vehicles, and completed the evaluation of the damage power of blasting ammunition hitting targets. In order to accurately evaluate the damaging effect of prefabricated fragments on human targets, Fu et al. [14] numerically simulated the scattering process of the fragment field and used Matlab programming to extract fragment-related information to study the damaging effect of prefabricated fragments on two human postures. The results show that on the battlefield, the squatting posture of combatants can reduce the probability of being hit by fragments, reduce the probability of disability of combatants, and reduce the damage area to a certain extent. The other authors [15,16,17] preliminarily gave the damage evaluation method of static explosion target around the modeling of warhead and target, from the initial interaction of ground projectile and target to the damage state of components, and then to the measurement of target engineering performance and target combat performance. At present, there are few studies on target damage in the intersection between projectile and target confrontation, and target damage under the confrontation system is an important manifestation of the current war. Based on the fact that the hit and defense game damage of projectile and target intersection is regarded as a two-person zero-sum non-cooperative game, this paper regards projectile and target as each other’s hitter and defender, establishes the target damage game model according to the game confrontation theory, and forms the theoretical method formed by the target damage mechanism under different game confrontation strategies. Therefore, this paper focuses on solving the Nash equilibrium solution of the game target damage model.
1.3. The Work and Highlights of This Thesis
This paper is mainly aimed at the evaluation of the target damage effect of uncertain projectile–target intersection confrontation game and carries out a target damage evaluation method with game confrontation. The main work of this paper is as follows:
- (1)
- Based on the basic model of a zero-sum game, this paper regards the projectile and the target as the participants in the model, regards the fragments formed by the explosion of the projectile as the incomes of the projectile in the strategy under the condition of effectively hitting the target, and regards the damage area by the projectile fragments as the target loss, forming a new game model of projectile and target confrontation, which is a highlight and innovation of this paper.
- (2)
- On the premise of the hit and defense strategy of the projectile and the target encounter, we established the target damage strategy model of the projectile–target encounter game and studied the game Nash equilibrium composed of the income-loss function in the game model. According to the definition of the possibility degree of the interval number in the uncertain multi-attribute decision-making, this paper proposed a method for solving the Nash equilibrium value of the payoff matrix of the two sides of the game by using the interval possibility degree.
- (3)
- According to the payoff matrix of the two sides of the interval possibility game, we proposed a method for solving the Nash equilibrium value of the game target damage based on a particle swarm optimization algorithm. This method is mainly to initialize the particle swarm by using the randomly generated position and velocity in the whole search space. By sorting each current particle and its corresponding individual optimal particle, a new individual optimal particle is obtained, and all the individual optimal particles are sorted to obtain a new global optimal particle so as to judge whether the iterative termination condition is satisfied, and the global optimal particle is output so as to obtain the Nash equilibrium value of the game target damage.
- (4)
- Through the quantitative calculation of typical cases, the feasibility and scientificity of the calculation model and the Nash equilibrium solution of the game are verified.
The highlights of this paper are as follows:
- (1)
- We establish the target damage model of projectile–target encounter game and give the calculation method of target damage evaluation.
- (2)
- We propose a method for solving the Nash equilibrium value of the payoff matrix of the two sides of the game by using the interval possibility degree.
The remainder of this paper is organized as follows. Section 2 states the target damage mechanism of the intersection between the projectile and the target game. Section 3 states the establishment of target damage payoff function in the game of projectile and target with uncertain information. Section 4 states the Nash equilibrium solution of offensive and defensive games based on uncertain information. Section 5 gives the calculation and analysis. Finally, Section 6 concludes the paper.
2. Target Damage Mechanism of the Intersection between Projectile and Target Game
2.1. The Intersection between Projectile and Target Game Model
Taking the projectile (projectile with certain hit and defense detection and guidance ability) and the target (projectile target with certain defense recognition ability) as the participants 1 and 2 participating in the game, the two-person zero-sum non-cooperative game model can be represented by , where and are the participants of the projectile and the target (often referring to the projectile target or aircraft, etc.) of the game, respectively. Define as the hitter and as the defender; is the strategy set with the projectile hitting the target, is the strategy set with the target effective defense projectile, and are the income function sets of projectile hit and target defense. Each participant has its own policy sets that are composed of limited strategies. Suppose that the strategy combination is , the expected game incomes of participants 1 and 2 are and , respectively, and the sum of the incomes is zero because participants 1 and 2 have a finite set of strategies, and the income of the two participants to any strategy combination is zero, then the random matrix game is also called the two-person finite zero-sum game [18,19].
The offensive/defensive game damage problem of the intersection between projectile and target can be regarded as the offensive/defensive game of participant 1 and participant 2. Participant 1 is the projectile (hitter) and participant 2 is the target (defender).
As the hitter, the projectile intersects with the target to form an explosive power fragment field, causing losses to the target. When the projectile hits the target, the fragment formed by the explosion can achieve the optimal damage to the target, which is regarded as the projectile to obtain the optimal income. When the target detects the incoming projectile, it uses its own defense system to interfere with the projectile so that the projectile does not explode, or the projectile explodes before reaching the effective damage area, that is, the detection guidance ability and detection distance of the projectile cannot meet the predetermined detonation set value. This phenomenon is called projectile loss. Under this condition, the target can preserve itself, which is called target income. In the process of confrontation between the two sides, both sides are looking for the best strategy to find the Nash equilibrium point of the game matrix.
2.2. Target Damage Probability Calculation Model
In order to solve the damage probability of the target in the state of the projectile target encounter game, it is necessary to grasp the density of the fragments formed by the projectile explosion to the projectile target coverage and establish the missile coordinate to determine the relative coordinates of the fragment intersection. The surface of the projectile target can be regarded as the sum of multiple unit square planes , such as Figure 1, and whether the fragment is effectively hit into the unit square plane area is used as a prerequisite for damage, and then the damage probability is calculated according to the ratio of the fragment coverage density and the fragment penetration target area in the area. In order to scientifically calculate the damage probability of the projectile target, we divide the projectile target into cabins; that is, . Each cabin can be equivalent to calculate the damage probability of the effective fragment hitting the cabin in the plane and coordinate planes and cabins are independent of each other.
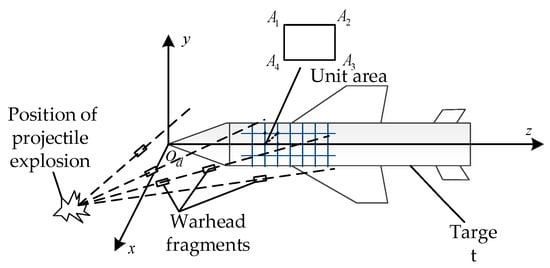
Figure 1.
Schematic diagram of fragment hitting target in the state of the intersection between projectile and target.
In section , let the coordinates of any fragment in the coordinate system be , be the hit fragment serial number of the section , , and be the total number of fragments hit section . The distribution density functions of fragments in plane and directions are established, which are as follows [20]:
In Equation (1), , , and are the mean square error of the dispersion of the projectile’s explosive fragments in the hit target [21].
For m fragments, the probability of a single fragment hitting any point of the -th segment is equal to [22]:
In (2), and are the width and length range of the equivalent square plane of the -th section of the target in the plane , , and are the width and length range of the equivalent square plane of the -th section of the target in the plane , here, .
The damage probability of section -th can be expressed by Formula (3).
In Formula (3), is the number of fragments required for damage to section , and is the mathematical expectation of hitting the damage ratio of the -th section, which is determined by the number of fragments in the planes and , denoted by and , respectively, so , and and are calculated from (4).
According to the damage criterion of each cabin, the damage probability of the whole projectile target is [23]
Based on Formulas (1)–(5), it is shown that the result of the projectile–target game against the target damage is related to the relative position of the projectile and the target and also related to the distribution of the fragment hitting the target. Therefore, we can reflect the damage effect of the target by the hit probability of the fragment hitting the target.
3. Establishment of Target Damage Payoff Function in the Game of Projectile and Target with Uncertain Information
The payoff function of the damage of the fragment -th to the -th target is [23]
In Formula (6), and are the weight of the target value income index and the weight of the intersection distance cost index, respectively, .
Considering that k projectiles simultaneously hit the j-th target, the payoff function is
Due to the uncertainty of information, each element in the calculated payment matrix is an interval number, each row vector of the matrix corresponds to a pure strategy of the projectile, and each column corresponds to a pure strategy of the target. The income matrix of the two sides of the game is , which has
In Formula (8), and refer to the strategies of the projectile hit and the target defense, respectively, and are the income of the projectile hit when the target defense adopts the strategies and the projectile hitter adopts the strategy . These incomes are all interval numbers, which are expressed as .
4. Nash Equilibrium Solution of Offensive and Defensive Game Based on Uncertain Information
In order to solve the solution of the game Nash equilibrium of the intersection between projectile and target confrontation, the definitions are as follows [24].
Definition 1.
Assuming that is the set of participants in the game, and for each participant , the pure strategy set of participant is . If participant chooses each pure strategy with probability , then is called a mixed strategy of the participant. Among them, .
Definition 2.
Assuming that is a hybrid strategy situation of non-cooperative game . If for each and every , there is , then is called a hybrid strategy Nash equilibrium point of , and is the corresponding equilibrium result.
According to the definition, the research ideas for solving the Nash equilibrium value of the income matrix of the two sides of the confrontation game are as follows.
Firstly, according to the definition of the possibility degree of interval number in uncertain multiple attribute decision-making, the Nash equilibrium value of the payment matrix of both sides of the game is solved using the interval possibility degree. Assuming that , , then can be expressed by Formula (9) [25].
Accordingly, the possibility degree of is expressed by Formula (10) [26].
Let be the payoff value of the projectile hit when the targeted defender takes the strategy , while the target adopts strategies . Finally, the probability matrix of Formula (11) can be obtained by comparing the interval number two by two:
In Formula (11), is the possibility degree of under ,, which means that there is no need to give any information for the interval number , . The matrix is a complementary judgment matrix. The value of is used to describe the degree to which the interval payment is superior to the interval payment . When , is superior to . When , is superior to .
Secondly, the Nash equilibrium value is solved based on the particle swarm optimization algorithm. Assuming that the hybrid strategy of Participant 1 in the game is , and the Nash equilibrium value can be obtained as [27].
The single matrix Nash equilibrium can be transformed into a linear programming problem. In an uncertain information environment, the income value of each scheme is an interval number. Let ; then, Formula (12) can be transformed into a mathematical programming problem, that is .
The solution of Nash linear programming is the optimal solution of Nash linear programming. In this paper, the particle swarm optimization algorithm is used to solve the single matrix game problem with interval value. Suppose that in an -dimensional search space and a population of particles, the position of the -th particle is represented by an -dimensional vector, that is, , and the position of each particle represents a candidate solution to the problem. The value of the fitness function determines the quality of these solutions. The fitness function value is larger, and the solution associated with it is better. At the same time, the fitness function is related to the objective function that is generally set according to specific problems. The flight velocity of the particle is also an -dimensional vector, that is, . The best position intersected during the flight of the -th particle is a point in space , which can be expressed as . represents the best position of the population obtained by the particle swarm in the previous flight and represents the position of the best particle in the population. After iterative optimization and random search, the final solution of the optimization problem is obtained. The iterative update calculation of particle velocity and position is expressed by Formula (14) [28].
In Formula (14), is the inertia weight coefficient, and is set to define the searching range of the solution; , , is the current number of iterations; and are learning factors; and are two independent random functions between (0, 1). The position variation range of the -dimension is , and the velocity variation range is . If exceeds the boundary value in the iteration, it is set to the boundary value or .
The optimal particle of each individual is the best position that the corresponding individual has reached. Its update method is as follows:
- (1)
- Assuming that the individual optimal particle of the previous generation is , the optimal particle of the current individual is , and the newly generated particle is . If , then , where represents the fitness function.
- (2)
- If , then .
The global optimal particle is the best position reached by all the current particles. The possibility matrix is obtained by comparing the interval fitness of the individual optimal particle of the current population. Then, the interval fitness is ranked according to the complementary possibility matrix ranking method, and the first is regarded as the global optimal particle. The specific processing algorithm steps are as follows:
Step 1: In the entire search space, the randomly generated position and velocity are used to initialize the particle swarm. Regarding the current particle as the individual optimal, the corresponding fitness of each particle is obtained, and then the global optimal is obtained according to the interval number ranking method.
Step 2: Update the particles to obtain a new generation of particles and find the corresponding fitness of each particle.
Step 3: Sorting each current particle and its corresponding individual optimal particle to obtain a new individual optimal particle and sorting all individual optimal particles to obtain a new global optimal particle. Finally, it is judged whether the iteration termination condition is satisfied. If not, the particle is re-updated, and the fitness of each example is searched for an income. The maximum number of iterations is searched to achieve the maximum number of iterations. After the cycle is completed, the global optimal particle is output. The flow chart of the global optimal particle algorithm is shown in Figure 2.
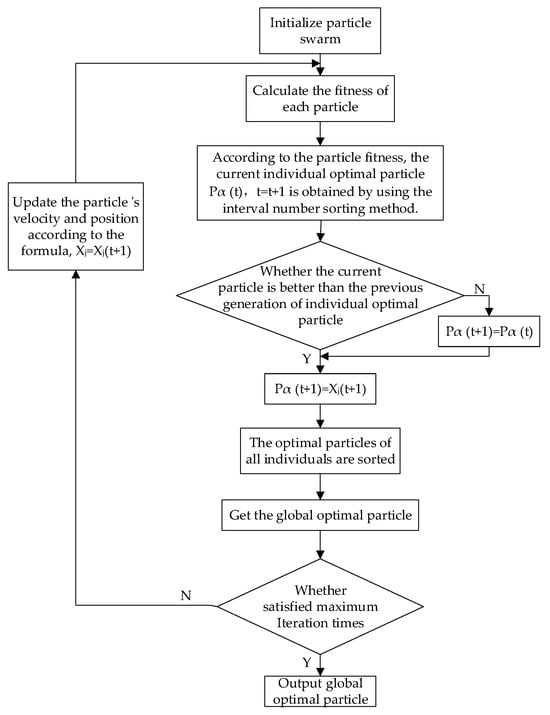
Figure 2.
Flow chart of global optimal particle algorithm.
According to the theory of Section 2, Section 3 and Section 4 of this paper, this paper proposes a calculation method for the target damage effect of the uncertain intersection between projectile and target confrontation game. The flow chart of the target damage algorithm of the intersection between the projectile and target confrontation game is shown in Figure 3.
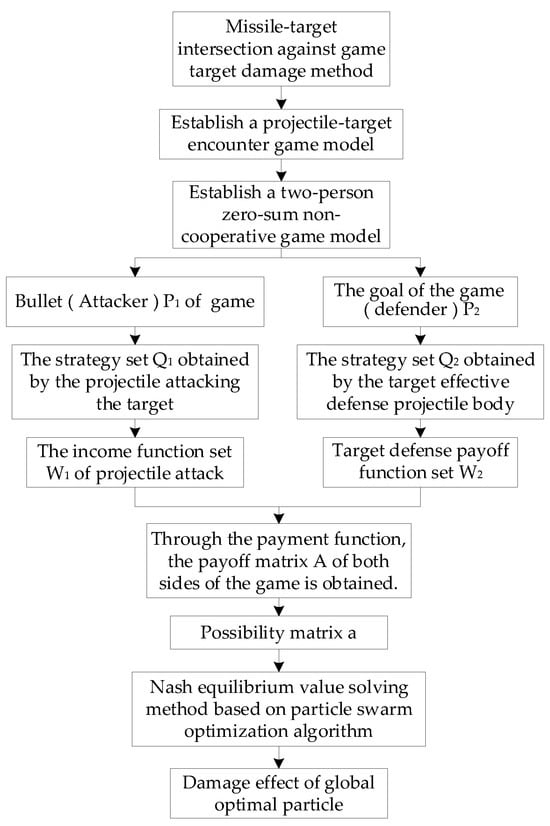
Figure 3.
Flow chart of target damage algorithm for the intersection between projectile and target confrontation game.
Referring to the flow chart of the target damage algorithm of the intersection between the projectile and target confrontation game in Figure 3, the damage calculation steps of this paper are as follows:
Step 1: Establishing an intersection between projectile and target game model;
Step 2: We establish a two-person zero-sum non-cooperative game model to obtain and, respectively, game the projectile and the target (often referring to the projectile target or aircraft, etc.) player, defined as the hitter, as the defender; the strategy set obtained for the projectile to hit the target, the strategy set obtained for the target to effectively defend the projectile, and the income function set for the projectile hit and target defense.
Step 3: The payoff matrix A of both sides of the game is obtained through the income function, then the possibility matrix A is obtained, and the damage evaluation effect of globally optimal particles is obtained by using the Nash equilibrium value solving method based on particle swarm optimization algorithm.
5. Case Calculation and Analysis
5.1. Calculation and Analysis of Game Strategy under Different Fragment Postures
According to the established target damage model of the projectile–target intersection confrontation game with uncertain income, the relationship between the corresponding game strategy and the target damage effect under different factors such as the number of fragments, the velocity of fragments, and the angle of hit of fragments is quantitatively calculated under the missile–target confrontation game. At the same time, the Nash equilibrium value solution method based on the particle swarm optimization algorithm can quantitatively calculate the fitness change relationship between the missile and the target under different strategy sets.
When the number of fragments in the hit state is 100, 200, and 300, the income of the game on both sides is divided into three levels: smaller, moderate, and larger. The income information between the projectile and the target is shown in Table 1.

Table 1.
Income of the game between projectile and target based on the number of fragments hit.
Based on the number of fragments hit the state of the projectile–target game income, player 1 is the target, the corresponding strategy set is ; player 2 is the projectile, the corresponding strategy set is , in which the strategy represents the smaller income when the number of fragments hit is 100; the strategy represents the moderate income when the number of fragments hit is 100; the strategy represents the larger income when the number of fragments hit is 100; the strategy represents the smaller income when the number of fragments hit is 200; the strategy represents the moderate income when the number of fragments hit is 200; and the strategy represents the larger income when the number of fragments hit is 200. The strategy represents a smaller income when the number of hits is 300, the strategy represents a moderate income when the number of hits is 300, and the strategy represents a larger income when the number of hits is 300. Under the same circumstances, the projectile’s response strategy income is . The game income matrix is
The mixed strategy distribution of the number of fragments hitting the state game is shown in Figure 4.
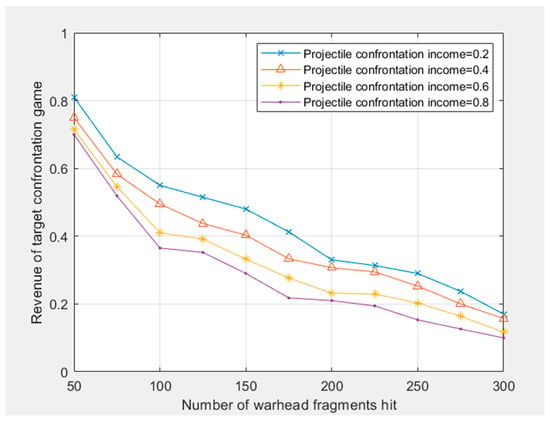
Figure 4.
Mixed strategy distribution based on the number of fragments hit state game.
According to Figure 4, the strategy set of the target is (0, 0.28, 0, 0, 0, 0, 0, 0, 0), and the strategy set of the projectile is (0, 0, 0, 0, 0.57, 0, 0, 0, 0). is the optimal strategy situation at this moment; that is, the income of the second strategy selected by the target party is 0.28, and the probability of other strategies is 0, indicating that the income of the target is the largest when the number of fragments hit is 100. At the same time, the income of the fifth strategy selected by the projectile side is 0.57, and the probability of other strategies is 0, indicating that the income of the projectile is the largest when the number of fragments hit is 200.
When the flight velocity of the fragment is 1000 m/s, 1500 m/s, or 2000 m/s, the target damage game model based on the mixed strategy of the fragment flight velocity is established. The degree of income of the game on the two sides at different fragment velocities is shown in Table 2.

Table 2.
Income of the game between projectile and target based on fragment flight velocities.
Based on the projectile–target game income of the fragment flight velocities, player 1 is the target, and the corresponding strategy set is , and player 2 is the projectile, and the corresponding strategy set is , where the strategy represents the smaller income when the fragment velocities are 1000 m/s, the strategy represents the moderate income when the fragment velocities are 1000 m/s, the strategy represents the larger income when the fragment velocities are 1000 m/s, the strategy represents the smaller income when the fragment velocity distance is 1500 m/s, and the strategy represents the moderate income when the fragment velocity is 1500 m/s. The strategy represents the larger income when the fragment velocity is 15,000 m/s, the strategy represents the smaller income when the fragment velocity is 2000 m/s, the strategy represents the moderate income when the fragment velocity is 2000 m/s, and the strategy represents the larger income when the fragment velocity is 2000 m/s. Under the same circumstances, the projectile’s coping strategy income is . Therefore, the corresponding game payoff matrix is
The mixed strategy distribution of the game between projectile and target income based on fragment flight velocities is shown in Figure 5.
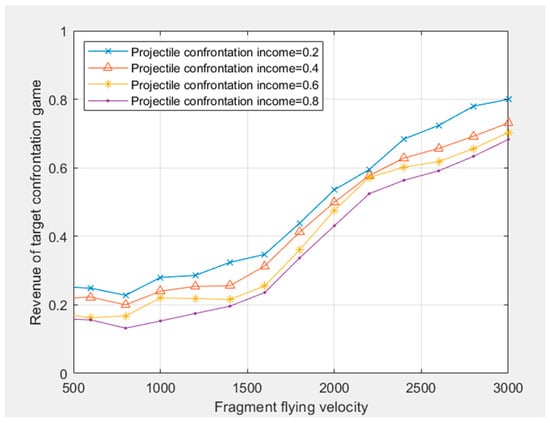
Figure 5.
Mixed strategy distribution based on fragment flight velocities game.
According to Figure 5, the strategy set of the target is (0, 0, 0.32, 0, 0, 0, 0, 0, 0); the strategy set of the projectile side is (0, 0, 0, 0.39, 0, 0, 0, 0, 0). is the optimal strategy at this moment; that is, the income of the target choosing the third strategy is 0.32, and the probability of other strategies is 0, indicating that the income of the target choosing the fragment intersection velocities of 1500 m/s is the largest. At the same time, the probability of the projectile choosing the fourth strategy is 0.39, and the probability of other strategies is 0, indicating that the projectile chooses the fragment intersecting velocities of 2000 m/s when its income is the largest.
For the curve change of Figure 5, the graph is formed under the condition of a certain income strategy set of both the projectile and the target. From the theoretical model of the game mixed strategy of the target damage of the projectile–target encounter, it can be found that different projectile–target encounter velocities have different effects on the damage effect. Although the damage income of the target confrontation game is closely related to the velocities of the fragment, it is not a linear relationship, especially since the fragment has a certain quality. Because the fragment has the factor of gravity acceleration, at the same distance between the projectile and the target, the velocities are low, and the probability of hitting the target will also become low. Because the number of fragments and the quality of the fragments of the same projectile are different, some fragments may not form a rendezvous with the target under the condition of low velocities, resulting in the target damage effect is not obvious. As the velocities of the fragment increase, the probability of hitting the target also increases for the same fragment. Therefore, from the distribution of the fragment velocities of 1000–2800 m/s, the target damage effect is gradually increasing.
When the intersection angle of the target is 15°, 30°, and 45° in the hit state, a mixed strategy of the intersection angle of the target is established. The intersection angle and income information of the two sides of the game are shown in Table 3.

Table 3.
Game income based on the intersection between projectile and target angle.
Based on the game income of the intersection angle of missile and target, player 1 is the target, and the corresponding strategy set is , and player 2 is the projectile, and the corresponding strategy set is , where strategy represents the smaller income when the intersection angle of missile and target is 30°, strategy represents the moderate income when the intersection angle of missile and target is 30°, strategy represents the larger income when the intersection angle of missile and target is 30°, strategy represents the smaller income when the intersection angle of missile and target is 45°, strategy represents the moderate income when the intersection angle of missile and target is 45°, strategy represents the larger income when the intersection angle of missile and target is 45°, strategy represents the smaller income when the intersection angle of the missile and target is 60°, strategy represents the moderate income when the intersection angle of missile and target is 60°, and strategy represents the larger income when the intersection angle of the missile and target is 60°. Therefore, the game payoff matrix is
The Nash equilibrium hybrid strategy distribution based on the intersection between projectile and target angle is shown in Figure 6.
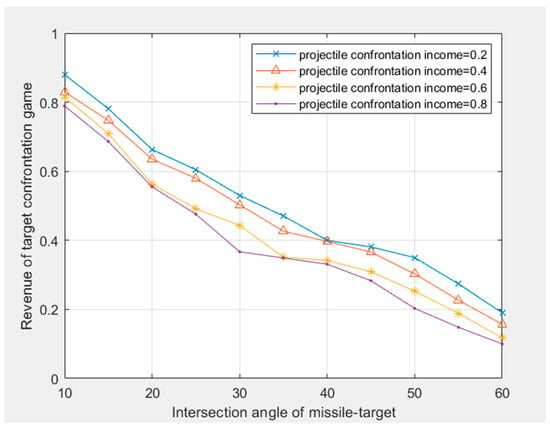
Figure 6.
Mixed strategy distribution based on the intersection between projectile and target angle game.
According to Figure 6, the strategy set of the target is (0, 0.44, 0, 0, 0, 0, 0, 0, 0); the strategy set of the projectile is (0, 0, 0, 0.31, 0, 0, 0, 0, 0). is the optimal strategy situation at this moment; that is, the income of the target party choosing the second strategy is 0.44, and the probability of other strategies is 0, indicating that the income of the target choosing the intersection angle of 15° is the largest. At the same time, the probability of the projectile choosing the fourth strategy is 0.31, and the probability of other strategies is 0, indicating that the projectile chooses the intersection angle of the projectile and the target to be 30°.
5.2. Damage Probability and Fitness Calculation
According to the intersection attitude of the projectile and the projectile target and the fragment dispersion of the projectile, in a test, in order to intuitively analyze the specific distribution position of the fragment in the projectile coordinate space, according to the spatial relationship between the projectile and the target, two groups of projectiles and projectiles were counted. There are 20 projectiles in each group. In the experiment, the projectile used is a radio fuze with a certain cooperative control ability. According to the mechanism of Figure 1, the spatial position relationship between the projectile and the target is sought. When the spatial position relationship is determined, the target is divided into three cabins, , , and , under the predetermined fragment parameters. The target damage probability is calculated according to Formulas (1)–(5). In order to achieve this probability result, it must be based on the game confrontation strategy set and solved using the Nash equilibrium method. The target is a flying fish projectile with guidance and control. Its length is about 4.71 m, and its diameter is about 385 mm. According to the statistical probability method, the average position coordinates of the two projectile explosion centers are and [29,30], respectively, and the unit used is meters. The average angle of the intersection attitude angle between the projectile and the target is 8.1° and 10.5°, respectively, and the number of uniform equal volume fragments formed by the projectile explosion is 200. The projectile target is divided into three cabins, mainly including the electronic guidance cabin , the fuel explosive cabin , and the other cabin . The size ratio of each cabin is 3:6:2. In the calculation, the damage weight factors are 0.3, 0.6, and 0.1, respectively. The damage to the electronic guidance cabin is mainly due to the fact that the fragment hits the projectile’s own electronic guidance and loses its combat capability, but it is not directly destroyed. The fuel explosion section is mainly related to the fragment hitting the projectile fuel component directly, which causes the projectile to ignite and explode to form damage. In this section, the number of fragments required is small. As long as the fragment reaches the energy that penetrates the projectile, the damage caused by the projectile to the target is the largest. In other cabins, the fragments hitting this part only cause a slight change in the flight state of the projectile, and the damage to the projectile is not fatal.
When the condition of the intersection between the fragment and the projectile is satisfied, the damage probability of the fragment to the three cabins is calculated. According to the test results of the two groups, the mean square error of the distribution position of the warhead fragments in each group is calculated, which are and , , and ; , and . On the basis of the statistical mean square error of the fragment distribution position, the damage probability of each group of fragments at and to three cabins is calculated, respectively, as shown in Figure 7 and Figure 8.
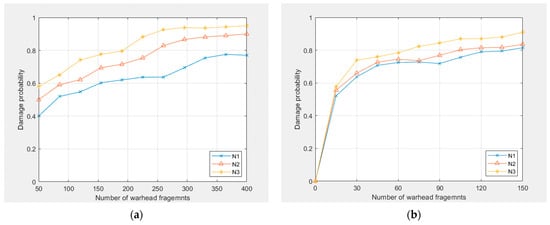
Figure 7.
The damage results of the first group of fragments to the three cabins: (a) the damage probability of three cabins when; (b) the damage probability of three cabins when .
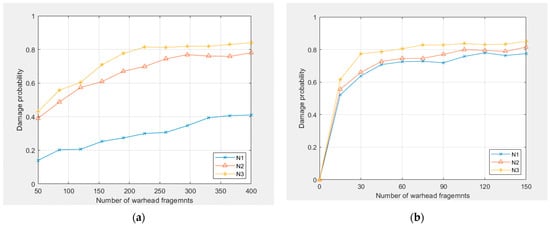
Figure 8.
The damage results of the second group of fragments to the three cabins: (a) the damage probability of three cabins when ; (b) the damage probability of three cabins when .
It can be seen from Figure 7 and Figure 8 that in the three cabins, when the minimum kinetic energy E of the fragment penetrating the projectile is satisfied, the damage probability of the cabin increases with the increase in the number of fragments hitting the cabin. On the other hand, the smaller the mean square error of the fragment distribution, the greater the damage probability of the cabin.
Using the particle swarm optimization algorithm and the possibility formula of the interval, the change interval of the projectile fitness value is obtained, as shown in Figure 9. The change interval of the target fitness value is obtained, as shown in Figure 10.
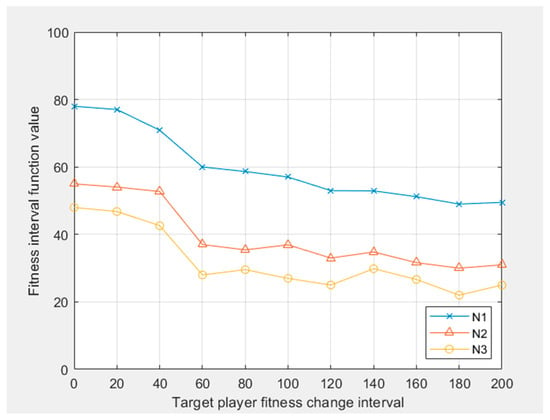
Figure 9.
The change interval of the fitness value of the projectile participant.
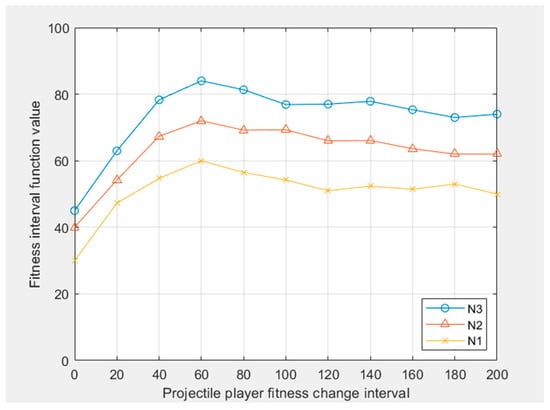
Figure 10.
Target participant fitness value change interval.
It can be seen from the simulation results that the projectile strategy set is , the target strategy set is , the intersection between projectile and target hit, and defense strategies adopt a mixed strategy set. The probabilities of the first strategy and the fifth strategy of the projectile are 0.32 and 0.68, respectively, and the probability of other strategies is 0. That is to say, the strategy probability of projectile 1 hitting target 1 and projectile 2 hitting target 2 is 0.095, and the strategy probability of projectile 1 hitting target 2 and projectile 2 hitting target 1 is 0.905. For the target strategy set , the probability of using the third strategy and the sixth strategy for target defense are 0.421 and 0.579, respectively, and the other probability is 0. In other words, the probability of selecting target 1 invalid defense projectile 1 and target 2 effective defense projectile 1 is 0.421, and the probability of selecting target 1 invalid defense projectile 2 and target 2 effective defense projectile 1 is 0.579.
In order to measure the damage effect of the target being hit, the target damage effect is calculated by using the probability of the fragment hitting the target formed by the projectile explosion and the income of the game between the projectile and target. According to the projectile strategy set and the target strategy set ,
It can be seen from Figure 5 that the income degree of the confrontation game between projectile and target is related to the number of fragments hitting the target, income fitness, and other parameters.
6. Conclusions
In this paper, by studying the spatial relationship between the position of the projectile explosion and the position of the missile relative to the ground coordinate system, taking the position of the missile target as the center of the damage effect calculation system, the damaging effect of the fragment group formed by the relative position of the projectile explosion on the missile target is discussed and analyzed. On the basis that the fragment satisfies the condition of hitting the projectile target cabin, the damage probability model of multiple fragments hitting the target of the projectile is established under the fragment distribution mechanism, and the damage income function of the game between the projectile and the target is established under the uncertain information. By quantitatively calculating the changes of game strategies and target damage under different fragment numbers, fragment velocities, fragment angles of hit, and other states under the background of confrontation game between projectile and target and based on the Nash equilibrium value solution method, which is about the particle swarm optimization algorithm, the fitness change relationship between the projectile and the target under different strategy sets is quantitatively calculated. The results show that under the same game strategy between projectile and target, the more the number of hits and the higher the intensity of the fragment hitting the target, the more obvious the damage effect of the target. The larger the angle of the intersection between the projectile and the target, the worse the effect of target damage. In addition, when the weight coefficient of the target cabin changes, although the probabilities of the fragment hitting each cabin are the same, the results of the target damage are also different, which reflects that the damage effects of the target are closely related to the damage weight of the target itself. At the same time, although the strategy sets adopted by both sides of the game between projectile and target are not the same, there is much uncertain information regarding the fragments formed by the explosion of the projectile, such as the number of fragments, the hit probability of fragments, the distribution of fragments, and the vulnerability of the target itself. Factors such as characteristics will form uncertain damage effects. This uncertainty is embodied in the intersection state of the projectile and missile target, which belongs to a dynamic confrontation game. This dynamic game needs to be analyzed and evaluated from the damage strategies of both projectile and target. Therefore, for the target damage effect of the confrontation game between projectile and target, more attention needs to be paid to the dynamic parameter changes under the strategy set of both the projectile and the target.
The projectile–target encounter target damage studied in this paper explores a calculation method of projectile–target encounter game against target damage from the projectile side and the target side as participants in the game confrontation. Because the target damage effect formed by the projectile and the target encounter involves many factors, in this paper, it is impossible to assign all the factors involved in the target damage assessment to the basic model. The target damage effect obtained in this paper is quantitatively calculated under the condition of conventional core parameters, which leads to the result of calculating the target damage. It is not an ideal effect, which is the deficiency of this paper. However, with the development of weapons and the strong demand for target damage assessment, the damage of multi-projectile cooperative confrontation targets will be an important development direction in the future. The target damage model of projectile–target encounter and the Nash equilibrium solution method of game confrontation strategy set proposed in this paper provide a new idea for the damage assessment of multi-projectile cooperative confrontation targets. Therefore, the research of this paper has important development prospects.
Author Contributions
Conceptualization and methodology, software and validation, writing—original draft, Y.H.; methodology, software and validation, writing—original draft, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 62073256.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, S.; Zhang, H.; Xu, X. Echo Characteristic of Planar Target in Pulsed Laser Fuze Detection. Army J. 2018, 39, 1095–1102. [Google Scholar]
- Wang, H.; Chen, Z.; Feng, X.; Di, X.; Liu, D.; Zhao, J.; Sui, X. Research on network security situation assessment and quantification method based on analytic hierarchy process. Wirel. Pers. Commun. 2018, 102, 1401–1420. [Google Scholar] [CrossRef]
- Chen, R.; Chen, D.; Ji, B.; Ni, J. Inversion method of the key structure parameters of light screen array measurement system using genetic algorithm. Optik 2020, 206, 164064. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X. Three-dimensional coordinates test method with uncertain projectile proximity explosion position based on dynamic seven photoelectric detection screen. Def. Technol. 2022, 18, 1643–1652. [Google Scholar] [CrossRef]
- Chen, R.; Ni, J. Optimization Method of Light-screen-array Structure Parameters of Photoelectric Target Based on Orthogonal Test. J. Ordnance Eng. 2017, 38, 2234–2239. [Google Scholar]
- Ma, W.; Dong, T.; Tian, H.; Ni, J. Line-scan CCD camera calibration in 2D coordinate measurement. Optik 2014, 125, 4795–4798. [Google Scholar] [CrossRef]
- Cui, Q.; Park, J.; Smith, R.T.; Gao, L. Snapshot hyperspectral light field imaging using image mapping spectrometry. Opt. Lett. 2020, 45, 772–775. [Google Scholar] [CrossRef]
- Liu, C.; Qiu, J.; Jiang, M. Light field reconstruction from projection modeling of focal stack. Opt. Express 2017, 25, 11377–11388. [Google Scholar] [CrossRef]
- Huijbregts, M.A.J.; Hellweg, S.; Hertwich, E. Average damage functions are not emission-rated distance to targets. Environ. Sci. Technol. 2012, 46, 569–572. [Google Scholar] [CrossRef]
- Fu, C.; Huang, K.; Tong, L.; Zhao, Y. Assess damage effectiveness for warhead to complex targets. J. Syst. Simul. 2009, 21, 5971–5976. [Google Scholar]
- Zhang, Z.; Zhang, L.; Xie, C.; Zhang, B.; Yang, B. Battle damage effect assessment based on improved GA-BP neural Network. Fire Control. Command. Control. 2021, 46, 42–48. [Google Scholar]
- Yu, B.; Li, X.; Lu, F. Fast analysis method for vulnerability of single fragment damage to missile cabin. Acta Ordnance Equip. Eng. 2020, 41, 82–86. [Google Scholar]
- Li, X.; Liu, Y.; Zhao, H.; Wang, G. Reduced-order vulnerability analysis and evaluation simulation of main battle tank weapon system. Technol. Bull. 2015, 33, 89–93. [Google Scholar]
- Fu, Z.; Fan, W.; Li, R.; Yang, L.; Wang, Y.; Chen, Y. Study on the damage effect of prefabricated fragments on human targets with two postures. Accord. J. Weapon Equip. Eng. 2024, 45, 62–69. [Google Scholar]
- Zhang, C.; Shu, J.; Wu, J.; Su, G. Current Status and Development of Target Damage Effect Evaluation Technology. Aviat. Proj. 2017, 45, 68–72. [Google Scholar]
- Liu, H.; Shi, X. Damage effectiveness calculation of hitting targets with ammunition based on bayesian multinomial distribution. Symmetry 2022, 14, 892. [Google Scholar] [CrossRef]
- Zhai, C.; Chen, X. Probability damage calculation of building targets under the projectile warhead strike. Reliab. Eng. Syst. Saf. 2020, 202, 107030. [Google Scholar] [CrossRef]
- Li, H.; Li, Y. Multi-burst location optical testing method and target damage efficiency assessment arithmetic. IEEE Sens. J. 2015, 15, 240–247. [Google Scholar]
- Chen, J.; Gao, X.; Ding, L. Design and operation strategies of the system for destroying time-sensitive target based on system effectiveness. J. Syst. Eng. Electron. 2008, 19, 1151–1156. [Google Scholar]
- Zhang, Y. Research on Damage Assessment Strategy of Projectile-Target Intersection Target. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2021. [Google Scholar]
- Orphal, D.L.; Anderson, C.E. Target damage from highly oblique hypervelocities impacts of steel spheres thin laminated targets. Int. J. Impact Eng. 2001, 26, 567–578. [Google Scholar] [CrossRef]
- Xu, Z.; Xue, J.; Liu, T.; Zhang, P.; Xie, X. Equivalent damage study of projectile due to energetic fragment warhead. Nanjing Univ. Technol. 2020, 44, 348–353. [Google Scholar]
- Lin, D.; Zhu, Y.; Yang, J. A Weapon-Target Assignment Method for Dynamic Damage Probability and Target Value. Fire Command Control 2024, 49, 138–143. [Google Scholar]
- Lu, D.; Chen, X.; Du, Z.; Pan, L. Simulation Research on Damage Probability of Distributed MEFP Warheads Hitting Air Target. J. Ballist. 2015, 27, 46–52. [Google Scholar]
- Fu, J.; Guo, G.; Feng, S.; Cehn, Z.; Zhao, T.; Hou, X. Damage Assessment Method and Application of Blast-fragmentation Warhead Ground Target. J. Ordnance Eng. 2016, 37, 7–12. [Google Scholar]
- Wang, Z.; Hu, J.; Zhu, X.; Zhang, Y. Damage effect evaluation of multiple missiles irregular surface targets under unascertained conditions. J. Natl. Univ. Def. Technol. 2024, 46, 213–221. [Google Scholar]
- Peng, Y.; Lu, F.; Li, X. Damage effectiveness evaluation method for penetrator. J. Weapon Equip. Eng. 2024, 45, 159–165. [Google Scholar]
- Qu, W. Research on Single Target Damage Effect Evaluation Model. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2023. [Google Scholar]
- Li, H.; Lei, Z. Measurement of spatial burst point position of projectile based on camera method. Opt. Precis. Eng. 2012, 20, 329–336. [Google Scholar]
- Li, H.; Lei, Z. Multi-screen optical method to measure the coordinates of projectile burst point and error analysis. Opt. J. 2012, 32, 136–142. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).