Dynamical Behaviors of a Stochastic Susceptible-Infected-Treated-Recovered-Susceptible Cholera Model with Ornstein-Uhlenbeck Process
Abstract
1. Introduction
2. Existence and Uniqueness of the Global Solution
3. Stationary Distribution
4. Density Function
5. Extinction
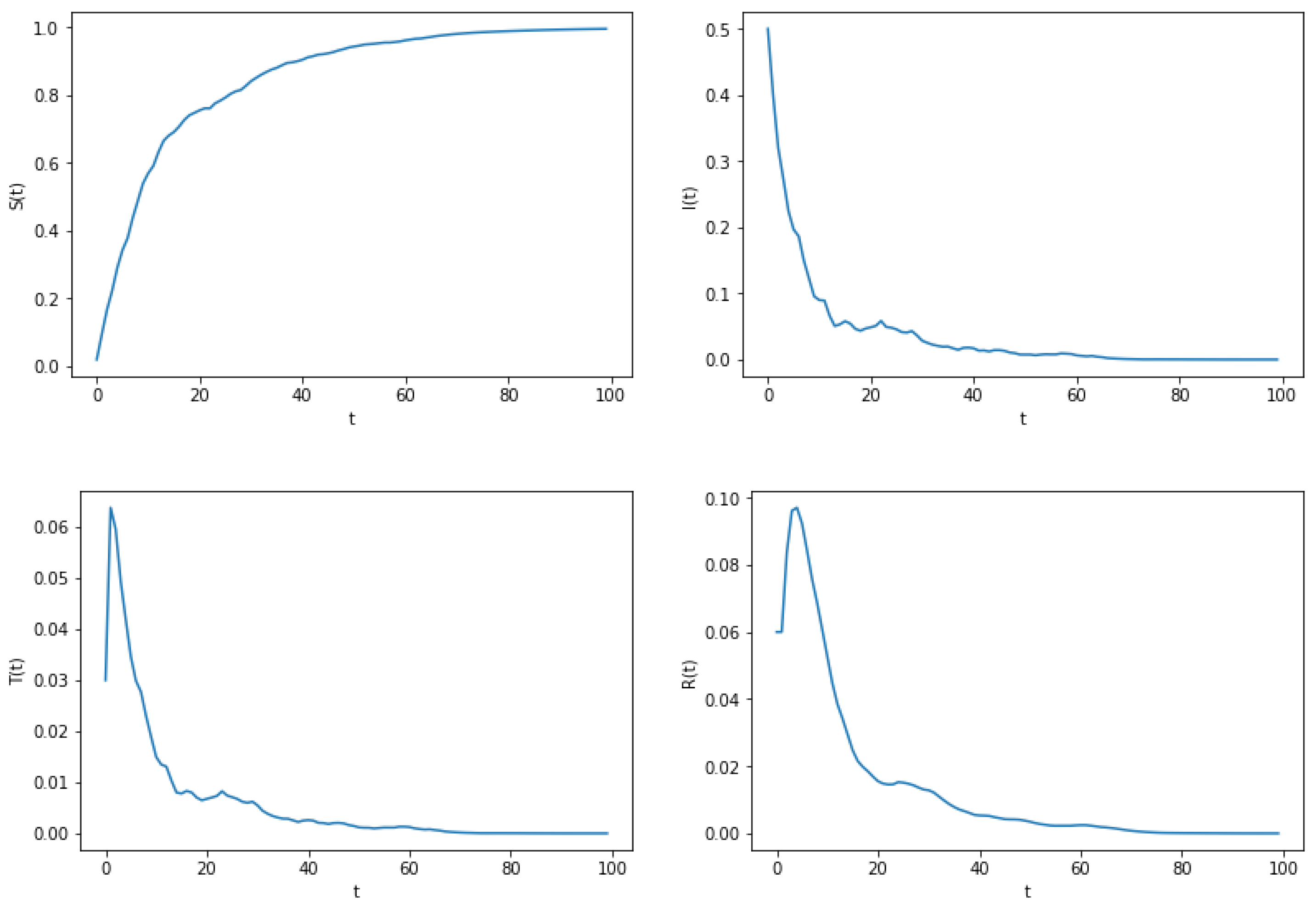
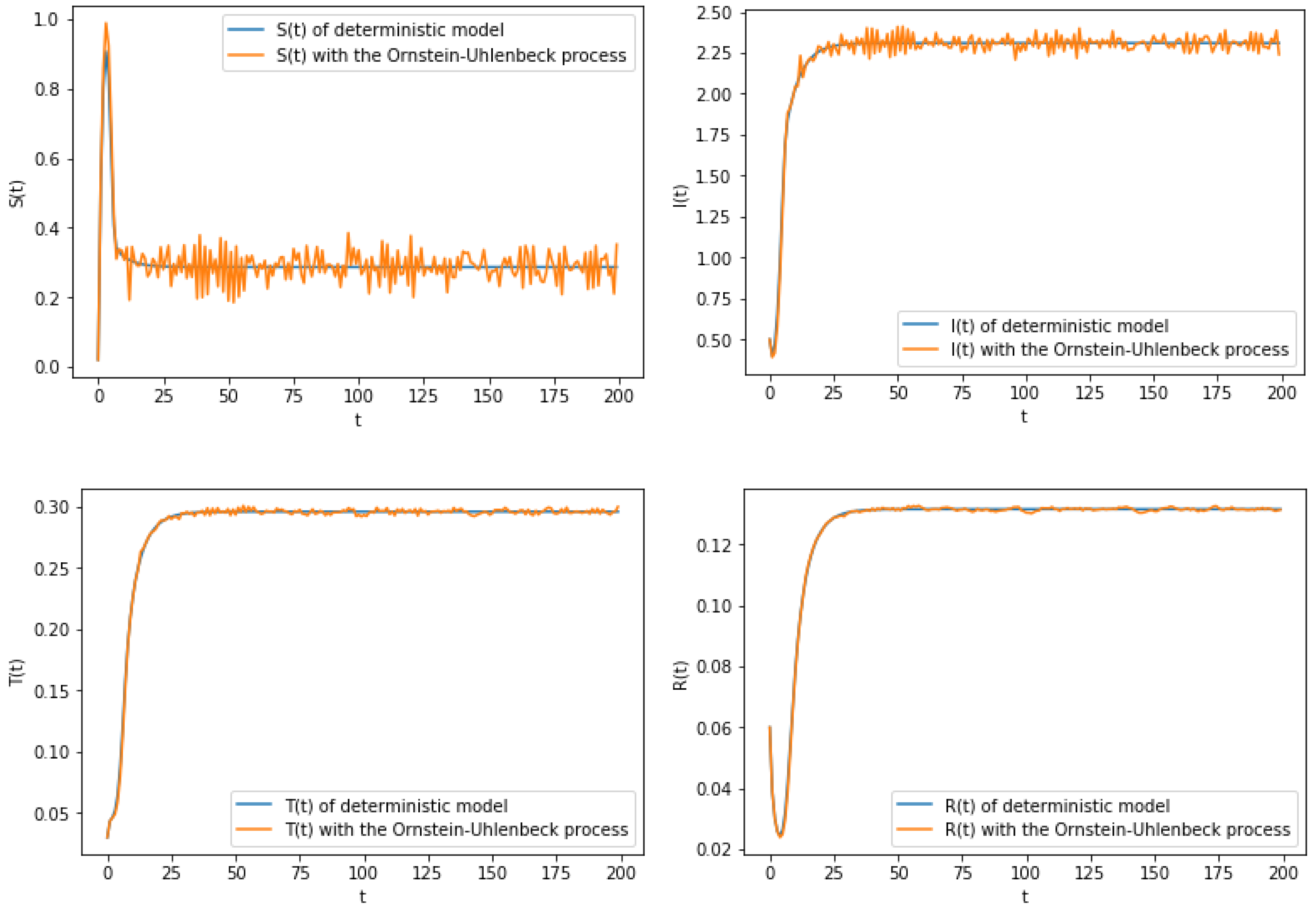
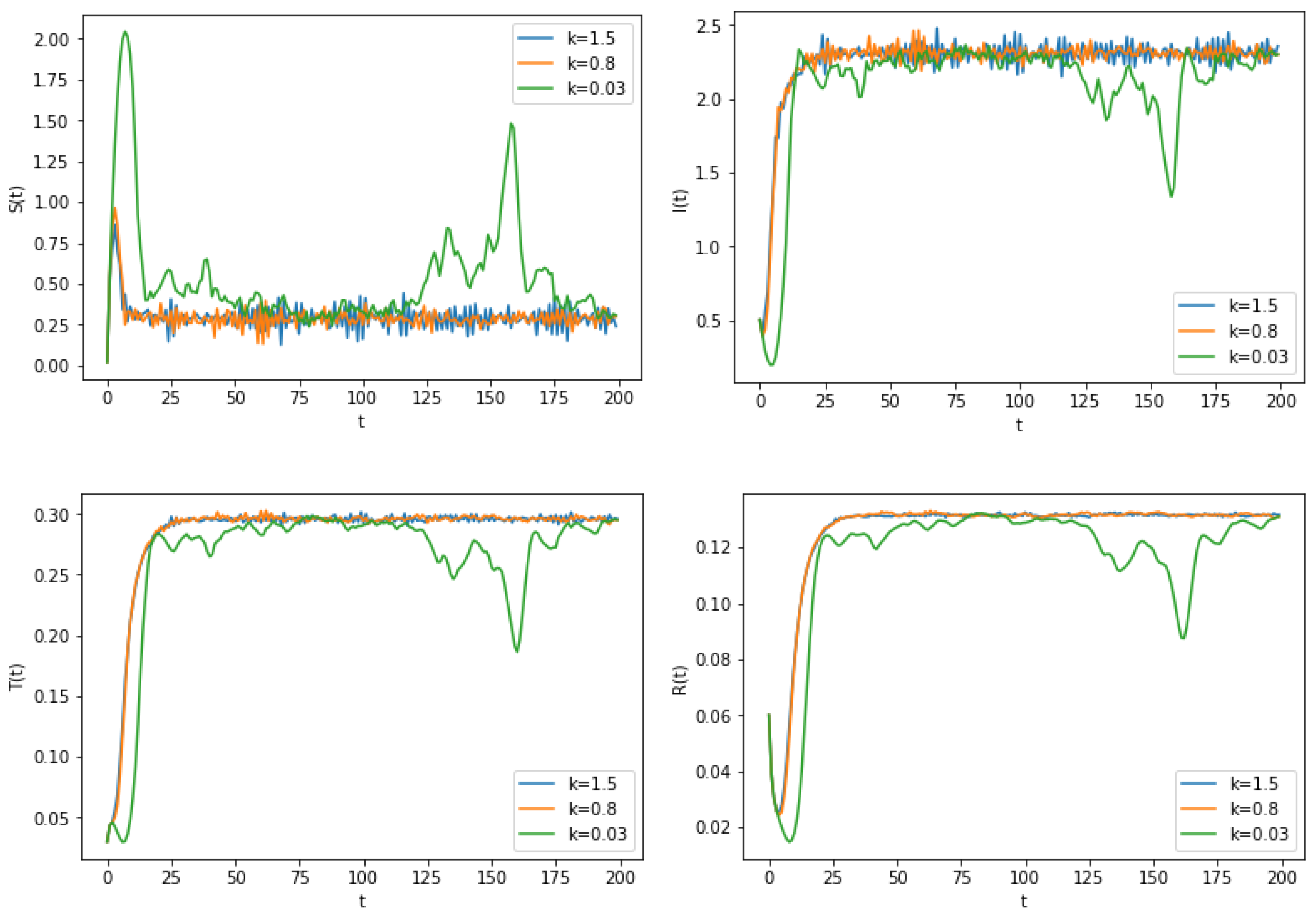
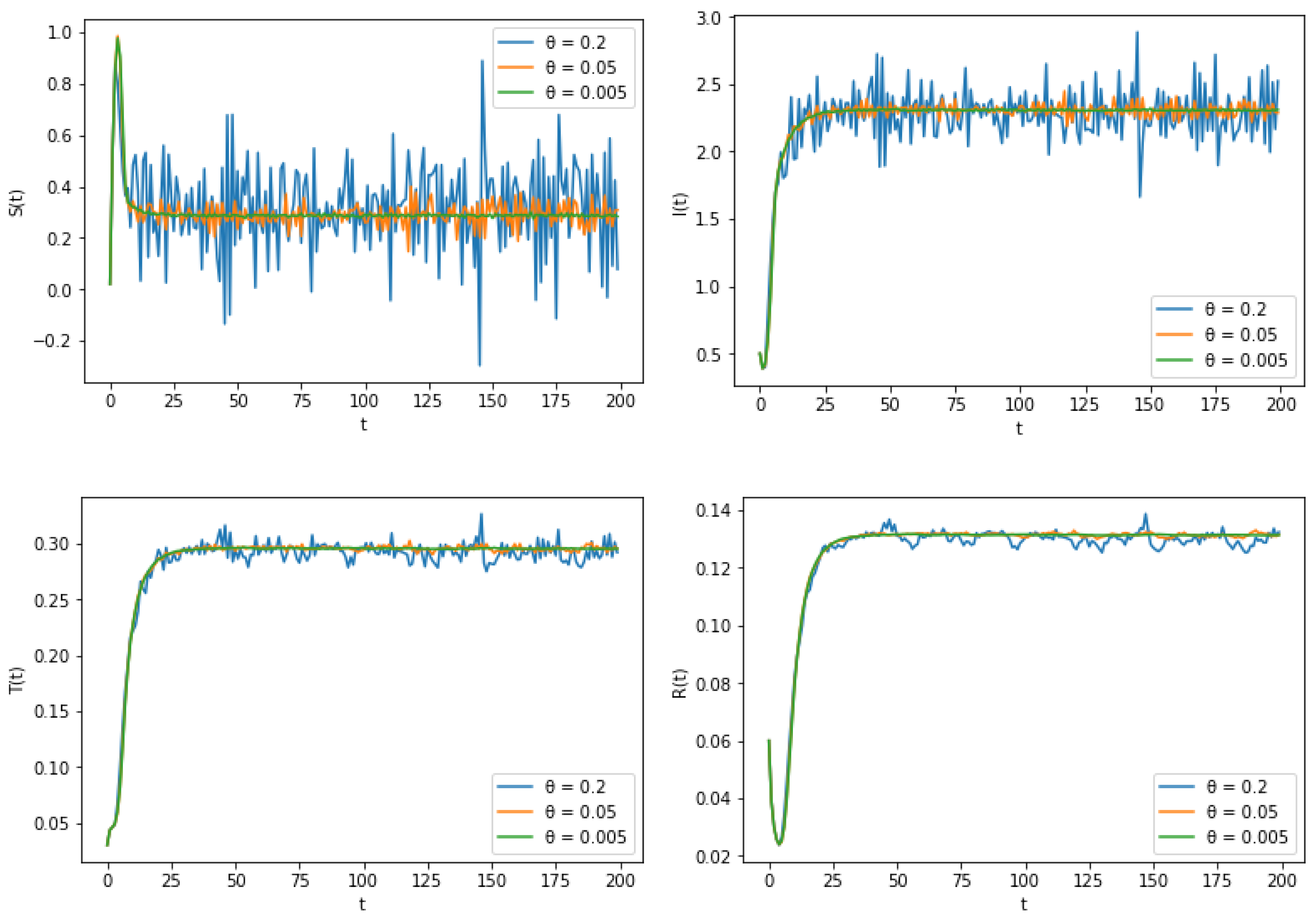
6. Numerical Simulation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, Z.; Zhou, Y.; Wu, J. Modeling and Dynamics of Infectious Diseases, 1st ed.; Higher Education Press: Beijing, China, 2009; pp. 1–35. [Google Scholar]
- Cai, Y.; Kang, Y.; Banerjee, M.; Wang, W. A stochastic epidemic model incorporating media coverage. Commun. Math. Sci. 2016, 14, 893–910. [Google Scholar] [CrossRef]
- World Health Organization (WHO). Cholera-Global Situation. Available online: https://www.who.int/emergencies/disease-outbreak-news/item/2023-DON437 (accessed on 11 February 2023).
- Beryl, M.O.; George, L.O.; Fredrick, N.O. Mathematical analysis of a cholera transmission model incorporating media coverage. Int. J. Pure. Appl. Math. 2016, 111, 219–231. [Google Scholar] [CrossRef]
- Fatima, S.; Krishnarajah, I.; Jaffar, M.Z.A.M.; Adam, M.B. A mathematical model for the control of cholera in Nigeria. Res. J. Environ. Earth Sci. 2014, 6, 321–325. [Google Scholar] [CrossRef]
- Nelson, E.J.; Harris, J.B.; Glenn, M.J.; Galderwood, S.B.; Camilli, A. Cholera transmission: The host, pathogen and bacteriophage dynamic. Nat. Rev. Microbiol. 2009, 7, 693–702. [Google Scholar] [CrossRef] [PubMed]
- Su, T.; Zhang, X. Stationary distribution and extinction of a stochastic generalized SEI epidemic model with Ornstein-Uhlenbeck process. Appl. Math. Lett. 2023, 143, 108690. [Google Scholar] [CrossRef]
- He, J.; Bai, Z. Global hopf bifurcation of a cholera model with media coverage. Math. Biosci. Eng. 2023, 20, 18468–18490. [Google Scholar] [CrossRef]
- Lemos-Paiao, A.P.; Silva, C.J.; Torres, D.F.M. A cholera mathematical model with vaccination and the biggest outbreak of world’s history. AIMS Math. 2018, 3, 448–463. [Google Scholar] [CrossRef]
- Zhou, X.; Shi, X.; Wei, M. Dynamical behavior and optimal control of a stochastic mathematical model for cholera. Chaos Solitons Fractals 2022, 156, 111854. [Google Scholar] [CrossRef]
- Hartley, D.M.; Morris, J.G., Jr.; Smith, D.L. Hyperinfectivity: A critical element in the ability of V. cholerae to cause epidemics? PLoS Med. 2005, 3, e7. [Google Scholar] [CrossRef]
- Lemos-Paiao, A.P.; Silva, C.J.; Torres, D.F.M. An epidemic model for cholera with optimal control treatment. J. Comput. Appl. Math. 2017, 318, 168–180. [Google Scholar] [CrossRef]
- Mwasa, A.; Tchuenche, J.M. Mathematical analysis of a cholera model with public health interventions. Biosystems 2011, 105, 190–200. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Yang, J.; Han, Y. Threshold dynamics of a chronological age and infection age structured cholera model with Neumann boundary condition. Z. Angew. Math. Phys. 2023, 74, 170. [Google Scholar] [CrossRef]
- Jiang, T.; Wang, J. Modeling and analysis of a diffusive cholera model with seasonally forced intrinsic incubation period and bacterial hyperinfectivity. J. Math. Anal. Appl. 2023, 527, 127414. [Google Scholar] [CrossRef]
- Tilahun, G.T.; Woldegerima, W.A.; Wondifraw, A. Stochastic and deterministic mathematical model of cholera disease dynamics with direct transmission. Adv. Differ. Equ. 2020, 2020, 670. [Google Scholar] [CrossRef]
- Zhou, Y.; Jiang, D. Dynamical behavior of a stochastic SIQR epidemic model with Ornstein-Uhlenbeck process and standard incidence rate after dimensionality reduction. Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106878. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X. Threshold behaviors and density function of a stochastic parasite-host epidemic model with Ornstein–Uhlenbeck process. Appl. Math. Lett. 2024, 153, 109079. [Google Scholar] [CrossRef]
- Bao, K.; Rong, L.; Zhang, Q. Analysis of a stochastic SIRS model with interval parameters. Discret. Contin. Dyn. Syst. Ser. B 2019, 24, 4827–4849. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.; Hayat, T.; Alsaedi, A. Dynamical behavior of a stochastic epidemic model for cholera. J. Frankl. Inst. 2019, 356, 7486–7514. [Google Scholar] [CrossRef]
- Zaho, Y.; Lin, Y.; Jiang, D.; Mao, X.; Li, Y. Stationary distribution of stochastic SIRS epidemic model with standard incidence. Discret. Contin. Dyn. Syst. Ser. B 2016, 21, 2363–2378. [Google Scholar] [CrossRef][Green Version]
- Zhang, X.; Yuan, R. A stochastic chemostat model with mean-reverting Ornstein-Uhlenbeck process and Monod-Haldane response function. Appl. Math. Comput. 2021, 394, 125833. [Google Scholar] [CrossRef]
- Allen, E. Environmental variability and mean-reverting processes. Discret. Contin. Dyn. Syst. Ser. B 2016, 21, 2073–2089. [Google Scholar] [CrossRef]
- Kutoyants, Y.A. Statistical Inference for Ergodic Diffusion Processes, 1st ed.; Springer: London, UK, 2004; pp. 50–103. [Google Scholar]
- Alshammari, F.S.; Akyildiz, F.T. Epidemic waves in a stochastic SIRVI epidemic model incorporating the Ornstein-Uhlenbeck process. Mathematics 2023, 11, 3876. [Google Scholar] [CrossRef]
- Zhou, B.; Jiang, D.; Hayat, T. Analysis of a stochastic population model with mean-reverting Ornstein-Uhlenbeck process and Allee effects. Commun. Nonlinear Sci. Numer. Simul. 2022, 111, 106450. [Google Scholar] [CrossRef]
- Wu, S.; Yuan, S.; Lan, G.; Zhang, T. Understanding the dynamics of hepatitis B transmission: A stochastic model with vaccination and Ornstein-Uhlenbeck process. Appl. Math. Comput. 2024, 476, 128766. [Google Scholar] [CrossRef]
- Zhou, B.; Jiang, D.; Han, B.; Hayat, T. Threshold dynamics and density function of a stochastic epidemic model with media coverage and mean-reverting Ornstein–Uhlenbeck process. Math. Comput. Simul. 2022, 196, 15–44. [Google Scholar] [CrossRef]
- Liu, Q. A stochastic predator-prey model with two competitive preys and Ornstein-Uhlenbeck process. J. Biol. Dyn. 2023, 17, 2193211. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Liang, G.; Chang, K. Stationary distribution of a reaction-diffusion hepatitis B virus infection model driven by the Ornstein-Uhlenbeck process. PLoS ONE 2023, 18, e0292073. [Google Scholar] [CrossRef] [PubMed]
- Mao, X. Stochastic Differential Equations and Applications, 2nd ed.; Horwood: Chichester, UK, 2008; pp. 149–155. [Google Scholar]
- Du, N.H.; Nguyen, D.H.; Yin, G.G. Conditions for permanence and ergodicity of certain stochastic predator–prey models. J. Appl. Probab. 2016, 53, 187–202. [Google Scholar] [CrossRef]
- Meyn, S.P.; Tweedie, R.L. Stability of Markovian processes III: Foster-Lyapunov criteria for continuous-time processes. Adv. Appl. Probab. 1993, 25, 518–548. [Google Scholar] [CrossRef]
- Dieu, N.T. Asymptotic Properties of a Stochastic SIR Epidemic Model with Beddington-DeAngelis Incidence Rate. J. Dyn. Differ. Equ. 2018, 30, 93–106. [Google Scholar] [CrossRef]
- Roozen, H. An asymptotic solution to a two-dimensional exit problem arising in population dynamics. SIAM J. Appl. Math. 1989, 49, 1793–1810. [Google Scholar] [CrossRef]
- Zhang, X.; Su, T.; Jiang, D. Dynamics of a Stochastic SVEIR Epidemic Model Incorporating General Incidence Rate and Ornstein–Uhlenbeck Process. J. Nonlinear Sci. 2023, 33, 76. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, J. Systems of reflected stochastic PDEs in a convex domain: Analytical approach. J. Differ. Equ. 2021, 284, 350–373. [Google Scholar] [CrossRef]
- Baccouch, M.; Temimi, H.; Ben-Romdhane, M. A discontinuous Galerkin method for systems of stochastic differential equations with applications to population biology, finance, and physics. J. Comput. Appl. Math. 2021, 388, 113297. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Li, W. Dynamical Behaviors of a Stochastic Susceptible-Infected-Treated-Recovered-Susceptible Cholera Model with Ornstein-Uhlenbeck Process. Mathematics 2024, 12, 2163. https://doi.org/10.3390/math12142163
Li S, Li W. Dynamical Behaviors of a Stochastic Susceptible-Infected-Treated-Recovered-Susceptible Cholera Model with Ornstein-Uhlenbeck Process. Mathematics. 2024; 12(14):2163. https://doi.org/10.3390/math12142163
Chicago/Turabian StyleLi, Shenxing, and Wenhe Li. 2024. "Dynamical Behaviors of a Stochastic Susceptible-Infected-Treated-Recovered-Susceptible Cholera Model with Ornstein-Uhlenbeck Process" Mathematics 12, no. 14: 2163. https://doi.org/10.3390/math12142163
APA StyleLi, S., & Li, W. (2024). Dynamical Behaviors of a Stochastic Susceptible-Infected-Treated-Recovered-Susceptible Cholera Model with Ornstein-Uhlenbeck Process. Mathematics, 12(14), 2163. https://doi.org/10.3390/math12142163





