Abstract
This article presents a new methodology for designing a robust, decentralized control structure that considers stochastic parametric uncertainty and uses a multi-objective approach. This design tunes the loop pairing and controller to be implemented. The proposed approach obtains the optimal and nearly optimal controllers relevant to the nominal scenario. Once obtained, the robustness of these solutions is analyzed. This methodology is compared with a traditional approach for selecting the most robust control pairings. The traditional approach obtains lightly robust controllers, i.e., the most robust controllers with an acceptable performance for the nominal scenario, and it obtains trade-offs between robustness and nominal performance. However, the traditional approach has a high computational cost because it is necessary to consider uncertainty in the optimization stage. The proposed approach mathematically guarantees the acquisition of at least one neighbor controller for each existing lightly robust controller. Therefore, this approach obtains solutions similar to lightly robust solutions with a significantly lower computational cost. Furthermore, the proposed approach provides the designer with more diversity and interesting solutions that are not lightly robust. The different approaches are compared using an example of a multi-variable process with two alternative control structures. The results show the usefulness of the proposed methodology.
Keywords:
multi-objective optimization problem; uncertainty; robustness; controller tuning; loop pairing MSC:
93B51
1. Introduction
Optimization tools are extensively used in many real-world engineering problems, such as control system design. In this task, the designer chooses a control structure and then adjusts its parameters. For this adjustment, design objectives related to the control system performance are defined (such as overshoot, rise or peak time, settling time, tracking error, and control effort for reference tracking and/or disturbance rejection). Many of these objectives conflict, which makes it appropriate to formulate the design problem as a multi-objective optimization problem (MOP) [1,2,3].
Another challenge in control system design is uncertainty [4]. Frequently, designers lack accurate information about the plant [5]. This raises the need for algorithms capable of providing solutions that work well, even under uncertain circumstances [6]. This uncertainty can come from measurement errors, inaccurate data, fluctuations, disturbances, etc. For instance, the model used in design and adjustment tasks typically has some degree of uncertainty [7]. This uncertainty negatively impacts the performance of the designed control system when it is implemented in the real plant [8]. Consequently, it is beneficial for the designer to analyze and/or incorporate uncertainties into the multi-objective optimization problem. This can be conducted by formulating an uncertain multi-objective optimization problem (MOP [9,10,11]). Such an approach enables the designer to choose a controller that performs well under nominal conditions and is robust (insensitive to uncertainties).
In order to formulate a MOP, it is first necessary to define a concept of robustness, i.e., when a solution is considered robust [12]. For single-objective problems, different concepts of robustness have been defined in the literature. One of the best known is the concept of minmax robustness [13,14]. According to this concept, a solution is robust if it minimizes the objective function in the worst case scenario (the worst case scenario may vary for each solution). In [15], a first attempt to extend these concepts to an MOP was provided. In particular, the authors used the supremum for each objective function separately in all scenarios. In the present study, this robustness concept is used and will be called point-based minmax robust efficiency.
However, optimizing for the worst case (or supremum for each objective separately) can be excessively conservative, resulting in solutions with poor performance for the nominal (most likely) scenario. Too much performance needs to be given up to ensure robustness [6]. For this reason, a trade-off between performance and robustness is necessary [16]. To address this issue and to better manage the cost of robustness (as defined in [17]), several concepts have been proposed, including reliability approaches [18], the method presented in [17], and the concept of adjustable robustness [19], as well as its extension to recovery robustness [20,21,22]. The reliability approach involves relaxing the constraints of the optimization problem to produce solutions that are nearly robust but offer significantly better nominal performance. The innovative concept of light robustness [10] integrates this idea. In this concept, only the solutions that are good enough for the nominal scenario (optimal or nearly optimal) are considered. Among these solutions, the most robust one is chosen (for example, the solution that minimizes the worst case scenario). This approach attains a trade-off between robustness and nominal performance [12]. Since its formulation, the concept of light robustness has been applied to robust railway timetabling [10], timetable information [23], and it has been compared to other robustness concepts in a study on aperiodic timetabling [24]. Additionally, light robustness has been used in several other studies [11,25,26,27].
Nevertheless, obtaining lightly robust solutions has a high computational cost since each controller must be evaluated on all the scenarios [12]. This fact has motivated a new and computationally more affordable approach, which was proposed in [28]. This new approach includes uncertainty in the analysis of alternatives at the decision stage. In the optimization stage, the design objectives are evaluated for a nominal model/scenario and, in addition to optimal controllers, the nearly optimal controllers that do not dominate in their neighborhood (called relevant nearly optimal solutions [29] in this work) are obtained. This procedure guarantees that there will be at least one neighboring solution to each existing lightly robust solution (see Theorem 1, as defined in [28]). This approach has a significantly lower computational cost, and it obtains similar (neighboring) controllers to the lightly robust solutions.
In this work, a novel methodology for the design of robust, decentralized multi-variable controllers (loop pairing tuning and controller tuning) is presented and its advantages are demonstrated. This latter task is performed by means of a comparison of different control structures for a robust control system (structure and controller) with an affordable computational cost. It is important to note that this new methodology is not limited to specific control structures and/or robustness concepts. In effect, it is possible to compare any control structures, and it can be achieved with any point-based robustness concept (where each solution is represented by a point, and not by a set, on the objective space). This methodology obtains the optimal and relevant nearly optimal controllers (nearly optimal meaning the controllers do not dominate in their neighborhood [29]) for the nominal scenario. The robustness is then analyzed in the decision stage on the obtained set of solutions. This methodology guarantees similar solutions (similar being defined by the designer) to the lightly robust solutions.
In this work, in order to show its validity, the methodology introduced was applied to the control system design of a multi-variable process, and two different multi-variable control structures (i.e., two design concepts) were compared. These concepts consist of multi-loop controls with simple PI-type controllers but different pairings between the controlled and manipulated variables. Furthermore, this new methodology is compared with a traditional approach for obtaining lightly robust controllers. It is not possible to compare the proposed methodology with other controller tuning techniques that do not contemplate nearly optimal solutions since their purposes are different. The results show how this novel methodology manages to obtain controllers that are similar to the lightly robust ones (in addition to other interesting controllers) at a much lower computational cost.
This paper is structured as follows. Section 2 presents some of the definitions introduced in the literature that describe MOPs and MOPs. Section 3 provides some new definitions that are needed to compare design concepts, as well as the steps required to obtain lightly robust controllers. Section 4 describes the new methodology presented in this paper. Section 5 presents the control design example used and discusses the results obtained in this paper. Finally, the conclusions are discussed in Section 6.
2. Background
A design problem is usually solvable in different ways or by design alternatives. Each of these alternatives is called a “design concept” or simply a “concept” [30]. For example, in a control context, a process could generally be controlled by different control structures or control pairings: such as a PID type controller, SMC (sliding mode control) controller, and fuzzy controller. In this scenario, each control structure to be analyzed is defined as a design concept, where the parameters of the controllers that make up each control structure must be tuned accordingly. This definition of design concept applies to all types of control structures. This work uses simple controllers that are commonly used in industrial applications. To control multi-variable processes, it is necessary to define the pairing between manipulated variables and controlled variables. Thus, a different design concept defines each pairing to be analyzed. Using the design concepts, it is possible to analyze the performance of each pairing in order to choose the most suitable for the designer’s preferences.
Thus, a design concept is defined as a given control pairing [30]. Each concept is characterized by its design parameters . In this work, we wish to fit using a multi-objective optimization approach that considers uncertainty in the process model. We assume that the uncertainty is associated with the parameters of the model. Uncertainty is incorporated in the problem formulation in the form of scenarios. A scenario is defined by values of the parameters . A nominal scenario/model is assumed to be known. This section presents the background related to the following: (1) MOP and (2) uncertainty in an MOP.
2.1. Multi-Objective Optimization Problems
Considering a given scenario and a given design concept, a multi-objective optimization problem (MOP) can be defined as follows: (a maximization problem can easily be converted into a minimization problem. Each of the objectives that must be maximized can be changed to ):
where can be defined (generally, any other constraints can be included) as follows:
with as a decision vector in the domain , and with : as the vector of the objective functions . In addition, and are the lower and upper bounds of each component of , and is the number of decision variables.
Moreover, incorporates different objectives that measure the quality of the control (performance, control efforts, etc.). Henceforth, to simplify the notation, in the nominal scenario , the vector of objective functions is represented as . The following definitions are particularized for a given scenario and concept.
Definition 1.
Dominance [2,31]: Given a scenario ξ, a decision vector is dominated by any other decision vector if for all , and for at least one j, . This is denoted as .
Definition 2.
Pareto set: The Pareto set (denoted by ) is the set of solutions in that are non-dominated by another solution in :
In addition to the Pareto set (see Definition 2), there is a set of nearly optimal solutions (see Definition 4) that may be useful to the designer.
Definition 3.
-dominance [32]: Given a scenario ξ and is defined as the maximum acceptable performance degradation, then a decision vector is -dominated by another decision vector if for all , and for at least one j, . This is denoted by .
Definition 4.
ϵ-efficiency [33]: The set of ϵ-efficient solutions (denoted by ) is the set of solutions in that are not ϵ-dominated by another solution in :
However, characterizing all nearly optimal solutions may have a high computational cost and could make the decision stage more difficult. To limit the number of solutions, it is proposed that one should only consider the non-dominated solutions in the neighborhood (see Definition 7). These solutions are potentially helpful and allow the designer to obtain diverse solutions without excessively increasing the number of possible alternatives.
Definition 5.
Neighborhood [29]: Define as the maximum distance between neighboring solutions, then the two decision vectors and are neighboring solutions () if for all .
Definition 6.
dominance [29]: A decision vector is dominated by another decision vector if they are neighboring solutions (Definition 5) and . This is denoted by .
Definition 7.
efficiency [29]: The set of efficient solutions (denoted by ) is the set of solutions of that are not dominated by another solution in :
2.2. Considering Uncertainties in MOP
For robustness analysis, uncertainty must be considered. For this purpose, a set of scenarios is defined . This uncertainty can be considered at the decision stage or the optimization stage.
When it is taken into account in the decision stage, we can achieve the following: (1) the Pareto set is obtained with the nominal scenario (or when relevant nearly optimal solutions are considered), and (2) the uncertainty (modeled through the different scenarios) is analyzed with the Pareto set obtained.
In the case where uncertainty is incorporated in the optimization process, we must pose a multi-objective optimization problem with uncertainty (MOP [12]), where the design objectives account for such uncertainty. Thus, to obtain a robust controller (which does not excessively degrade performance for all scenarios), it is necessary in the optimization to evaluate such a controller for the set of scenarios considered. Therefore, a controller generates a set of points in the objective space, one for each scenario considered in :
With , the robustness can be evaluated using different robustness criteria. In the literature, several possibilities have been presented as follows [11,12,34]: flimsy and highly robust efficiency; set-based minmax robust efficiency; lightly robust efficiency; point-based minmax robust efficiency, etc. A more wide-spread alternative is point-based minmax robust efficiency [12]. Under this approach, for each solution , the supremum value for every objective function is obtained separately by considering all scenarios . In this article, this definition will be used to obtain the robust solutions in a MOP.
However, optimizing the supreme value can significantly degrade performance in the nominal scenario. To limit this problem, the concept of light robustness for MOPs [11,12] arises, where the obtained robust solutions are guaranteed to have acceptable performance for the nominal scenario. This concept was introduced in [10] and generalized in [6]. Based on the point-based minmax robust efficiency concept, we defined a lightly robust MOP (hereafter referred to as MOP) as follows:
where
The Pareto set obtained with this MOP will be denoted as . All solutions of this set must have a nearly optimal performance with the nominal model and the concept (). In this paper, a solution is considered to be more robust than another solution if it obtains a better supreme value ().
2.3. Advantages of Using Nearly Optimal Solutions in MOP
In the previous subsections, the sets and for a given concept , which have been previously defined in the literature, were presented. These ensembles were already compared in [28] to analyze similarities from the point of view of robustness and computational cost differences.
To obtain both sets, it is necessary to define a nominal scenario , the maximum acceptable degradation (see Definition 3), and a set of scenarios for uncertainty analysis.
For a given concept , once the neighborhood is defined (see Definition 5), obtains the optimal and nearly optimal non-dominated solutions in its neighborhood for the nominal scenario . Once this set is obtained, the performance for the set is analyzed, e.g., through using . The computational cost associated with the robustness analysis is limited to the evaluation of all scenarios for each solution of the set .
The most robust solutions that have optimal or nearly optimal performance for are obtained by . To achieve this, in the optimization stage, it is necessary to evaluate, for each solution, the performance for each scenario of the set by . Obtaining this set has a notably higher computational cost than that required for obtaining and its robustness analysis.
Despite the computational advantage, must adequately characterize . Thus, obtaining will sensibly reduce the computational cost with solutions that are similar to the most robust ones (). Theorem 1 (proved mathematically in [28]) enables stating that any solution existing in the set has at least one neighboring solution in the set . Moreover, the neighborhood is chosen by the designer. Therefore, it is the designer who decides the similarity between neighboring solutions for these sets.
Theorem 1.
Any lightly robust solution has at least one neighboring solution in the set of optimal and non-dominated nearly optimal solutions in their neighborhood in the nominal scenario ().
A solution may fulfill the following: (1) belong to the set or (2) not belong to the set . In the first assumption, the solution is part of the sets and ; thus, there is a solution in neighboring ( itself). The second assumption is more complex. If belongs to the set , then it also belongs to the set (see MOP defined in (3)). Moreover, if , there is at least one solution such that dominates in its neighborhood (see Definition 7). Thus, is a solution belonging to and neighboring . Therefore, it can be stated that any solution in has a neighboring solution in .
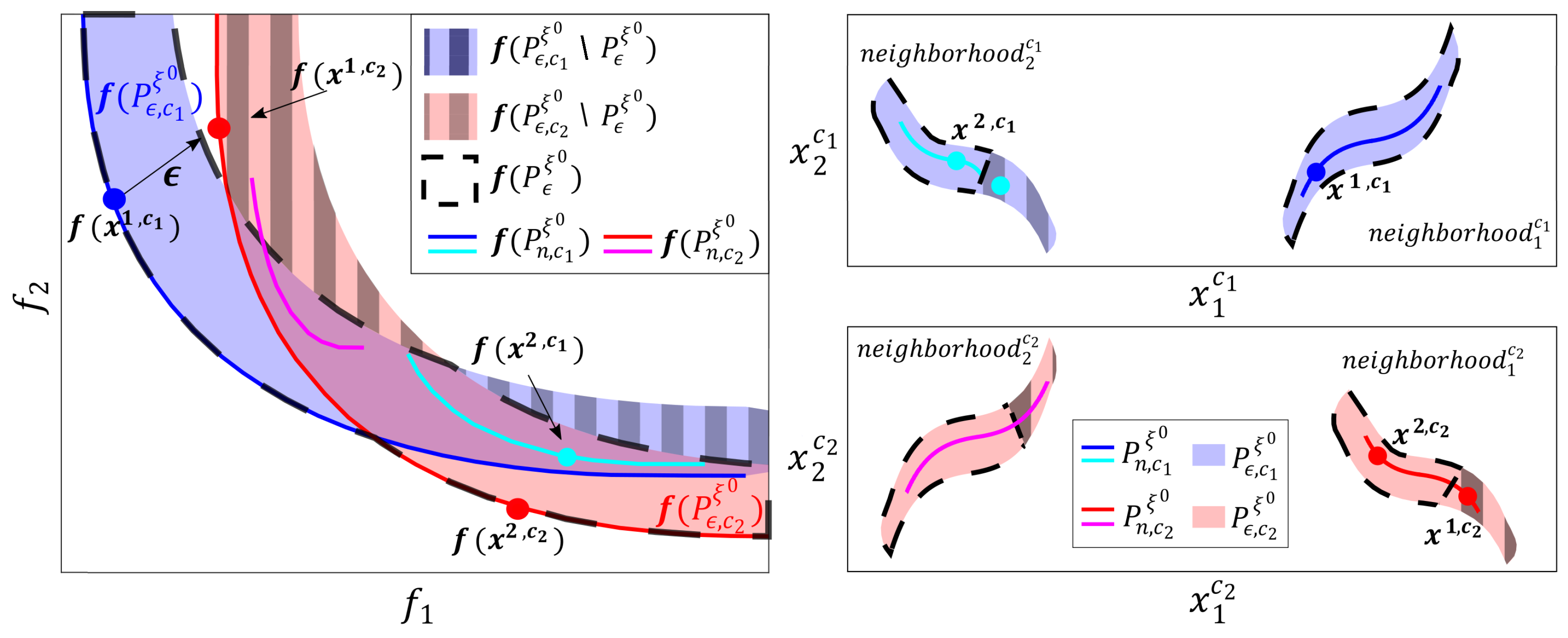
Let us take an example. Suppose you wish to design a control system. Two design objectives are defined: one evaluates the error in the output (), and the other evaluates the control effort (). We will use a design concept and a controller with two decision variables: and . The optimal and nearly optimal controllers with the nominal scenario were obtained using a multi-objective evolutionary algorithm. There were two different neighborhoods where the optimal or nearly optimal controllers were found ( and ). In , there are optimal controllers for . In , the most robust controllers (robust being understood as the controllers that obtain the best ) that were not optimal for were found. Figure 1 shows the sets of (blue and light blue controllers) and (red controllers). In the objective space, these sets are represented in the nominal scenario by (solid lines) and the set of scenarios is represented by (dashed lines).

Figure 1.
Illustrative example of a MOP. On the left, the objective space. On the right, the decision space.
obtains the most robust controllers with optimal or nearly optimal performance for . These solutions are found in (red controllers). The controllers were found to be appreciably more robust than those in the , and they obtained significantly better . Set can characterize all the neighborhoods where optimal and nearly optimal solutions exist under (blue and light blue controllers). Thus, it can characterize, in addition to , (see light blue line). These controllers (light blue) are neighbors of those obtained by ; thus, their robustness is similar.
An example of this is the controller. This controller is appreciably more robust than . However, obtains the controller . In addition, and are neighboring solutions; thus, their robustness is similar. Furthermore, performs slightly better than on . However, obtains a slightly better robustness than .
3. Comparison of Design Concepts in MOP
When comparing different design concepts , new situations arise because all the design concepts are being considered simultaneously. For example, an optimal solution under one design concept may be dominated by another solution of concept . In this case, such a solution would not be optimal if all design concepts were considered simultaneously. Thus, there is a global Pareto set (see Definition 8) under scenario that considers all concepts simultaneously.
Definition 8.
Pareto set: When comparing different design concepts , the Pareto set (denoted by ) that considers all concepts simultaneously is the set of solutions that is non-dominated by another solution for any defined design concept:
Analogously, when comparing design concepts, there is a set of globally optimal and nearly optimal solutions (see Definition 9) under scenario for all concepts simultaneously.
Definition 9.
ϵ-efficiency: When comparing different design concepts , the set of ϵ-efficient solutions for all concepts (denoted by ) is the set of solutions that are not ϵ-dominated by another solution for any defined design concept:
The same is true for the set of optimal and nearly optimal solutions that are non-dominated in their neighborhood. When different design concepts are compared, there is a global set (see Definition 10) under scenario that consists of the optimal and nearly optimal solution sets that are non-dominated in their neighborhood for all of the concepts at the same time.
Definition 10.
efficiency: When comparing different design concepts , the set of efficient solutions for all concepts (denoted by ) is the set of solutions of that are not dominated by another solution in :
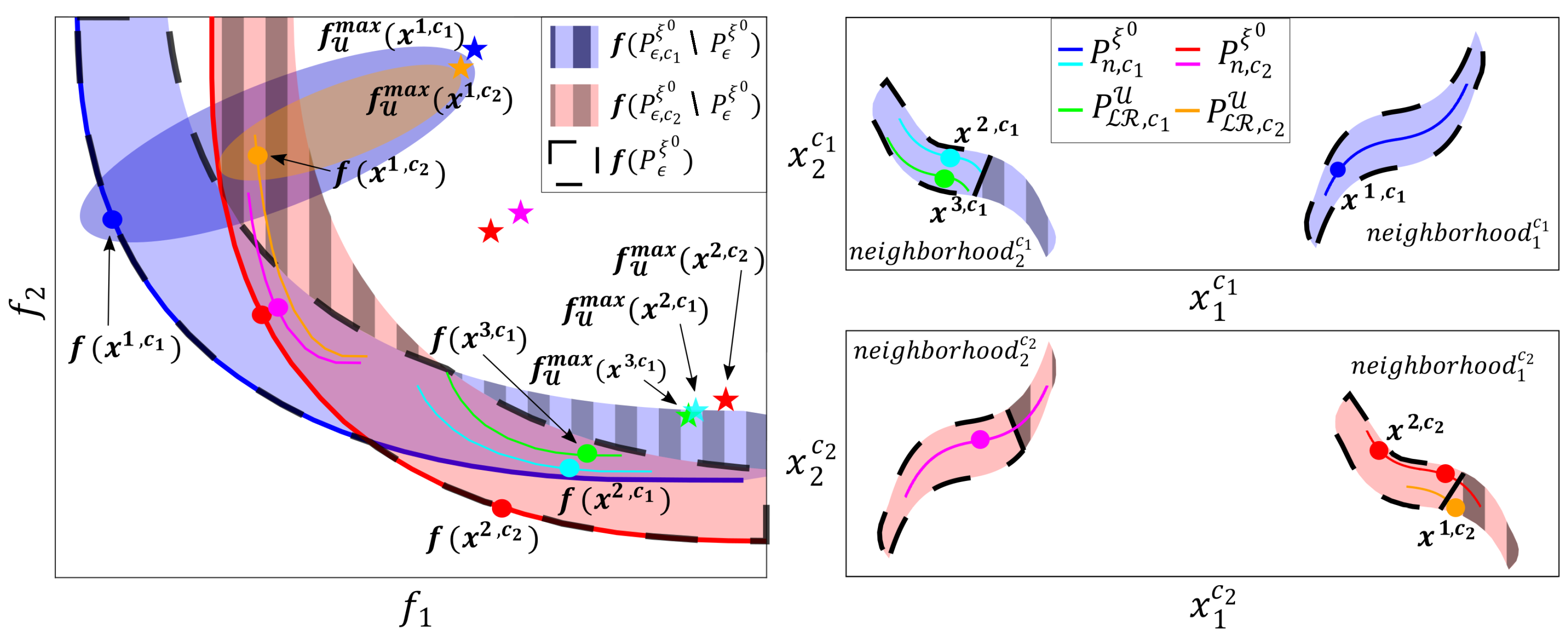
Let us return to the multi-variable control system design example introduced in the previous section to visualize the different scenarios that can occur when comparing different design concepts in an MOP. Two design concepts and were available in this case. Both design concepts defined a controller with two decision variables: and . In Figure 2, the sets and obtained for for each design concept are depicted. Both sets obtained solutions in two neighborhoods. In addition, the area of optimal and nearly optimal solutions for each design concept ( and ) was plotted.
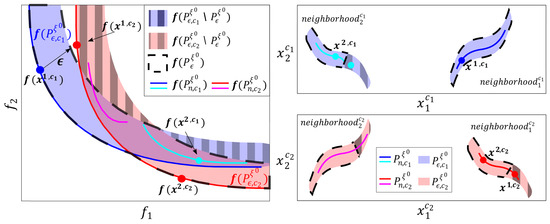
Figure 2.
Illustrative example of an MOP with two design concepts corresponding to different control pairings. On the left, is the objective space. On the right, is the decision space for each design concept.
Considering the fact that both concepts gives rise to the global optimal and nearly optimal solution area , which is delimited by the dashed black lines, there are controllers that, despite being optimal, or nearly optimal, for a concept, are not optimal when considering both concepts. This is the case of the areas shaded with vertical gray lines. For example, is an optimal controller for concept . However, it is -dominated by ; thus, it does not perform acceptably for (i.e., it is not part of the set ). The same is not true for concept , where the whole set is part of set (blue and cyan lines). This is the case with controller , which, despite being dominated, has acceptable performance for , i.e., it is not -dominated.
In a MOP, it is possible to compare different design concepts simultaneously. When this occurs, the MOP is slightly modified (due to the constraint) as follows:
The Pareto set obtained with this MOP for each design concept will be denoted as . All solutions of this set should obtain nearly optimal performance under the nominal model, and all concepts should be considered simultaneously ().
The global Pareto set (for all design concepts simultaneously) is formed by the union of different solutions in sets for each design concept . The same is true for set . Therefore, Theorem 1 is extrapolable to the and sets. Thus, for any solution in set , there exists a neighboring solution in set ().
Let us return to the previously introduced example to see what happens when analyzing robustness for a MOP with different design concepts. The sets are depicted in Figure 3 for each design concept as follows: , , and . In addition, we selected several controllers and represented their degradation against the set of scenarios by (stars). We selected the controllers and , where is an optimal controller under and concept ; is a lightly robust controller under concept ; and obtains higher degradation and, consequently, worse robustness than . However, was not part of the controllers with optimal or nearly optimal performance for the nominal scenario (). Therefore, this controller was not lightly robust when considering both concepts, and it was thus discarded.
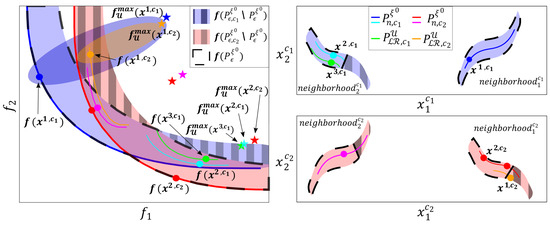
Figure 3.
An illustrative example of a MOP problem solved using two control pairings (concepts). On the left, is the objective space. On the right, is the decision space for each design concept.
We selected the controllers , , and , where is an optimal controller under and concept ; and are a nearly optimal and a lightly robust controller, respectively, for concept ; obtains the highest degradation; obtains the best robustness; and obtains slightly worse robustness than (obtaining a slightly better performance for the nominal scenario). Therefore, the designer could choose one of the and controllers in this area.
All the sets defined in this paper can have infinitely many solutions. Therefore, obtaining these is often unapproachable computationally. Typically, the designer obtains discrete sets denoted with a “*”. For example, the designer obtains the discrete set in such a way that it appropriately characterizes .
Obtaining a Lightly Robust Set
To obtain the global Pareto set (lightly robust set), for all design concepts simultaneously, it is necessary to perform the following steps:
is obtained by evaluating the uncertainty in the optimization process. In this work, the evMOGA (evMOGA [35]) algorithm, which is available at Matlabcentral https://es.mathworks.com/matlabcentral/fileexchange/31080-ev-moga-multiobjective-evolutionary-algorithm?s_tid=srchtitle_evMOGA_1, accessed on 5 July 2024, was used to determine sets and . However, any multi-objective optimization algorithm could be used.
4. Methodology Proposed
This section describes the new methodology presented in this article. The proposed methodology considers uncertainty in the decision stage. In addition, it enables an analysis of the different design concepts. This methodology obtains set through the following steps:
- Define as the maximum acceptable loss for the design objectives for .
- Define neighborhood as the maximum distance between neighboring controllers for each design concept .
- An MOP is defined for and each design concept (see MOP, as defined on (1)). In the optimization, , the optimal controllers, and the relevant nearly optimal controllers were obtained.
- The Pareto set is defined considering all concepts simultaneously, thus obtaining ().
- Finally, is obtained for each solution of set .
In this methodology, the parameters and are initially defined. When the necessary knowledge is unavailable, performing a sensitivity analysis for the definition of these parameters is recommended. This methodology has a significantly lower computational cost than that required in obtaining set (see Section Obtaining a Lightly Robust Set) since it is only necessary to evaluate the set of scenarios on a bounded set of . In addition, the relevant nearly optimal controllers offer greater diversity in the parameter space, which can, in turn, provide more robust solutions. characterizes all neighborhoods with nearly optimal solutions for the nominal scenario. Therefore, it can guarantee (Theorem 1) that will, at least, obtain solutions neighboring set (where all solutions are optimal or nearly optimal for ). The designer has the flexibility to define the similarity between these two sets ( and ) through the neighborhood parameter. If the neighborhood is reduced, the solutions obtained will closely resemble the lightly robust solutions. This, however, leads to a larger number of nearly optimal solutions. Conversely, if the neighborhood is increased, the solutions obtained will deviate more from the lightly robust solutions, but there will be fewer solutions.
In this work, the nevMOGA (nevMOGA [29] available at Matlabcentral https://es.mathworks.com/matlabcentral/fileexchange/71448-nevmoga-multiobjective-evolutionary-algorithm, accessed on 5 July 2024) algorithm was used to determine set (the optimal and relevant nearly optimal solutions for the concept). However, any other multi-objective optimization algorithm could be used.
5. Example 1: Control of a Linear System with Uncertainties
This section presents a robust controller design for a multi-variable linear process with uncertainty by applying multi-objective optimization. For this purpose, two alternative controllers (design concepts) were proposed. The two controllers were the same type of multi-loop controllers using 1DOF PI loops but with different pairings. This methodology enables the following: (1) determining which control pairing is more robust to model uncertainty in the designer’s area of interest; and (2) determining the controller best suited to the designer’s preference. The problem posed in this section was analyzed in [30], where the two control pairings posed in the present work were studied. In this paper, we expanded upon that study by considering uncertainty.
5.1. Description of the Problem
The model used in this example is defined as in [36]:
where and are the process outputs to be controlled, and and are the process inputs (control actions). The model inputs and outputs were normalized. This system is highly coupled, and the uncertainty was associated with all model delays, gains, and time constants. Therefore, the scenarios were defined by vector as follows:
and the nominal scenario was defined as follows:
In this example, the RGA (relative gain matrix [37]) loop-pairing technique recommends the use of diagonal pairing. However, the DRGA (dynamic relative gain matrix) technique presented in [36] suggests off-diagonal pairing. Therefore, this served an example where it was unclear which pairing to use, and this applied even more so if we considered uncertainty in the model parameters.
These will then be the design concepts to be compared: the controller with a multi-loop control structure using a diagonal pairing will be the concept; and the the concept will be the off-diagonal pairing. The PI controllers were fitted for both pairings:
- Diagonal PI controllers ():
- Off-diagonal PI controllers ():where is the proportional gains, is the integral time in seconds for each design concept and control loop i, and and are the output errors, with and being the set points for each closed loop.
Once the control system was defined, the MOP corresponding to each design concept was defined in accordance with [30]. Two design objectives were chosen. The first, , evaluated the performance of each of the outputs by applying the ISE (integral of the squared error). The second, , evaluated the control efforts of the system by applying the ISU (integral of the squared control action). The design objectives measured the ISE and ISU when unit steps were introduced in reference and independently. By aggregating errors and , identical relative importance was given to both outputs. The same procedure was performed for control actions and . Treating ISE and ISU as separate objectives in an MOP enables a controller to be chosen, and it is compensated in performance and control effort according to the preferences established a posteriori. Constraints on and determine the zone of interest so that the controllers from the Pareto front are neither aggressive nor conservative.
To compare both concepts ( and ), the design objectives must be the same under each compared concept, even though each MOP tries to fit a different set of parameters, as follows:
where
and
are subject to
and
For each design concept, the parameter vector and its constraints change as follows:
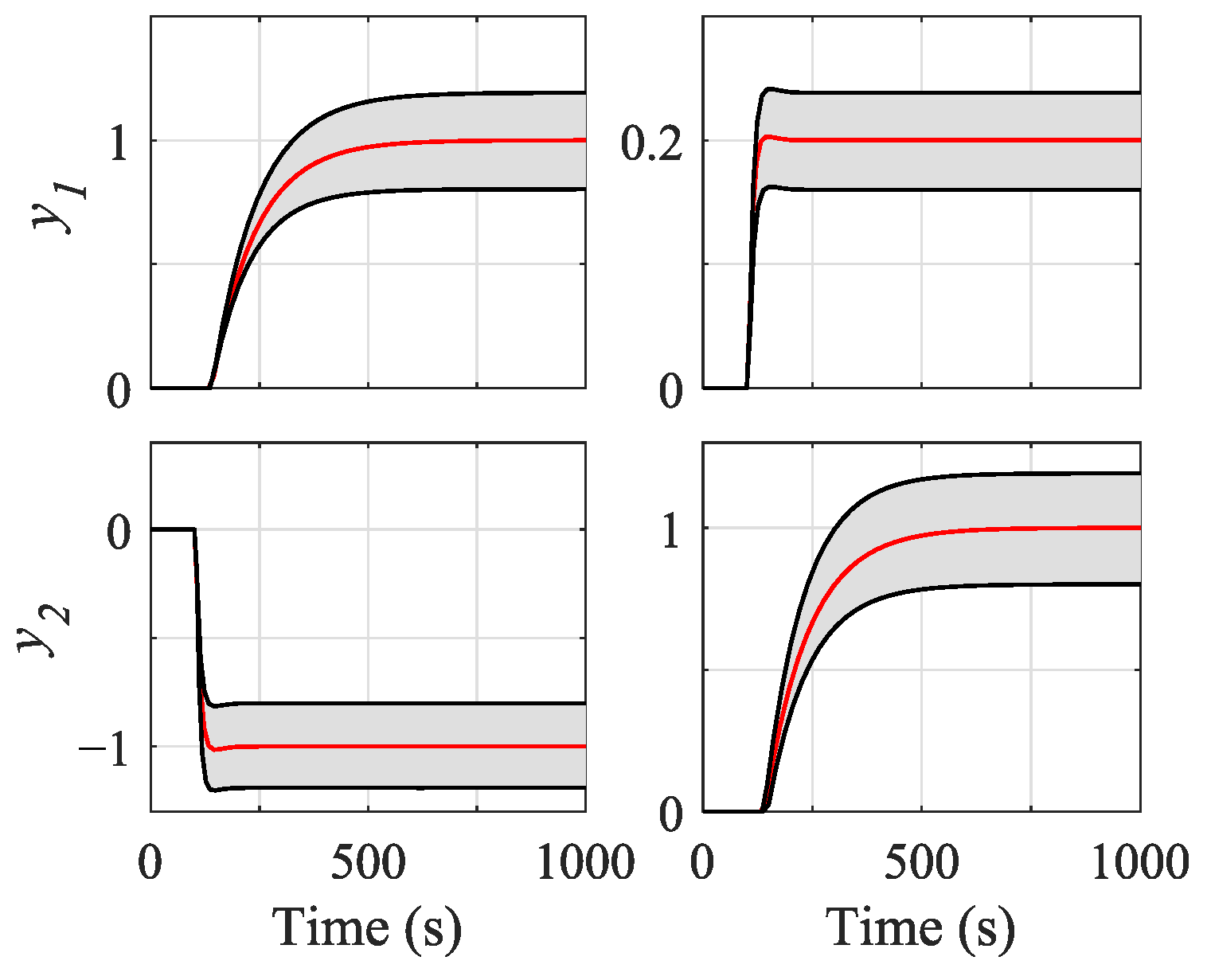
To account for uncertainty, a set of scenarios/models was considered. Each scenario was obtained by randomly varying the parameters of the nominal scenario by . In this case, a set of scenarios consisting of 50 models was defined. The open-loop envelope response seen in Figure 4 was obtained with this set. This envelope was 98% similar to that obtained with 25,000 different models. Therefore, the sample of 50 models was considered representative in the face of a variation. Thus, was the supremum value for every objective function separately for the set of 50 scenarios considered. This value will be the function that is to be minimized by the MOP (see Equation (16)). The controllers of the obtained set are guaranteed to have acceptable performance over the nominal model ().
is subject to
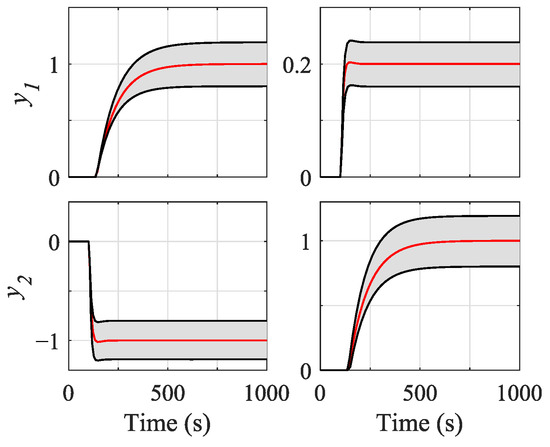
Figure 4.
Envelope response to the 50 scenarios/models of . On the left, is the response for input at s. On the right, is the response for at s. The response for the nominal model in both cases is plotted in red.
5.2. Results and Discussion
This section shows the results obtained after applying the approaches presented in Section Obtaining a Lightly Robust Set (traditional) and Section 4 (new methodology). The traditional approach obtains the lightly robust controllers , and the new methodology obtains the optimal and nearly optimal relevant controllers for the nominal scenario . These sets are analyzed for the nominal scenario and for the set of scenarios . The advantages and disadvantages of each of them, concerning the robustness of their obtained controllers, are exhibited. To make the comparison as fair as possible, the evMOGA and nevMOGA algorithms were used with the same settings (same population sizes, number of iterations, , etc.). The optimization stage was carried out with 10,000 evaluations of the objective function. No further evaluations were performed due to the high computational cost of taking uncertainty into account in the optimization stage.
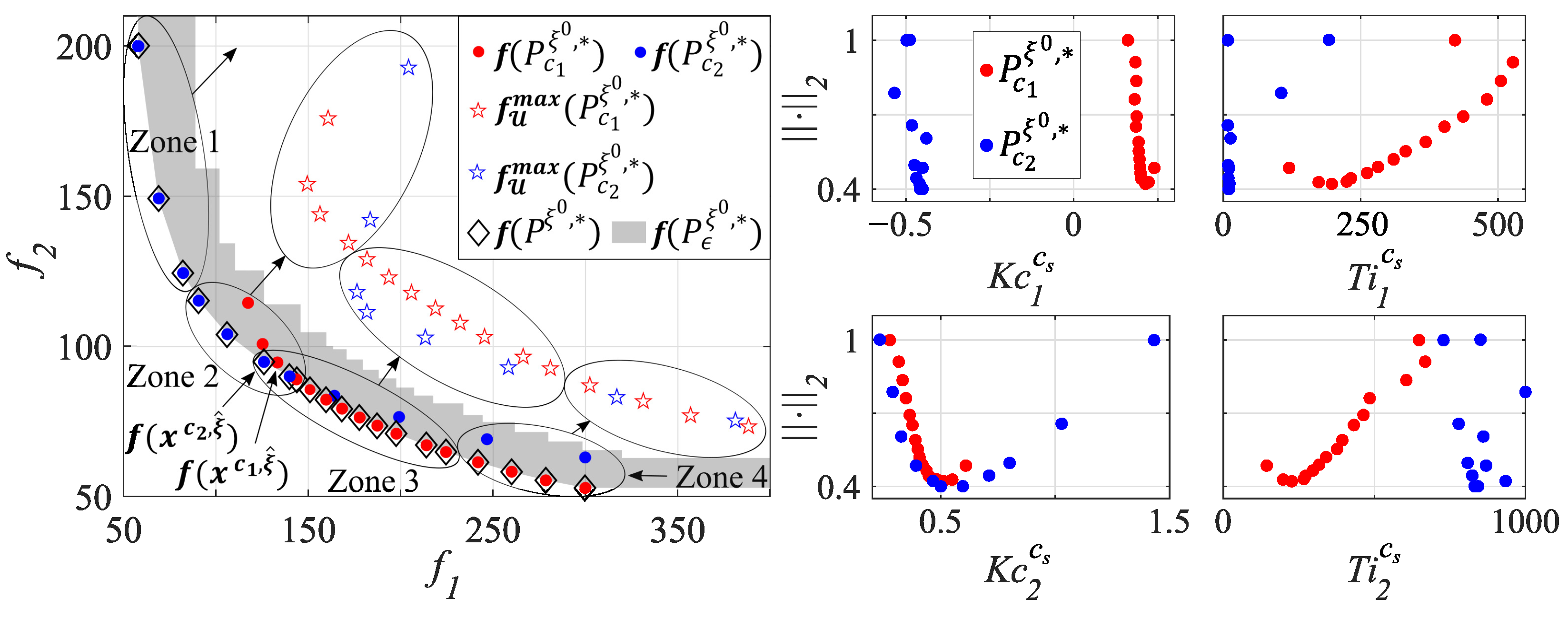
Figure 5 shows the Pareto sets obtained for each design concept (control pairings). These sets wwere obtained without considering the uncertainty in the optimization stage. The decision space is shown on the right. To show the decision variables, we used the level diagram (LD (available at Matlab Central: https://es.mathworks.com/matlabcentral/fileexchange/62224-interactive-tool-for-decision-making-in-multi-objective-optimization-with-level-diagrams, accessed on 5 July 2024) [38]) using 2-norm (). The LD tool is based on level diagrams, and each objective and design parameter is represented in a separate diagram. In this way, each level diagram represents the objective value or parameter on the abscissa axis and its norm value on the ordinate axis. The objective space is shown on the left. The performance of these controllers is plotted for the nominal scenario (using ) and for the set of scenarios (using ).
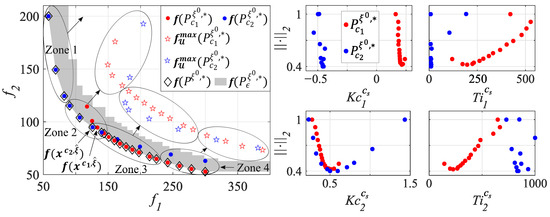
Figure 5.
In blue, is the off-diagonal concept (). In red, is the diagonal concept (). The dots represent , and the stars represent .
Once the sets and have been obtained, it is possible to obtain the global Pareto set (black diamonds in Figure 5) by considering all the design concepts simultaneously. With this set and parameter , the zone of optimal and nearly optimal controllers is defined for all concepts (the gray zone in Figure 5). All controllers obtained must be in .
It can be seen that both the Pareto fronts come into conflict. On these Pareto fronts, four zones are differentiated. Thus, under the nominal model, the following can be observed:
- The off-diagonal concept () is optimal in Zones 1 and 2.
- The diagonal concept () is optimal in Zones 3 and 4.
Therefore, neither design concept has complete dominance over the other.
Subsequently, we analyzed the robustness of the obtained controllers. To achieve this, we projected these controllers onto the objective space using , representing them with stars in Figure 5. The following could be observed:
- The off-diagonal concept (blue stars) was not very robust in Zone 1. In this zone, controllers were obtained with being very degraded and going off the graph’s scale.
- In Zone 2, diagonal concept was significantly more robust.
- In Zone 3, the most robust was the off-diagonal concept .
- Finally, in Zone 4, there was no clear preference between the compared concepts regarding their robustness.
Let us assume two situations:
- The designer prefers controllers with a small error in exchange for a worse control effort.
- The designer prefers controllers with low control effort in exchange for more error.
In the first situation, with the nominal scenario, the designer would choose a controller with an off-diagonal pairing (Zones 1 and 2). However, we observed how these controllers are not very robust when carrying out the uncertainty analysis. There were no robust controllers in Zone 1. In Zone 2, controllers with a diagonal pairing were significantly more robust. Therefore, in this situation, if the designer wants a robust controller, the designer should opt for a controller with a diagonal pairing (as opposed to if the designer relies on the nominal scenario).
In the second situation, with the nominal scenario, the designer would opt for a controller with a diagonal pairing (Zones 3 and 4). However, given the uncertainty in the model, controllers with an off-diagonal pairing are more robust in Zone 3. For this reason, considering robustness, the designer can opt for a controller with such a pairing (unlike under the nominal scenario).
Therefore, conducting an uncertainty analysis could completely change the designer’s decision. The designer could choose controllers with a different design concept than the one preferred for the nominal scenario.
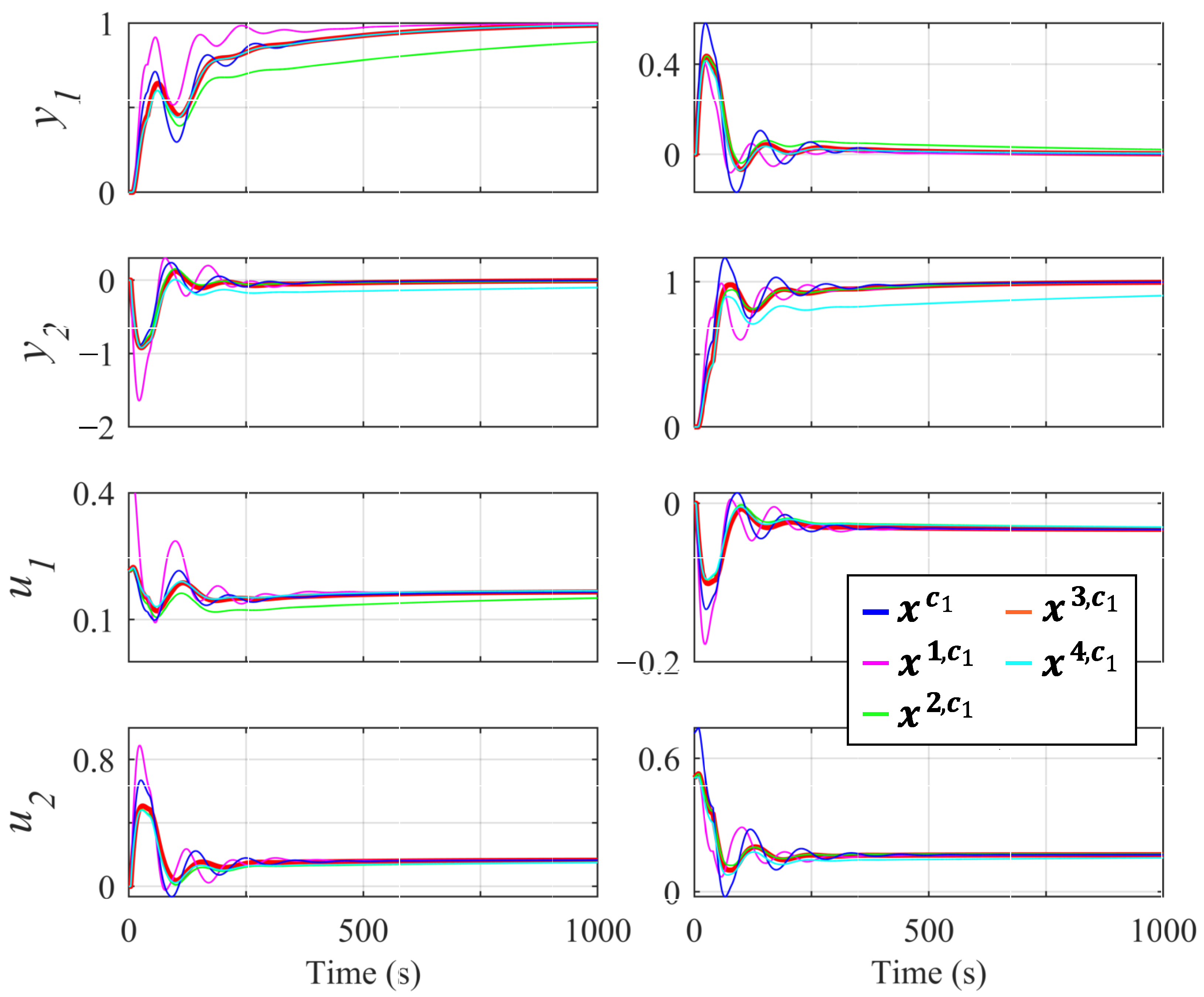
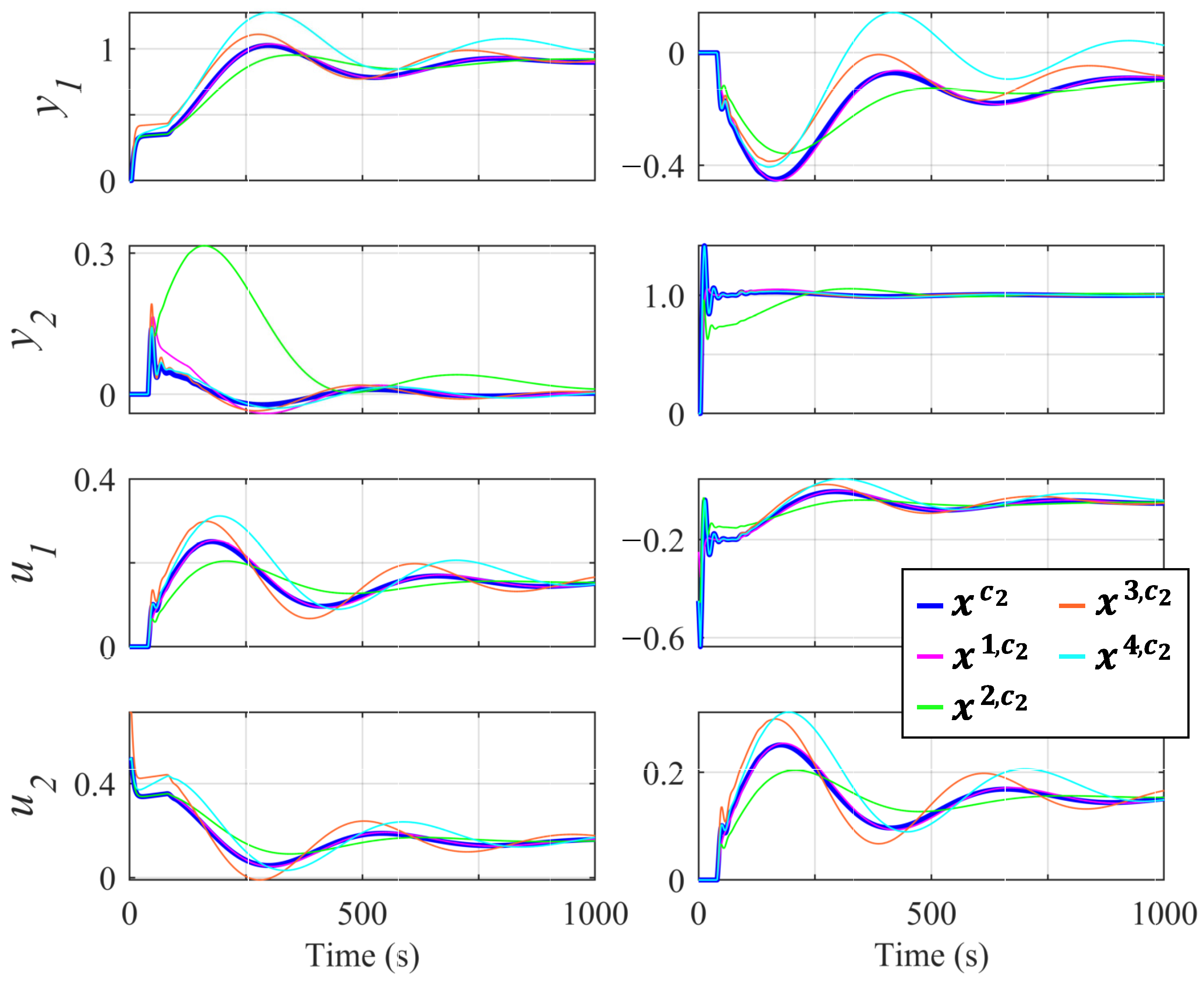
From sets and , the compromised controllers and were selected, respectively. These reference controllers enabled us to perform a sensitivity analysis for the choice of parameters and . To achieve this, we independently varied each parameter of these controllers until significant behavioral differences were achieved. For example, given reference controller , we obtained the following: (1) controller with an increase of over ; (2) controller with a 250 increase over ; (3) controller with an increase of over ; etc. Table 1 shows the new controllers and their performance with the nominal model. Furthermore, Figure 6 (diagonal pairing) and Figure 7 (off-diagonal pairing) show the output and control action of each of these controllers in the two proposed tests. Although the responses may seem poor, it can be verified in works where the same process is used and the same type of controller is tuned (see [30,36]) that the response exhibits similar behavior. As can be seen, all these controllers obtained a significantly different response than the initially selected compromise controllers. Therefore, neighborhood was defined (which was necessary to subsequently obtain set ). Furthermore, based on the results obtained, we defined (which was necessary to obtain sets and ) as the maximum acceptable degradation for the nominal model.

Table 1.
The controllers obtained for sensitivity analysis.
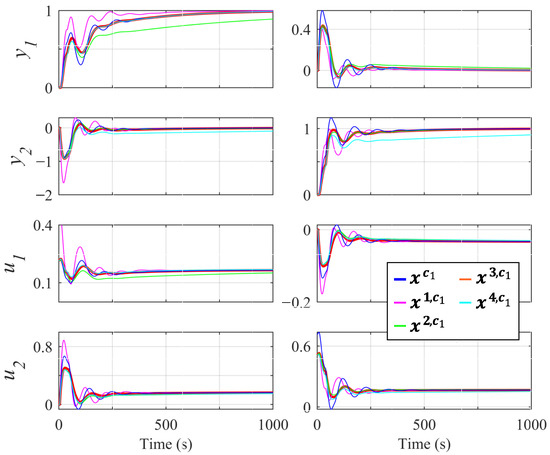
Figure 6.
Responses of the controllers with diagonal pairings of , , , , and . On the left, is the response with a unit step on . On the right, is the response with a unit step on .
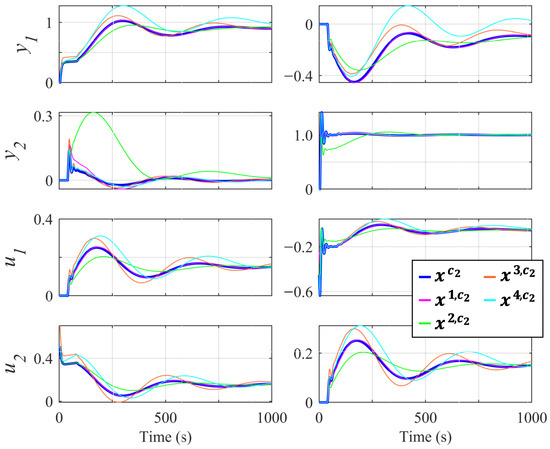
Figure 7.
Responses of the controllers with off-diagonal pairings of , , , , and . On the left, is the response with a unit step on . On the right, is the response with a unit step on .
We were thus in a position to analyze the two approaches compared in this work.
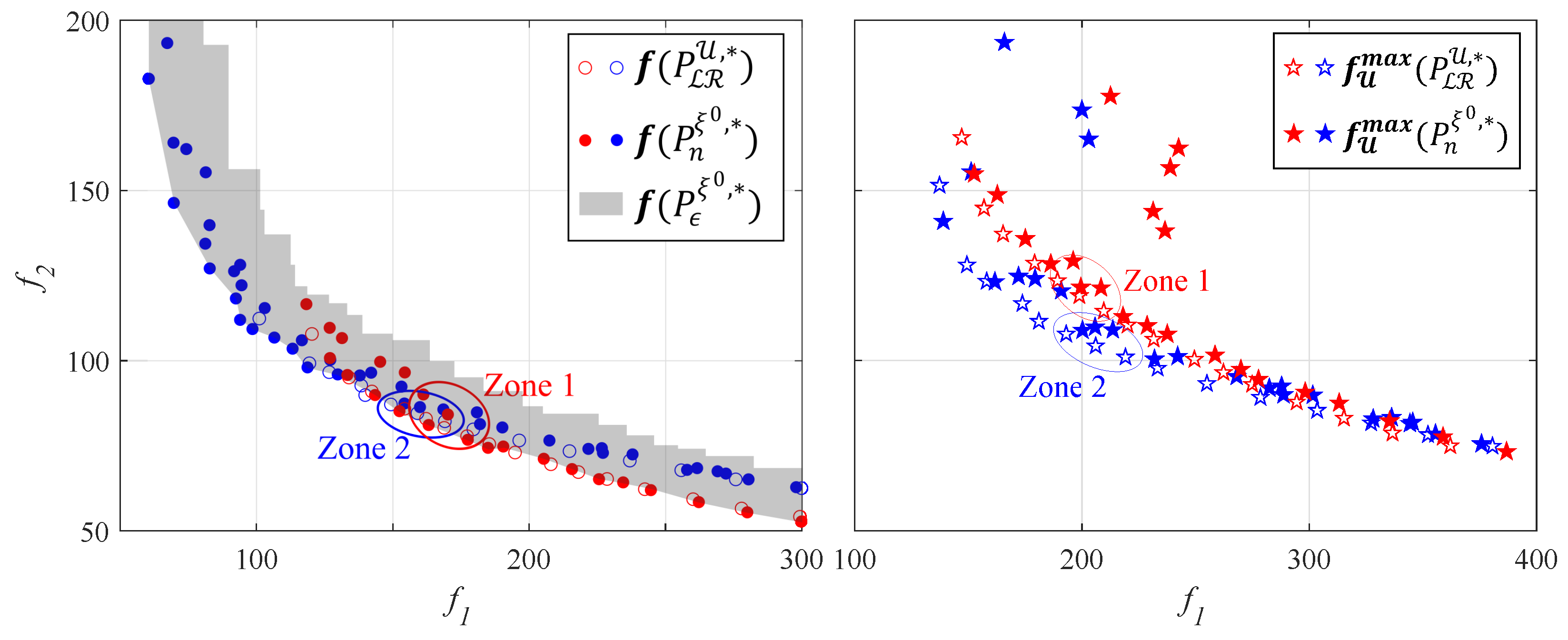
Figure 8 shows the performance of the and sets with the nominal scenario () and the set of scenarios (). In general, set was slightly better than with the nominal scenario. However, set was slightly more robust. As can be seen, both sets were similar, and the conclusions obtained from both were identical. Under the nominal model, the following can be seen:
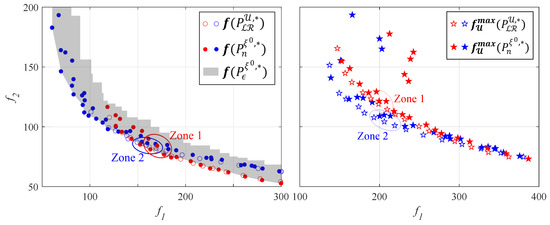
Figure 8.
In blue, is the off-diagonal concept (). In red, is the diagonal concept (). The circles represent , and the stars represent .
- The off-diagonal concept () is optimal in the range .
- The diagonal concept () is optimal in the range .
Subsequently, the robustness of the obtained controllers was analyzed. It must be taken into account that some of the controllers of set obtained poor robustness and were outside the scale of the figure. Under uncertainty, the following can be observed:
- The off-diagonal concept is now more robust for small values (unlike before).
- The off-diagonal concept is more robust in the range .
- The diagonal concept is optimal in the range .
Furthermore, in Figure 8, Zones 1 and 2 are defined with the controllers that have similar robustness. In Zone 1, six controllers are selected: three controllers from set and three controllers from set . In Zone 2, six controllers are selected: three controllers from set and three controllers from set . The parameters of these controllers are seen in Table 2. As can be seen, the three controllers belonging to in each design concept were very similar (, , and in Zone 1; , , and in Zone 2). Set had a controller similar to those controllers ( in Zone 1 and in Zone 2). However, in addition to that, had two significantly different controllers with similar robustness. In Zone 1, controllers and were obtained. In Zone 2, controllers and were obtained. These controllers had a similar robustness and were significantly different from the controllers. This occurred repeatedly along the obtained Pareto front. Therefore, the new methodology presented obtains greater diversity and enables the designer to choose the final controller with better information.

Table 2.
The controllers in the Zone 1 and 2 of Figure 8.
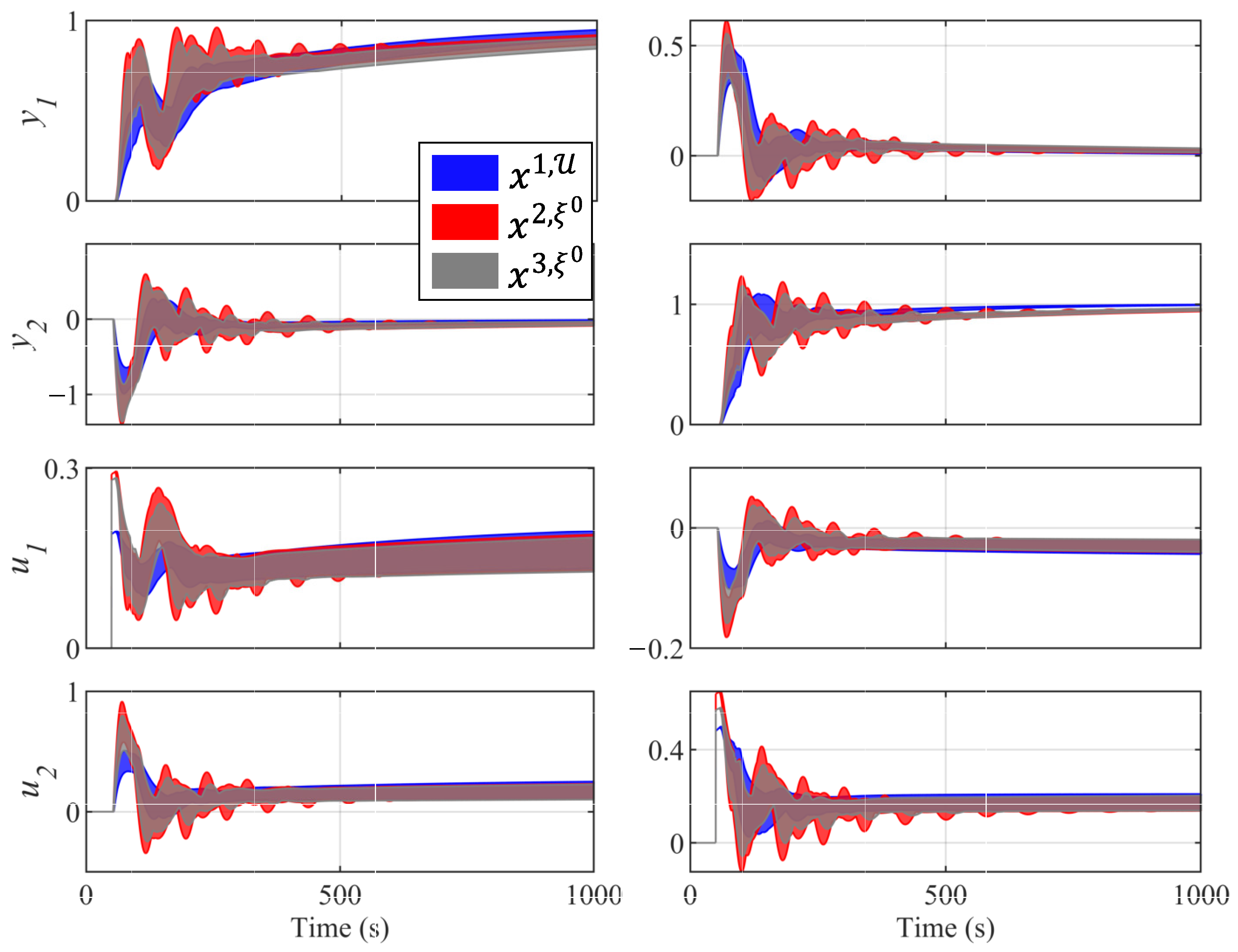
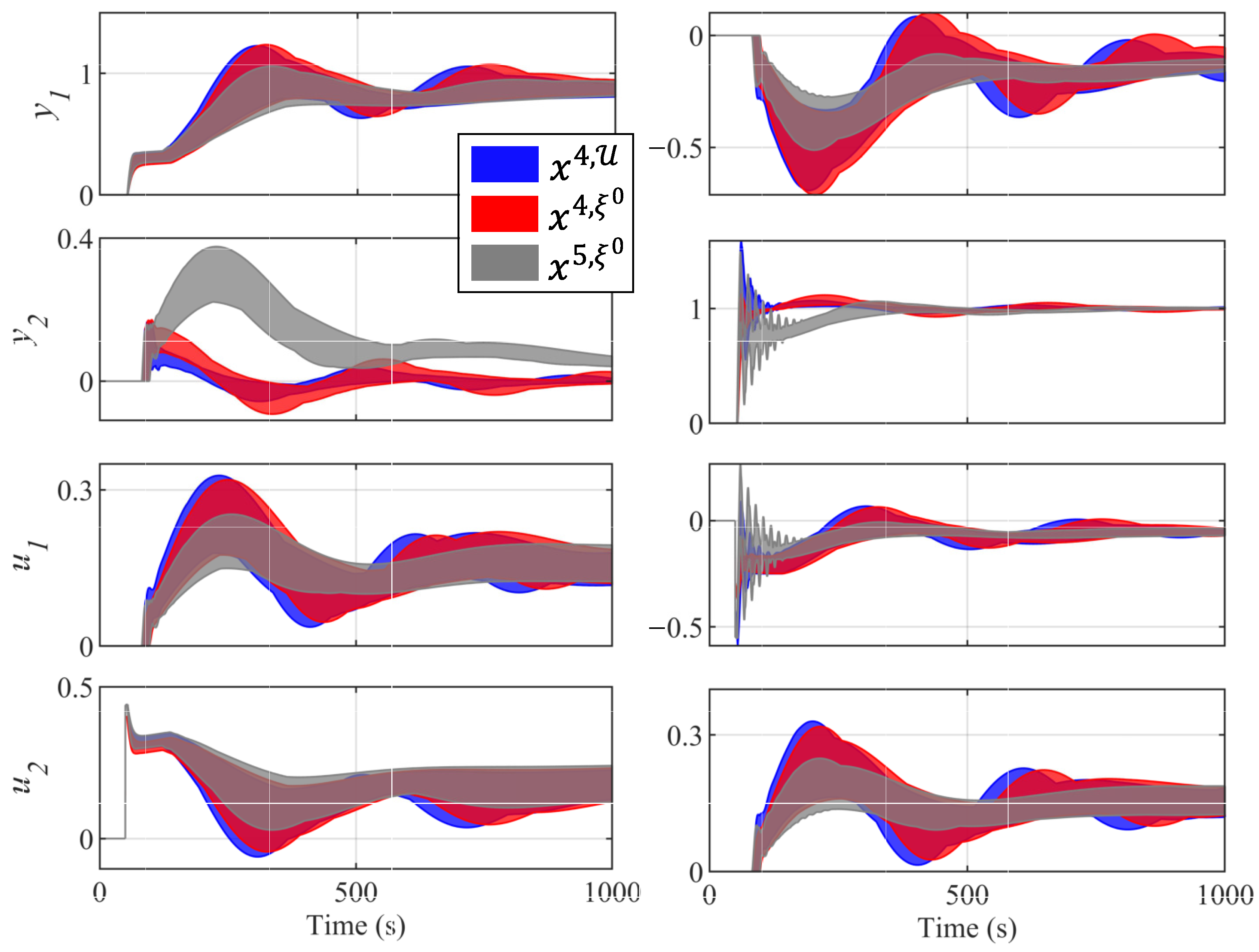
Figure 9 shows the envelope response to the 50 models of controllers , , and for diagonal pairings. The lightly robust controller obtained the envelope with the smallest oscillation at the outputs. In addition, it requireed less control effort. In set there was a controller very similar to this one (, see Table 2). Therefore, the designer could choose this controller with any of the approaches that were compared in this work. Furthermore, controllers and , which were obtained by set , had a significantly different envelope response. Therefore, the designer might prefer these controllers.
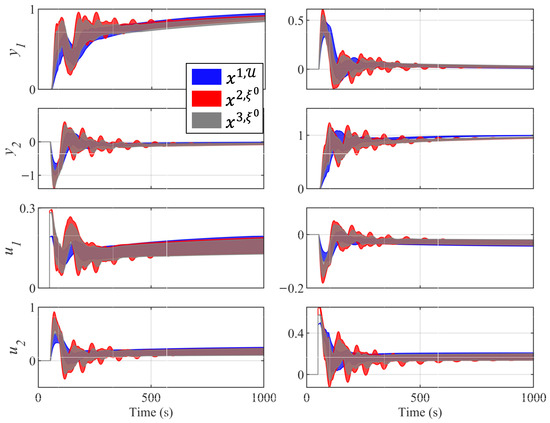
Figure 9.
Envelope response of controllers , , and for the 50 models . On the left, is the response with a unit step on . On the right, is the response with a unit step on .
Figure 10 shows the envelope response to the 50 models of controllers , , and for off-diagonal pairings, where is a lightly robust controller, and and belong to set . Controller obtained an envelope similar to . However, in some situations, controller obtained a better response. For example, output for controller had a smaller oscillation than the rest of the controllers. However, it produces a larger oscillation about . For all these reasons, the designer may choose the controller instead of the rest of the controllers. Therefore, the new methodology presented obtains a greater diversity of controllers, thus allowing the designer to decide with a greater number of criteria.
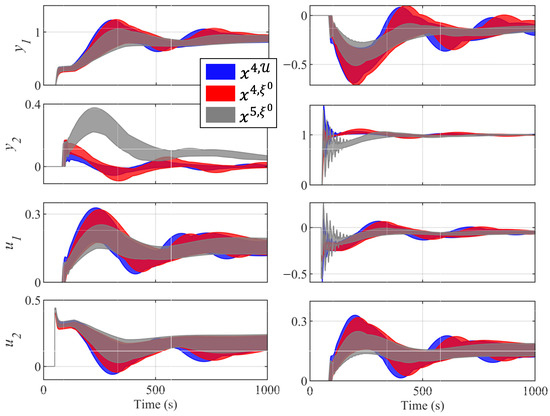
Figure 10.
Envelope response of controllers , , and for the 50 models . On the left, is the response with a unit step on . On the right, is the response with a unit step on .
Table 3 shows the computational cost (CPU processor Intel Core i7, 3.2 GHz with 16 GB RAM) required for each approach. Obtaining had a higher computational cost than obtaining because the controllers in the 50 scenarios in the optimization process had to be evaluated. The methodology presented only evaluated the 50 scenarios in the decision stage on the controller, which were previously obtained in the optimization stage.

Table 3.
Computational cost.
Some of the following conclusions can be drawn:
- (new methodology, see Section 4) mathematically guarantees (see Theorem 1) its similarity to the set of robust controllers (see Figure 8), with a notably lower computational cost (see Table 3). In addition, this methodology provides more information, and so enables a more reliable solution to be chosen.
6. Conclusions
In this article, a new methodology for the design of robust decentralized multi-variable controllers is presented. This methodology obtains the optimal and relevant nearly optimal controllers (nearly optimal non-dominated in their neighborhood) for the nominal scenario . The robustness is then analyzed in the decision stage on the obtained set. In this way, robust solutions with a nearly optimal performance for the nominal scenario are not ruled out.
This methodology guarantees obtaining similar solutions (where similar is defined by the designer) for the lightly robust (which was previously introduced in the literature) with a significantly lower computational cost. Lightly robust solutions obtain a trade-off between robustness and nominal performance. To obtain these solutions, it is necessary to evaluate the uncertainty of the optimization process. Considering uncertainty in the optimization stage enables us to obtain all the existing robust controllers in exchange for a high (sometimes unaffordable) computational cost.
The set of controllers obtained using the methodology presented in this article, and it was then compared with the lightly robust controllers . To achieve this, an example of a multi-variable process with two alternative control structures was used. These are multi-loop control structures with PI controllers but with different loop pairings. The consideration of uncertainty can modify the pairing chosen by the designer. The new methodology obtained results similar to the lightly robust controllers with a 95% lower computational cost. Furthermore, it obtained a greater diversity of controllers. Therefore, the methodology presented is a good alternative for the design of robust, decentralized multi-variable controllers.
Author Contributions
Conceptualization, A.P.; methodology, A.P., X.B. and J.M.H.; software developed, A.P.; validation, A.P.; writing—original draft preparation, A.P.; writing—review and editing, X.B., J.M.H., J.S. and R.S.; supervision, R.S. and J.S.; funding acquisition, X.B., J.M.H. and J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported, in part, by grant PID2021-124908NB-I00, which was funded by MCIN/AEI/10.13039/501100011033/; by “ERDF A way of making Europe”; and by the Generalitat Valenciana regional government through project CIAICO/2021/064.
Data Availability Statement
The data presented in this study are available on request from the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2001; Volume 16. [Google Scholar]
- Miettinen, K. Nonlinear Multiobjective Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 12. [Google Scholar]
- Gunantara, N. A review of multi-objective optimization: Methods and its applications. Cogent Eng. 2018, 5, 1502242. [Google Scholar] [CrossRef]
- Weinmann, A. Uncertain Models and Robust Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Xu, J.; Du, Y.; Chen, Y.H.; Guo, H. Optimal robust control design for constrained uncertain systems: A fuzzy-set theoretic approach. IEEE Trans. Fuzzy Syst. 2018, 26, 3494–3505. [Google Scholar] [CrossRef]
- Schöbel, A. Generalized light robustness and the trade-off between robustness and nominal quality. Math. Methods Oper. Res. 2014, 80, 161–191. [Google Scholar] [CrossRef]
- Laughlin, D.L.; Jordan, K.G.; Morari, M. Internal model control and process uncertainty: Mapping uncertainty regions for SISO controller design. Int. J. Control 1986, 44, 1675–1698. [Google Scholar] [CrossRef]
- Parnianifard, A.; Azfanizam, A.S. Metamodel-based robust simulation-optimization assisted optimal design of multiloop integer and fractional-order PID controller. Int. J. Numer. Model. Electron. Netw. Devices Fields 2020, 33, e2679. [Google Scholar] [CrossRef]
- Crespo, L.G.; Kenny, S.P. Robust Control Design for Systems with Probabilistic Uncertainty; Technical Report; NASA: Washington, DC, USA, 2005. [Google Scholar]
- Fischetti, M.; Monaci, M. Light robustness. In Robust and Online Large-Scale Optimization; Springer: Berlin/Heidelberg, Germany, 2009; pp. 61–84. [Google Scholar]
- Hernández Castellanos, C.I.; Schütze, O.; Sun, J.Q.; Ober-Blöbaum, S. Non-Epsilon Dominated Evolutionary Algorithm for the Set of Approximate Solutions. Math. Comput. Appl. 2020, 25, 3. [Google Scholar] [CrossRef]
- Ide, J.; Schöbel, A. Robustness for uncertain multi-objective optimization: A survey and analysis of different concepts. OR Spectr. 2016, 38, 235–271. [Google Scholar] [CrossRef]
- Soyster, A.L. Convex programming with set-inclusive constraints and applications to inexact linear programming. Oper. Res. 1973, 21, 1154–1157. [Google Scholar] [CrossRef]
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. Robust Optimization; Princeton University Press: Princeton, NJ, USA, 2009; Volume 28. [Google Scholar]
- Kuroiwa, D.; Lee, G.M. On robust multiobjective optimization. Vietnam J. Math 2012, 40, 305–317. [Google Scholar]
- Parnianifard, A.; Fakhfakh, M.; Kotti, M.; Zemouche, A.; Wuttisittikulkij, L. Robust tuning and sensitivity analysis of stochastic integer and fractional-order PID control systems: Application of surrogate-based robust simulation-optimization. Int. J. Numer. Model. Electron. Netw. Devices Fields 2021, 34, e2835. [Google Scholar] [CrossRef]
- Bertsimas, D.; Sim, M. The price of robustness. Oper. Res. 2004, 52, 35–53. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Nemirovski, A. Robust solutions of linear programming problems contaminated with uncertain data. Math. Program. 2000, 88, 411–424. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Goryashko, A.; Guslitzer, E.; Nemirovski, A. Adjustable robust solutions of uncertain linear programs. Math. Program. 2004, 99, 351–376. [Google Scholar] [CrossRef]
- Erera, A.L.; Morales, J.C.; Savelsbergh, M. Robust optimization for empty repositioning problems. Oper. Res. 2009, 57, 468–483. [Google Scholar] [CrossRef]
- Liebchen, C.; Lübbecke, M.; Möhring, R.; Stiller, S. The concept of recoverable robustness, linear programming recovery, and railway applications. In Robust and Online Large-Scale Optimization: Models and Techniques for Transportation Systems; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–27. [Google Scholar]
- Stiller, S. Extending Concepts of Reliability-Network Creation Games, Real-Time Scheduling, and Robust Optimization. Ph.D. Thesis, Technical University Berlin, Berlin, Germany, 2009. [Google Scholar]
- Goerigk, M.; Schmidt, M.; Schöbel, A.; Knoth, M.; Müller-Hannemann, M. The price of strict and light robustness in timetable information. Transp. Sci. 2014, 48, 225–242. [Google Scholar] [CrossRef]
- Goerigk, M.; Schöbel, A. An empirical analysis of robustness concepts for timetabling. In Proceedings of the 10th Workshop on Algorithmic Approaches for Transportation Modelling, Optimization, and Systems (ATMOS’10), Liverpool, UK, 6–10 September 2010. [Google Scholar]
- He, Y.; Li, Z.; Zhang, J.; Shi, G.; Cao, W. Day-ahead and intraday multi-time scale microgrid scheduling based on light robustness and MPC. Int. J. Electr. Power Energy Syst. 2023, 144, 108546. [Google Scholar] [CrossRef]
- Schöbel, A.; Zhou-Kangas, Y. The price of multiobjective robustness: Analyzing solution sets to uncertain multiobjective problems. Eur. J. Oper. Res. 2021, 291, 782–793. [Google Scholar] [CrossRef]
- Klamroth, K.; Köbis, E.; Schöbel, A.; Tammer, C. A unified approach for different concepts of robustness and stochastic programming via non-linear scalarizing functionals. Optimization 2013, 62, 649–671. [Google Scholar] [CrossRef]
- Pajares, A.; Blasco, X.; Herrero, J.M.; Veyna, U. Advantages of using relevant nearly optimal solutions in multi-objective tuning of robust controllers. ISA Trans. 2023, 139, 143–155. [Google Scholar] [CrossRef]
- Pajares, A.; Blasco, X.; Herrero, J.M.; Reynoso-Meza, G. A multiobjective genetic algorithm for the localization of optimal and nearly optimal solutions which are potentially useful: NevMOGA. Complexity 2018, 2018, 1792420. [Google Scholar] [CrossRef]
- Herrero, J.; Reynoso-Meza, G.; Ramos, C.; Blasco, X. Considerations on loop pairing in MIMO processes. A multi-criteria analysis. IFAC-PapersOnLine 2017, 50, 4454–4459. [Google Scholar] [CrossRef]
- Pareto, V.; Schwier, A.S.; Page, A.N. Manual of Political Economy; Macmillan: New York, NY, USA, 1971. [Google Scholar]
- Schütze, O.; Coello, C.A.C.; Talbi, E.G. Approximating the ε-efficient set of an MOP with stochastic search algorithms. In Proceedings of the Mexican International Conference on Artificial Intelligence, Aguascalientes, Mexico, 4–10 November 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 128–138. [Google Scholar]
- Schütze, O.; Vasile, M.; Coello, C.A.C. Computing the set of epsilon-efficient solutions in multiobjective space mission design. J. Aerosp. Comput. Inf. Commun. 2011, 8, 53–70. [Google Scholar] [CrossRef]
- Ehrgott, M.; Ide, J.; Schöbel, A. Minmax robustness for multi-objective optimization problems. Eur. J. Oper. Res. 2014, 239, 17–31. [Google Scholar] [CrossRef]
- Martínez-Iranzo, M.; Herrero, J.M.; Sanchis, J.; Blasco, X.; García-Nieto, S. Applied Pareto multi-objective optimization by stochastic solvers. Eng. Appl. Artif. Intell. 2009, 22, 455–465. [Google Scholar] [CrossRef]
- Mc Avoy, T.; Arkun, Y.; Chen, R.; Robinson, D.; Schnelle, P.D. A new approach to defining a dynamic relative gain. Control Eng. Pract. 2003, 11, 907–914. [Google Scholar] [CrossRef]
- Cai, L.J.; Erlich, I.; Fortmann, J. Dynamic voltage stability analysis for power systems with wind power plants using relative gain array (RGA). IFAC Proc. Vol. 2012, 45, 331–336. [Google Scholar] [CrossRef]
- Blasco, X.; Herrero, J.M.; Reynoso-Meza, G.; Iranzo, M.A.M. Interactive tool for analyzing multiobjective optimization results with level diagrams. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Berlin, Germany, 15–19 July 2017; pp. 1689–1696. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).