Approximation of the Interactions of Rarefaction Waves by the Wave Front Tracking Method
Abstract
1. Introduction
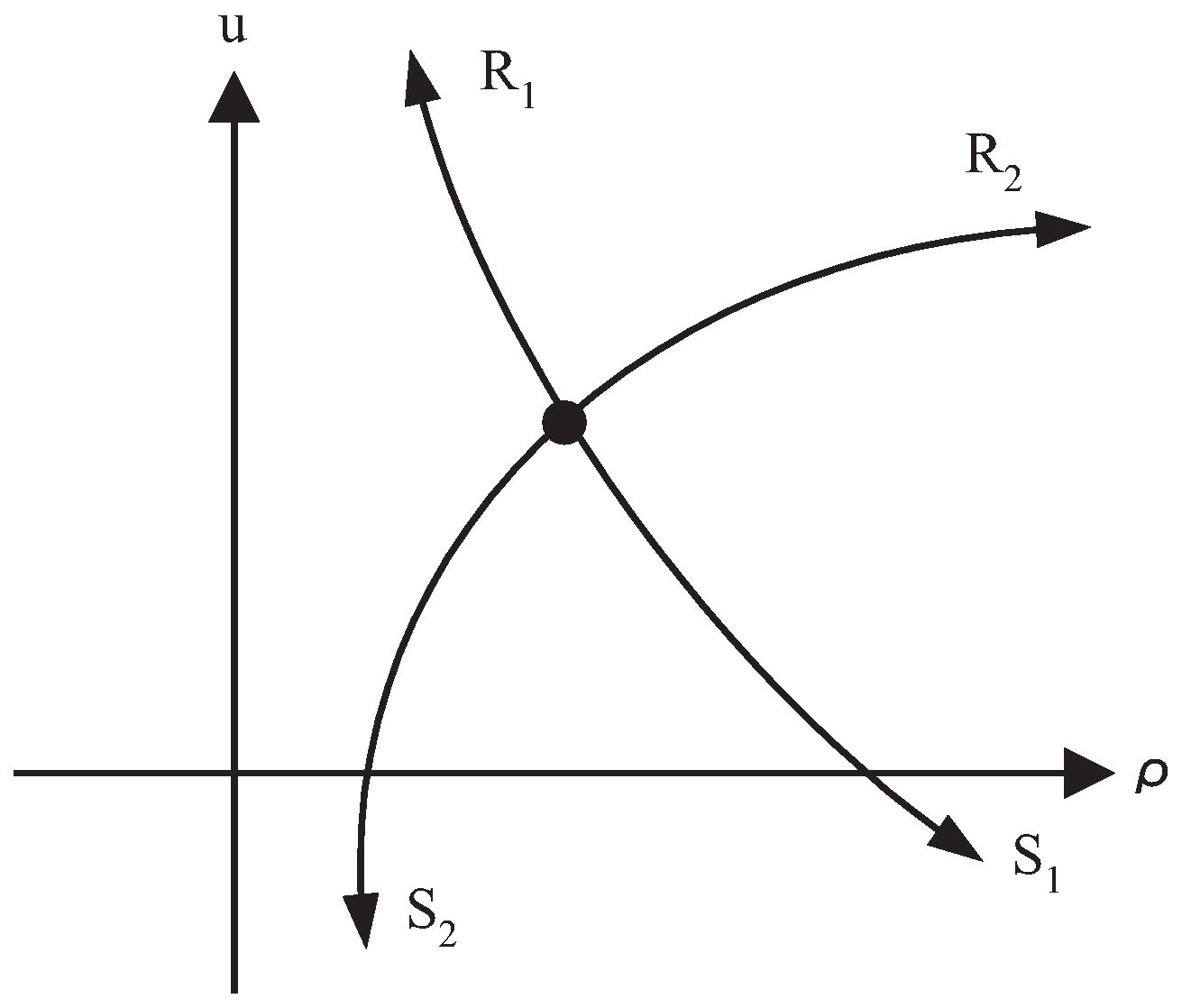
2. The Pressureless Gas Dynamics Model
Elementary Waves
- —a fixed speed of a non-physical wave,
- —a constant that controls rarefaction waves strength;
- —a number determining which type of Riemann solver is going to be used (accurate or approximative).
3. SDW Solutions to the Pressureless Gas Dynamics Model
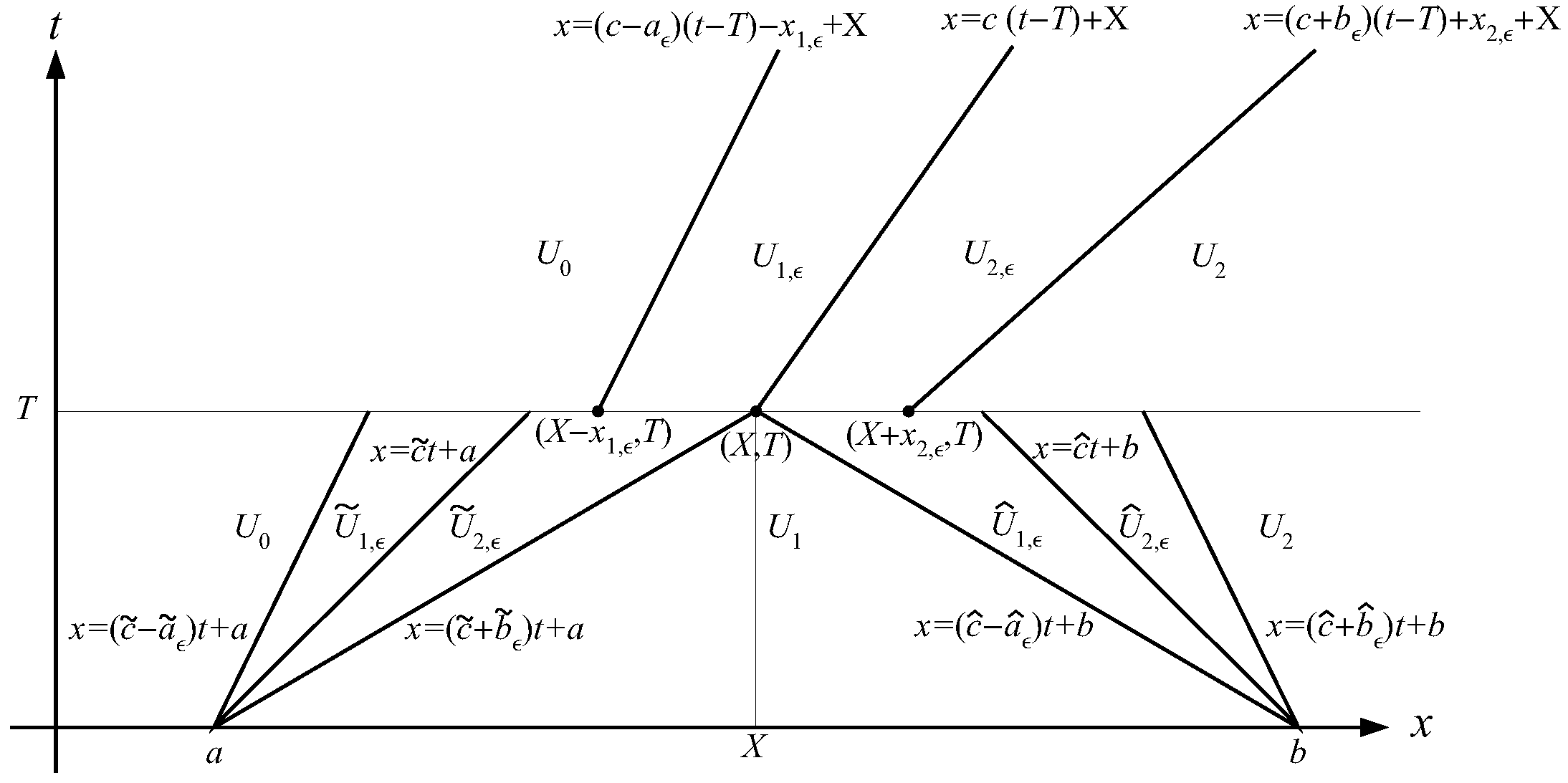
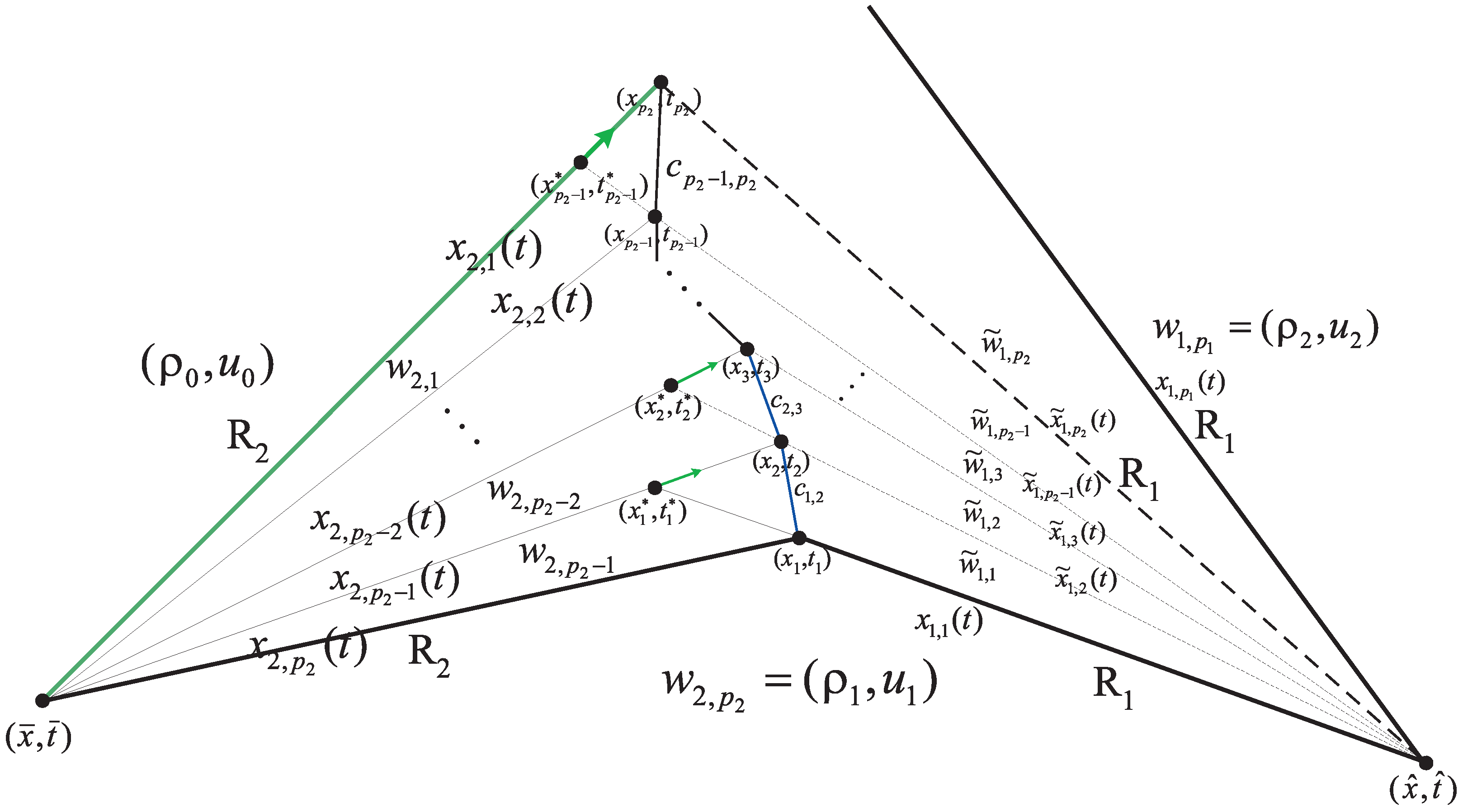
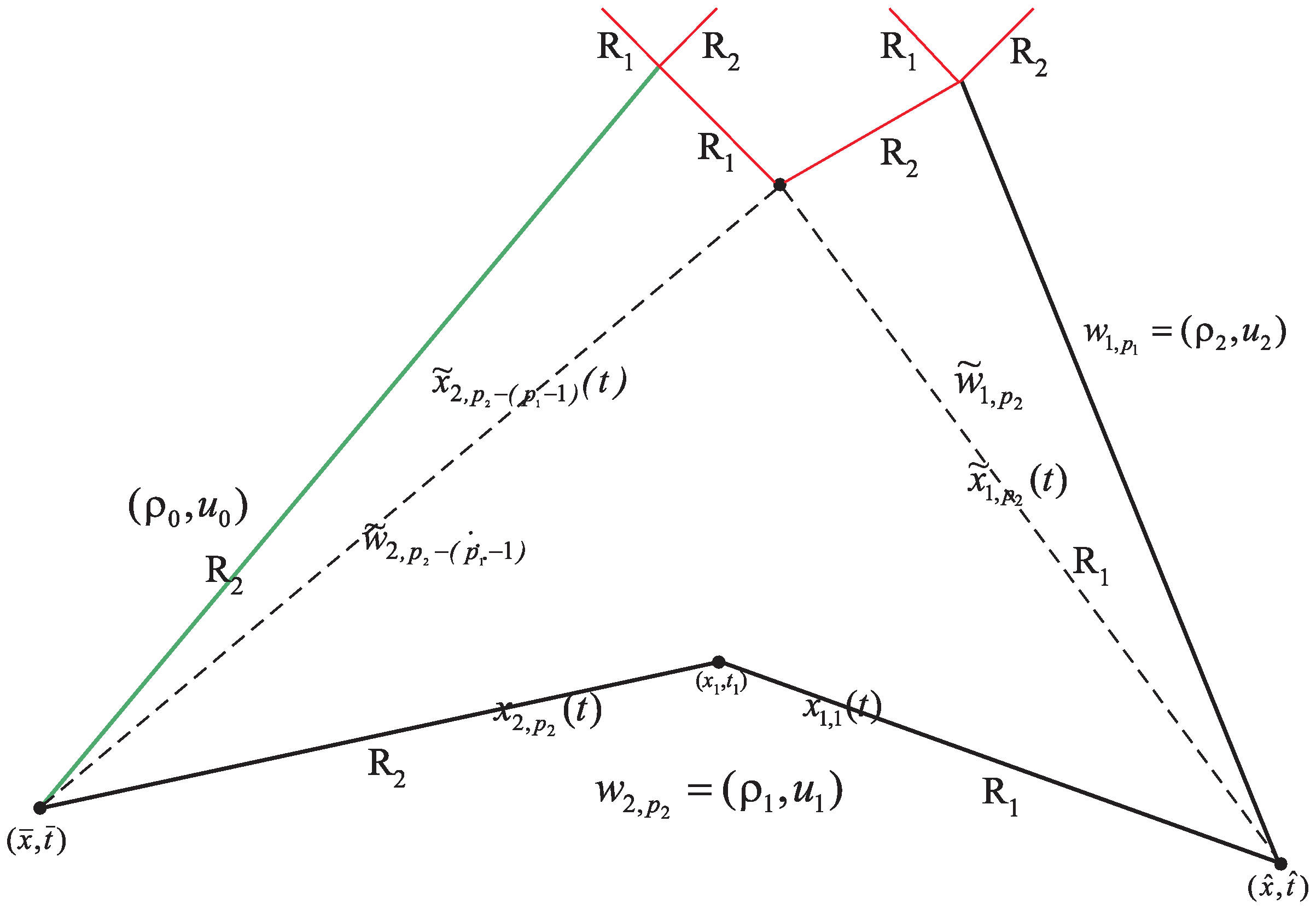
4. Algorithm of a New Concept of Rarefaction Wave Interactions Approximation
- Find the intersection point of the two half-lines and , solving the systemWe mark the solution as .
- Solving the systemwe find the intersection between and . Let us denote the solution of this system as .
- Choose to make the RH deficit as small as possible for . To be more precise, after is chosen, we check ifholds for . If it does not hold, we choose and check again, and so on. This stops after steps, even if the inequalities are not satisfied, and we accept new time . Here,holds, based on (17).
- Now, for each we do the following. Find the intersection between and , solving the systemWe denote the solution as . Then, choose to make the RH deficit as small as possible for . After is chosen, we check ifholds. If it does not hold, we choose or ,…until the upper inequalities are satisfied. If it is not a case, then after steps, we accept new time . Here,
- The half-lines that we keep during WFT approximation are , , .
- Find the intersection point of the two half-lines and , solving the systemWe mark the solution as .
- Solving the systemwe find the intersection between and . Let us denote the solution of this system as .
- Choose to make the RH deficit as small as possible for . To be more precise, after is chosen, we check ifholds for . If it does not hold, we choose and check again, and so on. This stops after steps, even if the inequalities are not satisfied, and we accept new time . Here,holds, based on (16).
- Now, for each we do the following. Find the intersection between and , solving the systemWe denote the solution as . Then, choose to make the RH deficit as small as possible for . To be more precise, after is chosen, we check ifholds. If it does not hold, we choose or ,…until the upper inequalities are satisfied. If it is not a case, then after steps, we accept new time . Here,
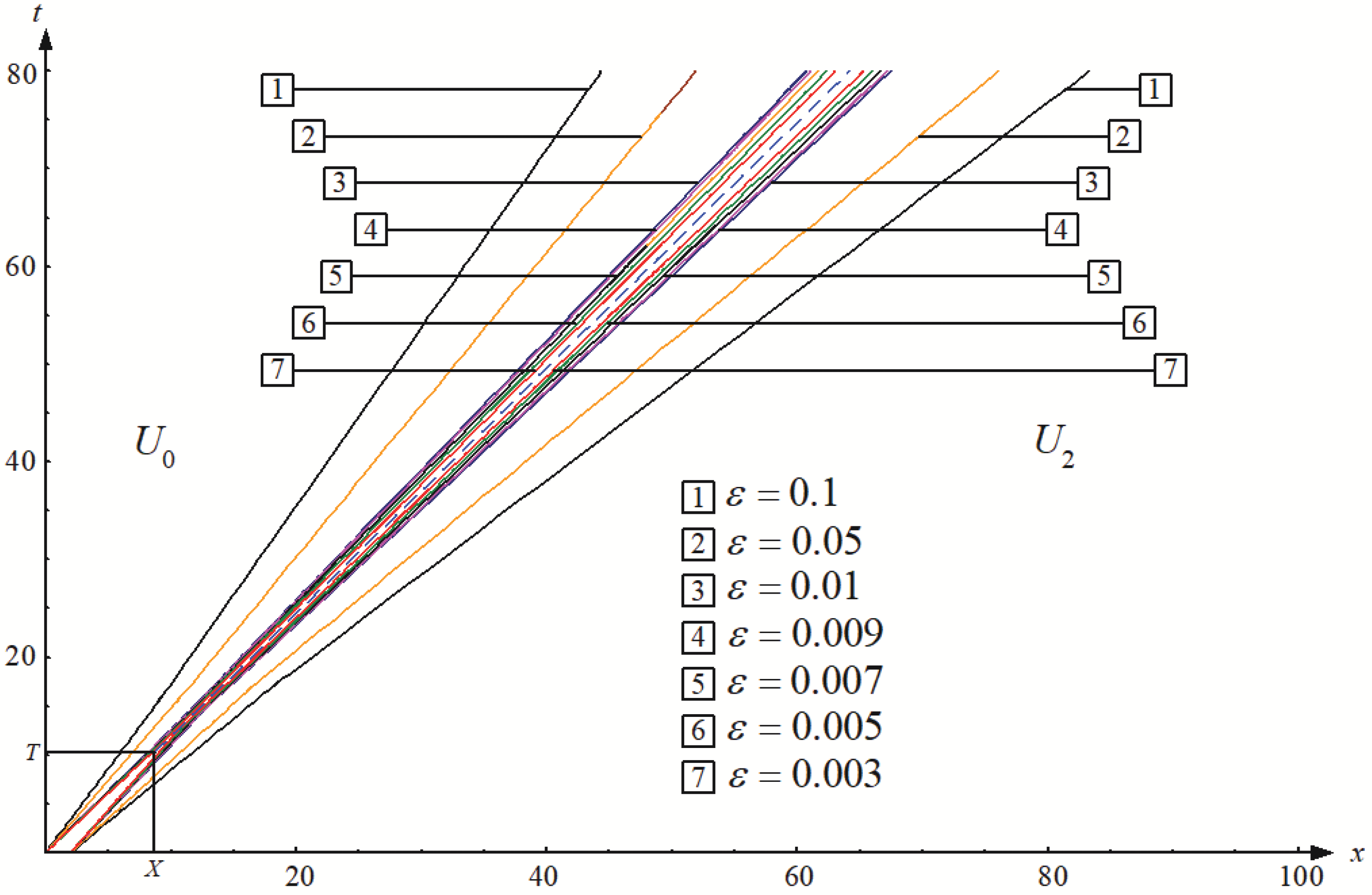
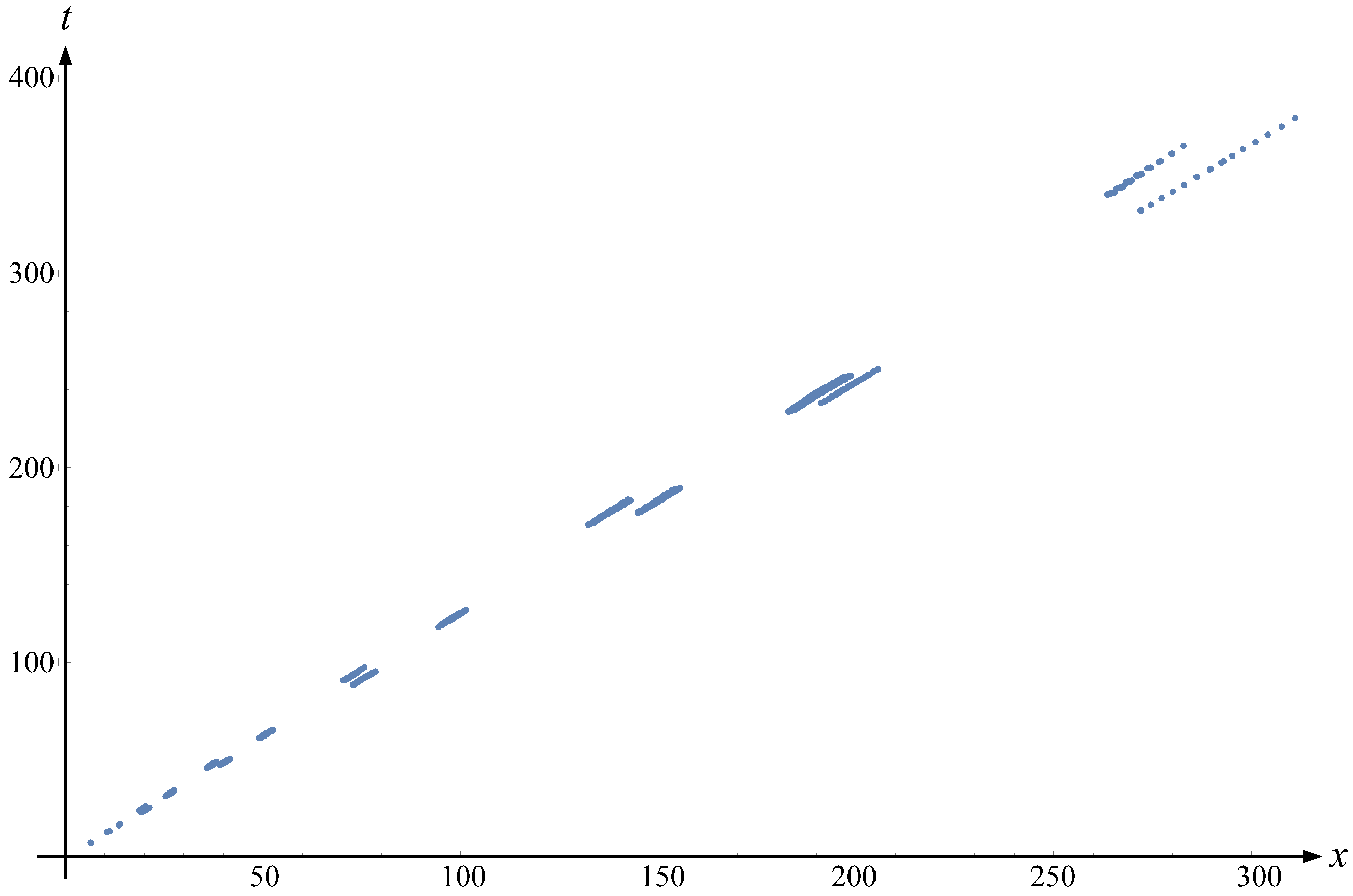
5. Numerical Results
- and are connected by an 1-shock;
- and are connected by a 2-shock;
- and are connected by an 1-shock;
- and are connected by a 2-shock.
- Example 1
- Example 2
- Example 3
- Example 4
- Example 5
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description |
| x | spatial variable |
| t | time variable |
| density | |
| u | velocity |
| small parameter | |
| parameter | |
| delta shock wave | |
| c | speed of the delta shock wave |
| speed of the shock waves of the both families | |
| strength of delta shock wave | |
| eigenvalues | |
| eigenvectors | |
| strength of the rarefaction wave | |
| number of the rarefaction waves of both families | |
| g | generation order |
| maximal allowed generation order | |
| fixed speed of non-physical wave | |
| shifts of the SDW | |
| Rankine–Hugoniot deficits | |
| strength of the divided rarefaction waves |
References
- Jeffrey, A. Quasilinear Hyperbolic Systems and Waves; Pitman: London, UK, 1976. [Google Scholar]
- Smoller, J. Shock Waves and Reaction-Diffusion Equations; Springer: New York, NY, USA, 1994. [Google Scholar]
- Bressan, A. Hyperbolic Systems of Conservation Laws. The One-Dimensional Cauchy Problem; Oxford University Press: New York, NY, USA, 2000. [Google Scholar]
- Holden, H.; Risbero, N.H. Front Tracking Method for Hyperbolic Conservaton Laws; Springer: New York, NY, USA, 2002. [Google Scholar]
- Kamrul, H.; Takia, H.; Rahaman, M.M.; Sikdar, M.H.; Hossain, B.; Hossen, K. Numerical Study of the Characteristics of Shock and Rarefaction Waves for Nonlinear Wave Equation. Am. J. Appl. Sci. Res. 2022, 8, 18–24. [Google Scholar]
- Lax, P.D. Shocks waves and entropy. In Contributions to Functional Analysis; Zarantonello, E.A., Ed.; Academic Press: New York, NY, USA, 1971; pp. 603–634. [Google Scholar]
- Chang, T.; Ling, H. The Reimann Problem and Interaction of Waves in Gas Dynamics; Longman Harlow: London, UK, 1989. [Google Scholar]
- Li, J.; Zhang, T.; Yang, S. The Two-Dimensional Riemann Problem in Gas Dynamics; Longman Harlow: London, UK, 1998. [Google Scholar]
- Chen, G.Q.; Liu, H. Formation of delta-shocks and vacuum states in the vanishing pressure limit of solutions to the isentropic Euler equations. SIAM J. Math. Anal. 2003, 34, 925–938. [Google Scholar] [CrossRef]
- Huang, F. Weak solution to pressureless type system. Comm. Part. Diff. Eqs. 2005, 30, 283–304. [Google Scholar] [CrossRef]
- Weinan, E.; Rykov, Y.G.; Sinai, Y.G. Generalized variotional principles, global weak solutions and behavior with random initial data for systems of consevation laws arising in adhesion particle dynamics. Comm. Math. Phys. 1996, 177, 349–380. [Google Scholar] [CrossRef]
- Keyfitz, B.L.; Kranzer, H.C. Spaces of weighted measures for conservation laws with singular shock solutions. J. Diff. Eq. 1995, 118, 420–451. [Google Scholar] [CrossRef]
- Nedeljkov, M. Delta and singular delta locus for one dimensional systems of conservation laws. Math. Methods Appl. Sci. 2004, 27, 931–955. [Google Scholar] [CrossRef]
- Nedeljkov, M. Shadow waves—Entropies and interactions for delta and singular shocks. Arch. Ration. Mech. Anal. 2010, 197, 489–537. [Google Scholar] [CrossRef]
- Bressan, A. Global solutions of systems of conservation laws by wave-front tracking. J. Math. Anal. Appl. 1992, 170, 414–432. [Google Scholar] [CrossRef]
- Risebro, N.H. A front-tracking alternative to the random choice method. Proc. Amer. Math. Soc. 1993, 117, 1125–1139. [Google Scholar] [CrossRef]
- LeVeque, R.J. Finite Difference Methods for Hyperbolic Problems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- LeVeque, R.J. Numerical Methods for Conservation Laws; Birkhäuser: Basel, Switzerland, 1990. [Google Scholar]
- Holdahl, R.; Holden, H.; Lie, K.-A. Unconditionally stable splitting methods for the shallow water equations. BIT 1999, 39, 451. [Google Scholar] [CrossRef]
- Nishida, T.; Smoller, J.A. Solutions in the Large for Some Nonlinear Hyperbolic Conservation Laws. Comm. Pure Appl. Math. 1973, 26, 183–200. [Google Scholar] [CrossRef]
- Witteveen, J.A.S.; Koren, B.; Bakker, P.G. An improved front tracking method for the Euler equations. J. Comput. Phys. 2007, 224, 712–728. [Google Scholar] [CrossRef]
- Asakura, F. Wave-front tracking method for the equations of isentropic gas dynamics. Quart. Appl. Math. 2005, 63, 20–33. [Google Scholar] [CrossRef][Green Version]
- Bouchut, F. On zero pressure gas dynamics, in Advances in Kinetic Theory and Computing. Ser. Adv. Math. Appl. Sci. 1994, 22, 171–190. [Google Scholar]
- Dedovic, N.; Nedeljkov, M. Delta Shocks Interactions and the Wave Front Tracking Method. J. Math. Anal. Appl. 2013, 403, 580–598. [Google Scholar] [CrossRef]
- Riemann, B. Ueber die Fortpflanzung ebener Luftwellen von endlicher Schwingungsweite. Gott. Abh. Math. Cl. 1860, 8, 43–65. [Google Scholar]
- Wolfram Research, Inc. Mathematica; Version 12.3; Wolfram Research, Inc.: Champaign, IL, USA, 2021. [Google Scholar]
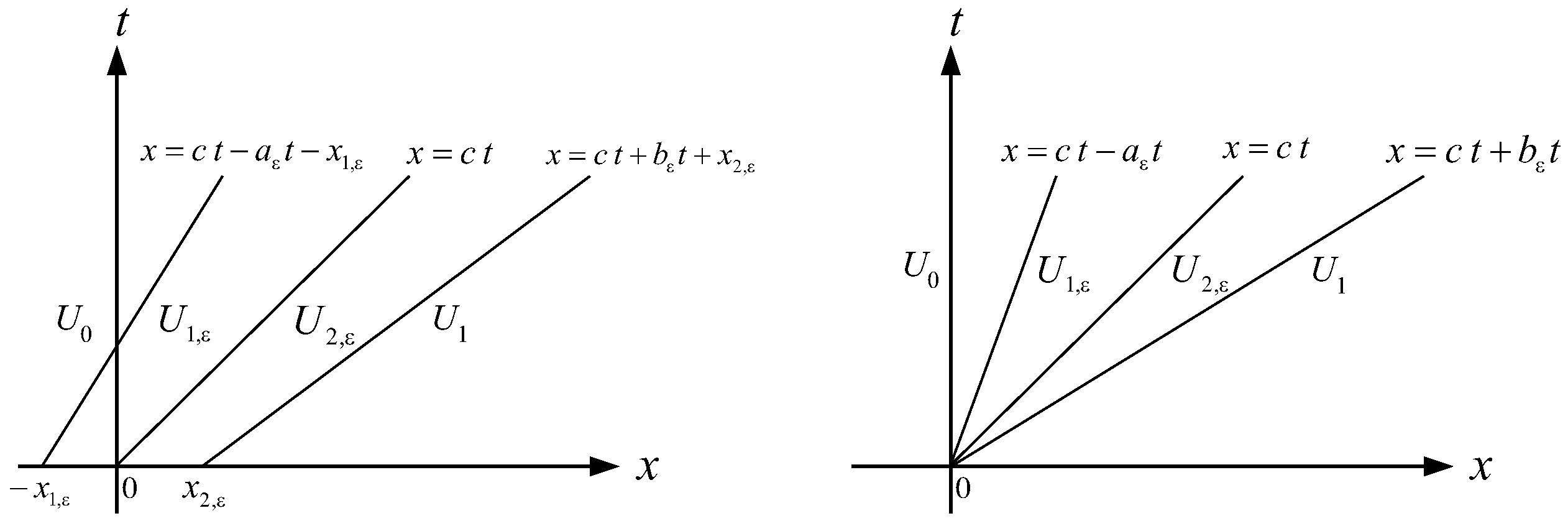

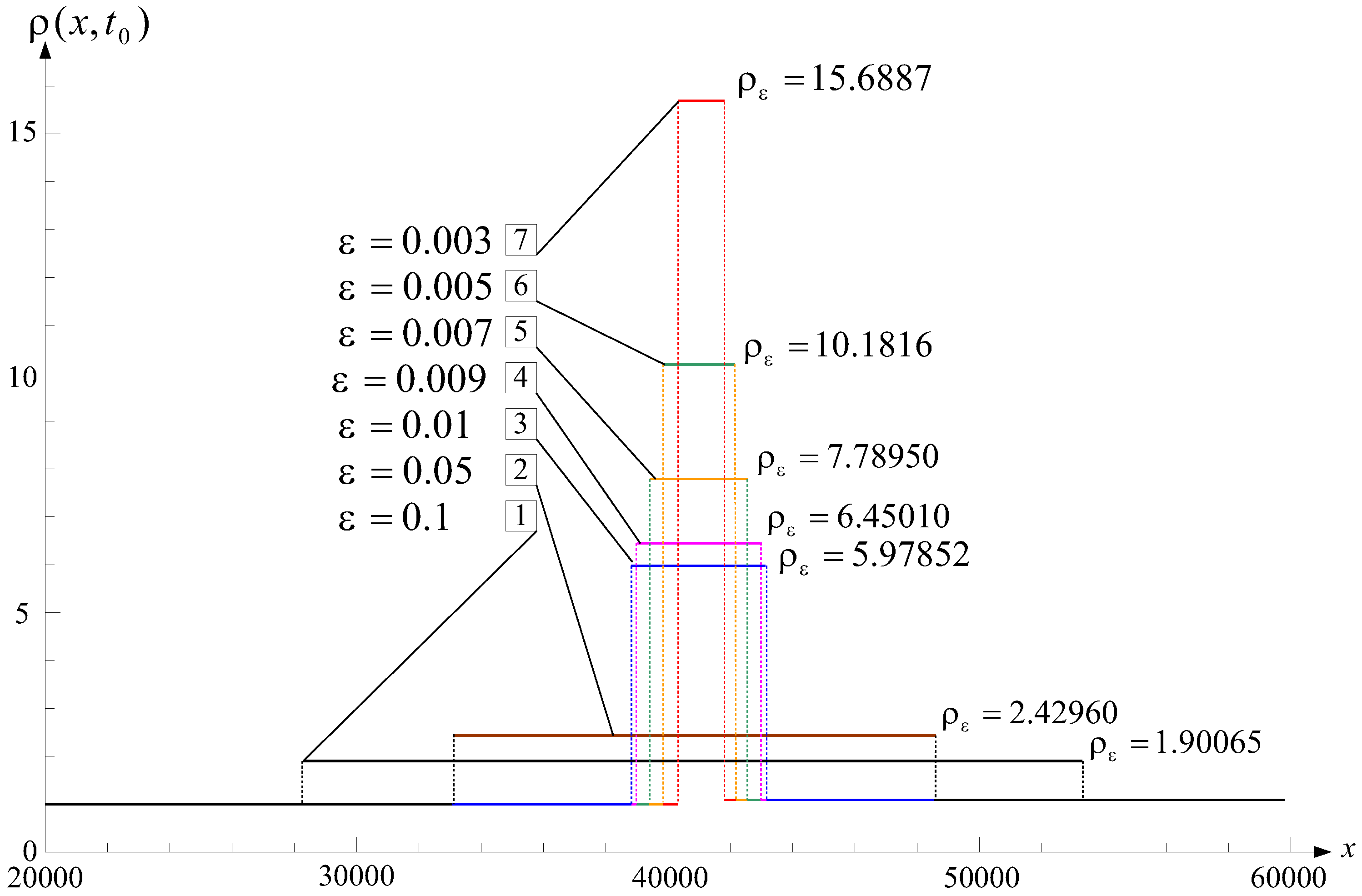
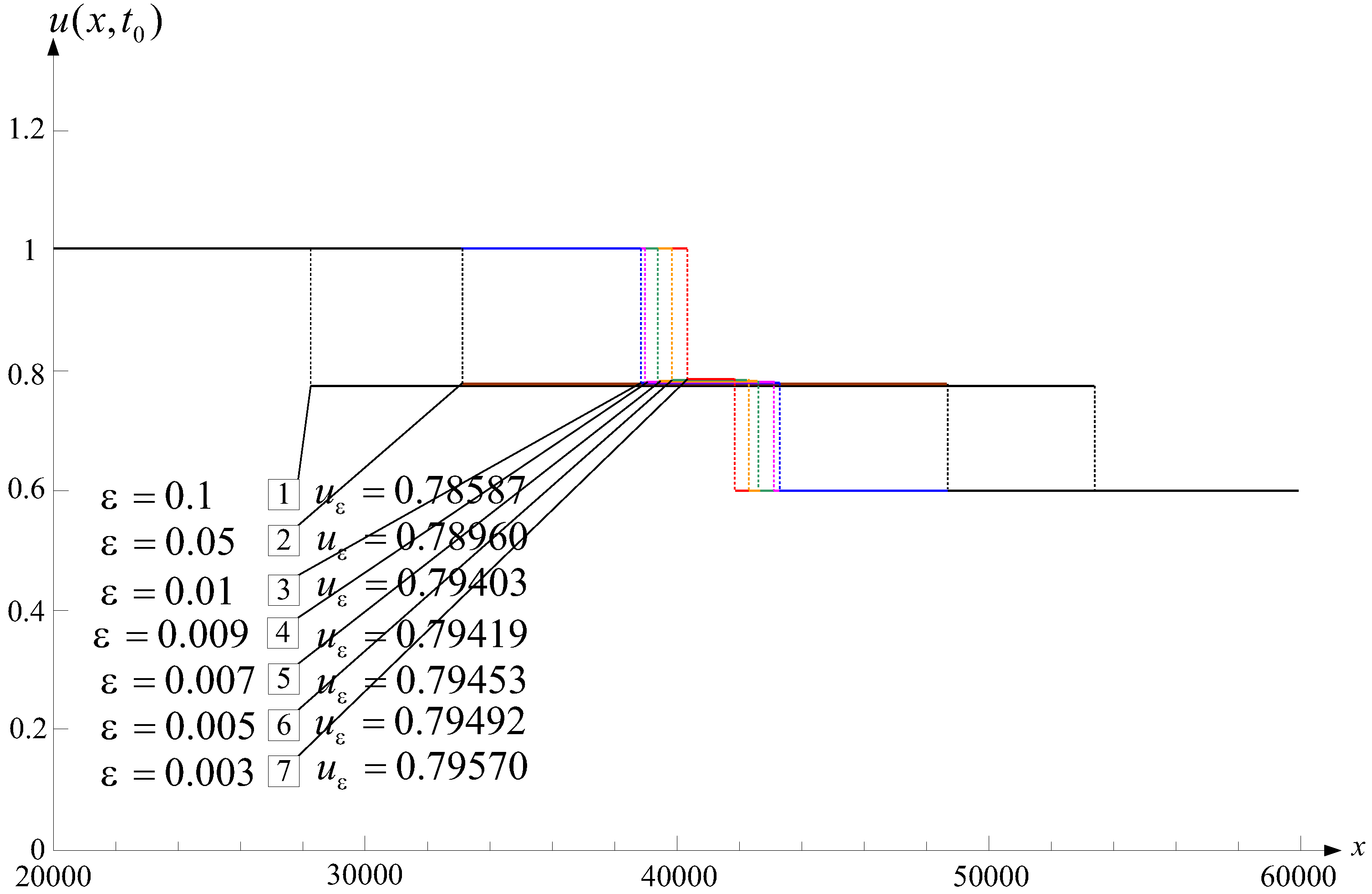
| 0.1 | 1.90065 | 0.78587 | 0.54812 | 1.03467 | 0.00014 | 0.00029 | 51539.2 |
| 0.05 | 2.42960 | 0.78960 | 0.64243 | 0.94334 | 0.00046 | 0.00091 | 44283.9 |
| 0.01 | 5.97852 | 0.79403 | 0.75266 | 0.83719 | 0.00197 | 0.01341 | 1280.45 |
| 0.009 | 6.45010 | 0.79419 | 0.75643 | 0.83359 | 0.00235 | 0.01775 | 1047.91 |
| 0.007 | 7.78950 | 0.79453 | 0.76426 | 0.82610 | 0.00152 | 0.02834 | 663.973 |
| 0.005 | 10.1816 | 0.79492 | 0.77259 | 0.81822 | 0.00037 | 0.04625 | 379.533 |
| 0.003 | 15.6887 | 0.79570 | 0.78179 | 0.81020 | 0.05231 | 0.05667 | 182.345 |
| 6 | 6.45010 | 0.79419 | 0.75643 | 0.83359 | 0.00235 | 0.01775 | 1047.91 |
| 7 | 6.45068 | 0.79418 | 0.75642 | 0.83357 | 0.00109 | 0.00696 | 2381.43 |
| 8 | 6.45058 | 0.79418 | 0.75642 | 0.83357 | 0.00029 | 0.00251 | 5703.15 |
| 9 | 6.45060 | 0.79418 | 0.75641 | 0.83356 | 0.00005 | 0.00203 | 12960.5 |
| 10 | 6.45059 | 0.79417 | 0.75641 | 0.83356 | 0.00001 | 0.00029 | 31037.1 |
| 0.1 | 1.74716 | 0.81567 | 0.56896 | 1.05016 | 0.00016 | 0.00004 | 37815.5 |
| 0.05 | 2.22987 | 0.81158 | 0.65838 | 0.95749 | 0.00042 | 0.00007 | 39901.9 |
| 0.01 | 5.47442 | 0.80668 | 0.76348 | 0.84789 | 0.00792 | 0.00948 | 1179.15 |
| 0.009 | 5.90553 | 0.80652 | 0.76708 | 0.84414 | 0.01313 | 0.01241 | 965.899 |
| 0.007 | 7.15678 | 0.80598 | 0.76987 | 0.83954 | 0.02456 | 0.02547 | 635.784 |
| 0.005 | 9.47854 | 0.80512 | 0.77259 | 0.82874 | 0.00037 | 0.04625 | 379.533 |
| 0.003 | 13.7598 | 0.80475 | 0.78815 | 0.81687 | 0.04255 | 0.04113 | 153.487 |
| Runtime | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 1.68612 | 0.828059 | 0.577459 | 1.097462 | 0.00014 | 0.00020 | 0.9 s | (54,245, 93,937) |
| 0.05 | 2.03792 | 0.834141 | 0.674341 | 1.005426 | 0.00037 | 0.00054 | 1.1 s | (62,255, 61,919) |
| 0.01 | 4.22713 | 0.841636 | 0.792563 | 0.894116 | 0.02266 | 0.00402 | 4.8 s | (5127.9, 5734.4) |
| 0.005 | 6.71266 | 0.843121 | 0.815659 | 0.872483 | 0.00501 | 0.02155 | 4477 s | (1229.6, 1408.6) |
| 0.003 | 9.95854 | 0.844183 | 0.826443 | 0.863428 | 0.01212 | 0.00688 | ≈168 h | (812.54, 1008.5) |
| 0.005 * | 6.71283 | 0.843118 | 0.815657 | 0.872480 | 0.00660 | 0.03910 | 15.3 s | (2598.4, 2977.4) |
| 0.003 * | 9.94664 | 0.843848 | 0.826450 | 0.862552 | 0.09700 | 0.05000 | 15.5 s | (894.2, 1036.1) |
| Runtime | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 4.22713 | 0.841636 | 0.792563 | 0.894116 | 0.02266 | 0.00402 | 13 s | (5127.9, 5734.4) |
| 0.05 | 4.22717 | 0.841634 | 0.792562 | 0.894115 | 0.00061 | 0.00786 | 25 s | (5122.8, 5728.6) |
| 0.04 | 4.22717 | 0.841634 | 0.792562 | 0.894115 | 0.00059 | 0.00690 | 39 s | (5123.0, 5728.9) |
| 0.03 | 4.22716 | 0.841634 | 0.792562 | 0.894115 | 0.00160 | 0.00691 | 289 s | (5121.2, 5726.9) |
| 0.02 | 4.22716 | 0.841635 | 0.792562 | 0.894115 | 0.00266 | 0.00641 | 1890 s | (5120.4, 5726.0) |
| 0.01 | 4.22716 | 0.841635 | 0.792562 | 0.894115 | 0.00352 | 0.00638 | ≈96 h | (5119.2, 5724.5) |
| 0.02 * | 4.22717 | 0.841634 | 0.792562 | 0.894115 | 0.00819 | 0.00969 | 5.5 s | (14,096, 15,765) |
| 0.01 * | 4.22717 | 0.841634 | 0.792562 | 0.894115 | 0.00690 | 0.01020 | 4.8 s | (14,104, 15,773) |
| 0.005 * | 4.22717 | 0.841634 | 0.792562 | 0.894115 | 0.00600 | 0.009801 | 4.83 s | (14,116, 15,787) |
| 0.001 * | 4.22717 | 0.841634 | 0.792562 | 0.894115 | 0.004487 | 0.014761 | 10.9 s | (14,260, 15,948) |
| 0.0001 * | 4.22717 | 0.841634 | 0.792562 | 0.894115 | 0.01231 | 0.02341 | 62.1 s | (14,347, 16,845) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dedović, N. Approximation of the Interactions of Rarefaction Waves by the Wave Front Tracking Method. Mathematics 2024, 12, 2099. https://doi.org/10.3390/math12132099
Dedović N. Approximation of the Interactions of Rarefaction Waves by the Wave Front Tracking Method. Mathematics. 2024; 12(13):2099. https://doi.org/10.3390/math12132099
Chicago/Turabian StyleDedović, Nebojša. 2024. "Approximation of the Interactions of Rarefaction Waves by the Wave Front Tracking Method" Mathematics 12, no. 13: 2099. https://doi.org/10.3390/math12132099
APA StyleDedović, N. (2024). Approximation of the Interactions of Rarefaction Waves by the Wave Front Tracking Method. Mathematics, 12(13), 2099. https://doi.org/10.3390/math12132099