Optimization of Interaction with Counterparties: Selection Game Algorithm under Uncertainty
Abstract
1. Introduction
- Game-theoretic approach—in accordance with this approach, the participants in the interaction try to self-organize in such a way that in the event of a force majeure situation, they do not suffer irreparable damage (reach a state of equilibrium).
- Integral estimates—synthetic estimates of complex objects, obtained by condensing various multifaceted indicators that characterize them into an indicator represented by one single number.
- Non-cooperative games—a situation where the parties of the interaction primarily pursue their own personal selfish goals, without trying to unite with other participants to solve their problem.
- Payment matrices—results presented in a tabular form and representing the ratio of actions of two interacting or opposing parties.
- Modeling of integral estimates—selection of a scheme for condensing various heterogeneous indicators characterizing a complex object into a single monosyllabic indicator.
2. Literature Review and Theoretical Analysis
2.1. Game-Theoretic Approach to Interaction Optimization
2.2. Multicriteria Analysis
2.3. Mathematical Statistics in Interaction Optimization
2.4. Interaction with Counterparties: From Theory to Practice
3. Research Methodology
3.1. Mutual Influence Indices
3.2. Risk and Cooperation Coefficients
3.3. Key Modeling Indicators
- the average cost of production;
- the average discount on products;
- the costs of cooperation;
- the time needed to search for a counterparty;
- the time of conclusion of the contract;
- the dates of transactions;
- the reliability of the counterparty;
- the product quality;
- the remoteness of the supplier; and
- the possibility of obtaining a deferred payment.
3.4. Game Interaction Algorithm
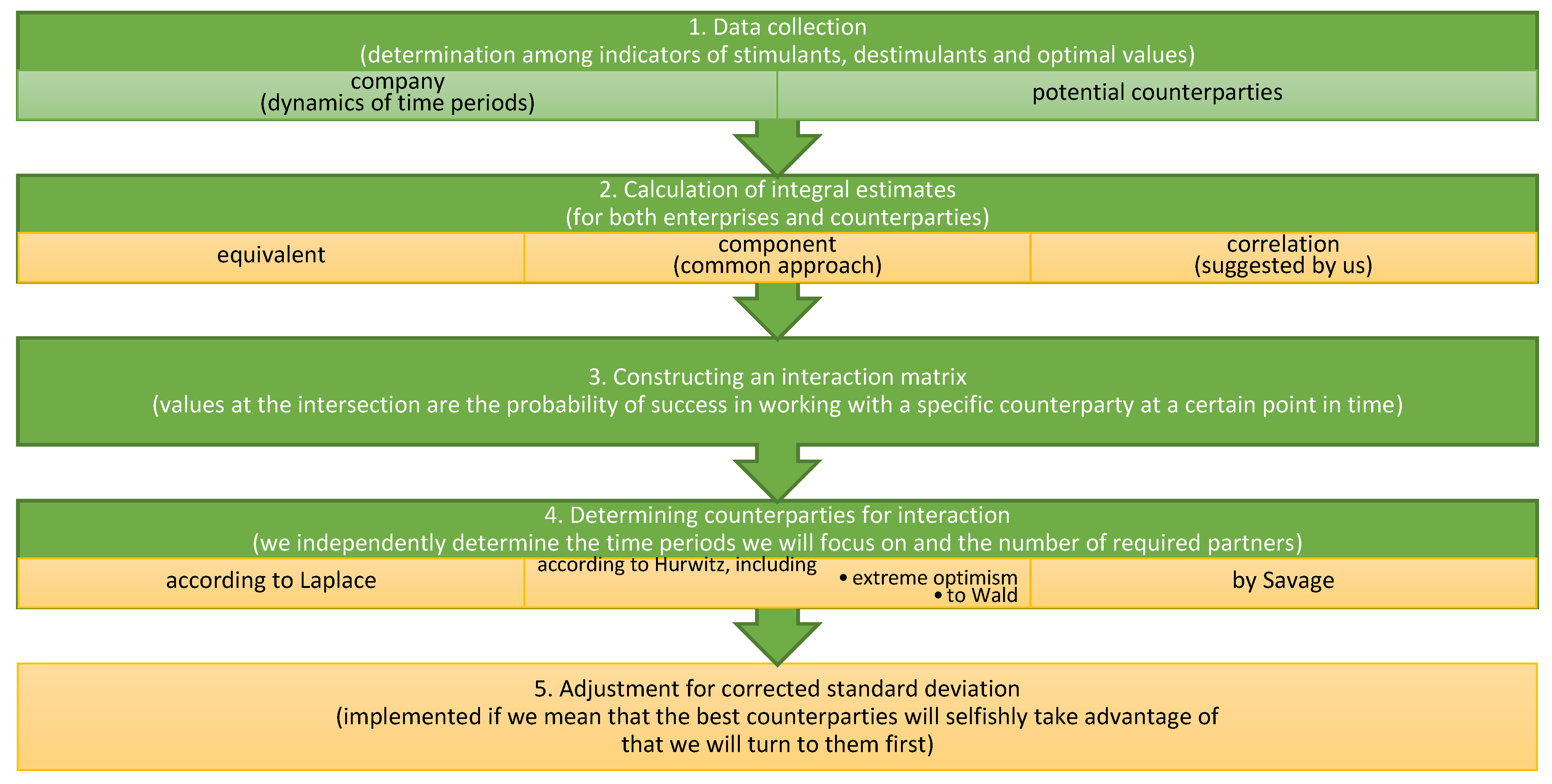
3.4.1. Development of a Set of Indicators for Assessing the Performance of Enterprises
3.4.2. Selection and Assessment of Counterparties
3.4.3. Modeling of Integral Estimates
- Data scaling
- Standardization
- Normalization
- 2.
- Weighting factors
- Equivalent indicators
- For the first principal component
- According to the correlation relation
- 3.
- Modeling the interaction of an enterprise with contractors
- Laplace criterion
- Bayes–Laplace criterion
- Extreme optimism criterion
- Wald criterion
- Hurwitz criterion
- Savage criterion
- 4.
- Review of the counterparties
4. Research Results
5. Discussion and Addition of Results
5.1. Extending the Game Component Using Heuristics
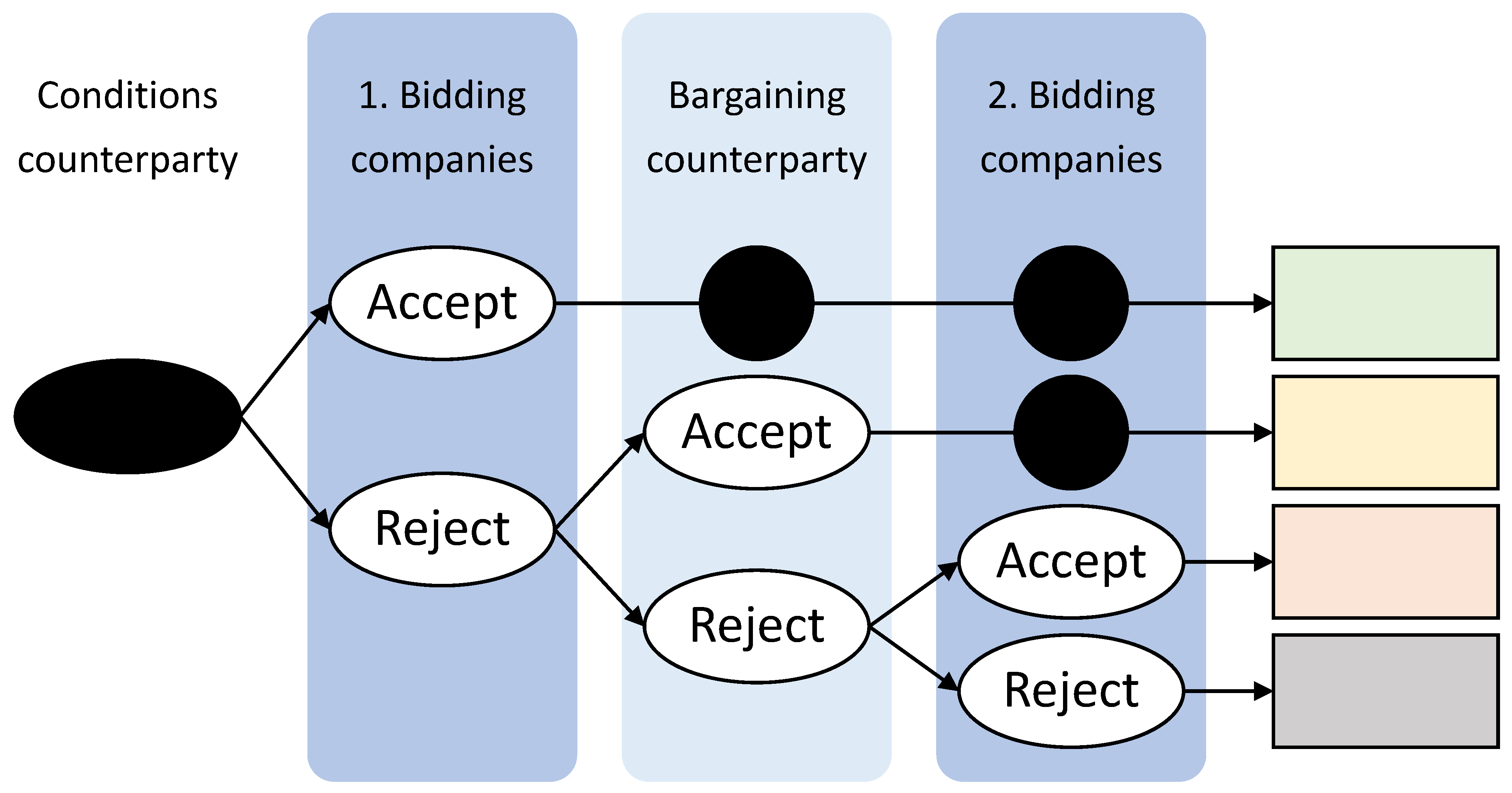
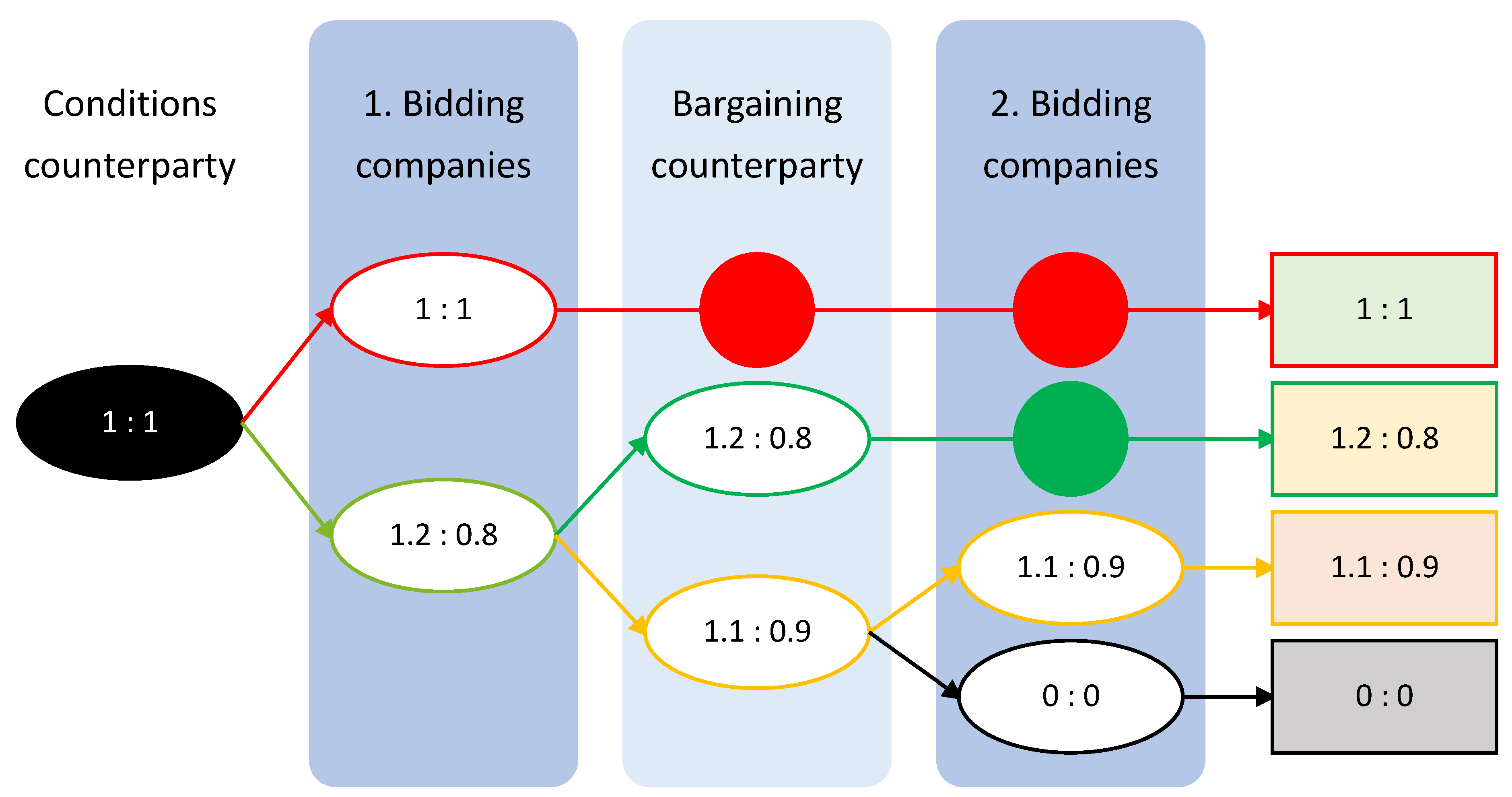
5.2. Game Interaction Algorithm
- In accordance with the order, the counterparty puts forward certain basic conditions, the assessment of which can be indicated by a unit—1.
- The subject can accept these conditions, and then, the winnings will be equal to 1, but can also try to push for a more advantageous position in the form of an increase in the discount, according to which the potential winnings can increase to 1.2 units.
- The counterparty may agree to this condition or make a partial concession, for example, increasing our winnings to 1.1 units, which is ultimately still better than the base position.
- If the final conditions of the subject are not satisfied, then, he proceeds to negotiations with the next counterparty, i.e., .
6. Conclusions and Practical Implications
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
% | % | % | % | % | % | days | days | days | days | days | days | rub./rub. | mln. rub. | mln. rub. | mln. rub. | % | % | % | % | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2012 | 54.6 | 37.7 | 11.7 | 47.9 | 34.7 | 92.7 | 129.8 | 67.1 | 27.5 | 8.7 | 41.3 | 87.4 | 6.1 | 5280.9 | 86,881.7 | 6249.2 | 12.2 | 17.1 | 28.8 | 154.8 |
| 2013 | 57.6 | 22.8 | 10.5 | 63.1 | 52.2 | 93.0 | 126.7 | 71.2 | 21.0 | 7.9 | 59.2 | 70.8 | 6.9 | 8712.4 | 105,948.7 | 10,977.7 | 9.0 | 23.7 | 50.6 | 95.9 |
| 2014 | 47.5 | 26.6 | 21.4 | 39.9 | 54.7 | 90.7 | 121.1 | 64.1 | 15.6 | 9.6 | 59.0 | 56.5 | 6.8 | 2491.2 | 110,591.8 | 2418.0 | 2.3 | 6.8 | 12.9 | 51.4 |
| 2015 | 41.3 | 32.3 | 41.5 | 16.3 | 49.4 | 92.7 | 152.7 | 67.5 | 19.8 | 21.1 | 68.1 | 73.4 | 4.6 | −1686.2 | 84,676.8 | −1657.3 | −1.7 | −4.8 | −8.9 | 50.6 |
| 2016 | 36.5 | 40.8 | 39.5 | 8.0 | 54.0 | 96.6 | 138.6 | 54.0 | 19.5 | 21.9 | 61.5 | 67.1 | 4.6 | −2613.6 | 94,587.2 | −3058.2 | −2.9 | −7.3 | −16.7 | 36.4 |
| 2017 | 53.5 | 22.7 | 25.7 | 42.5 | 56.5 | 97.3 | 116.7 | 53.6 | 15.6 | 16.4 | 61.0 | 52.1 | 6.3 | 3123.1 | 123,601.2 | 3846.3 | 2.9 | 7.9 | 21.0 | −49.7 |
| 2018 | 51.7 | 25.2 | 25.8 | 32.4 | 60.7 | 97.0 | 118.7 | 62.4 | 15.0 | 16.1 | 64.1 | 49.2 | 6.9 | 3603.5 | 137,286.4 | 4642.7 | 2.8 | 8.1 | 24.1 | −70.9 |
| 2019 | 47.0 | 26.3 | 25.1 | 32.0 | 68.9 | 97.5 | 118.9 | 58.6 | 15.1 | 15.0 | 68.9 | 41.7 | 6.3 | −171.7 | 143,529.9 | −318.6 | −0.1 | −0.4 | −1.8 | 1.7 |
| 2020 | 41.6 | 31.4 | 26.8 | 0.8 | 74.3 | 97.3 | 157.5 | 69.6 | 20.1 | 18.1 | 91.6 | 44.6 | 4.6 | −1385.1 | 117,358.1 | −1636.0 | −1.1 | −2.7 | −10.7 | 7.8 |
| 2021 | 41.6 | 23.8 | 19.6 | 28.6 | 76.1 | 97.9 | 136.5 | 56.8 | 15.5 | 13.0 | 89.2 | 33.7 | 5.6 | 1396.6 | 155,085.9 | 2010.0 | 1.0 | 2.4 | 13.1 | −6.5 |
% | % | % | % | % | % | days | days | days | days | days | days | rub./ rub. | mln. rub. | mln. rub. | mln. rub. | % | % | % | % | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Weights | equivalent | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | |||||
| 0.3 | 0.35 | 0.35 | ||||||||||||||||||||||||
| by component | 0.079 | 0.008 | 0.065 | 0.083 | 0.032 | 0.028 | 0.028 | 0.016 | 0.015 | 0.072 | 0.043 | 0.022 | 0.055 | 0.087 | 0.003 | 0.084 | 0.085 | 0.090 | 0.082 | 0.024 | ||||||
| 0.294 | 0.250 | 0.456 | ||||||||||||||||||||||||
| by correlation | 0.037 | 0.067 | 0.042 | 0.035 | 0.052 | 0.066 | 0.061 | 0.095 | 0.062 | 0.040 | 0.053 | 0.052 | 0.043 | 0.034 | 0.064 | 0.035 | 0.035 | 0.033 | 0.035 | 0.057 | ||||||
| 0.300 | 0.407 | 0.293 | ||||||||||||||||||||||||
| 2012 | 4.3925 | 3.5632 | 6.9339 | 4.4908 | 5.0282 | 7.7306 | 4.2252 | 3.1750 | 6.5150 | |||||||||||||||||
| 4.9917 | 6.1022 | 4.4695 | ||||||||||||||||||||||||
| 2013 | 2.8233 | 5.6255 | 8.3347 | 2.7552 | 7.1099 | 9.4255 | 2.7158 | 4.8305 | 7.7306 | |||||||||||||||||
| 5.7331 | 6.8848 | 5.0476 | ||||||||||||||||||||||||
| 2014 | 5.0452 | 7.1356 | 4.2728 | 6.2440 | 7.5260 | 4.2296 | 4.4226 | 6.7928 | 4.3001 | |||||||||||||||||
| 5.5065 | 5.6461 | 5.3513 | ||||||||||||||||||||||||
| 2015 | 4.7245 | 2.5645 | 1.4215 | 5.5612 | 1.9385 | 1.1412 | 4.2288 | 2.6886 | 1.5903 | |||||||||||||||||
| 2.8125 | 2.6405 | 2.8279 | ||||||||||||||||||||||||
| 2016 | 3.9048 | 4.1306 | 0.8800 | 3.9942 | 2.5956 | 0.2622 | 3.7319 | 5.0007 | 1.2340 | |||||||||||||||||
| 2.9252 | 1.9432 | 3.5155 | ||||||||||||||||||||||||
| 2017 | 3.4019 | 7.3320 | 4.3994 | 4.2317 | 6.3130 | 4.6559 | 2.9243 | 7.8160 | 4.2423 | |||||||||||||||||
| 5.1266 | 4.9454 | 5.3018 | ||||||||||||||||||||||||
| 2018 | 3.9204 | 7.1486 | 4.7481 | 5.1444 | 6.7095 | 4.8851 | 3.2997 | 7.0617 | 4.6501 | |||||||||||||||||
| 5.3399 | 5.4174 | 5.2270 | ||||||||||||||||||||||||
| 2019 | 4.1955 | 7.5740 | 3.1390 | 5.9417 | 6.8668 | 2.1836 | 3.3977 | 7.6999 | 3.6625 | |||||||||||||||||
| 5.0082 | 4.4597 | 5.2263 | ||||||||||||||||||||||||
| 2020 | 3.5698 | 3.9764 | 1.9728 | 4.8822 | 3.6569 | 1.2906 | 2.9878 | 3.7462 | 2.3537 | |||||||||||||||||
| 3.1532 | 2.9385 | 3.1104 | ||||||||||||||||||||||||
| 2021 | 3.9775 | 7.5960 | 4.3099 | 6.0508 | 6.9490 | 3.4637 | 3.0781 | 7.7645 | 4.7645 | |||||||||||||||||
| 5.3603 | 5.0959 | 5.4801 | ||||||||||||||||||||||||
rub. | % | thds. rub. | Days | Days | Units | Units | Units | km | Days | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1.0640 | 14.62 | 955.02 | 1.5 | 1.4 | 0.2800 | 0.87 | 88.51 | 28.27 | 56 | |
| 0.9420 | 7.10 | 1038.11 | 2.5 | 1.1 | 0.1200 | 0.59 | 87.58 | 22.74 | 0 | |
| 0.9990 | 13.34 | 1124.72 | 2.2 | 0.6 | 0.1700 | 0.70 | 93.01 | 18.43 | 14 | |
| 0.9690 | 7.00 | 945.47 | 1.3 | 1.6 | 0.9700 | 0.52 | 88.24 | 30.61 | 42 | |
| 0.9780 | 6.46 | 958.81 | 2.7 | 1.3 | 0.4400 | 0.54 | 93.88 | 16.12 | 28 | |
| 0.9980 | 10.20 | 1175.37 | 2.6 | 1.3 | 0.3400 | 0.88 | 84.76 | 31.20 | 7 | |
| 1.0480 | 9.02 | 1181.85 | 1.1 | 0.7 | 0.9000 | 0.55 | 81.42 | 26.46 | 28 | |
| 1.0910 | 6.07 | 1182.51 | 1.3 | 1.6 | 0.2400 | 0.69 | 88.80 | 27.83 | 63 | |
| 0.9820 | 13.69 | 1140.62 | 2.8 | 1.9 | 0.2900 | 0.67 | 89.54 | 17.24 | 63 | |
| 1.0510 | 7.04 | 965.73 | 1.9 | 1.2 | 0.1200 | 0.90 | 91.00 | 23.95 | 35 |
rub. | % | thds. rub. | Days | Days | Units | Units | Units | km | Days | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Weights | equivalent | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | ||
| by component | 0.1369 | 0.0076 | 0.0183 | 0.2692 | 0.0004 | 0.1176 | 0.0002 | 0.1787 | 0.2272 | 0.0438 | |||
| by correlation | 0.0849 | 0.1377 | 0.1352 | 0.0745 | 0.1178 | 0.0887 | 0.1003 | 0.0856 | 0.0827 | 0.0927 | |||
| 6.0517 | 4.6316 | 6.4135 | |||||||||||
| 3.7611 | 4.1260 | 3.7664 | |||||||||||
| 5.5962 | 5.6629 | 5.6950 | |||||||||||
| 5.2938 | 6.2241 | 5.1314 | |||||||||||
| 5.1416 | 6.0715 | 5.0514 | |||||||||||
| 3.3019 | 2.0497 | 3.3789 | |||||||||||
| 4.3148 | 5.1059 | 4.1206 | |||||||||||
| 3.5174 | 4.5476 | 3.1215 | |||||||||||
| 4.9716 | 5.0434 | 4.9105 | |||||||||||
| 5.1695 | 4.6832 | 5.2228 | |||||||||||
References
- Askari, G.; Gordji, M.E.; Park, C. The behavioral model and game theory. Palgrave Commun. 2019, 5, 57. [Google Scholar] [CrossRef]
- Gilliland, M.; Tashman, L.; Sglavo, U. Business Forecasting: Practical Problems and Solutions; John Wiley & Sons: Hoboken, NJ, USA, 2015; 374p. [Google Scholar]
- Taleb, N.N. The Black Swan: The Impact of the Highly Improbable, 2nd ed.; Random House: New York, NY, USA, 2010; 444p. [Google Scholar]
- Yemets, O.A.; Roskladka, A.A. Combinatorial optimization under uncertainty. Cybern. Syst. Anal. 2008, 44, 655–663. [Google Scholar] [CrossRef]
- Dmitriev, N.D.; Mihel, E.A. The algorithm for implementing game-theoretic tools of enterprise interaction in the strategic planning system. Econ. Sci. 2023, 55–63. (In Russian) [Google Scholar] [CrossRef]
- Mihel, E.A.; Dmitriev, N.D. Description of game-theoretic tools for interaction of enterprises in the strategic planning system. Econ. Sci. 2023, 226–231. (In Russian) [Google Scholar] [CrossRef]
- Fernandez, A.-S.; Chiambaretto, P.; Roy, F.L.; Czakon, W. The Routledge Companion to Coopetition Strategies; Routledge: London, UK, 2019; 444p. [Google Scholar]
- Heizer, J.; Render, B.; Munson, C. Operations Management: Sustainability and Supply Chain Management, 14th ed.; Pearson: London, UK, 2022. [Google Scholar]
- Kuznetsova, E.P. Changing the essence of a production cooperation in conditions of transition to the knowledge economy. Bull. NGIEL. 2020, pp. 67–77. Available online: https://disk.yandex.ru/i/GTJOdpjho52oKg (accessed on 10 April 2024). (In Russian).
- Le Breton, M.; Moreno-Ternero, J.D.; Savvateev, A.; Weber, S. Stability and fairness in models with a multiple membership. Int. J. Game Theory 2013, 42, 673–694. [Google Scholar] [CrossRef]
- Mazalov, V.V. Mathematical Game Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2014; 432p, Available online: http://matt-versaggi.com/mit_open_courseware/GameAI/MathematicalGameTheoryandApplications.pdf (accessed on 10 April 2024).
- Okura, M.; Carfì, D. Coopetition and Game Theory. J. Appl. Econ. Sci. 2014, 9, 458–469. Available online: https://researchgate.net/publication/282769586_Coopetition_and_Game_Theory (accessed on 10 April 2024).
- Petrosjan, L.A.; Zenkevich, N.A. Conditions for sustainable cooperation. Autom. Remote Control. 2015, 76, 1894–1904. [Google Scholar] [CrossRef]
- Rodionov, D.G.; Boiko, I.V.; Nadezhina, O.S. Pricing of the License Agreements: Improvement of the Methodology on the Basis of the Game Approach. Eurasian Stud. Bus. Econ. 2018, 9, 241–252. [Google Scholar] [CrossRef]
- Von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1944; 776p, Available online: https://jstor.org/stable/j.ctt1r2gkx (accessed on 10 April 2024).
- Greiner, D.; Periaux, J.; Emperador, J.M.; Galván, B.; Winter, G. Game Theory Based Evolutionary Algorithms: A Review with Nash Applications in Structural Engineering Optimization Problems. Arch. Comput. Methods Eng. 2017, 24, 703–750. [Google Scholar] [CrossRef]
- Lambertini, L. Chapter 20: The Genesis of Game Theory and its Role in Industrial Economics. In International Handbook on Industrial Policy; Edward Elgar Publishing: Cheltenham, UK, 2006. [Google Scholar] [CrossRef]
- Newton, J. Evolutionary Game Theory: A Renaissance. Games 2018, 9, 31. [Google Scholar] [CrossRef]
- Bieta, V.; Smelyanets, P. Game Theory and Financial Markets. Vopr. Ekon. 2007, 114–124. (In Russian) [Google Scholar] [CrossRef]
- Chernogorskiy, S.A.; Kozlov, A.V.; Teslya, A.B. Game-theoretic modeling of decision-making on state support for the infrastructure development in the Russian Far North. Int. J. Syst. Assur. Eng. Manag. 2020, 11, 10–18. [Google Scholar] [CrossRef]
- Zaytsev, A.; Dmitriev, N.; Fayzullin, R.; Mihel, E. Formation of Investment Behavior Strategy using the Game-theoretic Method. TEM J. 2021, 10, 673–681. [Google Scholar] [CrossRef]
- Rodionov, D.G.; Zaytsev, A.A.; Dmitriev, N.D.; Victorova, N.G. Game-theoretic rationalization method of economic entities’ investment policy. Bus. Educ. Law 2023, 63, 109–117. (In Russian) [Google Scholar] [CrossRef]
- Allen, F.; Morris, S. Game theory models in finance. Int. Ser. Oper. Res. Manag. Sci. 2014, 194, 17–41. [Google Scholar] [CrossRef]
- Samuelson, L. Game theory in economics and beyond. Vopr. Ekon. 2017, 89–115. (In Russian) [Google Scholar] [CrossRef]
- Smit, H.T.J.; Trigeorgis, L. Strategic Investment: Real Options and Games; Princeton University Press: Princeton, NJ, USA, 2004; Available online: http://hdl.handle.net/1765/12234 (accessed on 10 April 2024).
- Breen, R. Chapter 26: Game Theory. In The Oxford Handbook of Analytical Sociology; Bearman, P., Hedström, P., Eds.; Oxford Academic: Oxford, UK, 2011; pp. 619–638. [Google Scholar] [CrossRef]
- Bajari, P.; Hong, H.; Nekipelov, D. 1—Game Theory and Econometrics: A Survey of Some Recent Research. In Advances in Economics and Econometrics; Acemoglu, D., Arellano, M., Dekel, E., Eds.; Cambridge University Press: Cambridge, UK, 2013; pp. 3–52. [Google Scholar] [CrossRef]
- Liao, Y.-L.; Hong, Q.-L. Survey of option game theory of R&D investment. In Proceedings of the International Conference on E-Business and E-Government, Shanghai, China, 6–8 May 2011. [Google Scholar] [CrossRef]
- Shirokova, S.V.; Naidenysheva, E.G.; Dubgorn, A. Application of the Mathematical Tool of Game Theory for Project Management of Business Structures and Public-Private Partnerships Interaction (Information Systems Management—Project and Program Management). In Proceedings of the 29th IBIMA Conference, Vienna, Austria, 3–4 May 2017. [Google Scholar]
- Niazi, M.; Hussain, A. Agent-based computing from multi-agent systems to agent-based models: A visual survey. Scientometrics 2011, 89, 479–499. [Google Scholar] [CrossRef]
- Zaytsev, A.; Dmitriev, N.; Bunkovsky, D.; Faizullin, R. Audit of Intellectual Capital at an Industrial Enterprise: Open Data Analysis Digital-Model. Int. J. Technol. 2022, 13, 1473–1483. [Google Scholar] [CrossRef]
- Alferev, D.A.; Kremin, A.E. Multi-purpose optimization of the product release program. Vestn. Univ. 2019, 92–101. (In Russian) [Google Scholar] [CrossRef]
- Leider, S. Chapter 7: Behavioral Analysis of Strategic Interactions (Game Theory, Bargaining, and Agency). In The Handbook of Behavioral Operations; Donohue, K., Katok, E., Leider, S., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Mednikov, M.D.; Sokolitsyna, N.A.; Sokolitsyn, A.S.; Semenov, V.P. Game theory model of forming enterprise development strategy in market environment uncertainty. In Proceedings of the 20th IEEE International Conference on Soft Computing and Measurements, St. Petersburg, Russia, 24–26 May 2017. [Google Scholar] [CrossRef]
- Austin, A.A.; Carpenter, T.; Christ, M.H.; Nielson, C. The Data Analytics Journey: Interactions among Auditors, Managers, Regulation, and Technology. Contemp. Account. Res. 2021, 38, 1888–1924. [Google Scholar] [CrossRef]
- Lu, W.; Qin, H.-P. Research on Optimization of Webcast Income Distribution Based on Game Theory. In Proceedings of the International Conference on Physics, Mathematics, Statistics Modelling and Simulation, Wuzhen, China, 29–30 July 2018. [Google Scholar]
- Breton, M. Dynamic Games in Finance. In Handbook of Dynamic Game Theory; Başar, T., Zaccour, G., Eds.; Springer: Cham, Switzerland, 2018; pp. 827–863. [Google Scholar] [CrossRef]
- Geckil, I.K.; Anderson, P.L. Applied Game Theory and Strategic Behavior; CRC Press: New York, NY, USA, 2009; 230p. [Google Scholar] [CrossRef]
- Dmitriev, N.; Zaytsev, A.; Faizullin, R.; Bunkovsky, D. The Instrumental Apparatus of the Innovative Potential Audit of the Enterprise in the Implementation of Project Activities. Int. J. Technol. 2022, 13, 1484–1494. [Google Scholar] [CrossRef]
- Konnikov, E.; Konnikova, O.; Rodionov, D.; Yuldasheva, O. Analyzing Natural Digital Information in the Context of Market Research. Information 2021, 12, 387. [Google Scholar] [CrossRef]
- Mazilov, E.A.; Alferyev, D.A.; Zaripova, D.A. Forecasting scientific and technological development as a basis for the formation of the digital economy. In Proceedings of the 3th International Scientific and Practical Conference DEFIN, St. Petersburg, Russia, 19–20 March 2020. [Google Scholar] [CrossRef]
- Siegel, E. Predictive Analytics: The Power to Predict Who Will Click, Buy, Lie, or Die; John Wiley & Sons: Hoboken, NJ, USA, 2016; 374p. [Google Scholar]
- Mohammaditabar, D.; Ghodsypour, S.H.; Hafezalkotob, A. A game theoretic analysis in capacity-constrained supplier-selection and cooperation by considering the total supply chain inventory costs. Int. J. Prod. Econ. 2016, 181 Pt A, 87–97. [Google Scholar] [CrossRef]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. USA 2002, 99 (Suppl. S3), 7280–7287. [Google Scholar] [CrossRef]
- Farooqui, A.D.; Niazi, M.A. Game theory models for communication between agents: A review. Complex Adapt. Syst. Model. 2016, 4, 13. [Google Scholar] [CrossRef]
- Kleiner, G. The flagship of economic, mathematical and computer modeling: 60 years in line. Econ. Math. Methods 2023, 59, 5–20. (In Russian) [Google Scholar] [CrossRef]
- Kurz, S.; De Gersem, H.; Galetzka, A.; Klaedtke, A.; Liebsch, M.; Loukrezis, D.; Russenschuck, S.; Schmidt, M. Hybrid modeling: Towards the next level of scientific computing in engineering. J. Math. Ind. 2022, 12, 8. [Google Scholar] [CrossRef]
- Schweidtmann, A.M.; Zhang, D.; von Stosch, M. A review and perspective on hybrid modeling methodologies. Digit. Chem. Eng. 2024, 10, 100136. [Google Scholar] [CrossRef]
- Dorrah, D.H.; McCabe, B. Integrated Agent-Based Simulation and Game Theory Decision Support Framework for Cash Flow and Payment Management in Construction Projects. Sustainability 2024, 16, 244. [Google Scholar] [CrossRef]
- Michel, E.A.; Zaytsev, A.A.; Dmitriev, N.D. Game-theoretic tools of enterprises interaction in the strategic planning system. Bull. Altai Acad. Econ. Law 2022, 218–231. (In Russian) [Google Scholar] [CrossRef]
- Naumov, I.V.; Nikulina, N.L.; Bychkova, A.A. Scenario-Based Approach to Modeling Bankruptcy Risks for Enterprises in Various Industries. Econ. Soc. Changes Facts Trends Forecast. 2024, 17, 166–186. [Google Scholar] [CrossRef]
- Rudchenko, A.D.; Maleev, V.I. Features of the use of tools for analyzing information about procurement participants. Goszakaz Upr. Razmeshcheniye Obespecheniye 2014, 62–69. Available online: https://publications.hse.ru/articles/207789095 (accessed on 31 May 2024). (In Russian).
- Rodionov, D.G.; Zaytsev, A.A.; Konnikov, E.A.; Dmitriev, N.D.; Dubolazova, Y.A. Modeling Changes in the Enterprise Information Capital in the Digital Economy. J. Open Innov. Technol. Mark. Complex. 2021, 7, 166. [Google Scholar] [CrossRef]
- Aivazian, S.A. Quality of Life and Living Standards Analysis: An eEonometric Approach; Walter de Gruyter: Berlin, Germany, 2016; 419p. [Google Scholar]
- Gulin, K.A.; Mazilov, E.A.; Kuz’min, I.V.; Alfer’ev, D.A.; Ermolov, A.P. Scientific and Technological Potential of a Territory and its Comparative Appraisal. Probl. Territ. Dev. 2017, 21, 7–26. Available online: http://pdt.vscc.ac.ru/article/2102?_lang=en (accessed on 10 April 2024). (In Russian).
- Zhao, X.; Li, Y.; Song, H.; Jia, Y.; Liu, J. Agents Affecting the Productivity of Pine Plantations on the Loess Plateau in China: A Study Based on Structural Equation Modeling. Forests 2020, 11, 1328. [Google Scholar] [CrossRef]
- Alfer’ev, D.A.; Kremin, A.E.; Rodionov, D.G.; Velichenkova, D.S. On the methodology of checking integral estimates of socio-economic objects. Econ. Soc. Changes Facts Trends Forecast. 2021, 14, 86–106. [Google Scholar] [CrossRef]
- Minaker, V.Y.; Bykhovskiy, M.V. Problems of integral assessments of technical systems. In Proceedings of the Summit of TRIZ Developers, St. Petersburg, Russia, 13–14 October 2006; Available online: https://metodolog.ru/00821/00821.html (accessed on 10 April 2024). (In Russian).
- Kurbatskii, A.; Mironenko, A. Estimating the Quality of Life Using Weighted Principal Components Method. Montenegrin J. Econ. 2023, 19, 7–17. [Google Scholar] [CrossRef]
- Venttsel, Y.S. Elements of Game Theory; Central Books: Santa Cruz, Philippines, 1980; 69p. [Google Scholar]
- Kotova, V.V. A research of procedures used in the analytic hierarchy process and visualization in sensitivity analysis. Sci. Vis. 2016, 8, 59–84. Available online: https://sv-journal.org/2016-2/06.php?lang=en (accessed on 10 April 2024).
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw Hill: New York, NY, USA, 1980; 287p. [Google Scholar]
- Halicka, K. Technology Selection Using the TOPSIS Method. Foresight STI Gov. 2020, 14, 85–96. [Google Scholar] [CrossRef]
- Osborne, M.J.; Rubinstein, A. A Course in Game Theory; MIT Press: Cambridge, MA, USA, 1994; 368p, Available online: https://arielrubinstein.tau.ac.il/books/GT.pdf (accessed on 10 April 2024).
- Game Theoretic Software. Available online: https://gametheorysociety.org/game-theoretic-software (accessed on 12 April 2024).
- Savani, R.; von Stengel, B. Game Theory Explorer: Software for the applied game theorist. Comput. Manag. Sci. 2015, 12, 5–33. [Google Scholar] [CrossRef][Green Version]



| Approach | General Idea |
|---|---|
| 1. Game theory | Searching for equilibriums stable to shocks and beneficial to all participants in the interaction. |
| 2. Multicriteria analysis | Observation of an object from various sides and positions to characterize it. |
| 3. Mathematical statistics | Tracking of quantitative trends, dynamics, outliers, and recurring fluctuations. |
| 4. Hybrid approach | Integration of different heterogeneous tools adapted for narrow, local, and specific tasks to solve a more global problem. |
| Structure of the Enterprise’s Property and Sources of Its Formation | Business Activity (Turnover) | Financial Results |
|---|---|---|
|
|
|
| 3.1215 | 3.3789 | 3.7664 | 4.1206 | 4.9105 | 5.0514 | 5.1314 | 5.2228 | 5.6950 | 6.4135 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Normal | 0 | 0.0782 | 0.1959 | 0.3035 | 0.5434 | 0.5862 | 0.6105 | 0.6383 | 0.7817 | 1 | |||
| Normal | Counter | ||||||||||||
| Years | |||||||||||||
| 5.4801 | 1 | 2021 | 0 | 0 | 0 | 0 | 0.1599 | 0.2942 | 0.3621 | 0.4333 | 0.7208 | 1 | |
| 5.3513 | 0.9514 | 2014 | 0.0486 | 0.0527 | 0.0604 | 0.0697 | 0.2493 | 0.3771 | 0.4416 | 0.5094 | 0.7829 | 0.9514 | |
| 5.3018 | 0.9328 | 2017 | 0.0672 | 0.0729 | 0.0836 | 0.0965 | 0.2836 | 0.4089 | 0.4722 | 0.5386 | 0.8068 | 0.9328 | |
| 5.2270 | 0.9045 | 2018 | 0.0955 | 0.1036 | 0.1187 | 0.1371 | 0.3355 | 0.4571 | 0.5184 | 0.5829 | 0.8429 | 0.9045 | |
| 5.2263 | 0.9043 | 2019 | 0.0957 | 0.1038 | 0.1190 | 0.1374 | 0.3360 | 0.4575 | 0.5188 | 0.5832 | 0.8432 | 0.9043 | |
| 5.0476 | 0.8369 | 2013 | 0.1631 | 0.1769 | 0.2028 | 0.2341 | 0.4600 | 0.5724 | 0.6292 | 0.6888 | 0.9294 | 0.8369 | |
| 4.4695 | 0.6189 | 2012 | 0.3811 | 0.4134 | 0.4739 | 0.5471 | 0.8611 | 0.9442 | 0.9862 | 0.9697 | 0.7918 | 0.6189 | |
| 3.5155 | 0.2593 | 2016 | 0.7407 | 0.8036 | 0.9212 | 0.9365 | 0.4771 | 0.4422 | 0.4246 | 0.4062 | 0.3316 | 0.2593 | |
| 3.1104 | 0.1065 | 2020 | 0.8935 | 0.9693 | 0.8889 | 0.7172 | 0.1960 | 0.1817 | 0.1745 | 0.1669 | 0.1363 | 0.1065 | |
| 2.8279 | 0 | 2015 | 1 | 0.9152 | 0.7564 | 0.5643 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Laplace criterion (2020)—4.43. | ||
| 0.35 | 0.32 | 0.32 |
| Extreme optimism criterion (2020)—2.75 | ||
| 0.35 | 0.32 | 0.32 |
| Wald criterion (2020)—0.11 | ||
| 0.35 | 0.32 | 0.32 |
| Hurwitz criterion (2020) at —0.51 | ||
| 0.35 | 0.32 | 0.32 |
| Savage criterion (2019)—0.81 | ||
| 0.40 | 0.37 | 0.24 |
| Laplace criterion (2020 → 2019)—4.43 → 5.08 | ||
| → | → | |
| 0.35 | 0.32 → 0.33 | 0.32 |
| Extreme optimism criterion (2020)—2.75 → 2.79 | ||
| → | → | |
| 0.35 → 0.34 | 0.32 → 0.34 | 0.32 |
| Wald criterion (2020)—0.11 | ||
| → | → | |
| 0.35 → 0.34 | 0.32 → 0.34 | 0.32 |
| Hurwitz criterion (2020) at —0.51 → 0.52 | ||
| → | → | |
| 0.35 → 0.34 | 0.32 → 0.34 | 0.32 |
| Savage criterion (2019 → 2020)—0.81 → 0.88 | ||
| → | → | |
| 0.40 → 0.34 | 0.37 → 0.34 | 0.24 → 0.32 |
| Counterparty | Accept | Reject | |
|---|---|---|---|
| Company | |||
| Accept→accept | |||
| Accept→reject | |||
| Reject→accept | |||
| Reject→reject | |||
| Counterparty | |||||
|---|---|---|---|---|---|
| Accept | Reject | ||||
| Company | Accept → accept | 1 | 1 | 1 | |
| Accept → reject | 1 | 1 | 1 | ||
| Reject → accept | 1.2 | 1.1 | 1.1 | 1.1 | |
| Reject → reject | 1.2 | 0 | 0 | ||
| 1.2 | 1.1 | ||||
| 1.1 | |||||
| Company | |||||||
|---|---|---|---|---|---|---|---|
| Accept → Accept | Accept → Reject | Reject → Accept | Reject → Reject | ||||
| Counter party | Accept | 1 | 1 | 0.8 | 0.8 | 0.8 | 0.8 |
| Reject | 1 | 1 | 0.9 | 0 | 0 | ||
| 1 | 1 | 0.9 | 0.8 | ||||
| 0.8 | |||||||
| Counterparty | |||||
|---|---|---|---|---|---|
| Accept | Reject | ||||
| Company | Accept | 1 | 1 | 1 | 1 |
| Reject | 1.2 | 0 | 0 | ||
| 1.2 | 1 | ||||
| 1 | |||||
| Company | |||||
|---|---|---|---|---|---|
| Accept | Reject | ||||
| Counter party | Accept | 1 | 0.8 | 0.8 | 0.8 |
| Reject | 1 | 0 | 0 | ||
| 1 | 0.8 | ||||
| 0.8 | |||||
bargaining | bargaining | bargaining |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaytsev, A.; Mihel, E.; Dmitriev, N.; Alferyev, D.; Laszlo, U. Optimization of Interaction with Counterparties: Selection Game Algorithm under Uncertainty. Mathematics 2024, 12, 2079. https://doi.org/10.3390/math12132079
Zaytsev A, Mihel E, Dmitriev N, Alferyev D, Laszlo U. Optimization of Interaction with Counterparties: Selection Game Algorithm under Uncertainty. Mathematics. 2024; 12(13):2079. https://doi.org/10.3390/math12132079
Chicago/Turabian StyleZaytsev, Andrey, Ekaterina Mihel, Nikolay Dmitriev, Dmitry Alferyev, and Ungvari Laszlo. 2024. "Optimization of Interaction with Counterparties: Selection Game Algorithm under Uncertainty" Mathematics 12, no. 13: 2079. https://doi.org/10.3390/math12132079
APA StyleZaytsev, A., Mihel, E., Dmitriev, N., Alferyev, D., & Laszlo, U. (2024). Optimization of Interaction with Counterparties: Selection Game Algorithm under Uncertainty. Mathematics, 12(13), 2079. https://doi.org/10.3390/math12132079






