Estimating Cross-Border Mobility from the Difference in Peak Timing: A Case Study of Poland–Germany Border Regions
Abstract
1. Introduction
2. Methods
2.1. Deterministic Model
2.2. Stochastic Model
3. Results
Case Study: COVID-19 Incidence in Poland–Germany Border Region
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brockmann, D. Human mobility and spatial disease dynamics. Rev. Nonlinear Dyn. Complex. 2009, 2, 1–24. [Google Scholar]
- Findlater, A.; Bogoch, I.I. Human mobility and the global spread of infectious diseases: A focus on air travel. Trends Parasitol. 2018, 34, 772–783. [Google Scholar] [CrossRef] [PubMed]
- Alessandretti, L.; Aslak, U.; Lehmann, S. The scales of human mobility. Nature 2020, 587, 402–407. [Google Scholar] [CrossRef] [PubMed]
- Barbosa, H.; Barthelemy, M.; Ghoshal, G.; James, C.R.; Lenormand, M.; Louail, T.; Menezes, R.; Ramasco, J.J.; Simini, F.; Tomasini, M. Human mobility: Models and applications. Phys. Rep. 2018, 734, 1–74. [Google Scholar] [CrossRef]
- Schläpfer, M.; Dong, L.; O’Keeffe, K.; Santi, P.; Szell, M.; Salat, H.; Anklesaria, S.; Vazifeh, M.; Ratti, C.; West, G.B. The universal visitation law of human mobility. Nature 2021, 593, 522–527. [Google Scholar] [CrossRef]
- Wilder-Smith, A.; Gubler, D.J. Geographic expansion of dengue: The impact of international travel. Med. Clin. N. Am. 2008, 92, 1377–1390. [Google Scholar] [CrossRef]
- Cavallaro, F.; Dianin, A. Cross-border commuting in Central Europe: Features, trends and policies. Transp. Policy 2019, 78, 86–104. [Google Scholar] [CrossRef]
- Docquier, F.; Golenvaux, N.; Nijssen, S.; Schaus, P.; Stips, F. Cross-border mobility responses to COVID-19 in Europe: New evidence from facebook data. Glob. Health 2022, 18, 41. [Google Scholar] [CrossRef] [PubMed]
- Shyamsunder; Bhatter, S.; Jangid, K.; Abidemi, A.; Owolabi, K.M.; Purohit, S.D. A new fractional mathematical model to study the impact of vaccination on COVID-19 outbreaks. Decis. Anal. J. 2023, 6, 100156. [Google Scholar]
- Kumawat, S.; Bhatter, S.; Suthar, D.; Purohit, S.; Jangid, K. Numerical modeling on age-based study of coronavirus transmission. Appl. Math. Sci. Eng. 2022, 30, 609–634. [Google Scholar] [CrossRef]
- Shubin, M.; Brustad, H.K.; Midtbo, J.E.; Gunther, F.; Alessandretti, L.; Ala-Nissila, T.; Scalia Tomba, G.; Kivela, M.; Yat Hin Chan, L.; Leskela, L. The influence of cross-border mobility on the COVID-19 epidemic in Nordic countries. medRxiv 2023, 2023–11. [Google Scholar] [CrossRef] [PubMed]
- Kühn, M.J.; Abele, D.; Binder, S.; Rack, K.; Klitz, M.; Kleinert, J.; Gilg, J.; Spataro, L.; Koslow, W.; Siggel, M.; et al. Regional opening strategies with commuter testing and containment of new SARS-CoV-2 variants in Germany. BMC Infect. Dis. 2022, 22, 333. [Google Scholar] [CrossRef] [PubMed]
- Balcan, D.; Colizza, V.; Gonçalves, B.; Hu, H.; Ramasco, J.J.; Vespignani, A. Multiscale mobility networks and the spatial spreading of infectious diseases. Proc. Natl. Acad. Sci. USA 2009, 106, 21484–21489. [Google Scholar] [CrossRef] [PubMed]
- Jandarov, R.; Haran, M.; Bjørnstad, O.; Grenfell, B. Emulating a gravity model to infer the spatiotemporal dynamics of an infectious disease. J. R. Stat. Soc. Ser. (Appl. Stat.) 2014, 63, 423–444. [Google Scholar] [CrossRef]
- Xia, Y.; Bjørnstad, O.N.; Grenfell, B.T. Measles metapopulation dynamics: A gravity model for epidemiological coupling and dynamics. Am. Nat. 2004, 164, 267–281. [Google Scholar] [CrossRef] [PubMed]
- Senapati, A.; Sardar, T.; Ganguly, K.S.; Ganguly, K.S.; Chattopadhyay, A.K.; Chattopadhyay, J. Impact of adult mosquito control on dengue prevalence in a multi-patch setting: A case study in Kolkata (2014–2015). J. Theor. Biol. 2019, 478, 139–152. [Google Scholar] [CrossRef] [PubMed]
- Mari, L.; Bertuzzo, E.; Righetto, L.; Casagrandi, R.; Gatto, M.; Rodriguez-Iturbe, I.; Rinaldo, A. Modelling cholera epidemics: The role of waterways, human mobility and sanitation. J. R. Soc. Interface 2012, 9, 376–388. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, W.; Kargbo, D.; Yang, R.; Chen, Y.; Chen, Z.; Kamara, A.; Kargbo, B.; Kandula, S.; Karspeck, A.; et al. Transmission network of the 2014–2015 Ebola epidemic in Sierra Leone. J. R. Soc. Interface 2015, 12, 20150536. [Google Scholar] [CrossRef] [PubMed]
- Mertel, A.; Vyskočil, J.; Schüler, L.; Schlechte-Wełnicz, W.; Calabrese, J.M. Fine-scale variation in the effect of national border on COVID-19 spread: A case study of the Saxon-Czech border region. Spat. Spatio-Temporal Epidemiol. 2023, 44, 100560. [Google Scholar] [CrossRef]
- Simini, F.; González, M.C.; Maritan, A.; Barabási, A.L. A universal model for mobility and migration patterns. Nature 2012, 484, 96–100. [Google Scholar] [CrossRef]
- Timme, M. Revealing network connectivity from response dynamics. Phys. Rev. Lett. 2007, 98, 224101. [Google Scholar] [CrossRef] [PubMed]
- Casadiego, J.; Nitzan, M.; Hallerberg, S.; Timme, M. Model-free inference of direct network interactions from nonlinear collective dynamics. Nat. Commun. 2017, 8, 2192. [Google Scholar] [CrossRef] [PubMed]
- Shandilya, S.G.; Timme, M. Inferring network topology from complex dynamics. New J. Phys. 2011, 13, 013004. [Google Scholar] [CrossRef]
- Gao, T.T.; Yan, G. Autonomous inference of complex network dynamics from incomplete and noisy data. Nat. Comput. Sci. 2022, 2, 160–168. [Google Scholar] [CrossRef] [PubMed]
- Ching, E.S.; Lai, P.Y.; Leung, C. Reconstructing weighted networks from dynamics. Phys. Rev. 2015, 91, 030801. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.; Shen, C.; Jin, L.; Shi, Q.; Wang, Z.; Boccaletti, S. Inferring network structures via signal Lasso. Phys. Rev. Res. 2021, 3, 043210. [Google Scholar] [CrossRef]
- Alves, C.L.; Pineda, A.M.; Roster, K.; Thielemann, C.; Rodrigues, F.A. EEG functional connectivity and deep learning for automatic diagnosis of brain disorders: Alzheimer’s disease and schizophrenia. J. Phys. Complex. 2022, 3, 025001. [Google Scholar] [CrossRef]
- Sysoeva, M.V.; Sysoev, I.V.; Prokhorov, M.D.; Ponomarenko, V.I.; Bezruchko, B.P. Reconstruction of coupling structure in network of neuron-like oscillators based on a phase-locked loop. Chaos Solitons Fractals 2021, 142, 110513. [Google Scholar] [CrossRef]
- Hempel, K.; Earn, D.J. Estimating epidemic coupling between populations from the time to invasion. J. R. Soc. Interface 2020, 17, 20200523. [Google Scholar] [CrossRef]
- Bichara, D.; Kang, Y.; Castillo-Chavez, C.; Horan, R.; Perrings, C. SIS and SIR epidemic models under virtual dispersal. Bull. Math. Biol. 2015, 77, 2004–2034. [Google Scholar] [CrossRef]
- Bichara, D.; Iggidr, A. Multi-patch and multi-group epidemic models: A new framework. J. Math. Biol. 2018, 77, 107–134. [Google Scholar] [CrossRef]
- Espinoza, B.; Castillo-Chavez, C.; Perrings, C. Mobility restrictions for the control of epidemics: When do they work? PLoS ONE 2020, 15, e0235731. [Google Scholar] [CrossRef] [PubMed]
- Mhlanga, A.; Mupedza, T. A patchy theoretical model for the transmission dynamics of SARS-cov-2 with optimal control. Sci. Rep. 2022, 12, 17840. [Google Scholar] [CrossRef] [PubMed]
- Agusto, F.; Goldberg, A.; Ortega, O.; Ponce, J.; Zaytseva, S.; Sindi, S.; Blower, S. How do interventions impact malaria dynamics between neighboring countries? A case study with Botswana and Zimbabwe. In Using Mathematics to Understand Biological Complexity: From Cells to Populations; Association for Women in Mathematics Series; Springer: Cham, Switerland, 2021; Volume 22, pp. 83–109. [Google Scholar] [CrossRef]
- Gillespie, D.T. Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys. 2001, 115, 1716–1733. [Google Scholar] [CrossRef]
- Gillespie, D.T.; Petzold, L.R. Improved leap-size selection for accelerated stochastic simulation. J. Chem. Phys. 2003, 119, 8229–8234. [Google Scholar] [CrossRef]
- Linka, K.; Peirlinck, M.; Kuhl, E. The reproduction number of COVID-19 and its correlation with public health interventions. Comput. Mech. 2020, 66, 1035–1050. [Google Scholar] [CrossRef] [PubMed]
- Abdussalam, W.; Mertel, A.; Fan, K.; Schüler, L.; Schlechte-Wełnicz, W.; Calabrese, J.M. A scalable pipeline for COVID-19: The case study of Germany, Czechia and Poland. arXiv 2022, arXiv:2208.12928. [Google Scholar]
- Byrne, A.W.; McEvoy, D.; Collins, A.B.; Hunt, K.; Casey, M.; Barber, A.; Butler, F.; Griffin, J.; Lane, E.A.; McAloon, C.; et al. Inferred duration of infectious period of SARS-CoV-2: Rapid scoping review and analysis of available evidence for asymptomatic and symptomatic COVID-19 cases. BMJ Open 2020, 10, e039856. [Google Scholar] [CrossRef] [PubMed]
- Ma, J. Estimating epidemic exponential growth rate and basic reproduction number. Infect. Dis. Model. 2020, 5, 129–141. [Google Scholar] [CrossRef]
- Favier, C.; Dégallier, N.; Rosa-Freitas, M.G.; Boulanger, J.P.; Costa Lima, J.; Luitgards-Moura, J.F.; Menkes, C.E.; Mondet, B.; Oliveira, C.; Weimann, E.; et al. Early determination of the reproductive number for vector-borne diseases: The case of dengue in Brazil. Trop. Med. Int. Health 2006, 11, 332–340. [Google Scholar] [CrossRef]
- Pinho, S.T.R.d.; Ferreira, C.P.; Esteva, L.; Barreto, F.R.; Morato e Silva, V.; Teixeira, M. Modelling the dynamics of dengue real epidemics. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2010, 368, 5679–5693. [Google Scholar] [CrossRef] [PubMed]


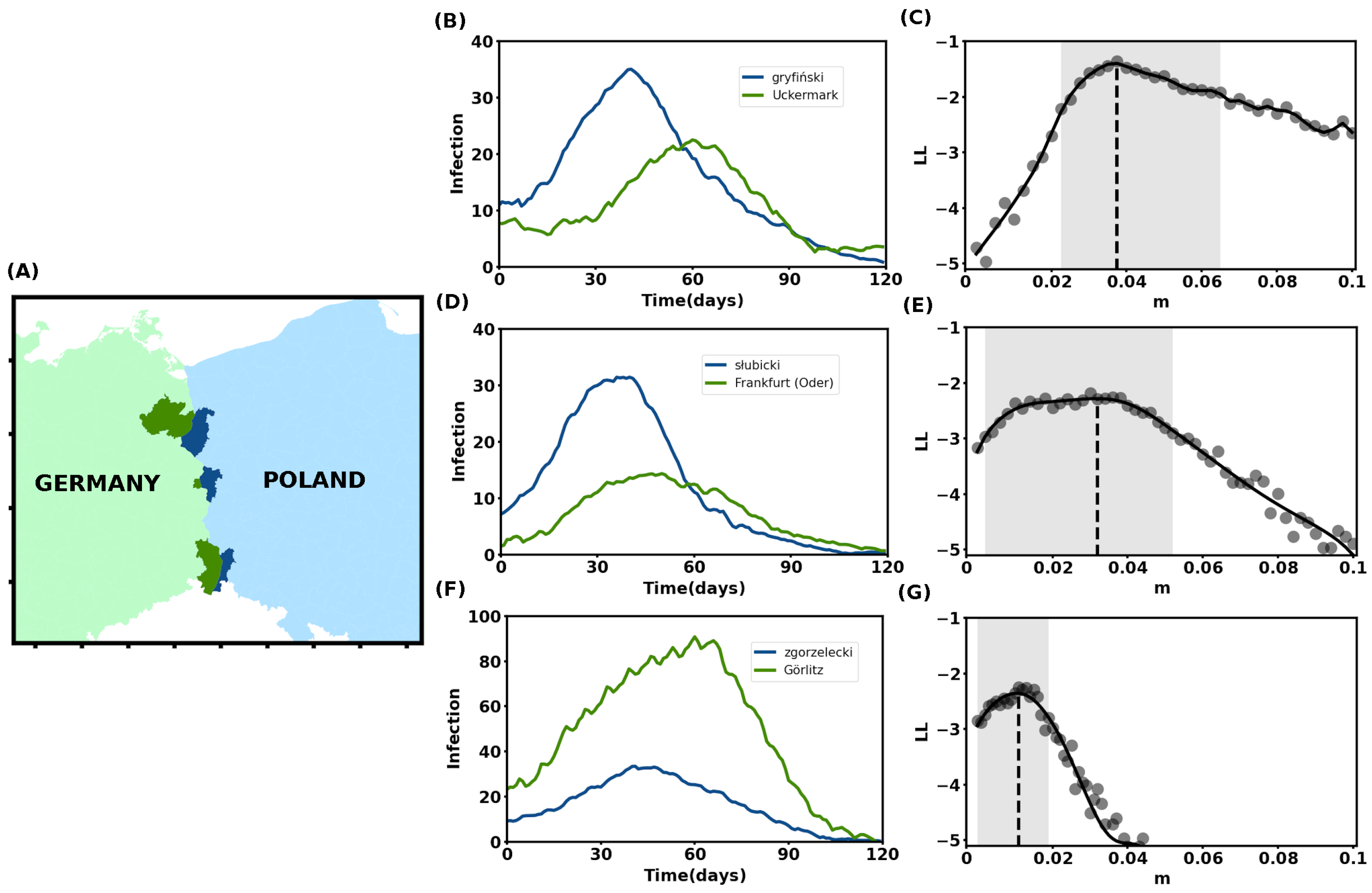
| Pair (Powiat, Kreise) | Transmission Rate (, ) | Total Population (, ) | Initial Infection | Observed Difference in Peak Timing () | Estimated Mobility Flux () |
|---|---|---|---|---|---|
| (Gryfiński, Uckermark) | (0.10, 0.075) | (82,951, 119,552) | (11, 8) | 20 days | 0.038 [0.022, 0.064] |
| (Słubicki, Frankfurt(Oder)) | (0.13, 0.14) | (47,068, 57,873) | (8, 1) | 10 days | 0.032 [0.004, 0.052] |
| (Zgorzelecki, Görlitz) | (0.10, 0.11) | (90,584, 254,894) | (9, 23) | 20 days | 0.012 [0.002, 0.018] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Senapati, A.; Mertel, A.; Schlechte-Welnicz, W.; Calabrese, J.M. Estimating Cross-Border Mobility from the Difference in Peak Timing: A Case Study of Poland–Germany Border Regions. Mathematics 2024, 12, 2065. https://doi.org/10.3390/math12132065
Senapati A, Mertel A, Schlechte-Welnicz W, Calabrese JM. Estimating Cross-Border Mobility from the Difference in Peak Timing: A Case Study of Poland–Germany Border Regions. Mathematics. 2024; 12(13):2065. https://doi.org/10.3390/math12132065
Chicago/Turabian StyleSenapati, Abhishek, Adam Mertel, Weronika Schlechte-Welnicz, and Justin M. Calabrese. 2024. "Estimating Cross-Border Mobility from the Difference in Peak Timing: A Case Study of Poland–Germany Border Regions" Mathematics 12, no. 13: 2065. https://doi.org/10.3390/math12132065
APA StyleSenapati, A., Mertel, A., Schlechte-Welnicz, W., & Calabrese, J. M. (2024). Estimating Cross-Border Mobility from the Difference in Peak Timing: A Case Study of Poland–Germany Border Regions. Mathematics, 12(13), 2065. https://doi.org/10.3390/math12132065






