Abstract
Since robustness only exists on the sliding mode/surface, sliding mode control is non-globally stable. Therefore, shortening the time to reach the sliding mode is an important method of improving sliding mode robustness. However, there is an inherent contradiction between rapidity and overshoot. Therefore, ensuring rapid convergence without overshoot is a worthwhile research problem. Consequently, this paper proposes a design for a fast variable speed reaching law (FVSRL) to improve the quality of sliding mode control. The constructed approach rate is based on a variable speed term, an exponential term, and a fast term, ensuring rapid convergence without overshoot. At the same time, a high-gain disturbance observer is employed for feedforward compensation. Finally, the designed reaching law is validated by comparing it with conventional exponential approach rates and a new sliding mode reaching law, demonstrating its superior performance. Detailed comparative and quantitative analyses of the simulation results using the conventional exponential reaching law, the new sliding mode reaching law, and the FVSRL are performed, utilizing metrics such as integrated square error, integral time square error, integrated absolute error, and integral time absolute error.
Keywords:
PMSM; sliding mode control; fast variable speed reaching law; high-gain disturbance observer MSC:
93C10; 93C40; 93C73
1. Introduction
The benefits of the permanent-magnet synchronous motor (PMSM) include a simple structure and high power density in addition to high efficiency [1]. Therefore, the PMSM has been extensively used in high-precision CNC machine tools, robotics, aerospace, and other fields [2,3,4]. However, PMSMs are multi-variable systems characterized by strong coupling and are subject to various disturbances and uncertainties, including load disturbance, parameter mismatch, friction, and so on [5]. Therefore, the performances obtained by traditional linear control methods, such as the PI control strategy, are hardly satisfactory, due to applying directly a linear PI controller in a nonlinear system. Although compensation is inherently automatic in PI regulators for modeling error, compensation may not always work effectively, even for predictive control systems [6]. In recent decades, in order to overcome some of the problems arising from traditional PI controllers, many nonlinear control theories have been proposed and developed. These methods include fuzzy control [7], auto-disturbance rejection control [8], model predictive control [9], and sliding mode control (SMC) [10]. Recently, the concept of designing several kinds of nonlinear control law has become very popular, and the SMC strategy is one of the important examples. SMC is a kind of a variable-structure control strategy that changes the dynamics of the system through a switching control law. The method is insensitive to parameter variations and has fast dynamic response [3,11,12,13].
However, it should be noted that the sliding mode method has some deficiencies too. In the context of the future implementation of the switching control law, time delays may result in high-frequency, oscillatory behavior, referred to as chattering. SMC consists of two key components: the reaching law and the sliding mode surface. The reaching law is useful in controlling the system states on the sliding mode surface; however, the task of maintaining the system states precisely on the sliding surface with zero error is a never-ending problem, as discussed in [14]. Moreover, the system states wander across both sides of the sliding surface and, thus, incorporate chattering. Furthermore, the SMC is only robust in the sliding mode and does not lend the system global robustness. Therefore, elimination of chattering and remedial action for the absence of global robustness are two paramount areas in SMC. The choice of the reaching law is especially critical since it affects the manner by which the system states progress towards the sliding mode surface [15].
However, it has been established that the regular SMC cannot be brought to the equilibrium point in a finite time duration; thus, there is the terminal SMC that can steer the tracking error to the equilibrium point in a finite time duration [16]. As to the singularity problem of the terminal SMC performing for the PMSM system, another nonsingular terminal SMC has been developed [17]. In addition, some new types of reaching law have been developed. The conventional exponential reaching law (CERL) was initially proposed and designed by Academician Weibing Gao [18]. A novel sliding mode control method utilizing a new sliding mode reaching law (NSMRL) has been introduced. This approach effectively reduces inherent chattering and enhances the velocity of the system state in reaching the sliding mode surface [19]. A new switching-type reaching law for sliding mode control of discrete-time systems was proposed. The refined reaching law ensures faster convergence and better robustness of the controlled plant compared to the earlier approach, while also helping to satisfy the constraints of important signals in the system [20].
Since disturbance observers can accommodate external disturbances, this can enhance the control quality of the system, as indicated in the work of [21]. By incorporating a disturbance observer to estimate random incidental disturbances and then feeding forward these estimates into the SMC, superior control performance can be attained, due to reduced effects from higher control gain values [22]. As the extended-state observer is simpler in application and more robust, it has been established that the expected performance based on the estimation of interference is realized by applying the observer of interference with the application of the sliding mode technique indicated in other studies [23,24].
As enhancing PMSM control can improve motor performance, based on the above research, this paper proposes a composite control strategy by introducing high-gain disturbance observer (HGDO) and fast variable-speed sliding mode control (FVSSMC) algorithms to achieve better speed control performance for PMSM systems. Additionally, a new fast variable speed reaching law (FVSRL) is incorporated into FVSSMC, to shorten the settling time. While ensuring convergence time without overshoot, robustness is greatly improved. The main contributions of this paper can be summarized as follows:
- An FVSRL was built to handle the contradiction between responding quickly and over-shooting, as far as embedded system certification is concerned.
- There was coordination between the HGDO and the FVSSMC, which aimed at doing 78 feedforward compensation.
- From the aspect of anti-interference, when applying the fast variable reaching law, the FVSSMC had good anti-interference ability.
- This was done through comparing with other similar models—namely, CERL and NSMRL—in order to substantiate the ease of use and accuracy of the FVSRL. Detailed comparative and quantitative analyses of the simulation results were conducted, using integrated square error (ISE), integral time square error (ITSE), integrated absolute error (IAE), and integral time absolute error (ITAE).
The remaining sections of this study are structured as follows: Section 2 presents the mathematical model for the three-phase PMSM. Section 3 provides an overview of how the HGDO gets involved in determining the unknown lumped disturbance and feeds back the estimated value to the FVSSMC. Section 4 covers the design of the controller, while Section 5 provides a simulation study to validate the proposed approaches. Our conclusions are presented in Section 6.
2. PMSM Modeling
Under the conditions of ignoring motor parameter variations and external disturbances, the mathematical model of a PMSM can be described by the following voltage equations [25]:
where the symbols represent the following:
- and are the d-axis and q-axis voltages, respectively.
- R is the stator resistance.
- and are the d-axis and q-axis currents, respectively.
- and are the d-axis and q-axis inductances, respectively.
- p is the number of pole pairs.
- is the mechanical angular velocity of the motor.
- is the flux linkage of the permanent magnet.
For a surface-mounted PMSM where the torque equation can be expressed as follows:
The motion equations of the PMSM [25] are given by
where B represents the viscous friction coefficient, J denotes the moment of inertia, and stands for the load torque.
3. Disturbance Estimation with High-Gain Disturbance Observer
3.1. Design of High-Gain Disturbance Observer
As shown by Equation (4), the disturbance term d, which is part of the PMSM system, has a significant impact on system performance, since d will appear in the control input directly. To improve the robustness of the system, it is essential to compensate for these disturbances. However, in practical applications, disturbance values are not directly measurable. This necessitates the development of a disturbance observer to obtain disturbance information. Consequently, this paper proposes the design of an HGDO for disturbance estimation.
Serving as a high-gain disturbance observer, it incorporates the disturbance into a new system state to be estimated. By setting up high-gain feedback for error compensation, the observer’s dynamics are designed to be significantly faster than those of the system, thereby ensuring accurate state tracking.
To establish the system’s state equation, let the state variable and the output . From Equation (4), Equation (6) can be obtained as follows:
We introduce the disturbance term as a new state variable . In practical PMSM systems, the disturbance d changes slowly, allowing us to approximate its first-order derivative as zero. Consequently, the state-space equation of the system is formulated as follows:
By using and as the observed variables, we establish a high-gain feedback for the speed estimation error e. The extended disturbance observer is designed as follows:
where , , and are positive real numbers, typically chosen to be very small, to ensure high gain. Using this HGDO, we can achieve and .
3.2. Observer Stability Analysis
To demonstrate that the observer converges within a finite time, we derive the error state equation of the observer and analyze its stability using the Lyapunov stability theory.
Theorem 1.
According to the Lyapunov stability theory, the observer can be stabilized when the convergence condition of the observer can be obtained as
Proof of Theorem 1.
We define the error state variables of the observer as :
where . Due to
Therefore, the error state equation of the extended observer can be written as
where . The characteristic equation of the matrix A is given by
where I represents the identity matrix, denotes the eigenvalue of A, and A can be made Hurwitz by appropriately choosing and . Then, for any symmetric positive-definite matrix Q, there exists a symmetric positive-definite matrix P satisfying
We define the Lyapunov function for the observer as
Taking the derivative of V and combining it with Equation (15), the next equation is given by
Remark 1.
From Equation (9), it can be seen that the convergence rate of ξ is inversely proportional to the parameter ε, i.e., the smaller ε is, the faster the convergence rate will be.
4. Controller Design
4.1. Design of Fast Terminal Variable Speed Reaching Law
Gao [18] proposed the concept of convergence rate and designed a widely used CERL, which is expressed as
where is the sliding surface, is the approach rate, q is the approach coefficient, and and . The phase portrait of the TERL is shown in Figure 1a.
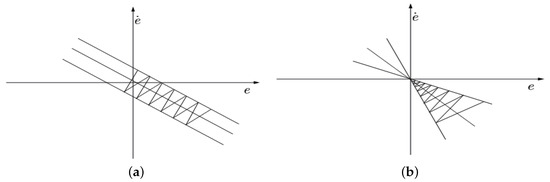
Figure 1.
(a) CERL. (b) FSVRL.
As is well known, the conventional pure exponential reaching law cannot reach the sliding mode surface in finite time. To address this, an isokinetic reach term is added, ensuring that when is close to zero, the reaching velocity is instead of zero. However, while this addition resolves the accessibility problem, the reaching speed to the sliding mode surface in the exponential reaching law is determined by the design value of the parameter q. This creates a contradiction, as increasing the reaching speed simultaneously increases sliding chattering.
In order to solve the inherent chattering problem of the exponential reaching law, the above exponential reaching law was improved, to obtain a new type of fast variable speed reaching law (FVSRL), which is expressed as
where x is the error between the desired value and the real value. Due to the introduction of the variable term, the system can adaptively approach the sliding surface with exponential and variable speed rates and obtain a faster convergence speed. When the system state is far away from the sliding mode surface and play a major role. When the system approaches the sliding surface, the exponential terms and approach zero, and its effect becomes smaller. The speed term plays a major role. The system enters the sliding mode process and the selected state quantity x enters the sliding surface and moves toward the origin. At this time, the speed term also decreases as x decreases and, finally, stabilizes at the origin. When x decreases to zero, the speed term becomes zero, and the chattering is suppressed. The phase portrait of the FVSRL is shown in Figure 1b.
4.2. Sliding Mode Control Controller Design
Based on the HGDO and the FVSSMC, an entire PMSM control diagram is shown in Figure 2. The PMSM state variables via Equation (4) are given by
The equation represents the target speed, while represents the motor output speed. Combining Equation (21) and taking the derivative of Equation (22) yields
The definition of a sliding surface function is
The derivative of the sliding surface function is referred to as the “sliding mode control law". Incorporating Equation (22) into this, we obtain
The integration of the HDGO and the SMC can be completed by using the observed value of d instead of d. This is also feedforward compensation. Combined with Equations (20) and (24) and substituting the observed disturbance and the perturbation value of the load torque into Equation (24) the output equation of the controller is obtained as
As seen from Equation (25), by incorporating parameter changes and load disturbances as feedforward compensation, the controller can counteract the effects of these disturbances on the system when the load and motor parameters vary.
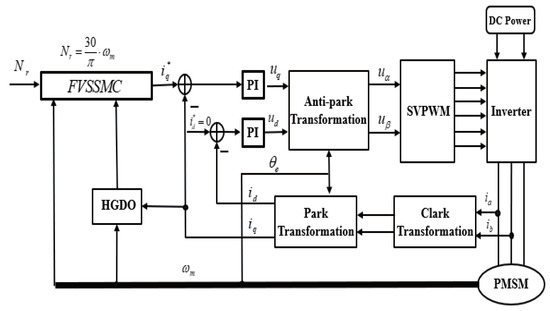
Figure 2.
FVSSMC control chart based on HGO.
Based on the CERL and the NSMRL, the controllers used for comparison reference are as follows:
Theorem 2.
When the controller is chosen as in Equation (25), the stability of the motion system can be guaranteed.
5. Simulation
In this section, we present simulation results to demonstrate the effectiveness of the proposed control strategy. The simulation parameters of the model, observer, and controllers used in this study are summarized in Table 1, Table 2 and Table 3, respectively. Figure 3 shows a comparison of the times required for the CERL, NSMRL, and FTSVRL systems to achieve speed regulation, with the desired value set to 1000 rpm. As depicted in Figure 3, the FTSVRL achieved the desired speed of 1000 rpm in the shortest time of 0.1014 s, whereas the CERL and NSMRL required 0.335 s and 0.4366 s, respectively. Hence, this comparison indicates that the FTSVRL outperformed the CERL and the NSMRL. Figure 4 shows the corresponding current variations, which represent the changes in the control inputs. Moreover, Figure 5 presents detailed comparative and quantitative analyses of the simulation results for speed regulation, utilizing the ISE, ITSE, IAE, and ITAE metrics.

Table 1.
Parameter values of the PMSM.

Table 2.
Parameter values of the HGDO.

Table 3.
Parameter values of the controllers.
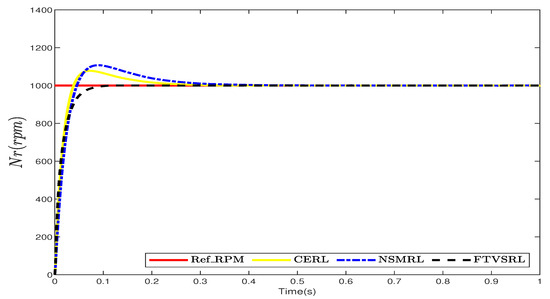
Figure 3.
Comparison between CERL, NSMRL, and FTVSRL for speed regulation.
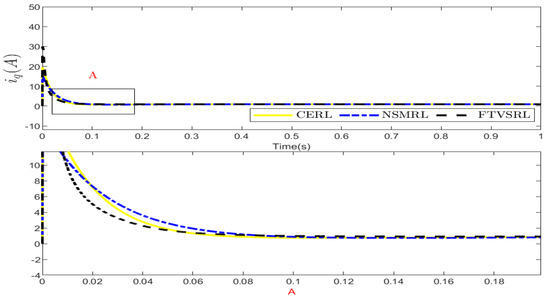
Figure 4.
Comparison between CERL, NSMRL, and FTVSRL for control input of speed regulation.
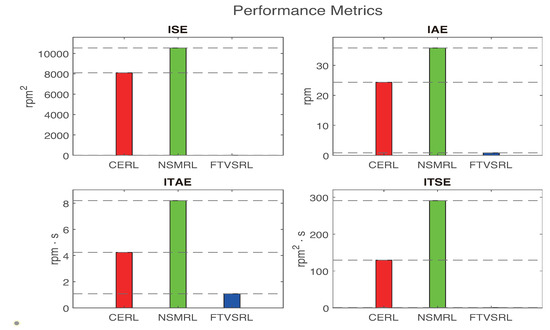
Figure 5.
Performance index using ISE, IAE, ITAE, and ITSE for speed regulation.
To verify the efficiency of the developed control strategy, simulation experiments were performed for this section. Table 1 shows the different simulation parameters that were used in the current study, while Table 2 and Table 3 depicts the different observers and controllers that were employed in the study, respectively. Figure 3 presents a comparison of the regulation times of the speed for the CERL, NSMRL, and FTSVRL systems, where the desired value was set to 1000 rpm. As seen in Figure 3, according to the requested performance, the FTSVRL rose to the required rotor speed of 1000 rpm within the shortest time of 0. The reaction times of the WSC, WEF, and Toll were 1014 s, whereas the CERL and the NSMRL required 0.335 s and 0.4366 s, respectively. Therefore, this comparison shows that the FTSVRL yielded better performance in comparison to the other two models, namely the CERL and the NSMRL. A similar but opposite result was obtained for the control inputs, as depicted in Figure 4, where the current differences are displayed. Furthermore, Figure 5 compares and quantifies the simulation results of the time–speed regulation, using the integrated square error (ISE), the integral time square error (ITSE), the integrated absolute error (IAE), and the integral time absolute error (ITAE).
Remark 2.
For a fair comparison, all three controllers were equipped with the same HGDO and the same parameters. The relevant parameters are listed in Table 2.
Remark 3.
Figure 6 presents a comparison of the speed-tracking performances of the CERL, the NSMRL, and the FTSVRL. The desired speed changed from 0 to 900 rpm at 0.0901 s, then from 900 to −500 rpm at 0.4983 s, and from −500 to 500 rpm at 0.7488 s. These figures demonstrate that the FTSVRL outperformed the CERL and the NSMRL in terms of tracking performance. Figure 7 shows the corresponding changes in the current, which represents the control input. Additionally, Figure 8 provides detailed comparative and quantitative analyses of the simulation results for speed tracking, using the ISE, ITSE, IAE, and ITAE metrics.
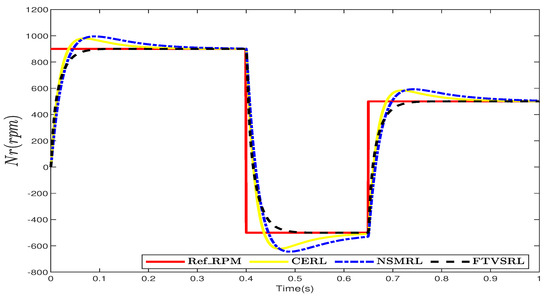
Figure 6.
Comparison between CERL, NSMRL, and FTVSRL for speed tracking.
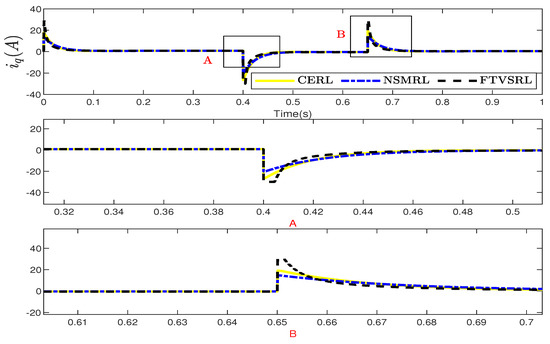
Figure 7.
Comparison between CERL, NSMRL, and FTVSRL for control input of speed tracking.
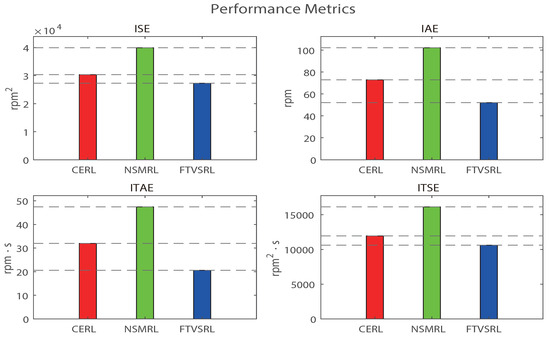
Figure 8.
Performance index using ISE, IAE, ITAE, and ITSE for speed tracking.
Figure 9 shows the speed response of the motor to a sudden load of 10 N·m applied at 0.6 s. The load duration was 0.4 s, meaning the load was applied at 0.6 s and removed at 1 s. As shown in Figure 9, the FTSVRL achieved a smaller speed deviation from the desired speed than the CERL and the NSMRL, respectively. The corresponding changes in the current are shown in Figure 10. Furthermore, Figure 11 offers detailed comparative and quantitative analyses of the simulation results for the sudden load test, employing ISE, ITSE, IAE, and ITAE metrics.
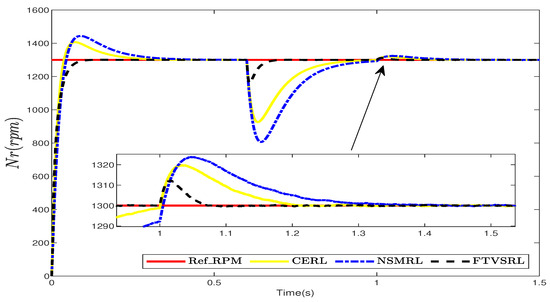
Figure 9.
Comparison between CERL, NSMRL, and FTVSRL for sudden load test.
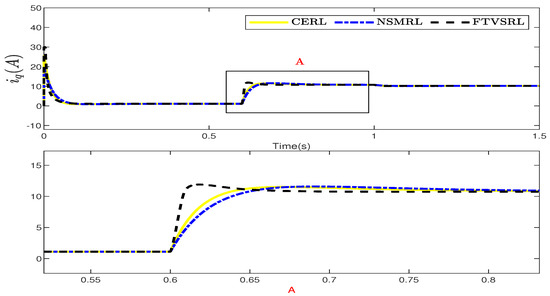
Figure 10.
Comparison between CERL, NSMRL, and FTVSRL for control input of sudden load test.
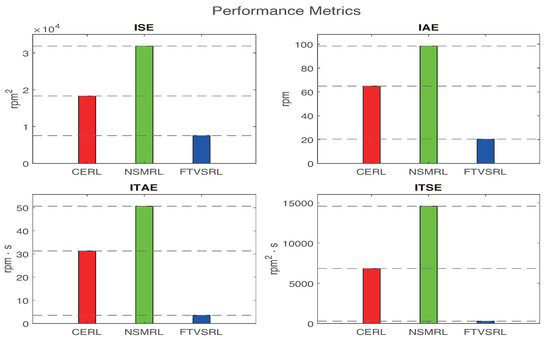
Figure 11.
Performance index using ISE, IAE, ITAE, and ITSE for sudden load test.
6. Conclusions
To address the tension between rapid market responsiveness and ensuring comprehensive certification for embedded systems, the FVSRL was established. Collaborating with the HGDO alongside the FVSSMC, it enables feedforward compensation. Integrating the fast variable reaching law enriches the FVSSMC by mitigating interferences. Performance comparisons with other models, the CERL and the NSMRL, validated the usability and reliability of the FVSRL. These analyses utilized key performance parameters, including ISE, ITSE, IAE, and ITAE, for quantitative comparisons and simulations. In the future, we will use the designed reaching law to verify its performance on real motors.
Author Contributions
This paper was accomplished by all the authors. H.W. and G.Z. conceived the idea, performed the analysis, and designed the simulation; H.W. and X.L. carried out the numerical simulations; and H.W. wrote the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Science and Technology Innovation Project of the National Shuohuang Railway Company (SHTL-22-17) and in part by the Key Research Development Project of Nanjing Polytechnic Institute under Grant NJPI-2021-14.
Data Availability Statement
The original contributions presented in the study are included in the article material, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, Z.; Yang, X.; Wang, W.; Chen, K.; Cheung, N.C.; Pan, J. Enhanced sliding mode control for PMSM speed drive systems using a novel adaptive sliding mode reaching law based on exponential function. IEEE Trans. Ind. Electron. 2024. [Google Scholar] [CrossRef]
- Shi, T.; Wang, Z.; Xia, C. Speed measurement error suppression for PMSM control system using self-adaption Kalman observer. IEEE Trans. Ind. Electron. 2014, 62, 2753–2763. [Google Scholar] [CrossRef]
- Xu, W.; Junejo, A.K.; Liu, Y.; Islam, M.R. Improved continuous fast terminal sliding mode control with extended state observer for speed regulation of PMSM drive system. IEEE Trans. Veh. Technol. 2019, 68, 10465–10476. [Google Scholar] [CrossRef]
- Sun, X.; Cao, J.; Lei, G.; Guo, Y.; Zhu, J. A composite sliding mode control for SPMSM drives based on a new hybrid reaching law with disturbance compensation. IEEE Trans. Transp. Electrif. 2021, 7, 1427–1436. [Google Scholar] [CrossRef]
- Sheng, L.; Li, W.; Wang, Y.; Fan, M.; Yang, X. Sensorless control of a shearer short-range cutting interior permanent magnet synchronous motor based on a new sliding mode observer. IEEE Access 2017, 5, 18439–18450. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, L.; Zhao, K.; Sun, L. Nonlinear speed control for PMSM system using sliding-mode control and disturbance compensation techniques. IEEE Trans. Power Electron. 2012, 28, 1358–1365. [Google Scholar] [CrossRef]
- Kung, Y.S.; Tsai, M.H. FPGA-based speed control IC for PMSM drive with adaptive fuzzy control. IEEE Trans. Power Electron. 2007, 22, 2476–2486. [Google Scholar] [CrossRef]
- Liu, X.; Deng, Y.; Cao, H.; Wang, J.; Li, H.; Lee, C.H. Modified ADRC based on quasi-resonant fixed-time-convergent extended state observer for PMSM current regulation. IEEE Trans. Transp. Electrif. 2024. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, X.; Xiao, D.; Ma, D.; Yang, X.; Wang, Z. Model predictive control of five-level open-end winding PMSM drives. IEEE Trans. Transp. Electrif. 2024. [Google Scholar] [CrossRef]
- Zwerger, T.; Mercorelli, P. Optimal control strategies for PMSM with a decoupling super twisting SMC and inductance estimation in the presence of saturation. J. Frankl. Inst. 2024, 361, 106934. [Google Scholar] [CrossRef]
- Sun, X.; Cao, J.; Lei, G.; Guo, Y.; Zhu, J. Speed sensorless control for permanent magnet synchronous motors based on finite position set. IEEE Trans. Ind. Electron. 2019, 67, 6089–6100. [Google Scholar] [CrossRef]
- Bai, C.; Yin, Z.; Zhang, Y.; Liu, J. Multiple-Models Adaptive Disturbance Observer-Based Predictive Control for Linear Permanent-Magnet Synchronous Motor Vector Drive. IEEE Trans. Power Electron. 2022, 37, 9596–9611. [Google Scholar] [CrossRef]
- Zheng, L.; Wu, C.; Shentu, F.; Wu, C. An Accurate Full-Speed Position Estimation for Permanent Magnet Synchronous Motors with a DC-Bus Current Sensor. IEEE Trans. Power Electron. 2024. [Google Scholar] [CrossRef]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Springer: Berlin/Heidelberg, Germany, 2014; Volume 10. [Google Scholar]
- Ma, H.; Wu, J.; Xiong, Z. A novel exponential reaching law of discrete-time sliding-mode control. IEEE Trans. Ind. Electron. 2017, 64, 3840–3850. [Google Scholar] [CrossRef]
- Ma, Y.; Li, D.; Li, Y.; Yang, L. A novel discrete compound integral terminal sliding mode control with disturbance compensation for PMSM speed system. IEEE/ASME Trans. Mechatronics 2021, 27, 549–560. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Su, J.; Yu, X. Continuous nonsingular terminal sliding mode control for systems with mismatched disturbances. Automatica 2013, 49, 2287–2291. [Google Scholar] [CrossRef]
- Gao, W.; Hung, J.C. Variable structure control of nonlinear systems: A new approach. IEEE Trans. Ind. Electron. 1993, 40, 45–55. [Google Scholar]
- Hou, Q.; Ding, S. Finite-time extended state observer-based super-twisting sliding mode controller for PMSM drives with inertia identification. IEEE Trans. Transp. Electrif. 2022, 8, 1918–1929. [Google Scholar] [CrossRef]
- Bartoszewicz, A.; Leśniewski, P. New switching and nonswitching type reaching laws for SMC of discrete time systems. IEEE Trans. Control Syst. Technol. 2016, 24, 670–677. [Google Scholar] [CrossRef]
- Ren, J.; Ye, Y.; Xu, G.; Zhao, Q.; Zhu, M. Uncertainty-and-disturbance-estimator-based current control scheme for PMSM drives with a simple parameter tuning algorithm. IEEE Trans. Power Electron. 2016, 32, 5712–5722. [Google Scholar] [CrossRef]
- Hou, Q.; Ding, S.; Yu, X. Composite super-twisting sliding mode control design for PMSM speed regulation problem based on a novel disturbance observer. IEEE Trans. Energy Convers. 2020, 36, 2591–2599. [Google Scholar] [CrossRef]
- Zhang, X.; Hou, B.; Mei, Y. Deadbeat predictive current control of permanent-magnet synchronous motors with stator current and disturbance observer. IEEE Trans. Power Electron. 2016, 32, 3818–3834. [Google Scholar] [CrossRef]
- Wu, Y.j.; Li, G.f. Adaptive disturbance compensation finite control set optimal control for PMSM systems based on sliding mode extended state observer. Mech. Syst. Signal Process. 2018, 98, 402–414. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, H.; Li, X.; Zhao, H.; Zhang, Y.; Wang, S.; Ahmad, T.; Liu, T.; Shuang, F.; Wu, T. A PMSM control system for electric vehicle using improved exponential reaching law and proportional resonance theory. IEEE Trans. Veh. Technol. 2023, 72, 8566–8578. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).