Multi-Soliton, Soliton–Cnoidal, and Lump Wave Solutions for the Supersymmetric Boussinesq Equation
Abstract
1. Introduction
2. Similarity Reductions of the BB Equation
| 0 | 0 | |||
| 0 | 0 | 0 | ||
| 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 |
3. Traveling Wave Solutions with the Mapping and Deformation Method
4. Novel Solutions Based on Prior Solutions and Symmetry of the Boussinesq Equation
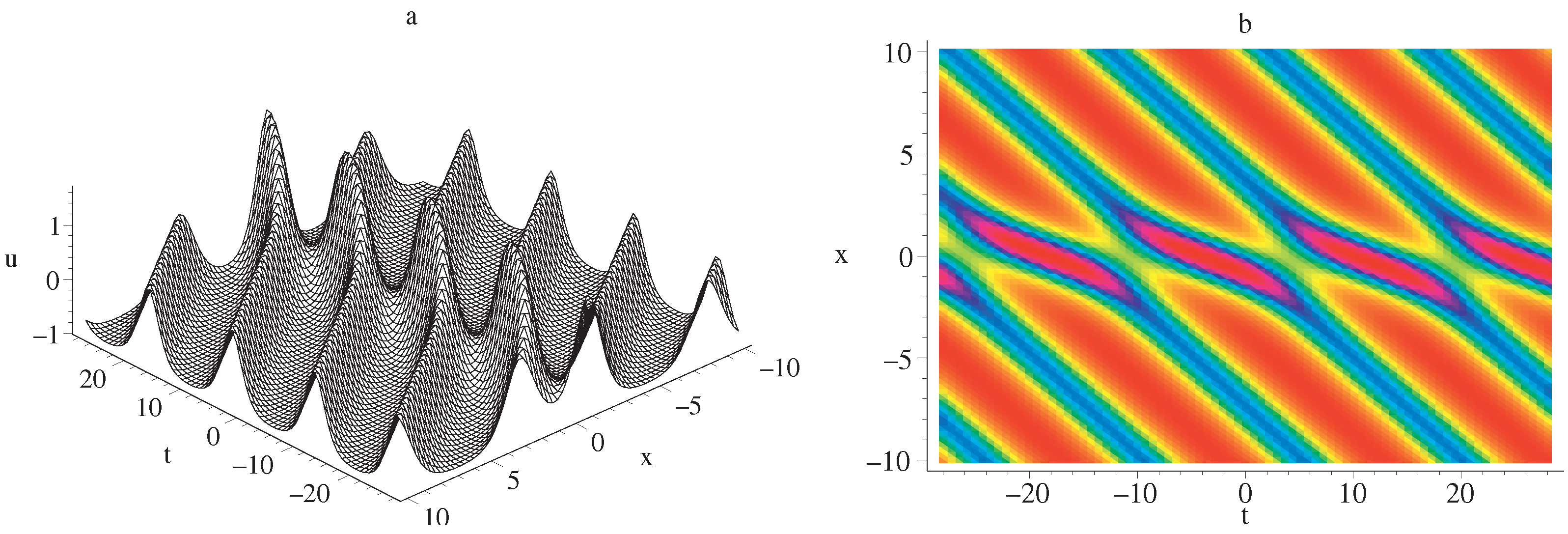
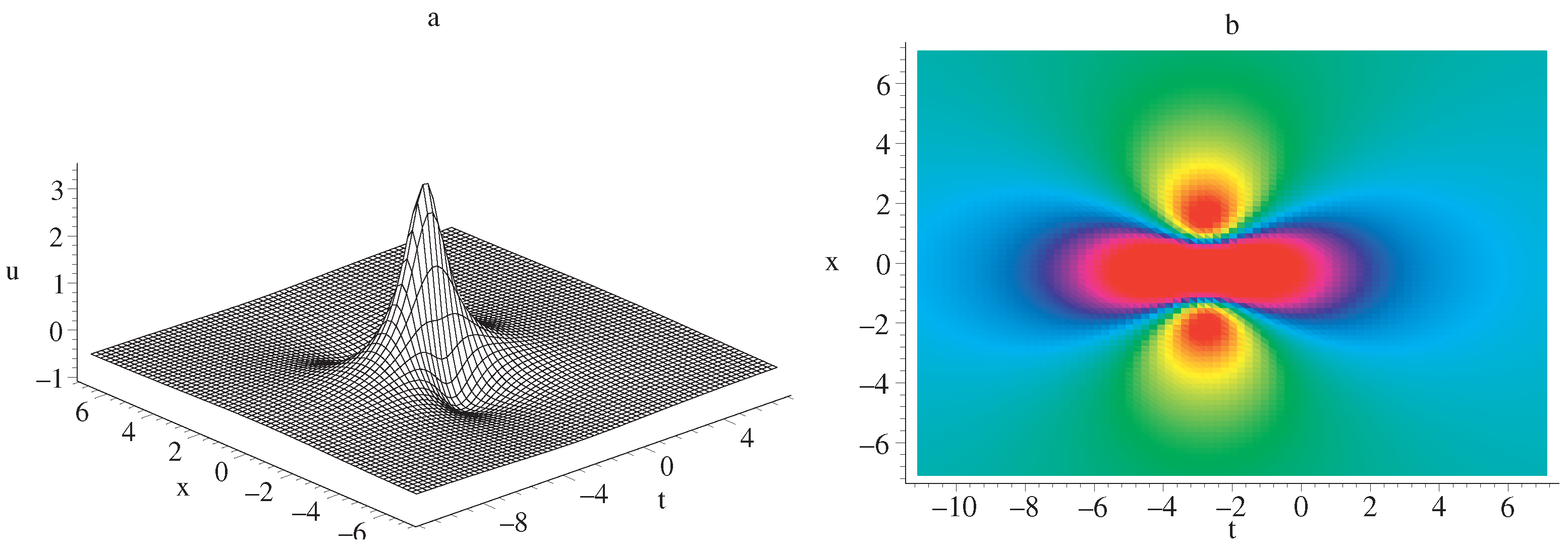
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hirota, R.; Satsuma, J. Nonlinear evolution equations generated from the Bäklund transformation for the Boussinesq equation. Prog. Theor. Phys. 1977, 57, 797–807. [Google Scholar] [CrossRef]
- Clarkson, P.A.; Kruskal, M.D. New similarity reductions of the Boussinesq equation. J. Math. Phys. 1989, 30, 2201. [Google Scholar] [CrossRef]
- Wang, Q.; Mihalache, D.; Beli, M.R.; Zeng, L.W.; Lin, J. Soliton transformation between different potential wells. Opt. Lett. 2023, 48, 747–750. [Google Scholar] [CrossRef]
- Jia, M.; Lou, S.Y. Searching For (2+1)-dimensional nonlinear Boussinesq equation from (1+1)-dimensional nonlinear Boussinesq equation. Commun. Theor. Phys. 2023, 75, 075006. [Google Scholar] [CrossRef]
- Tela, G.Y.; Zhang, D.J. On a special coupled lattice system of the discrete Boussinesq type. Rep. Math. Phys. 2023, 91, 219–235. [Google Scholar] [CrossRef]
- Kupershmidt, B.A. A supe Korteweg-de Vries equation: An integrable system. Phys. Lett. A 1984, 102, 213. [Google Scholar] [CrossRef]
- Martin, Y.I.; Radul, A.O. A supersymmetric extension of the Kadomtsev-Petviashvili hierarchy. Commun. Math. Phys. 1985, 65, 98. [Google Scholar]
- Mathieu, P. Supersymmetric extension of the Korteweg-de Vries equation. J. Math. Phys. 1988, 2499, 29. [Google Scholar] [CrossRef]
- Roelofs, G.H.M.; Kersten, P.H.M. Supersymmetric extensions of the nonlinear Schrödinger equation: Symmetries and coverings. J. Math. Phys. 1992, 2185, 33. [Google Scholar] [CrossRef]
- Zhang, C.F.; Zhao, Z.L.; Zhang, Y.F. Rational solutions consisting of multiple lump waves and line rogue waves in different spaces of the (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equation in incompressible fluid. Nonlinear Dyn. 2024, 112, 7377–7393. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Ren, B. Resonance solitons, soliton molecules and hybrid solutions for a (2+1)-dimensional nonlinear wave equation arising in the shallow water wave. Nonlinear Dyn. 2024, 112, 4793–4802. [Google Scholar] [CrossRef]
- Lou, S.Y.; Hu, X.R.; Chen, Y. Nonlocal symmetries related to Bäcklund transformation and their applications. J Phys. A Math. Theor. 2012, 45, 155209. [Google Scholar] [CrossRef]
- Ren, B. Symmetry reduction related with nonlocal symmetry for Gardner equation. Commun. Nonlinear Sci. Numer. Simulat. 2017, 42, 456–463. [Google Scholar] [CrossRef]
- Satsuma, J.; Ablowitz, M.J. Two-dimensional lumps in nonlinear dispersive systems. J. Math. Phys. 1979, 20, 1496–1503. [Google Scholar] [CrossRef]
- Yang, B.; Yang, J.K. Rogue waves in (2+1)-dimensional three-wave resonant interactions. Phys. D 2022, 432, 133160. [Google Scholar] [CrossRef]
- Younas, U.; Sulaiman, T.A.; Ren, J.L.; Yusuf, A. Lump interaction phenomena to the nonlinear ill-posed Boussinesq dynamical wave equation. J. Geom. Phys. 2022, 178, 104586. [Google Scholar] [CrossRef]
- Gao, X.N.; Lou, S.Y.; Tang, X.Y. Bosonization, singularity analysis, nonlocal symmetry reductions and exact solutions of supersymmetric KdV equation. J. High Energy Phys. 2013, 2013, 29. [Google Scholar] [CrossRef]
- Wei, P.F.; Liu, Y.; Zhan, X.R.; Zhou, J.L.; Ren, B. Bosonization, symmetry reductions, mapping and deformation method for B-extension of Sawada-Kotera equation. Results Phys. 2023, 54, 107132. [Google Scholar] [CrossRef]
- Das, A.; Huang, W.J.; Roy, S. The supersymmetric Boussinesq equation. Phys. Letts. A 2009, 157, 113. [Google Scholar] [CrossRef]
- Ren, B.; Lin, J.; Yu, J. Supersymmetric Ito equation: Bosonization and exact solutions. AIP Adv. 2013, 3, 042129. [Google Scholar] [CrossRef]
- Ren, B. Interaction solutions for supersymmetric mKdV-B equation. Chin. J. Phys. 2015, 53, 56. [Google Scholar] [CrossRef]
- Ren, B.; Lou, S.Y. A Super mKdV equation: Bosonization, Painlevé property and exact solutions. Commun. Theor. Phys. 2018, 69, 343. [Google Scholar] [CrossRef]
- Andrea, S.; Restuccia, A.; Sotomayor, A. An operator valued extension of the super Korteweg-de Vries equations. J. Math. Phys. 2001, 42, 2625. [Google Scholar] [CrossRef]
- Gao, X.N.; Lou, S.Y. Bosonization of supersymmetric KdV equation. Phys. Lett. B 2012, 209, 707. [Google Scholar] [CrossRef]
- Olver, P.J. Application of Lie Group to Differential Equation; Springer: Berlin, Germany, 1986. [Google Scholar]
- Tian, S.F.; Xu, M.J.; Zhang, T.T. A symmetry-preserving difference scheme and analytical solutions of a generalized higher-order beam equation. Proc. R. Soc. A 2021, 477, 20210455. [Google Scholar] [CrossRef]
- Ren, B.; Lin, J.; Wang, W.L. Painlevé analysis, infinite dimensional symmetry group and symmetry reductions for the (2+1)-dimensional Korteweg-de Vries-Sawada-Kotera-Ramani equation. Commun. Theor. Phys. 2023, 75, 085006. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Wazwaz, A.M. Multiple-soliton solutions for the Boussinesq equation. Appl. Math. Comput. 2007, 192, 479–486. [Google Scholar] [CrossRef]
- Lou, S.Y. Consistent Riccati expansion for integrable systems. Stud. Appl. Math. 2015, 134, 372–402. [Google Scholar] [CrossRef]
- Ma, W.X. Lump solutions to the Kadomtsev-Petviashvili equation. Phys. Lett. A 2015, 379, 2305. [Google Scholar] [CrossRef]
- Ren, B.; Ma, W.X.; Yu, J. Characteristics and interactions of solitary and lump waves of a (2+1)-dimensional coupled nonlinear partial differential equation. Nonlinear Dyn. 2019, 96, 717. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Satsuma, J. Solitons and rational solutions of nonlinear evolution equations. J. Math. Phys. 1978, 19, 2180. [Google Scholar] [CrossRef]
- Wei, P.F.; Long, C.X.; Zhu, C.; Zhou, Y.T.; Yu, H.Z.; Ren, B. Soliton molecules, multi-breathers and hybrid solutions in (2+1)-dimensional Korteweg-de Vries-Sawada-Kotera-Ramani equation. Chaos Solitons Fract. 2022, 158, 112062. [Google Scholar] [CrossRef]
- Lou, S.Y. Ren-integrable and ren-symmetric integrable systems. Commun. Theor. Phys. 2024, 76, 035006. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, P.-F.; Zhang, H.-B.; Liu, Y.; Lin, S.-Y.; Chen, R.-Y.; Xu, Z.-Y.; Wang, W.-L.; Ren, B. Multi-Soliton, Soliton–Cnoidal, and Lump Wave Solutions for the Supersymmetric Boussinesq Equation. Mathematics 2024, 12, 2002. https://doi.org/10.3390/math12132002
Wei P-F, Zhang H-B, Liu Y, Lin S-Y, Chen R-Y, Xu Z-Y, Wang W-L, Ren B. Multi-Soliton, Soliton–Cnoidal, and Lump Wave Solutions for the Supersymmetric Boussinesq Equation. Mathematics. 2024; 12(13):2002. https://doi.org/10.3390/math12132002
Chicago/Turabian StyleWei, Peng-Fei, Hao-Bo Zhang, Ye Liu, Si-Yu Lin, Rui-Yu Chen, Zi-Yi Xu, Wan-Li Wang, and Bo Ren. 2024. "Multi-Soliton, Soliton–Cnoidal, and Lump Wave Solutions for the Supersymmetric Boussinesq Equation" Mathematics 12, no. 13: 2002. https://doi.org/10.3390/math12132002
APA StyleWei, P.-F., Zhang, H.-B., Liu, Y., Lin, S.-Y., Chen, R.-Y., Xu, Z.-Y., Wang, W.-L., & Ren, B. (2024). Multi-Soliton, Soliton–Cnoidal, and Lump Wave Solutions for the Supersymmetric Boussinesq Equation. Mathematics, 12(13), 2002. https://doi.org/10.3390/math12132002





