Abstract
Uniaxial compressive strength is an essential mechanical parameter to adequately characterize any given material. Numerous standards have been developed to guarantee reliable testing execution, as well as the repeatability of results. In this sense, not only the geometric dimensions and tolerances of both the platen and the specimen have been prescribed, but also the testing parameters, such as the load application speed. However, all these recommendations are based on the assumption that the stresses are uniformly distributed across the contact interface between the platen and the specimen. Nevertheless, this is major elastic simplification that allows for obtaining a handy and useful formula to determine the compressive strength, but this strongly deviates the theoretical foundations from the actual experimental reality. Experimental and numerical research to determine the influence of relative stiffness between the specimen and the platen on the stress distribution generated during the execution of the uniaxial compressive test is performed. The results prove that the stresses are not uniformly distributed across the contact when the platen material is significantly stiffer or softer (less stiff) than that of the tested specimen, and additionally, an undesired triaxial stress field is induced inside the specimen. For these reasons, the use of platens with a similar stiffness to that of the specimen is strongly recommended, as it allows for the uniform distribution of the compressive contact stresses and minimizes the influence of the triaxial stress field.
Keywords:
uniaxial compressive strength; uniaxial compressive test; contact stress distribution; relative stiffness; standardized test; elastic behavior MSC:
65Z05
1. Introduction
An accurate characterization of the mechanical properties of any material is mandatory to address safety designs in all engineering fields. It also plays a relevant role in the stability analysis of dams, slopes, tunnels, etc. In this sense, the accurate determination of the uniaxial compressive strength (UCS) is a critical requirement to guarantee the execution of engineering projects under safety conditions, even though debate regarding its validity as a material property or merely as a design parameter is currently commonplace in the scientific community. Despite such controversy, numerous tests have been developed to determine the UCS numerical value. The most frequently performed test is the uniaxial compression test (UCT), in which a cylindrical specimen is compressed between two platens up to its failure [1,2]. The point load test has become commonplace, as no previous preparation of the tested sample is needed, allowing the test to be conducted on specimens of any shape [3,4].
To ensure the reliability and repeatability of UCT results, various standards and recommendations have been established [2,5,6,7,8,9,10,11]. It is important to note that although ISRM specifications are, technically speaking, recommendations and not standards, they will be referred to as standards in the following text. Standards related to rock materials [2,5,11] are particularly interesting, as many recommendations are aimed at overcoming complexities introduced by their inherent heterogeneity and brittleness. Nevertheless, all standards are primarily focused on the dimensional and geometrical tolerances for the involved elastic bodies, neglecting possible deviations in the stress and displacement specimen fields due to platen stiffness.
Regarding dimensional tolerances, the standards set recommended specimen diameter ( to length ratios. A minimum diameter is established to guarantee that the grain size is sufficiently small not to govern the failure mechanism at both the micro and macroscopic scale. Length restrictions are necessary to ensure a uniform compressive stress field inside the specimen at the moment of failure. During the contact between the specimen and the platen, shearing loads are generated across the contact, leading to a local stress field inside the specimen that does not match the desired homogeneous uniaxial compression field. Therefore, the length of the specimen is increased to allow for this undesired triaxial stress field induced near the contact to vanish. Therefore, a uniform compressive stress field at the mid-height of the specimen is ensured, although its length must be bounded to avoid buckling during the test execution. Hence, two presumed uniform stress distributions are involved in the UCT: one generated along the contact and another generated inside the specimen. For the latter, it is broadly assumed that if the restrictions imposed by the standards are met, a uniaxial and uniform compressive stress field is generated within the specimen.
Related to geometrical deviations for both the specimen and the platens, three main parameters are highlighted by most standards: flatness deviation at both ends, side straightness of the lateral surface, and perpendicularity, measured by angle, as schematically depicted in Figure 1.
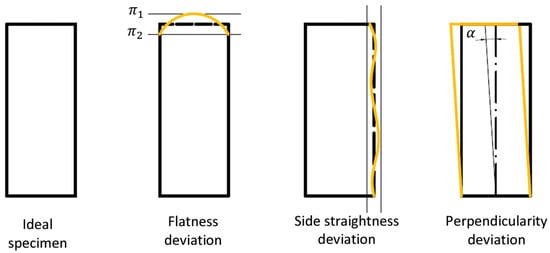
Figure 1.
Schematic representation of geometric tolerances, addressed by the standards, in both the specimen and the platen.
Although many standards propose different tolerance values, they are all in good agreement, as shown in Table 1 for the case of platens, and in Table 2 for the case of specimens, where and refers to diameter and length measures, and subscripts and refer to the specimen and the platen, respectively.

Table 1.
Tolerances of platens.

Table 2.
Tolerances allowed in specimens.
As evidenced by Table 1 and Table 2, tolerance values are recommended, disregarding the mechanical properties of the material under characterisation [2,11,12]. In this sense, it is worth highlighting the Spanish standard UNE 22950-1:1990, which recommends different specimen finishing qualities based on the stiffness of tested rock [5,13]. In this sense, three different stiffness levels are established: low, medium, and high deformability. Their boundaries are qualitatively set in accordance with representative properties of given materials for each range. Thus, no numerical value is used to define solid boundaries; instead, they are designated by simply naming some representative rock materials for each category. Furthermore, all standards set a minimum diameter that is at least 10 times higher than the largest grain size. However, provided this prerequisite is met, they permit minor variations in its minimum value.
The stress field within the specimen may be influenced not only by geometry, but also by the relative stiffness of the materials in contact, their preparation process, and the quality of the surface. Therefore, it is worth noting that only flatness tolerance has been established for platens (Table 2). Nevertheless, current literature accepts that possible deviations in testing results can be overcome for specimens with sufficient length [14,15,16], as due to the Saint-Venant’s principle, a homogeneous compression stress state will be developed at their mid-height points. However, the actual contact stress distribution will always be formed by the superposition of one normal and another shear load distribution (Figure 2). Only in those cases in which an adequate lubricant is used can the contact conditions be considered to produce neglectable shearing stresses. Nonetheless, no standard considers this last scenario.
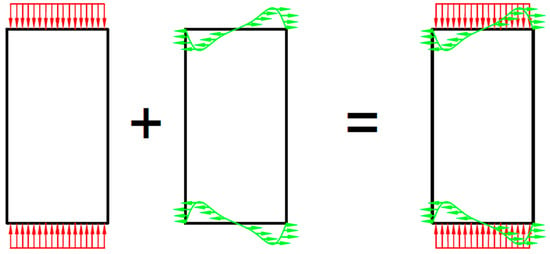
Figure 2.
Contact stress distribution as the superposition of normal (red arrows) and shearing (green arrows) stress distributions.
The induced shear load distribution across both ends provokes a local stress field close to the contact that vanishes at a certain distance from it [14,16,17,18]. Furthermore, the vertical load is assumed to be uniformly distributed along the contact, thereby generating a uniform compression stress field inside the specimen. The combination of these two phenomena allows standards to ensure that, for sufficiently long specimens, a homogeneous compressive stress field would be generated at the mid-height area of the specimens. Hence, they establish that the uniaxial compressive strength (UCS) can be determined as UCS = P/A, where P is the total applied load, and A the cross section of the specimen [15,19]. However, this may be a major simplification, as it will only hold true for the case of UCT in which the failure is initiated at a point located at the specimen’s mid-height, thus being subjected to uniaxial compression on the moment of failure initiation. Therefore, severe deviations may arise due to the inaccuracies of the final geometry of the specimen or its intrinsic heterogeneity, in the case of rock materials, which will lead to more complex loading schemes regarding the appearance of bending moment effects [20] or generating strain fluctuations, respectively [21,22,23].
Nonetheless, testing results lead to some contradictions when employing the aforementioned theoretical assumption. In this sense, if all induced stress fields are independent of the tested material properties, provided that specimens are sufficiently long, no differences should be registered in the obtained failure patterns. In contrast to this assumption, many authors have suggested different failure patterns when testing conditions are altered [17,24,25,26].
From an analytic perspective, induced stress fields in UCT specimens have been extensively analysed in the contemporary literature. The most prevalent approach considers arbitrary distributions of load or displacement in the vicinity of the contact to mathematically reproduce the involved physical phenomena of the end constraint. Nevertheless, the actual shape of the contact stress distribution remains unknown and may vary depending on the mechanical properties of the platen and specimen.
Although previous analytic approaches to the problem exist [27,28], the first major contribution is considered to have been made by Dougall [29], who proposed the solution to infinite circular cylinders subjected to a point load at any point inside the material or over its surface. The solution proposed by Power and Childs [30] significantly expanded the analytic possibilities, as it considered not only prescribed stresses, but also prescribed displacements as boundary conditions to solve the problem. Moghe and Neff [31] employed orthogonal Bessel and trigonometric functions to determine the stress field induced in constrained cylinders subjected to experimentally observed boundary conditions. Another major step forward was introduced by Benthem and Minderhoud [32], as their analytic solution considered that the elastic cylinder was compressed by the action of two stiff platens; therefore, they implemented a direct physical correlation between his formulation and the UCT. Al-Chalabi and Huang [33] developed an elastic solution based on the friction produced in the contact between the platen and the specimen, leading to major conclusions regarding the consequences of the triaxial stress state generated in the vicinity of the contact due to friction stresses. Kim and Steele present a novel solution for isotropic finite cylinders with mixed wall conditions, employing a Dini series [34]. Their contribution also overcame the singularities inherent in Benthem’s and Minderhound’s previous work [32]. Furthermore, with respect to the stress field developed inside isotropic cylinders due to arbitrary surface loads, the contributions of Wei and Chau cannot be ignored. Their research line allows for obtaining the stress field induced by any possible load distribution acting along the lateral surface or the ends of the specimen [35]. Indeed, the application of their general case to specific boundary conditions has resulted in direct applications in other pertinent tests in the field of rock mechanics, such as the double-punch test [36], the axial point load test [37], the diametral point load strength test [38,39], and the Brazilian test [40,41].
Due to the relevance of this elastic problem in the mechanical characterization of any given material, additional contributions that shed new light on the subject have arisen [42,43,44,45,46,47]. All these aforementioned elastic solutions are based on sophisticated mathematical treatments that lead to arduous stress analytic expressions, the management of which, for technical and practical purposes, can be extremely challenging without computational assistance. For this reason, no formulation is reproduced in this text, encouraging the readers to consult the original sources.
An induced stress field inside the specimen can be obtained not only through analytic treatment, but also by performing numerical simulations. The latter have proved to be of great relevance in a wide spectrum of rock mechanics applications, i.e., for addressing the stability of slopes [48,49,50,51], ensuring safety conditions in underground construction work [52,53], and even offering new testing insights at a laboratory scale [54,55,56,57]. However, the precise modeling of the compression phenomenon on rocks is still under debate, as numerous parameters can influence material behavior. Despite successful numerical simulations in the current literature [57,58,59,60], simulation results may deviate significantly from the expected test results due to factors such as the influence of grain size [56,61], the presence of weak planes [62], the existence of voids and initial cracks [63], the geometrical characteristic of the tested specimen [61,64], or even the instruments used to register all relevant data during the UCT [65,66,67]. All these sources of influence increase the complexity of accurately modeling rock behavior, as decisions by researchers should be made regarding the presence and distribution of natural heterogeneities inside the material [68], the contact conditions [57,69], or and even the meshing techniques applied [70,71,72,73]. Therefore, the deeper the understanding of how basic variables influence the standard UCT outputs, the more accurate the derived models and simulations will be. Hence, better predictions could be made regarding complex combined phenomena, as in the case of salt-frost cycles [74], cavern Y junctions [75], melting ice [76], rock containing gas [77], or the influence of the rift plane [78].
In light of the existing literature, the end effect produced by the contact between the specimen and the press plates is responsible for the shearing stress field generated in the vicinity of the contact. This local stress field disturbs the desired stress state in specimen points located close to the platen. Therefore, most standards recommend a minimum relationship of the diameter-to-length ratio, ensuring that the specimen is sufficiently long to remove the aforementioned contact effects. In this sense, previous research correlates different failure modes for the same specimen when subjected to different boundary conditions [25,57], although their straightforward relationship with platen stiffness remains a topic of ongoing debate.
To evaluate the influence of the platens’ elastic properties on the contact stress distribution generated during the test execution, a detailed analysis addressing the relative stiffness between the specimen and the platen has been conducted. Steel, aluminum, polymethylmethacrylate (PMMA), and rock specimens have been subjected to the action of steel, aluminum, and PMMA platens in combination with a novel technique, based on the use of pressure films, to register the real contact stress pattern for each case. Nevertheless, real specimens will always suffer from geometric deviations from the ideal straight cylinder shape that may also influence the final contact pattern and hence, the stress distribution. Therefore, FLAC3D 7.00 software was used to perform numerical simulations on a validated model to prove that differences in the stiffness values of the specimen and the platen play a significant role in the contact stress distribution, as well as in the induced stress field, even in those cases where the geometry of the specimen can be considered as an ideal cylinder. It is worth highlighting here that the performed analysis is limited to the elastic stress range, thereby enabling a direct comparison with the results obtained for the proposed materials. Both the numerical and experimental results prove that the contact stress distribution is more likely to be uniformly distributed when the platen and the specimen have similar elastic properties, with deviations arising from these behaviors as a consequence of geometry deviations. Consequently, when similar levels of surface quality can be guaranteed, it is recommendable to use cushions with elastic properties similar to those of the material being tested, guaranteeing a uniform distribution of stress and displacements across the contact.
Moreover, the results support that flatness tolerances may be established due to relative stiffness between the platen and the specimen, rather than resulting from the UCS of the material being tested or its mechanical properties. Additionally, it is worth mentioning here that the purpose of this article is to address, from a scientific perspective, the influence of the relative stiffness between the press plates and the specimen (the ratio between their Young’s modulus) on the different contact stress distributions. While according to best knowledge of the authors, no previous proposal regarding the use of press plates with different materials, depending on the tested specimen, can be found in the current literature, previous research proves that contact conditions influence the obtained failure pattern, the location of the failure initiation point, and hence, the registered material’s compressive strength [25,26]. The results expressed in this article confirm that the influence of shearing stresses across the contact can be minimized, reaching neglectable levels for practical engineering purposes, by using platens, or intermediate thick cushions, with similar elastic properties to those of the tested specimen. Consequently, the aim of this study is not to refuse the standardized uniaxial compressions test, but to identify testing alternatives that may nearly overcome the shearing stress concentration problem across the contact and therefore, improve the accuracy of the material’s mechanical characterization.
2. Testing Methodology
The findings and conclusions presented in this study are universally applicable to any material subjected to the standardized uniaxial compression test, with a primary emphasis on their application to rock materials.
The mechanical properties of rock materials can substantially vary depending on their place of origin; therefore, a significant level of uncertainty may be introduced regarding the tolerance range of a particular specimen classified in accordance with UNE 22950-1:1990. Through comprehensive bibliographic research [1,79,80], adequate correlations can be established between steel, aluminum, and PMMA and the cases of high, medium, and low deformability, respectively. The selection of these three materials was based on their capacity to be accurately machined to guarantee the dimensional and geometric tolerances set by the standards. Additionally, a fourth limestone specimen was selected to extend the analysis to the behavior of rock materials subjected to the UCT. All specimens used are shown in Figure 3.

Figure 3.
Employed specimens after the preparation process. From (left) to (right): aluminum, steel, PMMA, and limestone.
The theoretical size for the specimens was established at 50 mm in diameter and 125 mm in length, thereby simultaneously ensuring compliance with all standards. Given that the dimensions of the actual samples may exhibit minor deviations from these values, all tolerances set by UNE, ASTM, and ISRM were meticulously measured and verified for all tested specimens (Table 3). While considerations regarding the grain size of the metallic and plastic materials employed are deemed irrelevant due to their microscopic scale, they could potentially exhibit significance in the context of limestone. Nevertheless, the specimen diameter clearly fulfils the recommendations set by the standards.

Table 3.
Dimensional verified values for the tested specimens.
In order to properly address the load distribution along the contact during the execution of the test, it is mandatory to verify not only the geometric and dimensional tolerances of the specimen, but also those related to the platens. Hence, all specimens and platens have been checked using a coordinate measuring machine (CMM) in a temperature-controlled room to guarantee that they fulfil all the tolerances established by the standards. However, it is worth noting that the rock specimen cannot be machined with the same geometric accuracy as the other specimens, although the verification process using the CMM ensures its eligibility for UCT. In this sense, it is worth highlighting that the rock specimen was obtained from a sample using diamond core drilling to obtain the original cylinder, which was cut using a circular saw to obtain the resultant core. However, the unavoidable deflection of the cutting discs led to an unacceptable degree of deflection for the goals of the proposed research. Therefore, the sample was carefully polished to guarantee a sufficient level of parallelism and straightness in the tested core. Despite this conscientious finishing procedure, some influence of the tool marks was still registered, as shown in Section 3.
Furthermore, as was previously stated, the relative stiffness between the platen and the sample also influences the contact phenomenon. From a theoretical perspective, in those cases where the platen and specimen are made of the same material, no shearing loads should be generated at their contact, as they would share the same elastic properties. The closest real scenario matching this requirement involves a platen and a specimen obtained from the same original bar. Consequently, it could be stated that there should not be any shearing stresses at the interface between the platen and the specimen when they come into contact.
Once the specimens and platens have been properly shaped and verified, certain considerations regarding testing parameters must be addressed. The contact pattern and contact area will be profoundly influenced, not only by the mechanical properties of the materials, but also by the total applied load imposed during the execution of the test. In this sense, a fixed maximum load cannot be applied to all tested materials. In fact, it must be adjusted to induce a comparable level of exigency in all of them. This implies that the total applied load must be tailored to each material in accordance with its elastic properties. Therefore, the maximum applied load has been set to approximately 50% of each specimen’s yield stress, assuming that a uniform compressive stress field is generated inside the specimen.
The test setup for all conducted compression tests is based on its standardized modality. In this regard, the specimen, as well as the testing frame, fulfil the recommendations suggested by the most relevant guidelines. It is worth noting that this affirmation also includes the spherical seat recommended by the standards. The sole modification introduced is the utilization of Fujifilm Prescale pressure films, which are placed in the interface between the specimen and the platens at both the top and bottom ends, as shown in Figure 4.
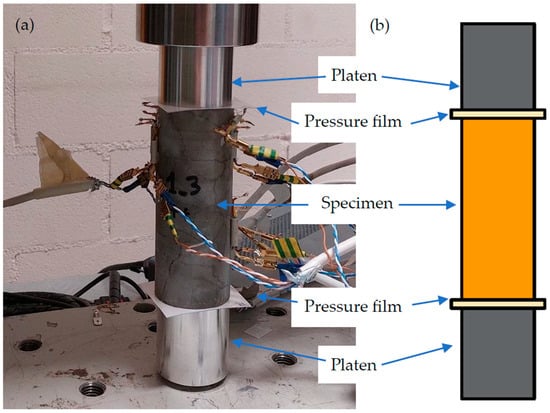
Figure 4.
Experimental setup used to register actual contact pattern: (a) experimental setup and (b) schematic setup representation.
Figure 5a shows the Fujifilm Prescale pressure film as it is delivered by the manufacturer. It is worth mentioning that prior to any testing, all pressure films employed are translucent and nearly colorless. They are composed of three different layers of material (Figure 5b): a polyester base, a color developing layer, and a micro-encapsulated color-forming layer. Thus, they can be placed between the matching surfaces, in this case, the specimen and platen ends, regardless of their particular orientation.
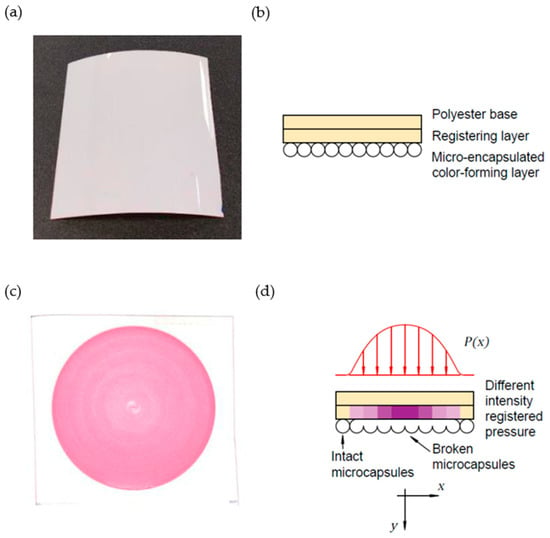
Figure 5.
Detailed explanation regarding the pressure film used based on: (a) pressure films in their delivered condition, (b) schematic representation of their internal structure, (c) pressure film after test execution, and (d) schematic explanation of the coloring process, based on microcapsule technology.
Initially, the microcapsules embedded within the film do not exhibit any discernible color, leading to the translucent appearance previously described. Once a certain pressure is applied on the film, due to the real contact between the two matching surfaces, points located on the contact change its color to one related to magenta tones (Figure 5c). This color change is caused by the breakage of the capsules involved in the contact process (Figure 5d). As a consequence of the applied pressure, the content of these capsules is released, forming minute color dots along the color-developing layer that directly relate to the areas where pressure was exerted. Additionally, the intensity of the applied pressure can be addressed within acceptable precision ranges. For this purpose, the manufacturer provides a calibration sheet and recommendations regarding the procedures for a reliable measurement. The typical accuracy claimed by the manufacturer on its specification sheet is approximately ±15% or better, as obtained by a simple visual comparison between the test results and its provided reference sample table and chart.
It is pertinent to underscore here that the thickness of the pressure films ranges from 100 to 120 µm, depending on the specific model employed. In any case, it can be considered that no deviations are induced in the test results as a consequence of a third elastic body simultaneously contacting with the specimen and the platen. Hence, their utilization does not significantly influence the contact conditions during the execution of the test.
Following the recommendations established in their technical sheet, tests employing pressure films were performed in a temperature-controlled room, maintaining the ambient temperature within the recommended range of 20 °C to 35 °C.
Pressure films are set up to cover a specific range of stress values. For example, pressure films designed to function between 50 and 130 MPa of applied stress will not exhibit evidence of contact under 50 MPa. Therefore, it is important to carefully select the most appropriate film in accordance with the elastic properties of the materials to be tested. Tests involving PMMA, aluminum, and limestone have been performed using MS (from 10 to 50 MPa) pressure films, whereas steel tests were executed with the HS version (from 50 to 130 MPa). Table 4 summarizes the pressure films employed in each test.

Table 4.
Pressure film used in each test.
3. Test Results
To address the influence of shearing stresses, a series of tests combining different stiffnesses for the platens and the specimens were conducted. It is worth highlighting here that the outer theoretical circumferences of the respective ends have been depicted in a solid, continuous black line in Table 5, Table 6, Table 7 and Table 8.
Prior to meticulously analyzing the experimental contact pattern registered in each test, it must be mentioned that the insertion of the pressure films may somehow distort the intended measurement of the actual contact stress distribution. Nevertheless, their extremely reduced thickness, coupled with their notably inferior mechanical properties, ensure that any deviation produced in the contact stress remains reasonable. Consequently, the addressed problem can still be analyzed under the proposed methodology. Due to the characteristics of the pressure films, their presence would produce a slight reduction in the shearing stresses generated along the contact between the platen and the specimen, not allowing the platen to constrain the specimen points with the same efficiency as that noted in the case without them. Therefore, the results shown in Section 3.1, Section 3.2, Section 3.3 and Section 3.4 strongly correlate to the behavior of normal stresses, whereas the influence of shear stresses in the pressure film may not be as direct. This last statement will be thoroughly discussed in Section 5.
3.1. Steel Specimen Tests
Contact patterns between the steel specimen and the different platens are depicted in Table 5. Contrary to what may be thought beforehand, the findings reveal that contact stresses are higher in the vicinity of the outer boundary. It is important to underscore that the central contact point observed in all the patterns is due to the turning technique employed to shape the specimens. Although in the case of platens and specimens made of the same material, tool marks are clearly visible on the pattern recorded by the paper film. However, all specimens have been meticulously machined to maintain their surface roughness to the minimum possible values that can be achieved with the available equipment at the research facilities. This fact, coupled with the fact that the stresses are limited to those in the elastic range, ensure the repeatability of the results presented.
It cannot be determined whether the white area (absence of magenta) in the center of the films corresponds to an area of null stress or just to an area with stress values below 50 or 10 MPa, depending on the film utilized. Regardless, a clear evolution from higher stress near the outer boundary to lower stress in the vicinity of the center has been registered. Thus, the generated load distribution is no longer uniform but rather distributed across the end. In this sense, linear or parabolic stress distributions exhibit a stronger correlation with the experimental results obtained. The deviation from uniformly distributed contact stresses seems to be significantly diminished in the case of PMMA platens. Actually, the softer the platen used, the more uniform the distribution becomes, according to the results provided by the contact patterns.


Table 5.
Contact patterns in steel specimen due to platens made of steel, aluminum, and PMMA.
Table 5.
Contact patterns in steel specimen due to platens made of steel, aluminum, and PMMA.
| Steel Specimen | |||
|---|---|---|---|
| Platen | Steel | Aluminum | PMMA |
| Top End | 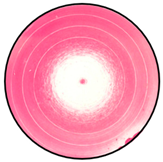 |  |  |
| Bottom End | 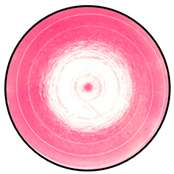 |  |  |
3.2. Aluminum Specimen Tests
Table 6 shows that the aluminum specimen behaves in a similar fashion to the steel specimen. The comparison between the platens of both metallic materials is particularly noteworthy. Although steel platens are recommended by the standards, those made of aluminum have clearly developed a higher uniform distribution in all cases. Nevertheless, after comparing aluminum and PMMA contact patterns for the aluminum specimen, it can be stated that the stresses have been almost uniformly distributed across both ends. Thus, the trend observed in the steel, where more uniform contact stress distributions occurred with decreasing platen stiffness, still holds true.


Table 6.
Contact patterns in aluminum specimen due to platens made of steel, aluminum, and PMMA.
Table 6.
Contact patterns in aluminum specimen due to platens made of steel, aluminum, and PMMA.
| Aluminum Specimen | |||
|---|---|---|---|
| Platen | Steel | Aluminum | PMMA |
| Top End |  |  |  |
| Bottom End |  |  |  |
3.3. PMMA Specimen Tests
Table 7 demonstrates that the PMMA specimen has developed the most uniformly distributed stress contact patterns of all specimens. It is worth highlighting that no white areas have been produced, and that the color intensity is approximately homogenous across all depicted ends. Therefore, the resultant contact pattern is less affected by platen stiffness in the case of soft specimens (relative low stiffness compared to the plate). However, imperfections related to the turning machining process are still noticeable in the contact patterns. Furthermore, stiffer platens exhibit a minor rim of greater stress concentration near the boundary than do the aluminum and PMMA platens. Consequently, the former deviate from the uniform case more dramatically than do the latter.


Table 7.
Contact patterns in PMMA specimen due to platens made of steel, aluminum, and PMMA.
Table 7.
Contact patterns in PMMA specimen due to platens made of steel, aluminum, and PMMA.
| PMMA Specimen | |||
|---|---|---|---|
| Platen | Steel | Aluminum | PMMA |
| Top End |  |  |  |
| Bottom End |  |  |  |
Regarding the results presented for the different platens, it may be affirmed that cushions of less or equally stiff materials than those of the tested specimen aid in spreading contact stresses more uniformly. Hence, the stress field generated inside the specimen is more likely to be a uniaxial compressive stress. However, as will be addressed in Section 5, this conclusion is tentative and requires further analysis.
Furthermore, it is noteworthy that the relevance of platen stiffness increases as the ratio of length to diameter () is reduced. For instance, UCT samples with , generally employed in the characterization of the dynamic properties of rock materials, may obtain significantly different UCS values than those tested under UNE and ISRM standards, where geometries with values of from 2.5 to 3.0 are permitted.
3.4. Case of Rock Materials
The heterogenities, inherent of rock materials, are a major inconvenience in obtaining a uniformly distributed contact stress. The presence of discontinuities and inclusions of other materials can profoundly influence the expected contact stress distribution. Thus, these two elements must be avoided during the sampling process whenever possible, if the UCS of the intact rock material is to be determined.
An experimental proof of this phenomenon can be observed in Table 8. Stiffer platens imposed a clearly non-uniform distribution on both ends of the rock specimen. Furthermore, contact patterns indicate that the assumption of axial symmetry may no longer be applicable. The pressure film at the bottom end recorded an approximate U-shaped contact pattern, which is completely inadequate to generate a uniform compression field inside the specimen. Consequently, major deviations with respect to the theoretical foundations of the UCT are produced. This phenomenon is lessened when aluminum platens, with elastic properties closer to those of the rock, are employed. However, local stress concentrations have also been registered in the vicinity of the outer boundary. All these effects seem to be minimized with PMMA platens. Nevertheless, even for platens softer than tested specimen, rock discontinuities and toolmarks caused by the preparation process can be clearly identified on the pressure film, similar to the results previously shown in this article.


Table 8.
Contact patterns in limestone specimen due to platens made of steel, aluminum, and PMMA.
Table 8.
Contact patterns in limestone specimen due to platens made of steel, aluminum, and PMMA.
| Limestone Specimen | |||
|---|---|---|---|
| Platen | Steel | Aluminum | PMMA |
| Top End |  | 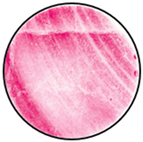 | 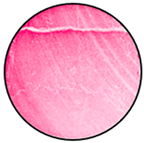 |
| Bottom End |  |  | 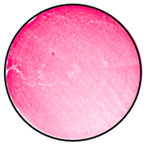 |
Due to this evidence, aluminum and PMMA could be considered suitable for testing rock specimens. However, tensile strains generated near the contact were responsible for the spalling phenomenon observed in the tested specimen (Figure 6). This evidence is especially relevant, as it leads to the presence of undesired tensile stress fields near the contact for softer platens. Moreover, it is particularly compelling for rock materials, as their compressive strength is usually around eight or ten times higher than their tensile strength , so local tensile failures may arise before complete macroscopic compressive failure is reached. Thus, equal stiff platens, or intermediate elastic cushions, may be preferable to uniformly distribute contact stresses during UCT execution on rock materials.
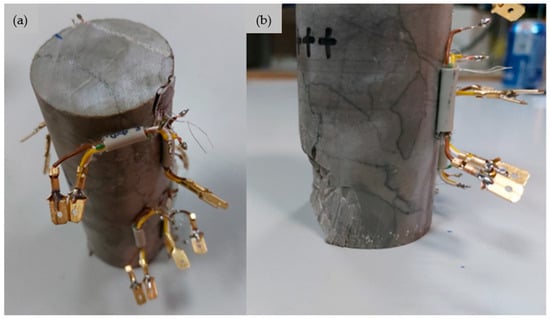
Figure 6.
Spalling in rock specimen due to the tensile stresses induced in the vicinity of the contact area at the (a) top and (b) bottom ends.
4. Numerical Verification of Contact Conditions
The prevailing consensus in the contemporary literature is that compressive stresses along the contact area during the execution of the UCT are uniformly distributed. Although the presence of friction or shearing stresses in conjunction with these compressive stresses are also considered, leading to various distribution shapes of the total applied load, the compressive component is predominantly considered constant across the contact. However, the experimental evidence shown in Table 5, Table 6 and Table 7 strongly suggests that this phenomenon only remains accurate under specific conditions of relative stiffness between the platen and the tested material.
In Section 3, particularly in Table 5, Table 6 and Table 7, the non-uniformity of contact stress distributions was experimentally proved. As these results may also be caused by fatness deviations or significant roughness in the ends of the specimen, their numerical verifications were conducted using a 3D model simulation to substantiate that compressive stresses are not uniformly distributed along the contact, even in the case of perfectly smooth and flat specimens.
The modeling was performed using FLAC3D v. 7.0 software, developed by Itasca Group Consulting. This software employs the finite difference method. Consequently, the continuity of the numerical solution is ensured, which is mandatory due to the isotropic, homogeneous, and linear elastic characteristics assigned to the materials. This software possesses a solid background in the analysis of real engineering situations and laboratory testing [81,82,83,84,85,86].
The analysis of the cylinders compressed by different stiffness platens has been addressed using an elastic model. In it, both the specimen and platen are considered as isotropic and homogeneous linear elastic solids. Hence, the physical model is governed by the well-known Hooke’s stress–strain relationships. The boundary conditions have been established, taking advantage of the symmetry of the stated problem. In this sense, neither horizontal nor vertical displacements have been permitted along the y axis (the axial symmetry axis) or at the specimen’s mid-height, respectively. Additionally, the lateral surface of the cylinder is free of applied stresses. The compression phenomenon has been reproduced, considering no interphase at the contact between the specimen and the platen. The principal rationale to avoid the implementation of an interphase in the model relates to the consequential necessity of introducing supplementary assumptions into the simulation and thereby engendering additional sources of uncertainty. Indeed, both solids have been meshed with common nodes along the contact. Hence, the latter is intimate and perfect. As all the stresses have been limited to ensure the elastic behavior, the results discussed in Section 4 and Section 5 are applicable to shearing stresses at the contact, only in those moments prior to the presence of friction. Consequently, it is worth highlighting here that these results cannot be related directly to cases where slippage between the platen’s and the specimen’s end points is reached. Furthermore, the compression load has been simulated by applying a displacement velocity on the upper face of the platen (y = −40 mm) equal to 1 × 10−10 m/s, similar to actual functioning of real rock testing frames. This speed is slow enough to ensure that the stresses are adequately redistributed in the different areas of the model, and the quasi-static testing conditions are ensured.
Due to the symmetry of the problem, only the upper plate (with a thickness of 40 mm) and half the height of the specimen were simulated. Furthermore, taking advantage of the axial symmetry, only a 45° portion of the cylinders has been considered, as shown in Figure 7.
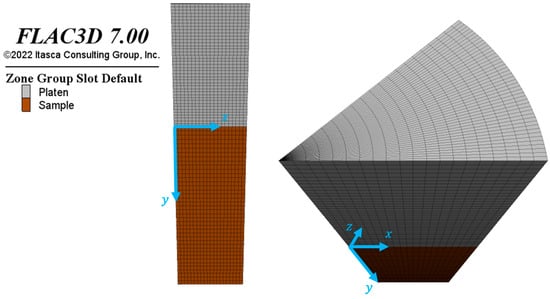
Figure 7.
Screenshot of the model used.
As the primary objective of the model is to delve into the influence of platen stiffness on the stress distribution generated along the contact, the entire analysis is conducted within the elastic range prior to material failure. Hence, no damage or failure criteria have been assigned to the elastic solids. It is worth noting here that in the numerical simulations performed, the specimen material was selected as limestone; whereas the platens were assigned using steel, aluminum, and PMMA.
Their properties are summarised in Table 9, which were in good agreement with those measured for the current samples used.

Table 9.
Values of elastic constants assigned to each material in the numerical model.
Section 4.1, Section 4.2 and Section 4.3 carefully analyzed the output results in a limestone specimen subjected to platens with the same geometry but different material properties. The stress field generated inside the specimen, as well as the displacement field of both elastic solids, are scrutinized to accurately justify the experimentally registered contact stress distributions.
4.1. Steel Platen
The distribution of compressive stresses across the contact is not uniform for the case of steel platens (Figure 8). This phenomenon is attributable to the difference in the Young’s modulus between steel and rock. As a result, the platen tends to retain specimen contact points during the execution of the test, impeding its free movement and resulting in a shear stress distribution (XY stress) across the contact, coupled with the vertical (YY stress) result.
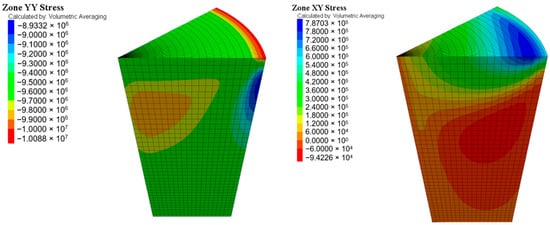
Figure 8.
Screenshot of the stress fields (Pa) in the specimen for the case of steel platens.
The aforementioned phenomenon is clearly depicted in Figure 9. While the vertical displacements (Y displacement) are approximately uniform, the horizontal displacements (X displacement) exhibit significant variation for the platen and the specimen. In the case of the latter, higher horizontal displacements are expected in points located far from the contact area, whereas in its vicinity, they are restricted due to the relative stiffness between both materials. Therefore, the model is successfully reproduces the observed experimental effect of sample widening at its mid-height. A direct correlation can be established between the horizontal displacements and the stress distribution generated along the contact, as greater impeded displacements lead to the generation of higher shear stresses. Consequently, the use of significantly stiffer platens than that of the material being tested can induce undesired behaviors in both the stress and displacements fields, potentially leading to unpredictable failure behavior.
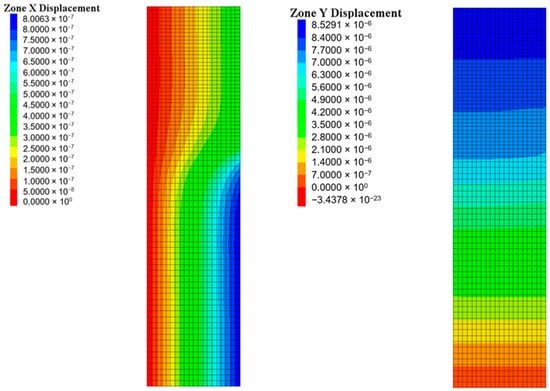
Figure 9.
Screenshot of the displacement fields (m) in the specimen for the case of steel platens.
4.2. Aluminum Platen
Based on the assumption that the shearing stresses generated across the contact are due to the stiffness difference between the platen and the specimen, they must be expected to vanish when both solids are of similar elastic properties. After simultaneously considering the testing results and those shown in Figure 10, it is proved that only minor differences in shearing stresses (XY stress) and horizontal displacements arise. Although different colormap levels are shown regarding shear stresses, the stress values are almost constant along the contact. Furthermore, the shear stresses (XY stress) are several orders of magnitude below the compressive stresses (YY Stress), and thus can be ignored for practical purposes, leading to the experimental reproduction of the desired contact stress conditions.
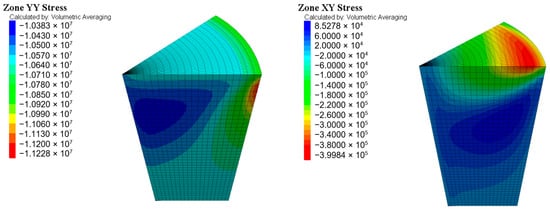
Figure 10.
Screenshot of the stress fields (Pa) in the specimen for the case of aluminum platens.
The stress and displacement fields induced by the aluminum platen are highly preferred to those imposed by the steel platen. As demonstrated in Figure 11, the vertical displacement smoothly decreases from the contact to the center of the specimen. Furthermore, the horizontal restrictions attributable to the stiffness mismatch have been significantly reduced when compared to those of the steel platen case.
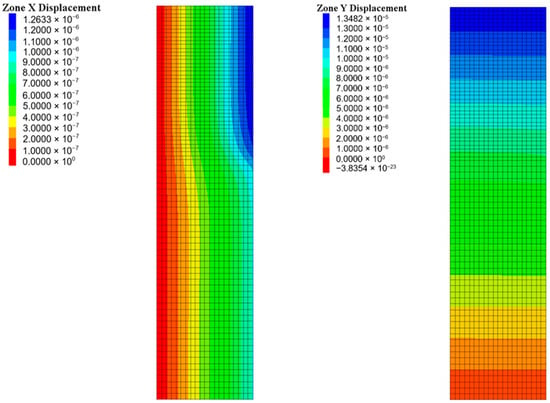
Figure 11.
Screenshot of the displacement fields (m) in the specimen for the case of aluminum platens.
4.3. PMMA Platen
Although it has already been proved that congruent elastic properties between the specimen and the platen yield the desired stress and displacement fields within the specimen, it is mandatory to determine whether this holds true for platens with lower stiffness. Figure 12 illustrates that the vertical compressive stress along the contact (YY stress) is not as uniformly distributed as in the case of materials of similar stiffness. This could lead to erroneous interpretations regarding the suitable correlation between the results depicted in Figure 12 and those presented in Table 5, Table 6 and Table 7. Even if some color intensity differences have been registered in the contact patterns, the possible stress value deviations between them may be caused by the actual shape of the ends of the specimen. Nevertheless, the testing and numerical results are in substantial agreement, as the lower stiffness of PMMA compared to the specimen facilitates the distribution of contact stresses across the entire surface, even though the compressive stress distribution is less uniform than that in the case of similar stiffness.
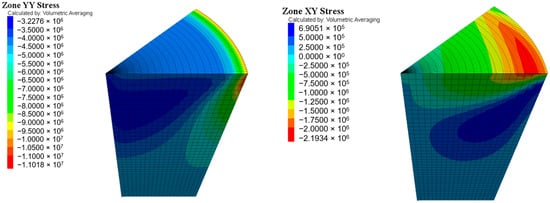
Figure 12.
Screenshot of the stress fields (Pa) in the specimen for the case of PMMA platens.
Upon concurrent consideration of the results shown in Figure 9 and Figure 13, it is proved that the results for the less stiff platens can be interpreted as the inverse case of the results for the stiffest platens. This implies that in the former situation, the specimen behaves in the same manner as the platen in the latter, and vice versa. Consequently, the displacement field exhibits a highly undesired effect in the vicinity of the contact, as the platens tend to excessively elongate at both ends during the test execution. This behavior is extremely relevant in brittle heterogeneous materials such as rocks due to their tendency to produce the spalling phenomenon, as evidenced in Figure 6.
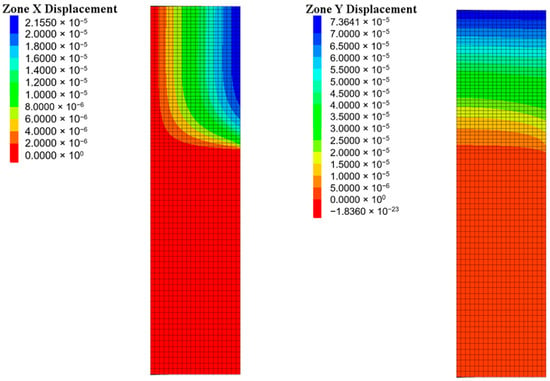
Figure 13.
Screenshot of the displacement fields (m) in the specimen for the case of PMMA platens.
5. Discussion of Testing and Numerical Results
Before meticulously addressing a discussion combining numerical and testing results, it is imperative to underscore that capsules embedded in the pressure films may reach failure due to the combined action of both normal and shear loads. Therefore, the comparison of contact patterns relating two different cases must be addressed cautiously, especially if significant differences between the induced contact shear load distributions are expected due to stiffness mismatches. In this regard, results concerning the contact stress distribution must be evaluated, simultaneously considering the evidence obtained by the pressure films and the numerical simulations. Although each method possesses its own limitations, they can be used to successfully complement each other. Pressure films cannot be used to straightforwardly identify normal or shearing stress distributions. However, they can accurately address the deviations caused by the shape and roughness of the ends of the specimens. On the contrary, the numerical simulations only apply for ideal cylinders, with no geometric or roughness deviations, but are extremely useful to analyze the evolution of shearing prior to the presence of friction.
Integrating results presented in Table 5, Table 6 and Table 7 accentuates the experimental reality of non-uniform contact stress distributions across the ends of the specimen. Nevertheless, the statement of the elastic problem can still be addressed, assuming the axial symmetry hypothesis. This assertion is supported by the symmetry registered on tested pressure films. Therefore, the mathematical problem to determine the strength of the material can be solved using 2D elasticity, provided that precise alignment between the platens and the specimen is guaranteed.
Conversely, Table 8 denotes that the heterogeneity of rock materials significantly influences the contact stress distribution, as they registered a strong variation of contact stress value at the discontinuity present on the top end. In this sense, the comparison between results obtained by numerical simulations and real testing must be performed with care. The geometry employed in the numerical model applies to the case in which the actual rock specimens could be considered as ideal isotropic cylinders. However, the contact patterns exhibit in Table 8 not only validate the substantial influence of heterogeneities, but also the impact of end roughness and geometric end deviations on the resultant contact stress distribution, as marks from the specimen preparation process and stress concentration areas are clearly observed on them.
Nevertheless, coupling numerical and experimental results ensured the hard-rock materials’ propensity to develop non-uniform contact stress distributions when subjected to the UCT, leading to elevated stress values generated in the vicinity of the outer circumference at both specimen ends, which decrease towards their center. Contrarily, contact stress distributions developed by softer materials (less stiff) seem to be significantly more homogeneous in their experimental contact patterns. Therefore, from an elastic perspective, it may be thought that the use of soft cushions could help to uniformly spread the stresses across the contact. However, when this tentative conclusion is checked with the numerical results, some objectionable implications are highlighted. In this regard, the numerical results evidence that horizontal displacements and shear stresses are relevant in the vicinity of the contact for PMMA platens. Indeed, softer platens exhibit induced tensile stresses and strains that have led to spalling failure in the tested specimen.
The contact patterns related to the PMMA platens, which generally seem to be more homogeneous than for the rest of the cases, may be explained by the relationship between the imposed load and the stiffness of the platens. The significantly lower stiffness of PMMA platens enables a better matching between the opposing surfaces, due to its higher deformation. An example of this behavior can be observed in the case of the aluminum specimen (Table 6), where the aluminum platen has induced concentric high value stress rings alternated with those of lower values, due to the actual undulating shape of the specimen’s end. Additionally, if the numerical simulation is performed by assigning the aluminum properties to both the platen and the material, direct evidence of this phenomenon can be observed after recalling the mentioned contact pattern (Figure 14). It is worth noting here that in the case in which the geometric deviations were overcome, the contact stress distribution was absolutely uniform. Moreover, these results apply for the complete elastic range of the specimen.

Figure 14.
Comparison of pressure films and numerical results (Pa) for the aluminum platen and specimen, proving the sensibility of the pressure films to geometry deviation: (a) real contact pattern and (b) ideal normal stress distribution due to numerical simulations performed on ideal cylinders.
Nevertheless, this undulation was low enough to be overcome by the deformation of the PMMA platen. This phenomenon, in conjunction with the tool marks registered in the different patterns, reiterates the suitability of introducing accurate roughness recommendations into the standards to ensure adequate sample preparation requirements.
Regardless of whether the platen stiffness exceeds or falls below that of the tested material, a triaxial stress state is induced in the vicinity of the contact. The primary distinction between them lies in the generation of mainly compressive stresses in the former case, whereas tensile stresses are induced in the latter. Hence, in the case of rock materials, it would be preferable to use steel rather than PMMA platens. In fact, the use of intermediate PMMA cushions should be cautiously considered, as its tendency to induce spalling failure may significantly alter the real UCS value when compared to the UCT obtained result.
To conclude this discussion section, the implications of these results in tests that replicate the setup of the uniaxial compression test may be considered. The differences registered in the contact pattern due to the relative stiffness between the specimen and the platen may not only apply for compressions tests performed under the standardized conditions, but also to all the tests in the universal frame in which a compression load is applied to the material by the use of flat platens. Even in the case of soft materials [87,88], each of the contacts produced with the platen would be subjected to the explained clamping phenomenon generated on the points constrained by the stiffer platens. This is also the case for the testing of soils in a similar setup to that of the UCT [89], although in those cases, most platen materials may constrain the movement of the end points on the soil specimen, unless water inherent to saturated specimens interacts with the contact, reducing the shearing stresses. In general, the results shown apply to the case of two flat, or approximately flat, surfaces formed by materials with different stiffness values that come into contact. In this sense, it is worth noting that the macroscopic dimension of the platen and the specimen may be significantly modified, and as long as the diameter of the specimen is at least equal to that of the plate, the presented results will also apply.
6. Conclusions
The determination of uniaxial compressive strength (UCS) values strongly relies on the assumption that a uniaxial compression stress field is generated inside the specimen. Despite the acceptance in contemporary literature of the existence of undesirable local triaxial stress states in the proximity of the contact area, attributable to the restricted movement of the specimen’s end points due to the employment of standardized platens (generally stiffer than the tested material), it is assumed that for long enough specimens, the desired uniform compression stress field is still generated at the specimen’s mid-height. To improve the current understanding of how different platen materials may influence the contact stress distributions, which play a major role in the induced stress field, Fujifilm Prescale pressure films have been employed to experimentally register the contact patterns from standardized uniaxial compression tests (UCT). Additionally, numerical simulations have been performed to ensure the validity of this novel testing procedure. The concurrence of both sources of evidence allows for the following conclusions:
- The contact stress distribution using standardized steel platens is non-uniform, presenting higher stress values in the vicinity of the outer circumference of the ends of the specimen, decreasing towards its center.
- Uniformly distributed contact stresses are achieved using platens with elastic properties similar to those of the tested material, as only a slight impediment to the horizontal movement of specimen ends is imposed. Therefore, this is a case when experimental tests would have better correlation, from an elastic perspective, with its theoretical foundations.
- As a corollary of points 1 and 2, contact patterns strongly change with different loading conditions. Even for the same tested materials, contact patterns vary depending on the stiffness of the platen utilized.
- To determine the compressive strength of brittle materials, the usage of cushions as devices to avoid local stress concentration areas is recommended. Nevertheless, the stiffness of the cushions must be similar to that of the tested material, or undesired triaxial stress states would be generated in the vicinity of the contact.
- Aluminum platens and/or cushions, rather than steel platens, may be selected to test hard rocks, unless the stiffness of tested material is approximately equal to that of steel.
- PMMA platens and/or cushions are only recommendable to test soft rocks. Nevertheless, prior to their reuse, it must be ensured that these platens do not reach plastic behavior during the test execution.
- Tolerances specified by standards must be proposed, considering the elastic properties of the tested specimen, as greater deformation related to less stiff materials would compensate for some minor deviations in the contact surface. Furthermore, the stiffer the material to be tested, the more suitable it would be to impose some roughness tolerance on its ends to avoid local stress concentrations on the main asperities.
- Considering different acceptable materials for testing platens within the same standard may be recommended to cover the entire spectrum of all possible rock materials.
- Due to the inherent heterogeneity of rock materials, whose properties differ from those of the intact rock, the prediction of load distributions may be challenging, even when similar materials of similar stiffness are employed.
Author Contributions
Conceptualization, C.G.-N.; numerical model, M.-I.Á.-F. and M.R.-B.; methodology, M.R.-B.; formal analysis, M.-I.Á.-F. and D.-J.G.-M.; writing—original draft preparation, M.-B.P.-G.; data curation, writing—review and editing, and visualization, D.-J.G.-M.; supervision, C.G.-N. and M.R.-B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Innovation of Spain through Grant MCIU-19-PGC2018-099695-B-100t and Grant MCINN-23-PID2022-142015OB-I00 funded by MCIN/AEI/10.13039/501100011033 and by “ERDF—A Way of Making Europe”.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Goodman, R.E. Introduction to Rock Mechanics, 2nd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1981; Volume 18, ISBN 0471812005. [Google Scholar]
- Ulusay, R.; Hudson, J. (Eds.) The Complete ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 1974-2006; ISRM Turkish National Group and the ISRM: Ankara, Turkey, 2007. [Google Scholar]
- Broch, E.; Franklin, J.A. The Point-Load Strength Test. Int. J. Rock Mech. Min. Sci. 1972, 9, 669–697. [Google Scholar] [CrossRef]
- ASTM D5731-16; Standard Test Method for Determination of the Point Load Strength Index of Rock Application to Rock Strength Classifications. ASTM: West Conshohocken, PA, USA, 2016.
- UNE 22950-1:1990; Propiedades Mecánicas de Las Rocas. Ensayos Para La Determinación de La Resistencia. Parte 1: Resistencia a La Compresión Uniaxial. AENOR: Madrid, Spain, 1990.
- ASTM C1358-18; Standard Test Method for Monotonic Compressive Strength Testing of Continuous Fiber-Reinforced Advanced Ceramics with Solid Rectangular Cross Section Test Specimens at Ambient Temperatures. ASTM: West Conshohocken, PA, USA, 2018.
- ASTM D695-15; Standard Test Method for Compressive Properties of Rigid Plastics. ASTM: West Conshohocken, PA, USA, 2016.
- ASTM E9-19; Standard Test Methods of Compression Testing of Metallic Materials at Room Temperature. ASTM: West Conshohocken, PA, USA, 2019.
- UNE-EN 12390-3:2020; Ensayos de Hormigón Endurecido. Parte 3: Determinación de La Resistencia a Compresión de Probetas. AENOR: Madrid, Spain, 2020.
- ASTM C39/39M-21; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM: West Conshohocken, PA, USA, 2021.
- ASTM D7012-23; Standard Test Method for Compressive Strength and Elastic Moduli of Intact Rock Core Specimens under Varying States of Stress and Temperatures. ASTM: West Conshohocken, PA, USA, 2023; Volume 04.09, pp. 1–10.
- ASTM D 4543-19; Standard Practices for Preparing Rock Core as Cylindrical Test Specimens and Verifying Conformance to Dimensional and Shape Tolerances. American Society For Testing and Materials: West Conshocken, PA, USA, 2019.
- UNE 22950-3:1990; Propiedades Mecánicas de Las Rocas. Ensayos Para La Determinación de La Resistencia. Parte 3: Determinación Del Módulo de Elasticidad (Young) y Del Coeficiente de Poisson. AENOR: Madrid, Spain, 1990.
- Timoshenko, S.; Goodier, J.N. Theory of Elasticity, 2nd ed.; McGraw-Hill: New York, NY, USA, 1951. [Google Scholar]
- Sadd, M.H. Elasticity, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2009; ISBN 9780123744463. [Google Scholar]
- Barber, J.R. Elasticity, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-90-481-3809-8. [Google Scholar]
- Kumar, S.; Mukhopadhyay, T.; Waseem, S.A.; Singh, B.; Iqbal, M.A. Effect of Platen Restraint on Stress–Strain Behavior of Concrete Under Uniaxial Compression: A Comparative Study. Strength Mater. 2016, 48, 592–602. [Google Scholar] [CrossRef]
- Kotsovos, M.D. Effect of Testing Techniques on the Post-Ultimate Behaviour of Concrete in Compression. Matériaux Et Constr. 1984, 16, 3–12. [Google Scholar] [CrossRef]
- Sokolnikoff, I.S. Mathematical Theory of Elasticity; McGraw-Hill Book Co.: New York, NY, USA, 1956. [Google Scholar]
- Gustkiewicz, J. Uniaxial Compression Testing of Brittle Rock Specimens with Special Consideration given to Bending Moment Effects. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1975, 12, 13–25. [Google Scholar] [CrossRef]
- Gustkiewicz, J. Strain Fluctuations in Heterogeneous Rocks. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1975, 12, 181–189. [Google Scholar] [CrossRef]
- Gustkiewicz, J. Strain Fluctuations within Some Rock Specimens under Uniaxial Compression. Part I—Local Fluctuations. Acta Geophys. Pol. 1985, 23, 389–405. [Google Scholar]
- Gustkiewicz, J. Strain Fluctuations within Some Rock Specimens under Uniaxial Compression. Part II—Certain Probabilistic Characteristics of the Fluctuations. Acta Geophys. Pol. 1985, 23, 407–427. [Google Scholar]
- Xu, Y.H.; Cai, M.; Zhang, X.W.; Feng, X.T. Influence of End Effect on Rock Strength in True Triaxial Compression Test. Can. Geotech. J. 2017, 54, 862–880. [Google Scholar] [CrossRef]
- Bandeira, M.V.V.; La Torre, K.R.; Kosteski, L.E.; Marangon, E.; Riera, J.D. Influence of Contact Friction in Compression Tests of Concrete Samples. Constr. Build. Mater. 2022, 317, 125811. [Google Scholar] [CrossRef]
- Guerrero-Miguel, D.J.; Álvarez-Fernández, M.I.; Gutiérrez-Moizant, R.; Prendes-Gero, M.B.; González-Nicieza, C. The Influence of Platen Stiffness on a Specimen’s Failure Initiation Point and the Failure Pattern of Brittle Materials in the Standardized Uniaxial Compression Test. Mathematics 2024, 12, 907. [Google Scholar] [CrossRef]
- Pochhammer, L. Über Die Fortpflanzungsgeschwindigkeiten Kleiner Schwingungen in Einem Unbegrenzten Isotropen Kreiszylinder. Trans. Camb. Phil. Soc. 1876, 81, 324–336. [Google Scholar]
- Chree, C. The Equation of an Isotropic Elastic Solid in Porlar and Cylindrical Co-Ordinates. Trans. Camb. Philos. Soc. 1889, 14, 250–369. [Google Scholar]
- Dougall, J. An Analytical Theory of the Equilibrium of an Isotropic Elastic Rod of Circular Section. Trans. R. Soc. Edinb. 1914, 49, 895–978. [Google Scholar] [CrossRef]
- Power, L.D.; Childs, S.B. Axisymmetric Stresses and Displacements in a Finite Circular Bar. Int. J. Eng. Sci. 1971, 9, 241–255. [Google Scholar] [CrossRef]
- Moghe, S.R.; Neff, H.F. Elastic Deformations of Constrained Cylinders. J. Appl. Mech. 1971, 38, 393–399. [Google Scholar] [CrossRef]
- Benthem, J.P.; Minderhoud, P. The Problem of the Solid Cylinder Compressed between Rough Rigid Stamps; Pergamon Press: Oxford, UK, 1972; Volume 8. [Google Scholar]
- Al-Chalabi, M.; Huang, C.L. Stress Distribution within Circular Cylinders in Compression. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1974, 11, 45–56. [Google Scholar] [CrossRef]
- Kim, Y.Y.; Steele, C.R. Static Axisymmetric End Problems in Semi-Infinite and Finite Solid Cylinders. J. Appl. Mech. 1992, 59, 69–76. [Google Scholar] [CrossRef]
- Wei, X.X.; Chau, K.T. Finite Solid Circular Cylinders Subjected to Arbitrary Surface Load. Part I—Analytic solution. Int. J. Solids Struct. 2000, 37, 5707–5732. [Google Scholar] [CrossRef]
- Wei, X.X.; Chau, K.T. Finite Solid Circular Cylinders Subjected to Arbitrary Surface Load. Part II—Application to Double-Punch Test. Int. J. Solids Struct. 2000, 37, 5733–5744. [Google Scholar] [CrossRef]
- Wei, X.X.; Chau, K.T. Analytic Solution for Finite Transversely Isotropic Circular Cylinders under the Axial Point Load Test. J. Eng. Mech. 2002, 128, 209–219. [Google Scholar] [CrossRef]
- Chau, K.T.; Wei, X.X. A New Analytic Solution for the Diametral Point Load Strength Test on Infinite Solid Circular Cylinders. Int. J. Solids Struct. 2001, 38, 1459–1481. [Google Scholar] [CrossRef]
- Wei, X.X.; Chau, K.T.; Wong, R.H.C. Analytic Solution for Axial Point Load Strength Test on Solid Circular Cylinders. J. Eng. Mech. 1999, 125, 1349–1357. [Google Scholar] [CrossRef]
- Chau, K.T.; Wei, X.X. A Three Dimensional Analytic Solution for the Brazilian Test. In Frontiers of Rock Mechanics and Sustainable Development in the 21st Century; CRC Press: Boca Raton, FL, USA, 2001; pp. 141–143. [Google Scholar]
- Wei, X.X.; Chau, K.T. Three Dimensional Analytical Solution for Finite Circular Cylinders Subjected to Indirect Tensile Test. Int J. Solids Struct. 2013, 50, 2395–2406. [Google Scholar] [CrossRef]
- Sburlati, R. Three-Dimensional Analytical Solution for an Axisymmetric Biharmonic Problem. J. Elast. 2009, 95, 79–97. [Google Scholar] [CrossRef]
- Meleshko, V.V.; Tokovyy, Y.V. Equilibrium of an Elastic Finite Cylinder under Axisymmetric Discontinuous Normal Loadings. J. Eng. Math. 2013, 78, 143–166. [Google Scholar] [CrossRef]
- Sirsat, A.V.; Padhee, S.S. Analytic Solution to Isotropic Axisymmetric Cylinder under Surface Loadings Problem through Variational Principle. Acta. Mech. 2024, 235, 2013–2027. [Google Scholar] [CrossRef]
- Meleshko, V.V. Equilibrium of an Elastic Finite Cylinder: Filon’s Problem Revisited. J. Eng. Math. 2003, 46, 355–376. [Google Scholar] [CrossRef]
- Zhao, B.S.; Gao, Y.; Zhao, Y.T.; Zhou, X.X. Boundary Conditions for an Axisymmetric Circular Cylinder. Comptes Rendus-Mec. 2010, 338, 255–259. [Google Scholar] [CrossRef]
- Rahnama, H.; Shokrieh, M.M. Axisymmetric Equilibrium of an Isotropic Elastic Solid Circular Finite Cylinder. Math. Mech. Solids 2019, 24, 996–1029. [Google Scholar] [CrossRef]
- Li, Z.X.; Fujii, Y.; Alam, A.K.M.B.; Li, Z.H.; Du, F.; Wei, W.J. Implementing a Simple 2D Constitutive Model for Rocks into Finite Element Method. Comput. Geotech. 2024, 167, 106095. [Google Scholar] [CrossRef]
- Hu, Y.; Lu, Y. Study on Soil-Rock Slope Instability at Mesoscopic Scale Using Discrete Element Method. Comput Geotech 2023, 157, 105268. [Google Scholar] [CrossRef]
- Sun, L.; Grasselli, G.; Liu, Q.; Tang, X.; Abdelaziz, A. The Role of Discontinuities in Rock Slope Stability: Insights from a Combined Finite-Discrete Element Simulation. Comput. Geotech. 2022, 147, 104788. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Q.; Tang, X.; Sun, L.; Deng, P.; Liu, H. Dynamic Stability Analysis of Jointed Rock Slopes Using the Combined Finite-Discrete Element Method (FDEM). Comput. Geotech. 2023, 160, 105556. [Google Scholar] [CrossRef]
- Lak, M.; Fatehi Marji, M.; Yarahmadi Bafghi, A.R.; Abdollahipour, A. Discrete Element Modeling of Explosion-Induced Fracture Extension in Jointed Rock Masses. J. Min. Environ. 2019, 10, 125–138. [Google Scholar] [CrossRef]
- Du, K.; Li, X.; Su, R.; Tao, M.; Lv, S.; Luo, J.; Zhou, J. Shape Ratio Effects on the Mechanical Characteristics of Rectangular Prism Rocks and Isolated Pillars under Uniaxial Compression. Int. J. Min. Sci. Technol. 2022, 32, 347–362. [Google Scholar] [CrossRef]
- Jiang, H.; Meng, D. 3D Numerical Modelling of Rock Fracture with a Hybrid Finite and Cohesive Element Method. Eng. Fract. Mech. 2018, 199, 280–293. [Google Scholar] [CrossRef]
- Fu, J.; Haeri, H.; Sarfarazi, V.; Asgari, K.; Ebneabbasi, P.; Fatehi Marji, M.; Guo, M. Extended Finite Element Method Simulation and Experimental Test on Failure Behavior of Defects under Uniaxial Compression. Mech. Adv. Mater. Struct. 2022, 29, 6966–6981. [Google Scholar] [CrossRef]
- Yu, Q.; Zhu, W.; Ranjith, P.G.; Shao, S. Numerical Simulation and Interpretation of the Grain Size Effect on Rock Strength. Geomech. Geophys. Geo-Energy Geo-Resour. 2018, 4, 157–173. [Google Scholar] [CrossRef]
- Wang, H.; Dyskin, A.; Pasternak, E.; Dight, P. Possible Mechanism of Spallation in Rock Samples under Uniaxial Compression. Eng. Fract. Mech. 2022, 269, 108577. [Google Scholar] [CrossRef]
- Ghazvinian, E.; Diederichs, M.S.; Quey, R. 3D Random Voronoi Grain-Based Models for Simulation of Brittle Rock Damage and Fabric-Guided Micro-Fracturing. J. Rock Mech. Geotech. Eng. 2014, 6, 506–521. [Google Scholar] [CrossRef]
- Li, X.F.; Li, H.B.; Zhao, J. 3D Polycrystalline Discrete Element Method (3PDEM) for Simulation of Crack Initiation and Propagation in Granular Rock. Comput. Geotech. 2017, 90, 96–112. [Google Scholar] [CrossRef]
- Ma, G.; Zhou, W.; Regueiro, R.A.; Wang, Q.; Chang, X. Modeling the Fragmentation of Rock Grains Using Computed Tomography and Combined FDEM. Powder Technol. 2017, 308, 388–397. [Google Scholar] [CrossRef]
- Peng, J.; Wong, L.N.Y.; Teh, C.I. A Re-Examination of Slenderness Ratio Effect on Rock Strength: Insights from DEM Grain-Based Modelling. Eng. Geol. 2018, 246, 245–254. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, M.; Zhou, L.; Zhu, Z.; Shu, Y.; Peng, T. Research on Uniaxial Compression Strength and Failure Properties of Stratified Rock Mass. Theor. Appl. Fract. Mech. 2022, 121, 103499. [Google Scholar] [CrossRef]
- Dyskin, A.V.; Sahouryeh, E.; Jewell, R.J.; Joer, H.; Ustinov, K.B. Influence of Shape and Locations of Initial 3-D Cracks on Their Growth in Uniaxial Compression. Eng. Fract. Mech. 2003, 70, 2115–2136. [Google Scholar] [CrossRef]
- Talaat, A.; Emad, A.; Tarek, A.; Masbouba, M.; Essam, A.; Kohail, M. Factors Affecting the Results of Concrete Compression Testing: A Review. Ain Shams Eng. J. 2021, 12, 205–221. [Google Scholar] [CrossRef]
- Alejano, L.R.; Arzúa, J.; Estévez-Ventosa, X.; Suikkanen, J. Correcting Indirect Strain Measurements in Laboratory Uniaxial Compressive Testing at Various Scales. Bull. Eng. Geol. Environ. 2020, 79, 4975–4977. [Google Scholar] [CrossRef]
- González-Fernández, M.A.; Estévez-Ventosa, X.; Alonso, E.; Alejano, L.R. Analysis of Size Effects on the Hoek-Brown Failure Criterion of Intact Granite Samples. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Turin, Italy, 20–25 September 2021; IOP Publishing Ltd.: Bristol, UK, 2021; Volume 833. [Google Scholar]
- Alejano, L.R.; Estévez-Ventosa, X.; González-Fernández, M.A.; Walton, G.; West, I.G.; González-Molano, N.A.; Alvarellos, J. A Method to Correct Indirect Strain Measurements in Laboratory Uniaxial and Triaxial Compressive Strength Tests. Rock Mech. Rock Eng. 2021, 54, 2643–2670. [Google Scholar] [CrossRef]
- Li, L.; Guan, J.; Liu, Z. A Random Discrete Element Method for Modeling Rock Heterogeneity. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 12. [Google Scholar] [CrossRef]
- Tang, C.A.; Tham, L.G.; Lee, P.K.K.; Tsui, Y.; Liu, H. Numerical Studies of the Infuence of Microstructure on Rock Failure in Uniaxial Compression Part II: Constraint, Slenderness and Size Effect. Int. J. Rock Mech. Min. Sci. 2000, 37, 571–583. [Google Scholar] [CrossRef]
- Khoei, A.R.; Vahab, M.; Haghighat, E.; Moallemi, S. A Mesh-Independent Finite Element Formulation for Modeling Crack Growth in Saturated Porous Media Based on an Enriched-FEM Technique. Int. J. Fract. 2014, 188, 79–108. [Google Scholar] [CrossRef]
- Jia, Z.M.; Zhou, X.P. Modelling Fracture of Rock Masses around Tunnels and Slopes by Field-Enriched Finite Element Method. Comput. Geotech. 2023, 163, 105756. [Google Scholar] [CrossRef]
- Bouchard, P.O.; Bay, F.; Chastel, Y. Numerical Modelling of Crack Propagation: Automatic Remeshing and Comparison of Different Criteria. Comput. Methods Appl. Mech. Eng. 2003, 192, 3887–3908. [Google Scholar] [CrossRef]
- Trädegård, A.; Nilsson, F.; Östlund, S. FEM-Remeshing Technique Applied to Crack Growth Problems. Comput. Methods Appl. Mech. Eng. 1998, 160, 115–131. [Google Scholar] [CrossRef]
- Hu, J.; Wu, J. Mechanical Properties and Uni-Axial Compression Stress-Strain Relation of Recycled Coarse Aggregate Concrete Subjected to Salt-Frost Cycles. Constr. Build. Mater. 2019, 197, 652–666. [Google Scholar] [CrossRef]
- Thirukumaran, S.; Oliveira, D. Innovative Design of Slender Rock Pillar Formed within Large Span Road Tunnels and Cavern Y-Junction in Hawkesbury Sandstone. Tunn. Undergr. Space Technol. 2023, 141, 105376. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Z.; Lei, R.; Lu, P.; Han, H. Estimation of the Uniaxial Compressive Strength of Arctic Sea Ice during Melt Season. Cold Reg. Sci. Technol. 2018, 151, 9–18. [Google Scholar] [CrossRef]
- Jin, C.; Liu, S.; Xu, P.; Guo, C. Scale Effect Stress–Strain Model of Coal Containing Gas. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 147. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, R.; Zhang, Q.; Du, S.; Yang, C. Experimental Study on the Rift Plane of Granite under Uniaxial Compression. J. Appl. Geophy. 2022, 199, 104590. [Google Scholar] [CrossRef]
- Pero-Sanz Elorz, J.A. Ciencia e Ingeniería de Materiales: Estructura, Transformaciones Propiedades y Selección; CIE Inversiones editoriales-DOSSAT 2000: Madrid, Spain, 2000; ISBN 8495312182. [Google Scholar]
- Budynas, R.G.; Nisbett, J.K. Shigley’s Mechanical Engineering Design; McGraw-Hill: New York, NY, USA, 2011; ISBN 0073529281. [Google Scholar]
- Wang, H.; Chen, Z.; Zhang, D. Rock Slope Stability Analysis Based on FLAC3D Numerical Simulation. Appl. Mech. Mater. 2012, 170–173, 375–379. [Google Scholar]
- Vuong, P.M.; Walentek, A.; Waclawik, P.; Souńcek, K.; Antoniuk, M. Numerical Modelling of Uniaxial Compressive Strength Laboratory Tests. J. Sustain. Min. 2023, 22, 280–294. [Google Scholar] [CrossRef]
- Zhao, H.; Su, H.; Qin, X.; Zhang, K.; Jiang, Y.; Wang, W. Experiment and Numerical Simulation of Strength and Stress Distribution Behaviors of Anchored Rock Mass in a Roadway. Geofluids 2023, 2023, 9311206. [Google Scholar] [CrossRef]
- Sitharam, T.G.; Maji, V.B.; Verma, A.K. Practical Equivalent Continuum Model for Simulation of Jointed Rock Mass Using FLAC3D. Int. J. Geomech. 2007, 7, 389–395. [Google Scholar] [CrossRef]
- Lin, H.; Liu, T.; Li, J.; Cao, P. A Simple Generation Technique of Complex Geotechnical Computational Model. Math. Probl. Eng. 2013, 2013, 863104. [Google Scholar] [CrossRef]
- Guo, F.; Gu, W.; Tang, J.; Murong, M. Research on Deformation Stability of Soft Rock Slope under Excavation Based on FLAC3D. Appl. Mech. Mater. 2013, 275–277, 290–294. [Google Scholar] [CrossRef]
- Shim, J.; Shan, S.; Košmrlj, A.; Kang, S.H.; Chen, E.R.; Weaver, J.C.; Bertoldi, K. Harnessing Instabilities for Design of Soft Reconfigurable Auxetic/Chiral Materials. Soft Matter 2013, 9, 8198–8202. [Google Scholar] [CrossRef]
- Wang, F.; Li, D.M.; Yang, Y.R.; Wu, Z. Progressive Compaction of Soft Cellular Structures with Layer-Wisely Designed Gradient Porosity. Thin-Walled Struct. 2023, 185, 110634. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, J.; Qiang, M.; Zhang, H.; Li, X.; Long, S.; Gao, Z.; Fan, H. Mechanical Characterization and Constitutive Modeling of Nano-Stabilized Soil under Uniaxial Compression. Materials 2023, 16, 1488. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).