Research on Vehicle AEB Control Strategy Based on Safety Time–Safety Distance Fusion Algorithm
Abstract
:1. Introduction
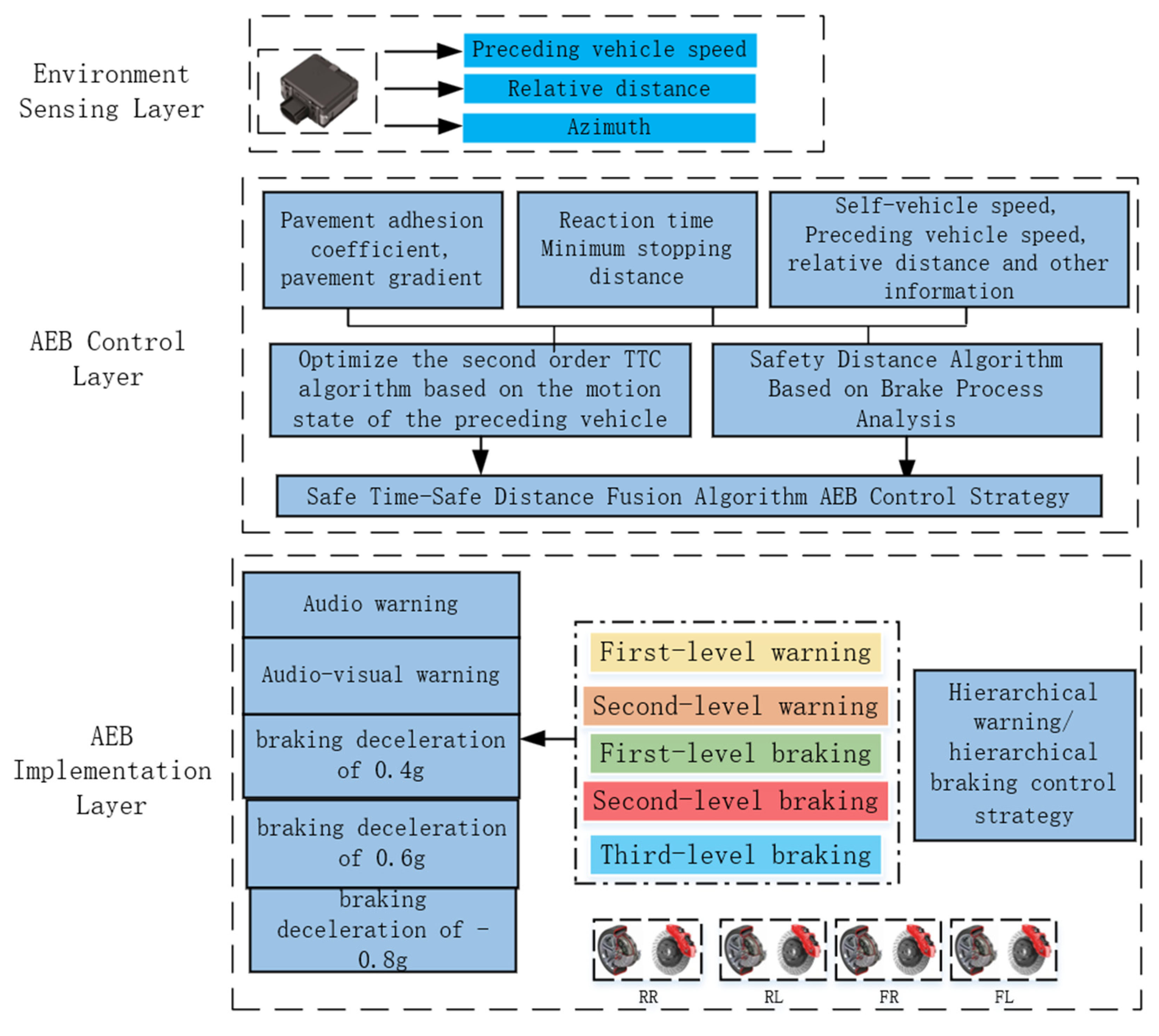
2. Safety Time–Safety Distance Fusion Algorithm
2.1. Optimized Second-Order TTC Safety Time Algorithm
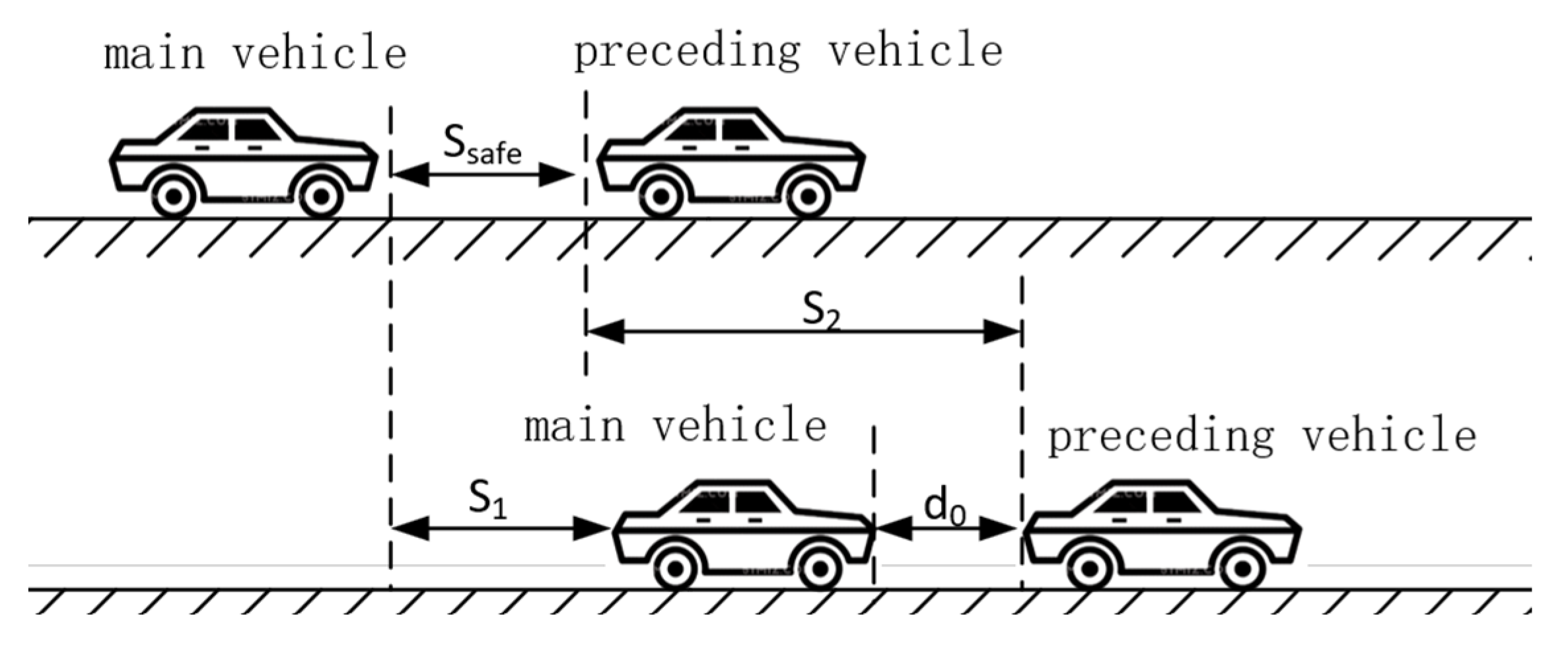
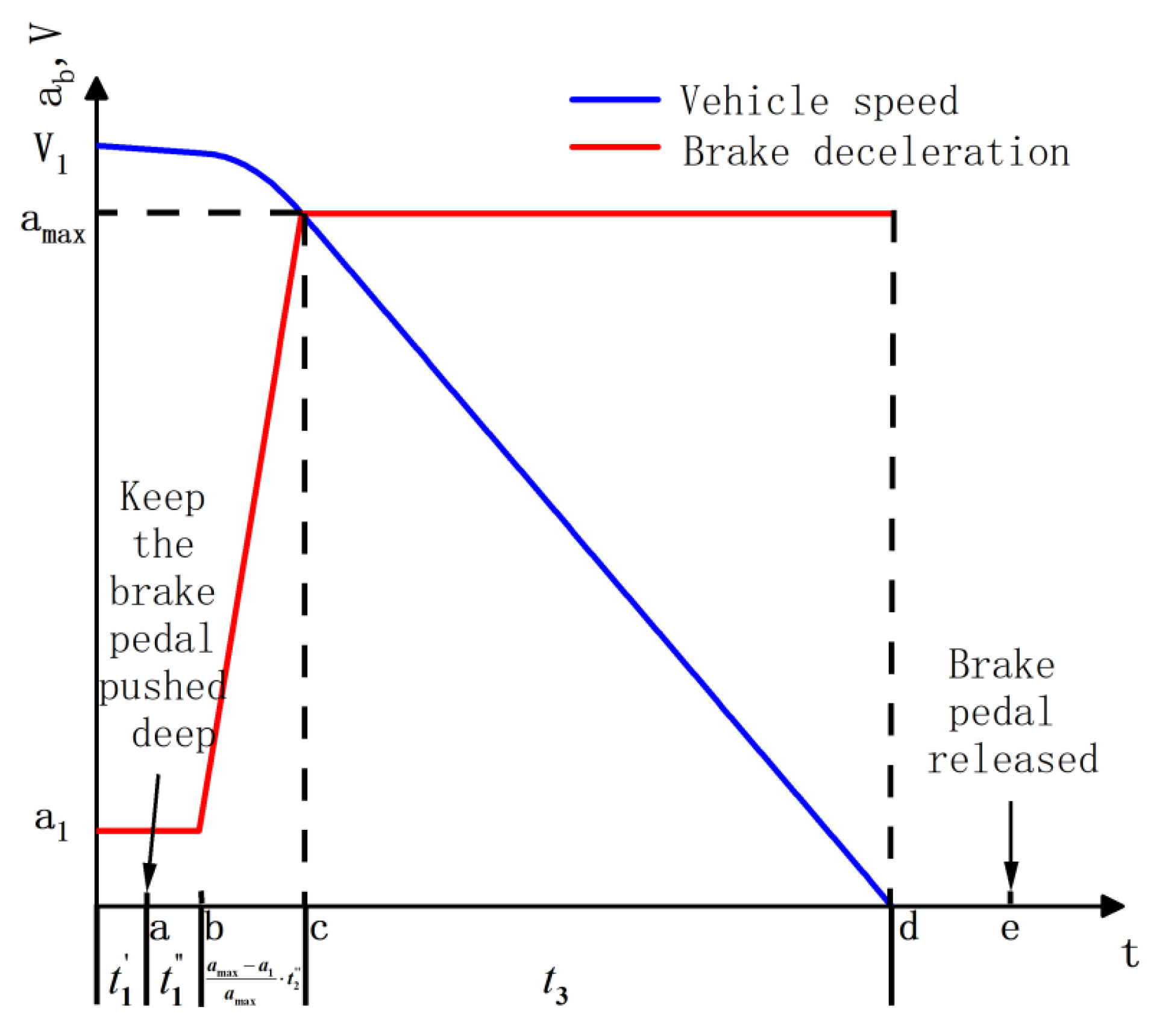
2.2. Safety Distance Algorithm Based on Brake Process Analysis
2.3. Safety Time–Safe Distance Fusion Algorithm
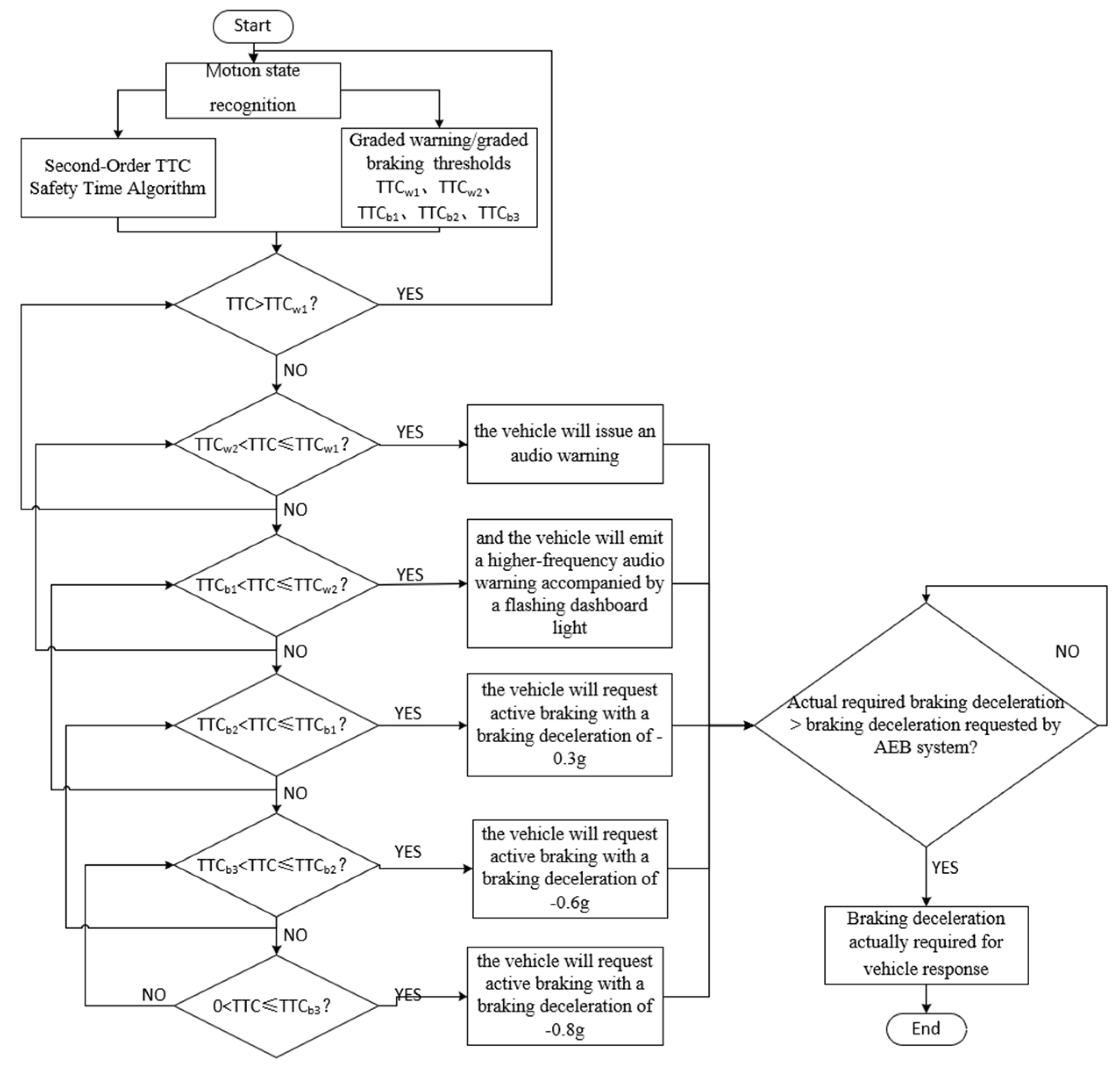
3. The Hierarchical Warning/Hierarchical Braking Control Strategy
4. Simulation Validation of AEB Control Strategy
4.1. Construction of the Joint Simulation Platform
4.2. Joint Simulation Comparative Models and Evaluation Metrics
4.3. Typical Test Scene Simulation and Analysis
4.3.1. Test Conditions for CCRs Scenario
4.3.2. Test Conditions for CCRm Scenario
4.3.3. Test Conditions for CCRb Scenario
4.3.4. Test Conditions for a Preceding Vehicle Accelerating Scenario
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, H.; Jin, H. Research on Personalized AEB Strategies Based on Self-Supervised Contrastive Learning. IEEE Trans. Intell. Transp. Syst. 2024, 25, 1303–1316. [Google Scholar] [CrossRef]
- Cao, W.; Yang, M.; Wei, Z.; Wang, J.; Yang, X. Autonomous Emergency Braking of Electric Vehicles with High Robustness to Cyber-Physical Uncertainties for Enhanced Braking Stability. IEEE Trans. Veh. Technol. 2023, 72, 4426–4441. [Google Scholar] [CrossRef]
- Veneroso, L.; Alfatti, F.; Annicchiarico, C.; Capitani, R. Modelling, testing and validation of an innovative AEB control logic on a Hardware in the loop test bench. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1275, 012041. [Google Scholar] [CrossRef]
- Park, M.-K.; Lee, S.-Y.; Kwon, C.-K.; Kim, S.-W. Design of Pedestrian target selection with Funnel Map for Pedestrian AEB System. IEEE Trans. Veh. Technol. 2017, 66, 3597–3609. [Google Scholar] [CrossRef]
- Youshiha, H.; Awano, S.; Nagai, M.; Kamada, T. Target Following Brake Control for Collision Avoidance Assist of Active Interface Vehicle. In Proceedings of the SICE-ICASE International Joint Conference, Busan, Republic of Korea, 18–26 October 2006; pp. 4436–4439. [Google Scholar]
- Liu, Z.; Cheng, S.; Wang, S. Control Strategy of Automatic Emergency Braking System under Complex Road Conditions. Chin. Sci. Technol. Pap. 2022, 17, 221–227. [Google Scholar]
- Xiaofei, P.E.I.; Zhaodu, L.I.U.; Guocheng, M.A.; Yang, Y.E. Safe Distance Model and Target Detection Algorithm for Vehicle Active Collision Avoidance System. J. Automob. Saf. Energy Conserv. 2012, 3, 26–33. [Google Scholar]
- Guo, L.; Sun, D.C.; Ge, P.S. Automatic Emergency Braking Model with Second-Order Collision Time under Complex Conditions. Mach. Des. Manuf. 2022, 375, 127–131. [Google Scholar]
- Gounis, K.; Bassiliades, N. Intelligent momentary assisted control for autonomous emergency braking. Simul. Model. Pract. Theory 2022, 115, 102450. [Google Scholar] [CrossRef]
- Luo, Q.; Xu, L.H. Research on Establishment and Simulation of Following Model Based on Minimum Safety Distance. Sci. Technol. Eng. 2010, 10, 569–573. [Google Scholar]
- Guan, Y.Y. Research on Longitudinal Collision Warning and Automatic Emergency Braking Controller of Electric Vehicle. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2018. [Google Scholar]
- Ao, H.W.; Chen, X.W.; Rong, T.K. Research on Layered Control Strategy of Vehicle Emergency Braking Based on Safety Distance—Time Model. J. Chongqing Univ. Technol. 2022, 36, 31–38. [Google Scholar]
- Cheng, S.; Li, L.; Guo, H.-Q.; Chen, Z.-G.; Song, P. Longitudinal Collision Avoidance and Lateral Stability Adaptive Control System Based on MPC of Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2019, 21, 2376–2385. [Google Scholar] [CrossRef]
- Han, I.C.; Luan, B.C.; Hsieh, F.C. Development of autonomous emergency braking control system based on road friction. In Proceedings of the 2014 IEEE International Conference on Automation Science and Engineering, Taipei, Taiwan, 18–22 August 2014; pp. 933–937. [Google Scholar]
- Yang, W.; Zhang, X.; Lei, Q.; Cheng, X. Research on longitudinal active collision avoidance of autonomous emergency braking pedestrian system (AEB-P). Sensors 2019, 19, 4671. [Google Scholar] [CrossRef] [PubMed]
- Zeng, D.; Yu, Z.; Xiong, L.; Zhao, J.; Zhang, P.; Li, Z.; Fu, Z.; Xia, L.; Wei, Y.; Yan, S.; et al. Improved AEB algorithm combined with estimating the adhesion coefficient of road ahead and considering the performance of EHB. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 237, 2415–2430. [Google Scholar] [CrossRef]
- Lai, F.; Yang, H. Integrated Longitudinal and Lateral Control of Emergency Collision Avoidance for Intelligent Vehicles under Curved Road Conditions. Appl. Sci. 2023, 13, 12–16. [Google Scholar] [CrossRef]
- Zhou, T.; Liu, W.; Zhang, M.; Jia, J. Optimization of AEB Decision System Based on Unsafe Control Behavior Analysis and Improved ABAS Algorithm. IEEE Trans. Intell. Transp. Syst. 2024, 25, 3152–3165. [Google Scholar] [CrossRef]
- Wang, Z.; Zang, L.; Jiao, J.; Mao, Y. Research on Hierarchical Control Strategy of Automatic Emergency Braking System. World Electr. Veh. J. 2023, 14, 6–9. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, C.; Yang, S.; Tang, X. Study on Top Hierarchy Control Strategy of AEBS over Regenerative Brake and Hydraulic Brake for Hub Motor Drive BEVs. Energies 2022, 15, 18–23. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, Z.; Xu, X.; Yan, Y. Research on Automatic Emergency Braking System Based on Target Recognition and Fusion Control Strategy in Curved Road. Electronics 2023, 12, 3490. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, X.; Deng, G.; Ou, J.; Yang, E.; Yang, S.; Li, T. Longitudinal and Lateral Control Strategies for Automatic Lane Change to Avoid Collision in Vehicle High–Speed Driving. Sensors 2023, 23, 23–28. [Google Scholar] [CrossRef] [PubMed]

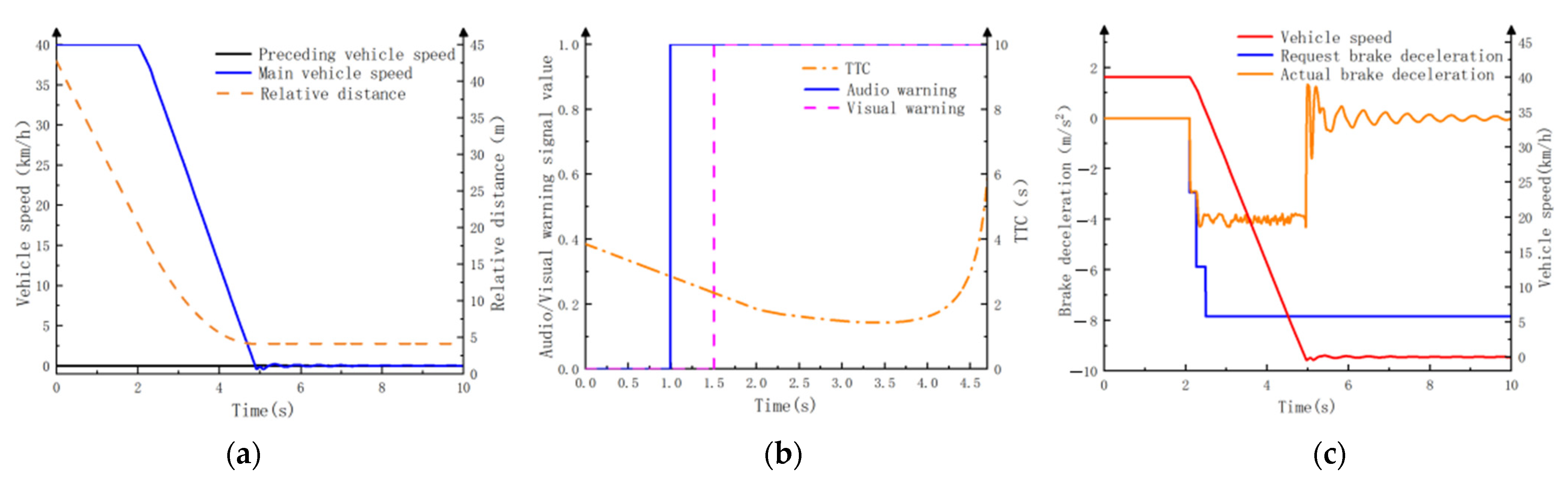
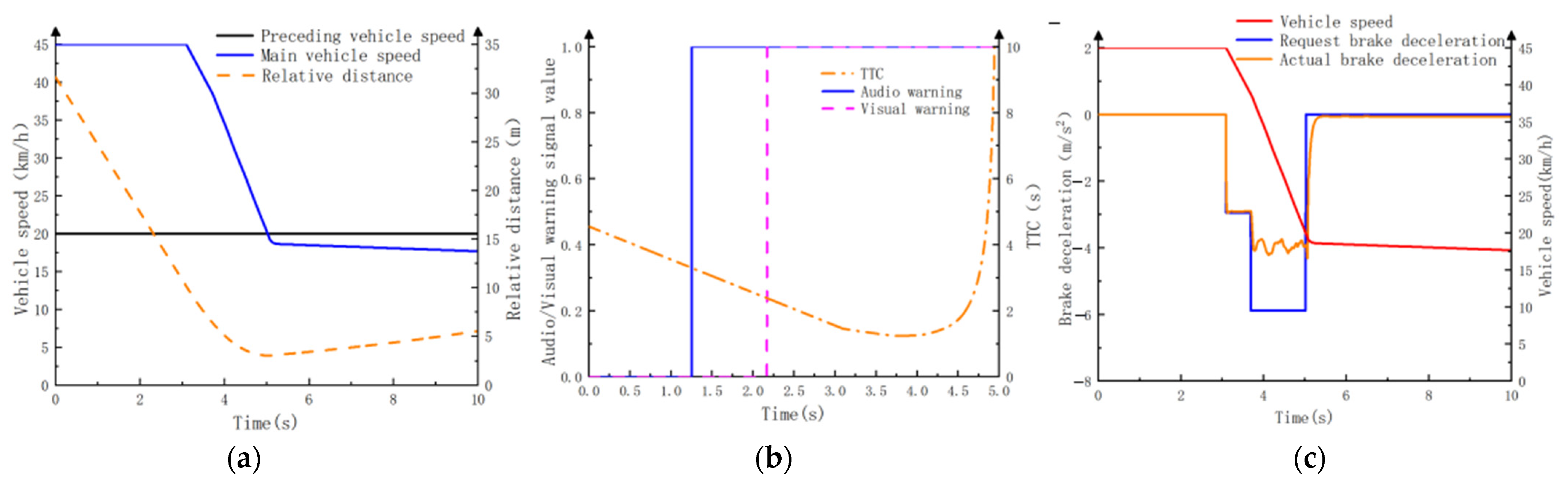


| Motion State | Conditions | Optimize the Second-Order TTC Algorithm |
|---|---|---|
| Stationary preceding vehicle | ||
| Preceding vehicle at a constant speed | ||
| Preceding vehicle decelerating | ||
| Preceding vehicle accelerating | ||
| The Function of Vehicle Speed-Time and Braking Deceleration-Time | ||
|---|---|---|
| The driver begins to apply the brake | ||
| The driver has begun to apply the brake | ||
| Motion State of the Preceding Vehicle | Warning/Braking Distance Thresholds |
|---|---|
| Stationary preceding vehicle | |
| Preceding vehicle at a constant speed | |
| Preceding vehicle decelerating | |
| Preceding vehicle accelerating. |
| Motion State of the Preceding Vehicle | Warning/Braking Distance Thresholds |
|---|---|
| Stationary preceding vehicle | |
| Preceding vehicle at a constant speed | |
| Preceding vehicle decelerating | |
| Preceding vehicle accelerating |
| Motion State | Conditions | Fusion Algorithm |
|---|---|---|
| Stationary preceding vehicle | ||
| Preceding vehicle at a constant speed | ||
| Preceding vehicle decelerating | ||
| Preceding vehicle accelerating | ||
| Deceleration | Distributions | ||||
|---|---|---|---|---|---|
| 5% | 25% | 50% | 75% | 95% | |
| The average braking deceleration | −0.15 | −0.29 | −0.38 | −0.42 | −0.55 |
| The maximum braking deceleration | −0.37 | −0.58 | −0.72 | −0.82 | −0.92 |
| Parameter Name | Parameter Information | Parameter Name | Parameter Information |
|---|---|---|---|
| Windward area A | 3.7 m2 | Effective wheel radius Re | 465 mm |
| Height of center of gravity hg | 860 mm | Wheelbases L | 3500 mm |
| Overall mass m | 4560 kg | Distance from center of mass to front axle lf | 1700 mm |
| Spring–loaded mass | 4080 kg | Distance from center of mass to rear axle lr | 1800 mm |
| Unsprung mass | 480 kg | Tread b | 2070 mm |
| Air resistance coefficient Cd | 0.4 | Moment of inertia about z-axis Iz | 10,080 kg·m2 |
| Model | Relative Distance at the Start of Collision Warning or TTC | Relative Distance at the Start of Active Braking or TTC | Full Collision Avoidance or Not | Rate of Velocity Reduction | Minimum Relative Distance | Relative Speed of Collision |
|---|---|---|---|---|---|---|
| Fusion algorithm model | 62.14 m/2.8 s | 39.47 m/1.78 s | Yes | 100% | 3.37 m | − |
| Honda model | 55.26 m/2.49 s | 29.4 m/1.32 s | No | 59.7% | 0 m | 32.24 km/h |
| Berkeley model | 70.79 m/3.19 s | 31.05 m/1.4 s | No | 66.3% | 0 m | 26.99 km/h |
| TTC model | 57.99 m/2.6 s | 35.67 m/1.6 s | No | 49.1% | 0 m | 40.71 km/h |
| Model | Relative Distance at the Start of Collision Warning or TTC | Relative Distance at the Start of Active Braking or TTC | Full Collision Avoidance or Not | Rate of Velocity Reduction | Minimum Relative Distance | Relative Speed of Collision |
|---|---|---|---|---|---|---|
| Fusion algorithm model | 46.95 m/2.81 s | 24.29 m/1.45 s | Yes | 100% | 3.09 m | − |
| Honda model | 42.99 m/2.57 s | 27.47 m/1.64 s | Yes | 100% | 7.61 m | − |
| Berkeley model | 68.29 m/4.08 s | 24.38 m/1.46 s | Yes | 100% | 4.51 m | − |
| TTC model | 43.49 m/2.6 s | 26.75 m/1.6 s | No | 80.6% | 0 m | 11.67 km/h |
| Model | Relative Distance at the Start of Collision Warning or TTC | Relative Distance at the Start of Active Braking or TTC | Full Collision Avoidance or Not | Rate of Velocity Reduction | Minimum Relative Distance | Relative Speed of Collision |
|---|---|---|---|---|---|---|
| Fusion algorithm model | 35.8 m/3.49 s | 29.16 m/2.47 s | Yes | 100% | 2.63 m | − |
| Honda model | 26.22 m/2.13 s | 15.44 m/1.12 s | No | 28.7% | 0 m | 35.66 km/h |
| Berkeley model | 31.8 m/2.82 s | 12.74 m/0.9 s | No | 22.4% | 0 m | 38.80 km/h |
| TTC model | 24.82 m/1.98 s | 18.28 m/1.36 s | No | 38% | 0 m | 30.98 km/h |
| Model | Relative Distance at the Start of Collision Warning or TTC | Relative Distance at the Start of Active Braking or TTC | Full Collision Avoidance or Not | Rate of Velocity Reduction | Minimum Relative Distance | Relative Speed of Collision |
|---|---|---|---|---|---|---|
| Fusion algorithm model | 43.25 m/4.24 s | 10.93 m/1.25 s | Yes | 100% | 3.06 m | − |
| Honda model | 31.02 m/3.19 s | 21.75 m/2.34 s | Yes | 100% | 14.7 m | − |
| Berkeley model | 64.84 m/6.05 s | 20.97 m/2.26 s | Yes | 100% | 14.0 m | − |
| TTC model | 28.83 m/3.0 s | 15.78 m/1.75 s | Yes | 100% | 5.55 m | − |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, X.; Wan, J.; Wu, D.; Jiang, W.; Ma, W.; Yang, T. Research on Vehicle AEB Control Strategy Based on Safety Time–Safety Distance Fusion Algorithm. Mathematics 2024, 12, 1905. https://doi.org/10.3390/math12121905
Fu X, Wan J, Wu D, Jiang W, Ma W, Yang T. Research on Vehicle AEB Control Strategy Based on Safety Time–Safety Distance Fusion Algorithm. Mathematics. 2024; 12(12):1905. https://doi.org/10.3390/math12121905
Chicago/Turabian StyleFu, Xiang, Jiaqi Wan, Daibing Wu, Wei Jiang, Wang Ma, and Tianqi Yang. 2024. "Research on Vehicle AEB Control Strategy Based on Safety Time–Safety Distance Fusion Algorithm" Mathematics 12, no. 12: 1905. https://doi.org/10.3390/math12121905
APA StyleFu, X., Wan, J., Wu, D., Jiang, W., Ma, W., & Yang, T. (2024). Research on Vehicle AEB Control Strategy Based on Safety Time–Safety Distance Fusion Algorithm. Mathematics, 12(12), 1905. https://doi.org/10.3390/math12121905





