A Method for Evaluating the Data Integrity of Microseismic Monitoring Systems in Mines Based on a Gradient Boosting Algorithm
Abstract
1. Introduction
2. Theoretical Background
2.1. Gradient Boosting Algorithm
2.2. Isolation Forest
2.3. Loss Function
2.4. Monitoring Capability of Seismic Networks
3. Engineering Background and Data Preprocessing
3.1. Project Overview
3.2. Data Preprocessing
3.3. Feature Engineering
4. Results and Analysis
4.1. Structure and Parameters
4.2. Performance Metrics
4.3. Input, Output, and Result
4.4. Comparison with the Traditional Method
5. Discussions
5.1. Influence of Feature Engineering
5.2. Influence of Oversampling
5.3. Subsequent Improvements
6. Conclusions
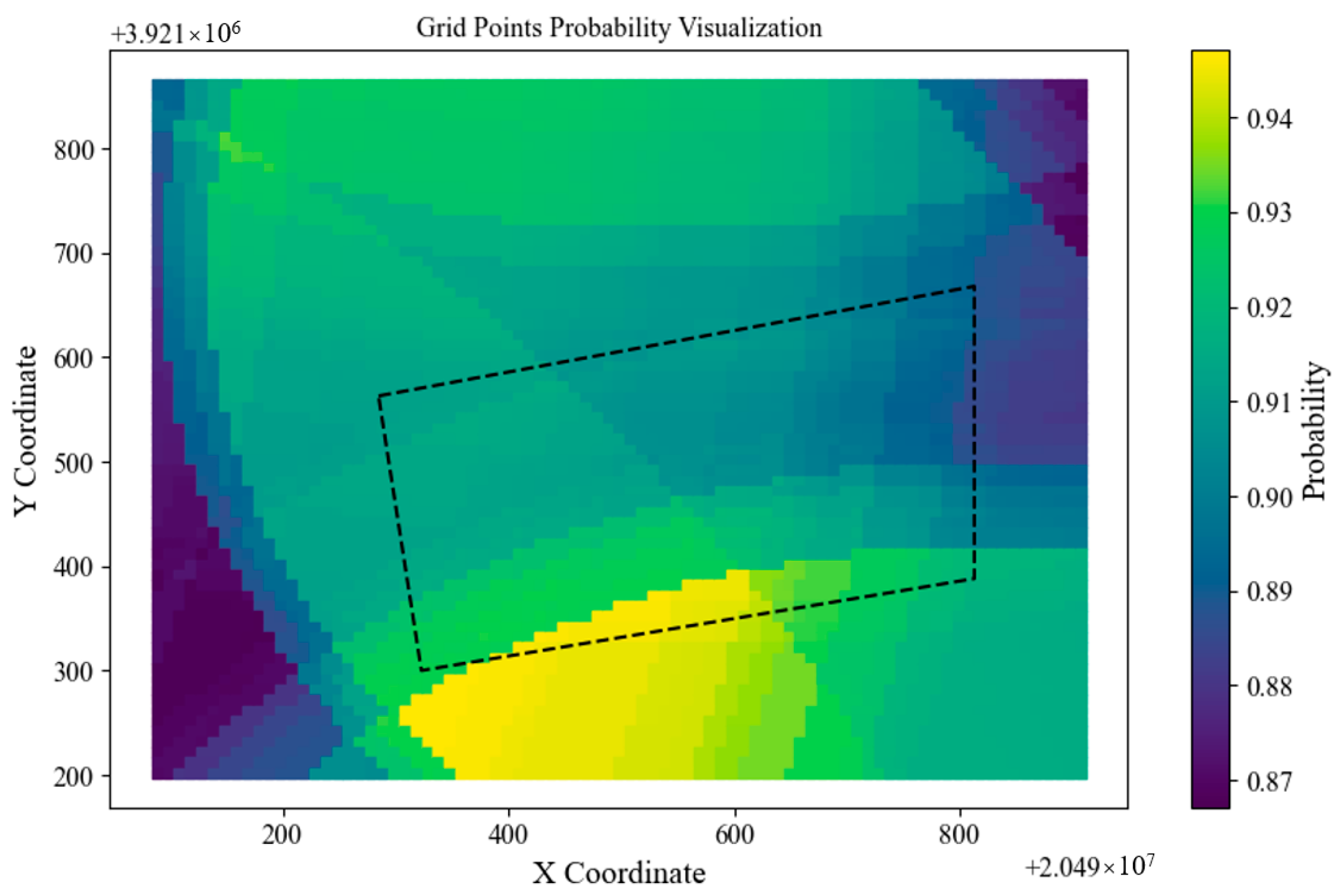
- This method clearly demonstrated the impact of heterogeneous mediums on the monitoring capability of seismic networks. For example, Station 0 exhibited significantly weaker monitoring capability in Areas A and B, Station 1 in Area B, and Station 2 in Area C. Conversely, Station 3 had significantly stronger monitoring capability in Areas B and D, Station 4 in Areas A and D, and Station 5 in Area B;
- The method calculated the detection probability of 3000-joule microseismic events in key monitoring areas to be 0.84, slightly lower than the 0.90 achieved by the traditional PDE method;
- Among the ensemble models, CatBoost performed the best, while LightGBM performed the worst. The ensemble of the three models effectively improved the stability of the results;
- The method overcame two major obstacles in applying the PDE method from earthquake monitoring to mining: the need for extensive nearby searches due to event concentration in specific areas and the necessity of acquiring the maximum amplitude of microseismic events detected by different stations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Parameter Name | Symbol | Parameter Name |
| s | The anomaly score | The average path length of data point x across all trees in the forest | |
| n | The number of samples | The harmonic function | |
| The average path length in a perfectly balanced binary tree | The actual label of sample | ||
| The probability predicted by the model that sample belongs to the positive class | The parameter for regularization strength | ||
| The model’s weight | The probability of an MS event being detected by network | ||
| The probability of an MS event being detected by i stations | The probability that the station i can detect the data point | ||
| The probability that station i does not detect the data point | s | The number of stations in the network | |
| The number of combinations of choosing i subsets from s elements | The weight for Algorithm i | ||
| The log loss values for Algorithm i | The precision values for Algorithm i | ||
| The recall values for Algorithm i |
References
- Zhang, C.; Canbulat, I.; Hebblewhite, B.; Ward, C.R. Assessing coal burst phenomena in mining and insights into directions for future research. Int. J. Coal Geol. 2017, 179, 28–44. [Google Scholar] [CrossRef]
- Cook, N. Seismicity associated with mining. Eng. Geol. 1976, 10, 99–122. [Google Scholar] [CrossRef]
- Iannacchione, A.T.; Tadolini, S.C. Occurrence, predication, and control of coal burst events in the U.S. Int. J. Min. Sci. Technol. 2016, 26, 39–46. [Google Scholar] [CrossRef]
- Patyńska, R.; Mirek, A.; Burtan, Z.; Pilecka, E. Rockburst of parameters causing mining disasters in Mines of Upper Silesian Coal Basin. E3S Web Conf. 2018, 36, 03005. [Google Scholar] [CrossRef]
- Cao, A.-Y.; Dou, L.-M.; Wang, C.-B.; Yao, X.-X.; Dong, J.-Y.; Gu, Y. Microseismic Precursory Characteristics of Rock Burst Hazard in Mining Areas Near a Large Residual Coal Pillar: A Case Study from Xuzhuang Coal Mine, Xuzhou, China. Rock Mech. Rock Eng. 2016, 49, 4407–4422. [Google Scholar] [CrossRef]
- Srinivasan, C.; Arora, S.; Benady, S. Precursory monitoring of impending rockbursts in Kolar gold mines from microseismic emissions at deeper levels. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1999, 36, 941–948. [Google Scholar] [CrossRef]
- Wang, G.; Gong, S.; Dou, L.; Wang, H.; Cai, W.; Cao, A. Rockburst characteristics in syncline regions and microseismic precursors based on energy density clouds. Tunn. Undergr. Space Technol. 2018, 81, 83–93. [Google Scholar] [CrossRef]
- Cai, W.; Dou, L.; Gong, S.; Li, Z.; Yuan, S. Quantitative analysis of seismic velocity tomography in rock burst hazard assessment. Nat. Hazards 2015, 75, 2453–2465. [Google Scholar] [CrossRef]
- Si, G.; Durucan, S.; Jamnikar, S.; Lazar, J.; Abraham, K.; Korre, A.; Shi, J.-Q.; Zavšek, S.; Mutke, G.; Lurka, A. Seismic monitoring and analysis of excessive gas emissions in heterogeneous coal seams. Int. J. Coal Geol. 2015, 149, 41–54. [Google Scholar] [CrossRef]
- Cai, W.; Dou, L.; Zhang, M.; Cao, W.; Shi, J.-Q.; Feng, L. A fuzzy comprehensive evaluation methodology for rock burst forecasting using microseismic monitoring. Tunn. Undergr. Space Technol. 2018, 80, 232–245. [Google Scholar] [CrossRef]
- Cai, W.; Bai, X.X.; Si, G.Y.; Cao, W.Z.; Gong, S.Y.; Dou, L.M. A Monitoring Investigation into Rock Burst Mechanism Based on the Coupled Theory of Static and Dynamic Stresses. Rock Mech. Rock Eng. 2020, 53, 5451–5471. [Google Scholar] [CrossRef]
- Duan, Y.; Shen, Y.; Canbulat, I.; Luo, X.; Si, G. Classification of clustered microseismic events in a coal mine using machine learning. J. Rock Mech. Geotech. Eng. 2021, 13, 1256–1273. [Google Scholar] [CrossRef]
- Wang, C.; Cao, A.; Zhu, G.; Jing, G.; Li, J.; Chen, T. Mechanism of rock burst induced by fault slip in an island coal panel and hazard assessment using seismic tomography: A case study from Xuzhuang colliery, Xuzhou, China. Geosci. J. 2017, 21, 469–481. [Google Scholar] [CrossRef]
- Wang, P.; Bi, B.; Lin, H.; Liu, F.; Shao, Y.; Wang, J. Assessment of Earthquake Monitoring Capability of Shanghai Seismic Network based on PMC Method. Seismol. Geomagn. Obs. Res. 2020, 41, 18–24. (In Chinese) [Google Scholar]
- Wang, C.; Cao, A.; Zhang, C.; Canbulat, I. A New Method to Assess Coal Burst Risks Using Dynamic and Static Loading Analysis. Rock Mech. Rock Eng. 2020, 53, 1113–1128. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Frequency of Earthquakes in California. Bull. Seismol. Soc. Am. 1994, 34, 185–188. [Google Scholar] [CrossRef]
- Sereno, T.J.; Bratt, S.R. Seismic detection capability at NORESS and implications for the detection threshold of a hypothetical network in the Soviet Union. J. Geophys. Res. 1989, 94, 10397–10414. [Google Scholar] [CrossRef]
- Gomberg, J. Seismicity and detection/location threshold in the Southern Great Basin Seismic Network. J. Geophys. Res. 1991, 96, 16401–16414. [Google Scholar] [CrossRef]
- Rydelek, P.A.; Sacks, I.S. Testing the completeness of earthquake catalogues and the hypothesis of self-similarity. Nature 1989, 337, 251–253. [Google Scholar] [CrossRef]
- Schorlemmer, D.; Woessner, J. Probability of Detecting an Earthquake. Bull. Seism. Soc. Am. 2008, 98, 2103–2117. [Google Scholar] [CrossRef]
- An, X.; Zhao, Q.; Wang, X.; Wang, S.; Xu, P. Assessment of Earthquake Monitoring Capability of Liaoning Seismic Network Based on PMC Method. China Earthq. Eng. J. 2019, 41, 1545–1552. (In Chinese) [Google Scholar]
- Peng, L.; Liu, L.; Chen, X.; Zeng, W.; Ding, Y.; Sun, P.; Li, J.; Li, D. Assessment of Earthquake Monitoring Capability of Hainan Seismic Network Based on PMC Method. South China J. Seismol. 2022, 42, 21–28. (In Chinese) [Google Scholar] [CrossRef]
- Liang, X.; Song, M.; Liu, F.; Liu, L. Assessment of Earthquake Monitoring Capability of Shanxi Seismic Network based on PMC Method. North China Earthq. Sci. 2022, 40, 62–71. (In Chinese) [Google Scholar]
- Wang, P.; Zheng, J.; Li, B. Analysis of detection capability of Shandong regional seismic network based on PMC method. Prog. Geophys. 2016, 31, 2408–2414. (In Chinese) [Google Scholar]
- Jiang, C.; Fang, L.; Han, L.; Wang, W.; Guo, L. Assessment of earthquake detection capability for the seismic array: A case study of the Xichang seismic array. Chin. J. Geophys. 2015, 58, 832–843. (In Chinese) [Google Scholar]
- Guo, Y.; Zhang, L.; Gu, Q.; Huang, H.; Li, Z.; Ma, L. Assessment of Earthquake Monitoring Capability of Qinghai Seismic Network Based on PMC Method. Seismol. Geomagn. Obs. Res. 2022, 43, 23–32. (In Chinese) [Google Scholar]
- Maghsoudi, S.; Cesca, S.; Hainzl, S.; Kaiser, D.; Becker, D.; Dahm, T. Improving the estimation of detection probability and magnitude of completeness in strongly heterogeneous media, an application to acoustic emission (AE). Geophys. J. Int. 2013, 193, 1556–1569. [Google Scholar] [CrossRef]
- Plenkers, K.; Schorlemmer, D.; Kwiatek, G.; JAGUARS Research Group. On the Probability of Detecting Picoseismicity. Bull. Seism. Soc. Am. 2011, 101, 2579–2591. [Google Scholar] [CrossRef]
- Wang, C.; Si, G.; Zhang, C.; Cao, A.; Canbulat, I. A Statistical Method to Assess the Data Integrity and Reliability of Seismic Monitoring Systems in Underground Mines. Rock Mech. Rock Eng. 2021, 54, 5885–5901. [Google Scholar] [CrossRef]
- Wang, C.; Si, G.; Zhang, C.; Cao, A.; Canbulat, I. Variation of seismicity using reinforced seismic data for coal burst risk assessment in underground mines. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2023, 165, 105363. [Google Scholar] [CrossRef]
- Li, H.; Cao, A.; Gong, S.; Wang, C.; Zhang, R. Evolution Characteristics of Seismic Detection Probability in Underground Mines and Its Application for Assessing Seismic Risks—A Case Study. Sensors 2022, 22, 3682. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the KDD ’16: 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Meng, Q. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Advances in Neural Information Processing Systems 30, Proceedings of the Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017; NeurIPS: San Diego, CA, USA, 2017; Volume 30. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. arXiv 2017. [Google Scholar] [CrossRef]
- Liu, F.; Ting, K.; Zhou, Z. Isolation Forest. In Proceedings of the IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008. [Google Scholar]
- Liu, F.T.; Ting, K.M.; Zhou, Z.-H. Isolation-Based Anomaly Detection. ACM Trans. Knowl. Discov. Data 2012, 6, 1–39. [Google Scholar] [CrossRef]












| Station ID | Location | Description |
|---|---|---|
| station_0 | (20,490,772.166, 3,921,683.424, −658.500) | operational base |
| station_1 | (20,490,811.790, 3,920,503.290, 47.506) | communication building |
| station_2 | (20,489,323.640, 3,920,445.053, −67.741) | silkworm farm |
| station_3 | (20,488,525.520, 3,921,936.055, −144.297) | airshaft |
| station_4 | (20,490,545.540, 3,922,838.660, −657.200) | equipment chamber |
| station_5 | (20,490,811.790, 3,920,503.290, −718.700) | substation |
| Event ID | x | y | z | Energy | Station ID |
|---|---|---|---|---|---|
| 0 | 20,489,977.04 | 3,921,589.92 | −674.14 | 576,000 | 5, 2, 4, 3 |
| 1 | 20,490,097.1 | 3,920,307.54 | −464.18 | 5490 | 5, 2, 4, 3 |
| 2 | 20,490,816.49 | 3,921,648.6 | −568.84 | 3130 | 5, 2, 4, 3 |
| 3 | 20,489,301.16 | 3,921,314.16 | −906.25 | 8380 | 0, 5, 3 |
| 4 | 20,490,259.05 | 3,921,625.64 | −578.04 | 6007 | 5, 2, 4 |
| 5 | 20,487,340.09 | 3,920,151.62 | −981.57 | 12,942 | 2, 3 |
| Feature Name | Data Type | Descriptions |
|---|---|---|
| z_distance | Float | The vertical distance between the MS event and the station |
| horizon_distance | Float | The horizontal distance between the MS event and the station |
| Area A | Boolean | Whether the MS event occurred in Area A |
| Area B | Boolean | Whether the MS event occurred in Area B |
| Area C | Boolean | Whether the MS event occurred in Area C |
| Area D | Boolean | Whether the MS event occurred in Area D |
| energy | Float | The energy released by the rupture of the MS event source |
| logenergy | Float | The logarithm of energy |
| Algorithm | Hyperparameters | Search Range | Stride | Optimal Values |
|---|---|---|---|---|
| XGBoost | booster | [gbtree, dart] | - | dart |
| learning_rate | [0.01, 0.5] | step = 0.01 | 0.15 | |
| gamma | [1, 10] | step = 0.1 | 2.6 | |
| max_depth | [3, 10] | step = 1 | 6 | |
| min_child_weight | [1, 100] | step = 0.01 | 14.4 | |
| grow_policy | [depthwise, lossguide] | - | depthwise | |
| max_leaves | [16, 64] | step = 1 | 41 | |
| subsample | [0.01, 1] | step = 0.01 | 0.86 | |
| lambda | [1 × 10−10, 100] | log = 10 | 1.91 × 10−9 | |
| alpha | [1 × 10−10, 100] | log = 10 | 2.37 × 10−3 | |
| sample_type | [uniform, weighted] | - | uniform | |
| normalize_type | [tree, forest] | - | forest | |
| rate_drop | [1 × 10−10, 1] | log = 10 | 7.68 × 10−2 | |
| skip_drop | [1 × 10−10, 1] | log = 10 | 2.02 × 10−6 | |
| LightGBM | boosting | [gbdt, dart] | - | dart |
| learning_rate | [0.01, 0.5] | step = 0.01 | 0.11 | |
| max_depth | [3, 10] | step = 1 | 6 | |
| num_leaves | [16, 64] | step = 1 | 30 | |
| min_data_in_leaf | [20, 200] | step = 2 | 24 | |
| lambda_l1 | [1 × 10−10, 100] | log = 10 | 7.80 × 10−7 | |
| lambda_l2 | [1 × 10−10, 100] | log = 10 | 2.25 × 10−7 | |
| bagging_fraction | [0.01, 1] | step = 0.01 | 0.58 | |
| bagging_freq | [1, 10] | step = 1 | 3 | |
| pos_bagging_fraction | [0.4, 1] | step = 0.01 | 0.69 | |
| neg_bagging_fraction | [0.4, 1] | step = 0.01 | 0.69 | |
| drop_rate | [1 × 10−10, 1] | log = 10 | 1.14 × 10−5 | |
| skip_rate | [1 × 10−10, 1] | log = 10 | 5.57 × 10−8 | |
| CatBoost | learning_rate | [0.01, 0.5] | step = 0.01 | 0.14 |
| l2_leaf_reg | [1 × 10−10, 100] | log = 10 | 27.13 | |
| depth | [3, 10] | step = 1 | 10 | |
| min_data_in_leaf | [20, 200] | step = 2 | 26 | |
| colsample_bylevel | [0.01, 1] | step = 0.01 | 0.84 |
| Station id | Model | Train | Test | ||||
|---|---|---|---|---|---|---|---|
| Log Loss | Precision | Recall | Log Loss | Precision | Recall | ||
| 0 | XGBoost_0 | 6.46 | 0.84 | 0.86 | 6.40 | 0.84 | 0.86 |
| LightGBM_0 | 6.43 | 0.83 | 0.89 | 6.13 | 0.85 | 0.87 | |
| CatBoost_0 | 7.24 | 0.81 | 0.86 | 6.60 | 0.83 | 0.87 | |
| 1 | XGBoost_1 | 6.62 | 0.79 | 0.13 | 6.80 | 0.64 | 0.12 |
| LightGBM_1 | 6.28 | 0.81 | 0.16 | 6.73 | 0.77 | 0.12 | |
| CatBoost_1 | 6.49 | 0.78 | 0.13 | 6.82 | 0.63 | 0.12 | |
| 2 | XGBoost_2 | 4.11 | 0.89 | 0.99 | 4.17 | 0.88 | 0.98 |
| LightGBM_2 | 4.06 | 0.89 | 0.99 | 4.03 | 0.89 | 0.99 | |
| CatBoost_2 | 4.18 | 0.88 | 0.99 | 4.19 | 0.88 | 0.99 | |
| 3 | XGBoost_3 | 8.81 | 0.76 | 0.99 | 9.09 | 0.75 | 0.99 |
| LightGBM_3 | 8.84 | 0.76 | 0.99 | 9.03 | 0.75 | 0.99 | |
| CatBoost_3 | 8.94 | 0.75 | 0.99 | 8.83 | 0.75 | 0.99 | |
| 4 | XGBoost_4 | 8.85 | 0.79 | 0.74 | 9.32 | 0.78 | 0.71 |
| LightGBM_4 | 8.84 | 0.79 | 0.75 | 9.47 | 0.77 | 0.74 | |
| CatBoost_4 | 9.15 | 0.78 | 0.73 | 9.96 | 0.77 | 0.70 | |
| 5 | XGBoost_5 | 7.37 | 0.80 | 0.84 | 5.79 | 0.86 | 0.93 |
| LightGBM_5 | 7.4 | 0.80 | 0.83 | 5.86 | 0.86 | 0.91 | |
| CatBoost_5 | 8.24 | 0.77 | 0.83 | 6.63 | 0.84 | 0.91 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Zhan, K.; Zheng, X.; Liu, C.; Kong, C. A Method for Evaluating the Data Integrity of Microseismic Monitoring Systems in Mines Based on a Gradient Boosting Algorithm. Mathematics 2024, 12, 1902. https://doi.org/10.3390/math12121902
Wang C, Zhan K, Zheng X, Liu C, Kong C. A Method for Evaluating the Data Integrity of Microseismic Monitoring Systems in Mines Based on a Gradient Boosting Algorithm. Mathematics. 2024; 12(12):1902. https://doi.org/10.3390/math12121902
Chicago/Turabian StyleWang, Cong, Kai Zhan, Xigui Zheng, Cancan Liu, and Chao Kong. 2024. "A Method for Evaluating the Data Integrity of Microseismic Monitoring Systems in Mines Based on a Gradient Boosting Algorithm" Mathematics 12, no. 12: 1902. https://doi.org/10.3390/math12121902
APA StyleWang, C., Zhan, K., Zheng, X., Liu, C., & Kong, C. (2024). A Method for Evaluating the Data Integrity of Microseismic Monitoring Systems in Mines Based on a Gradient Boosting Algorithm. Mathematics, 12(12), 1902. https://doi.org/10.3390/math12121902






