Analysis of Caputo Fractional-Order Co-Infection COVID-19 and Influenza SEIR Epidemiology by Laplace Adomian Decomposition Method

Abstract

Around the world, the people are simultaneously susceptible to or infected with several infections. This work aims at the analysis of the dynamics of transmission of two deadly viruses, COVID-19 and Influenza, using a co-infection epidemiological model by applying the Caputo fractional derivative. Fractional differential equations are currently used worldwide to model physical and biological phenomena. Our comprehension of complicated phenomena is improved when fractional-order derivatives are used to model systems with memory effects and long-range interactions. Mathematical depictions of infectious disease dynamics and dissemination across communities are provided by epidemiological models, which are essential resources for understanding and controlling infectious diseases. These models support informed decision making to prevent outbreaks, evaluate intervention measures, and help researchers and policymakers understand how diseases spread. A subclass of epidemiological models called co-infection models focuses on studying the dynamics of several infectious illnesses that occur in the same population at the same time. They are especially useful in situations where people are simultaneously susceptible to or infected with several infections. Co-infection models provide information on the development of effective control techniques, the progression of disease, and the interactions between several pathogens. The qualitative study via stability analysis is discussed at equilibrium, the reproduction number $R_0$ is computed, and the results are simulated using the Laplace Adomian Decomposition Method (LADM) for Fractional Differential Equations. We employ MATLAB R2023a for graphical presentations and numerical simulations.

1. Introduction

For many years, infectious diseases have been one of the largest issues facing humanity. SARS-CoV-2 (coronavirus), which causes the acute respiratory syndrome also known as COVID-19, was identified in Wuhan, China, towards the end of 2019 [1]. The infection quickly spread to almost every country in the world [1]. Fever, cough, headache, exhaustion, trouble breathing, and loss of taste and smell are just a few of this deadly infection’s typical symptoms. After 1 to 14 days of exposure, the infected person may show modest to severe symptoms [2]. Every year, seasonal Influenza, another infectious disease, kills over 500,000 people and impacts millions of individuals [3]. After exposure to the virus, Influenza symptoms start to manifest one to four days later and continue for the next two to eight days. Common symptoms include a high body temperature, coughing, shivers, pain in the head, painful muscles, lack of appetite, exhaustion, throat pain, and discomfort [3]. The COVID-19 pandemic is being intensified by the prevalence of Influenza in the community. Infections with several diseases have made it harder to diagnose and treat the affected persons, which worsens human health.

It should be noted that, in many situations, the conventional mathematical models based on derivatives of integer-order and nonlinear equations do not constitute suitable frameworks in many cases [4]. To adequately examine the dynamics of the two diseases in the general population, a deterministic mathematical model that integrates the biological dynamics of COVID-19 and Influenza, as studied in [4], is developed based on fractional calculus via the Caputo derivative. The degree to which these symptoms replicate those of COVID-19 may make diagnosis and treatment difficult [5,6,7]. It can be quite challenging to diagnose and start the right treatment for both COVID-19 and Influenza due to the similarities in their clinical presentations, modes of transmission, traits, and symptoms [8]. Traditional integer-order derivatives describe instantaneous rates of change, where the current value of a variable depends only on its current state. However, many real-world systems exhibit memory effects, meaning their behavior depends on past states and not just the current state [9]. Fractional-order derivatives capture these memory effects by incorporating the history of a variable’s behavior. This enables us to uncover hidden patterns, explain anomalous behavior, and address real-world challenges in diverse scientific disciplines.

Fractional calculus offers a powerful tool to provide more insight into complex systems and advance our knowledge in various fields of research. Compared to ODEs, FDEs offer a more accurate depiction of the course of natural occurrences and epidemics [10]. The Riemann–Liouville definition is one variation that is frequently used. The various kernels that can be used to satisfy the needs of various applications are the fundamental differences among the fractional derivatives [11]. The Riemann–Liouville and Caputo derivatives are two of the most widely used formulations of fractional derivatives that offer mathematically feasible methods for solving issues in applied sciences and engineering [12]. G. Adomian proposed the Adomian decomposition method (ADM) [13]. The ability to solve all varieties of integral and differential equations is one of the main benefits of the Adomian decomposition approach. It is an all-encompassing strategy that treats the approximation of a non-linear equation’s solution as an infinite series that typically converges to the precise solution. It should be emphasized that LADM has greater power than regular ADM [14]. We performed stability analysis to investigate the behavior of our epidemiological model over time [15,16]. Understanding the reproduction number is crucial in evaluating the possible consequences of infectious diseases and in directing public health initiatives [17,18]. Model variables, such as the model parameters of COVID-19, are taken as outlined in the referenced article [19]; those for Influenza are taken as outlined in the referenced articles [20,21]; and co-infection parametric values are taken from [22].

The paper is organized as follows. The definition of gamma function [23]; basic definitions of fractional-order derivatives [24,25,26]; and an introduction to deterministic compartment models, including the classical co-infection SEIR model, fractional order SEIR model, and SEIR model, are all covered in Section 2. The co-infection FO-SEIR model employing the Caputo derivative is constructed and examined in Section 3 as an alternative to the standard SEIR model [27,28]. In Section 4, the co-infection FO-SEIR model is numerically simulated using LADM [29,30,31], the convergence of LADM is examined [32,33], and MATLAB is used to provide a graphical depiction. The conclusion and the future scope are covered in Section 5.

2. Preliminaries

Many mathematical scholars have identified different definitions that suit the concept of a non-integer order integral or derivative over the years, each using their own notation and methods. In this article, we choose the Caputo fractional derivative to model the fractional-order co-infection SEIR epidemiological model.

2.1. Basic Definitions and Prepositions

Definition 1

([11]). Gamma function in terms of the variable $y*$

$$\Gamma (y*)={\displaystyle {\int }_0^{\infty }{e}^{-t}}{t}^{y^{*}-1}dt,y*\in {\Re }^{+}$$

Definition 2

([27,29]). Fractional integral operator of order q, which is greater than 0, by Riemann–Liouville of a function $f\mathsf{ϵ}{\mathrm{L}}^1{(\mathfrak{R}}^{+}$) is defined by

$$D_t^{-q}f\left(t\right)=\frac{1}{\Gamma (\mathrm{q})}{\int }_0^t{\left(t-x\right)}^{q-1}f\left(x\right)dx$$

where $\Gamma (.)$ denotes the Euler Gamma function.

Definition 3

([26]). The Riemann–Liouville fractional derivative:

$$D_t^{q}f\left(t\right)=\frac{1}{\Gamma (n-q)}\frac{d^n}{{dt}^n}{\int }_0^t{\left(t-x\right)}^{n-q-1}f\left(x\right)dx.$$

Definition 4

([27]). The Caputo integral of the function $f$: ${\Re }^{+}$ → ℜ is defined by

$$c_{D_t^{-\mathrm{q}*}f\left(\mathrm{t}\right)=\frac{1}{\Gamma (\alpha )}}{\int }_0^t{\left(t-x\right)}^{\mathrm{q}*-1}f\left(x\right)dx,0<\mathrm{q}*\le 1$$

$\mathrm{q}*$ is the fractional order.

Definition 5

([26]). The $\mathrm{q}*$ order Caputo derivative is defined by

$$c_{D_t^{\mathrm{q}*}f\left(t\right)=\frac{1}{\Gamma (n-\mathrm{q}*)}}{\int }_0^t{\left(t-x\right)}^{n-\mathrm{q}*-1}\frac{d^n}{{dx}^n}f\left(x\right)dx\mathrm{where}n-1<\mathrm{q}*<n,n\mathsf{ϵ}N$$

For simplicity, we denote the Caputo derivative in this article as $D^q$y(t).

Definition 6

([21]). Given a function f ($t$) defined for 0 < t < ∞, the following integral converges in a certain region of s, where s is a complex parameter. Then, the Laplace transform of f(t) is given by

$$F(s)=L[f(t)]={\int }_0^{\infty }f(t)e^{-st}dt.$$

For inverse Laplace transform, the formula is

$$f(t)=L^{-1}[F(s)]\frac{1}{2\pi j}{\int }_{m-j\infty }^{m+j\infty }F\left(s\right)e^{-st}ds.$$

Proposition 1

([24,25]). Let 0 < q < 1, then the Laplace transformation of the Caputo derivative is given by

$$L\{{}^{C}D^{q}f(t)\}=s^q[f(t)]-s^{q-1}f(0)$$

2.2. Mathematical Model Formulation

An infectious disease mathematical model aims to indicate the severity and possible extent of the epidemic and the spread of the disease, making recommendations for efficient approaches to preventing and controlling the epidemic [28].

2.2.1. Deterministic Epidemic Models—Compartment Approach

According to the disease’s natural history, the host population is split into compartments or groups that are mutually exclusive. Possible compartments for a simple infectious disease include S (susceptible individuals), I (infected individuals), and R (recovered individuals) [28].

2.2.2. SEIR Model [16]

In order to study the spread of contagious diseases, epidemiologists use a mathematical model known as the SEIR model. The SEIR model has four compartments: susceptible individuals (S), exposed individuals (E), infected individuals (I), and recovered individuals (R) [28].

The SEIR model uses a system of differential equations to explain how these compartments change over time. The sizes of the susceptible, infected, and recovered populations are taken into consideration in the equations, along with the rates of infection and recovery. These equations are used to simulate and forecast the dynamics of infectious illnesses within a population.

2.2.3. Fractional-Order SEIR (FO-SEIR) Model

The Fractional-order SEIR (FO-SEIR) model is a modification to the conventional SEIR model, which takes fractional calculus operators into account. The analysis of systems with memory and long-range dependencies is possible because of fractional calculus, which operates with derivatives and integrals of non-integer order. In the FO-SEIR model, the four compartments—susceptible individuals (S), exposed individuals (E), infected individuals (I), and recovered individuals (R) [21]—are still present, but the differential equations that govern the transitions between these compartments involve fractional derivatives. The Caputo fractional derivative is of order q, denoted as ${}^C\mathrm{D}^{\mathrm{q}}$y(t), which represents the rate of change of the variable y(t) with respect to time with a fractional power q.

2.2.4. Classical Co-Infection SEIR Model [4]

Ten mutually exclusive compartments make up the entire human population N (t) at the time t. These are susceptible individuals S(t); individuals who have been exposed to COVID-19, Influenza, or both diseases ($E_{Cv}$(t), $E_{If}$(t), and $E_{CI}$(t)); and individuals who are infected with COVID-19, Influenza, or both diseases $(I_{Cv}(t)$, $I_{If}\left(t\right),\mathrm{a}\mathrm{n}\mathrm{d}{I}_{CI}(t)),$ as well as those who have recovered from COVID-19, Influenza, aornd both diseases ($R_{Cv}(t)$, $R_{If}$(t), and $R_{CI}$(t)) [4].

Later on, we will remove t from the model variables for simplicity.

The entire human population consists of:

$$N=S+E_{Cv}+I_{Cv}+R_{Cv}+E_{If}+I_{If}+R_{If}+E_{CI}+I_{CI}+R_{CI}$$

(1)

Considering the system of integer-order nonlinear differential equations [4] applied to research the co-dynamics of COVID-19 and Influenza,

$$\frac{dS}{dt}=\pi -(\mu +{\lambda }_{Cv}+{\lambda }_{If}+{\lambda }_{CI}+{\lambda }_{IC})S,$$

$$\frac{d{E}_{Cv}}{dt}=({\lambda }_{Cv}+{\lambda }_{CI})S-({\sigma }_{Cv}+\mu )E_{Cv},$$

$$\frac{d{I}_{Cv}}{dt}={\sigma }_{Cv}{E}_{Cv}-({\gamma }_{Cv}+\mu +{\delta }_{Cv})I_{Cv},$$

$$\frac{d{R}_{Cv}}{dt}={\gamma }_{Cv}{I}_{Cv}-{\mu R}_{Cv},$$

$$\frac{d{E}_{If}}{dt}=({\lambda }_{If}+{\lambda }_{CI})S-({\sigma }_{If}+\mu )E_{If},$$

$$\frac{d{I}_{If}}{dt}={\sigma }_{If}{E}_{If}-({\gamma }_{If}+\mu +{\delta }_{If})I_{If},$$

(2)

$$\frac{d{R}_{If}}{dt}={\gamma }_{If}{I}_{If}-(\mu )R_{If},$$

$$\frac{d{I}_{CI}}{dt}={\sigma }_{CI}Ecf-({\gamma }_{CI}+\mu +{\delta }_{CI})I_{CI},$$

$$\frac{d{E}_{CI}}{dt}=({\lambda }_{CI}+{\lambda }_{IC})S-({\sigma }_{CI}+\mu )E_{CI},$$

$$\frac{d{R}_{CI}}{dt}={\gamma }_{CI}{I}_{CI}-{\mu R}_{CI}.$$

with the initial settings of $S\left(0\right)\mathrm{g}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{h}\mathrm{a}\mathrm{n}0,E_{Cv}$(0)$,E_{If}$(0), $E_{CI}$(0)$,I_{Cv}(0)$, $I_{If}\left(0\right),I_{CI}\left(0\right),R_{Cv}\left(0\right),R_{If}$(0), ${\mathrm{a}\mathrm{n}\mathrm{d}R}_{CI}$(0) greater than or equal to 0.

In Model (2), the forces of infection, λ = ${\lambda }_{Cv}$ +${\lambda }_{If}$ + ${\lambda }_{CI}$ +${\lambda }_{IC}$, ${\lambda }_{Cv},{\lambda }_{If}{,\lambda }_{CI},$ and ${\lambda }_{IC},$ are given below as

$${\lambda }_{Cv}=\frac{{\beta }_{Cv}{I}_{Cv}}{N},{\lambda }_{If}=\frac{{\beta }_{If}{I}_{If}}{N},{\lambda }_{CI}=\frac{{\beta }_{CI}{I}_{CI}}{N},{\lambda }_{IC}=\frac{{\beta }_{IC}{I}_{IC}}{N}.$$

The successful interactions with individuals who are affected with COVID-19, influenza, or both infections (co-infected) are at the rates of ${\lambda }_{Cv},{\lambda }_{If},{\lambda }_{CI}{,\lambda }_{IC},$ respectively. The parameters ${\beta }_{Cv}$, ${\beta }_{If}{,\beta }_{CI},$ and ${\beta }_{IC},$ respectively, reflect the effective contact rates resulting in the transmission of COVID-19, Influenza, and co-infections. Explanations of the model variables and parameters are given in

Table 1. An explanation of the model’s variable usage.

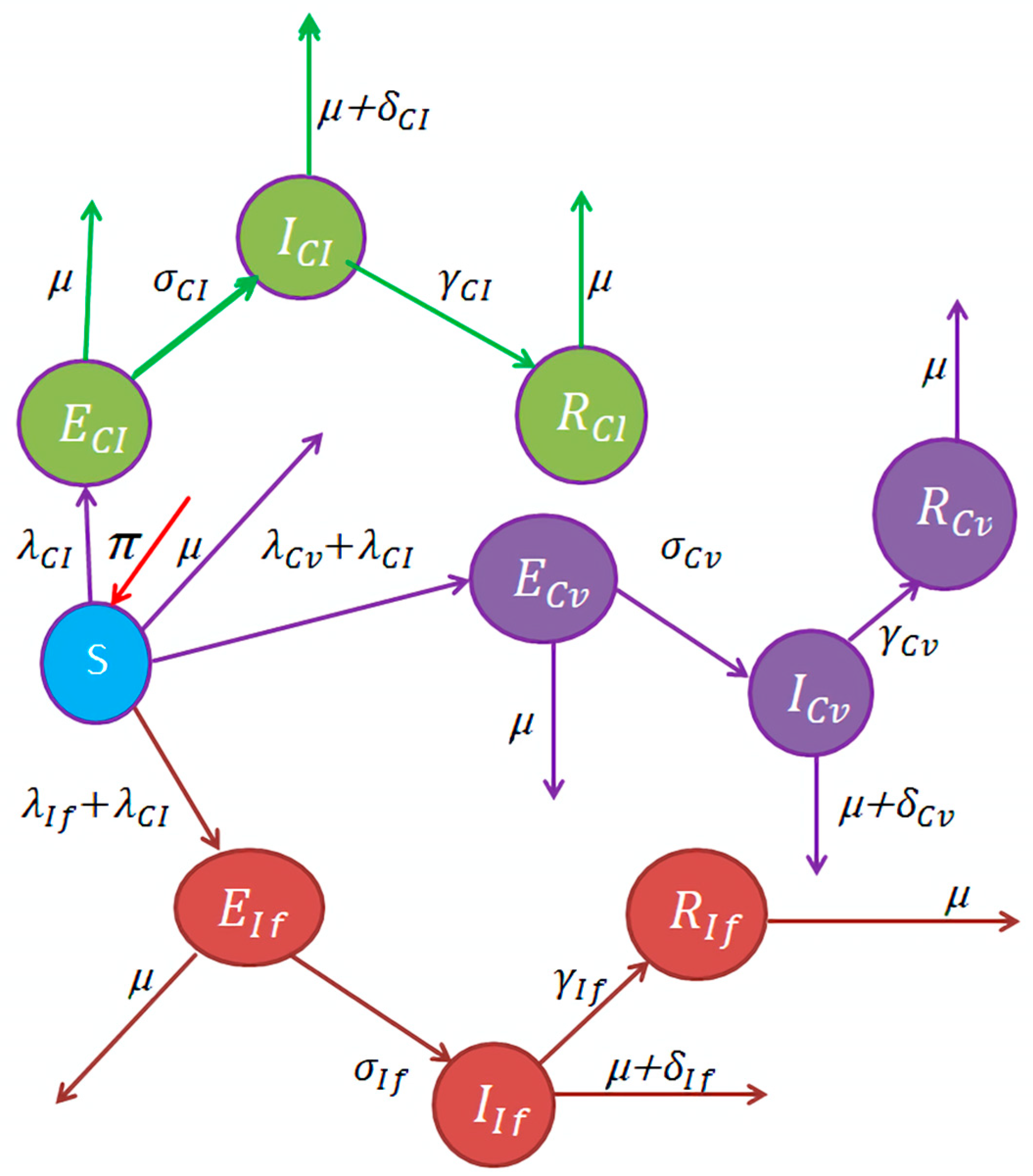
Variable	Explanation
S(t)	Vulnerable human population.
$E_{Cv}$(t)	Human population exposed to COVID-19 only.
$E_{If}$(t)	Individuals exposed to Influenza only.
$E_{CI}$(t)	Individuals exposed to COVID-19 and Influenza [4].
$I_{Cv}\left(t\right)$	Individuals infected with COVID-19 [4].
$I_{If}\left(t\right)$	Infectious individuals affected by Influenza [4].
$I_{CI}(t)$	Infectious individuals affected by COVID-19 and Influenza [4].
$R_{Cv}(t)$	Individuals recovered from COVID-19 [4].
$R_{If}$(t)	Individuals recovered from Influenza [4].
$R_{CI}$(t)	Individuals recovered from both COVID-19 and Influenza [4].

and

Table 2. Explanation of model parameters.

Parameters	Explanations	Specifications
Π	Susceptible individual’s entering rate	1.2 × ${10}^4\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{d}\mathrm{a}\mathrm{y}$ [4,19]
${\beta }_{Cv}$	COVID-19’s transmission rate	0.224334/day [19]
${\mathsf{\beta }}_{If}$	Influenza’s transmission rate	0.203 [20]
${\sigma }_{Cv}$	The progression rate of COVID-19 from the exposed to others [4]	0.40 [19]
${\sigma }_{If}$	The progression rate of Influenza from the exposed to others [4]	0.40 [22]
${\sigma }_{CI}$	The progression rate of infections caused by both (co-infection) from the exposed to others [4]	0.40 Assumed
μ	Natural mortality rate	0.0003516 [19]
${\delta }_{Cv}$	Death due to COVID-19	0.000573 per day [19]
${\delta }_{If}$	Death due to Influenza	0.021 [21]
${\delta }_{CI}$	Death due to co-infection	0.021–0.026 assumed
${\gamma }_{Cv}$	Rate of recovery from COVID-19	0.125 [19]
${\gamma }_{If}$	Influenza infectious individuals’ recovery rate	0.1998 [21]
${\gamma }_{cf}$	Co-infected infectious individuals’ recovery rate	0.125–0.1998 assumed

, and the process diagram is depicted in Figure 1.

2.3. Model Analysis—Stability Analysis and Equilibria [16,29]

To determine the dynamics of COVID-19 and Influenza transmission in a population, qualitative analysis is conducted in this section. This involves proving the stability and existence of steady-state solutions as well as computing the threshold values. To achieve this, we investigate the COVID-19-only and Influenza-only sub-models before presenting a more generalized result from the co-infection model.

Reproduction Number [18]

The average number of secondary cases produced by a typical infectious individual within a population lacking immunity is the basic reproduction number. The symbol for it is $R_0$ [17]. Research has demonstrated that $R_0$ may be mathematically described as virus transmission as in a “demographic process”, in which having children is not perceived as having children in the traditional sense, but as spreading the virus through communication. We will refer to birth as an epidemiological birth.

The next-generation matrix (NGM) approach is used to calculate ${\mathrm{R}}_0$. The next-generation matrix is given by G = F$V^{-1}$, where F is the transmission part and V is the transition part, describing changes in state (elimination of mortality or immunity) [17]. If $R_0<1,$ the sickness disappears. The assumption is that the disease spreads among the susceptible population if $R_0$ > 1 [17].

Theorem 1

([18]). The disease-free equilibrium $P_0$ is locally asymptotically stable if $R_0$ < 1, and is unstable if $R_0$ > 1.

3. Fractional-Order Co-Infection SEIR (Co-Infection FO-SEIR) Model

We introduce the Caputo fractional-order co-infection SEIR model, which is the modification of the classical integer-order co-infection SEIR model presented in (2).

3.1. Fractional-Order Co-Infection SEIR Model (Co-Infection FO-SEIR)

The fractional-order co-infection SEIR model is obtained by replacing the classical derivative operator in (2) with the Caputo fractional derivative [30]:

$${}^{C}D^{q}S(t)=\mathsf{\pi }-(\mu +{\lambda }_{Cv}+{\lambda }_{If}+{\lambda }_{CI}+{\lambda }_{IC})S,$$

$${}^{C}D^q{E}_{Cv}(t)=({\lambda }_{Cv}+{\lambda }_{CI})S-({\sigma }_{Cv}+\mu )E_{Cv},$$

$${}^{C}D^q{I}_{Cv}(t)={\sigma }_{Cv}{E}_{Cv}-({\gamma }_{Cv}+\mu +{\delta }_{Cv})I_{Cv},$$

$${}^{C}D^q{R}_{Cv}{(t)=\gamma }_{Cv}{I}_{Cv}-\mu R_{Cv},$$

$${}^{C}D^q{E}_{If}(t)=({\lambda }_{If}+{\lambda }_{IC})S-({\sigma }_{If}+\mu )E_{If},$$

$${}^{C}D^q{I}_{If}(t)={\sigma }_{If}{E}_{If}-({\gamma }_{If}+\mu +{\delta }_{If})I_{If},$$

(3)

$${}^{C}D^q{R}_{If}(t)={\gamma }_{If}{I}_{If}-(\mu )R_{If},$$

$${}^{C}D^q{E}_{CI}(t)=({\lambda }_{CI}+{\lambda }_{IC})S-({\sigma }_{CI}+\mu )E_{CI},$$

$${}^{C}D^q{I}_{CI}(t)={\sigma }_{CI}{E}_{CI}-({\gamma }_{CI}+\mu +{\delta }_{CI})I_{CI},$$

$${}^{C}D^q{R}_{CI}(t)={\gamma }_{CI}{I}_{CI}-\mu R_{CI},$$

$${S(0)>0,E}_{Cv}(0)\ge 0,E_{If}(0)\ge 0,E_{CI}(0)\ge 0,I_{Cv}(0)\ge 0,I_{If}\left(0\right)\ge 0,I_{CI}\left(0\right)\ge 0R_{Cv}\left(0\right)\ge 0,$$

$$R_{If}(0)\ge 0,R_{CI}(0)\ge 0$$

The initial conditions remain the same as provided earlier.

3.2. Local Stability Analysis of COVID-19-Only Model

This section contains the potential fixed points for the COVID-19-only model. Disease (COVID-19)-free equilibrium (DFE) and endemic equilibrium (EE) are the two potential equilibrium points that are computed. Additionally, the next-generation approach and discourse of the stability at these equilibrium points are used to produce the fundamental reproduction number [16].

The COVID-19-only model’s flow diagram is depicted in Figure 2, and its corresponding equations are obtained by setting:

$$E_{If}=0,E_{CI}=0,{\mathrm{I}}_{\mathrm{I}\mathrm{f}}=0,I_{CI}=0,R_{If}=0,R_{CI}=0.$$

$${}^{C}D^{q}S(t)=\mathsf{\pi }-(\mathsf{\mu }+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{v}})\mathrm{S},$$

$${}^{C}D^q{E}_{Cv}(t)={\lambda }_{Cv}S-({\sigma }_{Cv}+\mu )E_{Cv},$$

(4)

$${}^{C}D^q{I}_{Cv}(t)={\sigma }_{Cv}{E}_{Cv}-({\gamma }_{Cv}+\mu +{\delta }_{Cv})I_{Cv},$$

$${}^{C}D^q{R}_{Cv}{(t)=\gamma }_{Cv}{I}_{Cv}-\mu R_{Cv}$$

The initial conditions are:

$$S\left(0\right)>0,E_{Cv}(0)\ge 0,I_{Cv}(0)\ge 0,R_{Cv}\left(0\right)\ge 0.$$

The equation yields the model’s steady-state solution.

3.2.1. Disease (COVID-19)-Free Equilibrium (DFE)

To compute the equilibrium point,

$${}^{C}D^{q}S(t)=0,{}^{C}D^q{E}_{Cv}(t)=0,{}^{C}D^q{I}_{Cv}(t)=0,{}^{C}D^q{R}_{Cv}\left(t\right)=0.$$

The system’s solution asymptotically approaches a population or equilibrium devoid of sickness when the disease eventually dies out [29].

$$S=\raisebox{1ex}{$\mathsf{\pi }$}\!\left/ \!\raisebox{-1ex}{$\mathsf{\mu }$}\right.,E_{Cv}=0,I_{Cv}=0,R_{Cv}=0.$$

$$\mathrm{DFE}{P}_{Cv0}=(\raisebox{1ex}{$\mathsf{\pi }$}\!\left/ \!\raisebox{-1ex}{$\mathsf{\mu }$}\right.,0,0,0)$$

Using Theorem 1, the (DFE) disease-free equilibrium ${PCv}_0$ is locally and asymptotically stable if $R_{CV}$ < 1, and is unstable if $R_{Cv}$> 1 [29].

3.2.2. Non-Negative Solution [15]

From the dynamics described by the system of Equation (4),

Let $R_{+}^4$=$\left\{x\mathsf{ϵ}{R}^4,x\ge 0\right\},$ and $x\left(t\right)={\left(S(t),E_{Cv}(t),I_{Cv}(t),R_{Cv}\left(t\right)\right)}^{\mathrm{T}}$ is positively invariant (non-negative solutions).

Using Theorem 1, we can state the following theorem for the COVID-19-only model:

Theorem 2.

The initial value problem stated by (4) has a unique solution, which stays in $R^4,x\ge 0$ [29].

Proof. 

The uniqueness and existence of (4)’s solution in (0,q). It is necessary to demonstrate the positive invariance of the domain ${\mathrm{R}}^4,\mathrm{x}\ge 0.$

$${}^{C}D^{q}S(t){|}_{\mathrm{s}=0}=\mathsf{\pi }\ge 0$$

$${}^{C}D^q{E}_{Cv}(t){|E_{Cv}}_{=0}={\lambda }_{Cv}S\ge 0$$

$${}^{C}D^q{I}_{Cv}(t){|}_{I_{Cv}=0}={\sigma }_{Cv}{E}_{Cv}\ge 0$$

$${}^{C}D^q{R}_{Cv}{(t){|}_{R_{Cv}=0}=\gamma }_{\mathrm{C}\mathrm{v}}{I}_{Cv}\ge 0$$

The non-negative solution satisfies the vector field points into $R_{+}^4$ [29]. □

3.2.3. Reproduction Number (COVID-19-Only Model)

The reproduction number (threshold quantity) for the COVID-19-only model is denoted by $R_{Cv}$. $R_{Cv}$ is computed by employing the next-generation matrix method. The next-generation matrix is given by $G_{Cv}$ = $F_{Cv}{V_{Cv}}^{-1}$. The Jacobian matrix of the new infection terms ($F_{Cv}$) and the remaining transfer terms ($V_{Cv}$) is obtained as

$$F_{Cv}=\left[\begin{array}{cc}0& {\mathsf{\beta }}_{\mathrm{C}\mathrm{v}}\\ 0& 0\end{array}\right]\mathrm{and}{V}_{Cv}=\left[\begin{array}{cc}{\sigma }_{Cv}+\mu & 0\\ -{\sigma }_{Cv}& {\delta }_{Cv}+\mu +{\gamma }_{Cv}\end{array}\right]$$

$$G_{Cv}=F_{Cv}{V_{Cv}}^{-1}$$

$$G_{Cv}=\left[\begin{array}{cc}\frac{{\beta }_{Cv}{\sigma }_{Cv}}{({\sigma }_{Cv}+\mu )({\delta }_{Cv}+\mu +{\gamma }_{Cv})}& \frac{{\beta }_{Cv}}{({\delta }_{Cv}+\mu +{\gamma }_{Cv})}\\ 0& 0\end{array}\right]$$

Therefore, the reproduction number of the COVID-19-only model is defined as the largest eigenvalue of $G_{Cv}$ = $F_{Cv}{V_{Cv}}^{-1},$ which is given by [4]

$$R_{Cv0}=\frac{{\beta }_{Cv}{\sigma }_{Cv}}{({\sigma }_{Cv}+\mu )({\delta }_{Cv}+\mu +{\gamma }_{Cv})}.$$

Using Theorem 1, the disease-free equilibrium $P_{Cv0}$ is locally asymptotically stable if $R_{Cv0}$ < 1 and unstable if $R_{Cv0}$ > 1 [29].

3.3. Local Stability Analysis of Influenza-Only Model

This section contains the potential fixed points for the Influenza-only model. Disease (Influenza)-free equilibrium (DFE) and endemic equilibrium (EE) are the two potential equilibrium points that are computed. Additionally, the next-generation approach and the stable local analysis of these equilibrium points are used to produce the fundamental reproduction number [16].

The Influenza-only sub-model flow diagram is depicted in Figure 3, and its corresponding equations are obtained by setting:

$${\mathrm{E}}_{\mathrm{C}\mathrm{v}}=0,{\mathrm{E}}_{\mathrm{C}\mathrm{I}}=0,{\mathrm{I}}_{\mathrm{C}\mathrm{v}}=0,{\mathrm{I}}_{\mathrm{C}\mathrm{I}}=0,{\mathrm{R}}_{\mathrm{C}\mathrm{v}}=0,{\mathrm{R}}_{\mathrm{C}\mathrm{I}}=0.$$

$${}^{C}D^q\mathrm{S}(\mathrm{t})=\mathsf{\pi }-(\mathsf{\mu }+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{f}})\mathrm{S},$$

$${}^{C}D^q{\mathrm{E}}_{\mathrm{I}\mathrm{f}}(\mathrm{t})={\mathsf{\lambda }}_{\mathrm{I}\mathrm{f}}\mathrm{S}-({\mathsf{\sigma }}_{\mathrm{I}\mathrm{f}}+\mathsf{\mu }){\mathrm{E}}_{\mathrm{I}\mathrm{f}},$$

(5)

$${}^{C}D^q{\mathrm{I}}_{\mathrm{I}\mathrm{f}}(\mathrm{t})={\mathsf{\sigma }}_{\mathrm{I}\mathrm{f}}{\mathrm{E}}_{\mathrm{I}\mathrm{f}}-({\mathsf{\gamma }}_{\mathrm{I}\mathrm{f}}+\mathsf{\mu }+{\mathsf{\delta }}_{\mathrm{I}\mathrm{f}}){\mathrm{I}}_{\mathrm{I}\mathrm{f}},$$

$${}^{C}D^q{\mathrm{R}}_{\mathrm{I}\mathrm{f}}(\mathrm{t})={\mathsf{\gamma }}_{\mathrm{I}\mathrm{f}}{\mathrm{I}}_{\mathrm{I}\mathrm{f}}-\mathsf{\mu }{\mathrm{R}}_{\mathrm{I}\mathrm{f}}$$

The initial conditions are:

$${\mathrm{S}\left(0\right)>0,\mathrm{E}}_{\mathrm{I}\mathrm{f}}(0)\ge 0,{\mathrm{I}}_{\mathrm{I}\mathrm{f}}(0)\ge 0,{\mathrm{R}}_{\mathrm{I}\mathrm{f}}\left(0\right)\ge 0.$$

3.3.1. Influenza-Free Equilibrium

To compute the equilibrium point,

$${}^{C}D^q\mathrm{S}(\mathrm{t})=0,{}^{C}D^q{\mathrm{E}}_{\mathrm{I}\mathrm{f}}(\mathrm{t})=0,{}^{C}D^q{\mathrm{I}}_{\mathrm{I}\mathrm{f}}(\mathrm{t})=0,{}^{C}D^q{\mathrm{R}}_{\mathrm{I}\mathrm{f}}\left(\mathrm{t}\right)=0$$

The system’s solution asymptotically approaches a population or equilibrium devoid of sickness when the disease eventually dies out [29].

$$\mathrm{S}=\raisebox{1ex}{$\mathsf{\pi }$}\!\left/ \!\raisebox{-1ex}{$\mathsf{\mu }$}\right.,{\mathrm{E}}_{\mathrm{I}\mathrm{f}}=0,{\mathrm{I}}_{\mathrm{I}\mathrm{f}}=0,{\mathrm{R}}_{\mathrm{I}\mathrm{f}}=0.$$

$$\mathrm{DFE}{P}_{If0}=(\raisebox{1ex}{$\mathsf{\pi }$}\!\left/ \!\raisebox{-1ex}{$\mathsf{\mu }$}\right.,0,0,0).$$

3.3.2. Non-Negative Solution [15]

From the dynamics described by the system of Equation (6),

Let $R_{+}^4$=$\left\{x\mathsf{ϵ}{R}^4,x\ge 0\right\},$ and $\mathrm{x}(\mathrm{t})={\left(\mathrm{S}(\mathrm{t}),{\mathrm{E}}_{\mathrm{I}\mathrm{f}}(\mathrm{t}),{\mathrm{I}}_{\mathrm{I}\mathrm{f}}(\mathrm{t}),{\mathrm{R}}_{\mathrm{I}\mathrm{f}}\left(\mathrm{t}\right)\right)}^{\mathrm{T}}$ is positively invariant (non-negative solutions).

Using Theorem 1, we can state the following theorem for the Influenza-only model.

Theorem 3.

There is a unique solution for the IVP (initial value problem) given by (5), and the solution remains in $R^4,x\ge 0$ [29].

Proof. 

The existence and uniqueness of solution (5) is in interval (0,q), and we need to show that the domain $R^4,x\ge 0$ is positively invariant.

Since

$${}^{C}D^q\mathrm{S}(\mathrm{t}){|}_{\mathrm{s}=0}=\mathsf{\pi }\ge 0,{}^{C}D^q{\mathrm{E}}_{\mathrm{I}\mathrm{f}}(\mathrm{t}){|}_{{\mathrm{E}}_{\mathrm{I}\mathrm{f}}=0}={\mathsf{\lambda }}_{\mathrm{I}\mathrm{f}}\mathrm{S}\ge 0$$

$${}^{C}D^q{\mathrm{I}}_{\mathrm{I}\mathrm{f}}(\mathrm{t})={\mathsf{\sigma }}_{\mathrm{I}\mathrm{f}}{\mathrm{E}}_{\mathrm{I}\mathrm{f}}0\ge ,{}^{C}D^q{\mathrm{R}}_{\mathrm{I}\mathrm{f}}(\mathrm{t})={\mathsf{\gamma }}_{\mathrm{I}\mathrm{f}}{\mathrm{I}}_{\mathrm{I}\mathrm{f}}\ge 0$$

(6)

The non-negative solution satisfies the vector field points into $R_{+}^4$ [29]. □

3.3.3. Reproductive Number

The next-generation matrix (NGM) approach is used to calculate ${\mathrm{R}}_{\mathrm{I}\mathrm{f}0}$.

The next-generation matrix (NGM) is given by ${\mathrm{G}}_{\mathrm{I}\mathrm{f}}$ = ${\mathrm{F}}_{\mathrm{I}\mathrm{f}}{{\mathrm{V}}_{\mathrm{I}\mathrm{f}}}^{-1}$.

$${\mathrm{F}}_{\mathrm{I}\mathrm{f}}=\left[\begin{array}{cc}0& {\mathsf{\beta }}_{\mathrm{I}\mathrm{f}}\\ 0& 0\end{array}\right]\mathrm{and}{\mathrm{V}}_{\mathrm{C}\mathrm{v}}=\left[\begin{array}{cc}{\mathsf{\sigma }}_{\mathrm{I}\mathrm{f}}+\mathsf{\mu }& 0\\ -{\mathsf{\sigma }}_{\mathrm{I}\mathrm{f}}& {\mathsf{\delta }}_{\mathrm{I}\mathrm{f}}+\mathsf{\mu }+{\mathsf{\gamma }}_{\mathrm{I}\mathrm{f}}\end{array}\right]$$

$${\mathrm{G}}_{\mathrm{I}\mathrm{f}}={\mathrm{F}}_{\mathrm{I}\mathrm{f}}{{\mathrm{V}}_{\mathrm{I}\mathrm{f}}}^{-1}$$

$${\mathrm{G}}_{\mathrm{I}\mathrm{f}}=\left[\begin{array}{cc}\frac{{\mathsf{\beta }}_{\mathrm{I}\mathrm{f}}{\mathsf{\sigma }}_{\mathrm{I}\mathrm{f}}}{({\mathsf{\sigma }}_{\mathrm{I}\mathrm{f}}+\mathsf{\mu })({\mathsf{\delta }}_{\mathrm{I}\mathrm{f}}+\mathsf{\mu }+{\mathsf{\gamma }}_{\mathrm{I}\mathrm{f}})}& \frac{{\mathsf{\beta }}_{\mathrm{I}\mathrm{f}}}{({\mathsf{\delta }}_{\mathrm{I}\mathrm{f}}+\mathsf{\mu }+{\mathsf{\gamma }}_{\mathrm{I}\mathrm{f}})}\\ 0& 0\end{array}\right]$$

Therefore, the reproduction number of the Influenza-only model (5) is defined as the highest eigenvalue of ${\mathrm{G}}_{\mathrm{I}\mathrm{f}}$ = ${\mathrm{F}}_{\mathrm{I}\mathrm{f}}{{\mathrm{V}}_{\mathrm{I}\mathrm{f}}}^{-1},$ given by

$${\mathrm{R}}_{\mathrm{I}\mathrm{f}0}=\frac{{\mathsf{\beta }}_{\mathrm{I}\mathrm{f}}{\mathsf{\sigma }}_{\mathrm{I}\mathrm{f}}}{({\mathsf{\sigma }}_{\mathrm{I}\mathrm{f}}+\mathsf{\mu })({\mathsf{\delta }}_{\mathrm{I}\mathrm{f}}+\mathsf{\mu }+{\mathsf{\gamma }}_{\mathrm{I}\mathrm{f}})}$$

Using Theorem 1, the disease-free equilibrium $P_{If0}$ is locally asymptotically stable if $R_{If0}$< 1 and unstable if $R_{If0}$> 1.

3.4. The Co-Infection SEIR Model of COVID-19 and Influenza

3.4.1. Disease (Co-Infection)-Free Equilibrium

To compute the equilibrium point,

$${}^{C}D^q\mathrm{S}(\mathrm{t})=0,{}^{C}D^q{\mathrm{E}}_{\mathrm{C}\mathrm{v}}(\mathrm{t})=0,{}^{C}D^q{\mathrm{I}}_{\mathrm{C}\mathrm{v}}(\mathrm{t})=0,{}^{C}D^q{\mathrm{R}}_{\mathrm{C}\mathrm{v}}\left(\mathrm{t}\right)=0$$

$${}^{C}D^q{\mathrm{E}}_{\mathrm{I}\mathrm{f}}(\mathrm{t})=0,{}^{C}D^q{\mathrm{I}}_{\mathrm{I}\mathrm{f}}(\mathrm{t})=0,{}^{C}D^q{\mathrm{R}}_{\mathrm{I}\mathrm{f}}\left(\mathrm{t}\right)=0,$$

$${}^{C}D^q{\mathrm{E}}_{\mathrm{C}\mathrm{I}}(\mathrm{t})=0,{}^{C}D^q{\mathrm{I}}_{\mathrm{C}\mathrm{I}}(\mathrm{t})=0,{}^{C}D^q{\mathrm{R}}_{\mathrm{C}\mathrm{I}}\left(\mathrm{t}\right)=0.$$

The system’s solution asymptotically approaches a population or equilibrium devoid of sickness when the disease eventually dies out [29]:

$$\mathrm{S}=\raisebox{1ex}{$\mathsf{\pi }$}\!\left/ \!\raisebox{-1ex}{$\mathsf{\mu }$}\right.,{\mathrm{E}}_{\mathrm{C}\mathrm{v}}=0,{\mathrm{I}}_{\mathrm{C}\mathrm{v}}=0,{\mathrm{R}}_{\mathrm{C}\mathrm{v}}=0,{\mathrm{E}}_{\mathrm{I}\mathrm{f}}=0,{\mathrm{I}}_{\mathrm{I}\mathrm{f}}=0,{\mathrm{R}}_{\mathrm{I}\mathrm{f}}=0,{\mathrm{E}}_{\mathrm{C}\mathrm{I}}=0,{\mathrm{I}}_{\mathrm{C}\mathrm{I}}=0,{\mathrm{R}}_{\mathrm{C}\mathrm{I}}=0.$$

$$\mathrm{DFE}{\mathrm{P}}_0=(\raisebox{1ex}{$\mathsf{\pi }$}\!\left/ \!\raisebox{-1ex}{$\mathsf{\mu }$}\right.0,0,0,0,0,0,0,0,0)$$

3.4.2. Non-Negative Solution

From the dynamics described by the system of Equation (3),

Let ${\mathit{R}}_{+}^{10}$=$\left\{\mathit{x}\mathit{ϵ}{\mathit{R}}^{10},\mathit{x}\ge 0\right\},$ and $\mathit{x}\left(\mathit{t}\right)$=${\left(\mathrm{S}\left(\mathrm{t}\right),{\mathrm{E}}_{\mathrm{C}\mathrm{v}}\left(\mathrm{t}\right),{\mathrm{I}}_{\mathrm{C}\mathrm{v}}\left(\mathrm{t}\right),{\mathrm{R}}_{\mathrm{C}\mathrm{v}}\left(\mathrm{t}\right),{\mathrm{E}}_{\mathrm{I}\mathrm{f}}\left(\mathrm{t}\right),{\mathrm{I}}_{\mathrm{I}\mathrm{f}}\left(\mathrm{t}\right),{\mathrm{R}}_{\mathrm{I}\mathrm{f}}\left(\mathrm{t}\right),{\mathrm{E}}_{\mathrm{C}\mathrm{I}}(\mathrm{t}),{\mathrm{I}}_{\mathrm{C}\mathrm{I}}(\mathrm{t}),{\mathrm{R}}_{\mathrm{C}\mathrm{I}}\left(\mathrm{t}\right)\right)}^{\mathrm{T}}$ is positively invariant (non-negative solutions).

Theorem 4.

There is a unique solution for the initial value problem given by (3), and the solution remains in $R^{10},x\ge 0$ [29].

Proof of Theorem 4.

The existence and uniqueness of the solution of (3) in (0, q) can be proven by similar argument as the per proof of Theorems 3 and 4; that is, the domain in $R^{10},x\ge 0$ is positively invariant. □

3.4.3. Reproductive Number for COVID-19 and Influenza [4]

The reproduction number of the co-infection model (2) is given by:

$$R_0=\max \{R_{Cv0},R_{If0}\}$$

where ${\mathrm{R}}_{\mathrm{C}\mathrm{v}0}$ is the computed reproduction number of COVID-19 and ${\mathrm{R}}_{\mathrm{I}\mathrm{f}0}$ is the computed reproduction number of Influenza [4].

Using Theorem 1, the disease-free equilibrium ${\mathrm{P}}_0$ is locally asymptotically stable if $R_0$ < 1 and unstable if $R_0$ > 1. The COVID-19–Influenza co-infection model (3) is therefore said to be well-posed, both mathematically and epidemiologically, in the feasible zone.

Also, for the parameters (Table 2) $R_{Cv0}$ = 1.622 and $R_{If0}$ = 14.87, $R_0$ = max {$R_{Cv0}$, $R_{If0}$} = 14.87. The disease-free equilibrium $P_0$ is locally asymptotically unstable, since $R_0$ > 1.

4. Numerical Simulations

4.1. Using LADM [14]

The basic idea of LADM is to apply the Laplace transformation to the fractional differential equation after assuming an infinite solution of the type $\mathrm{u}\left(\mathrm{t}\right)={\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{\mathrm{u}}_{\mathrm{n}}(\mathrm{t})$. After that, the nonlinear term is broken down into terms of Adomian polynomials, and a recursive iterative algorithm is created to determine the ${\mathrm{u}}^n$’s [31].

The present part is devoted to expound how to use the LADM to solve Equation (3). Taking Laplace transformation on either side of the model,

$$\mathrm{L}\left[\mathrm{S}(\mathrm{t})\right]=\mathrm{L}\left[\mathsf{\pi }-(\mathsf{\mu }+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{v}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{f}}+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{I}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{C}})\mathrm{S}\right],$$

$$\mathrm{L}\left[{\mathrm{E}}_{\mathrm{C}\mathrm{v}}(\mathrm{t})\right]=\mathrm{L}\left[({\mathsf{\lambda }}_{\mathrm{C}\mathrm{v}}+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{I}})\mathrm{S}-({\mathsf{\sigma }}_{\mathrm{C}\mathrm{v}}+\mathsf{\mu }){\mathrm{E}}_{\mathrm{C}\mathrm{v}}\right],$$

$$\mathrm{L}\left[{\mathrm{I}}_{\mathrm{C}\mathrm{v}}(\mathrm{t})\right]=\mathrm{L}\left[{\mathsf{\sigma }}_{\mathrm{C}\mathrm{v}}{\mathrm{E}}_{\mathrm{C}\mathrm{v}}-({\mathsf{\gamma }}_{\mathrm{C}\mathrm{v}}+\mathsf{\mu }+{\mathsf{\delta }}_{\mathrm{C}\mathrm{v}}){\mathrm{I}}_{\mathrm{C}\mathrm{v}}\right],$$

$$\mathrm{L}\left[{\mathrm{R}}_{\mathrm{C}\mathrm{v}}(\mathrm{t})\right]=\mathrm{L}\left[{\mathsf{\gamma }}_{\mathrm{C}\mathrm{v}}{\mathrm{I}}_{\mathrm{C}\mathrm{v}}-\mathsf{\mu }{\mathrm{R}}_{\mathrm{C}\mathrm{v}}\right],$$

$$\mathrm{L}\left[{\mathrm{E}}_{\mathrm{I}\mathrm{f}}(\mathrm{t})\right]=\mathrm{L}\left[({\mathsf{\lambda }}_{\mathrm{I}\mathrm{f}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{C}})\mathrm{S}-({\mathsf{\sigma }}_{\mathrm{I}\mathrm{f}}+\mathsf{\mu }){\mathrm{E}}_{\mathrm{I}\mathrm{f}}\right],$$

(7)

$$\mathrm{L}\left[{\mathrm{I}}_{\mathrm{I}\mathrm{f}}(\mathrm{t})\right]=\mathrm{L}\left[{\mathsf{\sigma }}_{\mathrm{I}\mathrm{f}}{\mathrm{E}}_{\mathrm{I}\mathrm{f}}-({\mathsf{\gamma }}_{\mathrm{I}\mathrm{f}}+\mathsf{\mu }+{\mathsf{\delta }}_{\mathrm{I}\mathrm{f}}){\mathrm{I}}_{\mathrm{I}\mathrm{f}}\right],$$

$$\mathrm{L}\left[{\mathrm{E}}_{\mathrm{C}\mathrm{I}}(\mathrm{t})\right]=\mathrm{L}\left[({\mathsf{\lambda }}_{\mathrm{C}\mathrm{I}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{C}})\mathrm{S}-({\mathsf{\sigma }}_{\mathrm{C}\mathrm{I}}+\mathsf{\mu }){\mathrm{E}}_{\mathrm{C}\mathrm{I}}\right],$$

$$\mathrm{L}\left[{\mathrm{I}}_{\mathrm{C}\mathrm{I}}(\mathrm{t})\right]=\mathrm{L}\left[{\mathsf{\sigma }}_{\mathrm{C}\mathrm{I}}{\mathrm{E}}_{\mathrm{C}\mathrm{I}}-({\mathsf{\gamma }}_{\mathrm{C}\mathrm{I}}+\mathsf{\mu }+{\mathsf{\delta }}_{\mathrm{C}\mathrm{I}}){\mathrm{I}}_{\mathrm{C}\mathrm{I}}\right],$$

$$\mathrm{L}\left[{\mathrm{R}}_{\mathrm{C}\mathrm{I}}(\mathrm{t})\right]=\mathrm{L}\left[{\mathsf{\gamma }}_{\mathrm{C}\mathrm{I}}{\mathrm{I}}_{\mathrm{C}\mathrm{I}}-\mathsf{\mu }{\mathrm{R}}_{\mathrm{C}\mathrm{I}}\right].$$

Expressing the solutions as an infinite series,

$$\mathrm{S}\left(\mathrm{t}\right)={\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{\mathrm{S}}_{\mathrm{n}}(\mathrm{t}),{\mathrm{E}}_{\mathrm{C}\mathrm{v}}(\mathrm{t})={\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{E}}_{\mathrm{C}\mathrm{v}}}_{\mathrm{n}}(\mathrm{t}),{\mathrm{E}}_{\mathrm{I}\mathrm{f}}(\mathrm{t})={\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{E}}_{\mathrm{I}\mathrm{f}}}_{\mathrm{n}}(\mathrm{t}),$$

$${\mathrm{E}}_{\mathrm{C}\mathrm{I}}(\mathrm{t})={\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{E}}_{\mathrm{C}\mathrm{I}}}_{\mathrm{n}}\left(\mathrm{t}\right),{\mathrm{I}}_{\mathrm{C}\mathrm{v}}\left(\mathrm{t}\right)={\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{I}}_{\mathrm{C}\mathrm{v}}}_{\mathrm{n}}\left(\mathrm{t}\right),$$

$${\mathrm{I}}_{\mathrm{I}\mathrm{f}}\left(\mathrm{t}\right)={\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{I}}_{\mathrm{I}\mathrm{f}}}_{\mathrm{n}}\left(\mathrm{t}\right),{\mathrm{I}}_{\mathrm{C}\mathrm{I}}\left(\mathrm{t}\right)={\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{I}}_{\mathrm{C}\mathrm{I}}}_{\mathrm{n}}(\mathrm{t}),{\mathrm{R}}_{\mathrm{C}\mathrm{v}}\left(\mathrm{t}\right)={\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{R}}_{\mathrm{C}\mathrm{v}}}_{\mathrm{n}}(\mathrm{t}),$$

(8)

$${\mathrm{R}}_{\mathrm{I}\mathrm{f}}(\mathrm{t})={\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{R}}_{\mathrm{I}\mathrm{f}}}_{\mathrm{n}}(\mathrm{t}),{\mathrm{R}}_{\mathrm{C}\mathrm{I}}(\mathrm{t})={\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{R}}_{\mathrm{C}\mathrm{I}}}_{\mathrm{n}}(\mathrm{t})$$

Substituting initial conditions and the infinite series (8) into Equation (7), we have

$$\mathrm{L}\left[{\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{\mathrm{S}}_{\mathrm{n}}(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}\mathrm{L}\left[\mathsf{\pi }-(\mathsf{\mu }+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{v}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{f}}+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{I}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{C}}){\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{\mathrm{S}}_{\mathrm{n}}(\mathrm{t})\right],$$

$$\mathrm{L}\left[{\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{E}}_{\mathrm{C}\mathrm{v}}}_{\mathrm{n}}(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}\mathrm{L}\left[({\mathsf{\lambda }}_{\mathrm{C}\mathrm{v}}+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{I}}){\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{\mathrm{S}}_{\mathrm{n}}(\mathrm{t})-({\mathsf{\sigma }}_{\mathrm{C}\mathrm{v}}+\mathsf{\mu }){\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{E}}_{\mathrm{C}\mathrm{v}}}_{\mathrm{n}}(\mathrm{t})\right],$$

$$\mathrm{L}\left[{\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{I}}_{\mathrm{C}\mathrm{v}}}_{\mathrm{n}}(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}\mathrm{L}\left[{\mathsf{\sigma }}_{\mathrm{C}\mathrm{v}}{\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{E}}_{\mathrm{C}\mathrm{v}}}_{\mathrm{n}}(\mathrm{t})-({\mathsf{\gamma }}_{\mathrm{C}\mathrm{v}}+\mathsf{\mu }+{\mathsf{\delta }}_{\mathrm{C}\mathrm{v}}){\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{I}}_{\mathrm{C}\mathrm{v}}}_{\mathrm{n}}(\mathrm{t})\right],$$

$$\mathrm{L}\left[{\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{R}}_{\mathrm{C}\mathrm{v}}}_{\mathrm{n}}(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}\mathrm{L}\left[{\mathsf{\gamma }}_{\mathrm{C}\mathrm{v}}{\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{I}}_{\mathrm{C}\mathrm{v}}}_{\mathrm{n}}(\mathrm{t})-\mathsf{\mu }{\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{R}}_{\mathrm{C}\mathrm{v}}}_{\mathrm{n}}(\mathrm{t})\right],$$

$$\mathrm{L}\left[{\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{E}}_{\mathrm{I}\mathrm{f}}}_{\mathrm{n}}(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}\mathrm{L}\left[({\mathsf{\lambda }}_{\mathrm{I}\mathrm{f}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{C}}){\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{\mathrm{S}}_{\mathrm{n}}(\mathrm{t})-({\mathsf{\sigma }}_{\mathrm{I}\mathrm{f}}+\mathsf{\mu }){\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{E}}_{\mathrm{I}\mathrm{f}}}_{\mathrm{n}}(\mathrm{t})\right],$$

(9)

$$\mathrm{L}\left[{\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{I}}_{\mathrm{I}\mathrm{f}}}_{\mathrm{n}}(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}\mathrm{L}\left[{\mathsf{\sigma }}_{\mathrm{I}\mathrm{f}}{\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{E}}_{\mathrm{I}\mathrm{f}}}_{\mathrm{n}}(\mathrm{t})-({\mathsf{\gamma }}_{\mathrm{I}\mathrm{f}}+\mathsf{\mu }+{\mathsf{\delta }}_{\mathrm{I}\mathrm{f}}){\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{I}}_{\mathrm{I}\mathrm{f}}}_{\mathrm{n}}(\mathrm{t})\right],$$

$$\mathrm{L}\left[{\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{R}}_{\mathrm{I}\mathrm{f}}}_{\mathrm{n}}(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}\mathrm{L}\left[{\mathsf{\gamma }}_{\mathrm{I}\mathrm{f}}{\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{I}}_{\mathrm{I}\mathrm{f}}}_{\mathrm{n}}(\mathrm{t})-(\mathsf{\mu }){\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{R}}_{\mathrm{I}\mathrm{f}}}_{\mathrm{n}}(\mathrm{t})\right],$$

$$\mathrm{L}\left[{\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{E}}_{\mathrm{C}\mathrm{I}}}_{\mathrm{n}}(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}\mathrm{L}\left[({\mathsf{\lambda }}_{\mathrm{C}\mathrm{I}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{C}}){\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{\mathrm{S}}_{\mathrm{n}}(\mathrm{t})-({\mathsf{\sigma }}_{\mathrm{C}\mathrm{I}}+\mathsf{\mu }){\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{E}}_{\mathrm{C}\mathrm{I}}}_{\mathrm{n}}(\mathrm{t})\right],$$

$$\mathrm{L}\left[{\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{I}}_{\mathrm{C}\mathrm{I}}}_{\mathrm{n}}(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}\mathrm{L}\left[{\mathsf{\sigma }}_{\mathrm{C}\mathrm{I}}{\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{E}}_{\mathrm{C}\mathrm{I}}}_{\mathrm{n}}(\mathrm{t})-({\mathsf{\gamma }}_{\mathrm{C}\mathrm{I}}+\mathsf{\mu }+{\mathsf{\delta }}_{\mathrm{C}\mathrm{I}}){\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{I}}_{\mathrm{C}\mathrm{I}}}_{\mathrm{n}}(\mathrm{t})\right],$$

$$\mathrm{L}\left[{\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{R}}_{\mathrm{C}\mathrm{I}}}_{\mathrm{n}}(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}\mathrm{L}\left[{\mathsf{\gamma }}_{\mathrm{C}\mathrm{I}}{\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{I}}_{\mathrm{C}\mathrm{I}}}_{\mathrm{n}}(\mathrm{t})-\mathsf{\mu }{\sum }_{\mathrm{n}=0}^{\mathrm{\infty }}{{\mathrm{R}}_{\mathrm{C}\mathrm{I}}}_{\mathrm{n}}(\mathrm{t})\right].$$

Equating the terms on either side of Equation (9), we can obtain the following iterative algorithm:

$$\left\{\begin{array}{c}\mathrm{L}\left[S_0\left(t\right)\right]=\frac{\pi }{s^{q+1}},\\ \mathrm{L}\left[S_1\left(t\right)\right]=\frac{-\mathsf{\pi }\left(\mathsf{\mu }+{\lambda }_{Cv}+{\lambda }_{If}+{\lambda }_{CI}+{\lambda }_{IC}\right)}{s^q}\mathrm{L}\left[S_0\left(t\right)\right],\\ \mathrm{L}\left[S_2\left(t\right)\right]=\frac{-\mathsf{\pi }\left(\mathsf{\mu }+{\lambda }_{Cv}+{\lambda }_{If}+{\lambda }_{CI}+{\lambda }_{IC}\right)}{s^q}\mathrm{L}\left[S_1\left(t\right)\right],\\ \dots \\ \mathrm{L}\left[S_{n+1}\left(t\right)\right]=\frac{-\mathsf{\pi }\left(\mathsf{\mu }+{\lambda }_{Cv}+{\lambda }_{If}+{\lambda }_{CI}+{\lambda }_{IC}\right)}{s^q}\mathrm{L}\left[S_n\left(t\right)\right].\end{array}\right.\left\{\begin{array}{c}\mathrm{L}\left[{E_{Cv}}_0\left(t\right)\right]=0,\\ \mathrm{L}\left[{E_{Cv}}_1(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[({\lambda }_{Cv}+{\lambda }_{CI})S_0(t)-({\sigma }_{Cv}+\mu ){E_{Cv}}_0(\mathrm{t})\right],\\ \mathrm{L}\left[{E_{Cv}}_2(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[({\lambda }_{Cv}+{\lambda }_{CI})S_1(t)-({\sigma }_{Cv}+\mu ){E_{Cv}}_1(\mathrm{t})\right],\\ \dots \\ \mathrm{L}\left[{E_{Cv}}_{\mathrm{n}+1}(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[({\lambda }_{Cv}+{\lambda }_{CI})S_n(t)-({\sigma }_{Cv}+\mu ){E_{Cv}}_{\mathrm{n}}(\mathrm{t})\right].\end{array}\right.$$

$$\left\{\begin{array}{c}\mathrm{L}\left[{I_{Cv}}_0\left(t\right)\right]=0,\\ \mathrm{L}\left[{I_{Cv}}_1(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[{\sigma }_{Cv}{E_{Cv}}_0(\mathrm{t})-({\gamma }_{Cv}+\mu +{\delta }_{Cv}){I_{Cv}}_0(\mathrm{t})\right],\\ \mathrm{L}\left[{I_{Cv}}_2(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[{\sigma }_{Cv}{E_{Cv}}_1(\mathrm{t})-({\gamma }_{Cv}+\mu +{\delta }_{Cv}){I_{Cv}}_1(\mathrm{t})\right],\\ \dots \\ \mathrm{L}\left[{I_{Cv}}_{\mathrm{n}+1}(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[{\sigma }_{Cv}{E_{Cv}}_{\mathrm{n}}(\mathrm{t})-({\gamma }_{Cv}+\mu +{\delta }_{Cv}){I_{Cv}}_{\mathrm{n}}(\mathrm{t})\right].\end{array}\right.\left\{\begin{array}{c}\mathrm{L}\left[{R_{Cv}}_0\left(t\right)\right]=0,\\ \mathrm{L}\left[{R_{Cv}}_1(\mathrm{t})\right]=\frac{1}{s^q}L\left[{\gamma }_{Cv}{I_{Cv}}_0(\mathrm{t})-\mu {R_{Cv}}_0(\mathrm{t})\right],\\ \mathrm{L}\left[{R_{Cv}}_2(\mathrm{t})\right]=\frac{1}{s^q}L\left[{\gamma }_{Cv}{I_{Cv}}_1(\mathrm{t})-\mu {R_{Cv}}_1(\mathrm{t})\right],\\ \dots \\ \mathrm{L}\left[{R_{Cv}}_{\mathrm{n}+1}(\mathrm{t})\right]=\frac{1}{s^q}L\left[{\gamma }_{Cv}{I_{Cv}}_{\mathrm{n}}(\mathrm{t})-\mu {R_{Cv}}_{\mathrm{n}}(\mathrm{t})\right].\end{array}\right.$$

$$\left\{\begin{array}{c}\mathrm{L}\left[{E_{If}}_0\left(t\right)\right]=0,\\ \mathrm{L}\left[{E_{If}}_1(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[({\lambda }_{If}+{\lambda }_{CI})S_0(t)-({\sigma }_{If}+\mu ){E_{If}}_0(\mathrm{t})\right],\\ \mathrm{L}\left[{E_{If}}_2(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[({\lambda }_{If}+{\lambda }_{CI})S_1(t)-({\sigma }_{If}+\mu ){E_{If}}_1(\mathrm{t})\right],\\ \dots \\ \mathrm{L}\left[{E_{If}}_{\mathrm{n}+1}(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[({\lambda }_{If}+{\lambda }_{IC})S_n(t)-({\sigma }_{If}+\mu ){E_{If}}_{\mathrm{n}}(\mathrm{t})\right].\end{array}\right.\left\{\begin{array}{c}\mathrm{L}\left[{I_{If}}_0\left(t\right)\right]=0,\\ \mathrm{L}\left[{I_{If}}_1(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[{\sigma }_{If}{E_{If}}_0(\mathrm{t})-({\gamma }_{If}+\mu +{\delta }_{If}){I_{If}}_0(\mathrm{t})\right],\\ \mathrm{L}\left[{I_{If}}_2(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[{\sigma }_{If}{E_{If}}_1(\mathrm{t})-({\gamma }_{If}+\mu +{\delta }_{If}){I_{If}}_1(\mathrm{t})\right],\\ \dots \\ \mathrm{L}\left[{I_{If}}_{\mathrm{n}+1}(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[{\sigma }_{If}{E_{If}}_{\mathrm{n}}(\mathrm{t})-({\gamma }_{If}+\mu +{\delta }_{If}){I_{If}}_{\mathrm{n}}(\mathrm{t})\right].\end{array}\right.$$

(10)

$$\left\{\begin{array}{c}\mathrm{L}\left[{R_{If}}_0\left(t\right)\right]=0,\\ \mathrm{L}\left[{R_{If}}_1(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[{\gamma }_{If}{I_{If}}_0(\mathrm{t})-(\mu ){R_{If}}_0(\mathrm{t})\right],\\ \mathrm{L}\left[{R_{If}}_2(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[{\gamma }_{If}{I_{If}}_1(\mathrm{t})-(\mu ){R_{If}}_1(\mathrm{t})\right],\\ \dots \\ \mathrm{L}\left[{R_{If}}_{\mathrm{n}+1}(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[{\gamma }_{If}{I_{If}}_{\mathrm{n}}(\mathrm{t})-(\mu ){R_{If}}_{\mathrm{n}}(\mathrm{t})\right].\end{array}\right.\left\{\begin{array}{c}\mathrm{L}\left[{E_{CI}}_0(\mathrm{t})\right]=0,\\ \mathrm{L}\left[{E_{CI}}_1(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[({\lambda }_{CI}+{\lambda }_{IC})S_0(t)-({\sigma }_{CI}+\mu ){E_{CI}}_0(\mathrm{t})\right],\\ \mathrm{L}\left[{E_{CI}}_2(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[({\lambda }_{CI}+{\lambda }_{IC})S_1(t)-({\sigma }_{CI}+\mu ){E_{CI}}_1(\mathrm{t})\right],\\ \dots \\ \mathrm{L}\left[{E_{CI}}_{\mathrm{n}+1}(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[({\lambda }_{CI}+{\lambda }_{IC})S_n(t)-({\sigma }_{CI}+\mu ){E_{CI}}_{\mathrm{n}}(\mathrm{t})\right].\end{array}\right.$$

$$\left\{\begin{array}{c}\mathrm{L}\left[{I_{CI}}_0(\mathrm{t})\right]=0,\\ \mathrm{L}\left[{I_{CI}}_1(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[{\sigma }_{CI}{E_{CI}}_0(t)-({\gamma }_{CI}+\mu +{\delta }_{CI}){I_{CI}}_0(\mathrm{t})\right],\\ \mathrm{L}\left[{I_{CI}}_2(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[{\sigma }_{CI}{E_{CI}}_1(t)-({\gamma }_{CI}+\mu +{\delta }_{CI}){I_{CI}}_1(\mathrm{t})\right],\\ \dots \\ \mathrm{L}\left[{I_{CI}}_{\mathrm{n}+1}(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[{\sigma }_{CI}{E_{CI}}_{\mathrm{n}}(t)-({\gamma }_{CI}+\mu +{\delta }_{CI}){I_{CI}}_{\mathrm{n}}(\mathrm{t})\right].\end{array}\right.\left\{\begin{array}{c}\mathrm{L}\left[{R_{CI}}_0(\mathrm{t})\right]=0,\\ \mathrm{L}\left[{R_{CI}}_1(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[{\gamma }_{CI}{I_{CI}}_0(\mathrm{t})-\mu {R_{CI}}_0(\mathrm{t})\right],\\ \mathrm{L}\left[{R_{CI}}_2(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[{\gamma }_{CI}{I_{CI}}_1(\mathrm{t})-\mu {R_{CI}}_1(\mathrm{t})\right],\\ \dots \\ \mathrm{L}\left[{R_{CI}}_{\mathrm{n}+1}(\mathrm{t})\right]=\frac{1}{{\mathrm{s}}^{\mathrm{q}}}L\left[{\gamma }_{CI}{I_{CI}}_{\mathrm{n}}(\mathrm{t})-\mu {R_{CI}}_{\mathrm{n}}(\mathrm{t})\right].\end{array}\right.$$

Using inverse Laplace transform for first three terms of each equation:

$$\left\{\begin{array}{c}{S}_0\left(t\right)=\frac{\pi t^q}{\Gamma (q+1)},\\ {\mathrm{S}}_1\left(\mathrm{t}\right)=\frac{-{\mathsf{\pi }}^2(\mathsf{\mu }+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{v}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{f}}+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{I}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{C}})t^{2\mathrm{q}}}{\Gamma (2q+1)},\\ S_2\left(t\right)=\frac{{\mathsf{\pi }}^3{\left(\mathsf{\mu }+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{v}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{f}}+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{I}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{C}}\right)}^2{t}^{3\mathrm{q}}}{\Gamma (3q+1)},\\ \dots \end{array}\right.\left\{\begin{array}{c}{E_{Cv}}_0\left(t\right)=0,\\ E_{Cv1}\left(\mathrm{t}\right)=\frac{\pi ({\mathsf{\lambda }}_{\mathrm{C}\mathrm{v}}+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{I}})t^{2\mathrm{q}}}{\Gamma (2q+1)},\\ {E_{Cv}}_2(t)=\frac{-\pi ({\mathsf{\lambda }}_{\mathrm{C}\mathrm{v}}+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{I}})t^{3\mathrm{q}}[\pi \left(\mathsf{\mu }+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{v}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{f}}+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{I}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{C}}\right)+\left({\sigma }_{Cv}+\mathsf{\mu }\right)]}{\Gamma (3q+1)},\\ \dots \end{array}\right.$$

$$\left\{\begin{array}{c}{I_{Cv}}_0\left(t\right)=0,\\ I_{Cv1}\left(\mathrm{t}\right)=0,\\ I_{Cv2}\left(\mathrm{t}\right)=\frac{\pi {\sigma }_{Cv}({\mathsf{\lambda }}_{\mathrm{C}\mathrm{v}}+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{I}})t^{3\mathrm{q}}}{\Gamma (3q+1)},\\ \dots \end{array}\right.\left\{\begin{array}{c}{R_{Cv}}_0\left(t\right)=0,\\ R_{Cv1}\left(\mathrm{t}\right)=0,\\ R_{Cv2}\left(\mathrm{t}\right)=0\\ R_{Cv3}\left(\mathrm{t}\right)=\frac{\pi {\gamma }_{Cv}({\mathsf{\lambda }}_{\mathrm{C}\mathrm{v}}+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{I}})t^{4\mathrm{q}}}{\Gamma (4q+1)}\\ \dots \end{array}\right.,\left\{\begin{array}{c}{E_{If}}_0\left(t\right)=0,\\ E_{If1}\left(\mathrm{t}\right)=\frac{\pi ({\lambda }_{If}+{\lambda }_{IC})t^{2\mathrm{q}}}{\Gamma (2q+1)},\\ {E_{If}}_2(t)=\frac{-\pi ({\mathsf{\lambda }}_{\mathrm{I}\mathrm{f}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{C}})[\pi \left(\mathsf{\mu }+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{v}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{f}}+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{I}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{C}}\right)+\left({\sigma }_{If}+\mathsf{\mu }\right)]t^{3\mathrm{q}}}{\Gamma (3q+1)},\\ \dots \end{array}\right.$$

(11)

$$\left\{\begin{array}{c}{I_{If}}_0\left(t\right)=0,\\ I_{If1}\left(\mathrm{t}\right)=0,\\ {I_{If}}_2(t)=\frac{\pi {\sigma }_{If}({\mathsf{\lambda }}_{\mathrm{I}\mathrm{f}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{C}})]t^{3\mathrm{q}}}{\Gamma (3q+1)},\\ \dots \end{array}\right.\left\{\begin{array}{c}{R_{If}}_0\left(t\right)=0,\\ R_{If1}\left(\mathrm{t}\right)=0,\\ R_{If2}\left(\mathrm{t}\right)=0\\ {R_{If}}_3(t)=\frac{\pi {{\gamma }_{If}\sigma }_{If}({\mathsf{\lambda }}_{\mathrm{I}\mathrm{f}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{C}})]t^{4\mathrm{q}}}{\Gamma (4q+1)},\\ \dots \end{array}\right.\left\{\begin{array}{c}{E_{CI}}_0\left(t\right)=0,\\ E_{CI1}\left(\mathrm{t}\right)=\frac{\pi ({\lambda }_{CI}+{\lambda }_{IC})t^{2\mathrm{q}}}{\Gamma (2q+1)},\\ {E_{CI}}_2(t)=\frac{-\pi ({\mathsf{\lambda }}_{CI}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{C}})[\pi \left(\mathsf{\mu }+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{v}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{f}}+{\mathsf{\lambda }}_{\mathrm{C}\mathrm{I}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{C}}\right)+\left({\sigma }_{CI}+\mathsf{\mu }\right)]t^{3\mathrm{q}}}{\Gamma (3q+1)},\\ \dots \end{array}\right.$$

$$\left\{\begin{array}{c}{I_{CI}}_0\left(t\right)=0,\\ I_{CI1}\left(\mathrm{t}\right)=0,\\ {I_{CI}}_2\left(\mathrm{t}\right)=\frac{\pi {\sigma }_{CI}({\mathsf{\lambda }}_{\mathrm{C}\mathrm{I}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{C}})]t^{3\mathrm{q}}}{\Gamma (3q+1)},\\ \dots \end{array}\right.\left\{\begin{array}{c}{R_{CI}}_0\left(t\right)=0,\\ R_{CI1}\left(\mathrm{t}\right)=0,\\ R_{CI2}\left(\mathrm{t}\right)=0\\ {R_{CI}}_3\left(\mathrm{t}\right)=\frac{\pi {{\gamma }_{CI}\sigma }_{CI}({\mathsf{\lambda }}_{\mathrm{C}\mathrm{I}}+{\mathsf{\lambda }}_{\mathrm{I}\mathrm{C}})]t^{4\mathrm{q}}}{\Gamma (4q+1)}.\\ \dots \end{array}\right.$$

When all the terms are calculated, the precise answer can be found. We find the few initial finite terms. Cherruault et al. [32,33] have shown that the Adomian decomposition approach converges, and the first three or four terms combined together have a high degree of accuracy. When we include more terms in the computations, the accuracy improves [24]. To approximate the exact solution, we simply need the first few terms; to obtain the values of S, ${\mathrm{E}}_{\mathrm{C}\mathrm{v}}$, ${\mathrm{I}}_{\mathrm{C}\mathrm{v}}$, ${\mathrm{R}}_{\mathrm{C}\mathrm{v}}$, ${\mathrm{E}}_{\mathrm{I}\mathrm{f}}$, ${\mathrm{I}}_{\mathrm{I}\mathrm{f}}$, ${\mathrm{R}}_{\mathrm{I}\mathrm{f}}$, ${\mathrm{E}}_{\mathrm{C}\mathrm{I}}$, ${\mathrm{I}}_{\mathrm{C}\mathrm{I}}$, and ${\mathrm{R}}_{\mathrm{C}\mathrm{I}}$ for a different fractional order q, the respective terms of equation (11) are added, and the numerical result is quite precise. Due to the nonlinear variables, some differential equations can be challenging to solve. This approach does not require linearization or perturbation [10].

4.2. Graphical Analysis Using LADM

In this part, we will use the parameters given in the Table 2. Considering first few (3 or 4) terms from the above Equation (11), we can compare the graph of S, ${\mathrm{E}}_{\mathrm{C}\mathrm{v}}$, ${\mathrm{I}}_{\mathrm{C}\mathrm{v}}$, ${\mathrm{R}}_{\mathrm{C}\mathrm{v}}$, ${\mathrm{E}}_{\mathrm{I}\mathrm{f}}$, ${\mathrm{I}}_{\mathrm{I}\mathrm{f}}$, ${\mathrm{R}}_{\mathrm{I}\mathrm{f}}$, ${\mathrm{E}}_{\mathrm{C}\mathrm{I}}$, ${\mathrm{I}}_{\mathrm{C}\mathrm{I}}$, and ${\mathrm{R}}_{\mathrm{C}\mathrm{I}}$ for a different fractional order q (Figure 4).

5. Conclusions

Fractional differential equations are essential in many fields of science and engineering because they offer a strong mathematical foundation for simulating complicated processes with memory, non-locality, and anomalous behavior. Co-infection models provide important insights into the complex interactions between many pathogens and their consequences for disease control, treatment, and public health policy. These insights are particularly important in epidemiology, where understanding and treating infectious illnesses is critical. These models outperform traditional ones by exposing subtle patterns in co-infection dynamics, which helps with the creation of complex disease control plans like immunization and therapy schedules. Sensitivity analysis identifies important factors influencing co-infection dynamics, which helps to direct future studies and data collection initiatives. Comparative evaluations show that fractional calculus may perform better than integer-order models when used to simulate biological systems. In summary, fractional-order models play a critical role in influencing public health responses and minimizing the impact of outbreaks, underscoring their value in understanding and managing infectious illnesses. This work aims at constructing a fractional-order co-infection SEIR model using the Caputo derivative to observe the variations in the behavior of S, ${\mathrm{E}}_{\mathrm{C}\mathrm{v}}$, ${\mathrm{I}}_{\mathrm{C}\mathrm{v}}$, ${\mathrm{R}}_{\mathrm{C}\mathrm{v}}$, ${\mathrm{E}}_{\mathrm{I}\mathrm{f}}$, ${\mathrm{I}}_{\mathrm{I}\mathrm{f}}$, ${\mathrm{R}}_{\mathrm{I}\mathrm{f}}$, ${\mathrm{E}}_{\mathrm{C}\mathrm{I}}$, ${\mathrm{I}}_{\mathrm{C}\mathrm{I}}$, and ${\mathrm{R}}_{\mathrm{C}\mathrm{I}}$ for a different fractional order q, which is depicted in the graphs. In future work, the derivatives can be changed to Atangana–Baleanu derivatives, and in addition, the number of compartments can be increased, parameters can be changed, and the obtained solutions can be compared.