Novel Machine Learning Based Credit Card Fraud Detection Systems

Abstract

This research deals with the critical issue of credit card fraud, a problem that has escalated in the last decade due to the significant increase in credit card usage, largely driven by advances in international trade, e-commerce, and FinTech. With global losses projected to exceed USD 400 billion in the next decade, the urgent need for effective fraud detection systems is apparent. Our study leverages the power of machine learning (ML) and presents a novel approach to credit card fraud detection. We used the European cardholders dataset for model training, addressing the data imbalance issue that often hinders the effectiveness of the learning process. As a key innovative element, we introduce compact data learning (CDL), a powerful tool for reducing the size and complexity of the training dataset without sacrificing the accuracy of the ML system. Comparative experiments have shown that our CDL-adapted feature reduction outperforms various ML algorithms and feature reduction methods. The findings of this research not only contribute to the theoretical foundations of fraud detection but also provide practical implications for the financial sector, which can benefit immensely from the enhanced fraud detection system.

1. Introduction

There has been a marked and swift surge in credit card users and transaction volume over the previous decade. This escalation is tied to advancements in international commerce, e-commerce, and financial technology, which have notably amplified the convenience of credit card use. Consequently, the ubiquity of credit card transactions has spurred an ongoing rise in credit card fraud. Credit card fraud involves unauthorized use of a credit card account, taking place when the cardholder or card issuer remains unaware of third-party usage. Fraudulent actors engage in acts such as procuring goods or services without payment or illicitly accessing account funds, including offline fraud, application fraud, bankruptcy fraud, and behavioral fraud [1]. The detection and prevention of credit card fraud are vital elements of financial systems aiming to identify and halt fraudulent transactions [2]. The deployment of efficient fraud surveillance strategies curbs economic losses, bolsters customer trust, and diminishes complaints [3,4]. Addressing the substantial financial losses tied to such fraudulent activities is pivotal. Recent data indicate that global losses from credit card fraud were USD 9.84 billion in 2011 [5], escalating to USD 28.65 billion in 2019 [6], an increase of USD 18.81 billion over eight years. Moreover, forecasts suggest that global credit card fraud losses may surpass USD 400 billion in the ensuing decade [7]. In 2020, there were 365,597 instances of fraud involving new credit accounts [8,9]. According to Federal Trade Commission (FTC) data [10,11], there were 459,297 credit card fraud cases in 2020, with 393,207 identified as credit card theft, a 44.6% increase from 271,927 cases in 2019. Consequently, the rapid development and implementation of credit card fraud detection systems by enterprises, particularly within the financial sector, is a pressing priority. The detection of credit card fraud within the financial sector could potentially be integrated with the field of economic criminology [12]. The efficiency and effectiveness of fraud detection systems could be enhanced by recognizing the limitations inherent in policing fraud through the application of modern technologies [13]. Leveraging the continual progress in machine learning (ML), a broad array of diverse ML systems is deployed for credit card fraud detection across various datasets. Numerous datasets used in preceding studies include the Credit Card Fraud dataset [1], European Cardholders dataset [14,15,16,17], and Lending Club Issued Loans dataset [18,19]. Several of these datasets are characterized by substantial data volume [1,18] and are trained with an extensive set of features [19]. Furthermore, it has been noted that data imbalance issues can potentially impede the effectiveness of the learning process in certain studies [17,20]. For our research, we utilized the European Cardholders dataset for ML model training and evaluation [14,17,21,22,23]. The escalating volume and rapid expansion of data in contemporary enterprises, coupled with their increasing diversity, have resulted in data becoming increasingly complex and high-dimensional. The primary contribution of this paper is the proposition of a unique compact data learning (CDL) approach aimed at enhancing model training efficiency. This approach seeks to optimize runtime speed by diminishing the sample size and minimizing data features. Through the use of reduced sampling to decrease the dataset size and the implementation of a robust comparison and selection procedure for feature reduction methods, we effectively tackled the difficulties associated with training models on expansive datasets. Importantly, our methodology not only boosts runtime efficiency but also ensures negligible impact on the original accuracy performance. The outcomes of this study offer insightful understanding and pragmatic techniques for augmenting model training efficiency, particularly in situations involving data volume reduction and feature selection.

This article proceeds in three additional sections. Section 2 explores the preliminaries, primarily presenting the theoretical foundations of our study, including data balancing and diverse machine learning algorithms previously implemented in existing research [8,14,17,24]. A brief overview of current feature reduction techniques is also provided in this section. Moreover, it suggests a novel feature reduction approach utilizing compact data learning [25,26]. CDL is a simple yet potent tool for downsizing the training dataset in terms of features and/or sample size with no harm to the accuracy of a machine learning system. Section 3 offers the experiment outcomes, comparing various ML algorithms and feature reduction methods with CDL adapted feature reduction. Lastly, Section 4 encapsulates the performance comparisons with the innovative feature reduction.

2. Preliminaries

Due to the limited access to real-world credit card transaction data from companies, the European credit cardholders dataset, which contains 284,807 non-fraud category and 492 fraud category (i.e., $0.172\%$ out of the total) samples, was applied in this paper. This dataset, which is publicly available on Kaggle, has been widely used in the related studies [14,15,21,22,23].

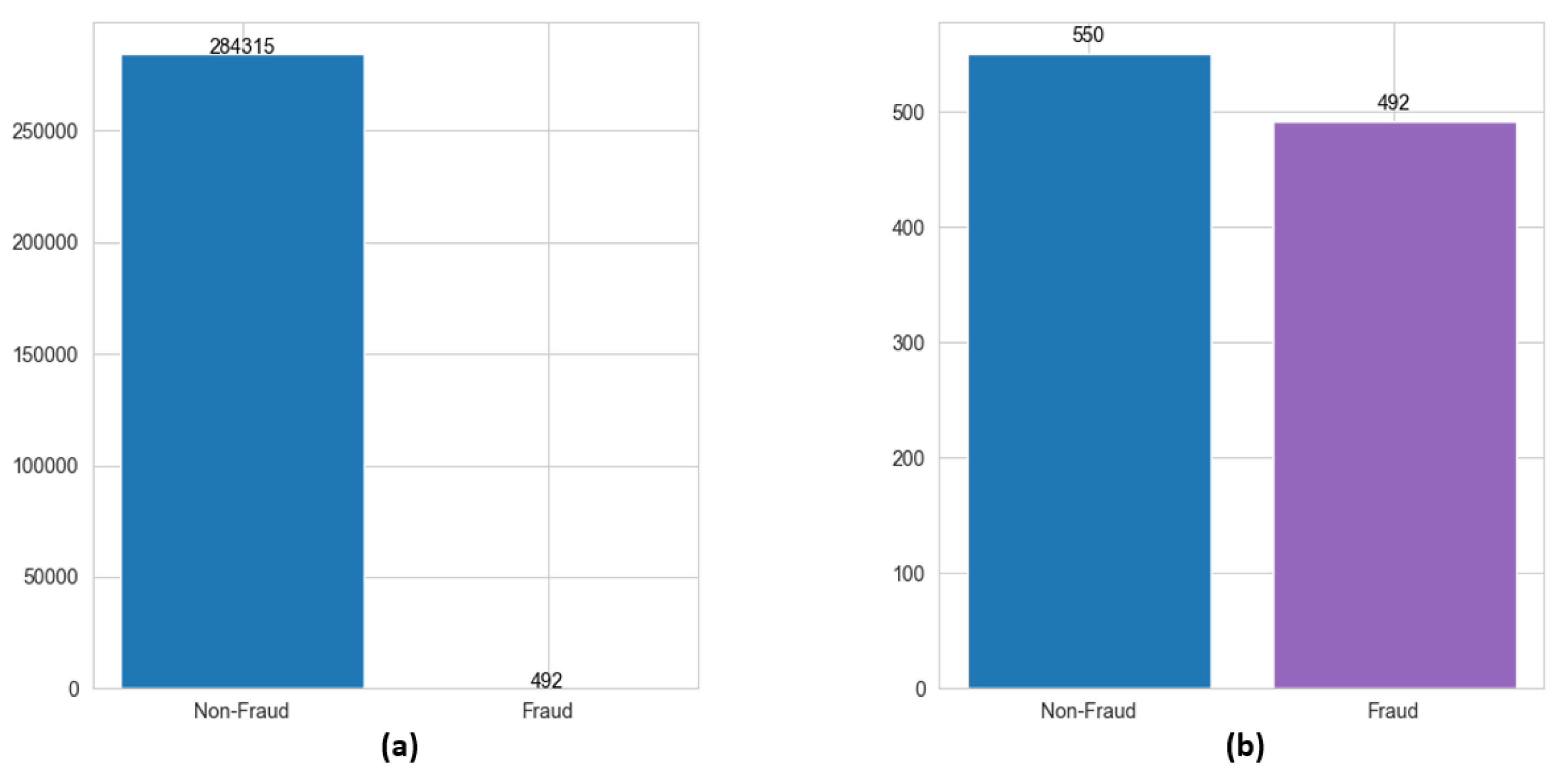
2.1. Data Balancing

The resampling approach, encompassing both over-sampling and under-sampling methods, is often utilized to mitigate issues of data imbalance. This process involves generating synthetic samples either by duplicating minority class samples or interpolating between them [27]. Nevertheless, over-sampling via the duplication of minority class samples may amplify the noise present in the data [2]. The Synthetic Minority Oversampling Technique (SMOTE) [27] and ensemble-based sampling approaches, which are typical over-sampling techniques, are found to be highly susceptible to the quality of the synthetically created samples. However, these techniques might introduce imprecision and lead to unstable model performance, as the learning process becomes overly dependent on the characteristics of the artificially generated samples [2]. On the other hand, under-sampling, targeted at addressing class imbalance in datasets and reducing computational burden for improved efficiency, involves either randomly eliminating samples from the majority class or replacing them with cluster centroids from a subset of samples [2,28]. In alignment with compact data learning (CDL) principles, under-sampling is considered more suitable for enhancing machine learning (ML) training efficiency. Consequently, the random under-sampling technique was applied to reduce the number of non-fraud samples, with the goal of attaining an almost equal distribution between fraud and non-fraud classes, aiming for approximately 50% representation in each class. As a result of the random under-sampling method, we obtained 550 non-fraud transactions and 492 fraud transactions (see Figure 1).

In this research, the dataset was divided into the training and testing (or inference) datasets for training and testing various ML models. The training dataset accounts for $74\%$ of the entire dataset, while the testing dataset accounts for $26\%$ (see

Table 1. Training and testing transaction samples.

Dataset/ Classification	Class 0 (Non-Fraud)	Class 1 (Fraud)
Training	400	369
Testing	150	123

). This study utilized five ML models for conducting model training and analysis, including the RF method with the AdaBoost, GBDT, KNN, CNN, and SVM models. These five algorithms were employed in training with the optimized and balanced dataset.

Our experiments demonstrate that basic data balancing can boost training time efficiency by up to 24,000 times compared to unbalanced data. It is important to note that unbalanced training datasets can introduce bias into ML systems. While reducing data samples may potentially impair key performance metrics (e.g., accuracy, precision, and recall), unbalanced training datasets should be adjusted to develop a proper ML system for the above reason.

2.2. Various Machine Learning Models for Credit Card Fraud Detection

In this section, we provide an overview of our research methodology in this study. Various machine learning algorithms were tested for selecting the best model for the credit card fraud detection. Among these models, we chose ensemble-based learning models and traditional machine learning models for our analysis [8,14,15,17]. There are five ML algorithms which were applied to the same datasets. These ML models with the balanced datasets are considered for this research:

• The random forest (RF) + adaptive boosting (AB) [14] method constructs a stronger classifier through training the random forest model, which is an ensemble learning model consisting of multiple decision trees based on random feature selection and a boot program [24]. This combined model adjusts the weights of samples based on the performance of the previous round’s classifier and strengthens the training of misclassified samples in the next round. The pairing of AdaBoost with the RF method enhances its robustness and improves the quality of classification for imbalanced credit card data.
• The Gradient Boosted Decision Tree (GBDT) [17] model is an ensemble learning algorithm which iteratively trains a series of decision trees to build a powerful predictive model. The GBDT model has also been used in previous papers as a base learner for fixed-size decision trees to overcome the problem of decision trees limiting their depth due to exponential growth.
• K-Nearest Neighbor (KNN) [8] is a model that involves voting on local neighboring data points to build the classifier function [15,29,30]. The user sets the number k, and the ‘neighbors’ value is initially chosen randomly, but it can be fine-tuned through iterative evaluation.
• A Convolutional Neural Network (CNN) [8] is a deep learning method that is widely used in images, text, audio and time series data, etc. There are six different layers in the CNN model, namely, the input layer, convolutional layer, pooling layer, fully connected layer, SoftMax/Logic layer, and output layer, of which hidden layers with the same structure can have different numbers of channels per layer.
• A Support Vector Machine (SVM) [15] utilizes both classification and regression tasks. The SVM is known for its capability to derive optimal decision boundaries between classes. However, it is not well-suited for datasets exhibiting imbalanced class distribution, noise, and overlapping class samples.

The reproduced results based on the above models with the balanced dataset are presented in

Table 2. Performance results of various machine learning algorithms.

Algorithm	Accuracy $(\%)$	Precision $(\%)$	Recall $(\%)$	F1-Score	Training Time (s)
RF + AB [14]	94.14	94.61	93.72	0.940	0.345
GBDT [17]	93.41	93.86	92.98	0.933	0.937
SVM [15]	93.77	94.49	93.24	0.936	0.041
CNN [8]	92.67	93.87	91.94	0.925	31.30
KNN [8]	92.31	92.80	91.83	0.922	0.076

in Section 3.1. It is noted that the performance results for the above ML models are not the same as the results from the original research because all above mentioned studies were completed using an unbalanced dataset.

2.3. Various Feature Reduction Methods

Feature selection methods have been widely adopted in addressing high-dimensional problems due to their simplicity and efficiency [31]. Feature selection aids in data understanding, reduces computational demands, mitigates the curse of dimensionality, and enhances predictor performance [32]. The essence of feature selection lies in selecting a subset of variables from the input and effectively captures the input data while minimizing the influence of noise or irrelevant variables to generate robust predictive outcomes [32,33].

• Analysis of Variance (ANOVA) is a statistical method used to compare means across different groups by analyzing data variance. It is commonly used in feature selection to aid in inference and decision-making processes. This method has reused in a previous paper [34].
• The feature importance method is a technique used to evaluate and quantify the importance of features in a machine learning model, which helps the user to understand the critical role of specific features in the predictive performance of a model.
• The correlation heatmap is a graphical representation that visualizes pairwise correlations between variables in a dataset and is generated based on linear correlation coefficients. In the correlation heatmap, darker blue indicates a stronger negative correlation, while darker red indicates a stronger positive correlation.
• The linear correlation coefficient is employed to quantify the strength and direction of the linear relationship between two variables [35].

The above four feature reduction methods were employed to select the features for training the machine learning models. The outputs of these methods were compared to determine the optimal feature reduction approach for further training. Resampling techniques were utilized to eliminate redundant data instances from the dataset.

2.4. Compact Data Learning

Compact data design for machine learning entails the development of an optimized training dataset that maintains comparable machine learning accuracy while minimizing data volume [25]. Compact Data Learning (CDL) introduces a novel and applicable structure for enhancing a classification system by reducing the machine learning training data size [26]. Since CDL is an enhanced feature reduction method which is based on correlation, a correlation heatmap is directly applied to calculate the pair-wise comparison between the input features of the dataset. A correlation heatmap is a visualization instrument utilized to display the intensity of the correlation among variables. The Pearson Correlation Coefficient serves as a significant method for quantifying the affinity or relationship between multiple data variables [36,37,38]. The correlation score heatmap of all input features in the training dataset is shown in Figure A1 in Appendix A. Originating from the idea of compact data design, which provides optimal resources without the necessity of managing intricate big data, CDL distinguishes itself by offering a general, output-independent structure to optimize the ML training dataset. CDL serves as a specific framework intended to accelerate the machine learning training phase without sacrificing system precision. A typical form of absolute correlation is as [26]:

$$r=\left|\frac{\mathbb{E}\left[\left(X-{\mu }_X\right)\left(Y-{\mu }_Y\right)\right]}{\sqrt{\mathbb{E}\left[{\left(X-{\mu }_X\right)}^2\right]·\mathbb{E}\left[{\left(Y-{\mu }_Y\right)}^2\right]}}\right|,r\in \left[0,1\right],$$

(1)

where ${\mu }_X=\mathbb{E}\left[X\right],{\mu }_Y=\mathbb{E}\left[Y\right]$. The closer the absolute correlation value r is to 1, the higher correlation. An absolute correlation value close to 0 indicates weak or no correlation between two variables. It is noted that the CDL can be easily implemented from the correlation heatmap by using a simple algorithm (see Algorithm A1 in Appendix B). In our research, we employed the CDL-based feature reduction, and the accuracy of the trained models was evaluated using the two-sample Z-test method to determine the significance of the results, which would help us determine whether to accept or reject the outcomes of the model. In the subsequent section, we present and analyze the results and compare the outcomes of applying the CDL method. Identifying the optimal threshold for diminishing input features could serve as another research subject to enhance CDL. The absolute correlation threshold, denoted as $r^{*}$, is formally defined as follows [26]:

$$r^{*}=\underset{r}{argmin}\left\{\mathbf{True}\mathrm{for}{H}_0:\mathbb{E}\left[G\left(\xi \left(r\right)\right)\right]-\mathbb{E}\left[G\left(\xi \left(1\right)\right)\right]=0\right\},$$

(2)

where $H_0$ is the null hypothesis for the two-sample Z-test and the revised set of the input features, the function $G\left(\xi \left(r\right)\right)$ provides the accuracy of a machine learning function, and $\xi \left(r\right)$ is the selected input feature based on the correlation threshold from the correlation heatmap. It is noted that several ML evaluations are required to obtain the optimal threshold $r^{*}$ from (2), and this threshold is data-dependent. But the absolute correlation threshold is conventionally set based on industrial practices [26]. According to our industrial practices, CDL-based feature reduction gives the best performance when $r*$ is around $0.7$ to $0.9$. Hence, we chose the threshold of the CDL feature reduction from the best practice (i.e., $r^{*}=0.7$).

2.5. Performance Measures

The performance of the selected models was evaluated using a performance matrix, which compared the actual observations with the model predictions. The performance matrix encompassed metrics such as accuracy, precision, recall, and F1-score. The metrics were calculated across different classes: True Positives (TPs) refer to the number of correctly classified positive instances, while True Negatives (TNs) represent the number of correctly classified negative instances. False Positives (FPs) indicate the number of instances that are falsely classified as positive, and False Negatives (FNs) denote the instances that are falsely classified as negative [18,39]. Let N represent the total number of samples, and the evaluation metrics can be expressed using the following formulas:

$$Accuracy=\frac{N_{TP}+N_{TN}}{N},$$

(3)

$$Precision=\frac{N_{TP}}{N_{TP}+N_{FP}},$$

(4)

$$Recall=\frac{N_{TP}}{N_{TP}+N_{FN}},$$

(5)

$$F1-score=\frac{2\times Precision\times Recall}{Precision+Recall}.$$

(6)

Accuracy is the most commonly used and simplest model evaluation metric, providing a direct measure of the proportion of correctly classified samples. Precision measures the proportion of true positive samples among all predicted positive samples by the model. Recall measures the proportion of true positive samples among all actual positive samples. F1-score is the harmonic mean of precision and recall, which combines both accuracy and recall performance. In this study, these four model metrics were utilized to comprehensively evaluate the ML models, and their respective scores are presented to provide objective measures to evaluate the performance of the models and aid in decision-making. Furthermore, we continuously examined accuracy in the application of the CDL method to ensure the performance level of the models.

3. Experiment Results

The upcoming discussion presents the optimization results of the five machine learning algorithms detailed in Section 2.5. Section 3.1 illustrates the performance metrics, namely, accuracy, precision, recall, f1-score, as well as the execution time of algorithms, when deployed on a balanced dataset using the testing dataset. Advancing to Section 3.2, three feature reduction methods, specifically ANOVA, feature importance, and correlation heatmap, were implemented to generate accuracy results and determine the most effective feature reduction method. In conclusion, as detailed in Section 3.3, we applied the feature reduction method chosen in Section 3.2 to conduct feature filtering during training, aiming to confirm the acceptability of the accuracy results. Simultaneously, we also recorded the execution time performance of the ML algorithms.

3.1. Result Comparisons for ML Algorithms

The subsequent discussion features the performance results of the test dataset, which were also analyzed. Displayed in Table 2 are the original performance results for the five machine learning models. Notably, all models achieved performance scores ranging from $91.83\%$ to $94.61\%$ across the evaluation metrics. It is noted that the RF + AB model achieved the highest performance across all accuracy-related indicators, but the SVM provided highest performance in terms of the training time. Among all models, the CNN model exhibited the longest running time, requiring $31.3$ s to complete.

3.2. Result Comparisons for Feature Reduction

Based on the accuracy results shown in Table 2 in the previous section, the ANOVA, feature importance, and correlation heatmap methods were utilized to reduce the number of features in the dataset, and the training results of the models are presented in

Table 3. Accuracy comparisons of different feature reduction methods.

Algorithm	Original $(\%)$	ANOVA $(\%)$	Feat. Imp. $(\%)$	Heatmap $(\%)$
RF + AB [14]	94.14	93.40	93.68	94.14
SVM [15]	93.77	93.04	93.77	93.77
GBDT [17]	93.41	93.77	94.04	94.87
CNN [8]	92.67	94.87	92.67	93.41
KNN [8]	92.31	92.31	92.31	93.77

. In ANOVA, a significance level ($\alpha$) of $0.05$, representing a $95\%$ confidence level, was selected. Subsequently, features with p-values lower than the established significance level were selected for model training. In feature importance analysis, features with a score of zero were removed as they have no predictive capability for the target variable. Similarly, in the correlation heatmap, features with a score of zero were not selected because they show no significant correlation with the target variable.

As shown in Table 3, the accuracy scores of the correlation heatmap group were consistently higher or equal to those of the original group. In contrast, the ANOVA group and feature importance group have one or two accuracy scores that decreased. Consequently, the correlation heatmap approach might be adapted for further model training.

3.3. Feature Reduction with CDL

The accuracy results obtained using different correlation threshold limits for feature selection in machine model training are showcased in

Table 4. Performance comparisons of different correlation threshold limits.

Algorithm	Original (%)	CDL (${\mathit{r}}^{*}=0.7$, $\mathit{\alpha }=0.05$)
		Accuracy (%)	${\mathit{H}}_{\mathbf{0}}$ Accepted?	Training Time (s)
GBDT [17]	93.41	93.77	Yes	0.578
RF + AB [14]	94.14	92.67	Yes	0.343
SVM [15]	93.77	91.94	Yes	0.040
CNN [8]	92.67	90.84	Yes	21.834
KNN [8]	92.31	87.18	No	0.058

, with the correlation threshold between each feature represented in the correlation heatmap in Figure A1. In this study, the null hypothesis assumes no significant accuracy difference between the two samples, at a significance level of $0.05$. The findings indicate that when the correlation threshold $r^{*}$ is $0.7$, the GBDT model showed a slight accuracy improvement, while the other four models experienced a decrease in accuracy. By applying the Z-test method, it was found that only the KNN model had a Z-score exceeding the critical value, leading to the rejection of the null hypothesis, implying that the accuracy of the KNN model is not acceptable. By using the Z-test method, it was determined that there is no significant accuracy difference among all models, leading to the acceptance of the null hypothesis, suggesting that the accuracy of all models is acceptable. The running times for all models are shorter than their original running times, indicating a decrease in running time achieved after feature reduction. The GBDT model showed an improvement in accuracy, while the RF + AB, SVM, CNN, and KNN models experienced a decrease in accuracy but still acceptable performance (i.e., no differences). On the other hand, the performance of the KNN model is unacceptable, as indicated by the rejection of the null hypothesis. The training times of all models were shorter than their original times (see Table 4).

Figure 2 presents the quantity and ratio of features prior to any feature removal, subsequent to feature selection using the heatmap, and following feature selection using the CDL technique. According to our experiments, the CDL-based feature reduction is theoretically based on the absolute correlation and is easily transformed from the correlation heatmap, but this simple method is more practical, and its efficiency is even better than the performance using a correlation heatmap (see Figure 2). Before feature selection, the original dataset consisted of 30 features. After applying heatmap-based feature selection, 24 features were selected, accounting for $80\%$ of the total features. Employing the CDL technique for feature selection resulted in the selection of 18 features, representing $60\%$ of the total features. Using $60\%$ of the CDL-selected features, we trained the model and achieved comparable accuracy performance to the initial selection of 30 features, as indicated in Table 4. These results highlight the potential effectiveness of our proposed CDL technique in reducing features while maintaining the desired accuracy performance.

4. Conclusions

This research deals with the development of a credit card fraud detection system that leverages machine learning, and innovatively incorporates a compact data learning method (CDL) for feature reduction. The CDL method not only reduces the sample size through data balancing but also optimizes the feature size, all while maintaining the accuracy of the fraud detection system. The simplicity and universality of the CDL method make it an ideal choice for almost any machine learning training process. The CDL serves as a guide for adopting this cutting-edge method to boost ML training efficiency for credit card fraud detection. By integrating the CDL method into machine learning training, we can create more robust and reliable models. This not only improves the accuracy of fraud detection but also reduces the computational complexity, thus delivering quicker and more reliable outcomes. Therefore, this research offers a promising direction in the field of credit card fraud detection, demonstrating that the CDL method could be a game-changer in improving the detection of fraudulent activities, thereby enhancing the security of credit card transactions. While numerous challenges remain to be addressed in future research, this framework shows promise for application across various multidisciplinary domains, including economic criminology, accountancy, and legal matters. This research opens new avenues for enhancing the efficiency and effectiveness of fraud detection systems. Scholars active in these areas might find the research particularly beneficial, recognizing the broader context that could be potential topics for our future research.