An Efficient Numerical Method for Solving a Class of Nonlinear Fractional Differential Equations and Error Estimates
Abstract
1. Introduction
2. Numerical Method
3. The Convergence of the Method and Error Estimate
4. Applications of the Method
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sandev, T.; Tomovski, Z. Fractional Equations and Models, Theory and Applications; Springer Nature: Cham, Switzerland, 2019. [Google Scholar]
- Sandev, T.; Tomovski, Z.; Dubbeldam, J.L.; Chechkin, A. Generalized diffusion-wave equation with memory kernel. J. Phys. Math. Theor. 2018, 52, 015201. [Google Scholar] [CrossRef]
- Tomovski, Ž.; Dubbeldam, J.L.; Korbel, J. Applications of hilfer-prabhakar operator to option pricing financial model. Fract. Calc. Appl. Anal. 2020, 23, 996–1012. [Google Scholar] [CrossRef]
- Kilbas, A. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Marynets, K.; Pantova, D. Successive approximations and interval halving for fractional BVPs with integral boundary conditions. J. Comput. Appl. Math. 2024, 436, 115361. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Hashemi, M.; Liu, C.-S. The Lie-group shooting method for solving the bratu equation. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 4238–4249. [Google Scholar] [CrossRef]
- Abu Arqub, O. Adaptation of reproducing kernel algorithm for solving fuzzy Fredholm–Volterra integrodifferential equations. Neural Comput. Appl. 2017, 28, 1591–1610. [Google Scholar] [CrossRef]
- Arqub, O.A.; Al-Smadi, M.; Momani, S.; Hayat, T. Numerical solutions of fuzzy differential equations using reproducing kernel hilbert space method. Soft Comput. 2016, 20, 3283–3302. [Google Scholar] [CrossRef]
- Arqub, O.A.; Maayah, B. Solutions of Bagley–Torvik and Painlevé equations of fractional order using iterative reproducing kernel algorithm with error estimates. Neural Comput. Appl. 2018, 29, 1465–1479. [Google Scholar] [CrossRef]
- Akram, G.; Rehman, H.U. Solution of fifth order boundary value problems in reproducing kernel space. Middle-East J. Sci. Res. 2011, 10, 191–195. [Google Scholar]
- Al-Said, E.A.; Noor, M.A. Cubic splines method for a system of third-order boundary value problems. Appl. Math. Comput. 2003, 142, 195–204. [Google Scholar] [CrossRef]
- Bai, Z. On positive solutions of a nonlocal fractional boundary value problem. Nonlinear Anal. Theory Methods Appl. 2010, 72, 916–924. [Google Scholar] [CrossRef]
- Caglar, H.; Caglar, S.; Twizell, E. The numerical solution of fifth-order boundary value problems with sixth-degree B-spline functions. Appl. Math. Lett. 1999, 12, 25–30. [Google Scholar] [CrossRef]
- Caglar, H.; Caglar, N.; Özer, M.; Valarıstos, A.; Anagnostopoulos, A.N. B-spline method for solving Bratu’s problem. Int. J. Comput. Math. 2010, 87, 1885–1891. [Google Scholar] [CrossRef]
- Momani, S.; Noor, M.A. Numerical comparison of methods for solving a special fourth-order boundary value problem. Appl. Math. Comput. 2007, 191, 218–224. [Google Scholar] [CrossRef]
- Yousif, M.A.; Hamasalh, F.K. The fractional non-polynomial spline method: Precision and modeling improvements. Math. Comput. Simul. 2024, 218, 512–525. [Google Scholar] [CrossRef]
- Jassim, H.K.; Hussein, M.A. A new approach for solving nonlinear fractional ordinary differential equations. Mathematics 2023, 11, 1565. [Google Scholar] [CrossRef]
- Temimi, H.; Ben-Romdhane, M. A highly accurate discontinuous galerkin method for solving nonlinear Bratu’s problem. Alex. Eng. J. 2024, 95, 50–58. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. An effective approach for numerical solutions of high-order Fredholm integro-differential equations. Appl. Math. Comput. 2014, 227, 384–398. [Google Scholar] [CrossRef]
- Kreyszig, E. Introductory Functional Analysis with Applications; John Wiley & Sons: Hoboken, NJ, USA, 1991; Volume 17. [Google Scholar]
- Rivlin, T.J. An Introduction to the Approximation of Functions; Courier Corporation: North Chelmsford, MA, USA, 1981. [Google Scholar]
- Torvik, P.J.; Bagley, R.L. On the appearance of the fractional derivative in the behavior of real materials. J. Appl. Mech. 1984, 51, 294–298. [Google Scholar] [CrossRef]
- Wang, Y.-L.; Tian, D.; Bao, S.-H.; Li, Z.-Y. Using the iterative reproducing kernel method for solving a class of nonlinear fractional differential equations. Int. J. Comput. Math. 2017, 94, 2558–2572. [Google Scholar] [CrossRef]
- Liao, S.; Tan, Y. A general approach to obtain series solutions of nonlinear differential equations. Stud. Appl. Math. 2007, 119, 297–354. [Google Scholar] [CrossRef]
- McGough, J.S. Numerical continuation and the Gelfand problem. Appl. Math. Comput. 1998, 89, 225–239. [Google Scholar] [CrossRef]
- Noor, M.A.; Mohyud-Din, S.T. Variational iteration method for fifth-order boundary value problems using he’s polynomials. Math. Probl. Eng. 2008, 2008, 954794. [Google Scholar] [CrossRef]
- Noor, M.A.; Mohyud-Din, S.T. A new approach to fifth-order boundary value problems. Int. J. Nonlinear Sci. 2009, 7, 143–148. [Google Scholar]
- Wazwaz, A.-M. The numerical solution of fifth-order boundary value problems by the decomposition method. J. Comput. Appl. Math. 2001, 136, 259–270. [Google Scholar] [CrossRef]
- Zhang, J. The numerical solution of fifth-order boundary value problems by the variational iteration method. Comput. Math. Appl. 2009, 58, 2347–2350. [Google Scholar] [CrossRef]
- Ali, J.; Islam, S.; Islam, S.; Zaman, G. The solution of multipoint boundary value problems by the optimal homotopy asymptotic method. Comput. Math. Appl. 2010, 59, 2000–2006. [Google Scholar] [CrossRef]
- Saadatmandi, A.; Dehghan, M. The use of Sinc-collocation method for solving multi-point boundary value problems. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 593–601. [Google Scholar] [CrossRef]
- Tatari, M.; Dehghan, M. The use of the Adomian decomposition method for solving multipoint boundary value problems. Phys. Scr. 2006, 73, 672. [Google Scholar] [CrossRef]
- Tatari, M.; Dehghan, M. An efficient method for solving multi-point boundary value problems and applications in physics. J. Vib. Control. 2012, 18, 1116–1124. [Google Scholar] [CrossRef]
- Xie, L.-j.; Zhou, C.-l.; Xu, S. A new algorithm based on differential transform method for solving multi-point boundary value problems. Int. J. Comput. Math. 2016, 93, 981–994. [Google Scholar] [CrossRef]
- Temimi, H.; Kurkcu, H. An accurate asymptotic approximation and precise numerical solution of highly sensitive Troesch’s problem. Appl. Math. Comput. 2014, 235, 253–260. [Google Scholar] [CrossRef]


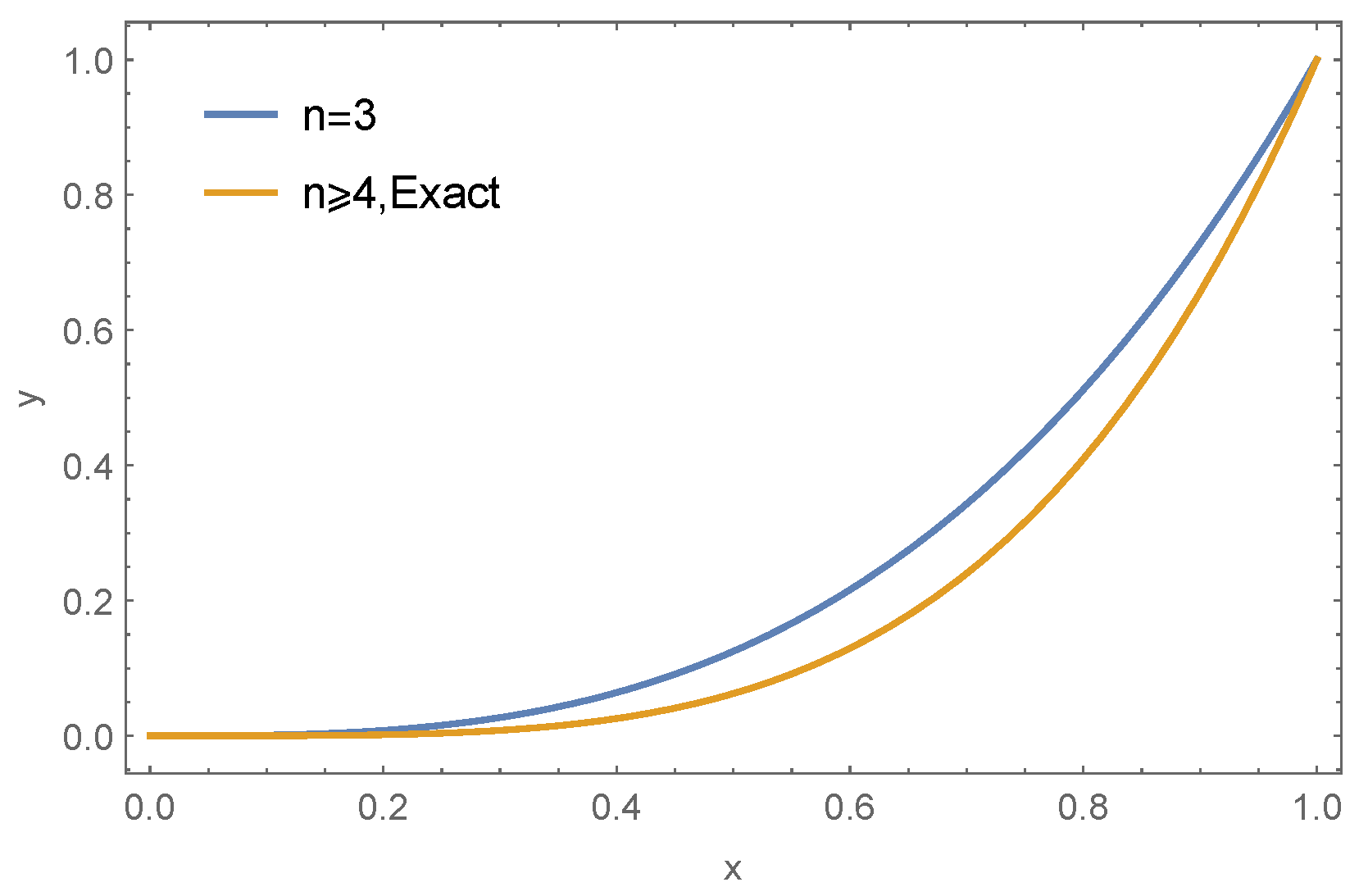
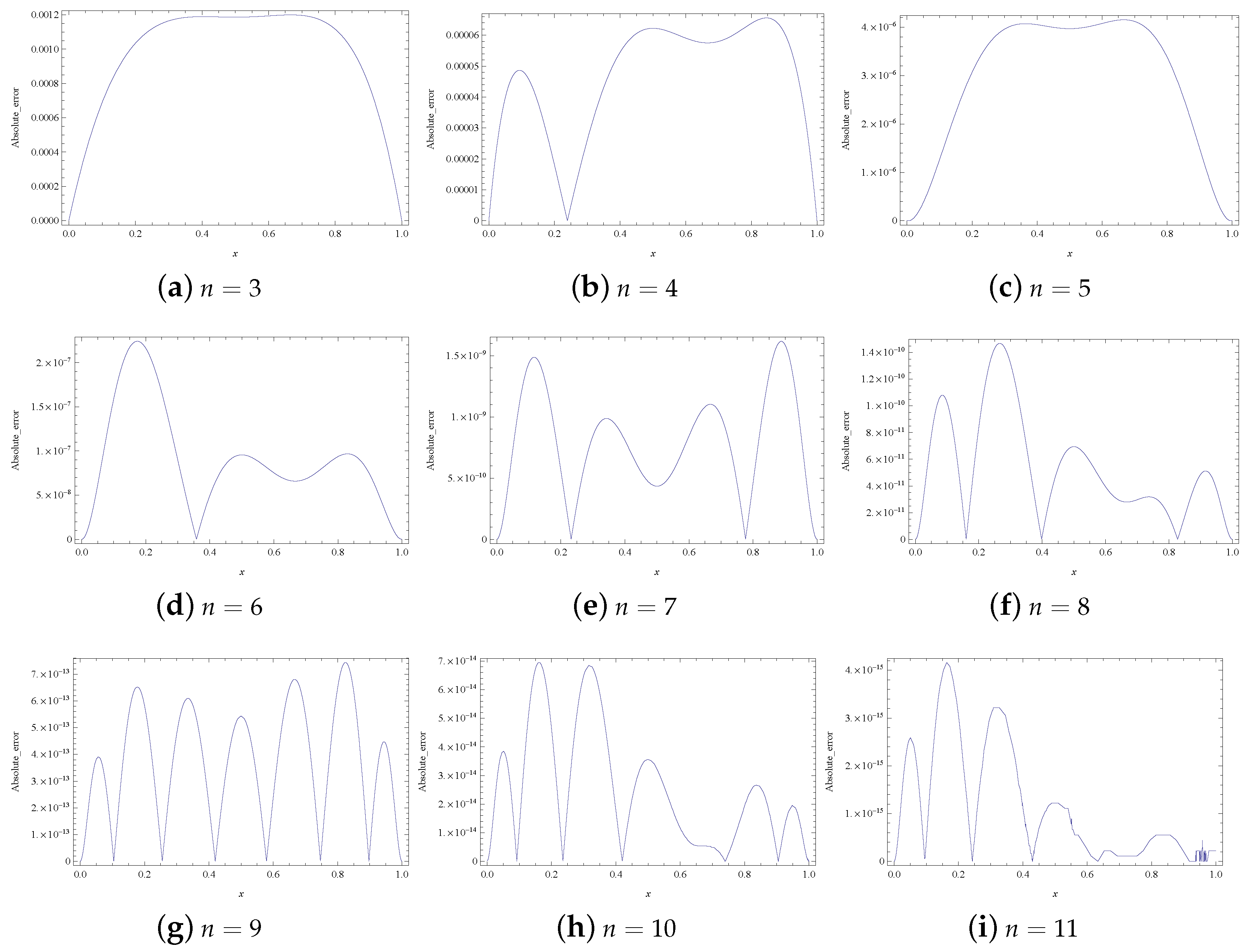
| Node | LGSM [6] | B-spline [7] | Laplace [8] | ADM [9] | RKSM [23] | Present Method | |
|---|---|---|---|---|---|---|---|
| 0.1 | 7.5 | 3.0 | 2.0 | 2.7 | 6.2 | 2.8 | |
| 0.2 | 1.0 | 5.5 | 3.9 | 2.0 | 1.1 | 3.6 | |
| 0.4 | 5.2 | 8.5 | 7.7 | 2.2 | 1.7 | 2.5 | |
| 0.6 | 5.1 | 8.5 | 1.1 | 2.2 | 1.6 | 2.5 | |
| 0.9 | 7.4 | 3.0 | 1.2 | 2.7 | 5.6 | 2.8 | |
| 0.2 | 5.7 | 1.9 | 4.2 | 1.5 | 5.8 | 5.0 | |
| 0.3 | 5.2 | 2.8 | 6.2 | 5.9 | 7.9 | 2.0 | |
| 0.5 | 1.5 | 1.1 | 9.6 | 7.0 | 9.7 | 6.6 | |
| 0.7 | 5.2 | 6.9 | 1.2 | 5.9 | 7.8 | 2.0 | |
| 0.9 | 4.0 | 2.6 | 1.1 | 1.5 | 3.0 | 4.4 |
| Node | ADM [10] | HPM [11] | VIMHP [11] | VIM [11] | B-Spline [12] | Method in [13] | Method in [14] | RKSM [23] | Present Method |
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 1.0 | 1.0 | 1.0 | 1.0 | 7.0 | 2.3 | 0 | 7.1 | 1.1 |
| 0.2 | 2.0 | 2.0 | 2.0 | 2.0 | 7.2 | 1.6 | 1.0 | 4.6 | 1.7 |
| 0.3 | 1.0 | 1.0 | 1.0 | 1.0 | 4.1 | 4.6 | 1.0 | 1.2 | 5.4 |
| 0.4 | 2.0 | 2.0 | 2.0 | 2.0 | 4.6 | 8.9 | 1.0 | 2.2 | 7.6 |
| 0.5 | 3.1 | 3.1 | 3.1 | 3.1 | 4.7 | 1.3 | 3.2 | 3.1 | 5.6 |
| 0.6 | 3.7 | 3.7 | 3.7 | 3.7 | 4.8 | 1.6 | 3.6 | 3.5 | 1.7 |
| 0.7 | 4.1 | 4.1 | 4.1 | 4.1 | 3.9 | 1.6 | 1.4 | 3.3 | 3.4 |
| 0.8 | 3.1 | 3.1 | 3.1 | 3.1 | 3.1 | 1.2 | 3.1 | 2.2 | 1.1 |
| 0.9 | 1.4 | 1.4 | 1.4 | 1.4 | 1.6 | 5.1 | 5.8 | 8.1 | 1.6 |
| Node | ADM [15] | HPM [15] | DTM [15] | RKSM [23] | Present Method |
|---|---|---|---|---|---|
| 0.1 | 6.5 | 6.5 | 1.5 | 1.8 | 1.2 |
| 0.2 | 8.8 | 8.8 | 3.7 | 2.8 | 4.6 |
| 0.3 | 3.6 | 3.6 | 9.0 | 4.6 | 6.5 |
| 0.4 | 9.1 | 9.1 | 8.5 | 5.5 | 1.8 |
| 0.5 | 1.6 | 1.6 | 4.8 | 6.3 | 3.6 |
| 0.6 | 2.3 | 2.3 | 1.9 | 6.4 | 1.2 |
| 0.7 | 2.6 | 2.6 | 6.4 | 5.8 | 4.9 |
| 0.8 | 2.1 | 2.1 | 1.7 | 4.5 | 1.9 |
| 0.9 | 9.1 | 9.1 | 4.2 | 2.1 | 3.3 |
| Node | ||||||
|---|---|---|---|---|---|---|
| Method in [34] | Method in [34] | Method in [34] | Present Method | Present Method | Present Method | |
| 0.1 | 6.2 | 4.2 | 1.1 | 3.7 | 2.2 | 2.6 |
| 0.2 | 1.2 | 8.1 | 2.3 | 6.7 | 4.5 | 5.1 |
| 0.3 | 1.6 | 1.2 | 4.2 | 9.1 | 7.4 | 7.6 |
| 0.4 | 2.0 | 1.4 | 4.9 | 1.1 | 1.1 | 1.0 |
| 0.5 | 2.3 | 1.7 | 5.2 | 1.2 | 1.3 | 1.2 |
| 0.6 | 2.5 | 2.0 | 7.6 | 1.2 | 1.4 | 1.2 |
| 0.7 | 2.6 | 2.1 | 7.3 | 1.1 | 1.3 | 1.1 |
| 0.8 | 2.4 | 2.1 | 1.2 | 8.2 | 1.0 | 9.0 |
| 0.9 | 1.8 | 1.7 | 1.1 | 4.7 | 6.6 | 5.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, X.; Wu, R. An Efficient Numerical Method for Solving a Class of Nonlinear Fractional Differential Equations and Error Estimates. Mathematics 2024, 12, 1824. https://doi.org/10.3390/math12121824
Song X, Wu R. An Efficient Numerical Method for Solving a Class of Nonlinear Fractional Differential Equations and Error Estimates. Mathematics. 2024; 12(12):1824. https://doi.org/10.3390/math12121824
Chicago/Turabian StyleSong, Xin, and Rui Wu. 2024. "An Efficient Numerical Method for Solving a Class of Nonlinear Fractional Differential Equations and Error Estimates" Mathematics 12, no. 12: 1824. https://doi.org/10.3390/math12121824
APA StyleSong, X., & Wu, R. (2024). An Efficient Numerical Method for Solving a Class of Nonlinear Fractional Differential Equations and Error Estimates. Mathematics, 12(12), 1824. https://doi.org/10.3390/math12121824




