TPoison: Data-Poisoning Attack against GNN-Based Social Trust Model
Abstract
:1. Introduction and Preliminaries
1.1. Introduction
- 1.
- Based on the characteristics of online social networks, we propose a data-poisoning attack method in a gray-box environment for GNN-based social trust models.
- 2.
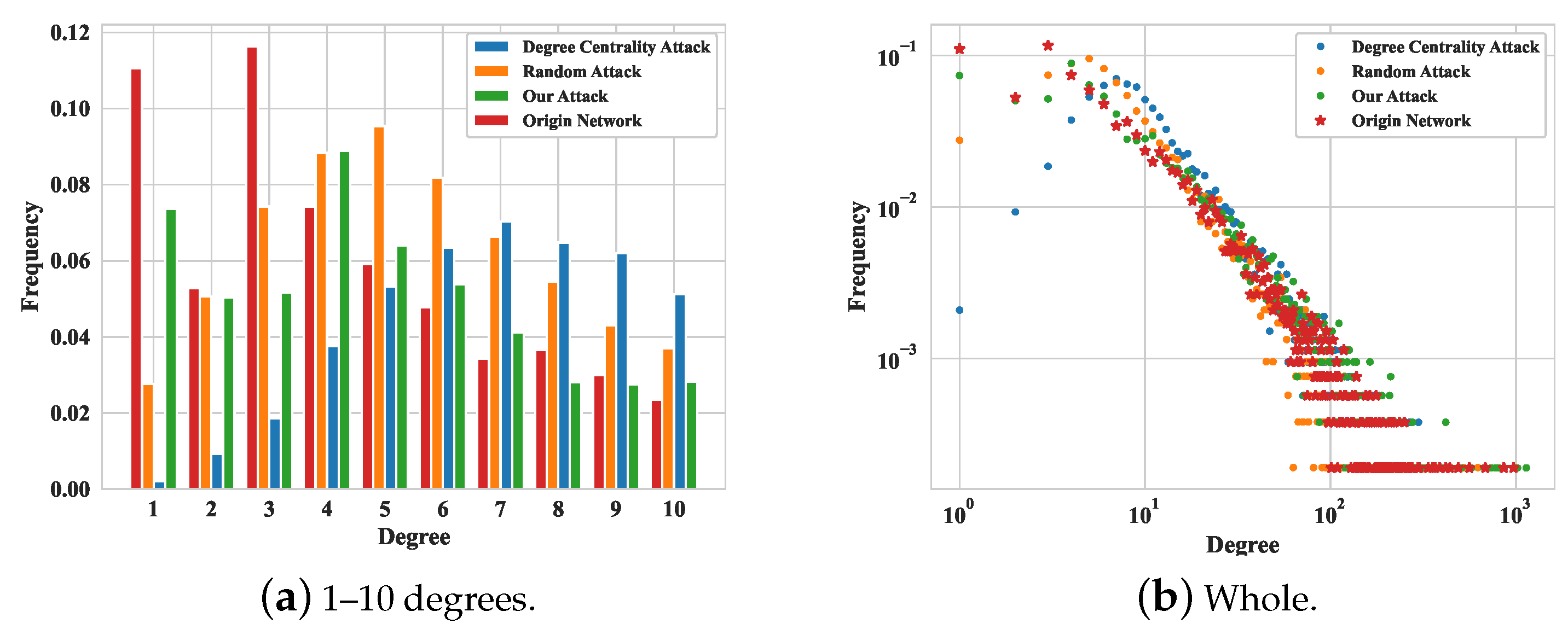
- If the node degree distribution changes significantly, the attack will be very easy to detect. To overcome this problem, we used a two-sample test for power-law distributions of discrete data to keep the node degree distribution relatively unchanged and preserve important social relationships.
- 3.
- To showcase the effectiveness of the method, we performed a series of quantitative and qualitative experiments on three real-world datasets. The results demonstrate that our method exhibited superior attack performance compared with the other attack methods.
1.2. Problem Scope
1.3. Preliminaries
2. Poisoning Method
2.1. Avoidance Detection Module
2.2. Gray-Box Attack Module
2.3. Attack Evaluation Module
| Algorithm 1 An algorithm to find the best poisoning sample under constrained conditions. |
|
3. Experimental Results
3.1. Dataset Description
3.2. Experimental Settings
3.3. Experimental Results and Analysis
3.3.1. Effectiveness of the Avoidance Detection Module
3.3.2. Impact of Attacks on Model Performance
3.3.3. Impact of Attacks on Model Training
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, H.; Gibbons, P.B.; Kaminsky, M.; Xiao, F. SybilLimit: A Near-Optimal Social Network Defense against Sybil Attacks. In Proceedings of the 29th IEEE Symposium on Security and Privacy, Oakland, CA, USA, 18–21 May 2008; pp. 3–17. [Google Scholar]
- Yu, H.; Kaminsky, M.; Gibbons, P.B.; Flaxman, A.D. SybilGuard: Defending Against Sybil Attacks via Social Networks. IEEE/ACM Trans. Netw. 2008, 16, 576–589. [Google Scholar] [CrossRef]
- Samreen, S.; Jabbar, M. Countermeasures for Conflicting Behavior Attack in a Trust Management Framework for a Mobile Ad hoc Network. In Proceedings of the IEEE International Conference on Computational Intelligence and Computing Research, Coimbatore, India, 14–16 December 2017; pp. 1–4. [Google Scholar]
- Sun, Y.L.; Han, Z.; Yu, W.; Ray Liu, K.J. Attacks on Trust Evaluation in Distributed Networks. In Proceedings of the 40th IEEE Annual Conference on Information Sciences and Systems, Princeton, NJ, USA, 22–24 March 2006; pp. 1461–1466. [Google Scholar]
- Xue, L.; Wang, Q.; An, L.; He, Z.; Feng, S.; Zhu, J. A nonparametric adaptive EWMA control chart for monitoring mixed continuous and categorical data using self-starting strategy. Comput. Ind. Eng. 2024, 188, 109930. [Google Scholar] [CrossRef]
- Yeganeh, A.; Shadman, A.; Shongwe, S.C.; Abbasi, S.A. Employing evolutionary artificial neural network in risk-adjusted monitoring of surgical performance. Neural Comput. Appl. 2023, 35, 10677–10693. [Google Scholar] [CrossRef]
- Salmasnia, A.; Namdar, M.; Abolfathi, M.; Ajaly, P. Statistical design of a VSI-EWMA control chart for monitoring the communications among individuals in a weighted social network. Int. J. Syst. Assur. Eng. Manag. 2021, 12, 495–508. [Google Scholar] [CrossRef]
- Flossdorf, J.; Fried, R.; Jentsch, C. Online monitoring of dynamic networks using flexible multivariate control charts. Soc. Netw. Anal. Min. 2023, 13, 87. [Google Scholar] [CrossRef]
- Noorossana, R.; Hosseini, S.S.; Heydarzade, A. An overview of dynamic anomaly detection in social networks via control charts. Qual. Reliab. Eng. Int. 2018, 34, 641–648. [Google Scholar] [CrossRef]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive Representation Learning on Large Graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 1025–1035. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the 5th International Conference on Learning Representations, Toulon, France, 24–26 April 2017; pp. 1–14. [Google Scholar]
- Zhang, M.; Chen, Y. Link Prediction Based on Graph Neural Networks. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 5171–5181. [Google Scholar]
- Lin, W.; Gao, Z.; Li, B. Guardian: Evaluating Trust in Online Social Networks with Graph Convolutional Networks. In Proceedings of the 39th IEEE Conference on Computer Communications, Toronto, ON, Canada, 6–9 July 2020; pp. 914–923. [Google Scholar]
- Zügner, D.; Borchert, O.; Akbarnejad, A.; Günnemann, S. Adversarial attacks on graph neural networks: Perturbations and their patterns. ACM Trans. Knowl. Discov. Data 2020, 14, 1–31. [Google Scholar] [CrossRef]
- Jin, W.; Li, Y.; Xu, H.; Wang, Y.; Ji, S.; Aggarwal, C.; Tang, J. Adversarial Attacks and Defenses on Graphs. SIGKDD Explor. Newsl. 2021, 22, 19–34. [Google Scholar] [CrossRef]
- Chen, J.; Wu, Y.; Xu, X.; Chen, Y.; Zheng, H.; Xuan, Q. Fast gradient attack on network embedding. arXiv 2018, arXiv:1809.02797. [Google Scholar]
- Wang, X.; Cheng, M.; Eaton, J.; Hsieh, C.J.; Wu, F. Attack graph convolutional networks by adding fake nodes. arXiv 2018, arXiv:1810.10751. [Google Scholar]
- Chen, J.; Chen, Y.; Zheng, H.; Shen, S.; Yu, S.; Zhang, D.; Xuan, Q. MGA: Momentum gradient attack on network. IEEE Trans. Comput. Soc. Syst. 2020, 8, 99–109. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, J.; Chen, Z.; Du, M.; Xuan, Q. Time-aware gradient attack on dynamic network link prediction. IEEE Trans. Knowl. Data Eng. 2021, 35, 2091–2102. [Google Scholar] [CrossRef]
- Sharma, A.K.; Kukreja, R.; Kharbanda, M.; Chakraborty, T. Node injection for class-specific network poisoning. Neural Netw. 2023, 166, 236–247. [Google Scholar] [CrossRef]
- Zong, W.; Chow, Y.; Susilo, W.; Do, K.; Venkatesh, S. TrojanModel: A Practical Trojan Attack against Automatic Speech Recognition Systems. In Proceedings of the 44th IEEE Symposium on Security and Privacy, San Francisco, CA, USA, 21–25 May 2023; pp. 1667–1683. [Google Scholar]
- Nelson, B.; Barreno, M.; Chi, F.J.; Joseph, A.D.; Rubinstein, B.I.P.; Saini, U.; Sutton, C.; Tygar, J.D.; Xia, K. Exploiting Machine Learning to Subvert Your Spam Filter. In Proceedings of the 1st Usenix Workshop on Large-Scale Exploits and Emergent Threats, San Francisco, CA, USA, 15 April 2008; pp. 1–9. [Google Scholar]
- Li, B.; Wang, Y.; Singh, A.; Vorobeychik, Y. Data Poisoning Attacks on Factorization-Based Collaborative Filtering. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 1893–1901. [Google Scholar]
- Fang, M.; Yang, G.; Gong, N.Z.; Liu, J. Poisoning Attacks to Graph-Based Recommender Systems. In Proceedings of the 34th ACM Annual Computer Security Applications Conference, San Juan, PR, USA, 3–7 December 2018; pp. 381–392. [Google Scholar]
- Fang, M.; Gong, N.Z.; Liu, J. Influence Function Based Data Poisoning Attacks to Top-N Recommender Systems. In Proceedings of the Web Conference, New York, NY, USA, 20–24 April 2020; pp. 3019–3025. [Google Scholar]
- Shan, S.; Wenger, E.; Zhang, J.; Li, H.; Zheng, H.; Zhao, B.Y. Fawkes: Protecting Privacy against Unauthorized Deep Learning Models. In Proceedings of the 29th USENIX Security Symposium, Boston, MA, USA, 12–14 August 2020; pp. 1589–1604. [Google Scholar]
- Jiang, Y.; Xia, H. Adversarial attacks against dynamic graph neural networks via node injection. High-Confid. Comput. 2024, 4, 100185. [Google Scholar] [CrossRef]
- Douceur, J.R. The sybil attack. In Proceedings of the International Workshop on Peer-to-Peer Systems, Cambridge, MA, USA, 7–8 March 2002; Springer: Berlin/Heidelberg, Germany, 2002; pp. 251–260. [Google Scholar]
- Gürses, S.; Berendt, B. The social web and privacy: Practices, reciprocity and conflict detection in social networks. In Privacy-Aware Knowledge Discovery, Novel Applications and New Techniques; CRC Press: Boca Raton, FL, USA, 2010; pp. 395–429. [Google Scholar]
- Costa, H.; Merschmann, L.H.; Barth, F.; Benevenuto, F. Pollution, bad-mouthing, and local marketing: The underground of location-based social networks. Inf. Sci. 2014, 279, 123–137. [Google Scholar] [CrossRef]
- Sony, S.M.; Sasi, S.B. On-Off attack management based on trust. In Proceedings of the 2016 Online International Conference on Green Engineering and Technologies (IC-GET), Coimbatore, India, 19 November 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–4. [Google Scholar]
- Li, S.; Yang, J.; Liang, G.; Li, T.; Zhao, K. SybilFlyover: Heterogeneous graph-based fake account detection model on social networks. Knowl.-Based Syst. 2022, 258, 110038. [Google Scholar] [CrossRef]
- Adekunle, T.S.; Alabi, O.O.; Lawrence, M.O.; Ebong, G.N.; Ajiboye, G.O.; Bamisaye, T.A. The Use of AI to Analyze Social Media Attacks for Predictive Analytics. J. Comput. Theor. Appl. 2024, 2, 169–178. [Google Scholar]
- Bessi, A. Two samples test for discrete power-law distributions. arXiv 2015, arXiv:1503.00643. [Google Scholar]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-Law Distributions in Empirical Data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Sherchan, W.; Nepal, S.; Paris, C. A Survey of Trust in Social Networks. ACM Comput. Surv. 2013, 45, 47:1–47:33. [Google Scholar] [CrossRef]
- Zügner, D.; Akbarnejad, A.; Günnemann, S. Adversarial Attacks on Neural Networks for Graph Data. In Proceedings of the 24th ACM International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 2847–2856. [Google Scholar]
- Massa, P.; Salvetti, M.; Tomasoni, D. Bowling Alone and Trust Decline in Social Network Sites. In Proceedings of the 8th IEEE International Conference on Dependable, Autonomic and Secure Computing, Chengdu, China, 12–14 December 2009; pp. 658–663. [Google Scholar]
- Boguñá, M.; Pastor-Satorras, R.; Díaz-Guilera, A.; Arenas, A. Models of social networks based on social distance attachment. Phys. Rev. E 2004, 70, 056122. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Hooi, B.; Makhija, D.; Kumar, M.; Faloutsos, C.; Subrahmanian, V. Rev2: Fraudulent user prediction in rating platforms. In Proceedings of the Eleventh ACM International Conference on Web Search and Data Mining, Marina Del Rey, CA, USA, 5–9 February 2018; pp. 333–341. [Google Scholar]








| Title | Authors | Year | Innovation Points |
|---|---|---|---|
| The sybil attack [28]. | Douceur, J.R. | 2002 | The first attack method on social networks. |
| SybilGuard: Defending Against Sybil Attacks via Social Networks [2]. | Yu, H.; Kaminsky, M.; Gibbons, P.B.; Flaxman, A.D. | 2008 | A decentralized defense method against a sybil attack is proposed based on user characteristics. |
| SybilLimit: A Near-Optimal Social Network Defense against Sybil Attacks [1]. | Yu, H.; Gibbons, P.B.; Kaminsky, M.; Xiao, F. | 2008 | Based on Sybilguard, the use of the near-optimal approach allows for a further increase in the number of attack edges. |
| The social web and privacy: Practices, reciprocity and conflict detection in social networks [29]. | Gürses, S.; Berendt, B. | 2010 | Detecting conflict behavior attacks and modeling the real-world impacts of such attacks in social networks. |
| Pollution, bad-mouthing, and local marketing: The underground of location-based social networks [30]. | Costa, H.; Merschmann, L. H.; Barth, F.; Benevenuto, F. | 2014 | Research into attack and defense measures against bad-mouthing attacks within social networks, alongside the initial validation of the impact of such attacks in real environments. |
| On-off attack management based on trust [31]. | Sony, S.M.; Sasi, S.B. | 2016 | Defense mechanisms against on–off attacks utilizing predictability trust and sliding windows, coupled with a practical assessment to validate the efficacy of on–off attacks within social networks. |
| SybilFlyover: Heterogeneous graph-based fake account detection model on social networks [32]. | Siyu, L.; Jin, Y.; Gang, L.; Tianrui, L.; Kui, Z. | 2022 | Using the utilization of social data sourced from social networks for attacks and defenses. |
| Adversarial attacks against dynamic graph neural networks via node injection [27]. | Yanan, J.; Hui, X. | 2024 | Node injection attacks on dynamic graph neural networks based on graph structure vulnerability. |
| Advogato | PGP | BitcoinOTC | |
|---|---|---|---|
| # of nodes | 5.2 K | 10.7 K | 5.8 K |
| # of edges | 47.1 K | 24.3 K | 35.5 K |
| Density | 0.003548 | 0.000426 | 0.002490 |
| Maximum degree | 941 | 205 | 1298 |
| Minimum degree | 1 | 1 | 1 |
| Average degree | 18 | 4 | 12 |
| Parameters | Settings |
|---|---|
| Embedding_dim | 128 |
| Learning rate | 0.01 |
| Dropout rate | 0 |
| Normalization factor | |
| Layer numbers | [32, 64, 32] |
| Advogato | ||||
| Origin Network | 0.73 | |||
| Poisoning ratio | 5% | 10% | 15% | 20% |
| Random attack | 0.720 | 0.716 | 0.711 | 0.705 |
| Degree-centrality attack | 0.747 | 0.729 | 0.718 | 0.705 |
| Our attack | 0.680 | 0.660 | 0.632 | 0.604 |
| PGP | ||||
| Origin Network | 0.873 | |||
| Poisoning ratio | 5% | 10% | 15% | 20% |
| Random attack | 0.842 | 0.832 | 0.814 | 0.8 |
| Degree-centrality attack | 0.846 | 0.823 | 0.81 | 0.797 |
| Our attack | 0.688 | 0.67 | 0.654 | 0.645 |
| BitcoinOTC | ||||
| Origin Network | 0.898 | |||
| Poisoning ratio | 5% | 10% | 15% | 20% |
| Random attack | 0.878 | 0.856 | 0.836 | 0.824 |
| Degree-centrality attack | 0.869 | 0.848 | 0.842 | 0.829 |
| Our attack | 0.801 | 0.788 | 0.771 | 0.76 |
| Advogato | ||||
| Origin Network | 0.729 | |||
| Poisoning ratio | 5% | 10% | 15% | 20% |
| Random attack | 0.719 | 0.715 | 0.709 | 0.703 |
| Degree-centrality attack | 0.746 | 0.729 | 0.717 | 0.704 |
| Our attack | 0.678 | 0.658 | 0.628 | 0.6 |
| PGP | ||||
| Origin Network | 0.873 | |||
| Poisoning ratio | 5% | 10% | 15% | 20% |
| Random attack | 0.839 | 0.832 | 0.814 | 0.799 |
| Degree-centrality attack | 0.846 | 0.823 | 0.809 | 0.796 |
| Our attack | 0.672 | 0.652 | 0.635 | 0.628 |
| BitcoinOTC | ||||
| Origin Network | 0.889 | |||
| Poisoning ratio | 5% | 10% | 15% | 20% |
| Random attack | 0.871 | 0.848 | 0.828 | 0.815 |
| Degree-centrality attack | 0.862 | 0.841 | 0.835 | 0.823 |
| Our attack | 0.757 | 0.739 | 0.708 | 0.696 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Jiang, N.; Pei, K.; Wen, J.; Zhan, H.; Tu, Z. TPoison: Data-Poisoning Attack against GNN-Based Social Trust Model. Mathematics 2024, 12, 1813. https://doi.org/10.3390/math12121813
Zhao J, Jiang N, Pei K, Wen J, Zhan H, Tu Z. TPoison: Data-Poisoning Attack against GNN-Based Social Trust Model. Mathematics. 2024; 12(12):1813. https://doi.org/10.3390/math12121813
Chicago/Turabian StyleZhao, Jiahui, Nan Jiang, Kanglu Pei, Jie Wen, Hualin Zhan, and Ziang Tu. 2024. "TPoison: Data-Poisoning Attack against GNN-Based Social Trust Model" Mathematics 12, no. 12: 1813. https://doi.org/10.3390/math12121813
APA StyleZhao, J., Jiang, N., Pei, K., Wen, J., Zhan, H., & Tu, Z. (2024). TPoison: Data-Poisoning Attack against GNN-Based Social Trust Model. Mathematics, 12(12), 1813. https://doi.org/10.3390/math12121813






