Research on Quantile Regression Method for Longitudinal Interval-Censored Data Based on Bayesian Double Penalty
Abstract
1. Introduction
2. Model Building and Estimation Methods
2.1. Bayesian Tobit Hierarchical Quantile Regression Model for Longitudinal Interval-Censored Data
2.2. Bayesian Double Lasso Penalized Quantile Regression Method for Tobit Model
2.3. Bayesian Dual Adaptive Lasso Penalized Quantile Regression for Tobit Models
2.4. Gibbs Sampling Algorithm for Parameter Estimation and Variable Selection
2.4.1. Gibbs Sampling Algorithm for DL-BTQR
- (1)
- Given the initial value α(0), β(0), σ(0), from truncated normal distributions to generate unobserved latent variables ;
- (2)
- From conditional posterior distribution to generate νij;
- (3)
- From conditional posterior distribution to generate σ;
- (4)
- From conditional posterior distribution to generate sl;
- (5)
- From conditional posterior distribution to generate ;
- (6)
- From conditional posterior distribution to update the fixed effects coefficient β;
- (7)
- From conditional posterior distribution to generate rit;
- (8)
- From conditional posterior distribution to generate ;
- (9)
- From conditional posterior distribution to update the random effect coefficients αi;
2.4.2. Gibbs Sampling Algorithm for DAL-BTQR
- (1)
- Given the initial value α0, β0, τ, σ;
- (2)
- From conditional posterior distribution to generate νij; from truncated normal distributions to generate unobserved latent variables ;
- (3)
- From conditional posterior distribution to generate σ;
- (4)
- From conditional posterior distribution to generate rl;
- (5)
- From conditional posterior distribution to generate ;
- (6)
- From conditional posterior distribution to update the fixed effects coefficient β;
- (7)
- From conditional posterior distribution to generate sit;
- (8)
- From conditional posterior distribution to generate ;
- (9)
- From conditional posterior distribution to update the random effect coefficients αi;
3. Comparative Analysis of Monte Carlo Simulations
3.1. Comparative Analysis of Simulation Results at Different Quartiles
3.1.1. Simulation Results under Different Quartiles of Sparse Longitudinal Data
3.1.2. Simulation Results under Different Quartiles of Dense Longitudinal Data
3.2. Comparative Analysis of Simulation Results under Different Censoring Ratios
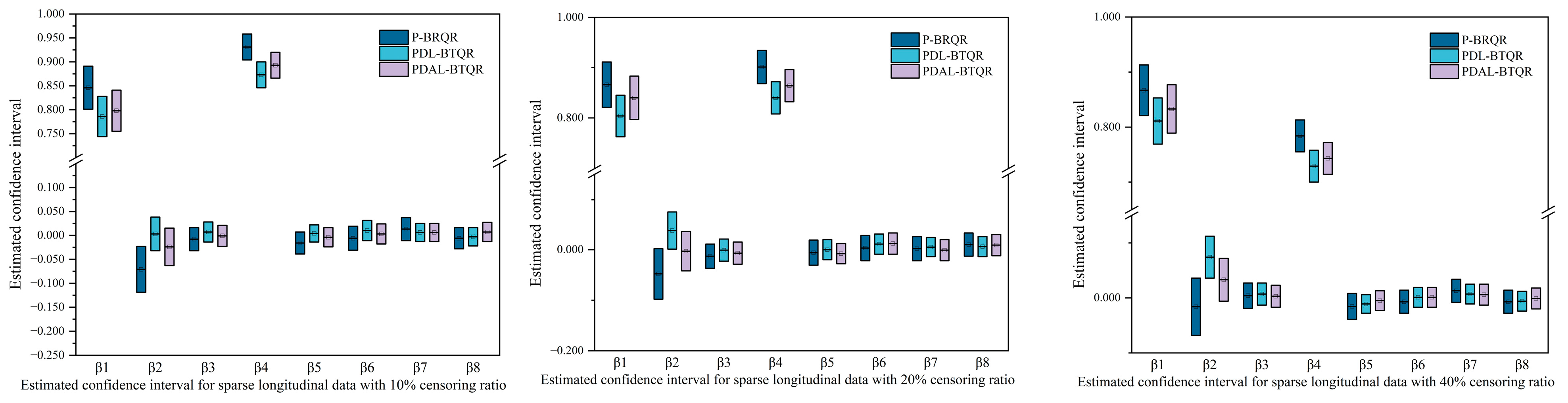
3.2.1. Simulation Results under Different Censoring Ratios of Sparse Longitudinal Data
3.2.2. Simulation Results under Different Censoring Ratios for Dense Longitudinal Data
3.3. Comparative Analysis of Simulation Results under Different Random Error Distributions
3.3.1. Simulation Results under Different Random Error Distributions for Sparse Longitudinal Data
3.3.2. Simulation Results under Different Random Error Distributions for Dense Longitudinal Data
3.4. Time Consumption for the Methods
- (1)
- Unpenalized Bayesian Tobit quantile regression for interval-censored data (P-BTQR);
- (2)
- Single-Lasso penalized Bayesian Tobit quantile regression for interval-censored data (PL-BTQR);
- (3)
- Single-Adaptive Lasso penalized Bayesian Tobit quantile regression for interval-censored data (PAL-BTQR);
- (4)
- Double-Lasso penalized Bayesian Tobit quantile regression for interval-censored data (PDL-BTQR);
- (5)
- Double-Adaptive Lasso penalized Bayesian Tobit quantile regression for interval-censored data (PDAL-BTQR)
4. Interprovincial Longitudinal Crime Rate Data Analysis
5. Discussion
6. Conclusions
- (1)
- Significantly improved model accuracy and efficiency
- (2)
- Demonstrated robustness in handling complex and variable datasets
- (3)
- New and effective tool for dealing with interval-censored data
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, X.K.; Ming, T. Marginal Models for Longitudinal Continuous Proportional Data. Biometrics 2000, 56, 496–502. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, S.; Cribari-Neto, F. Beta Regression or Modeling Rates and Proportions. J. Appl. Stat. 2004, 31, 799–815. [Google Scholar] [CrossRef]
- Lesaffre, E.; Rizopoulos, D.; Tsonaka, R. The logistic transform for bounded outcomes scores. Biostatistics 2007, 8, 72–85. [Google Scholar] [CrossRef] [PubMed]
- Espinheira, P.L.; Ferrari, S.L.P.; Cribari-Neto, F. Infuence diagnostics in beta regression. Comput. Stat. Data Anal. 2008, 52, 4417–4431. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, R.; Lv, Y.; Liu, J. Variable selection for varying dispersion beta regression model. J. Appl. Stat. 2014, 41, 95–108. [Google Scholar] [CrossRef]
- Ying, Z.L.; Yu, W.; Zhao, Z.Q.; Zheng, M. Regression Analysis of Doubly Truncated Data. J. Am. Stat. Assoc. 2019, 115, 810–821. [Google Scholar] [CrossRef] [PubMed]
- Tobin, J. Estimation of relationships for limited dependent variables. Econometrica 1958, 26, 24–36. [Google Scholar] [CrossRef]
- Cunha Danúbia, R.; Angelo, J.D.; Helton, S. On a log-symmetric quantile Tobit model applied to female labor supply data. J. Appl. Stat. 2022, 49, 4225–4253. [Google Scholar] [CrossRef]
- Powell, J.L. Censored regression quantiles. J. Econom. 1986, 32, 143–155. [Google Scholar] [CrossRef]
- Frumento, P. A quantile regression estimator for interval-censored data. Int. J. Biostat. 2023, 19, 81–96. [Google Scholar] [CrossRef]
- Li, L.; Hao, R.; Yang, X. Data Augmentation Based Quantile Regression Estimation for Censored Partially Linear Additive Model. Comput. Econ. 2023, 1–30. [Google Scholar] [CrossRef]
- Hao, R.; Weng, C.; Liu XYang, X. Data augmentation based estimation for the censored quantile regression neural network model. Expert Syst. Appl. 2023, 214, 119097. [Google Scholar] [CrossRef]
- Yu, R.; Long, X.; Quddus, M.; Wang, J.H. A Bayesian Tobit quantile regression approach for naturalistic longitudinal driving capability assessment. Accid. Anal. Prev. 2020, 147, 105779. [Google Scholar] [CrossRef] [PubMed]
- Tibshirani, R.J. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable Selection via Non-concave Penalized Likelihood and Its Oracle Properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Kim, S.M.; Lee, S.B.; Lee, S.H.; Kim, W. Robust estimation of outage costs in South Korea using a machine learning technique: Bayesian Tobit quantile regression. Appl. Energy 2020, 278, 115702. [Google Scholar] [CrossRef]
- Alhamzawi, R.; Keming, Y.; Dries, F.B. Bayesian adaptive Lasso quantile regression. Stat. Model. 2012, 12, 279–297. [Google Scholar] [CrossRef]
- Alhamzawi, R. Bayesian Elastic Net Tobit Quantile Regression. Commun. Stat.—Simul. Comput. 2016, 45, 2409–2427. [Google Scholar] [CrossRef]
- Alhusseini, F. New Bayesian Lasso in Tobit Quantile Regression. Rom. Statal Rev. Suppl. 2017, 65, 213–229. [Google Scholar]
- Alhamzawi, R.; Ali, M.T.H. Bayesian tobit quantile regression with penalty. Commun. Stat.—Simul. Comput. 2018, 47, 1739–1750. [Google Scholar] [CrossRef]
- Abbas, H.K. Bayesian Lasso Tobit regression. J. Al-Qadisiyah Comput. Sci. Math. 2019, 11, 1–13. [Google Scholar] [CrossRef]
- Kottas, A.; Krnjaji, M. Bayesian Semiparametric Modelling in Quantile Regression. Scand. J. Stat. 2009, 36, 297–319. [Google Scholar] [CrossRef]
- Narjes, G.; Reza, P. The likelihood and Bayesian analyses for asymmetric Laplace nonlinear regression model. Comput. Appl. Math. 2024, 43, 21. [Google Scholar]
- Mallows, D.F.; Andrews, L. Scale Mixtures of Normal Distributions. J. R. Stat. Soc. Ser. B Methodol. 1974, 36, 99–102. [Google Scholar]
- Zou, H. The Adaptive Lasso and Its Oracle Properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Alhamzawi, R.; Yu, K. Bayesian Lasso-mixed Quantile Regression. J. Stat. Comput. Simul. 2012, 84, 868–880. [Google Scholar] [CrossRef]
- Luo, Y.X.; Li, H.F. The Research of Double Adaptive Lasso Quantile Regression Model with Random Effects. J. Quant. Technol. Econ. 2017, 34, 136–148. [Google Scholar]
- Alhamzawi, R.; Ali, H.T.M. The Bayesian adaptive lasso regression. Math. Biosci. 2018, 303, 75–82. [Google Scholar] [CrossRef]
- Bhattacharya, A. Analysis of the Factors Affecting Violent Crime Rates in the US. Int. J. Eng. Manag. Res. 2020, 10, 106–109. [Google Scholar] [CrossRef]
- Shen, P.S. Median regression model with left truncated and interval-censored data. J. Korean Stat. Soc. 2013, 42, 469–479. [Google Scholar] [CrossRef]
- Zhou, X.; Feng YDu, X. Quantile regression for interval censored data. Commun. Stat.-Theory Methods 2017, 46, 3848–3863. [Google Scholar] [CrossRef]
- Cox David, R. Regression models and life-tables. J. R. Stat. Soc. Ser. B 1972, 34, 187–202. [Google Scholar]
- Angelov, A.G.; Magnus, E.; Klarizze, P.; Arcenas, A.; Bengt, K. Quantile regression with interval-censored data in questionnaire-based studies. Comput. Stat. 2022, 39, 583–603. [Google Scholar] [CrossRef]
- Dengluan, D.; Anmin, T.; Jinli, Y. High-Dimensional Variable Selection for Quantile Regression Based on Variational Bayesian Method. Mathematics 2023, 11, 2232. [Google Scholar] [CrossRef]
- Wang, Z.F.; Li, T.; Xiao, L.Q.; Tu, D.S. A threshold longitudinal Tobit quantile regression model for identification of treatment-sensitive subgroups based on interval-bounded longitudinal measurements and a continuous covariate. Stat. Med. 2023, 42, 4618–4631. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Wu, Y.; Cheng, W.L. Variational inference on a Bayesian adaptive lasso Tobit quantile regression model. Stat 2023, 12, 13. [Google Scholar] [CrossRef]
- Kobayashi, G. Bayesian Endogenous Tobit Quantile Regression. Bayesian Anal. 2017, 12, 161–191. [Google Scholar] [CrossRef]
- Alhusseini, H.H.F.; Georgescu, V. Bayesian composite Tobit quantile regression. J. Appl. Stat. 2017, 45, 727–739. [Google Scholar] [CrossRef]
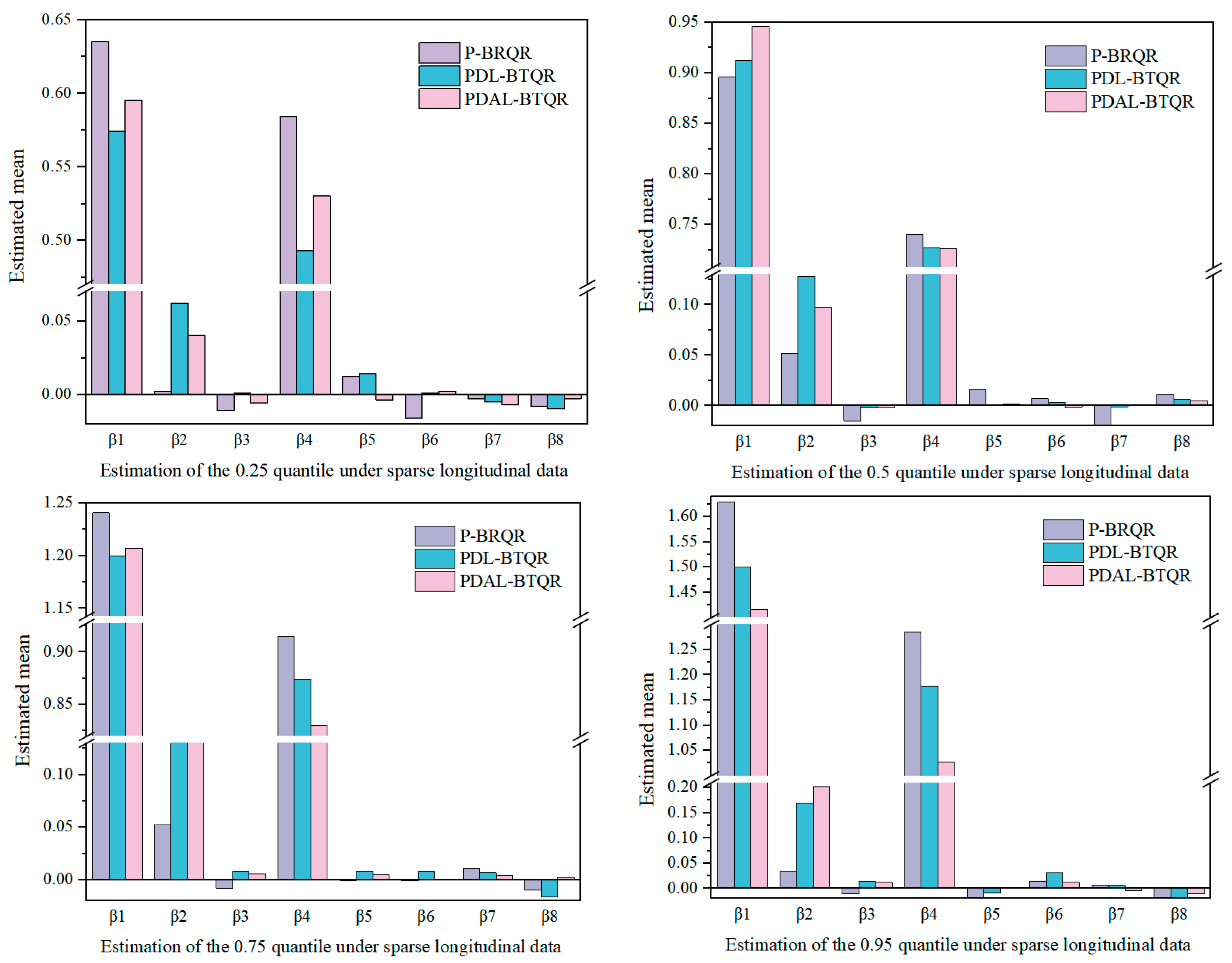


















| Method | Estimation | MSE | β1 | β2 | β3 | β4 | β5 | β6 | β7 | β8 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |||
| τ = 0.25 | ||||||||||
| P-BTQR | Mean | 0.070 | 0.635 | 0.002 | −0.011 | 0.584 | 0.012 | −0.016 | −0.003 | −0.008 |
| Sd | 0.152 | 0.227 | 0.251 | 0.107 | 0.241 | 0.190 | 0.139 | 0.108 | 0.105 | |
| Confidence interval | - | [0.591, 0.679] | [−0.047, 0.051] | [−0.032, 0.010] | [0.537, 0.631] | [−0.027, 0.051] | [−0.043, 0.011] | [−0.024, 0.018] | [−0.029, 0.013] | |
| PDL-BTQR | Mean | 0.079 | 0.574 | 0.062 | 0.001 | 0.493 | 0.014 | 0.001 | −0.005 | −0.010 |
| Sd | 0.137 | 0.198 | 0.195 | 0.081 | 0.244 | 0.170 | 0.999 | 0.083 | 0.078 | |
| Confidence interval | - | [0.536, 0.612] | [0.024, 0.099] | [−0.015, 0.017] | [0.445, 0.541] | [−0.019, 0.047] | [−0.019, 0.021] | [−0.021, 0.011] | [−0.026, 0.006] | |
| PDAL-BTQR | Mean | 0.067 | 0.595 | 0.040 | −0.006 | 0.530 | −0.004 | 0.002 | −0.007 | −0.003 |
| Sd | 0.061 | 0.209 | 0.216 | 0.085 | 0.163 | 0.096 | 0.082 | 0.086 | 0.072 | |
| Confidence interval | - | [0.555, 0.635] | [−0.003, 0.083] | [−0.022, 0.010] | [0.498, 0.562] | [−0.023, 0.015] | [−0.014, 0.018] | [−0.024, 0.010] | [−0.017, 0.011] | |
| τ = 0.5 | ||||||||||
| P-BTQR | Mean | 0.054 | 0.896 | 0.052 | −0.015 | 0.740 | 0.016 | 0.007 | −0.023 | 0.011 |
| Sd | 0.141 | 0.311 | 0.330 | 0.125 | 0.246 | 0.172 | 0.137 | 0.116 | 0.117 | |
| Confidence interval | - | [0.834, 0.958] | [−0.012, 0.116] | [−0.038, 0.008] | [0.690, 0.790] | [−0.017, 0.049] | [−0.021, 0.035] | [−0.044, −0.002] | [−0.011, 0.033] | |
| PDL-BTQR | Mean | 0.041 | 0.912 | 0.128 | −0.002 | 0.727 | 0.000 | 0.003 | −0.001 | 0.006 |
| Sd | 0.070 | 0.263 | 0.273 | 0.101 | 0.204 | 0.106 | 0.102 | 0.092 | 0.098 | |
| Confidence interval | - | [0.859, 0.965] | [0.075, 0.181] | [−0.021, 0.017] | [0.688, 0.766] | [−0.021, 0.021] | [−0.017, 0.023] | [−0.019, 0.017] | [−0.013, 0.025] | |
| PDAL-BTQR | Mean | 0.039 | 0.946 | 0.097 | −0.002 | 0.726 | 0.002 | −0.002 | 0.001 | 0.005 |
| Sd | 0.052 | 0.283 | 0.248 | 0.104 | 0.207 | 0.100 | 0.099 | 0.092 | 0.095 | |
| Confidence interval | - | [0.890, 1.002] | [0.049, 0.146] | [−0.023, 0.019] | [0.685, 0.767] | [−0.017, 0.021] | [−0.021, 0.017] | [−0.017, 0.019] | [−0.014, 0.024] | |
| τ = 0.75 | ||||||||||
| P-BTQR | Mean | 0.071 | 1.241 | 0.052 | −0.008 | 0.915 | −0.001 | −0.011 | 0.011 | −0.010 |
| Sd | 0.125 | 0.329 | 0.395 | 0.167 | 0.301 | 0.204 | 0.181 | 0.143 | 0.161 | |
| Confidence interval | - | [−0.024, 0.128] | [1.177, 1.305] | [−0.041, 0.025] | [0.853, 0.977] | [−0.041, 0.039] | [−0.047, 0.025] | [−0.018, 0.040] | [−0.040, 0.020] | |
| PDL-BTQR | Mean | 0.051 | 1.200 | 0.149 | 0.008 | 0.874 | 0.008 | 0.008 | 0.007 | −0.016 |
| Sd | 0.058 | 0.330 | 0.304 | 0.130 | 0.236 | 0.129 | 0.148 | 0.116 | 0.122 | |
| Confidence interval | - | [1.138, 1.262] | [0.088, 0.210] | [−0.018, 0.034] | [0.827, 0.921] | [−0.017, 0.033] | [−0.022, 0.038] | [−0.015, 0.029] | [−0.040, 0.008] | |
| PDAL-BTQR | Mean | 0.050 | 1.207 | 0.141 | 0.006 | 0.830 | 0.005 | 0.000 | 0.004 | 0.002 |
| Sd | 0.046 | 0.333 | 0.287 | 0.125 | 0.215 | 0.114 | 0.133 | 0.117 | 0.112 | |
| Confidence interval | - | [1.139, 1.275] | [0.086, 0.196] | [−0.018, 0.030] | [0.787, 0.873] | [−0.017, 0.027] | [−0.026, 0.026] | [−0.019, 0.027] | [−0.020, 0.024] | |
| τ = 0.95 | ||||||||||
| P-BTQR | Mean | 0.225 | 1.629 | 0.034 | −0.011 | 1.285 | −0.037 | 0.015 | 0.006 | −0.050 |
| Sd | 0.239 | 0.438 | 0.600 | 0.325 | 0.500 | 0.358 | 0.357 | 0.292 | 0.275 | |
| Confidence interval | - | [1.544, 1.714] | [−0.082, 0.150] | [−0.072, 0.050] | [1.188, 1.382] | [−0.106, 0.032] | [−0.054, 0.084] | [−0.052, 0.064] | [−0.104, 0.004] | |
| PDL-BTQR | Mean | 0.132 | 1.500 | 0.170 | 0.015 | 1.178 | −0.009 | 0.031 | 0.006 | −0.031 |
| Sd | 0.096 | 0.452 | 0.438 | 0.224 | 0.365 | 0.218 | 0.242 | 0.188 | 0.190 | |
| Confidence interval | - | [1.413, 1.587] | [0.084, 0.256] | [−0.029, 0.059] | [1.105, 1.251] | [−0.051, 0.033] | [−0.016, 0.078] | [−0.030, 0.042] | [−0.068, 0.006] | |
| PDAL-BTQR | Mean | 0.108 | 1.416 | 0.202 | 0.012 | 1.027 | 0.000 | 0.012 | −0.004 | −0.010 |
| Sd | 0.086 | 0.469 | 0.408 | 0.197 | 0.316 | 0.170 | 0.201 | 0.150 | 0.148 | |
| Confidence interval | - | [1.325, 1.507] | [0.125, 0.279] | [−0.027, 0.051] | [0.965, 1.089] | [−0.032, 0.033] | [−0.028, 0.052] | [−0.032, 0.025] | [−0.039, 0.019] | |
| Method | Estimation | MSE | β1 | β2 | β3 | β4 | β5 | β6 | β7 | β8 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | |||
| τ = 0.25 | ||||||||||
| P-BTQR | Mean | 0.074 | 0.642 | 0.704 | 0.314 | 0.349 | 0.315 | 0.316 | 0.304 | 0.329 |
| Sd | 0.021 | 0.204 | 0.207 | 0.127 | 0.151 | 0.143 | 0.107 | 0.151 | 0.129 | |
| Confidence interval | - | [0.602, 0.682] | [0.665, 0.743] | [0.289, 0.339] | [0.318, 0.380] | [0.286, 0.344] | [0.296, 0.336] | [0.275, 0.333] | [0.303, 0.355] | |
| PDL-BTQR | Mean | 0.070 | 0.663 | 0.755 | 0.302 | 0.328 | 0.318 | 0.294 | 0.319 | 0.319 |
| Sd | 0.025 | 0.187 | 0.207 | 0.118 | 0.148 | 0.137 | 0.114 | 0.127 | 0.119 | |
| Confidence interval | - | [0.626, 0.700] | [0.714, 0.796] | [0.279, 0.325] | [0.300, 0.356] | [0.291, 0.345] | [0.271, 0.317] | [0.295, 0.343] | [0.296, 0.342] | |
| PDAL-BTQR | Mean | 0.062 | 0.728 | 0.761 | 0.294 | 0.346 | 0.324 | 0.298 | 0.323 | 0.325 |
| Sd | 0.017 | 0.179 | 0.191 | 0.127 | 0.162 | 0.133 | 0.110 | 0.126 | 0.118 | |
| Confidence interval | - | [0.693, 0.763] | [0.723, 0.799] | [0.269, 0.319] | [0.312, 0.380] | [0.300, 0.349] | [0.278, 0.319] | [0.298, 0.348] | [0.303, 0.347] | |
| τ = 0.5 | ||||||||||
| P-BTQR | Mean | 0.040 | 0.899 | 1.058 | 0.358 | 0.402 | 0.366 | 0.359 | 0.366 | 0.398 |
| Sd | 0.018 | 0.237 | 0.243 | 0.126 | 0.146 | 0.143 | 0.136 | 0.127 | 0.126 | |
| Confidence interval | - | [0.851, 0.947] | [1.011, 1.105] | [0.333, 0.383] | [0.374, 0.430] | [0.338, 0.394] | [0.332, 0.386] | [0.342, 0.390] | [0.373, 0.423] | |
| PDL-BTQR | Mean | 0.039 | 0.902 | 1.040 | 0.365 | 0.404 | 0.359 | 0.376 | 0.370 | 0.390 |
| Sd | 0.018 | 0.227 | 0.230 | 0.129 | 0.138 | 0.138 | 0.138 | 0.131 | 0.129 | |
| Confidence interval | - | [0.860, 0.944] | [0.996, 1.084] | [0.340, 0.390] | [0.377, 0.431] | [0.331, 0.387] | [0.349, 0.403] | [0.344, 0.396] | [0.365, 0.415] | |
| PDAL-BTQR | Mean | 0.040 | 0.905 | 1.013 | 0.352 | 0.395 | 0.367 | 0.365 | 0.362 | 0.382 |
| Sd | 0.018 | 0.224 | 0.240 | 0.131 | 0.142 | 0.142 | 0.134 | 0.131 | 0.129 | |
| Confidence interval | - | [0.861, 0.949] | [0.965, 1.061] | [0.326, 0.378] | [0.366, 0.424] | [0.339, 0.395] | [0.339, 0.391] | [0.336, 0.388] | [0.357, 0.407] | |
| τ = 0.75 | ||||||||||
| P-BTQR | Mean | 0.059 | 1.085 | 1.290 | 0.372 | 0.466 | 0.399 | 0.404 | 0.425 | 0.426 |
| Sd | 0.033 | 0.284 | 0.302 | 0.172 | 0.169 | 0.155 | 0.160 | 0.171 | 0.175 | |
| Confidence interval | - | [1.027, 1.143] | [1.230, 1.350] | [0.337, 0.407] | [0.433, 0.499] | [0.369, 0.429] | [0.373, 0.435] | [0.393, 0.457] | [0.392, 0.460] | |
| PDL-BTQR | Mean | 0.056 | 1.099 | 1.297 | 0.383 | 0.460 | 0.389 | 0.430 | 0.421 | 0.405 |
| Sd | 0.033 | 0.269 | 0.298 | 0.149 | 0.148 | 0.146 | 0.164 | 0.148 | 0.171 | |
| Confidence interval | - | [1.044, 1.154] | [1.237, 1.357] | [0.353, 0.413] | [0.431, 0.489] | [0.361, 0.417] | [0.398, 0.462] | [0.393, 0.449] | [0.372, 0.438] | |
| PDAL-BTQR | Mean | 0.058 | 1.087 | 1.272 | 0.347 | 0.428 | 0.367 | 0.396 | 0.396 | 0.375 |
| Sd | 0.031 | 0.264 | 0.300 | 0.151 | 0.150 | 0.154 | 0.168 | 0.154 | 0.173 | |
| Confidence interval | - | [1.034, 1.140] | [1.214, 1.330] | [0.318, 0.376] | [0.399, 0.457] | [0.336, 0.398] | [0.363, 0.429] | [0.366, 0.426] | [0.341, 0.409] | |
| τ = 0.95 | ||||||||||
| P-BTQR | Mean | 0.245 | 1.469 | 1.806 | 0.524 | 0.645 | 0.576 | 0.546 | 0.641 | 0.572 |
| Sd | 0.124 | 0.438 | 0.478 | 0.316 | 0.339 | 0.327 | 0.329 | 0.330 | 0.320 | |
| Confidence interval | - | [1.380, 1.558] | [1.710, 1.902] | [0.462, 0.586] | [0.578, 0.712] | [0.511, 0.641] | [0.481, 0.611] | [0.580, 0.703] | [0.510, 0.634] | |
| PDL-BTQR | Mean | 0.201 | 1.399 | 1.765 | 0.498 | 0.590 | 0.495 | 0.532 | 0.544 | 0.493 |
| Sd | 0.116 | 0.410 | 0.449 | 0.265 | 0.287 | 0.264 | 0.300 | 0.288 | 0.307 | |
| Confidence interval | - | [1.320, 1.478] | [1.677, 1.853] | [0.446, 0.550] | [0.533, 0.646] | [0.445, 0.545] | [0.475, 0.589] | [0.489, 0.599] | [0.433, 0.553] | |
| PDAL-BTQR | Mean | 0.193 | 1.295 | 1.753 | 0.371 | 0.506 | 0.431 | 0.419 | 0.479 | 0.406 |
| Sd | 0.117 | 0.409 | 0.504 | 0.255 | 0.284 | 0.230 | 0.282 | 0.271 | 0.285 | |
| Confidence interval | - | [1.216, 1.374] | [1.655, 1.851] | [0.323, 0.419] | [0.451, 0.561] | [0.387, 0.475] | [0.365, 0.473] | [0.428, 0.530] | [0.350, 0.462] | |
| Method | Estimation | MSE | β1 | β2 | β3 | β4 | β5 | β6 | β7 | β8 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |||
| Censoring ratio = 10% | ||||||||||
| P-BTQR | Mean | 0.029 | 0.846 | −0.071 | −0.008 | 0.931 | −0.016 | −0.006 | 0.013 | −0.006 |
| Sd | 0.026 | 0.232 | 0.242 | 0.127 | 0.138 | 0.116 | 0.129 | 0.120 | 0.115 | |
| Confidence interval | - | [0.801, 0.891] | [−0.119, −0.023] | [−0.032, 0.016] | [0.904, 0.958] | [−0.039, 0.007] | [−0.031, 0.019] | [−0.011, 0.037] | [−0.028, 0.016] | |
| PDL-BTQR | Mean | 0.026 | 0.786 | 0.003 | 0.007 | 0.873 | 0.004 | 0.010 | 0.006 | −0.003 |
| Sd | 0.016 | 0.215 | 0.183 | 0.108 | 0.132 | 0.092 | 0.105 | 0.100 | 0.096 | |
| Confidence interval | - | [0.744, 0.828] | [−0.032, 0.038] | [−0.014, 0.028] | [0.846, 0.900] | [−0.014, 0.022] | [−0.011, 0.031] | [−0.013, 0.025] | [−0.022, 0.016] | |
| PDAL-BTQR | Mean | 0.025 | 0.798 | −0.024 | −0.001 | 0.893 | −0.004 | 0.003 | 0.006 | 0.007 |
| Sd | 0.015 | 0.224 | 0.197 | 0.111 | 0.134 | 0.101 | 0.106 | 0.098 | 0.101 | |
| Confidence interval | - | [0.755, 0.841] | [−0.063, 0.015] | [−0.023, 0.021] | [0.866, 0.920] | [−0.024, 0.016] | [−0.018, 0.024] | [−0.013, 0.025] | [−0.013, 0.027] | |
| Censoring ratio = 20% | ||||||||||
| P-BTQR | Mean | 0.030 | 0.866 | −0.048 | −0.013 | 0.901 | −0.006 | 0.003 | 0.002 | 0.010 |
| Sd | 0.018 | 0.228 | 0.248 | 0.123 | 0.162 | 0.129 | 0.124 | 0.126 | 0.118 | |
| Confidence interval | - | [0.821, 0.911] | [−0.098, 0.002] | [−0.037, 0.011] | [0.868, 0.934] | [−0.031, 0.019] | [−0.022, 0.028] | [−0.022, 0.026] | [−0.013, 0.033] | |
| PDL-BTQR | Mean | 0.027 | 0.804 | 0.038 | −0.001 | 0.840 | 0.000 | 0.011 | 0.005 | 0.006 |
| Sd | 0.017 | 0.212 | 0.188 | 0.106 | 0.160 | 0.102 | 0.101 | 0.104 | 0.102 | |
| Confidence interval | - | [0.763, 0.845] | [0.001, 0.075] | [−0.023, 0.021] | [0.808, 0.872] | [−0.020, 0.020] | [−0.009, 0.031] | [−0.014, 0.024] | [−0.014, 0.026] | |
| PDAL-BTQR | Mean | 0.026 | 0.840 | −0.003 | −0.007 | 0.864 | −0.008 | 0.012 | −0.001 | 0.009 |
| Sd | 0.016 | 0.223 | 0.199 | 0.112 | 0.158 | 0.103 | 0.108 | 0.105 | 0.106 | |
| Confidence interval | - | [0.797, 0.883] | [−0.042, 0.036] | [−0.029, 0.015] | [0.832, 0.896] | [−0.028, 0.012] | [−0.009, 0.033] | [−0.022, 0.020] | [−0.012, 0.030] | |
| Censoring ratio = 40% | ||||||||||
| P-BTQR | Mean | 0.033 | 0.867 | −0.016 | 0.004 | 0.784 | −0.014 | −0.007 | 0.013 | −0.007 |
| Sd | 0.018 | 0.234 | 0.253 | 0.124 | 0.148 | 0.115 | 0.108 | 0.107 | 0.107 | |
| Confidence interval | - | [0.821, 0.913] | [−0.068, 0.036] | [−0.019, 0.027] | [0.755, 0.813] | [−0.039, 0.008] | [−0.028, 0.014] | [−0.008, 0.034] | [−0.028, 0.014] | |
| PDL-BTQR | Mean | 0.032 | 0.811 | 0.074 | 0.007 | 0.729 | −0.011 | 0.001 | 0.007 | −0.006 |
| Sd | 0.019 | 0.219 | 0.197 | 0.102 | 0.145 | 0.090 | 0.092 | 0.096 | 0.092 | |
| Confidence interval | - | [0.769, 0.853] | [0.036, 0.112] | [−0.013, 0.027] | [0.700, 0.758] | [−0.028, 0.006] | [−0.017, 0.019] | [−0.011, 0.025] | [−0.024, 0.012] | |
| PDAL-BTQR | Mean | 0.031 | 0.833 | 0.033 | 0.003 | 0.743 | −0.005 | 0.001 | 0.006 | −0.001 |
| Sd | 0.018 | 0.225 | 0.200 | 0.103 | 0.147 | 0.094 | 0.092 | 0.099 | 0.095 | |
| Confidence interval | - | [0.789, 0.877] | [−0.006, 0.072] | [−0.017, 0.023] | [0.714, 0.772] | [−0.023, 0.013] | [−0.017, 0.019] | [−0.013, 0.025] | [−0.020, 0.018] | |
| Method | Estimation | MSE | β1 | β2 | β3 | β4 | β5 | β6 | β7 | β8 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | |||
| Censoring ratio = 10% | ||||||||||
| P-BTQR | Mean | 0.042 | 0.810 | 0.787 | 0.441 | 0.492 | 0.431 | 0.464 | 0.474 | 0.459 |
| Sd | 0.015 | 0.255 | 0.257 | 0.147 | 0.143 | 0.164 | 0.143 | 0.119 | 0.134 | |
| Confidence interval | - | [0.759, 0.861] | [0.736, 0.838] | [0.413, 0.469] | [0.464, 0.520] | [0.399, 0.463] | [0.437, 0.491] | [0.450, 0.498] | [0.434, 0.484] | |
| PDL-BTQR | Mean | 0.040 | 0.793 | 0.826 | 0.444 | 0.466 | 0.428 | 0.435 | 0.459 | 0.441 |
| Sd | 0.020 | 0.226 | 0.248 | 0.137 | 0.144 | 0.149 | 0.151 | 0.140 | 0.131 | |
| Confidence interval | - | [0.748, 0.838] | [0.778, 0.874] | [0.417, 0.471] | [0.438, 0.494] | [0.399, 0.457] | [0.405, 0.465] | [0.433, 0.485] | [0.416, 0.466] | |
| PDAL-BTQR | Mean | 0.041 | 0.793 | 0.817 | 0.436 | 0.465 | 0.430 | 0.443 | 0.451 | 0.440 |
| Sd | 0.021 | 0.235 | 0.256 | 0.140 | 0.150 | 0.160 | 0.149 | 0.140 | 0.139 | |
| Confidence interval | - | [0.748, 0.838] | [0.766, 0.868] | [0.408, 0.464] | [0.435, 0.495] | [0.399, 0.461] | [0.413, 0.473] | [0.424, 0.478] | [0.413, 0.467] | |
| Censoring ratio = 20% | ||||||||||
| P-BTQR | Mean | 0.044 | 0.848 | 0.845 | 0.425 | 0.482 | 0.434 | 0.417 | 0.427 | 0.455 |
| Sd | 0.019 | 0.269 | 0.286 | 0.160 | 0.171 | 0.155 | 0.136 | 0.151 | 0.127 | |
| Confidence interval | - | [0.796, 0.900] | [0.789, 0.901] | [0.393, 0.457] | [0.448, 0.516] | [0.403, 0.465] | [0.391, 0.443] | [0.398, 0.456] | [0.430, 0.480] | |
| PDL-BTQR | Mean | 0.038 | 0.840 | 0.904 | 0.420 | 0.456 | 0.418 | 0.431 | 0.430 | 0.421 |
| Sd | 0.020 | 0.233 | 0.258 | 0.143 | 0.157 | 0.145 | 0.138 | 0.151 | 0.131 | |
| Confidence interval | - | [0.795, 0.885] | [0.852, 0.956] | [0.392, 0.448] | [0.426, 0.486] | [0.390, 0.446] | [0.402, 0.460] | [0.403, 0.457] | [0.395, 0.447] | |
| PDAL-BTQR | Mean | 0.039 | 0.841 | 0.890 | 0.418 | 0.453 | 0.422 | 0.421 | 0.434 | 0.439 |
| Sd | 0.020 | 0.234 | 0.266 | 0.144 | 0.165 | 0.149 | 0.137 | 0.154 | 0.138 | |
| Confidence interval | - | [0.796, 0.886] | [0.838, 0.942] | [0.389, 0.447] | [0.420, 0.486] | [0.393, 0.451] | [0.393, 0.449] | [0.404, 0.464] | [0.412, 0.466] | |
| Censoring ratio = 40% | ||||||||||
| P-BTQR | Mean | 0.048 | 0.793 | 0.830 | 0.375 | 0.388 | 0.362 | 0.355 | 0.371 | 0.382 |
| Sd | 0.018 | 0.233 | 0.237 | 0.145 | 0.147 | 0.152 | 0.137 | 0.129 | 0.130 | |
| Confidence interval | - | [0.748, 0.838] | [0.784, 0.876] | [0.346, 0.404] | [0.360, 0.416] | [0.332, 0.392] | [0.328, 0.382] | [0.345, 0.397] | [0.357, 0.407] | |
| PDL-BTQR | Mean | 0.046 | 0.794 | 0.876 | 0.373 | 0.382 | 0.356 | 0.374 | 0.371 | 0.374 |
| Sd | 0.019 | 0.214 | 0.228 | 0.139 | 0.147 | 0.134 | 0.135 | 0.139 | 0.134 | |
| Confidence interval | - | [0.752, 0.836] | [0.830, 0.922] | [0.346, 0.400] | [0.354, 0.410] | [0.329, 0.383] | [0.347, 0.401] | [0.345, 0.397] | [0.348, 0.400] | |
| PDAL-BTQR | Mean | 0.047 | 0.800 | 0.861 | 0.358 | 0.372 | 0.356 | 0.368 | 0.366 | 0.384 |
| Sd | 0.021 | 0.209 | 0.237 | 0.145 | 0.148 | 0.145 | 0.131 | 0.140 | 0.135 | |
| Confidence interval | - | [0.761, 0.839] | [0.815, 0.907] | [0.329, 0.387] | [0.343, 0.401] | [0.327, 0.385] | [0.342, 0.394] | [0.339, 0.393] | [0.358, 0.410] | |
| Method | Estimation | MSE | β1 | β2 | β3 | β4 | β5 | β6 | β7 | β8 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |||
| N(0,1) | ||||||||||
| P-BTQR | Mean | 0.054 | 0.896 | 0.052 | −0.015 | 0.740 | 0.016 | 0.007 | −0.023 | 0.011 |
| Sd | 0.141 | 0.311 | 0.330 | 0.125 | 0.246 | 0.172 | 0.137 | 0.116 | 0.117 | |
| Confidence interval | - | [0.834, 0.958] | [−0.012, 0.116] | [−0.038, 0.008] | [0.690, 0.790] | [−0.017, 0.049] | [−0.021, 0.035] | [−0.044, −0.002] | [−0.011, 0.033] | |
| PDL-BTQR | Mean | 0.041 | 0.912 | 0.128 | −0.002 | 0.727 | 0.000 | 0.003 | −0.001 | 0.006 |
| Sd | 0.070 | 0.263 | 0.273 | 0.101 | 0.204 | 0.106 | 0.102 | 0.092 | 0.098 | |
| Confidence interval | - | [0.859, 0.965] | [0.075, 0.181] | [−0.021, 0.017] | [0.688, 0.766] | [−0.021, 0.021] | [−0.017, 0.023] | [−0.019, 0.017] | [−0.013, 0.025] | |
| PDAL-BTQR | Mean | 0.039 | 0.946 | 0.097 | −0.002 | 0.726 | 0.002 | −0.002 | 0.001 | 0.005 |
| Sd | 0.052 | 0.283 | 0.248 | 0.104 | 0.207 | 0.100 | 0.099 | 0.092 | 0.095 | |
| Confidence interval | - | [0.890, 1.002] | [0.049, 0.146] | [−0.023, 0.019] | [0.685, 0.767] | [−0.017, 0.021] | [−0.021, 0.017] | [−0.017, 0.019] | [−0.014, 0.024] | |
| t(3) | ||||||||||
| P-BTQR | Mean | 0.077 | 1.248 | 0.133 | −0.029 | 0.944 | −0.016 | 0.058 | −0.075 | 0.006 |
| Sd | 0.041 | 0.324 | 0.347 | 0.229 | 0.207 | 0.237 | 0.227 | 0.231 | 0.227 | |
| Confidence interval | - | [1.186, 1.310] | [0.064, 0.202] | [−0.072, 0.015] | [0.903, 0.985] | [−0.061, 0.029] | [0.013, 0.103] | [−0.121, −0.029] | [−0.037, 0.049] | |
| PDL-BTQR | Mean | 0.057 | 1.178 | 0.250 | 0.010 | 0.918 | 0.022 | 0.051 | −0.047 | −0.003 |
| Sd | 0.034 | 0.308 | 0.254 | 0.172 | 0.215 | 0.201 | 0.179 | 0.162 | 0.175 | |
| Confidence interval | - | [1.120, 1.236] | [0.200, 0.300] | [−0.022, 0.042] | [0.877, 0.959] | [−0.017, 0.061] | [0.017, 0.085] | [−0.079, −0.015] | [−0.035, 0.029] | |
| PDAL-BTQR | Mean | 0.056 | 1.190 | 0.208 | −0.009 | 0.901 | 0.008 | 0.044 | −0.043 | 0.006 |
| Sd | 0.033 | 0.305 | 0.257 | 0.168 | 0.201 | 0.201 | 0.189 | 0.178 | 0.178 | |
| Confidence interval | - | [1.129, 1.251] | [0.158, 0.258] | [−0.042, 0.024] | [0.862, 0.940] | [−0.031, 0.047] | [0.008, 0.080] | [−0.077, −0.009] | [−0.027, 0.039] | |
| ALD | ||||||||||
| P-BTQR | Mean | 0.044 | 1.118 | 0.054 | 0.006 | 0.852 | 0.007 | −0.022 | −0.006 | 0.016 |
| Sd | 0.028 | 0.327 | 0.306 | 0.123 | 0.173 | 0.128 | 0.152 | 0.138 | 0.134 | |
| Confidence interval | - | [1.057, 1.179] | [−0.005, 0.113] | [−0.019, 0.031] | [0.818, 0.886] | [−0.018, 0.032] | [−0.051, 0.007] | [−0.033, 0.021] | [−0.010, 0.042] | |
| PDL-BTQR | Mean | 0.037 | 1.059 | 0.138 | 0.024 | 0.837 | 0.010 | −0.012 | 0.007 | 0.004 |
| Sd | 0.025 | 0.328 | 0.246 | 0.112 | 0.176 | 0.099 | 0.122 | 0.110 | 0.112 | |
| Confidence interval | - | [0.997, 1.121] | [0.090, 0.186] | [0.002, 0.046] | [0.802, 0.872] | [−0.009, 0.029] | [−0.036, 0.012] | [−0.014, 0.028] | [−0.018, 0.026] | |
| PDAL-BTQR | Mean | 0.037 | 1.091 | 0.110 | 0.010 | 0.836 | 0.008 | −0.022 | 0.007 | 0.001 |
| Sd | 0.025 | 0.320 | 0.253 | 0.113 | 0.171 | 0.100 | 0.125 | 0.106 | 0.111 | |
| Confidence interval | - | [1.029, 1.153] | [0.061, 0.159] | [−0.013, 0.033] | [0.802, 0.870] | [−0.012, 0.028] | [−0.046, 0.002] | [−0.013, 0.027] | [−0.021, 0.023] | |
| Method | Estimation | MSE | β1 | β2 | β3 | β4 | β5 | β6 | β7 | β8 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | |||
| N(0,1) | ||||||||||
| P-BTQR | Mean | 0.040 | 0.899 | 1.058 | 0.358 | 0.402 | 0.366 | 0.359 | 0.366 | 0.398 |
| Sd | 0.018 | 0.237 | 0.243 | 0.126 | 0.146 | 0.143 | 0.136 | 0.127 | 0.126 | |
| Confidence interval | - | [0.851, 0.947] | [1.011, 1.105] | [0.333, 0.383] | [0.374, 0.430] | [0.338, 0.394] | [0.332, 0.386] | [0.342, 0.390] | [0.373, 0.423] | |
| PDL-BTQR | Mean | 0.039 | 0.902 | 1.040 | 0.365 | 0.404 | 0.359 | 0.376 | 0.370 | 0.390 |
| Sd | 0.018 | 0.227 | 0.230 | 0.129 | 0.138 | 0.138 | 0.138 | 0.131 | 0.129 | |
| Confidence interval | - | [0.860, 0.944] | [0.996, 1.084] | [0.340, 0.390] | [0.377, 0.431] | [0.331, 0.387] | [0.349, 0.403] | [0.344, 0.396] | [0.365, 0.415] | |
| PDAL-BTQR | Mean | 0.040 | 0.905 | 1.013 | 0.352 | 0.395 | 0.367 | 0.365 | 0.362 | 0.382 |
| Sd | 0.018 | 0.224 | 0.240 | 0.131 | 0.142 | 0.142 | 0.134 | 0.131 | 0.129 | |
| Confidence interval | - | [0.861, 0.949] | [0.965, 1.061] | [0.326, 0.378] | [0.366, 0.424] | [0.339, 0.395] | [0.339, 0.391] | [0.336, 0.388] | [0.357, 0.407] | |
| t(3) | ||||||||||
| P-BTQR | Mean | 0.074 | 1.056 | 1.231 | 0.370 | 0.438 | 0.362 | 0.434 | 0.355 | 0.376 |
| Sd | 0.041 | 0.293 | 0.323 | 0.215 | 0.214 | 0.213 | 0.218 | 0.218 | 0.214 | |
| Confidence interval | - | [0.999, 1.113] | [1.171, 1.291] | [0.330, 0.410] | [0.397, 0.479] | [0.320, 0.404] | [0.391, 0.477] | [0.312, 0.398] | [0.335, 0.417] | |
| PDL-BTQR | Mean | 0.065 | 1.061 | 1.208 | 0.381 | 0.447 | 0.380 | 0.453 | 0.357 | 0.375 |
| Sd | 0.034 | 0.280 | 0.293 | 0.199 | 0.205 | 0.200 | 0.208 | 0.208 | 0.204 | |
| Confidence interval | - | [1.006, 1.116] | [1.152, 1.264] | [0.343, 0.419] | [0.407, 0.487] | [0.341, 0.419] | [0.413, 0.493] | [0.316, 0.398] | [0.336, 0.414] | |
| PDAL-BTQR | Mean | 0.068 | 1.039 | 1.184 | 0.350 | 0.425 | 0.346 | 0.424 | 0.335 | 0.354 |
| Sd | 0.035 | 0.278 | 0.296 | 0.199 | 0.213 | 0.207 | 0.201 | 0.199 | 0.207 | |
| Confidence interval | - | [0.984, 1.094] | [1.128, 1.240] | [0.312, 0.388] | [0.385, 0.465] | [0.306, 0.386] | [0.385, 0.463] | [0.300, 0.373] | [0.315, 0.393] | |
| ALD | ||||||||||
| P-BTQR | Mean | 0.046 | 1.011 | 1.155 | 0.400 | 0.411 | 0.419 | 0.374 | 0.414 | 0.410 |
| Sd | 0.030 | 0.296 | 0.297 | 0.144 | 0.142 | 0.133 | 0.146 | 0.137 | 0.145 | |
| Confidence interval | - | [0.953, 1.069] | [1.097, 1.213] | [0.372, 0.428] | [0.383, 0.439] | [0.393, 0.445] | [0.346, 0.402] | [0.387, 0.441] | [0.382, 0.438] | |
| PDL-BTQR | Mean | 0.043 | 1.022 | 1.133 | 0.407 | 0.422 | 0.416 | 0.402 | 0.406 | 0.397 |
| Sd | 0.026 | 0.283 | 0.287 | 0.137 | 0.143 | 0.132 | 0.144 | 0.138 | 0.147 | |
| Confidence interval | - | [0.968, 1.076] | [1.076, 1.190] | [0.381, 0.433] | [0.395, 0.449] | [0.391, 0.441] | [0.373, 0.431] | [0.379, 0.433] | [0.368, 0.426] | |
| PDAL-BTQR | Mean | 0.044 | 1.015 | 1.112 | 0.393 | 0.404 | 0.413 | 0.383 | 0.406 | 0.396 |
| Sd | 0.025 | 0.282 | 0.279 | 0.142 | 0.148 | 0.139 | 0.153 | 0.148 | 0.151 | |
| Confidence interval | - | [0.961, 1.069] | [1.056, 1.168] | [0.366, 0.420] | [0.375, 0.433] | [0.386, 0.440] | [0.354, 0.412] | [0.376, 0.436] | [0.367, 0.424] | |
| Methods | User Time | System Time | Elapsed Time |
|---|---|---|---|
| P-BTQR | 0.224 | 0.069 | 54.840 |
| PL-BTQR | 0.247 | 0.084 | 102.377 |
| PAL-BTQR | 0.219 | 0.043 | 104.179 |
| PDL-BTQR | 0.241 | 0.028 | 95.354 |
| PDAL-BTQR | 0.238 | 0.033 | 98.353 |
| Variant | Name | Define | Mean | Sd | Max | Min |
|---|---|---|---|---|---|---|
| Y | Crime rate | Number of criminal suspects arrested by the Public Prosecutor’s Office per 10,000 population | 6.684 | 2.301 | 14.840 | 3.549 |
| X1 | Per capita GDP | GDP output per unit of population | 4.277 | 2.088 | 12.319 | 1.299 |
| X2 | Urbanization rate | Ratio of regional urban population to total population | 0.543 | 0.137 | 0.896 | 0.222 |
| X3 | Regional income gap | Difference between per capita disposable income of regional residents and per capita disposable income of national residents | 0.545 | 0.543 | 3.048 | 0.002 |
| X4 | Educational level | Average number of students enrolled in higher education per 100,000 population | 0.247 | 0.086 | 0.620 | 0.108 |
| X5 | Unemployment rate | Urban registered unemployment rate | 3.369 | 0.654 | 4.500 | 1.200 |
| Variant | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| PDL-BTQR | |||||||||
| Per capita GDP | −0.097 | −0.079 | −0.060 | −0.068 | −0.099 | −0.134 | −0.153 | −0.117 | −0.010 |
| Urbanization rate | 0.456 | 0.423 | 0.406 | 0.424 | 0.449 | 0.442 | 0.380 | 0.334 | 0.264 |
| Regional income disparities | 0.161 | 0.178 | 0.175 | 0.182 | 0.201 | 0.232 | 0.273 | 0.229 | 0.125 |
| Educational level | −0.399 | −0.366 | −0.359 | −0.392 | −0.428 | −0.430 | −0.413 | −0.358 | −0.298 |
| Unemployment rate | −0.102 | −0.117 | −0.135 | −0.171 | −0.211 | −0.240 | −0.249 | −0.212 | −0.151 |
| PDAL-BTQR | |||||||||
| Per capita GDP | −0.162 | −0.129 | −0.111 | −0.119 | −0.153 | −0.195 | −0.230 | −0.208 | −0.046 |
| Urbanization rate | 0.610 | 0.581 | 0.536 | 0.546 | 0.572 | 0.563 | 0.510 | 0.473 | 0.356 |
| Regional income disparities | 0.187 | 0.199 | 0.206 | 0.212 | 0.240 | 0.281 | 0.319 | 0.277 | 0.169 |
| Educational level | −0.592 | −0.592 | −0.585 | −0.602 | −0.646 | −0.643 | −0.630 | −0.556 | −0.475 |
| Unemployment rate | −0.126 | −0.149 | −0.166 | −0.190 | −0.239 | −0.257 | −0.259 | −0.218 | −0.163 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, K.; Shu, T.; Hu, C.; Luo, Y. Research on Quantile Regression Method for Longitudinal Interval-Censored Data Based on Bayesian Double Penalty. Mathematics 2024, 12, 1782. https://doi.org/10.3390/math12121782
Zhao K, Shu T, Hu C, Luo Y. Research on Quantile Regression Method for Longitudinal Interval-Censored Data Based on Bayesian Double Penalty. Mathematics. 2024; 12(12):1782. https://doi.org/10.3390/math12121782
Chicago/Turabian StyleZhao, Ke, Ting Shu, Chaozhu Hu, and Youxi Luo. 2024. "Research on Quantile Regression Method for Longitudinal Interval-Censored Data Based on Bayesian Double Penalty" Mathematics 12, no. 12: 1782. https://doi.org/10.3390/math12121782
APA StyleZhao, K., Shu, T., Hu, C., & Luo, Y. (2024). Research on Quantile Regression Method for Longitudinal Interval-Censored Data Based on Bayesian Double Penalty. Mathematics, 12(12), 1782. https://doi.org/10.3390/math12121782






