Exploring the Extended Beta-Logarithmic Function: Matrix Arguments and Properties

Abstract

The beta-logarithmic function substantially generalizes the standard beta function, which is widely recognized for its significance in many applications. This article is devoted to the study of a generalization of the classical beta-logarithmic function in a matrix setting called the extended beta-logarithmic matrix function. The proofs of some essential properties of this extension, such as convergence, partial derivative formulas, functional relations, integral representations, inequalities, and finite and infinite sums, are established. Moreover, an application of the extended beta-logarithmic function in matrix arguments is proposed in probability theory. Further, numerical examples and graphical presentations of the new generalization are obtained.

1. Introduction and Preliminaries

Special functions, which are natural generalizations of elementary functions, are derived by solving partial differential equations that satisfy a specific set of conditions. For centuries, many special functions have been developed and implemented in various fields, including combinatorics, chemistry, statistics, physics, and engineering (see, e.g., [1,2,3]).

On the other hand, recent extensions of special functions build upon the work of esteemed researchers such as Abdalla et al. [4,5], Abd-Elmageed et al. [6], Hidan et al. [7], Fuli He et al. [8], and Cuchta et al. [9], who have shown a strong interest in studying the extension of special functions in matrix arguments. Contributions to the field by considering various extensions of the gamma, beta, and hypergeometric matrix functions have been documented in [10,11,12,13,14]. Inspired by earlier studies, a new extension of the beta function in its matrix version is presented: the extended beta-logarithmic matrix function (EBLMF). An application and discussion of some of its analytic and numerical properties were also provided. One can easily obtain various applications from the close relationship of EBLMF with several special functions.

This paper is structured as follows: Section 2 gives the definition of the extended beta-logarithmic matrix function and studies its convergence properties and partial derivative formulas. Section 3 presents various properties of the EBLMF, including functional relations, inequalities, infinite sums, finite sums, and integral formulas. In Section 4, an application of the extended beta-logarithmic function in matrix arguments is offered. Section 5 provides numerical illustration examples and graphical descriptions of the EBLMF and some exceptional cases. Finally, in Section 6, we conclude with some final remarks.

Following [15,16], let ${\mathcal{M}}_{\kappa }$ be the vector space of all the $\kappa \times \kappa$ Hermitian positive stable matrices of order $\kappa \in \mathbb{N}$ whose entries are in the set of complex number $\mathcal{C}.$ For a matrix $\mathsf{\Lambda }\in {\mathcal{M}}_{\kappa },$ let $\rho \left(\mathsf{\Lambda }\right)$ be the set of all eigenvalues of $\mathsf{\Lambda }$, which is called the spectrum of $\mathsf{\Lambda },$ and

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mu }_{max}\left(\mathsf{\Lambda }\right)=max\{\mathrm{Re}\left(w\right):w\in \rho \left(\mathsf{\Lambda }\right)\},{\mu }_{min}\left(\mathsf{\Lambda }\right)=min\{\mathrm{Re}\left(w\right):w\in \rho \left(\mathsf{\Lambda }\right)\},\end{array}\end{array}$$

(1)

where ${\mu }_{max}\left(\mathsf{\Lambda }\right)$ is referred to the spectral abscissa and ${\mu }_{max}(-\mathsf{\Lambda })=-{\mu }_{min}\left(\mathsf{\Lambda }\right).$ For $\mathsf{\Lambda }\in {\mathcal{M}}_{\kappa }$, the norm of a matrix $\mathsf{\Lambda }$ is defined by

$$\begin{array}{c}\hfill \parallel \mathsf{\Lambda }\parallel =\underset{x\ne 0}{max}\frac{\parallel \mathsf{\Lambda }x\parallel }{\parallel x\parallel }.\end{array}$$

(2)

The matrix norm of the maximum absolute row sum of the matrix $\mathsf{\Lambda }\in {\mathcal{M}}_{\kappa }$ is given [17] by

$$\begin{array}{c}\hfill {\parallel \mathsf{\Lambda }\parallel }_{\infty }=\underset{1\le i\le \kappa }{max}\sum _{j=1}^{\kappa }\left|{\lambda }_{ij}\right|.\end{array}$$

(3)

Taking into account the Schur decomposition of a matrix $\mathsf{\Lambda }\in {\mathcal{M}}_{\kappa }$ (see [17], pp. 192–193), we have

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \parallel \exp \left(\mathsf{\Lambda }w\right)\parallel \le \exp \left(w{\mu }_{max}\left(\mathsf{\Lambda }\right)\right)\sum _{s=0}^{\kappa -1}\frac{(\parallel \mathsf{\Lambda }\parallel {\kappa }^{\frac{1}{2}}{w)}^s}{s!};w\ge 0.\end{array}\end{array}$$

(4)

The Gamma function $\mathsf{\Gamma }\left(\upsilon \right)$ is defined by (see, e.g., [18] (Chapter 11, p. 231) and [19] (Section 1.1))

$$\begin{array}{c}\hfill \mathsf{\Gamma }\left(\upsilon \right)={\int }_0^{\infty }\exp (-x)x^{\upsilon -1}dx(\mathrm{Re}\left(\upsilon \right)>0).\end{array}$$

(5)

If $\mathsf{\Lambda },\mathrm{T}\in {\mathcal{M}}_{\kappa },$ then the Gamma matrix function $\mathsf{\Gamma }\left(\mathsf{\Lambda }\right)$ and the extended Gamma matrix function ${\mathsf{\Gamma }}_T\left(\mathsf{\Lambda }\right)$ are well defined, respectively, as follows (see, e.g., [12,20]):

$$\begin{array}{c}\hfill \mathsf{\Gamma }\left(\mathsf{\Lambda }\right)={\int }_0^{\infty }\exp (-w)w^{\mathsf{\Lambda }-I}dw,w^{\mathsf{\Lambda }-I}:=\exp \left((\mathsf{\Lambda }-I)lnw\right),\end{array}$$

(6)

and

$$\begin{array}{c}\hfill {\mathsf{\Gamma }}_T\left(\mathsf{\Lambda }\right)={\int }_0^{\infty }\exp \left(-wI-\mathrm{T}{w}^{-1}\right)w^{\mathsf{\Lambda }-I}dw,\end{array}$$

(7)

where I denotes the identity matrix of any order $\kappa .$ The beta function $\mathbf{B}({\lambda }_1,{\lambda }_2)$ is defined by (see, e.g., [18] (Chapter 11, p. 235))

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathbf{B}({\lambda }_1,{\lambda }_2)=\left\{\begin{array}{c}{\int }_0^1{w}^{{\lambda }_1-1}{(1-w)}^{{\lambda }_2-1}dw,(\min \{\mathrm{Re}\left({\lambda }_1\right),\mathrm{Re}\left({\lambda }_2\right)\}>0),\hfill \\ \\ \frac{\mathsf{\Gamma }\left({\lambda }_1\right)\mathsf{\Gamma }\left({\lambda }_2\right)}{\mathsf{\Gamma }({\lambda }_1+{\lambda }_2)},\left({\lambda }_1,{\lambda }_2\in \mathcal{C}\setminus {\mathbb{Z}}_0^{-}\right).\hfill \end{array}\right.\end{array}\end{array}$$

(8)

Let $\mathsf{\Theta },\mathsf{\Psi }\in {\mathcal{M}}_{\kappa }$ such that $\mathsf{\Theta }\mathsf{\Psi }=\mathsf{\Psi }\mathsf{\Theta }.$ Then, the beta matrix function $\mathcal{B}(\mathsf{\Theta },\mathsf{\Psi })$ is well defined as follows (cf. [20]):

$$\begin{array}{c}\hfill \mathcal{B}(\mathsf{\Theta },\mathsf{\Psi })={\int }_0^1{w}^{\mathsf{\Theta }-I}{(1-w)}^{\mathsf{\Psi }-I}dw=\mathsf{\Gamma }\left(\mathsf{\Theta }\right)\mathsf{\Gamma }\left(\mathsf{\Psi }\right){\mathsf{\Gamma }}^{-1}(\mathsf{\Theta }+\mathsf{\Psi })=\mathcal{B}(\mathsf{\Psi },\mathsf{\Theta }).\end{array}$$

(9)

The extended beta function (EBF) is defined by Choudhary et al. [21] in the form

$$\begin{array}{c}\hfill \begin{array}{cc}& \mathrm{EB}\left(u,v;\ell \right)={\int }_0^1{w}^{u-1}{(1-w)}^{v-1}\exp (\frac{-\ell }{w(1-w)})dw,\hfill \\ & \left(\mathrm{Re}\right(u)>0,\mathrm{Re}(v)>0\mathrm{and}\mathrm{Re}(\ell )>0).\hfill \end{array}\end{array}$$

(10)

For $\mathsf{\Theta },\mathsf{\Psi },$ and $\mathrm{T}\in {\mathcal{M}}_{\kappa },$ the extended beta function (10) in the matrix setting is defined by Abdalla and Bakhet in [11] as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}& {\mathbb{EB}}^{\mathbf{T}}\left(\mathsf{\Theta },\mathsf{\Psi }\right)={\int }_0^1{w}^{\mathsf{\Theta }-1}{(1-w)}^{\mathsf{\Psi }-1}\exp (\frac{-\mathrm{T}}{w(1-w)})dw.\hfill \end{array}\end{array}$$

(11)

In the view of integral (11), they introduced types of extended hypergeometric matrix functions and provided numerous characteristics in [4,12,22].

Further, the logarithmic mean of $\theta ,\vartheta \in {\mathbb{R}}^{+}$ is defined in [23,24] by

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathrm{L}}_{mean}\left(\theta ,\vartheta \right)={\int }_0^1{\theta }^{1-x}{\vartheta }^{x}dx=\left\{\begin{array}{cc}\frac{\theta -\vartheta }{ln\left(\theta \right)-ln\left(\vartheta \right)},\hfill & \mathrm{if}\theta \ne \vartheta ,\hfill \\ \\ \theta ,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}\end{array}$$

(12)

where

$$\begin{array}{c}\hfill \sqrt{\theta \vartheta }<{\mathrm{L}}_{mean}\left(\theta ,\vartheta \right)<\frac{\theta +\vartheta }{2}.\end{array}$$

(13)

Raïssouli and Chergui [25] applied Equation (12) in presenting the beta-logarithmic function ($\mathrm{B}{\mathrm{L}}_{mean}$) as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}& \mathrm{B}{\mathrm{L}}_{mean}\left(\theta ,\varphi ;{\delta }_1,{\delta }_2\right)={\int }_0^1{\theta }^{1-x}{\varphi }^x{x}^{{\delta }_1-1}{(1-x)}^{{\delta }_2-1}dx,\hfill \\ & \left(\mathrm{Re}\left({\delta }_1\right)>0,\mathrm{Re}\left({\delta }_2\right)>0,\theta ,\varphi \in {\mathbb{R}}^{+}\right).\hfill \end{array}\end{array}$$

(14)

Lately, Alqarni and Abdalla [26] introduced the following extension of the beta-logarithmic function

$$\begin{array}{c}\hfill \begin{array}{cc}& \mathrm{EBL}\left[a,b;x,y;\ell \right]={\int }_0^1{a}^{1-w}{b}^w{w}^{x-1}{(1-w)}^{y-1}\exp \left(-\frac{\ell }{w(1-w)}\right)dw,\hfill \\ & \left(a,b\in {\mathbb{R}}^{+}\mathrm{with}\mathrm{Re}\left(x\right)>0,\mathrm{Re}\left(y\right)>0,\mathrm{and}\mathrm{Re}(\ell )>0\right).\hfill \end{array}\end{array}$$

(15)

2. The Extended Beta-Logarithmic Matrix Function

2.1. Convergence Property

Assume that $\mathrm{Re}\left(z_1\right)>0,\mathrm{Re}\left(z_2\right)>0$, and $\mathrm{Re}\left(z_3\right)>0,$ for all $z_1\in \rho \left({\mathsf{\Lambda }}_1\right),z_2\in \rho \left({\mathsf{\Lambda }}_2\right)$ and $z_3\in \rho \left(\mathrm{T}\right),$ where ${\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2,$ and $\mathrm{T}$ are matrices in ${\mathcal{M}}_{\kappa }$, and if $\alpha ,\beta >0$ fixed, the function $w\rightarrowtail {\alpha }^{1-w}{\beta }^w$ is continuous on $[0,1]$ and so it is bounded on $[0,1].$ Let $ϵ\ge 0$, from (4) and using $lnw<w$ and $ln(1-w)<(1-w)$ for $0<w<1,$ and it follows that

$$\begin{array}{c}\hfill \begin{array}{cc}& {\int }_0^1\parallel w^{{\mathsf{\Lambda }}_1-I}{\parallel \parallel (1-w)}^{{\mathsf{\Lambda }}_2-I}\parallel \parallel {\alpha }^{1-w}{\beta }^w\parallel \parallel \exp (\frac{-\mathrm{T}}{w(1-w)})\parallel dw\hfill \\ \hfill \le & ϵ\sum _{i=0}^{\kappa -1}\sum _{j=0}^{\kappa -1}\sum _{s=0}^{\kappa -1}\frac{(\parallel {\mathsf{\Lambda }}_1{\parallel +1)}^i(\parallel {\mathsf{\Lambda }}_2{\parallel +1)}^j{(\parallel \mathrm{T}\parallel )}^s{\left(\sqrt{\kappa }\right)}^{i+j+s}}{i!j!s!}\hfill \\ \hfill \times & {\int }_0^1{w}^{{\mu }_{max}\left({\mathsf{\Lambda }}_1\right)-1}{(1-w)}^{{\mu }_{max}\left({\mathsf{\Lambda }}_2\right)-1}{ln}^i\left(w\right){ln}^j(1-w){\left(w(1-w)\right)}^{-s}\exp (\frac{-{\mu }_{max}\left(\mathrm{T}\right)}{w(1-w)})dw\hfill \\ \hfill \le & \sum _{i=0}^{\kappa -1}\sum _{j=0}^{\kappa -1}\sum _{s=0}^{\kappa -1}\frac{(\parallel {\mathsf{\Lambda }}_1{\parallel +1)}^i(\parallel {\mathsf{\Lambda }}_2{\parallel +1)}^j(\parallel -{\mathrm{T}\parallel )}^s{\left(\sqrt{\kappa }\right)}^{i+j+s}}{i!j!s!}\hfill \\ \hfill \times & {\int }_0^1{w}^{{\mu }_{max}\left({\mathsf{\Lambda }}_1\right)+i-s-1}{(1-w)}^{{\mu }_{max}\left({\mathsf{\Lambda }}_2\right)+j-s-1}\exp (\frac{-{\mu }_{max}\left(\mathrm{T}\right)}{w(1-w)})dw\hfill \\ \hfill =& \sum _{i=0}^{\kappa -1}\sum _{j=0}^{\kappa -1}\sum _{s=0}^{\kappa -1}\frac{(\parallel {\mathsf{\Lambda }}_1{\parallel +1)}^i(\parallel {\mathsf{\Lambda }}_2{\parallel +1)}^j(\parallel -{\mathrm{T}\parallel )}^s{\left(\sqrt{\kappa }\right)}^{i+j+s}}{i!j!s!}\hfill \\ \hfill \times & \mathrm{EB}\left({\mu }_{max}\left({\mathsf{\Lambda }}_1\right)+i-s,{\mu }_{max}\left({\mathsf{\Lambda }}_2\right)+j-s;{\mu }_{max}\left(\mathrm{T}\right)\right)<+\infty .\hfill \end{array}\end{array}$$

(16)

The EBLMF is revealed in the following definition.

Definition 1.

The EBLMF is defined by

$$\begin{array}{c}\hfill \begin{array}{cc}& {\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]={\int }_0^1{w}^{{\mathsf{\Lambda }}_1-I}{(1-w)}^{{\mathsf{\Lambda }}_2-I}{\alpha }^{1-w}{\beta }^w\exp \left(-\frac{\mathrm{T}}{w(1-w)}\right)dw,\hfill \end{array}\end{array}$$

(17)

where $\alpha ,\beta \in {\mathbb{R}}^{+}$ with $\alpha \ne \beta$ and ${\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2,\mathrm{T}\in {\mathcal{M}}_{\kappa }.$

Remark 1.

One can deduce some special cases of Definition (1) as follows:

a- 

If $\alpha =\beta =1,$ the (17) reduces to the extended beta matrix function defined in (11).

b- 

When $\mathrm{T}={\mathbf{0}}_{\kappa }$ in (17), a new matrix version of the beta-logarithmic function (14) is brought in as

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathcal{BL}}_{\alpha ,\beta }\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right]={\int }_0^1{w}^{{\mathsf{\Lambda }}_1-I}{(1-w)}^{{\mathsf{\Lambda }}_2-I}{\alpha }^{1-w}{\beta }^{w}dw,\end{array}\end{array}$$

(18)

where ${\mathbf{0}}_{\kappa }$ denotes the zero matrix of any order $\kappa .$

c- 

To attain the beta matrix function defined in (9), set $\alpha =\beta =1$ in (18).

d- 

For $\alpha ,\beta \in {\mathbb{R}}^{+}$ with $\alpha \ne \beta$ and let $\mathrm{T}\in {\mathcal{M}}_{\kappa }.$ Then, the extended logarithmic mean of a matrix argument is defined by

$$\begin{array}{c}\hfill \begin{array}{cc}& {\mathbb{L}}_{Matrix}\left[\alpha ,\beta ;\mathrm{T}\right]={\int }_0^1{\alpha }^{1-w}{\beta }^w\exp \left(-\frac{\mathrm{T}}{w(1-w)}\right)dw.\hfill \end{array}\end{array}$$

(19)

e- 

When $\mathrm{T}={\mathbf{0}}_{\kappa }$ in (19), one obtains a scalar logarithmic mean given in (12).

f- 

Taking $\alpha =\beta$ in (19), one obtains the following:

$$\begin{array}{c}\hfill \begin{array}{cc}& {\mathbb{L}}_{Matrix}\left[\alpha ,\alpha ;\mathrm{T}\right]=\alpha {\int }_0^1\exp \left(-\frac{\mathrm{T}}{w(1-w)}\right)dw.\hfill \end{array}\end{array}$$

(20)

g- 

If the matrices ${\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2,$ and $\mathrm{T}$ are in ${\mathcal{M}}_1\equiv \mathcal{C},$ then the matrix functions in (17), (18), and (19) reduce to the new extensions of classical functions (see, e.g., [21,25,26]).

Remark 2.

The ${\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]$ can provide the following identities directly:

$$\begin{array}{c}\hfill {\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]={\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_2,{\mathsf{\Lambda }}_1;\beta ,\alpha \right],\end{array}$$

(21)

$$\begin{array}{c}\hfill {\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\alpha \right]=\alpha {\mathbb{EB}}^{\mathrm{T}}\left({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right),\end{array}$$

(22)

and

$$\begin{array}{c}\hfill {\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\mu \alpha ,\mu \beta \right]=\mu {\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right],\mu >0.\end{array}$$

(23)

2.2. Partial Derivative Formulas

Here, the higher-order derivative formulas of EBLMF where the matrices ${\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2,$ $\mathrm{T}\in {\mathcal{M}}_{\kappa }$ and the parameters $\alpha ,\beta \ge 0$ are discussed in the following theorem.

Theorem 1.

For $\alpha ,\beta \in {\mathbb{R}}^{+}$ such that $\alpha \ne \beta$ and let ${\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2,$ and $\mathrm{T}$ be mutually commutative matrices in ${\mathcal{M}}_{\kappa },$ we have

$$\begin{array}{c}\hfill \begin{array}{cc}& \frac{{\partial }^{(h+s)}}{\partial {\mathsf{\Lambda }}_1^{\left(h\right)}\partial {\mathsf{\Lambda }}_2^{\left(s\right)}}\left\{{\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]\right\}\hfill \\ & ={\int }_0^1{w}^{{\mathsf{\Lambda }}_1-I}{(1-w)}^{{\mathsf{\Lambda }}_2-I}{\alpha }^{1-w}{\beta }^w\hfill \\ & \times {ln}^h\left(w\right){ln}^s(1-w)\exp \left(-\frac{\mathrm{T}}{w(-w)}\right)dw,s,h\in {\mathbb{N}}_0,\hfill \end{array}\end{array}$$

(24)

$$\begin{array}{c}\hfill \begin{array}{cc}& \frac{{\partial }^{\left(m\right)}}{\partial {\mathrm{T}}^{\left(m\right)}}\left\{{\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]\right\}\hfill \\ & ={(-1)}^m{\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1-mI,{\mathsf{\Lambda }}_2-mI;\alpha ,\beta \right],m\in {\mathbb{N}}_0,\hfill \end{array}\end{array}$$

(25)

$$\begin{array}{c}\hfill \begin{array}{cc}& \frac{{\partial }^{\left(m\right)}}{\partial {\alpha }^{\left(m\right)}}\left\{{\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]\right\}\hfill \\ & =\sum _{r=0}^{\infty }\frac{{\alpha }^{-m}}{(r-m)!}{(ln\left(\alpha \right))}^{r-m}{\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+rI,{\mathsf{\Lambda }}_2;1,\beta \right],m\in {\mathbb{N}}_0,\hfill \end{array}\end{array}$$

(26)

and

$$\begin{array}{c}\hfill \begin{array}{cc}& \frac{{\partial }^{\left(m\right)}}{\partial {\beta }^{\left(m\right)}}\left\{{\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]\right\}\hfill \\ & =\sum _{r=0}^{\infty }\frac{{\beta }^{-m}}{(r-m)!}{(ln\left(\beta \right))}^{r-m}{\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2+rI;\alpha ,1\right],m\in {\mathbb{N}}_0.\hfill \end{array}\end{array}$$

(27)

Proof. 

To prove (24), we compute the partial derivatives of $B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]$ with respect to ${\mathsf{\Lambda }}_1$ and ${\mathsf{\Lambda }}_2,$ and then apply Leibniz integral rule [27] (Chapter 8, pp. 421–426), we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}& \frac{{\partial }^{\left(2\right)}}{\partial {\mathsf{\Lambda }}_1\partial {\mathsf{\Lambda }}_2}\left\{B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]\right\}\hfill \\ & ={\int }_0^1{w}^{{\mathsf{\Lambda }}_1-I}{(1-w)}^{{\mathsf{\Lambda }}_2-I}{\alpha }^{1-w}{\beta }^w\hfill \\ & \times ln\left(w\right)ln(1-w)\exp \left(-\frac{\mathrm{T}}{w(-w)}\right)dw.\hfill \end{array}\end{array}$$

(28)

Repeating this technique yields the result in (24). Equations (25)–(27) are derived using a similar procedure. □

Setting $\mathrm{T}={\mathbf{0}}_{\kappa }$ in Theorem 1, the higher-order derivative formulas for the beta-logarithmic matrix function defined in (18) are given in the following corollary.

Corollary 1.

For $\alpha ,\beta \in {\mathbb{R}}^{+}$ such that $\alpha \ne \beta$ and let ${\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\in {\mathcal{M}}_{\kappa },$ we have

$$\begin{array}{c}\hfill \begin{array}{cc}& \frac{{\partial }^{(h+s)}}{\partial {\mathsf{\Lambda }}_1^{\left(h\right)}\partial {\mathsf{\Lambda }}_2^{\left(s\right)}}\left\{{\mathcal{BL}}_{\alpha ,\beta }\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right]\right\}\hfill \\ & ={\int }_0^1{w}^{{\mathsf{\Lambda }}_1-I}{(1-w)}^{{\mathsf{\Lambda }}_2-I}{\alpha }^{1-w}{\beta }^w\hfill \\ & \times {ln}^h\left(w\right){ln}^s(1-w)\exp \left(-\frac{\mathrm{T}}{w(-w)}\right)dw,s,h\in {\mathbb{N}}_0,\hfill \end{array}\end{array}$$

(29)

$$\begin{array}{c}\hfill \begin{array}{cc}& \frac{{\partial }^{\left(m\right)}}{\partial {\alpha }^{\left(m\right)}}\left\{{\mathcal{BL}}_{\alpha ,\beta }\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right]\right\}\hfill \\ & =\sum _{r=0}^{\infty }\frac{{\alpha }^{-m}}{(r-m)!}{(ln\left(\alpha \right))}^{r-m}{\mathcal{BL}}_{1,\beta }\left[{\mathsf{\Lambda }}_1+rI,{\mathsf{\Lambda }}_2\right],\hfill \end{array}\end{array}$$

(30)

and

$$\begin{array}{c}\hfill \begin{array}{cc}& \frac{{\partial }^{\left(m\right)}}{\partial {\beta }^{\left(m\right)}}\left\{{\mathcal{BL}}_{\alpha ,\beta }\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right]\right\}\hfill \\ & =\sum _{r=0}^{\infty }\frac{{\beta }^{-m}}{(r-m)!}{(ln\left(\alpha \right))}^{r-m}{\mathcal{BL}}_{\alpha ,1}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2+rI\right].\hfill \end{array}\end{array}$$

(31)

Similarly, the following result gives the partial differentiations of the logarithmic function in a matrix argument (19).

Corollary 2.

For $\alpha ,\beta \in {\mathbb{R}}^{+}$ such that $\alpha \ne \beta$ and let $\mathrm{T}\in {\mathcal{M}}_{\kappa },$ we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}& \frac{{\partial }^{\left(m\right)}}{\partial {\mathrm{T}}^{\left(m\right)}}\left\{{\mathbb{L}}_{Matrix}\left[\alpha ,\beta ;\mathrm{T}\right]\right\}\hfill \\ & ={(-1)}^m{\int }_0^1\frac{{\alpha }^{1-w}{\beta }^w}{w^m{(1-w)}^m}\exp \left(-\frac{\mathrm{T}}{w(1-w)}\right)dw,m\in {\mathbb{N}}_0,\hfill \end{array}\end{array}$$

(32)

$$\begin{array}{c}\hfill \begin{array}{cc}& \frac{{\partial }^{\left(m\right)}}{\partial {\alpha }^{\left(m\right)}}\left\{{\mathbb{L}}_{Matrix}\left[\alpha ,\beta ;\mathrm{T}\right]\right\}\hfill \\ & =\sum _{r=0}^{\infty }{w}^r\frac{{\alpha }^{-m}}{(r-m)!}{(ln\left(\alpha \right))}^{r-m}{\mathbb{L}}_{Matrix}\left[1,\beta ;\mathrm{T}\right],\hfill \end{array}\end{array}$$

(33)

and

$$\begin{array}{c}\hfill \begin{array}{cc}& \frac{{\partial }^{\left(m\right)}}{\partial {\beta }^{\left(m\right)}}\left\{{\mathbb{L}}_{Matrix}\left[\alpha ,\beta ;\mathrm{T}\right]\right\}\hfill \\ & =\sum _{r=0}^{\infty }{(1-w)}^r\frac{{\beta }^{-m}}{(r-m)!}{(ln\left(\alpha \right))}^{r-m}{\mathbb{L}}_{Matrix}\left[\alpha ,1;\mathrm{T}\right].\hfill \end{array}\end{array}$$

(34)

Remark 3.

When considering the results in Remark 1 and Theorem 1, various other outcomes in the literature, including those in (see, e.g., [20,21,25]), can be demonstrated as special cases.

3. Some Analytic Characteristics

The essential analytic properties are established in this section.

Theorem 2.

The EBLMF defined in (17) satisfies the following functional relation:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+I,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]+{\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2+I;\alpha ,\beta \right]={\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right].\end{array}\end{array}$$

(35)

Proof. 

Using Definition 1, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}& B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+I,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]+B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2+I;\alpha ,\beta \right]\hfill \\ & ={\int }_0^1\left[w^{{\mathsf{\Lambda }}_1}{(1-w)}^{{\mathsf{\Lambda }}_2-1}+w^{{\mathsf{\Lambda }}_1-1}{(1-w)}^{{\mathsf{\Lambda }}_2}\right]{\alpha }^{1-w}{\beta }^w\exp \left(-\frac{\mathrm{T}}{w(1-w)}\right)dw.\hfill \end{array}\end{array}$$

(36)

Thus, the desired result is attained. □

Corollary 3.

For $\mathrm{T}={\mathbf{0}}_{\kappa }$ in (35), we have

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathcal{BL}}_{\alpha ,\beta }\left[{\mathsf{\Lambda }}_1+I,{\mathsf{\Lambda }}_2\right]+{\mathcal{BL}}_{\alpha ,\beta }\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2+I\right]={\mathcal{BL}}_{\alpha ,\beta }\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right].\end{array}\end{array}$$

(37)

Corollary 4.

For $\mathrm{T}={\mathbf{0}}_{\kappa }$ and $\alpha =\beta =1$ in (35), we have

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathcal{B}\left({\mathsf{\Lambda }}_1+I,{\mathsf{\Lambda }}_2\right)+\mathcal{B}\left({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2+I\right)=\mathcal{B}\left({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right).\end{array}\end{array}$$

(38)

The following theorem delivers a bound of the EBLMF given in (17).

Theorem 3.

For $\alpha ,\beta \in {\mathbb{R}}^{+}$ such that $\alpha \ne \beta$ and let ${\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2,$ and $\mathrm{T}$ be matrices in ${\mathcal{M}}_{\kappa },$ we obtain

$$\begin{array}{c}\min \{\alpha ,\beta \}\parallel {\mathbb{EB}}^{\mathrm{T}}\left({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right)\parallel \hfill \\ \le \parallel {\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]\parallel \hfill \\ \le max\{\alpha ,\beta \}\parallel {\mathbb{EB}}^{\mathrm{T}}\left({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right)\parallel ,\hfill \end{array}$$

(39)

where $\parallel .\parallel$ is defined in (2).

Proof. 

From (11) and (13), we obtain

$$\begin{array}{c}\hfill \begin{array}{c}\hfill min\left\{\alpha ,\beta \right\}\parallel {\mathbb{EB}}^{\mathrm{T}}\left({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right)\parallel \le \parallel B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]\parallel .\end{array}\end{array}$$

(40)

After applying Young’s inequality and simplifying, we find

$$\begin{array}{c}\hfill \begin{array}{cc}& 0\le \parallel B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]\parallel \hfill \\ & \le max\left\{\alpha ,\beta \right\}\parallel {\mathbb{EB}}^{\mathrm{T}}\left({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right)\parallel .\hfill \end{array}\end{array}$$

(41)

We can derive the desired assertion in (39) by making use of (40) and (41). □

Corollary 5.

For $\mathrm{T}={\mathbf{0}}_{\kappa }$ in Theorem 3, the following inequality for ${\mathcal{BL}}_{\alpha ,\beta }\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right]$ holds true:

$$\begin{array}{c}\hfill \begin{array}{cc}& \min \{\alpha ,\beta \}\parallel \mathcal{B}\left({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right)\parallel \le \parallel {\mathcal{BL}}_{\alpha ,\beta }\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right]\parallel \hfill \\ & \le max\{\alpha ,\beta \}\parallel \mathcal{B}\left({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right)\parallel .\hfill \end{array}\end{array}$$

(42)

Corollary 6.

For $\alpha =\beta =1,$ let ${\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2,$ and $\mathrm{T}$ be reciprocally commutative matrices in ${\mathcal{M}}_{\kappa },$ we derive

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \parallel {\mathbb{EB}}^{\mathrm{T}}\left({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right)\parallel \le \exp (-4\parallel \mathrm{T}\parallel )\parallel \mathcal{B}\left({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right)\parallel .\end{array}\end{array}$$

(43)

The following theorem gives various integral representations of the EBLMF defined in (17).

Theorem 4.

For $\alpha ,\beta \in {\mathbb{R}}^{+}$ such that $\alpha \ne \beta$ and let ${\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2,\mathrm{T}\in {\mathcal{M}}_{\kappa },$ the ${\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]$ satisfies the following integral formulas:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]=& 2\alpha {\int }_0^{\frac{\pi }{2}}{\left(\beta {\alpha }^{-1}\right)}^{{cos}^2\left(\phi \right)}{cos}^{2{\mathsf{\Lambda }}_1-I}\left(\phi \right){sin}^{2{\mathsf{\Lambda }}_2-I}\left(\phi \right)\hfill \\ \hfill \times & \exp (-\mathrm{T}{sec}^2\left(\phi \right){csc}^2\left(\phi \right))d\phi ,\hfill \end{array}\end{array}$$

(44)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]& =e^{-2\mathrm{T}}{\int }_0^{\infty }\frac{{\tau }^{{\mathsf{\Lambda }}_2-I}}{{(1+\tau )}^{{\mathsf{\Lambda }}_1+{\mathsf{\Lambda }}_2}}\hfill \\ & \times {\left(\alpha \right)}^{\frac{\tau }{\tau +1}}{\left(\beta \right)}^{\frac{1}{\tau +1}}\exp (-\mathrm{T}(\tau +{\tau }^{-1}))d\tau ,\hfill \end{array}\end{array}$$

(45)

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]=& \sqrt{\alpha \beta }{2}^{I-({\mathsf{\Lambda }}_1+{\mathsf{\Lambda }}_2)}{\int }_0^{\infty }{\left(\beta {\alpha }^{-1}\right)}^{\frac{\tau }{2}}{(1+\tau )}^{{\mathsf{\Lambda }}_1-I}{(1-\tau )}^{{\mathsf{\Lambda }}_2-I}\hfill \\ \hfill \times & \exp (-4\mathrm{T}/(1-{\tau }^2))d\tau .\hfill \end{array}\end{array}$$

(46)

Proof. 

Setting $w=cos\left(\phi \right)$ in (17) yields (44). Next, replacing $w=\frac{\tau }{\tau +1}$ in (17) provides Formula (45). Finally, substituting $w=\frac{1+\tau }{2}$ in (17) gives the result (46). □

Corollary 7.

Let ${\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2,\mathrm{T}\in {\mathcal{M}}_{\kappa },$ we observe that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathbb{EB}}^{\mathrm{T}}\left({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right)=& 2{\int }_0^{\frac{\pi }{2}}{cos}^{2{\mathsf{\Lambda }}_1-I}\left(\phi \right){sin}^{2{\mathsf{\Lambda }}_2-I}\left(\phi \right)\hfill \\ \hfill \times & \exp \left(-\mathrm{T}{sec}^2\left(\phi \right){csc}^2\left(\phi \right)\right)d\phi ,\hfill \end{array}\end{array}$$

(47)

and

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathsf{\Gamma }}_{\mathrm{T}}\left({\mathsf{\Lambda }}_1\right){\mathsf{\Gamma }}_{\mathrm{T}}\left({\mathsf{\Lambda }}_2\right)={\int }_0^{\infty }{z}^{({\mathsf{\Lambda }}_1+{\mathsf{\Lambda }}_2)-I}{e}^{-z}{\mathbb{EB}}^{\frac{\mathrm{T}}{\sqrt{z}}}\left({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right)dz,\end{array}\end{array}$$

(48)

where ${\mathsf{\Gamma }}_{\mathrm{T}}\left(\mathsf{\Lambda }\right)$ is defined in (7).

Remark 4.

Applying Remark 1’s results into Theorem 4 generates the other conformable results found in [12,20,25,28].

Now, we archive some finite and infinite sums of the $B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]$.

Theorem 5.

The following sums hold for the ${\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]$:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]=\sum _{\mathsf{ȷ}=0}^m\left(\genfrac{}{}{0pt}{}{m}{\mathsf{ȷ}}\right){\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+\mathsf{ȷ}I,{\mathsf{\Lambda }}_2+(m-\mathsf{ȷ})I;\alpha ,\beta \right],\end{array}\end{array}$$

(49)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]=\sum _{\mathsf{ȷ}=0}^{\infty }{\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+\mathsf{ȷ}I,{\mathsf{\Lambda }}_2+I;\alpha ,\beta \right],\end{array}\end{array}$$

(50)

and

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]=\sum _{r,s=0}^{\infty }{\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+rI,{\mathsf{\Lambda }}_2+sI;\alpha ,\beta \right]\frac{{(ln\left(\alpha \right))}^r{(ln\left(\beta \right))}^s}{r!s!}.\end{array}\end{array}$$

(51)

Proof. 

To demonstrate (49), we use induction on $m,$ for $m=1,$ we find

$$\begin{array}{c}\hfill \begin{array}{cc}& B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+I,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]+B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2+I;\alpha ,\beta \right]\hfill \\ & {\int }_0^1{w}^{{\mathsf{\Lambda }}_1}{(1-w)}^{{\mathsf{\Lambda }}_2}[w^{-1}+{(1-w)}^{-1}]\hfill \\ & \times {\alpha }^{1-w}{\beta }^w\exp \left(-\frac{\mathrm{T}}{w(1-w)}\right)dw=B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right].\hfill \end{array}\end{array}$$

(52)

Assume that Equation (49) is true for $m=\ell$, it follows that

$$\begin{array}{c}\hfill \begin{array}{c}\hfill B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]=\sum _{\mathsf{ȷ}=0}^{\ell }\left(\genfrac{}{}{0pt}{}{\ell }{\mathsf{ȷ}}\right)B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+\mathsf{ȷ}I,{\mathsf{\Lambda }}_2+(\ell -\mathsf{ȷ})I;\alpha ,\beta \right].\end{array}\end{array}$$

Using the binomial identity $\left(\genfrac{}{}{0pt}{}{\ell +1}{\mathsf{ȷ}}\right)=\left(\genfrac{}{}{0pt}{}{\ell }{\mathsf{ȷ}}\right)+\left(\genfrac{}{}{0pt}{}{\ell }{\mathsf{ȷ}-1}\right)$ and taking $m=\ell +1$, one finds

$$\begin{array}{c}\hfill \begin{array}{cc}& \sum _{\mathsf{ȷ}=0}^{\ell +1}\left(\genfrac{}{}{0pt}{}{\ell +1}{\mathsf{ȷ}}\right)B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+\mathsf{ȷ}I,{\mathsf{\Lambda }}_2+(\ell -\mathsf{ȷ})I;\alpha ,\beta \right]\hfill \\ & =\sum _{\mathsf{ȷ}=0}^{\ell +1}\left(\genfrac{}{}{0pt}{}{\ell }{\mathsf{ȷ}}\right)B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+\mathsf{ȷ}I,{\mathsf{\Lambda }}_2+(\ell -\mathsf{ȷ})I;\alpha ,\beta \right]\hfill \\ & +\sum _{\mathsf{ȷ}=0}^{\ell +1}\left(\genfrac{}{}{0pt}{}{\ell }{\mathsf{ȷ}-1}\right)B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+\mathsf{ȷ}I,{\mathsf{\Lambda }}_2+(\ell -\mathsf{ȷ})I;\alpha ,\beta \right]\hfill \\ & =\sum _{\mathsf{ȷ}=0}^{\ell }\left(\genfrac{}{}{0pt}{}{\ell }{\mathsf{ȷ}}\right)B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+\mathsf{ȷ}I,{\mathsf{\Lambda }}_2+(\ell -\mathsf{ȷ})I;\alpha ,\beta \right]\hfill \\ & +\sum _{\mathsf{ȷ}=1}^{\ell +1}\left(\genfrac{}{}{0pt}{}{\ell }{\mathsf{ȷ}-1}\right)B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+\mathsf{ȷ}I,{\mathsf{\Lambda }}_2+(\ell -\mathsf{ȷ})I;\alpha ,\beta \right]\hfill \\ & =\sum _{\mathsf{ȷ}=0}^{\ell }\left(\genfrac{}{}{0pt}{}{\ell }{\mathsf{ȷ}}\right)B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+\mathsf{ȷ}I,{\mathsf{\Lambda }}_2+(\ell -\mathsf{ȷ})I;\alpha ,\beta \right]\hfill \\ & +\sum _{\mathsf{ȷ}=0}^{\ell }\left(\genfrac{}{}{0pt}{}{\ell }{\mathsf{ȷ}}\right)B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+\mathsf{ȷ}I,{\mathsf{\Lambda }}_2+(\ell -\mathsf{ȷ}+1)I;\alpha ,\beta \right]=B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right].\hfill \end{array}\end{array}$$

Thus, we attain the desired result (49).

To prove (50), substitute ${(1-w)}^{{\mathsf{\Lambda }}_2-I}$ in (17) with ${(1-w)}^{{\mathsf{\Lambda }}_2}{\sum }_{r=0}^{\infty }{w}^r,\mathrm{for}w\in (0,1),$ which yields

$$\begin{array}{c}\hfill B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]=\sum _{r=0}^{\infty }{\int }_0^1{\alpha }^{1-w}{\beta }^w{w}^{{\mathsf{\Lambda }}_1+(r-1)I}{(1-w)}^{{\mathsf{\Lambda }}_2}\exp \left(-\frac{\mathrm{T}}{w(1-w)}\right)dw,\end{array}$$

Hence, (50) is obtained.

To prove (51), replacing ${\alpha }^{1-w}$ and ${\beta }^w$ in (17) with ${\sum }_{r=0}^{\infty }\frac{{(ln\alpha )}^r}{r!}{(1-w)}^r$ and ${\sum }_{s=0}^{\infty }\frac{{(ln\beta )}^s}{s!}{w}^r$, respectively, yields

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]& ={\int }_0^1\sum _{r,s=0}^{\infty }\frac{{(ln\alpha )}^r{(ln\beta )}^s}{r!s!}\hfill \\ & \times w^{{\mathsf{\Lambda }}_2+(s-1)I}{(1-w)}^{{\mathsf{\Lambda }}_2+(r-1)I}\exp \left(-\frac{\mathrm{T}}{w(1-w)}\right)dw.\hfill \end{array}\end{array}$$

Thus, the infinite sum in (51) is seized after simplification. □

Corollary 8.

For $\alpha ,\beta \in {\mathbb{R}}^{+}$ such that $\alpha \ne \beta$ and let $\mathrm{T}\in {\mathcal{M}}_{\kappa },$ we have

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathbb{L}}_{Matrix}\left[\alpha ,\beta ;\mathrm{T}\right]=\sum _{r,s=0}^{\infty }{w}^s{(1-w)}^r\frac{{(ln\left(\alpha \right))}^r{(ln\left(\beta \right))}^s}{r!s!}{\mathbb{L}}_{Matrix}\left[1,1;\mathrm{T}\right].\end{array}\end{array}$$

(53)

Remark 5.

There are also matrix versions of some known infinite sums in [25].

4. The Beta-Logarithmic Distribution: Matrix Arguments

As is well known, the beta distribution is one of the essential variate distributions in statistical analysis, and its importance is that it is in deriving moments and can help us understand the different probabilities associated with the random variable $\mathcal{X}$ (cf. [29]). Traditional beta distributions were introduced in [11,12,13,28,30] using extended beta functions. They suggested that these distributions could help analyze and review techniques employed in specific circumstances during project evaluation and review. They pointed out that these distributions could be advantageous for evaluating and reviewing the method used in particular cases during project evaluation and review. Here, the generalized beta-logarithmic distribution of matrix arguments is defined as

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathcal{F}\left(w\right)=\left\{\begin{array}{cc}\frac{1}{B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]}{\alpha }^{1-w}{\beta }^w{w}^{{\mathsf{\Lambda }}_1-I}{(1-w)}^{{\mathsf{\Lambda }}_2-I}\exp \left(-\frac{\mathrm{T}}{w(1-w)}\right),& (0<w<1).\hfill \\ \\ 0,& \mathrm{otherwise},\hfill \end{array}\right.\end{array}\end{array}$$

(54)

where $\alpha ,\beta \in {\mathbb{R}}^{+}$ with $\alpha \ne \beta$ and let ${\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2,\mathrm{T}\in {\mathcal{M}}_{\kappa }.$ It will be said that a random variable $\mathcal{X}$ with probability density matrix function defined by (54) has the extended beta-logarithmic distribution with matrix arguments ${\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2,$ and $\mathrm{T}$ in ${\mathcal{M}}_{\kappa }.$ If the incomplete extended beta-logarithmic matrix function is expressed by

$$\begin{array}{c}\hfill \begin{array}{cc}& B_{Log}^{\mathrm{T};z}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]={\int }_0^z{w}^{{\mathsf{\Lambda }}_1-I}{(1-w)}^{{\mathsf{\Lambda }}_2-I}{\alpha }^{1-w}{\beta }^w\exp \left(-\frac{\mathrm{T}}{w(1-w)}\right)dw,(0<w<1),\hfill \end{array}\end{array}$$

(55)

then the cumulative distribution of (54) can be given as

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathsf{ϝ}}_{\alpha ,\beta }\left(z\right)={\int }_0^z\mathcal{F}\left(w\right)dw=B_{Log}^{\mathrm{T};z}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]{\left(B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]\right)}^{-1};{\mathsf{ϝ}}_{\ell }\left(1\right)=1.\end{array}\end{array}$$

(56)

Remark 6.

The incomplete generalized beta-logarithmic matrix function in (55) can be reduced to numerous simple incomplete extended beta matrix functions (see, e.g., [4,13]).

Also, let $\wp \in {\mathbb{R}}^{+},$ then one obtains (cf. [11,28])

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathbf{E}\left({\mathcal{X}}^{\mathrm{T}}\right)=B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+\wp I,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]{\left(B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]\right)}^{-1}.\end{array}\end{array}$$

(57)

Following the particular case of (57) at $\wp =1$, the mean of the distribution is provided as

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mu }_{\alpha ,\beta }=\mathbf{E}\left(\mathcal{X}\right)=B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+I,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]{\left(B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]\right)}^{-1}.\end{array}\end{array}$$

(58)

Further, the variance of the generalized beta-logarithmic distribution of matrix arguments is shown as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\sigma }_{\alpha ,\beta }^2& =\mathbf{E}\left({\mathcal{X}}^2\right)-{\left\{\mathbf{E}\left(\mathcal{X}\right)\right\}}^2\hfill \\ & =\{B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+2I,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]\hfill \\ & -{\left(B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+I,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]\right)}^2\}{\left(B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]\right)}^{-2}.\hfill \end{array}\end{array}$$

(59)

In addition, the moment-generating function of the distribution can be expressed as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathcal{M}}_{\mathrm{T}}\left(w\right)& =\sum _{m=0}^{\infty }\mathbf{E}\left({\mathcal{X}}^m\right)\frac{w^m}{m!}={\left(B_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]\right)}^{-1}\hfill \\ & \times \sum _{m=0}^{\infty }{B}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1+mI,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]\frac{w^m}{m!}.\hfill \end{array}\end{array}$$

(60)

Remark 7.

The results in [11] can be achieved when $\alpha =\beta =1$ in the above results. Also, setting $\alpha =\beta =1,$ in (54), corresponding to (g) in Remark 2.1, one can achieve various results in [28] (Chapter 5, p. 258).

Remark 8.

The generalized results of the matrix setting in [25] (p. 137) are obtained by taking $\mathrm{T}={\mathbf{0}}_{\kappa }$ in the above results.

5. Numerical and Graphical Representations

5.1. Numerical Illustration Examples

Example 1.

For $\alpha =2,\beta =4,$ ${\mathsf{\Lambda }}_1=\left(\begin{array}{cc}5& 3\\ 3& 2\end{array}\right),$ ${\mathsf{\Lambda }}_2=\left(\begin{array}{cc}2& 4\\ 4& 10\end{array}\right),$ and $\mathrm{T}=\left(\begin{array}{cc}13& 7\\ 7& 5\end{array}\right).$

Then

$w^{{\mathsf{\Lambda }}_1-I}=w^{\left(\begin{array}{cc}4& 3\\ 3& 1\end{array}\right)},$ ${(1-w)}^{{\mathsf{\Lambda }}_2-I}={(1-w)}^{\left(\begin{array}{cc}1& 4\\ 4& 9\end{array}\right)},$ and $\exp \left[\left(\begin{array}{cc}13{\left[w(w-1)\right]}^{-1}& 7{\left[w(w-1)\right]}^{-1}\\ 7{\left[w(w-1)\right]}^{-1}& 5{\left[w(w-1)\right]}^{-1}\end{array}\right)\right].$

Thus, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;2,4\right]& ={\int }_0^1{w}^{\left(\begin{array}{cc}4& 3\\ 3& 1\end{array}\right)}{(1-w)}^{\left(\begin{array}{cc}1& 4\\ 4& 9\end{array}\right)}\hfill \\ & \times 2^{1+w}\exp \left[\left(\begin{array}{cc}13{\left[w(w-1)\right]}^{-1}& 7{\left[w(w-1)\right]}^{-1}\\ 7{\left[w(w-1)\right]}^{-1}& 5{\left[w(w-1)\right]}^{-1}\end{array}\right)\right]dw\hfill \\ & =\left(\begin{array}{cc}97/6837& -187/7649\\ -53/2431& 626/16663\end{array}\right).\hfill \end{array}\end{array}$$

(61)

Example 2.

For $\alpha =4,\beta =2,$ ${\mathsf{\Lambda }}_1=\left(\begin{array}{cc}5& 3\\ 3& 2\end{array}\right),$ ${\mathsf{\Lambda }}_2=\left(\begin{array}{cc}2& 4\\ 4& 10\end{array}\right),$ and $\mathrm{T}=\left(\begin{array}{cc}13& 7\\ 7& 5\end{array}\right).$

Then,

$w^{{\mathsf{\Lambda }}_1-I}=w^{\left(\begin{array}{cc}4& 3\\ 3& 1\end{array}\right)},$ ${(1-w)}^{{\mathsf{\Lambda }}_2-I}={(1-w)}^{\left(\begin{array}{cc}1& 4\\ 4& 9\end{array}\right)},$ and $\exp \left[\left(\begin{array}{cc}13{\left[w(w-1)\right]}^{-1}& 7{\left[w(w-1)\right]}^{-1}\\ 7{\left[w(w-1)\right]}^{-1}& 5{\left[w(w-1)\right]}^{-1}\end{array}\right)\right].$

Thus, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;4,2\right]& ={\int }_0^1{w}^{\left(\begin{array}{cc}4& 3\\ 3& 1\end{array}\right)}{(1-w)}^{\left(\begin{array}{cc}1& 4\\ 4& 9\end{array}\right)}\hfill \\ & \times 2^{2-w}\exp \left[\left(\begin{array}{cc}13{\left[w(w-1)\right]}^{-1}& 7{\left[w(w-1)\right]}^{-1}\\ 7{\left[w(w-1)\right]}^{-1}& 5{\left[w(w-1)\right]}^{-1}\end{array}\right)\right]dw\hfill \\ & =\left(\begin{array}{cc}142/9951& -385/15657\\ -58/2613& 339/8863\end{array}\right).\hfill \end{array}\end{array}$$

(62)

Example 3.

For $\alpha =2,\beta =4,$ ${\mathsf{\Lambda }}_1=\left(\begin{array}{cccc}10& 9& 11& 11\\ 9& 10& 11& 11\\ 11& 11& 13& 13\\ 11& 11& 13& 13\end{array}\right),$ ${\mathsf{\Lambda }}_2=\left(\begin{array}{cccc}7& 8& 6& 5\\ 8& 10& 7& 6\\ 6& 7& 7& 5\\ 5& 6& 5& 4\end{array}\right),$ and $\mathrm{T}=\left(\begin{array}{cccc}10& 10& 7& 7\\ 10& 10& 7& 7\\ 7& 7& 7& 6\\ 7& 7& 6& 7\end{array}\right).$

Then,

$w^{{\mathsf{\Lambda }}_1-I}=w^{\left(\begin{array}{cccc}9& 9& 11& 11\\ 9& 9& 11& 11\\ 11& 11& 12& 13\\ 11& 11& 13& 12\end{array}\right)},$ ${(1-w)}^{{\mathsf{\Lambda }}_2-I}={(1-w)}^{\left(\begin{array}{cccc}6& 8& 6& 5\\ 8& 9& 7& 6\\ 6& 7& 6& 5\\ 5& 6& 5& 3\end{array}\right)},$ and $\exp \left[\left(\begin{array}{cccc}10& 10& 7& 7\\ 10& 10& 7& 7\\ 7& 7& 7& 6\\ 7& 7& 6& 7\end{array}\right)\right].$

Thus, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;2,4\right]& ={\int }_0^1{w}^{\left(\begin{array}{cccc}9& 9& 11& 11\\ 9& 9& 11& 11\\ 11& 11& 12& 13\\ 11& 11& 13& 12\end{array}\right)}{(1-w)}^{\left(\begin{array}{cccc}6& 8& 6& 5\\ 8& 9& 7& 6\\ 6& 7& 6& 5\\ 5& 6& 5& 3\end{array}\right)}\hfill \\ & \times 2^{1+w}\exp \left[\left(\begin{array}{cccc}10& 10& 7& 7\\ 10& 10& 7& 7\\ 7& 7& 7& 6\\ 7& 7& 6& 7\end{array}\right)\right]dw\hfill \\ & =\left(\begin{array}{cccc}3338/659& -1479/292& 85/16709& -69/12977\\ -4563/901& 15776/3115& 96/12727& 56/7235\\ -619/306& 2389/1181& 114/3803& -55/1836\\ 3082/1027& -2413/804& -69/1693& 233/5669\end{array}\right).\hfill \end{array}\end{array}$$

(63)

Remark 9.

The previous examples show that if ${\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2,$ and $\mathrm{T}$ do not commute with $\alpha \ne \beta$, then the property symmetry of the function ${\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]$ does not hold.

Remark 10.

The following example shows that if ${\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2,$ and $\mathrm{T}$ are commutes with $\alpha =\beta ,$ then the property symmetry of the functions ${\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;\alpha ,\beta \right]$ and ${\mathbb{EB}}^{\mathrm{T}}\left({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right)$, respectively, does hold.

Example 4.

For $\alpha =3,\beta =3,$ ${\mathsf{\Lambda }}_1=\left(\begin{array}{cc}0& 1\\ -1& 1\end{array}\right),$ ${\mathsf{\Lambda }}_2=\left(\begin{array}{cc}1& 2\\ -2& 1\end{array}\right),$ and $\mathrm{T}=\left(\begin{array}{cc}2& 3\\ -3& 2\end{array}\right).$

Then,

$w^{{\mathsf{\Lambda }}_1-I}=w^{\left(\begin{array}{cc}-1& 1\\ 1& -1\end{array}\right)},$ ${(1-w)}^{{\mathsf{\Lambda }}_2-I}={(1-w)}^{\left(\begin{array}{cc}0& 2\\ -2& 0\end{array}\right)},$ and $\exp \left[\left(\begin{array}{cc}2{\left[w(w-1)\right]}^{-1}& 3{\left[w(w-1)\right]}^{-1}\\ -3{\left[w(w-1)\right]}^{-1}& 2{\left[w(w-1)\right]}^{-1}\end{array}\right)\right].$

Thus, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;3,3\right]& =3{\int }_0^1{w}^{\left(\begin{array}{cc}-1& 1\\ 1& -1\end{array}\right)}{(1-w)}^{\left(\begin{array}{cc}0& 2\\ -2& 0\end{array}\right)}\hfill \\ & \times \exp \left[\left(\begin{array}{cc}2{\left[w(w-1)\right]}^{-1}& 3{\left[w(w-1)\right]}^{-1}\\ -3{\left[w(w-1)\right]}^{-1}& 2{\left[w(w-1)\right]}^{-1}\end{array}\right)\right]dw\hfill \\ & =\left(\begin{array}{cc}-10/54137& -2/4813\\ 2/4813& -10/54137\end{array}\right)={\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_2,{\mathsf{\Lambda }}_1;3,3\right].\hfill \end{array}\end{array}$$

(64)

Example 5.

For $\alpha =1,\beta =1,$ ${\mathsf{\Lambda }}_1=\left(\begin{array}{cc}0& 1\\ -1& 1\end{array}\right),$ ${\mathsf{\Lambda }}_2=\left(\begin{array}{cc}1& 2\\ -2& 1\end{array}\right),$ and $\mathrm{T}=\left(\begin{array}{cc}2& 3\\ -3& 2\end{array}\right).$

Then

$w^{{\mathsf{\Lambda }}_1-I}=w^{\left(\begin{array}{cc}-1& 1\\ 1& -1\end{array}\right)},$ ${(1-w)}^{{\mathsf{\Lambda }}_2-I}={(1-w)}^{\left(\begin{array}{cc}0& 2\\ -2& 0\end{array}\right)},$ and $\exp \left[\left(\begin{array}{cc}2{\left[w(w-1)\right]}^{-1}& 3{\left[w(w-1)\right]}^{-1}\\ -3{\left[w(w-1)\right]}^{-1}& 2{\left[w(w-1)\right]}^{-1}\end{array}\right)\right].$

Thus, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathbb{EB}}^{\mathrm{T}}\left({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2\right)& ={\int }_0^1{w}^{\left(\begin{array}{cc}-1& 1\\ 1& -1\end{array}\right)}{(1-w)}^{\left(\begin{array}{cc}0& 2\\ -2& 0\end{array}\right)}\hfill \\ & \times \exp \left[\left(\begin{array}{cc}2{\left[w(w-1)\right]}^{-1}& 3{\left[w(w-1)\right]}^{-1}\\ -3{\left[w(w-1)\right]}^{-1}& 2{\left[w(w-1)\right]}^{-1}\end{array}\right)\right]dw\hfill \\ & =\left(\begin{array}{cc}-9/146170& -2/14439\\ 2/14439& -9/146170\end{array}\right)={\mathbb{EB}}^{\mathrm{T}}\left({\mathsf{\Lambda }}_2,{\mathsf{\Lambda }}_1\right).\hfill \end{array}\end{array}$$

(65)

Example 6.

For $\alpha =1.2,\beta =3.2,$ ${\mathsf{\Lambda }}_1=\left(\begin{array}{ccc}9& 9& 7\\ 9& 9& 7\\ 7& 7& 6\end{array}\right),$ ${\mathsf{\Lambda }}_2=\left(\begin{array}{ccc}6& 9& 6\\ 9& 17& 13\\ 6& 13& 11\end{array}\right),$

and $\mathrm{T}=\left(\begin{array}{ccc}14& 20& 13\\ 20& 34& 19\\ 13& 19& 14\end{array}\right).$ Then, $w^{{\mathsf{\Lambda }}_1-I}=w^{\left(\begin{array}{ccc}8& 9& 7\\ 9& 8& 7\\ 7& 7& 5\end{array}\right)},$ ${(1-w)}^{{\mathsf{\Lambda }}_2-I}={(1-w)}^{\left(\begin{array}{ccc}5& 9& 6\\ 9& 16& 13\\ 6& 13& 10\end{array}\right)},$

and $\exp \left[{\left[w(w-1)\right]}^{-1}\left(\begin{array}{ccc}14& 20& 13\\ 20& 34& 19\\ 13& 19& 14\end{array}\right)\right].$

Thus, we find that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathrm{B}}_{Log}^{\mathrm{T}}\left[{\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2;1.2,3.2\right]& ={\int }_0^1{w}^{\left(\begin{array}{ccc}8& 9& 7\\ 9& 8& 7\\ 7& 7& 5\end{array}\right)}{(1-w)}^{\left(\begin{array}{ccc}5& 9& 6\\ 9& 16& 13\\ 6& 13& 10\end{array}\right)}\hfill \\ & \times {\left(1.2\right)}^{1-w}{\left(3.2\right)}^w\exp \left[{\left[w(w-1)\right]}^{-1}\left(\begin{array}{ccc}14& 20& 13\\ 20& 34& 19\\ 13& 19& 14\end{array}\right)\right]dw\hfill \\ & =\left(\begin{array}{ccc}101/5372& -80/20229& -89/6901\\ -148/9867& 64/20253& 67/6517\\ -47/9854& 60/60179& 57/17368\end{array}\right).\hfill \end{array}\end{array}$$

(66)

5.2. Graphical Representations

This section illustrates the generalization presented in this paper with the previous results in [20] in their graphical forms to provide a comprehensive understanding. The differences were handled using the infinite norm (3) since the comparisons run over matrices. The size of all matrices used here is $2\times 2$. The choice of the used matrices is ${\mathsf{\Lambda }}_1=\left(\begin{array}{cc}1& 0\\ 1& 2\end{array}\right)$ and ${\mathsf{\Lambda }}_2=\left(\begin{array}{cc}1& 1\\ 0& 2\end{array}\right)$, as in [20], while $\mathrm{T}$ is a matrix chosen to be approaching the zero matrices, ${\mathbf{0}}_{\kappa },\kappa =2$.

Figure 1 shows the graph of the differences between the EBLMF and beta matrix function against various values of $\alpha$ in the interval $(0,20)$ for multiple choice of $\mathrm{T}$ matrix having infinity-norm starting from 0.5 and approaching 0 and taking $\beta =1$. As ${\alpha }^{\prime }s$ value increases, the difference decreases when $\mathrm{T}$ is not close to ${\mathbf{0}}_{\kappa }$. However, for $\mathrm{T}$ approaching zero matrices, the difference decreases for small values of $\alpha ,$ and then it changes direction. That is because of the trade-off between $\alpha$ and the choice of $\mathrm{T}$ in (17). Similar observations can be made when fixing $\alpha =1$ and plotting the differences versus $\beta \in (0,20)$, as shown in Figure 2.

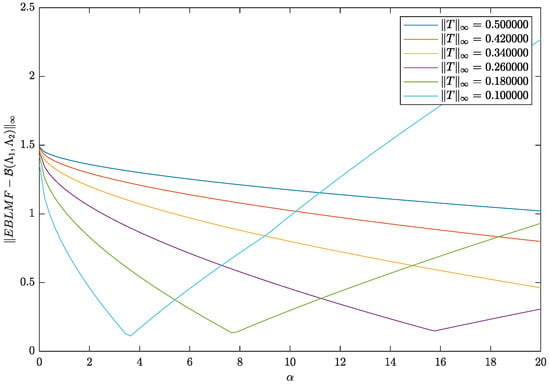
Figure 1. Graphical representation of $\parallel EBLMF-\mathcal{B}({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2){\parallel }_{\infty }$ various values of $\alpha$.

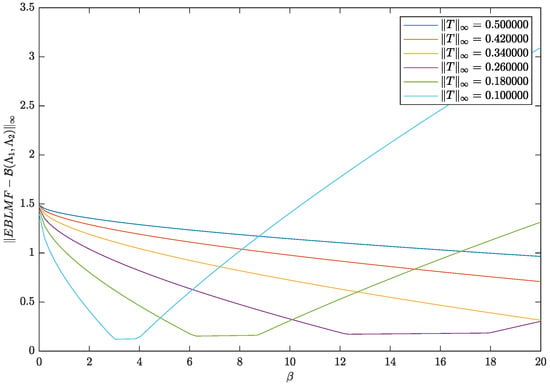
Figure 2. Graphical representation of $\parallel EBLMF-\mathcal{B}({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2){\parallel }_{\infty }$ various values of $\beta$.

When the matrix $\mathrm{T}$ approaches zero, $\parallel EBLMF-\mathcal{B}({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2){\parallel }_{\infty }$ should go to zero when $\alpha ,\beta =1$, and the result in [20] is obtained. To show the generalization introduced in this paper, Figure 3 depicts the graphs of the differences $\parallel EBLMF-\mathcal{B}({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2){\parallel }_{\infty }$ versus $\parallel \mathrm{T}-{\mathbf{0}}_{\kappa }{\parallel }_{\infty }$ when the matrix $\mathrm{T}$ is chosen to approach zero, and the values of $\alpha$ and $\beta =0.2,0.4,0.6.$ One can conclude that the differences decrease for all the values of $\alpha$ and $\beta$ when $\mathrm{T}$ tends to zero in its infinity norm. Similar results can be obtained from Figure 4 when the values of $\alpha$ and $\beta =0.5,1.5,3$ for a suitable choice of $\mathrm{T}$ matrix.

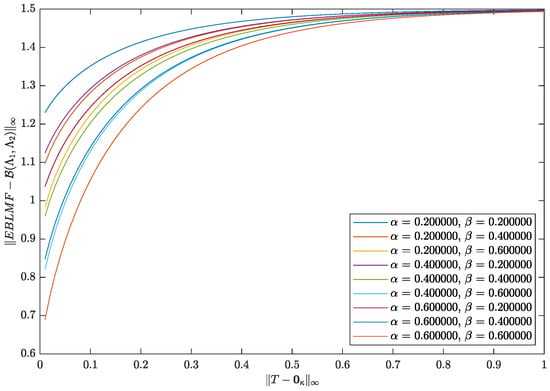
Figure 3. Graphical representation of $\parallel EBLMF-\mathcal{B}({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2){\parallel }_{\infty }$ with $\parallel \mathrm{T}-{\mathbf{0}}_{\kappa }{\parallel }_{\infty }$ for various values of $\alpha ,\beta \in [0.2,0.6]$.

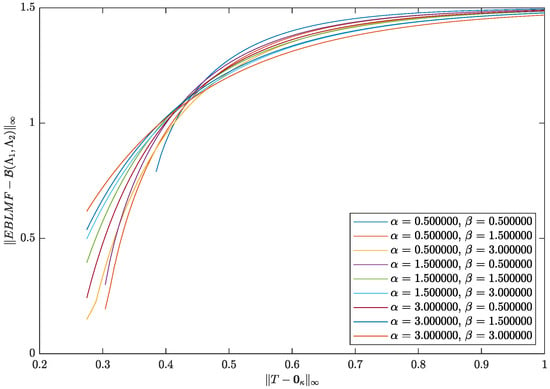
Figure 4. Graphical representation of $\parallel EBLMF-\mathcal{B}({\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2){\parallel }_{\infty }$ with $\parallel \mathrm{T}-{\mathbf{0}}_{\kappa }{\parallel }_{\infty }$ for various values of $\alpha ,\beta \in [0.5,3]$.

6. Conclusions

Later, many researchers contemplated the extension of the classical beta function to the matrix framework. The extended beta-logarithmic matrix function extends the extended beta matrix function [10] and the beta matrix function [20]. This manuscript explores several analytical properties of this function and employs this extension to derive the generalized beta distribution of matrix arguments. In addition, some numerical illustration examples and graphical descriptions were presented to show the efficacy of this extension by using MATLAB R2023b. Finally, the extended beta-logarithmic matrix function has the potential to extend several known applications based on numerous special functions in the literature.