Hermite Finite Element Method for One-Dimensional Fourth-Order Boundary Value Problems
Abstract
1. Introduction
2. One-Dimensional Fourth-Order Boundary Value Problems
2.1. Preliminaries
2.2. Problem Model
2.3. Weak Formulation
3. Finite Element Approximation
3.1. Hermite Finite Element Method
- Hermite cubic basis function:
- Hermite quintic basis function:
3.2. Discrete Scheme
4. Error Estimations
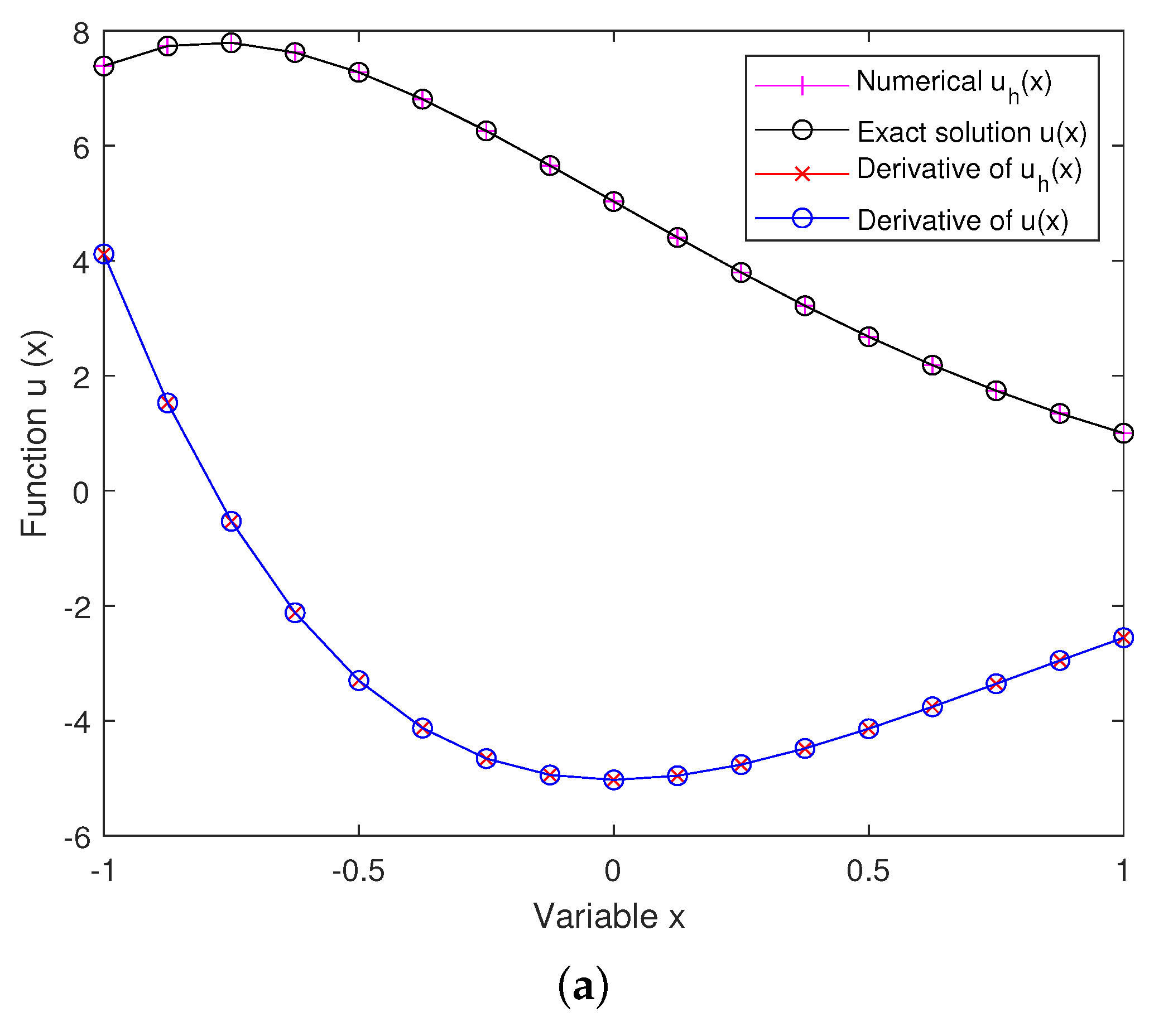
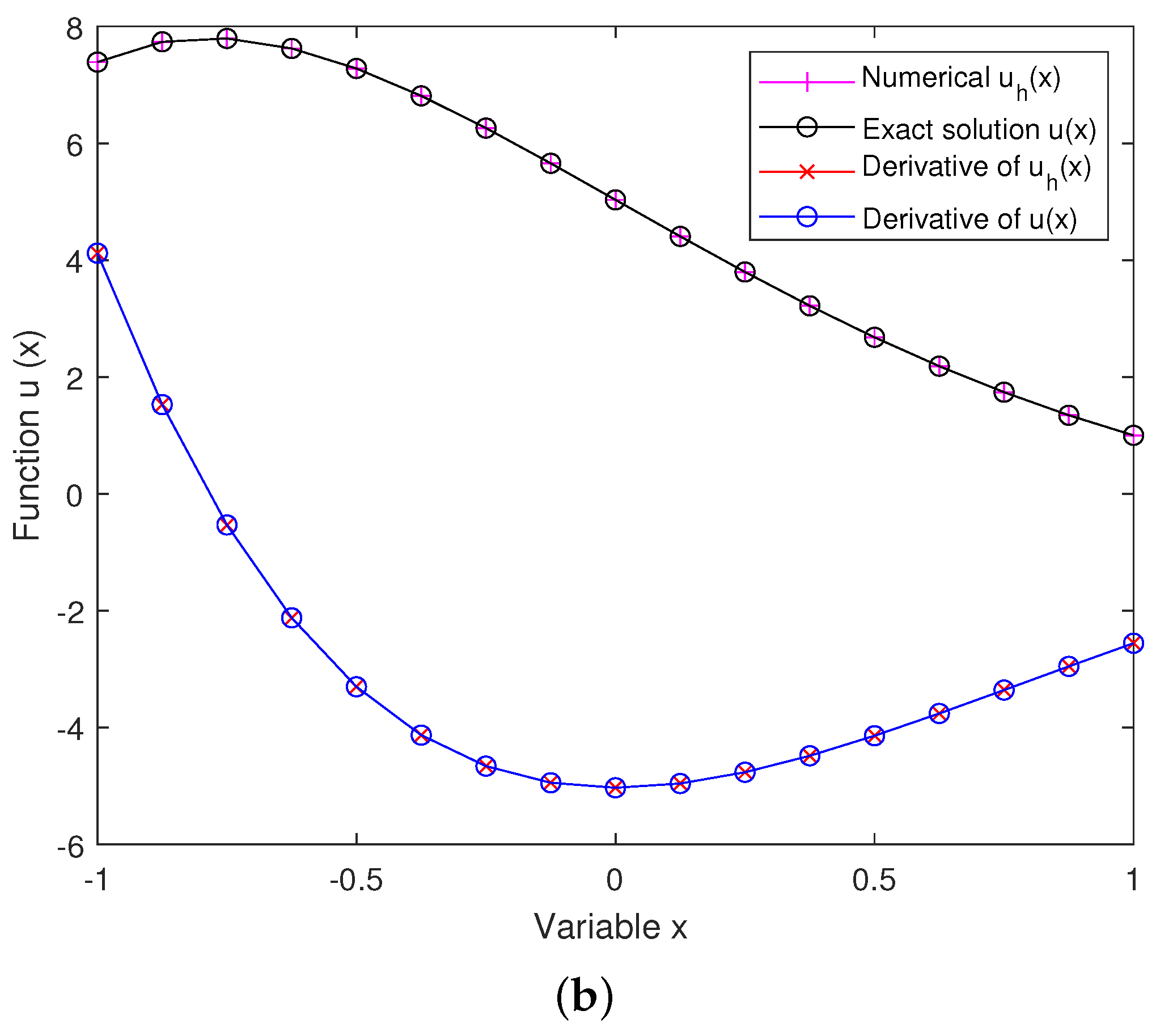
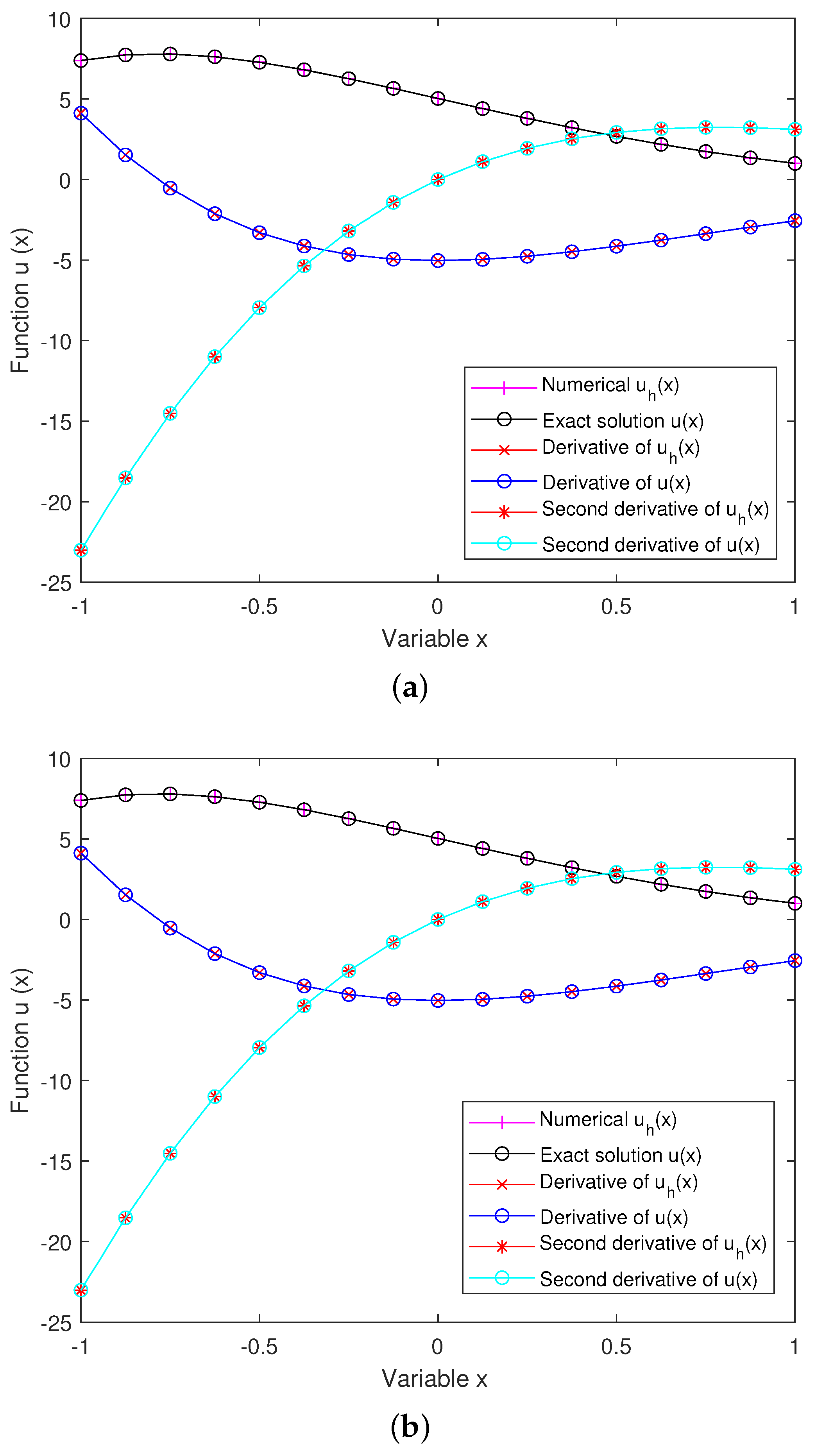
5. Numerical Simulations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, J.; Chen, S.; Zhang, B. The nonconforming virtual element method for plate bending problems. Math. Meth. Appl. Sci. 2016, 26, 1671–1687. [Google Scholar] [CrossRef]
- Arita, S.; Okumiya, T.; Miyazaki, Y. Numerical model for prediction of wrinkling behavior on a thin-membrane structure. J. Mech. Eng. 2014, 1, SE0041. [Google Scholar] [CrossRef]
- Firouzi, N.; Zur, K.K. On the generalized nonlinear mechanics of compressible, incompressible, isotropic, and anisotropic hyperelastic membranes. Int. J. Solids. Struct. 2023, 264, 1671–1687. [Google Scholar] [CrossRef]
- Schmitz, T.L.; Smith, K.S. Mechanical Vibrations Modeling and Measurement; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- LeVeque, R.J. Finite Difference Methods for Ordinary and Partial Differential Equations: Steady-State and Time-Dependent Problems; SIAM: Philadelphia, PA, USA, 2007. [Google Scholar]
- Ebrahimzadeh, A.; Panjeh Ali Beik, S. Application of spectral methods to solve nonlinear buckling analysis of an elastic beam. Casp. J. Math. Sci. 2021, 10, 68–76. [Google Scholar]
- Akano, T.; Fakinlede, O.A. An effective finite element method for beam based compliant mechanism. J. Eng. Mech. 2013, 3, 407–419. [Google Scholar]
- Lu, F.; Song, Z.; Zhang, Z. A compact fourth-order finite difference scheme for the improved Boussinesq equation with damping terms. J. Comput. Math. 2016, 34, 462–478. [Google Scholar] [CrossRef]
- Bernardi, C.; Maday, Y. Spectral methods for the approximation of fourth-order problems: Application to the stokes and Navier-Stokes equations. Comput. Struct. 1988, 30, 205–216. [Google Scholar] [CrossRef]
- Balasundaram, S.; Bhattacharyya, P.K. A mixed finite element method for fourth order partial differential equations. Z. Angew. Math. Mech. 2010, 66, 489–499. [Google Scholar] [CrossRef]
- Chen, G.; Feng, M. A C0-weak Galerkin finite element method for fourth-order elliptic problems. Numer. Methods Partial. Differ. Equ. 2016, 32, 1090–1104. [Google Scholar] [CrossRef]
- Holdeman, J.T. A Hermite finite element method for incompressible fluid flow. Int. J. Numer. Methods Fluids 2010, 64, 376–408. [Google Scholar] [CrossRef]
- Tang, Y.; Yin, Z. Hermite finite element method for a class of viscoelastic beam vibration problem. Engineering 2021, 13, 463–471. [Google Scholar] [CrossRef]
- Wang, Q.S.; Chen, S.; Li, F. Superconvergence and high accuracy combination formula of Hermite finite element for fourth-order equation. Int. J. Numer. Meth. Eng. 2009, 1, 131–137. [Google Scholar]
- Evans, L.C. Partial Differential Equations; American Mathematical Society: Providence, RI, USA, 2010; Volume 19. [Google Scholar]
- Brenner, S.C.; Scott, L.R. The Mathematical Theory of Finite Element Methods, 2nd ed.; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Ciarlet, P.G. The Finite Element Method for Elliptic Problems; North-Holland: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Brenner, S.C.; Wang, K.; Zhao, J. Poincaré–friedrichs inequalities for picewise H2 function. Numer. Funct. Anal. Opt. 2004, 25, 463–478. [Google Scholar] [CrossRef]
- Khalifa, A.K.; Aziz, M.A. Collocation finite element and spectral methods for one dimensional biharmonic equations. Int. J. Comput. Math. 2000, 74, 537–550. [Google Scholar] [CrossRef]
- Santos, H.A.F.A. A new finite element formulation for the dynamic analysis of beams under moving loads. Comput. Struct. 2024, 298, 107347. [Google Scholar] [CrossRef]
- Ben-Romdhane, M.; Temimi, H.; Baccouch, M. An iterative finite difference method for approximating the two-branched solution of Bratu’s problem. Appl. Numer. Math. 2019, 139, 62–76. [Google Scholar] [CrossRef]

| Mesh Size (h) | Semi-Error | Error Order | Error | Error Order |
|---|---|---|---|---|
| 1 | 1.1405 | 0.0499 | ||
| 1/2 | 0.2843 | 2.0043 | 0.0031 | 4.0035 |
| 1/4 | 0.0710 | 2.0017 | 1.9405 × 10 | 4.0042 |
| 1/8 | 0.0177 | 2.0004 | 1.2118 × 10 | 4.0013 |
| 1/16 | 0.0044 | 2.0001 | 7.5718 × 10 | 4.0003 |
| 1/32 | 0.0010 | 2.0000 | 4.7220 × 10 | 4.0031 |
| Mesh Size (h) | Semi-Error | Error Order | Error | Error Order |
|---|---|---|---|---|
| 1 | 1.1421 | 0.0378 | ||
| 1/2 | 0.2843 | 2.0062 | 0.0024 | 3.9537 |
| 1/4 | 0.0710 | 2.0019 | 1.5303 × 10 | 3.9945 |
| 1/8 | 0.0177 | 2.0004 | 9.5705 × 10 | 3.9990 |
| 1/16 | 0.0044 | 2.0001 | 5.9824 × 10 | 3.9998 |
| 1/32 | 0.0011 | 2.0000 | 3.7066 × 10 | 4.0125 |
| Mesh Size (h) | Semi-Error | Error Order | Error | Error Order |
|---|---|---|---|---|
| 1 | 0.0081 | 7.7134 × 10 | ||
| 1/2 | 5.7698 × 10 | 3.8129 | 1.3077 × 10 | 5.8852 |
| 1/4 | 3.6226 × 10 | 3.9934 | 1.9897 × 10 | 6.0384 |
| 1/8 | 2.2574 × 10 | 4.0034 | 3.0660 × 10 | 6.0020 |
| 1/16 | 1.4090 × 10 | 4.0019 | 4.5808 × 10 | 2.7427 |
| Mesh Size (h) | Semi-Error | Error Order | Error | Error Order |
|---|---|---|---|---|
| 1 | 0.0081 | 7.7198 × 10 | ||
| 1/2 | 5.7698 × 10 | 3.8130 | 1.3078 × 10 | 5.8833 |
| 1/4 | 3.6226 × 10 | 3.9934 | 1.9897 × 10 | 6.0385 |
| 1/8 | 2.2574 × 10 | 4.0043 | 3.0662 × 10 | 6.0200 |
| 1/16 | 1.4090 × 10 | 4.0019 | 1.5879 × 10 | 0.9493 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, B.; Qiu, J. Hermite Finite Element Method for One-Dimensional Fourth-Order Boundary Value Problems. Mathematics 2024, 12, 1613. https://doi.org/10.3390/math12111613
Wu B, Qiu J. Hermite Finite Element Method for One-Dimensional Fourth-Order Boundary Value Problems. Mathematics. 2024; 12(11):1613. https://doi.org/10.3390/math12111613
Chicago/Turabian StyleWu, Bangmin, and Jiali Qiu. 2024. "Hermite Finite Element Method for One-Dimensional Fourth-Order Boundary Value Problems" Mathematics 12, no. 11: 1613. https://doi.org/10.3390/math12111613
APA StyleWu, B., & Qiu, J. (2024). Hermite Finite Element Method for One-Dimensional Fourth-Order Boundary Value Problems. Mathematics, 12(11), 1613. https://doi.org/10.3390/math12111613





