Abstract
A technique for the reduction in the CPU-time in the analysis of electromagnetic problems using the Characteristic Basis Function Method (CBFM) is presented here, allowing for analysis of electrically large cases where an iterative solution process cannot be avoided. This technique is based on the use of the Adaptive Cross Approximation (ACA) for the fast computation of the coupling matrix between CBFs belonging to adjacent blocks, as well as the Multilevel Fast Multipole Method (MLFMM) for the computation of matrix−vector products in the solution of the full system. This combination allows for a noticeable reduction in the computational resources during the analysis of electrically large and complex scenarios while maintaining a very good degree of accuracy. A number of test cases serve to validate the presented approach in terms of accuracy, memory and CPU-time compared with conventional techniques.
Keywords:
computational electromagnetics; numerical methods; full-wave analysis; moment methods; macro basis functions MSC:
78M05; 78M15; 78M16
1. Introduction
It is widely acknowledged that, while the Method of Moments (MoM) [1] is commonly employed as a boundary element reference technique for the analysis of scattering or radiation problems, its application in real world cases is hindered by very high computational requirements posed by the size and density of the impedance matrix. Over the years, various improvements have emerged to mitigate these restrictions through following different strategies. Notable among these is the Fast Multipole Method (FMM) [2], or its multilevel implementation (MLFMM) [3,4], which facilitates fast matrix−vector product calculations during the iterative solution process and notably reduces memory requirements by storing only the near-field coupling terms. Nonetheless, it is important to note that certain practical challenges may persist, presenting difficult convergences due to either the scale of the problem at hand or the intricate geometric characteristics involved. The MLFMM can be combined with additional approaches that allow for extending its applicability to larger or more complex scenarios. The use of spherical harmonics can noticeably reduce [5] the memory requirements for the storage of the Fourier Transforms of the basis functions required by the MLFMM, maintaining the CPU-time of the iterative process. The efficiency of FFT computations is combined with MLFMM in [6], allowing for the analysis of large problems with mixed memory systems.
The interest in the use of techniques dealing with Macro Basis Functions (MBFs) [7,8,9,10,11,12,13,14,15,16,17] has increased sharply during the last decade, based on the computational advantages of reducing the effective numerical size of the problems under analysis. This family of methods requires the computation of a new set of basis functions defined on a number of blocks in which the scenario has been previously partitioned. The new high-level basis functions on a given block can be obtained by considering the set of currents induced by the external sources (primary CBFs) and those induced by the rest of the blocks, (secondary CBFs) [8] or by a number of sources artificially placed around each isolated block [9], in which case the redundancy of the information contained in those current vectors is usually minimized by performing the Singular Value Decomposition (SVD) and truncating the number of singular vectors retained as the new base after setting a threshold on the magnitude of the singular values. Each of those singular vectors is then identified as a Macro Basis Function on that block. In [10], the authors describe an approach for the acceleration of the generation of the MBFs by considering only near-field coupling terms for each isolated block, taking advantage of the fact that the MBFs can be very effective even when the corresponding current distributions used for their computation are not very accurate.
The Characteristic Basis Function Method (CBFM) makes use of MBFs called Characteristic Basis Functions (CBFs), which are defined over blocks with typical sizes of one or a few wavelengths. It is important to highlight, in the context of the work presented here, that the CBFM can be effectively combined with MLFMM [10]. Existing works make use of a preliminary ray-tracing analysis of the scenario to further reduce the size of the problem [11,12]. The CBFM requires a preprocessing stage for the generation of the CBFs and the matrix that contains the coupling terms between CBFs, often called a reduced matrix. The CBFs can then be reused when some blocks are replicated in the scenario, which can reduce processing time [13]. A variation in the CBFM for the analysis of complex radome antennas is described in [14], defining two domains containing currents that are updated iteratively. The calculation of the reduced matrix can pose an important computational bottleneck for MLFMM-CBFM when considering large blocks, since it is necessary to obtain all the low-level impedance terms inside each block as well as between neighboring blocks. In [15], the CBFs are used as a sparse base over which a Compressive Sensing approach is used to analyze the bistatic RCS of 3D targets. The work described in [16] makes use of CBFs in order to improve the alternating GMRES-Jacobi (AGJ) iterative solver, where the reduced system is built based on the previous iterations. The authors of [17] have presented a fast technique for the computation of the CBFs, making use of a Sparse Approximate Inverse (SAI) matrix used as a direct operator to obtain an estimation of the currents induced by a large number of plane wave sources on each block. A technique for the analysis of scattering by dielectric objects based on the Poggio–Miller–Chang–Harrington–Wu–Tsai (PMCHWT) formulation is shown in [18], where the bases for electric and magnetic currents are orthogonalized via the SVD and applied as dual basis functions, with a Krylov-Calderón preconditioner also being used for better convergence. In turn, ref. [19] shows a method making use of piecewise sinusoidal (PS) basis functions for the approximation of surface currents, making use of CBFs and a new generation strategy, setting a number of auxiliary sources on the cubical surface bounding the entire target.
It is worthwhile to mention an additional type of fast technique based on the compression of the right-hand side vectors [20,21] or parts of the coupling matrix by taking advantage of their low-rank approximation. This is especially well suited when the analytical representation of the Green’s Function is not available, and the application of multipole expansions can be difficult because of its dependence on an explicit form of the Green’s Function kernel. The Dual-MGS method [22] or the Adaptive Cross Approximation (ACA) [23] provide approximate QR decompositions without having to compute and store all the coefficients of the original matrices. A fast evaluation of the Frobenius norm as the convergence criterion for the ACA based on a stochastic approach is described in [24]. A multilevel subdivision approach for the analysis of dielectric objects is applied in [25], making use of the Multiscale Adaptive Cross Approximation (MS-ACA) for an efficient filling of parts of the impedance matrix. An additional work regarding the generation of multilevel MBFs is described in [26], featuring a recursive decomposition of the impedance matrix and its compression by means of a fast Adaptive Cross Approximation algorithm. A weighted-average ACA is proposed in [27] to mitigate the loss of error control in cases where the matrix alternates between zero and non-zero sub-blocks. A kernel independent Nested Cross Approximation (NCA) approach is presented in [28] for the solution of large Volume Integral Equations (VIEs) with controlled accuracy. A fast parallel direct solver based on the ACA is described in [29] where the off-diagonal blocks are compressed after performing an LU decomposition. A combination of ACA and a Domain Decomposition Method (DDM) is shown in [30] in order to address layered media scattering problems efficiently.
The main contribution of this work is the development of a numerical scheme that makes use of the ACA for the generation of the near-field reduced matrix, compressing the off-diagonal blocks and making use of CBFs, combined with MLFMM for the computation of the final current distribution. Our primary goal is to use moderately large block sizes for a better reduction in the number of unknowns while avoiding the computational penalty in terms of CPU-time suffered by conventional methods. Section 2 of this paper lays out the specific MLFMM-CBFM framework considered in this work and describes in detail the reduced matrix filling using ACA. Section 3 presents some representative results, and, finally, Section 4 contains the conclusions derived from this work.
2. Materials and Methods
2.1. CBF Generation and Block Size Considerations
The CBFM performs a substitution of basis functions with MBFs over the blocks, allowing for a reduction in the number of unknowns without loss of accuracy. This reduction results in an improvement in computational resources both in terms of memory and CPU-time. This reduction is closely related to the size of the blocks: the larger the size, the greater the reduction in the number of unknowns. To obtain this improvement, it is necessary to include a preprocessing stage for the construction of the CBFs and the reduced matrix. This additional CPU-time becomes greater as the block size increases. The block size is generally chosen to be around λ, as it provides a considerable reduction in the number of unknowns without rendering the technique inefficient. Figure 1a shows the reduction in the number of unknowns when increasing the block size for a Perfect Electric Conductor (PEC) sphere with a radius of 1 m, while the variation in the preprocessing time needed for each block size is depicted in Figure 1b.
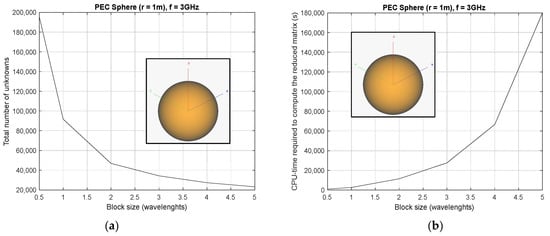
Figure 1.
Results obtained for different block sizes regarding (a) the number of unknowns and (b) the CPU-Time required for the computation of the reduced matrix.
With these considerations, the benefit of seeking improvements that allow for enlarging the block size while easing the CPU-time penalty seems clear, and it is the goal of the approach proposed in this paper. The CBFM is especially efficient when the preprocessing time is compensated by the faster iteration time in the solution process, making it especially well suited for the analysis of problems with multiple right hand sides, as is the case with monostatic RCS. Note that there are some published works that deal with the reduction in the CBF generation time [12] or that of the reduced matrix. The authors have developed in [31] a technique in which MLFMM-MoM is used inside each block for the acceleration of the reduced matrix computation, avoiding the need to obtain the full low-level coupling matrix.
2.2. Generation of the Reduced Matrix Using ACA and Solution via MLFMM-CBFM
The CBFM relies on the definition of a number of high-level basis functions (CBFs) which can be expressed as weighted aggregations of low-level (conventional) basis functions:
where refers to the i-th CBF on the k-th block, is the number of low-level basis functions contained in that block, denotes the n-th basis function on the block, and is the weight of the n-th low-level basis function for that CBF. Using this expansion, the reduced coupling term between the i-th CBF contained in the m-th block and the j-th CBF contained in the k-th block can be computed using the low-level coupling terms as follows:
where the superscript (R) indicates that the term is related to the reduced matrix and not to the conventional coupling matrix. represents the testing CBF, which can be analogously expanded as a set of weighted low-level testing functions, as shown in (1). If we consider the submatrix containing all the coupling terms between the source CBFs on the k-th block and the testing CBFs on the m-th block, it is possible to express it more compactly as:
where, as mentioned above, is the sub-matrix containing all the coupling terms between both blocks, is the corresponding low-level coupling submatrix, and each column of contains the weights of all the low-level basis functions used to represent each CBF on the k-th block, arranged as columns, as follows:
taking into account that Mk stands for the number of CBFs in the block.
Considering how the reduced matrix can be obtained by source-testing block pairs using (3), it becomes apparent that, as previously mentioned, one important computational drawback from the use of large blocks is that we need to compute and store in advance. Note that, since the MLFMM is combined with CBFM, the reduced matrix does not need to be complete, and the far-field interactions between CBFs will be considered in the iterative solution process by means of efficient matrix−vector products involving aggregation, translation and disaggregation stages [4]. It is, therefore, only necessary to compute the coupling terms between CBFs located in the same and neighboring blocks. Since the CBF generation involves isolating each block and obtaining the currents due to a number of conveniently arranged sources, the reduced submatrix of each block can be stored at that stage. For the off-diagonal submatrices, we propose making use of the ACA factorization in order to obtain the following approximation:
where r is much smaller than either Nm or Nk, and the application of this factorization does not need to have the full original matrix stored or to compute all its coefficients.
The ACA is exclusively based on algebraic manipulations [23] and does not depend on the kernel of the integral equation (unlike MLFMM). It allows for the generation of rows and columns of the original matrix on the fly to build the Q and R factors, making use of a tolerance parameter ε that allows for controlling the degree of accuracy of this compression process:
where [Rm,k] is the error matrix, and represents the Frobenius norm. Substituting (5) in (3) results:
which, due to the size of these matrices, can be calculated much faster than directly applying (3). Note that, since we are considering a compression based on a reduced rank approximation of the original submatrices, we are not including diagonal submatrices in the ACA factorization process, although, as previously mentioned, the full submatrix is available after the CBF generation stage.
The reduced matrix can be obtained as discussed above and stored in compact form. The non-neighboring coupling terms between CBFs do not require storage and are taken into account by means of their corresponding multipole expansions with MLFMM-CBFM. More specifically, the coupling term between CBFs m and n when both are located in the non-neighboring blocks b1 and b2, respectively, is given by:
where contains the contribution of the CBF m at the center of its block, denoted as , on the directions of the Ewald sphere, which can be computed as follows:
and the translation operator is given by:
where is a spherical Hankel function of the second kind and is a Legendre polynomial of degree l.
The approach described in this section aims to improve the efficiency of existing MBF-based techniques by making use of a low-rank compression of the coupling matrix for each block in order to speed up the computation of the reduced matrix by means of the ACA method, and the subsequent acceleration of the matrix-vector products during the iterative solution process by applying the MLFMM, reducing at the same time the memory requirements, since it is only necessary to store the near-field part of the reduced matrix. Note that, even though ACA is notably faster than the full SVD, it offers a less accurate approximation of the original matrix for the same error threshold. It is worthwhile to mention that it is possible to combine both approaches as seen in [32], where ACA is used as a preliminary stage using a safe threshold value (about ten times lower than the desired one), and the result is post-compressed using the SVD with the final error threshold. This approach could also be used in the generation of the CBFs, compressing the matrices containing the currents induced by the external excitations around each block before applying the SVD to obtain the final CBFs.
3. Results
This section includes test cases selected in order to show the accuracy and efficiency of the previously described approach.
The first example consists of the monostatic RCS computation of a 32λ dihedral structure, taking into account an angular sweep for ϕ = 0° and θ ranging from 0° to 45° in 0.5° steps. The total number of unknowns using MoM has been 413,770, and this number has been brought down to 36,158 when applying CBFM. Figure 2 compares the results obtained using MLFMM-MoM, conventional MLFMM-CBFM and MLFMM-CBFM using the proposed approach to obtain the reduced matrix via ACA compression.
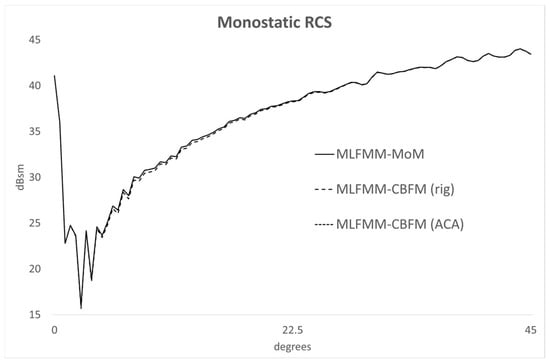
Figure 2.
Monostatic RCS of the 32λ 90° dihedron test case.
Good agreement can be observed between the three simulations. Table 1 shows the comparison of the CPU-time required for the computation of the reduced matrix and its influence on the total CPU-time, as well as the peak memory requirements.

Table 1.
Comparison of computational resources for the first test case (Block size: 2λ).
The CPU-time required for the simulation using MLFMM-MoM has been 42,720 s, where most of the time has been used in the system solution (42,546 s), since the preprocessing time has been only 174 s.
The next test case considered has been the monostatic RCS of the geometry shown in Figure 3 at a frequency of 25 GHz. This geometry has a size of 0.1 m × 0.02 m × 0.06 m.
Figure 3.
Resonant pipe geometry.
An angular observation cut on the θ = 90° plane has been considered in this analysis, with 181 samples in ϕ from ϕ = 0° to ϕ = 90°. The predicted RCS is compared between the conventional MLFMM-CBFM, the presented approach and a variation where the reduced matrix has been computed using MLFMM-MoM instead of ACA (as seen in Figure 4). In the latter case, we have made use of a previously developed approach, presented in [31], in which the acceleration in the computation of (3) is based on the use of multipole expansions and the corresponding aggregation, translation and disaggregation stages.
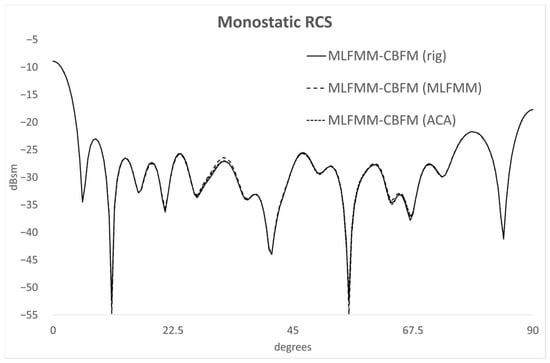
Figure 4.
Monostatic RCS of the resonant pipe geometry.
Aside from the good agreement shown in these results, it is necessary to compare the computational requirements of these simulations. Regarding the solution stage, MLFMM-MoM has required 5792 s, and the total number of unknowns has been 69,655. With respect to MLFMM-CBFM, we have considered two different block sizes: 2λ and 4λ. Table 2 and Table 3 show the CPU-time and memory results for both configurations.

Table 2.
Comparison of computational resources for the second test case (Block size: 2λ).

Table 3.
Comparison of computational resources for the second test case (Block size: 4λ).
The first conclusion that can be derived from the comparison between MLFMM-CBFM and MLFMM-MoM is that the total CPU-time is lower when using CBFM for both configurations. MLFMM-MoM uses most of the simulation time for the system solution, while MLFMM-CBFM balances the total time between the preprocessing and solution stages.
In addition, it can be observed that the proposed approach requires less CPU-time to compute the reduced matrix than the rest. Note that this specific case contains parts where different surfaces are close to each other, which entails more near-field coupling terms, and the use of ACA benefits greatly from not having to assemble the full near-field coupling submatrices. There are also many adjacent blocks around the central part of the target, where using the proposed approach contributes to the reduction in the CPU-time.
There is, in turn, a reduction in the memory requirements for the computation of the reduced matrix. As mentioned in the previous section, the coupling submatrix between off-diagonal blocks is not required to be stored with the presented approach, and it is substituted by its factors Q and R with smaller sizes.
As the block size increases, the reduced matrix filling time using the conventional approach increments significantly due to the need to obtain all the coupling coefficients of the submatrices involved. The proposed approach based on ACA compression presents a much smoother behavior with the block size. When using MLFMM instead of ACA to obtain the reduced matrix, as the block size increases, it is necessary to consider new MLFMM levels to compute the couplings, resulting in additional CPU-time, although it presents a weaker dependence in regard to the block size than the conventional technique.
The last test case considered for the validation of the method described in this work is the monostatic RCS of the aircraft shown in Figure 5 at a frequency of 150 Mhz. The set of observation directions is given by θ = 90° and ϕ ranges from 90° to 270° in 0.5° steps. The number of unknowns using MLFMM-MoM has been 107,770 and reduced to 9398 using MLFMM-CBFM.
Figure 5.
Aircraft geometry.
Figure 6 shows a good agreement between the results returned by the proposed approach, MLFMM-MoM and the conventional MLFMM-CBFM. The CPU-time required for the full simulation using MLFMM-MoM has been 6456 s. The conventional MLFMM-CBFM analysis has taken 4382 s, and the presented approach has required a CPU-time of 3252 s.
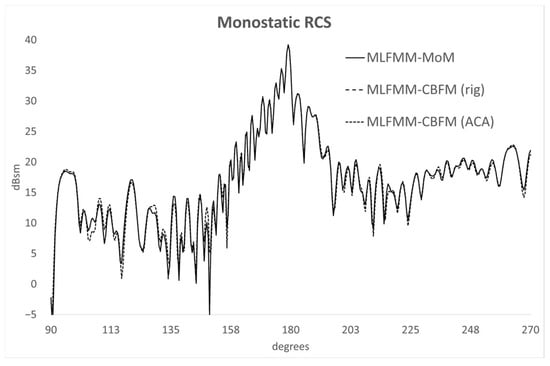
Figure 6.
Monostatic RCS of the aircraft test case.
4. Discussion
This paper presents a new technique based on the CBFM where the computation of the reduced matrix is accelerated by introducing an ACA-based approach for the compression of the off-diagonal near-field coupling submatrices. This method is then combined with MLFMM for the analysis of the full problem. Several test cases have validated the improved efficiency achieved by this approach compared to the conventional MLFMM-CBFM while maintaining a good degree of accuracy. The contribution introduced by this approach allows for increasing the block size, for a more pronounced reduction in the total number of unknowns, while reducing the computational penalty of the preprocessing CPU-time that arises with other conventional techniques. We have seen that using ACA for the block-wise computation of the reduced matrix is in general faster than using MLFMM, and it is also more efficient in regard to the memory required. Additionally, as expected, the number of CBFs decreased drastically as we increased the block size in all the cases analyzed. We believe that this improvement can be combined with future lines of work addressing, for example, a faster generation of the CBFs by using a low-rank-based compression of the matrix factorized by the SVD, with an efficient interpolation of the currents for dense angular monostatic RCS analyses, or other approaches.
Author Contributions
Conceptualization, C.D. and E.G.; data curation, F.C.; formal analysis, C.D.; funding acquisition, C.D. and E.G.; investigation, C.D.; methodology, E.G.; project administration, F.C.; resources, F.C.; software, C.D. and E.G.; supervision, E.G.; validation, E.G. and F.C.; visualization, C.D.; writing—original draft, C.D.; writing—review and editing, C.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the Spanish Ministerio de Ciencia e Innovación (MICINN) under project PID2020-114362RB-I00/AEI/10.13039/501100011033, by Junta de Comunidades de Castilla—La Mancha, project SBPLY/21/180501/000264 and by Altair Inc., contracts ART. 83/LOU 181/2019 and 183/2019.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to thank Altair, Inc. for the technical and material support provided in the development of this work, including the use of Altair newFASANT and Altair Feko for the validation of the presented approach.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Harrington, R.F. Field Computation by Moment Methods; McMillan: New York, NY, USA, 1993. [Google Scholar]
- Engheta, N.; Murphy, W.D.; Rokhlin, V.; Vassiliou, M.S. The fast multipole method (FMM) for electro-magnetic scattering problems. IEEE Trans. Antennas Propag. 1992, 40, 634–641. [Google Scholar] [CrossRef]
- Chew, W.C.; Jin, J.; Michielssen, E.; Song, J. (Eds.) Fast and Efficient Algorithms in Computational Electromagnetics; Artech House: Norwood, MA, USA, 2001. [Google Scholar]
- Song, J.M.; Chew, W.C. Multilevel fast multipole algorithm for solving combined field integral equa-tions of electromagnetic scattering. Microw. Opt. Technol. Lett. 1995, 10, 14–19. [Google Scholar] [CrossRef]
- Eibert, T. A diagonalized multilevel fast multipole method with spherical harmonics expansion of the k-space Integrals. IEEE Trans. Antennas Propag. 2005, 53, 814–817. [Google Scholar] [CrossRef]
- Taboada, J.M.; Araujo, M.G.; Basteiro, F.O.; Rodriguez, J.L.; Landesa, L. MLFMA-FFT Parallel Algo-rithm for the Solution of Extremely Large Problems in Electromagnetics. Proc. IEEE 2013, 101, 350–363. [Google Scholar] [CrossRef]
- Suter, E.; Mosig, J.R. A subdomain multilevel approach for the efficient MoM analysis of large planar antennas. Microw. Opt. Technol. Lett. 2000, 26, 270–277. [Google Scholar] [CrossRef]
- Prakash, V.V.S.; Mittra, R. Characteristic basis function method: A new technique for efficient solution of method of moments matrix equations. Microw. Opt. Technol. Lett. 2003, 36, 95–100. [Google Scholar] [CrossRef]
- Matekovits, L.; Laza, V.A.; Vecchi, G. Analysis of Large Complex Structures with the Synthetic-Functions Approach. IEEE Trans. Antennas Propag. 2007, 55, 2509–2521. [Google Scholar] [CrossRef]
- García, E.; Delgado, C.; Cátedra, F. Flexible Approach for the Generation of Macro-Basis Functions Using the Characteristic Basis Function Method. Electronics 2024, 13, 657. [Google Scholar] [CrossRef]
- Delgado, C.; Catedra, M.F. Efficient Generation of Macro Basis Functions for Radiation Problems Using Ray-Tracing Derived Dynamic Thresholds. IEEE Trans. Antennas Propag. 2018, 66, 3231–3236. [Google Scholar] [CrossRef]
- Delgado, C.; Cátedra, M.F. Combination of Ray-Tracing and the Method of Moments for Electromagnetic Radiation Analysis Using Reduced Meshes. J. Comput. Phys. 2018, 361, 412–423. [Google Scholar] [CrossRef]
- Gonzalez-Ovejero, D.; Craeye, C. Interpolatory macro basis functions analysis of non-periodic arrays. IEEE Trans. Antennas Propag. 2011, 59, 3117–3122. [Google Scholar] [CrossRef]
- García, E.; Delgado, C.; Cátedra, F. Efficient Iterative Analysis Technique of Complex Radome Antennas Based on the Characteristic Basis Function Method. IEEE Trans. Antennas Propag. 2021, 69, 5881–5891. [Google Scholar] [CrossRef]
- Wang, Z.G.; Nie, W.Y.; Lin, H. Characteristic basis functions enhanced compressive sensing for solving the bistatic scattering problems of three-dimensional targets. Microw. Opt. Technol. Lett. 2020, 62, 3132–3138. [Google Scholar] [CrossRef]
- Marinović, T.; Maaskant, R.; Mittra, R.; Vandenbosch, G.A.E. Comparison of CBFM-Enhanced Iterative Methods for MoM-Based Finite Antenna Array Analysis. IEEE Trans. Antennas Propag. 2022, 70, 3538–3548. [Google Scholar] [CrossRef]
- García, E.; Delgado, C.; Cátedra, F. A Computationally Efficient Technique Using Characteristic Basis Functions and Large Block Sizes. IEEE Antennas Wirel. Propag. Lett. 2024, 23, 1341–1345. [Google Scholar] [CrossRef]
- Tanaka, T.; Niino, K.; Nishimura, N. Characteristic Basis Function Method Combined with Krylov-Calderón Preconditioner for PMCHWT Formulation. IEEE Trans. Antennas Propag. 2024, 72, 2578–2591. [Google Scholar] [CrossRef]
- Li, C.; Sharawi, M.S.; Mittra, R. Fast Computation of Electromagnetic Scattering from Dielectric Objects Using Quadrilateral Piecewise Sinusoidal Basis and Characteristic Basis Function Method. IEEE Trans. Antennas Propag. 2022, 70, 5683–5692. [Google Scholar] [CrossRef]
- Lü, Z.-Q.; An, X. Fast monostatic radar cross-section computation for perfectly electric conducting targets using low-rank compression and adaptive integral method. IET Microw. Antennas Propag. 2014, 8, 46–51. [Google Scholar] [CrossRef]
- Li, M.; Ding, D.; Heldring, A.; Hu, J.; Chen, R.; Vecchi, G. Low-Rank Matrix Factorization Method for Multiscale Simulations: A Review. IEEE Open J. Antennas Propag. 2021, 2, 286–301. [Google Scholar] [CrossRef]
- Burkholder, R.J.; Lee, J.F. Fast Dual-MGS Block-Factorization Algorithm for Dense MoM Matrices. IEEE Trans. Antennas Propag. 2004, 52, 1693–1699. [Google Scholar] [CrossRef]
- Zhao, K.; Vouvakis, N.M.; Lee, J.-F. The adaptive cross approximation algorithm for accelerated method of moments computations of EMC problems. IEEE Trans. Electromagn. Compat. 2005, 47, 763–773. [Google Scholar] [CrossRef]
- Heldring, A.; Ubeda, E.; Rius, J.M. Stochastic Estimation of the Frobenius Norm in the ACA Conver-gence Criterion. IEEE Trans. Antennas Propag. 2015, 63, 1155–1158. [Google Scholar] [CrossRef]
- Huang, F.; Sun, Y.F. Efficient solution of electromagnetic scattering from dielectric objects via characteristic basis function method based on large-size blocks with multilevel subdivision. IEEE Access 2019, 7, 71741–71748. [Google Scholar] [CrossRef]
- Fang, X.X.; Cao, Q.S.; Wang, Y. Accelerated direct solver with multiscale compressed block decomposition and multilevel characteristic basis function method. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 2226–2229. [Google Scholar] [CrossRef]
- Blackburn, J.N.; Young, J.C.; Adams, R.J. A Weighted Average Adaptive Cross Approximation. IEEE Trans. Antennas Propag. 2023, 71, 8121–8129. [Google Scholar] [CrossRef]
- Wang, Y.; Jiao, D. Fast O(N log N) Algorithm for Generating Rank-Minimized H2-Representation of Electrically Large Volume Integral Equations. IEEE Trans. Antennas Propag. 2022, 70, 6944–6956. [Google Scholar] [CrossRef]
- Jia, R.; Zuo, S.; Zhao, X.; Lin, Z.; Zhang, Y.; Yang, M. A Novel Parallel Direct Solver Using Adaptive Cross Approximation for Analysis of Electromagnetic Radiation Problems with Complex Structures. IEEE Trans. Antennas Propag. 2024, 72, 2962–2967. [Google Scholar] [CrossRef]
- Wang, D.; Hu, Y.; Fang, Y.; Mao, Y.; Liu, Q.H. Fast VIE-DDM for 3-D Electromagnetic Scattering of Complicated Anomalies in Layered Media Using Adaptive Cross Approximation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4507709. [Google Scholar] [CrossRef]
- García, E.; Lozano, L.; Delgado, C.; Cátedra, F. Efficient computation of the reduced matrix of MLFMA–CBFM for electrically large blocks. IET Microwaves Antennas Propag. 2020, 14, 539–546. [Google Scholar] [CrossRef]
- Heldring, A.; Rius, J.M.; Tamayo, J.M.; Parrón, J.; Ubeda, E. Multiscale Compressed Block Decomposition for Fast Direct Solution of Method of Moments Linear System. IEEE Trans. Antennas Propag. 2011, 59, 526–536. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).