Static Bipartite Consensus Problems of Heterogeneous Signed Networks

Abstract

This paper aims to study the distributed control problems of heterogeneous signed networks whose communication topologies are undirected. A distributed control protocol is designed based on neighboring state information. With this protocol be employed, the convergence results of the heterogeneous signed network are provided. It is shown that the heterogeneous signed network can achieve the static bipartite consensus (respectively, state stability) if and only if the signed graph is structurally balanced (respectively, unbalanced). The associated convergence analyses can be developed by constructing a suitable Lyapunov function. In addition, two simulation examples are presented to validate the correctness of the obtained results.

1. Introduction

Networked systems mainly consist of multiple agents and interactions among agents, which can accomplish the tasks that are difficult for single agent. When the dynamics of all agents in the networked system are identical, we refer to this networked system as a homogeneous networked system. The dynamics of agents can include first-order integrators [1], second-order integrators [2], higher-order integrators [3], or general linear dynamics [4]. In order to improve the convergence speed of the networked system, distributed control problems with finite-time/fixed-time convergence have been studied [5]. If the dynamics of agents in the network are different, we refer to this network system as a heterogeneous networked system. Heterogeneous networked systems are quite common in our daily lives [6,7]. Some of these applications include the following:

(1)

Internet of Things (IoT): Heterogeneous networks play an important role in IoT applications, where diverse devices such as sensors, actuators, and smart appliances communicate and collaborate to collect and exchange data for monitoring, automation, and optimization purposes.

(2)

Smart cities: In urban environments, heterogeneous networked systems enable the integration of various infrastructures such as transportation systems, energy grids, public safety systems, and environmental monitoring systems. This integration facilitates efficient resource management, traffic optimization, waste management, and enhanced public services.

(3)

Military and defense: Heterogeneous networked systems are deployed in military and defense applications for situational awareness, battlefield communications, unmanned vehicle control, and intelligence gathering. Integration of various sensors, platforms, and communication technologies enhances military capabilities and mission effectiveness.

When considering only cooperative interactions between agents, this kind of networked systems is referred to as unsigned networks. The distributed control problems of unsigned network systems whose agents contains heterogeneous dynamics have attracted widespread attentions. When the communication topology of unsigned networks is undirected, Ref. [8] has provided the conditions for achieving consensus when the agents’ dynamic simultaneously includes first-order integrators and second-order integrators. Ref. [9] has extended the results of [8] to the case of directed fixed and switching topologies. When the communication topology is disconnected, Ref. [10] investigates the group consensus control problem of heterogeneous unsigned networks. To ensure the convergence speed of the unsigned networks, nonlinear distributed control protocols have been proposed to achieve finite-time consensus [11], fixed-time consensus [12,13], and predetermined-time consensus [14] objectives for all agents. Considering the agent structure as general linear dynamics, Refs. [15,16,17,18] have studied the output consensus problem of heterogeneous unsigned networks. Ref. [19] has further investigated the output control problems under switching topologies based on Lyapunov stability analysis methods. Ref. [20] has designed a sub-linear control protocol based on sliding mode control, which can guarantee achieving consensus within finite time. Ref. [21] has studied the predetermined-time consensus problem, and the distributed control protocol designed can ensure consensus within the predetermined time. In addition, Ref. [22] has investigated the controllability problem of heterogeneous unsigned networks and provided conditions for the controllability.

When the interactions between agents involve not only cooperative but also antagonistic relationships, this class of networked systems is referred to as signed networks. They are termed as signed networks because this class of networked systems can be represented using a signed graph, where positive edge weights represent cooperative relationships between agents and negative edge weights represent antagonistic relationships between agents. Similarly, the distributed control problem of signed networks has also attracted significant attention. Ref. [23] has induced a distributed control protocol based on the Laplacian potential function to ensure the bipartite consensus and established a framework for studying the distributed control problem of signed networks. Considering agents with general linear dynamics, Ref. [24] has provided conditions for how to select the control gain matrix to achieve the bipartite consensus in signed networks. Ref. [25] has investigated the presence of input saturation constraints on agents and designed a distributed control protocol to achieve the bipartite consensus goals, which validated the effectiveness of the proposed protocol through experiments with obstacle avoidance using mobile robots. Ref. [26] has studied the bipartite consensus problems among agents with communication noise and provided solvable conditions. Ref. [27] has designed distributed control protocols using state feedback and output feedback and provided conditions for solving the bipartite consensus problems of signed networks. Ref. [28] has investigated distributed control problems with multiple fixed communication delays among agents, providing an upper bound for the allowable communication delay. Although recent research has yielded many promising results in the analyses of dynamic behaviors in signed networks, most of these studies focus on signed networks with homogeneous dynamics. Currently, there is relatively limited research on the distributed control problems of heterogeneous signed networks. Additionally, due to the existence of different dynamics of signed networks, the eigenvalue-based methods that are suitable for analyzing the convergence of homogeneous signed networks are no longer effective for studying the convergence of heterogeneous signed networks. Therefore, there is a challenge in finding a new approach to study the convergence of dynamic behaviors in heterogeneous signed networks.

Motivated by the above discussions, this paper aims to study the distributed control problems of signed networks with heterogeneous dynamics, where both first-order integrators and second-order integrators are considered. The contributions of this paper include three aspects:

• We propose a distributed control protocol based on the neighbor agents’ information. The proposed protocol can ensure the static bipartite consensus (respectively, state stability) if and only if the communication topology is structurally balanced (respectively, structurally unbalanced).
• We provide a Lyapunov-based approach to analyze the convergence of dynamic behaviors in heterogeneous signed networks. This method is applicable not only to structurally balanced signed networks but also to those that are structurally unbalanced.
• We extend the distributed control problems of homogeneous signed networks to heterogeneous signed networks. We give a method for designing suitable distributed control protocols and analyzing their convergence, which can significantly generalize the existing results of signed networks [23].

The remainder of this paper is organized as follows: Section 2 provides some basic knowledge of signed graphs. Section 3 presents the problem statement. Section 4 gives the main results of static bipartite consensus. Section 5 gives the simulation results. In addition, the conclusions are provided in Section 6.

Notations: we denote ${\mathcal{I}}_n=\{1$, 2, ⋯, $n\}$, $1_n=[1$, 1, ⋯, ${1]}^T$, $0_n=[0$, 0, ⋯, ${0]}^T$, and $\mathrm{diag}\{{\sigma }_1$, ${\sigma }_2$, ⋯, ${\sigma }_n\}$ as a diagonal matrix whose diagonal elements are ${\sigma }_1$, ${\sigma }_2$, ⋯, ${\sigma }_n$ and non-diagonal elements are zero. For any real number $a\in \mathbb{R}$, let $\left|a\right|$ be its absolute value and $\mathrm{sgn}\left(a\right)$ be its sign, i.e.,

$$\mathrm{sgn}\left(a\right)=\left\{\begin{array}{ccc}1,\hfill & \hfill & a>0\hfill \\ 0,\hfill & \hfill & a=0\hfill \\ -1,\hfill & \hfill & a<0.\hfill \end{array}\right.$$

2. Preliminaries

A signed network can be described by a signed graph, where nodes can represent agents, and edges with positive and negative weights can denote the cooperative and antagonistic interactions among agents.

Let $\mathcal{G}=(\mathcal{V}$, $\mathcal{E}$, $A)$ denote a signed graph of n-order, where $\mathcal{V}=\{v_1$, $v_2$, ⋯, $v_n\}$ is a node set with n nodes, $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}=\{(v_i,v_j):$$\forall v_i\in \mathcal{V}$, $v_j\in \mathcal{V}\}$ is an edge set, and $A={\left[a_{ij}\right]}_{n\times n}$ is the adjacent weight matrix whose element $a_{ij}$ satisfies $a_{ij}\ne 0\iff (v_j,v_i)\in \mathcal{E}$. We assume that there are no self-loops in the signed graph $\mathcal{G}$, i.e., $a_{ii}=0$ for $\forall i\in \{1,2,\cdots ,n\}$. If the edge $(v_j,v_i)$ exists, then we say that $v_j$ is a neighbor of $v_i$ and all neighbors of $v_i$ can be denoted by $N\left(i\right)=\{j:(v_j,v_i)\in \mathcal{E}\}$. The in-degree of $v_i$ is ${\Delta }_i={\sum }_{j\in N\left(i\right)}\left|a_{ij}\right|$ and the in-degree matrix is given by

$$\Delta =\mathrm{diag}\{{\Delta }_1,{\Delta }_2,\cdots ,{\Delta }_n\}.$$

The Laplacian matrix $L={\left[l_{ij}\right]}_{n\times n}$ of $\mathcal{G}$ is defined as $L=\Delta -A$ and its element satisfies

$$l_{ij}=\left\{\begin{array}{ccc}{\displaystyle \sum _{k\in N\left(i\right)}}\left|a_{ik}\right|,\hfill & \hfill & i=j\hfill \\ -a_{ij},\hfill & \hfill & i\ne j.\hfill \end{array}\right.$$

There is a directed path $\mathcal{P}=\left\{\right(v_i$, $v_{k_1})$, $(v_{k_1}$, $v_{k_2})$, ⋯, $(v_{k_{m-1}}$, $v_j\left)\right\}$ with m edges, in which $v_i$, $v_{k_1}$, $v_{k_2}$, ⋯, $v_{k_{m-1}}$, $v_j$ are different nodes. For a signed graph $\mathcal{G}$, if there exists a directed path between any two nodes, then $\mathcal{G}$ is referred to as strongly connected. If $A=A^T$ holds, we refer to the signed graph $\mathcal{G}$ as undirected. It can be easily developed that $L=L^T$ also holds when the signed graph $\mathcal{G}$ is undirected. Below, we present the concepts of structural balance and unbalance, which play a significant role in studying distributed control problems of signed networks.

Definition 1.

For a signed graph $\mathcal{G}$, all of its nodes can be divided into two sets: ${\mathcal{V}}_1$ and ${\mathcal{V}}_2$, such that $\mathcal{V}={\mathcal{V}}_1\bigcup {\mathcal{V}}_2$ and ${\mathcal{V}}_1\bigcap {\mathcal{V}}_2=\varnothing$. If the two following conditions hold:

1. 

When two nodes $v_i$ and $v_j$ belong to the same set, i.e., $v_i$, $v_j\in {\mathcal{V}}_k$, $\forall k\in \{1,2\}$, the weight $a_{ij}\ge 0$ holds;

2. 

When two nodes $v_i$ and $v_j$ belong to different sets, i.e., $v_i\in {\mathcal{V}}_k$ and $v_j\in {\mathcal{V}}_{3-k}$, $\forall k\in \{1,2\}$, the weight $a_{ij}\le 0$ holds.

then we say that $\mathcal{G}$ is structurally balanced, and, otherwise, $\mathcal{G}$ is structurally unbalanced.

When all negative weights in the signed graph $\mathcal{G}$ are transformed into the associated positive weights, a new induced unsigned graph $\overline{\mathcal{G}}=(\mathcal{V}$, $\mathcal{E}$, $\overline{A})$ is obtained, where $\overline{A}=\left|A\right|=\left[\right|a_{ij}{\left|\right]}_{n\times n}$. When the signed graph $\mathcal{G}$ is structurally balanced, there is a diagonal matrix $D_n=\mathrm{diag}\{{\sigma }_1$, ${\sigma }_2$, ⋯, ${\sigma }_n\}$, ${\sigma }_i\in \{-1$, $1\}$, $\forall i\in {\mathcal{I}}_n$ such that $\overline{A}=D_{n}A{D}_n$ holds. In the following, we provide an example.

Example 1.

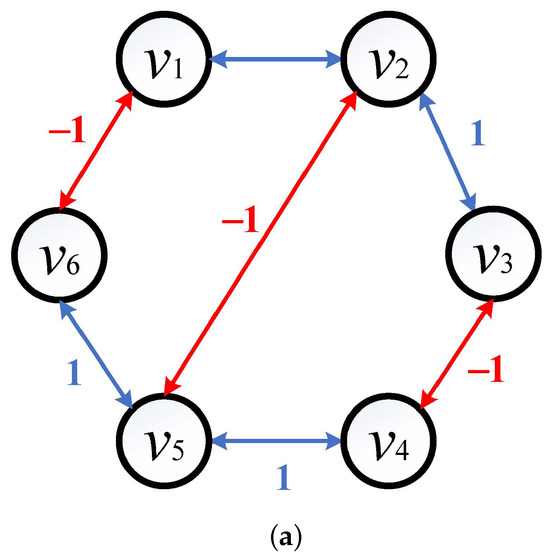
There are two signed undirected graphs in Figure 1. It is easy to see that all the vertices in ${\mathcal{G}}_1$ can be divided into two groups: ${\mathcal{V}}_1=\{v_1$, $v_2$, $v_3\}$ and ${\mathcal{V}}_2=\{v_4$, $v_5$, $v_6\}$. The weights of all edges within each group are non-negative and the weights of all edges between the two groups are non-positive, which satisfy the definition of structural balance. Therefore, the signed graph ${\mathcal{G}}_1$ is structurally balanced. Conversely, for the signed graph ${\mathcal{G}}_2$, it is impossible to find two such subsets, which does not satisfy the definition of structural balance. Hence, the signed graph ${\mathcal{G}}_2$ is structurally unbalanced.

Figure 1. Two signed undirected graphs, (a): ${\mathcal{G}}_1$ and (b): ${\mathcal{G}}_2$.

It follows from Figure 1 that the adjacent weight matrix $A_1$ of ${\mathcal{G}}_1$ is given by

$$A_1=\left[\begin{array}{cccccc}0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & -1\hfill \\ 1\hfill & 0\hfill & 1\hfill & 0\hfill & -1\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill & -1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & -1\hfill & 0\hfill & 1\hfill & 0\hfill \\ 0\hfill & -1\hfill & 0\hfill & 1\hfill & 0\hfill & 1\hfill \\ -1\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill \end{array}\right].$$

Since the signed undirected graph ${\mathcal{G}}_1$ is structurally balanced, there exists a diagonal matrix $D_6=\{1,1,1,-1,-1,-1\}$ such that ${\overline{A}}_1=D_6{A}_1{D}_6$ holds, i.e.,

$${\overline{A}}_1=\left[\begin{array}{cccccc}0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill \\ 1\hfill & 0\hfill & 1\hfill & 0\hfill & 1\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill & 0\hfill & 1\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill & 1\hfill & 0\hfill & 1\hfill \\ 1\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill \end{array}\right].$$

3. Problem Statements

A signed network can be depicted through a signed graph, wherein nodes symbolize agents and edges denote interactions between these agents. Positive weights indicate cooperative relationships among agents, while negative weights denote antagonistic relationships. We consider a heterogeneous signed network with n agents whose dynamics are described by

$$\left\{\begin{array}{ccccc}\hfill {\dot{x}}_i\left(t\right)& ={\nu }_i\left(t\right),\hfill & \hfill & i\in {\mathcal{I}}_m,\hfill & \\ \hfill {\dot{\nu }}_i\left(t\right)& =u_i\left(t\right),\hfill & \hfill & i\in {\mathcal{I}}_m,\hfill & \\ \hfill {\dot{x}}_i\left(t\right)& =u_i\left(t\right)\hfill & \hfill & i\in {\mathcal{I}}_n-{\mathcal{I}}_m\hfill \end{array}\right.$$

(1)

where $x_i\left(t\right)$ and ${\nu }_i\left(t\right)$ are the position state and velocity state, respectively, and $u_i\left(t\right)$ is the control input to be designed. For any initial states, we say that the system (1) can achieve the following:

• Static bipartite consensus if

  $$\begin{array}{cc}\hfill & {\displaystyle \underset{t\to \infty }{lim}}\left(\right|x_i\left(t\right)|-|x_j\left(t\right)\left|\right)=0,\forall i,j\in {\mathcal{I}}_n\hfill \\ \hfill & {\displaystyle \underset{t\to \infty }{lim}}{\nu }_i\left(t\right)=0,\forall i\in {\mathcal{I}}_m\hfill \end{array}$$
• State stability if

  $$\begin{array}{cc}\hfill & {\displaystyle \underset{t\to \infty }{lim}}{x}_i\left(t\right)=0,\forall i\in {\mathcal{I}}_n\hfill \\ \hfill & {\displaystyle \underset{t\to \infty }{lim}}{\nu }_i\left(t\right)=0,\forall i\in {\mathcal{I}}_m.\hfill \end{array}$$

Next, we aim to explore how to ensure that the system (1) can achieve the bipartite consensus and state stability, respectively.

4. Main Results

The distributed control protocol is designed as follows:

$$u_i\left(t\right)=\left\{\begin{array}{c}-{\displaystyle \sum _{j\in N_i}}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]+{\dot{\xi }}_i\left(t\right),\forall i\in {\mathcal{I}}_m\hfill \\ -{\displaystyle \sum _{j\in N_i}}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right],\forall i\in {\mathcal{I}}_n-{\mathcal{I}}_m\hfill \end{array}\right.$$

(2)

with

$${\dot{\xi }}_i\left(t\right)=-{\xi }_i\left(t\right)-{\displaystyle \sum _{j\in N_i}}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]$$

where $\xi \left(t\right)$ is an auxiliary variable.

Theorem 1.

We consider the system (1) under a signed undirected connected graph $\mathcal{G}$. Let the distributed protocol (2) be applied to the system (1). Then, the following results hold:

1. 

The system (1) can achieve the bipartite consensus if and only if $\mathcal{G}$ is structurally balanced;

2. 

The system (1) can reach the state stability if and only if $\mathcal{G}$ is structurally unbalanced.

Proof. 

We can write (1) and (2) as

$$\left\{\begin{array}{ccccc}\hfill {\dot{x}}_i\left(t\right)& ={\nu }_i\left(t\right),\hfill & \hfill & i\in {\mathcal{I}}_m,\hfill & \\ \hfill {\dot{\nu }}_i\left(t\right)& =-{\displaystyle \sum _{j\in N\left(i\right)}}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]+{\dot{\xi }}_i\left(t\right),\hfill & \hfill & i\in {\mathcal{I}}_m,\hfill & \\ \hfill {\dot{\xi }}_i\left(t\right)& =-{\xi }_i\left(t\right)-{\displaystyle \sum _{j\in N\left(i\right)}}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right],\hfill & \hfill & i\in {\mathcal{I}}_m,\hfill & \\ \hfill {\dot{x}}_i\left(t\right)& =-{\displaystyle \sum _{j\in N\left(i\right)}}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right],\hfill & \hfill & i\in {\mathcal{I}}_n-{\mathcal{I}}_m\hfill \end{array}\right.$$

(3)

We can construct a candidate Lyapunov function:

$$\begin{array}{cc}\hfill V\left(t\right)& ={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}\left|a_{ij}\right|\frac{{\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]}^2}{2}+{\displaystyle \sum _{i=1}^m}{\left({\xi }_i\left(t\right)\right)}^2+{\displaystyle \sum _{i=1}^m}{\left[{\nu }_i\left(t\right)-{\xi }_i\left(t\right)\right]}^2.\hfill \end{array}$$

We can easily verify that $V\left(x\right)$ is positive definite. Taking the derivative of $V\left(x\right)$ with respect to the time t, we can obtain

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)& ={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]\left[{\dot{x}}_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right){\dot{x}}_j\left(t\right)\right]\hfill \\ \hfill & +2{\displaystyle \sum _{i=1}^m}{\xi }_i\left(t\right){\dot{\xi }}_i\left(t\right)+2{\displaystyle \sum _{i=1}^m}\left[{\nu }_i\left(t\right)-{\xi }_i\left(t\right)\right]\left[{\dot{\nu }}_i\left(t\right)-{\dot{\xi }}_i\left(t\right)\right]\hfill \end{array}$$

We bring Equation (3) into $\dot{V}\left(t\right)$ to get

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)& ={\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{j=1}^m}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]\left[{\nu }_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right){\nu }_j\left(t\right)\right]\hfill \\ \hfill & +{\displaystyle \sum _{i=m+1}^n}{\displaystyle \sum _{j=1}^m}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]\left[{\dot{x}}_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right){\nu }_j\left(t\right)\right]\hfill \\ \hfill & +{\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{j=m+1}^n}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]\left[{\nu }_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right){\dot{x}}_j\left(t\right)\right]\hfill \\ \hfill & +{\displaystyle \sum _{i=m+1}^n}{\displaystyle \sum _{j=m+1}^n}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]\left[{\dot{x}}_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right){\dot{x}}_j\left(t\right)\right]\hfill \\ \hfill & +2{\displaystyle \sum _{i=1}^m}{\xi }_i\left(t\right)\left[-{\xi }_i\left(t\right)-{\displaystyle \sum _{j=1}^n}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]\right]\hfill \\ \hfill & +2{\displaystyle \sum _{i=1}^m}\left[{\nu }_i\left(t\right)-{\xi }_i\left(t\right)\right]\left(-{\displaystyle \sum _{j=1}^n}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]\right).\hfill \end{array}$$

Because of the fact that the signed graph $\mathcal{G}$ is undirected and connected, we can deduce that its adjacency weight matrix A is symmetric, i.e., $a_{ij}=a_{ji}$, $\forall i,j\in {\mathcal{I}}_n$. We can further induce

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{j=1}^m}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]{\nu }_i\left(t\right)\hfill \\ \hfill & ={\displaystyle \sum _{j=1}^m}{\displaystyle \sum _{i=1}^m}\left|a_{ji}\right|\left[x_j\left(t\right)-\mathrm{sgn}\left(a_{ji}\right)x_i\left(t\right)\right]{\nu }_j\left(t\right)\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{j=1}^m}\left|a_{ij}\right|\left[x_j\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_i\left(t\right)\right]{\nu }_j\left(t\right)\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{j=1}^m}\left|a_{ij}\right|\left[\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)-x_i\left(t\right)\right]\mathrm{sgn}\left(a_{ij}\right){\nu }_j\left(t\right)\hfill \\ \hfill & =-{\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{j=1}^m}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]\mathrm{sgn}\left(a_{ij}\right){\nu }_j\left(t\right).\hfill \end{array}$$

Therefore, we can deduce

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{j=1}^m}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]\left[{\nu }_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right){\nu }_j\left(t\right)\right]\hfill \\ \hfill & =2{\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{j=1}^m}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]{\nu }_i\left(t\right).\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{i=m+1}^n}{\displaystyle \sum _{j=1}^m}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]\left[{\dot{x}}_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right){\nu }_j\left(t\right)\right]\hfill \\ \hfill & ={\displaystyle \sum _{j=m+1}^n}{\displaystyle \sum _{i=1}^m}\left|a_{ji}\right|\left[x_j\left(t\right)-\mathrm{sgn}\left(a_{ji}\right)x_i\left(t\right)\right]\left[{\dot{x}}_j\left(t\right)-\mathrm{sgn}\left(a_{ji}\right){\nu }_i\left(t\right)\right]\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{j=m+1}^n}\left|a_{ij}\right|\left[x_j\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_i\left(t\right)\right]\left[{\dot{x}}_j\left(t\right)-\mathrm{sgn}\left(a_{ij}\right){\nu }_i\left(t\right)\right]\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{j=m+1}^n}\left|a_{ij}\right|\left[\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)-x_i\left(t\right)\right]\left[\mathrm{sgn}\left(a_{ij}\right){\dot{x}}_j\left(t\right)-{\nu }_i\left(t\right)\right]\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{j=m+1}^n}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]\left[{\nu }_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right){\dot{x}}_j\left(t\right)\right].\hfill \end{array}$$

(5)

Due to

$$\begin{array}{cc}\hfill & -{\displaystyle \sum _{i=m+1}^n}{\displaystyle \sum _{j=m+1}^n}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]\mathrm{sgn}\left(a_{ij}\right){\dot{x}}_j\left(t\right)\hfill \\ \hfill & =-{\displaystyle \sum _{j=m+1}^n}{\displaystyle \sum _{i=m+1}^n}\left|a_{ji}\right|\left[x_j\left(t\right)-\mathrm{sgn}\left(a_{ji}\right)x_i\left(t\right)\right]\mathrm{sgn}\left(a_{ji}\right){\dot{x}}_i\left(t\right)\hfill \\ \hfill & =-{\displaystyle \sum _{i=m+1}^n}{\displaystyle \sum _{j=m+1}^n}\left|a_{ij}\right|\left[\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)-x_i\left(t\right)\right]{\dot{x}}_i\left(t\right)\hfill \\ \hfill & ={\displaystyle \sum _{i=m+1}^n}{\displaystyle \sum _{j=m+1}^n}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]{\dot{x}}_i\left(t\right),\hfill \end{array}$$

we have

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{i=m+1}^n}{\displaystyle \sum _{j=m+1}^n}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]\left[{\dot{x}}_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right){\dot{x}}_j\left(t\right)\right]\hfill \\ \hfill & =-2{\displaystyle \sum _{i=m+1}^n}{\displaystyle \sum _{j=m+1}^n}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]\mathrm{sgn}\left(a_{ij}\right){\dot{x}}_j\left(t\right).\hfill \end{array}$$

(6)

Substituting Equations (4)–(6) into $\dot{V}\left(x\right)$ and further simplifying, we can obtain

$$\begin{array}{cc}\hfill \dot{V}\left(x\right)& =-2{\displaystyle \sum _{i=1}^m}{\xi }_i^2\left(t\right)-2{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=m+1}^n}\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]\mathrm{sgn}\left(a_{ij}\right){\dot{x}}_j\left(t\right)\hfill \\ \hfill & =-2{\displaystyle \sum _{i=1}^m}{\xi }_i^2\left(t\right)-2{\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{i=m+1}^n}\left|a_{ji}\right|\left[x_j\left(t\right)-\mathrm{sgn}\left(a_{ji}\right)x_i\left(t\right)\right]\mathrm{sgn}\left(a_{ji}\right){\dot{x}}_i\left(t\right)\hfill \\ \hfill & =-2{\displaystyle \sum _{i=1}^m}{\xi }_i^2\left(t\right)-2{\displaystyle \sum _{i=m+1}^n}{\dot{x}}_i\left(t\right){\displaystyle \sum _{j=1}^n}\left|a_{ij}\right|\left[-x_i\left(t\right)+\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]\hfill \\ \hfill & =-2{\displaystyle \sum _{i=1}^m}{\xi }_i^2\left(t\right)-2{\displaystyle \sum _{i=m+1}^n}{\dot{x}}_i^2\left(t\right)\le 0.\hfill \end{array}$$

(7)

$\dot{V}\left(x\right)=0$ implies ${lim}_{t\to \infty }{\dot{x}}_i\left(t\right)=0$ for $\forall i\in \{m+1$, $m+2$, ⋯, $n\}$ and ${lim}_{t\to \infty }{\xi }_i\left(t\right)=0$ for $\forall i\in \{1$, 2, ⋯, $m\}$. Because of ${\dot{x}}_i\left(t\right)=-{\sum }_{j=1}^n\left|a_{ij}\right|\left[x_i\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_j\left(t\right)\right]$, we can induce

$$\begin{array}{c}\hfill {\displaystyle \sum _{i=1}^n}{x}_i(\infty ){\displaystyle \sum _{j=1}^n}\left|a_{ij}\right|\left[x_i(\infty )-\mathrm{sgn}\left(a_{ij}\right)x_j(\infty )\right]\\ \hfill ={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}\left|a_{ij}\right|{\left[x_i(\infty )-\mathrm{sgn}\left(a_{ij}\right)x_j(\infty )\right]}^2=0.\end{array}$$

(8)

(1) When $\mathcal{G}$ is structurally balanced, we can derive

$${\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}\left|a_{ij}\right|{\left[x_i(\infty )-\mathrm{sgn}\left(a_{ij}\right)x_j(\infty )\right]}^2=x^T(\infty )Lx(\infty ).$$

(9)

Because $\mathcal{G}$ is structurally balanced, there exists a diagonal matrix $D_n$ such that $\overline{L}=D_{n}L{D}_n$ holds. Then, we can rewrite (9) as

$$\begin{array}{cc}\hfill x^T(\infty )Lx(\infty )& =x^T(\infty )D_n^{2}L{D}_n^{2}x(\infty )\hfill \\ \hfill & ={\left(D_{n}x(\infty )\right)}^T\left(D_{n}L{D}_n\right)\left(D_{n}x(\infty )\right)=0.\hfill \end{array}$$

Therefore, we can derive that $x^T(\infty )Lx(\infty )=0$ implies $D_{n}x(\infty )=c{1}_n$ for some $c\in \mathbb{R}$. We can further develop $x(\infty )=c{D}_n{1}_n$. The position’s states of the system (1) can achieve the bipartite consensus. Based on this, we can further develop ${\nu }_i(\infty )={\dot{x}}_i(\infty )=0$, $\forall i\in {\mathcal{I}}_m$. Hence, we can induce

$$\begin{array}{cc}\hfill & {\displaystyle \underset{t\to \infty }{lim}}\left(|x_i\left(t\right)|-|x_j\left(t\right)|\right)=0,\forall i,j\in {\mathcal{I}}_n,\hfill \\ \hfill & {\displaystyle \underset{t\to \infty }{lim}}\left|{\nu }_i\left(t\right)\right|=0,\forall i\in {\mathcal{I}}_m.\hfill \end{array}$$

Hence, the system (1) can achieve the static bipartite consensus under the control of the protocol (2).

(2) When $\mathcal{G}$ is structurally unbalanced, we can deduce

$$x^T(\infty )Lx(\infty )=0.$$

Because L is symmetric, it can be written as $L=M^{T}M$. We can derive

$$\begin{array}{cc}\hfill x^T(\infty )Lx(\infty )& =x^T(\infty )M^{T}Mx(\infty )\hfill \\ \hfill & ={\left(Mx(\infty )\right)}^T\left(Mx(\infty )\right)=0\hfill \end{array}$$

(10)

Hence, $Mx(\infty )=0_n$ holds, which implies $x(\infty )=0_n$. This, together with $\nu (\infty )=\dot{x}(\infty )$, ensures $\nu (\infty )=0_m$. Thus,

$$\begin{array}{cc}\hfill & {\displaystyle \underset{t\to \infty }{lim}}\left|x_i\left(t\right)\right|=0,\forall i\in {\mathcal{I}}_n,\hfill \\ \hfill & {\displaystyle \underset{t\to \infty }{lim}}\left|{\nu }_i\left(t\right)\right|=0,\forall i\in {\mathcal{I}}_m\hfill \end{array}$$

which indicates the static state stability of the system (1) when the distributed protocol (2) is applied. We complete this proof. □

Remark 1.

According to Theorem 1, we can develop the convergence results of signed networks with heterogeneous dynamics. It is shown that with the proposed protocol being used, the signed network subject to both first-order and second-order integrators can achieve the static bipartite consensus (respectively, state stability) if and only if the associated signed graph is structurally balanced (respectively, unbalanced). Additionally, we should point out that the computational complexity of Theorem 1 is related to the number of agents in signed networks. This computational complexity may grow as the number of nodes increases.

5. Simulations

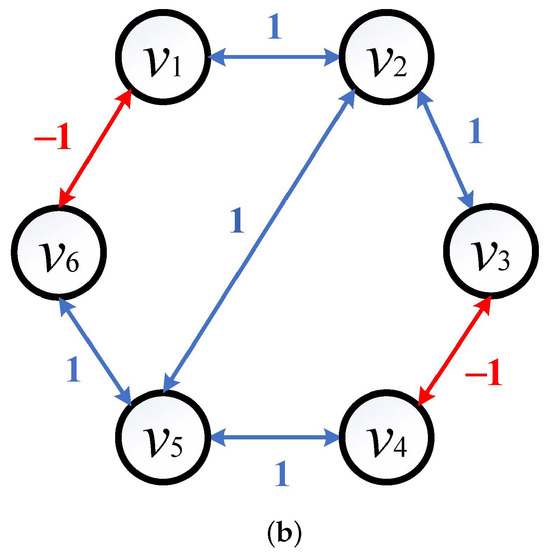
In this section, we introduce two examples to validate the correctness of the obtained results. We consider the system (1) consisting of eight agents, whose communication topology can be represented by Figure 2, where the dynamics of four agents $v_1$, $v_2$, $v_3$, and $v_4$ are second-order integrators and the dynamics of four agents $v_5$, $v_6$, $v_7$, and $v_8$ are first-order integrators. The initial states of these eight agents are selected as follows:

$$\begin{array}{cc}\hfill x\left(0\right)& ={\left[200,110,60,40,-60,-80,-50,10\right]}^T,\hfill \\ \hfill \nu \left(0\right)& ={\left[2,2,2,1\right]}^T.\hfill \end{array}$$

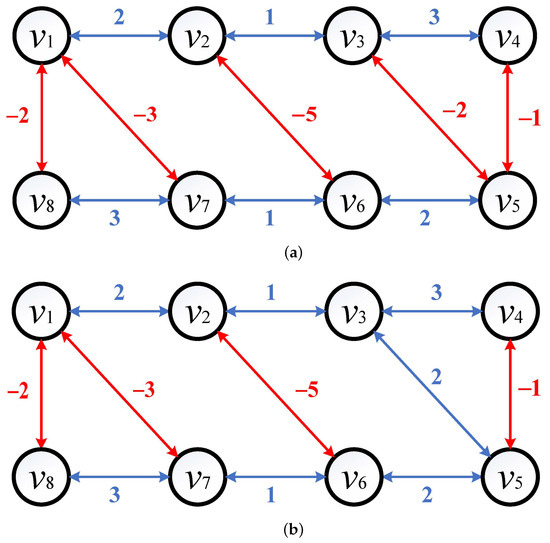
Figure 2. Two signed undirected graphs, (a): ${\mathcal{G}}_3$ and (b): ${\mathcal{G}}_4$.

Example 2.

We consider the system (1) whose communication topology is described by Figure 2a. We can easily see that the signed graph ${\mathcal{G}}_3$ is structurally balanced and all nodes can be divided into two groups: ${\mathcal{V}}_1=\{v_1,v_2,v_3,v_4\}$ and ${\mathcal{V}}_2=\{v_5,v_6,v_7,v_8\}$. The Laplacian matrix of ${\mathcal{G}}_3$ is given by

$$L_3=\left[\begin{array}{cccccccc}7& -2& 0& 0& 0& 0& 3& 2\\ -2& 8& -1& 0& 0& 5& 0& 0\\ 0& -1& 6& -3& 2& 0& 0& 0\\ 0& 0& -3& 4& 1& 0& 0& 0\\ 0& 0& 2& 1& 5& -2& 0& 0\\ 0& 5& 0& 0& -2& 8& -1& 0\\ 3& 0& 0& 0& 0& -1& 7& -3\\ 2& 0& 0& 0& 0& 0& -3& 5\end{array}\right].$$

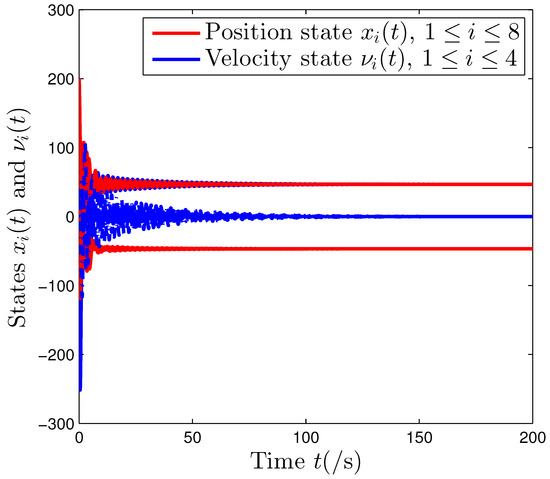
Applying the distributed control protocol (2) to the system (1), the state evolutions of eight agents are shown in Figure 3.

Figure 3. State evolutions of the system (1) under the signed graph ${\mathcal{G}}_3$.

From Figure 3, it can be seen that the position states of the eight agents (as indicated by the red lines) can achieve the bipartite consensus, and the velocity states of four agents (as indicated by the blue lines) with second-order integrator dynamics eventually converge to zero. This indicates that, under the distributed control algorithm (2), the system (1) can achieve the goal of static bipartite consensus, which validates the correctness of the results of Theorem 1.

Example 3.

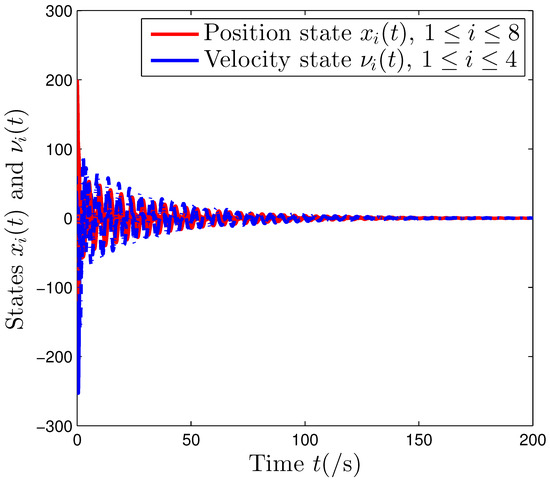
For the system (1) under the signed graph ${\mathcal{G}}_4$ in Figure 2b, let the distributed control protocol (2) be employed. It can be easily seen that the signed graph ${\mathcal{G}}_4$ is structurally unbalanced based on the definition of structural balance. The Laplacian matrix of ${\mathcal{G}}_4$ is given by

$$L_4=\left[\begin{array}{cccccccc}7& -2& 0& 0& 0& 0& 3& 2\\ -2& 8& -1& 0& 0& 5& 0& 0\\ 0& -1& 6& -3& -2& 0& 0& 0\\ 0& 0& -3& 4& 1& 0& 0& 0\\ 0& 0& -2& 1& 5& -2& 0& 0\\ 0& 5& 0& 0& -2& 8& -1& 0\\ 3& 0& 0& 0& 0& -1& 7& -3\\ 2& 0& 0& 0& 0& 0& -3& 5\end{array}\right].$$

The evolution of the states of all eight agents is shown in Figure 4.

Figure 4. State evolutions of the system (1) under the signed graph ${\mathcal{G}}_4$.

From Figure 4, it can be observed that when the communication topology is structurally unbalanced, the positional states of eight agents (as indicated by the red lines) and the velocity states of four agents (as indicated by the blue lines) eventually converge to zero under the control of the distributed protocol (2), which denotes that the system (1) can reach the state stability. Hence, these derived results satisfy Theorem 1.

6. Conclusions

In this paper, we have studied the distributed control problems of heterogeneous signed networks under undirected communication topologies, in which both first-order integrators and second-order integrators are considered. We have designed a distributed control protocol based on only position information. With this protocol being employed, we have developed the convergence results of signed networks. It is shown that the signed network can achieve the static bipartite consensus (respectively, state stability) if and only if the signed undirected graph is structurally balanced (respectively, unbalanced). In addition, we have given two examples to verify the correctness of our derived results.

In our future work, we aim to explore the distributed control problems of heterogeneous signed networks under directed topologies, in addition to those with communication delays and external disturbances.