Abstract
The smart grid, as a crucial part of modern energy systems, handles extensive and diverse data, including inputs from various sensors, metering devices, and user interactions. Outsourcing data storage to remote cloud servers presents an economical solution for enhancing data management within the smart grid ecosystem. However, ensuring data privacy before transmitting it to the cloud is a critical consideration. Therefore, it is common practice to encrypt the data before uploading them to the cloud. While encryption provides data confidentiality, it may also introduce potential issues such as limiting data owners’ ability to query their data. The searchable attribute-based encryption (SABE) not only enables fine-grained access control in a dynamic large-scale environment but also allows for data searches on the ciphertext domain, making it an effective tool for cloud data sharing. Although SABE has become a research hotspot, existing schemes often have limitations in terms of computing efficiency on the client side, weak security of the ciphertext and the trapdoor. To address these issues, we propose an efficient server-aided ciphertext-policy searchable attribute-based encryption scheme (SA-CP-SABE). In SA-CP-SABE, the user’s data access authority is consistent with the search authority. During the search process, calculations are performed not only to determine whether the ciphertext matches the keyword in the trapdoor, but also to assist subsequent user ciphertext decryption by reducing computational complexity. Our scheme has been proven under the random oracle model to achieve the indistinguishability of the ciphertext and the trapdoor and to resist keyword-guessing attacks. Finally, the performance analysis and simulation of the proposed scheme are provided, and the results show that it performs with high efficiency.
Keywords:
searchable encryption; attribute-based encryption; server-aided decryption; trapdoor indistinguishability; random oracle model MSC:
68P25
1. Introduction
The smart grid stands as a pivotal advancement in the future of energy, marking a transformative leap forward and modernization of traditional power systems. Compared to conventional grids, the smart grid harnesses advanced technologies and digital solutions to make the processes of transmitting, distributing, and monitoring electricity more intelligent, efficient, and reliable. It represents a critical pathway for the future evolution of power systems. Through continuous real-time monitoring, control, and optimization of power system operations, the smart grid enhances energy utilization efficiency and system stability. Moreover, big data technology offers robust support to the smart grid by gathering, storing, and analyzing vast data sets, unveiling patterns, trends, and potential issues within power system operations. Harnessing big data analytics enables the smart grid to accurately forecast load demands, optimize energy distribution, and achieve intelligent maintenance and management of power supply equipment. Consequently, the integration of smart grid and big data not only elevates energy systems’ intelligence and efficiency, but also bolsters efforts toward sustainable energy development and heightened energy security. Nevertheless, it faces security challenges, especially concerning cryptographic and network security issues. In the smart grid, safeguarding the security and privacy of data is paramount given the implications for energy supply stability, user privacy, and critical infrastructure operation. Hence, addressing security concerns in the smart grid demands vigilant attention and the implementation of robust cryptographic measures to protect system security. Cloud computing [1] provides ubiquitous access, high flexibility, low cost and scalability, making the cloud an attractive option for storing and managing data due to almost unlimited storage space and powerful processing capabilities. Outsourcing data storage to remote cloud servers presents an economical solution for enhancing data management within the smart grid ecosystem. Data sharing [2] is critical in data management. Attribute-based encryption has proven effective in enabling fine-grained access control and is considered as a valuable tool for realizing cloud data sharing. The concept of attribute-based encryption was first proposed by Sahai et al. [3]. Subsequently, Goyal et al. [4] discussed the differences and connections between key-policy attribute-based encryption (KP-ABE) and ciphertext-policy attribute-based encryption (CP-ABE), and proposed a KP-ABE scheme based on a tree access structure. At the same time, Bethencourt et al. [5] introduced the first CP-ABE scheme. In practice, users typically only need access to specific data rather than all data they can be permitted to access. Therefore, it is often necessary to control data access privileges and ensure encrypted data searchability in cloud computing environments. To achieve both encrypted data searchability and access control simultaneously, scholars have combined searchable encryption with attribute encryption and proposed numerous searchable attribute-based encryption schemes [6,7,8,9,10,11,12,13,14,15,16].
1.1. Motivation
We consider an example of the application of SABE for smart grids.
Smart grids integrate advanced communication and information technologies into the power system, enabling real-time monitoring and control of power flow, distribution, and management. Smart meters are a crucial component of smart grids, collecting and transmitting consumer electricity usage data as well as monitoring the status and load of the grid.
In such a system, ensuring the security of smart meter data is of the utmost importance. The SABE can be employed to securely store and control access to the data while allowing for authorized users to effectively search encrypted data without revealing sensitive information. For instance, in smart grids, smart meter data typically include vital information such as user details, electricity consumption, and grid status. By utilizing SABE, these data can be securely encrypted and associated with multiple attributes, such as “User ID”, “Timestamp”, and “Electricity Consumption”, while grid status data may be labeled with “Geographic Location” and “Date”.
Authorized users can search the encrypted data based on their access privileges. For instance, when an authorized user, such as an operator from a utility company, needs to inquire about a user’s electricity consumption within a specific time period, they can utilize SABE to perform an encrypted search within the encrypted smart meter data. The system matches the encrypted data based on the search keywords provided by the user, which are within their permissions, such as the specific user’s ID and a timestamp for a designated time period. The system then returns the matched ciphertext data as search results to the search user without revealing any other sensitive data information.
This application of SABE in smart grids not only ensures the security and privacy of data, but also enables efficient searching and access control of encrypted data, thereby enhancing the security and efficiency of smart grid systems.
Despite the significant benefits and conveniences to smart grids, SABE still faces two main challenges. One is that many existing SABE schemes are unable to resist keyword guessing attacks. The other is that many existing SABE schemes require expensive pairing operations which pose a formidable challenge to search efficiency. Thus, it is essential to design a novel SABE scheme that can simultaneously resist keyword guessing attacks and mitigate the decryption burden.
1.2. Contributions
To fill the above-mentioned gaps, in this paper, we propose a new searchable attribute-based encryption scheme (SA-CP-SABE) with the following contributions:
(1) We propose a searchable attribute-based encryption scheme (SA-CP-SABE) utilizing a ciphertext policy based on the tree access structure. Our SA-CP-SABE scheme has two distinctive features: first, it employs the same tree structure for both data encryption and keyword encryption, thereby ensuring consistent search rights and access permissions; second, it includes assisted decryption functionality, that is, it can enable a third party to verify whether a ciphertext matches a user’s query based on the trapdoor. Additionally, the third party can leverage the search outcome to aid the user in decrypting the ciphertext. To the best of our knowledge, none of the existing SABE schemes in the smart grid can simultaneously resist keyword guessing attacks and mitigate the decryption burden so far.
(2) In the random oracle model, we prove that SA-CP-SABE satisfies indistinguishability between keyword ciphertexts and trapdoors. Compared with schemes in the literature [9,10,11,12,13,14,15,16], SA-CP-SABE can prevent keyword substitution attacks in both ciphertexts and trapdoors while also providing resistance against keyword guessing attacks. Furthermore, we conduct theoretical and experimental analyses of the SA-CP-SABE scheme, demonstrating its superior performance compared to that of the existing schemes.
1.3. Related Work
To enable user searching on the ciphertext domain, Song et al. [17] initially introduced the concept of searchable encryption and developed a symmetric searchable encryption scheme. In 2004, Boneh et al. [18] devised the first public key searchable encryption (PEKS) scheme. The PEKS scheme can delegate the search trapdoor to a third party to perform the search, while ensuring that the search trapdoor does not reveal any plaintext information. PEKS has attracted significant research attention in the realm of information security. Literature [19,20] discusses the keyword guessing attack based on the fact that the keyword space is much smaller than the key space in practical applications. Additionally, literature [21] explores the utilization of server assistance to enhance the efficiency of the scheme and proposes a server-aided PEKS scheme.
In 2005, Sahai et al. [3] initially introduced the concept of attribute-based encryption (ABE) where ciphertexts and keys are associated with sets of descriptive attributes. This allows a ciphertext to be decrypted by multiple users, overcoming the traditional limitation of decrypting a ciphertext with only a single key. Since the detailed work on attribute encryption provided by Goyal et al. [4] and Bethencourt et al. [5], attribute-based encryption has attracted widespread attention. ABE schemes have been applied in various domains such as video-on-demand [22], electronic medical health record access [23], and social networking site access operations [24]. To meet the data searchability requirement in data sharing environments, Li et al. [25] proposed a ciphertext policy-based searchable attribute-based encryption scheme by integrating ABE and PEKS concepts. In recent years, with the maturation of cloud computing technology, numerous searchable attribute-based encryption schemes have been proposed, providing ideal application scenarios for searchable attribute-based encryption [6,7,8,9,10,11,12,13,14,15,16]. However, searchable attribute-based encryption means that a keyword index must be searchable by a group of users. This leads to its construction method being more complex than traditional public key searchable schemes. From a construction perspective, the searchable attribute-based encryption schemes mentioned above can generally be divided into two categories. One category [6,7,8] combines attribute encryption with public-key searchable encryption. Specifically, it encrypts data using attribute encryption to achieve access control, and then utilizes traditional searchable encryption techniques to process keywords, thus enabling ciphertext searchability. However, this approach may lead to the separation of data access rights and search rights. In other words, it could expose keyword information (which may be sensitive) during searches conducted by users without data access permissions.The other category [9,10,11,12,13,14,15,16] utilizes attribute encryption techniques to regulate user search privileges with a construction process similar to attribute encryption. However, these schemes possess certain drawbacks. The ciphertext models featuring indistinguishable keywords in the literature [9,10,11,12] are relatively weak as these security models lack the capability to perform trapdoor queries. In other words, these security models assume that attackers cannot access the trapdoor. This assumption is only suitable for scenarios where the search is conducted by the data owner themself or a fully trusted third party. Clearly, such security models are inadequate in a cloud computing environment where ciphertext searches are primarily conducted by a semi-trusted cloud. Although the security models in the literature [13,14,15,16] incorporate trapdoor queries, their schemes fail to meet the defined security criteria because the keywords in the ciphertexts can be replaced with other keywords. More specifically, after obtaining keyword w and its corresponding trapdoor through a trapdoor query, an attacker can carry out a keyword-guessing attack by modifying the attacked ciphertext (associated with keyword w) into another ciphertext (associated with keyword ) and then using the trapdoor for verification. Consequently, during the security game’s challenge phase, the attacker can win the game by altering the keywords of the challenging ciphertext to another valid ciphertext contained within the intercepted trapdoor. Additionally, in the schemes presented in the literature [9,10,11,12,13,14,15,16], the keywords in the trapdoor can also be substituted with other keywords, thus failing to prevent insider keyword guessing attacks [26].
ABE schemes often involve a significant number of pairing and exponential operations, which means that the devices at the user side need more computations to share or access the data. This is obviously unacceptable for some devices with limited computational resources or in scenarios with high real-time demands. To meet the real-time encryption requirements of certain applications, scholars have recognized this issue and employed offline/online encryption techniques [9,11]. Additionally, outsourced decryption techniques [12,14,27] have been utilized to mitigate the decryption burden on the user side. A summary of the related work is provided in Table 1, where “√” indicates that the specified scheme (row) satisfies the security property (column), “×” indicates that the specified scheme (row) does not satisfy the security property (column), and “-” indicates that the attack is not considered in this work.

Table 1.
Security Analysis for Existing Schemes.
1.4. Organization
The remainder of the paper is organized as follows. We present some preliminaries in Section 2. In Section 3, we define the system model and the security model of our scheme. In Section 4, we propose the concrete construction of the proposed SA-CP-SABE scheme. In Section 5, we provide the security analysis as well as the performance evaluation of our scheme. Finally, we draw the conclusion of the whole paper in Section 6.
2. Preliminaries
2.1. Notations
Table 2 provides the summary of notations used in our proposed scheme.

Table 2.
Notations and their meanings.
2.2. Bilinear Pairs
We let and be the cyclic multiplicative groups of order q where q is a large prime, and we let be a bilinear map between the two groups satisfying the following conditions:
- (1)
- Bilinearity: , such that holds.
- (2)
- Non-degeneracy: , such that , where 1 is the unit element of .
- (3)
- Computability: For , there exist efficient algorithms that can compute .
2.3. Difficult Assumptions
Assumption 1.
Let be a bilinear group system and g be a generator of group . Given , we determine whether R is equal to . Drawing on the analysis of the literature [26,28], the difficult assumption above translates into proving whether is independent of , i.e., proving that there are no coefficients satisfying equation . Obviously, due to , there always exists an expression in with some coefficient of no matter how is combined to take values. Therefore, determining whether R is equal to is a difficult problem.
Based on the above analysis, the following difficult problem can be obtained.
Assumption 2.
We let be a bilinear group system and be a generator. Given , we determine whether R is equal to .
2.4. Access Tree
Definition 1
(Access Tree). An access tree is used to describe an access structure. Each intermediate node of tree x represents a relation function, which can be “or”, “with”, or other threshold. Assuming that denotes the number of children of a node and represents its threshold, is satisfied. Each leaf node of tree x represents an attribute item and threshold . In implementation, it is generally necessary to adopt a top-down approach to select a polynomial of degree , for each node x, satisfying . Here, denotes the parent of node x, and is the index of node x.
We let denote the subtree of T with node x as the root. When x is a leaf node, represents the attribute value of the output leaf node. We say that attribute set S satisfies (denoted by ) if and only if the following two conditions are met:
- (1)
- When x is a leaf node, if and only if is an attribute in attribute set S.
- (2)
- When x is an internal node, we compute for each child z of x. if and only if there are at least children.
3. System Model and Security Model
3.1. System Model
The system consists of a Key Generation Center (KGC), a Data Owner (DO), a Cloud Server Provider (CSP), and a Data User (DU). The system model is illustrated in Figure 1.
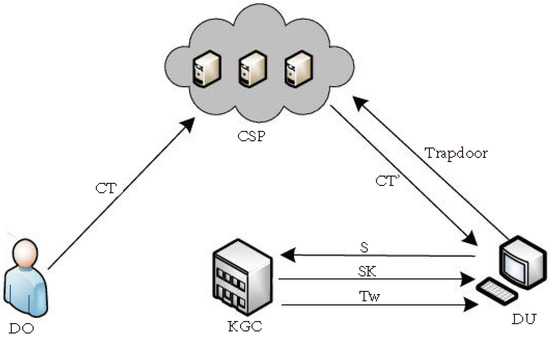
Figure 1.
System model of the SA-CP-SABE scheme.
KGC: Responsible for generating private keys for data users and assisting them in generating trapdoors.
DO: The DO acts as the ciphertext generator, i.e., it performs encryption of keywords and uploads the encrypted ciphertext to the cloud server.
CSP: The CSP stores the ciphertext and conducts ciphertext search and transform tasks.
DU: The user of the data who generates the trapdoor and delegates it to the cloud for data search and performs decryption operations.
Definition 2.
The proposed SA-CP-SABE scheme comprises the following six probabilistic polynomial-time (PPT) algorithms:
- (1)
- System Initialization: This PPT algorithm is executed by the to initialize the global system. Taking security parameter λ as input, it outputs the system master key, , and the system public parameters, .
- (2)
- Encryption: This PPT algorithm is executed by the to perform encryption. Taking the system public parameters, , data m, keywords and access structure T as input, it outputs the ciphertext, , which is then uploaded to the cloud.
- (3)
- User Private Key Generation: This PPT algorithm is executed by the to generate a user private key. Taking the system public parameters, , the system master key, , and attribute set S as input, it outputs a user private key, .
- (4)
- Trapdoor Generation: This PPT algorithm is executed by the to generate a search trapdoor. Taking the system public parameters, , the user private key, , and keyword w as input, it outputs the trapdoor, .
- (5)
- Search and Transformation: This PPT algorithm is executed by the to perform search and transformation operations. Taking the system public parameters, , the keyword ciphertext, , and trapdoor as input, it outputs the search result and server-aided decrypted ciphertext and returns them to the search user.
- (6)
- Decryption: This PPT algorithm is executed by the to perform decryption. Taking the system public parameters, , the ciphertext, , and private key as input, it outputs plaintext data m.
3.2. Security Model
In this section, we define two security models for our SA-CP-SABE scheme to specify the capabilities and possible actions of the attacker by a game involving two participants: the challenger and the attacker. In the security model, the challenger assumes a dual role. First, the challenger interacts with the attacker, responding to queries that essentially serve to ascertain the attacker’s capabilities and the type of information they can obtain. Second, the challenger acts as a problem solver for challenging tasks, leveraging the attacker’s capabilities and the information provided during the challenge phase to tackle difficult problems. In searchable encryption schemes, two main security properties are typically considered: ciphertext privacy security (IND-CKA) and trapdoor privacy security (IND-KGA).
Ciphertext privacy security means that the ciphertext of a keyword does not reveal any information about the keyword to an unauthorized attacker. The specific security model is as follows:
Definition 3
(IND-CKA). Assuming is the attacker and is the challenger, the IND-CKA security model is defined by security game between the challenger, , and the attacker, . The game, , is described as follows:
Initialization: Challenger executes the system initialization algorithm, obtains system parameters and master key , and offers to attacker .
Phase 1: Attacker can initiate the following queries:
Hash queries: An attacker can, at any time, initiate hash queries of any message, and the challenger returns the corresponding hash value.
Key queries: Upon receiving a set of attributes S by the attacker, the challenger simulates private key and sends it to the attacker.
Trapdoor Queries: Upon receiving a set of attributes S and keyword w from the attacker, the challenger simulates trapdoor and returns it to the attacker.
Challenge phase: At the end of Phase 1 queries, the attacker outputs with the same length and an access tree (where the set of attributes required to satisfy its access rights has not been queried by the key queries). Challenger randomly selects , performs the encryption algorithm on , and returns ciphertext to the attacker.
Phase 2: The attacker continues to initiate the same queries as in Phase 1 with the following restrictions:
- (1)
- If attribute set S satisfies access tree , key queries of S are prohibited.
- (2)
- If attribute set S satisfies access tree , trapdoor queries with and are prohibited.
Guess: At the end of the game, attacker outputs ; if , the attacker wins the game.
Attacker has the advantage of winning the game defined as .
If advantage of attacker in winning the game is negligible, the scheme satisfies IND-CKA security.
Trapdoor privacy means that trapdoors do not reveal any information about relevant keywords to unauthorized attackers. The specific security model is as follows.
Definition 4
(INA-KGA). Assuming that is the attacker and is the challenger, the INA-KGA security model can be defined by security game between the challenger, , and the attacker, , and game is described as follows:
Initialization: Challenger executes the system initialization algorithm, obtains the system parameters, , and the master key, and offers to attacker .
Phase 1: The attacker at can initiate the following queries:
Hash queries: An attacker can, at any time, initiate hash queries of any message, and the challenger returns the corresponding hash value.
Key queries: Upon receiving a set of attributes S from the attacker, the challenger simulates the private key, , and sends it to the attacker.
Trapdoor Queries: Upon receiving a set of attributes S and keyword w from the attacker, the challenger simulates trapdoor and returns it to the attacker.
Challenge phase: The attacker selects the given set of challenge attributes (no private key queries are queried) and keyword . The challenger randomly selects and returns challenge trapdoor . Here, data m, , and access structure T ( meets T) are never encrypted.
Phase 2: The attacker continues to initiate queries as in Phase 1 with the following restrictions:
- (1)
- Encryption of data m, , and access structures T ( satisfies T) is not permitted.
- (2)
- Private key queries on attribute set are not permitted.
Guess: At the end of the game, attacker outputs . If , the attacker wins the game.
Attacker has the advantage of winning the game defined as .
If advantage of attacker in winning the game is negligible, the scheme satisfies INA-KGA security.
4. Construction of the SA-CP-SABE Scheme
Next, we present the design of our SA-CP-SABE scheme. There are six polynomial-time algorithms described as follows:
- 1.
- System initialization: this algorithm selects two multiplicative groups with the same prime order q. We define bilinear map , and g is the generator of group . We choose four random numbers and compute , and . We define hash function . Finally, PKG publishes system parameters and the secret system master key . We use to denote the Lagrange coefficients of and .
- 2.
- Encryption: Given data and keyword , the DO selects a symmetric encryption algorithm and encryption key and encrypts m with algorithm and key represented as . Then, we define access structure T and encrypt and keyword according to T in the following steps:
- (1)
- We randomly select and calculate , , .
- (2)
- Using a top-down approach, we start from the root node, and for each node x, we select polynomial of degree . When x is the root node, we make . Otherwise, we let where is the parent of node x and is the index of node x. We let Y denote the set of all leaf nodes. Each leaf node y corresponds to a specific attribute value, which is denoted as . We compute .
- (3)
- Finally, we upload ciphertext to the cloud.
- 3.
- User Private Key Generation: Once the KGC receives a request from a data user (with attribute set S) to generate a key, it first randomly selects and calculates and . Then, we randomize and calculate . Finally, we send to the data user.
- 4.
- Trapdoor Generation: When the data user requests the search permission of keyword w from the KGC, the KGC randomly selects k and calculates and , and returns it to the data user. After receiving it, the data user calculates the trapdoor,and sends it to the cloud server.
- 5.
- Search and Transform: Upon receiving , the cloud first verifies whether the user’s attribute set S satisfies access control tree T in ciphertext . If not, it returns ⊥. Otherwise, the search is conducted as follows:
- (1)
- The cloud defines two recursive algorithms, and , which take as input ciphertext , trapdoor , attribute set S, and node x in access tree T and return the result as follows. The actual attribute is used to represent leaf node x.
- (i)
- If x is a leaf node and , then we define
- (ii)
- If x is a leaf node and , then we define , .
- (iii)
- If x is a non-terminal node, then we create the set where z is the left child of node x. When is less than the threshold , we make . Otherwise, we choose a subset of that satisfies , and denote the set by . Finally, we define
- (2)
- The cloud calls and to obtain and , respectively, where R is the root node.
- (3)
- Ciphertext Verification.The cloud server verifies whether holds.
- (i)
- If it holds, it implies that the keyword of the ciphertext matches the keyword in the trapdoor. Therefore, the cloud returns the ciphertext as follows:
- (ii)
- If it does not hold, it indicates that the ciphertext is not the one searched by the data user.In fact, here are
- 6.
- Decryption: The data user receives and calculates . Finally, the data user can obtain the plaintext .
5. Analysis of the SA-CP-SABE Scheme
5.1. Security Analysis
Theorem 1.
Under the random model, if there exists an attacker A who can win game with probability ε in polynomial time, then there exists a challenger who can solve the hard problem defined in Definition 1 with probability in polynomial time.
Proof.
Given an instance , challenger performs the game with attacker A and solves the hard problem in Definition 1 by using attacker A’s ability to determine whether R is equal to as follows:
Initialization: Challenger selects four random numbers and calculates , , and . We define hash function . Finally, PKG issues system parameter . In fact, the system parameters set in this way can be regarded as the system master key owned by KGC, denoted as .
Phase 1: Attacker A adaptively initiates the following queries:
queries: Upon receiving w from the attacker, challenger first looks up list , and if , returns . Otherwise, it randomly selects , computes and returns , and writes to list .
Key queries: Upon receiving a set of attributes S from the attacker, challenger , randomly computes and . Then, it randomly selects and computes
Finally, we send to the user. Here, satisfies and can be obtained by querying .
Trapdoor queries: Given an attribute set S and keyword w by the attacker, the challenger first performs key queries with attribute set S to obtain . We randomly select k and compute and . Finally, we compute the trapdoor as
and return it to the attacker. Here, satisfies , which can be obtained by querying .
Challenge phase: Once the decision is made to end the queries in Phase 1, the attacker is given A with the same length and an access tree (the set of attributes required to satisfy its access rights is not interrogated by the key). Challenger randomly selects and , obtains by the method in the encryption algorithm based on the access tree, , and returns the following ciphertext:
Phase 2: The attacker continues to initiate the same queries as in Phase 1, with the following restrictions:
- (1)
- If attribute set S satisfies access tree , key queries of S are prohibited.
- (2)
- If attribute set S satisfies access tree , trapdoor queries with and are prohibited.
Guess: At the end of the game, attacker A outputs , and if , the attacker wins the game.
Obviously, when , the above ciphertext is a legitimate ciphertext. Assuming that the attacker has the advantageous attack scheme of , when the ciphertext is valid, the attacker can guess it correctly with the probability of . When , which is some random number to the attacker, the attacker can guess accurately with probability . Therefore, the challenger also has probability of solving the hard problem in Definition 1. □
Theorem 2.
Under the stochastic prediction model, if there exists an attacker A who can win with ε probability in polynomial time, then there exists a challenger who can win the hard problem in Definition 2 with probability in polynomial time.
Proof.
Given instance , challenger performs the game with attacker A and uses the difficult problem in the definition of attacker A’s ability to determine whether R is equal to , as follows:
Initialization: Challenger selects four random numbers and calculates , and . We define hash function . Finally, PKG issues system parameter . In fact, the system parameters set in this way can be regarded as PKC with the system master key as .
Phase 1: Attacker A adapts to initiate the following queries:
The query: Given w by the attacker, challenger first looks up list , and if , it returns . Otherwise, it randomly selects , computes and returns , and appends to list .
Key queries: The attacker is given a set of attributes S, challenger randomly computes and . Then, it randomly selects , and computes . Finally, it sends to the user. Here, satisfies and can be obtained by asking .
Trapdoor queries: Given an attribute set S and keyword w by the attacker, the challenger first performs key queries with attribute set S to obtain . It randomly selects k and computes and , and finally computes the trapdoor,
and returns it to the attacker. Here, satisfies , which can be obtained by interrogating .
Challenge phase: The attacker selects the given set of challenge attributes (no private key queries performed) and keyword . The challenger randomly selects and returns the challenge trapdoor . Here, data m, and access structure T ( meets T) are never encrypted. The specific challenge trapdoor is generated as follows:
- (1)
- We randomly select and calculate
- (2)
- We calculate .
- (3)
- We return .
Phase 2: The attacker continues to initiate the queries as in Phase 1 with the following restrictions:
- (1)
- It is not possible to encrypt data m, and access structures T ( meets T).
- (2)
- Private key queries cannot be performed on attribute set .
Guess: At the end of the game, attacker A outputs , if . The attacker wins the game.
Obviously, considering random number s in key generation and k in trapdoor generation as being opposite to each other (i.e., ), and when , the trapdoor described above is a legitimate one. Assuming the attacker has an advantage of in breaking the scheme, under the condition of valid ciphertexts, the attacker can correctly guess with a probability of . When , it appears as a collection of some random numbers to the attacker, and the probability of the attacker’s accurate guess is . Therefore, the challenger also has a probability of to solve the difficult BDDH problem. □
5.2. Performance Analysis
5.2.1. Functionality Comparison
In this section, we compare the security and functionality features of our searchable attribute-based encryption scheme with current searchable attribute-based encryption schemes [9,10,13,16]. The comparison specifically includes ciphertext indistinguishability, trapdoor indistinguishability, resistance to keyword guessing attacks, whether it employs ciphertext policy or key policy, and whether it supports aided decryption. The comparison results are presented in Table 3. Table 3 demonstrates that our scheme has significant advantages in terms of security features.

Table 3.
Comparison of security properties.
5.2.2. Storage Cost
In this subsection, we compare our schemes with the ABKS-HD [10] scheme and the DSF [9] scheme in terms of user key length, ciphertext length, and trapdoor length, as shown in Table 4. There are two reasons why we chose to conduct performance analysis on the ABKS-HD [10] scheme and the DSF [9] scheme. First, they are both based on ciphertext-policy attribute-based encryption (CP-ABE), similar to our proposed SA-CP-SABE scheme. Second, they both have server-assisted decryption capabilities. These factors make them appropriate candidates for comparative performance evaluations. It should be noted that the calculation of ciphertext length for the CP-ABESA scheme does not include the part , as this component is consistent across all three schemes. Therefore, when comparing storage and computational costs, this part is not taken into account.

Table 4.
Comparison of storage cost.
5.2.3. Computation Cost
For the encryption algorithm, the trapdoor generation algorithm, the search algorithm, and the decryption algorithm, we first perform a theoretical estimation of the computation time for the ABKS-HD [10] scheme and the SA-CP-SABE scheme, as shown in Table 5. Note that , respectively, denote the inverse, multiplication, and exponential operations in the group. denotes the pair operation. represents the size of the smallest subset of attributes in the user attribute set that satisfies the access tree. denotes the number of internal nodes of the subtree from which the subset forms the access tree. d represents the average threshold value of the internal nodes.

Table 5.
Comparison of computation cost.
Evidently, as depicted in Table 5, in our scheme, the exponential operations in the encryption algorithm are linearly related to the number of leaf nodes in the access control tree, the multiplication operations in the trapdoor generation algorithm are linearly correlated with the size of user attributes, and the pairing operations in the search and transformation algorithm are linearly related to the size of the smallest subset of attributes in the user attribute set that satisfies the access tree.
Subsequently, we compare their computational costs through simulation experiments. The experimental simulation platform is as follows: Intel(R) Core(TM) i3-4130 CPU @3.40GHz processor, 4GB memory, Ubuntu 14.04.3 operating system, and the programming language is Python 3.7. To handle group operations, we utilize the PBC library. Additionally, we conduct testing on the “SS512” super-singular symmetric group. The time cost of each phase (encryption, trapdoor generation, search and transform and user decryption) are illustrated in Figure 2, Figure 3, Figure 4 and Figure 5, respectively.
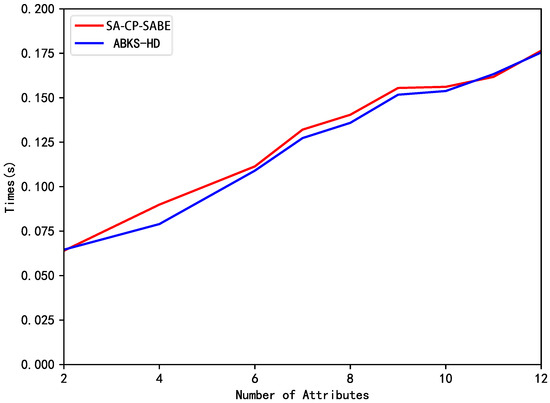
Figure 2.
Comparison of encryption time.
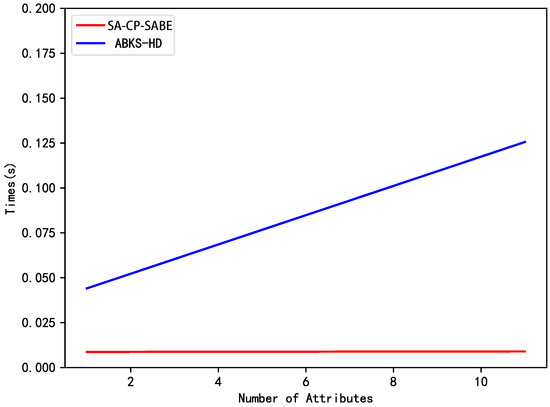
Figure 3.
Comparison of trapdoor generation time.
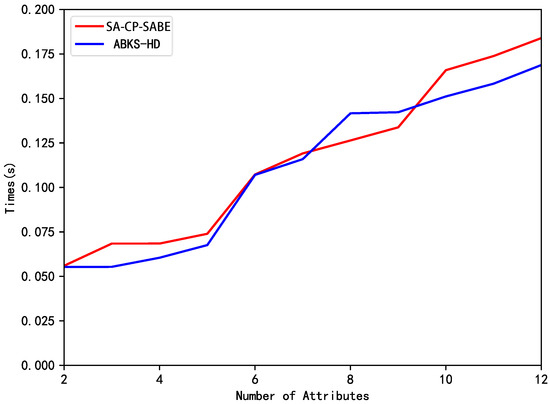
Figure 4.
Comparison of search transform times.
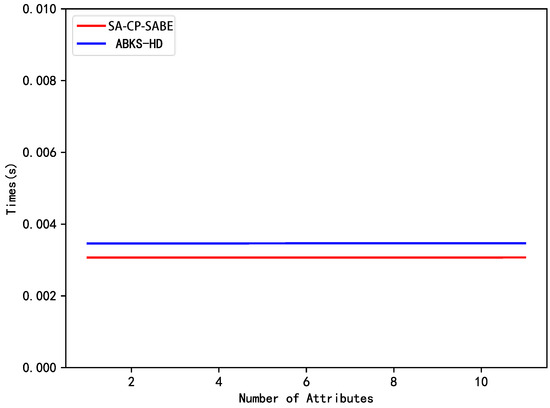
Figure 5.
Comparison of decryption time.
5.2.4. Discussion
Figure 2 illustrates the encryption time (in seconds) as it varies with the number of leaf nodes in the access tree. It should be noted that the encryption time is not solely determined by the number of leaf nodes but also relates to the structural form of the access tree. However, the computationally intensive operations (such as multiplication, exponentiation, etc.) mainly occur at the leaf nodes. Therefore, only the number of leaf nodes is calculated.
Figure 3 depicts the execution time (in seconds) for trapdoor generation corresponding to keywords as it varies with the number of attributes. Under the condition of disregarding other non-algorithmic factors, the trapdoor generation time exhibits a linear function of the number of attributes. Therefore, based on the raw data obtained from the simulation results, we utilized the least squares method to model the trend of the generation time with the number of attributes.
Figure 4 illustrates the variation of the search and transform time (in seconds) with the number of attributes. From the graph, it is evident that the search and transform time are linearly related to the number of attributes, which confirms the theoretical analysis discussed in the previous section.
Figure 5 illustrates the variation of decryption time with the number of attributes. Since the ciphertext decryption performed by the user is independent of the number of attributes after the computation by the cloud server in the search and transform phase, Figure 5 also employs the least squares method to model the trend of the decryption time with the number of attributes.
From the analysis above, it can be concluded that the overall performance of the SA-CP-SABE scheme is comparable to that of the ABKS-HD scheme, but it offers higher security.
6. Conclusions
In this paper, we propose a new ciphertext policy-based searchable attribute-based encryption scheme (SA-CP-SABE) to enhance the security for cloud-based smart grids and efficiency which achieves the control of user data access rights and data search rights. SA-CP-SABE has both the unforgeability of the ciphertext and the indistinguishability of the trapdoor, overcoming the security problems of many similar existing schemes. In addition, the performance analysis shows that the proposed SA-CP-SABE scheme also offers superior performance benefits. However, the limitation of the current scheme is that, to prevent offline keyword guessing attacks, data users need to request authorization from the KGC for each search trapdoor generation, which increases the operational load on the KGC. In our future work, we will focus on developing a one-time authorization system to eliminate the need for repeated permissions with each trapdoor generation and design more functional, more efficient, and more secure searchable encryption schemes.
Author Contributions
Conceptualization, J.W., H.L. and C.L.; methodology, J.W., H.L. and C.L.; software, C.L.; validation, H.L., L.L. and C.L.; security analysis, H.L. and C.L.; resources, H.L.; writing—original draft preparation, J.W. and L.L.; writing—review and editing, C.L. and L.L.; visualization, H.L. and C.L.; supervision, H.L., L.L. and C.L.; funding acquisition, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported, in part, by “Kunlun Elite” Talent Recruitment Research Project under Grant No. 2023-QLGKLYCZX-028, and New Faculty (Ph.D.) Extended Research and Cultivation Program under Grant No. 202302lwys018.
Data Availability Statement
The authors confirm that the data supporting the findings of this study are available within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ABE | Attribute-Based Encryption |
| KP-ABE | Key-Policy Attribute-Based Encryption |
| CP-ABE | Ciphertext-Policy Attribute-Based Encryption |
| PEKS | Public Key Searchable Encryption |
| SABE | Searchable Attribute-Based Encryption |
| KGC | Key Generation Center |
| DO | Data Owner |
| DU | Data User |
| CSP | Cloud Server Provider |
References
- Mell, P.; Grance, T. The NIST Definition of Cloud Computing. Available online: http://nvlpubs.nist.gov/nistpubs/Legacy/SP/nistspecialpublication800-145.pdf (accessed on 7 May 2024).
- Tabrizchi, H.; Rafsanjani, M.K. A survey on security challenges in cloud computing: Issues, threats, and solutions. J. Supercomput. 2020, 76, 9493–9532. [Google Scholar] [CrossRef]
- Sahai, A.; Waters, B. Fuzzy Identity-Based Encryption. In Advances in Cryptology—EUROCRYPT 2005; Cramer, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 457–473. [Google Scholar]
- Goyal, V.; Pandey, O.; Sahai, A.; Waters, B. Attribute-based encryption for fine-grained access control of encrypted data. In Proceedings of the 13th ACM Conference on Computer and Communications Security, OCT 2006, Alexandria, VA, USA, 30 October–3 November 2006. [Google Scholar] [CrossRef]
- Bethencourt, J.; Sahai, A.; Waters, B. Ciphertext-Policy Attribute-Based Encryption. In Proceedings of the 2007 IEEE Symposium on Security and Privacy (SP ’07), Oakland, CA, USA, 20–23 May 2007; pp. 321–334. [Google Scholar] [CrossRef]
- Wang, S.; Ye, J.; Zhang, Y. A keyword searchable attribute-based encryption scheme with attribute update for cloud storage. PLoS ONE 2018, 13, e0197318. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Jing, T. A lightweight fine-grained searchable encryption scheme in fog-based healthcare IoT networks. Wirel. Commun. Mob. Comput. 2019, 2019, 1019767. [Google Scholar] [CrossRef]
- Zhang, K.; Long, J.; Wang, X.; Dai, H.N.; Liang, K.; Imran, M. Lightweight Searchable Encryption Protocol for Industrial Internet of Things. IEEE Trans. Ind. Inform. 2021, 17, 4248–4259. [Google Scholar] [CrossRef]
- Miao, Y.; Tong, Q.; Choo, K.K.R.; Liu, X.; Deng, R.H.; Li, H. Secure Online/Offline Data Sharing Framework for Cloud-Assisted Industrial Internet of Things. IEEE Internet Things J. 2019, 6, 8681–8691. [Google Scholar] [CrossRef]
- Miao, Y.; Ma, J.; Liu, X.; Li, X.; Jiang, Q.; Zhang, J. Attribute-Based Keyword Search over Hierarchical Data in Cloud Computing. IEEE Trans. Serv. Comput. 2020, 13, 985–998. [Google Scholar] [CrossRef]
- Chen, D.; Cao, Z.; Dong, X. Online/offline ciphertext-policy attribute-based searchable encryption. J. Comput. Res. Dev. 2016, 53, 2365–2375. [Google Scholar] [CrossRef]
- Niu, S.; Xie, Y.; Yang, P.; Du, X. Cloud-Assisted Attribute-Based Searchable Encryption Scheme on Blockchain. J. Comput. Res. Dev. 2021, 50, 811–821. [Google Scholar] [CrossRef]
- Yin, H.; Zhang, J.; Xiong, Y.; Ou, L.; Li, F.; Liao, S.; Li, K. CP-ABSE: A Ciphertext-Policy Attribute-Based Searchable Encryption Scheme. IEEE Access 2019, 7, 5682–5694. [Google Scholar] [CrossRef]
- Li, J.; Lin, X.; Zhang, Y.; Han, J. KSF-OABE: Outsourced Attribute-Based Encryption with Keyword Search Function for Cloud Storage. IEEE Trans. Serv. Comput. 2017, 10, 715–725. [Google Scholar] [CrossRef]
- Wang, H.; Ning, J.; Huang, X.; Wei, G.; Poh, G.S.; Liu, X. Secure Fine-Grained Encrypted Keyword Search for E-Healthcare Cloud. IEEE Trans. Dependable Secur. Comput. 2021, 18, 1307–1319. [Google Scholar] [CrossRef]
- Bao, Y.; Qiu, W.; Cheng, X. Secure and lightweight fine-grained searchable data sharing for IoT-oriented and cloud-assisted smart healthcare system. IEEE Internet Things J. 2022, 9, 2513–2526. [Google Scholar] [CrossRef]
- Song, D.X.; Wagner, D.; Perrig, A. Practical techniques for searches on encrypted data. In Proceedings of the Proceeding 2000 IEEE Symposium on Security and Privacy, S&P 2000, Berkeley, CA, USA, 14–17 May 2000; pp. 44–55. [Google Scholar] [CrossRef]
- Boneh, D.; Di Crescenzo, G.; Ostrovsky, R.; Persiano, G. Public Key Encryption with Keyword Search. In Advances in Cryptology—EUROCRYPT 2004; Cachin, C., Camenisch, J.L., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 506–522. [Google Scholar]
- Rhee, H.S.; Park, J.H.; Susilo, W.; Lee, D.H. Trapdoor security in a searchable public-key encryption scheme with a designated tester. J. Syst. Softw. 2010, 83, 763–771. [Google Scholar] [CrossRef]
- Yang, N.; Zhou, Q.; Xu, S. Public-Key Authenticated Encryption with Keyword Search without Pairings. J. Comput. Res. Dev. 2020, 57, 2125–2135. [Google Scholar] [CrossRef]
- Chen, R.; Mu, Y.; Yang, G.; Guo, F.; Huang, X.; Wang, X.; Wang, Y. Server-Aided Public Key Encryption With Keyword Search. IEEE Trans. Inf. Forensics Secur. 2016, 11, 2833–2842. [Google Scholar] [CrossRef]
- Yu, S.; Ren, K.; Lou, W.; Li, J. Defending against Key Abuse Attacks in KP-ABE Enabled Broadcast Systems. In Security and Privacy in Communication Networks; Chen, Y., Dimitriou, T.D., Zhou, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 311–329. [Google Scholar]
- Wei, J.; Chen, X.; Huang, X.; Hu, X.; Susilo, W. RS-HABE: Revocable-Storage and Hierarchical Attribute-Based Access Scheme for Secure Sharing of e-Health Records in Public Cloud. IEEE Trans. Dependable Secur. Comput. 2021, 18, 2301–2315. [Google Scholar] [CrossRef]
- Liang, K.; Liu, J.K.; Lu, R.; Wong, D.S. Privacy Concerns for Photo Sharing in Online Social Networks. IEEE Internet Comput. 2015, 19, 58–63. [Google Scholar] [CrossRef]
- Li, S.; Xu, M. Attribute-based public encryption with keyword search. Chin. J. Comput. 2014, 37, 1017–1024. [Google Scholar]
- Zhou, R.; Zhang, X.; Du, X.; Wang, X.; Yang, G.; Guizani, M. File-centric multi-key aggregate keyword searchable encryption for industrial internet of things. IEEE Trans. Ind. Inform. 2018, 14, 3648–3658. [Google Scholar] [CrossRef]
- Lai, J.; Deng, R.H.; Guan, C.; Weng, J. Attribute-Based Encryption With Verifiable Outsourced Decryption. IEEE Trans. Inf. Forensics Secur. 2013, 8, 1343–1354. [Google Scholar] [CrossRef]
- Delerablée, C.; Pointcheval, D. Dynamic Threshold Public-Key Encryption. In Advances in Cryptology—CRYPTO 2008; Wagner, D., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 317–334. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).