Key Vulnerable Nodes Discovery Based on Bayesian Attack Subgraphs and Improved Fuzzy C-Means Clustering
Abstract
1. Introduction
- An analysis method based on Bayesian attack subgraphs is proposed. It divides the attack graph based on the idea of community division, quantifies the threat of nodes, constructs and analyzes Bayesian attack subgraphs to form the subgraph analysis information group, and aggregates information groups to quickly obtain the final analysis results of all paths so as to improve the spatiotemporal efficiency of the results;
- A method based on improved FCM to discover key vulnerable nodes is proposed. It uses variance to design the total difference value between classes (TDVC) and determines the optimal number of FCM by maximizing the TDVC. Then, the actual threat features and inherent threat features of vulnerabilities are extracted based on the Common Vulnerability Scoring System (CVSS) and the analysis results of the attack graph. Next, FCM is used to cluster the vulnerability nodes based on the extracted features so as to improve the accuracy of the results. Finally, the feature priority is set, and the key vulnerability node cluster with the highest threat level is found according to the results.
- The experimental scenario is designed and the data from the National Vulnerability Database (NVD) are collected for the experiment. The temporal and spatial efficiency improvement of attack graph analysis and the accuracy improvement of key vulnerability nodes search results are verified by comparing with other methods.
2. Related Works
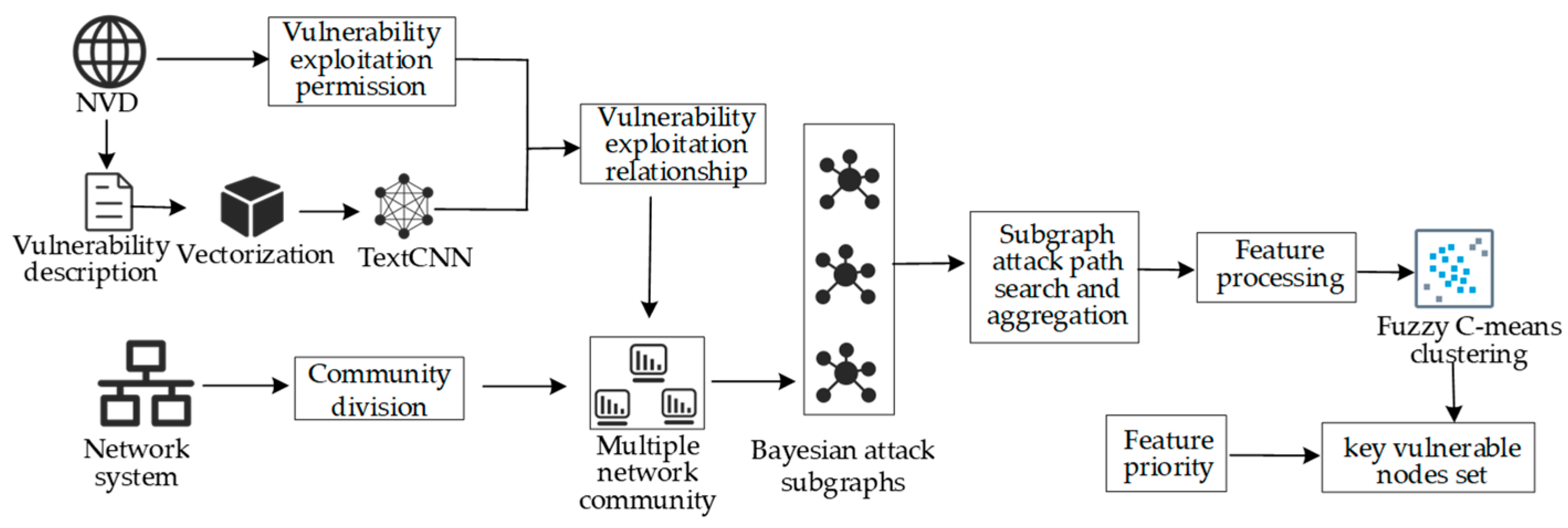
3. Key Nodes Discovery Model Based on Attack Subgraph Aggregation Search and Fuzzy C-Means Clustering
4. Attack Path Aggregation Search Based on Bayesian Attack Subgraph
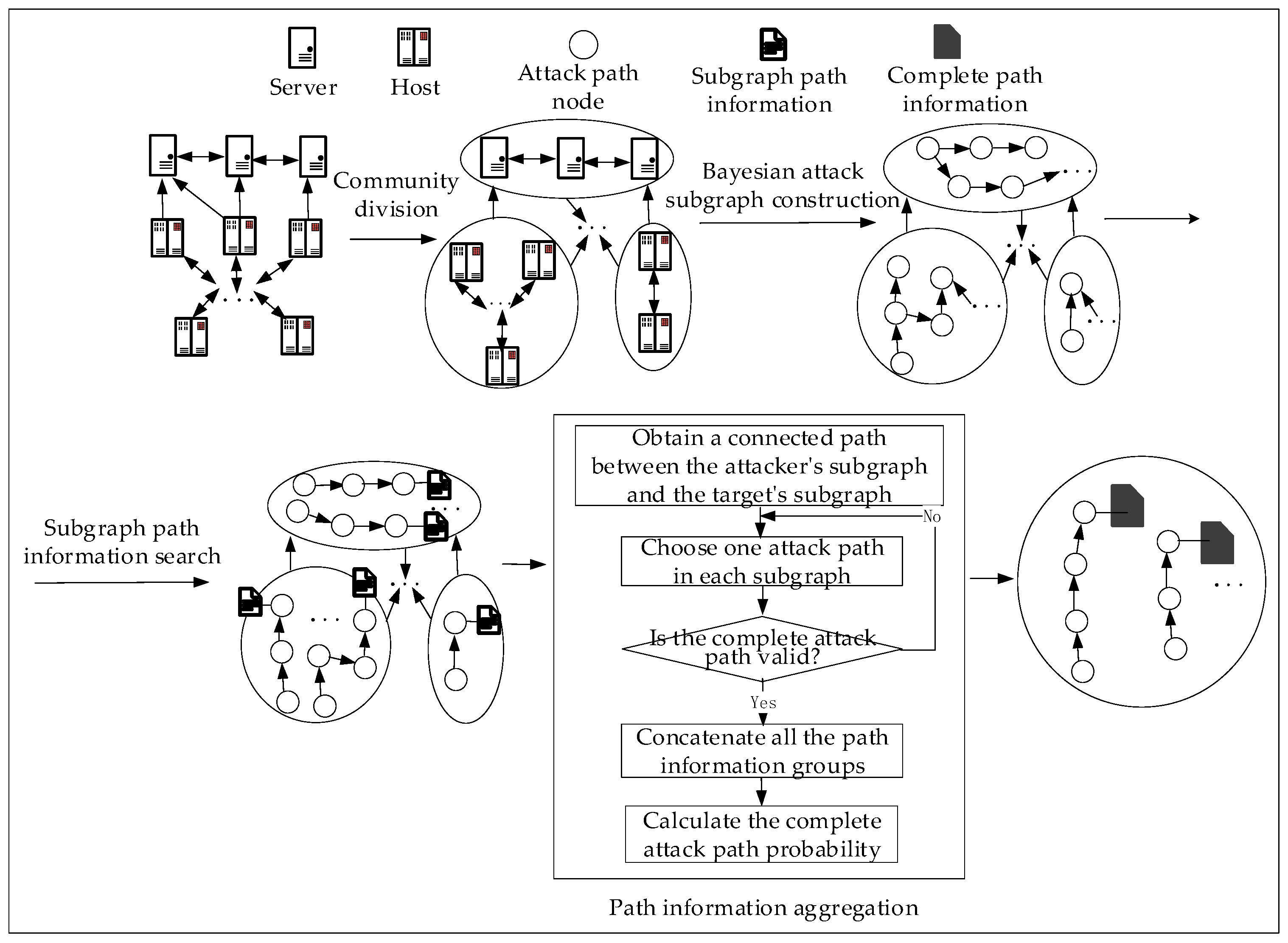
4.1. Bayesian Attack Subgraph Construction
- is the set of nodes. . is the set of nodes where the attacker is located in the Bayesian attack graph. is the node set of the attack target. is the set of the remaining nodes. The value of can be 0 or 1. means that the node has been compromised. means that the node is not compromised;
- is the set of directed edges between nodes. . means that an attacker at node can attack node after having sufficient privileges;
- is the set of parent–child node relationships in the attack graph. . is the set of parents of node . means that node can be attacked when any of its parents has been compromised. means that node can only be attacked after all its parents have been compromised;
- is the set of node breach probabilities. . means the probability that node is successfully attacked;
- is the set of node selection probabilities. . means the probability that node is selected by the attacker as an attack target;
- is the set of conditional probabilities of nodes. . means the conditional probability that the node i will be attacked after its parent is compromised.
4.2. Attack Subgraph Paths Search
| Algorithm 1: BasicPathSearch |
| Input: The Bayesian attack subgraph set |
| Output: The basic path set Ls in the Bayesian attack subgraph, the information group set Is, and the basic path reachability probability set Probs |
|
4.3. Attack Paths and Its Information Aggregation
| Algorithm 2: AttackPathAggregation |
| Input: The attack connection information C between subgraphs, the utilization relation U of nodes, the basic path reachability probability P, the basic path information group I |
| Output: The aggregated reachability probability of the attack path and its corresponding information group |
|
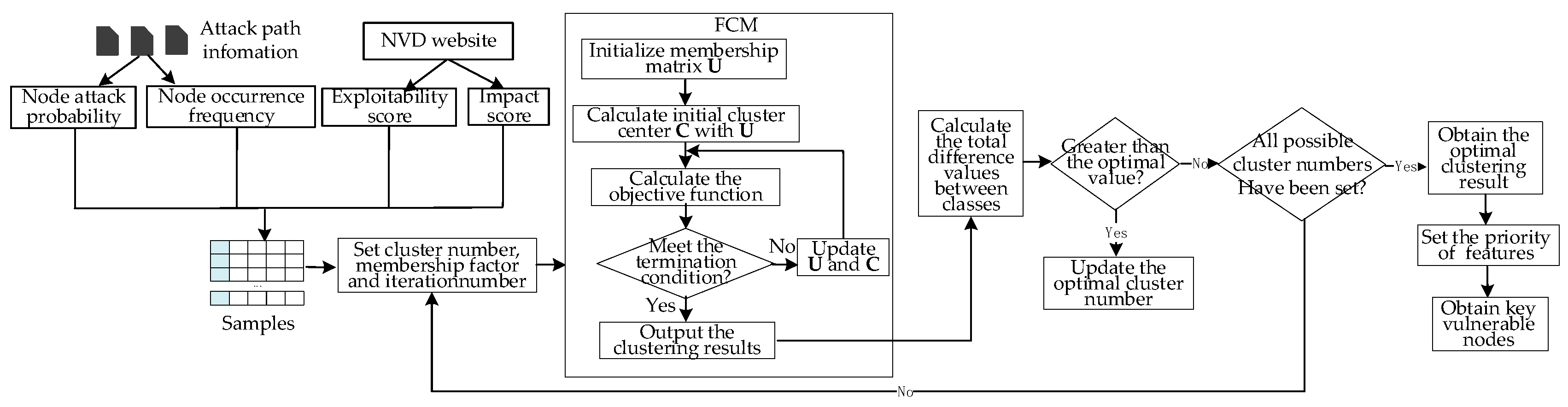
5. Discovery of Key Vulnerable Nodes Based on Improved FCM
| Algorithm 3: VulnerabilityClusteringByImprovedFCM |
| Input: The vulnerability node samples , the total number of samples |
| Output: The number of optimal clusters , and the corresponding clustering result |
|
6. Results
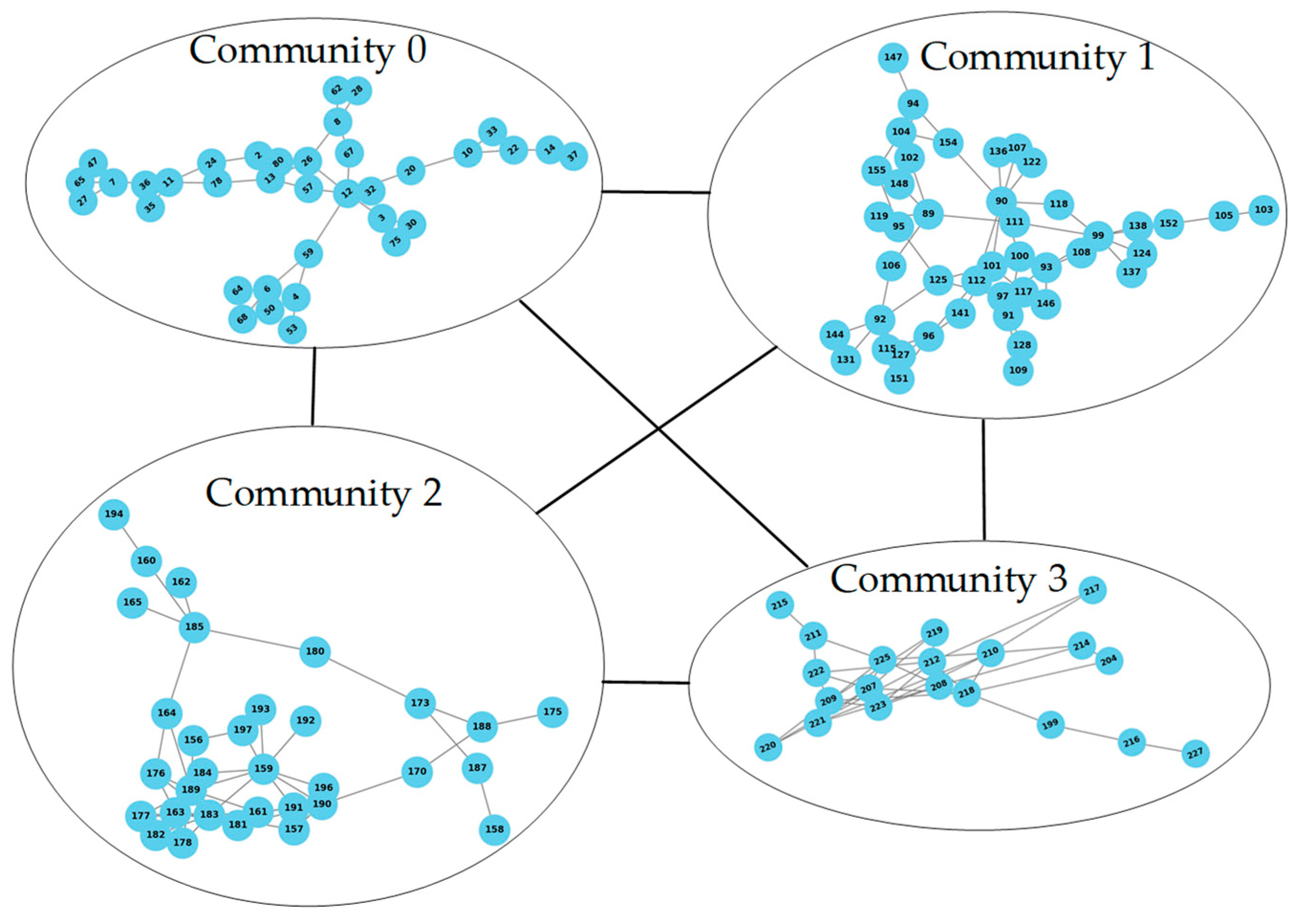
6.1. Experimental Scenario
6.2. Experimental Process
6.3. Experiment Results Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aslan, Ö.; Aktuğ, S.S.; Ozkan-Okay, M.; Yilmaz, A.A.; Akin, E. A comprehensive review of cyber security vulnerabilities, threats, attacks, and solutions. Electronics 2023, 12, 1333. [Google Scholar] [CrossRef]
- Ferrara, P.; Mandal, A.K.; Cortesi, A.; Spoto, F. Static analysis for discovering IoT vulnerabilities. Int. J. Softw. Tools Technol. Transf. 2021, 23, 71–88. [Google Scholar] [CrossRef]
- Vallabhaneni, R.; Vaddadi, S.; Maroju, A.; Dontu, S. Analysis on Security Vulnerabilities of the Modern Internet of Things (IOT) Systems. Int. J. Recent Innov. Trends Comput. Commun. 2024, 11, 9. [Google Scholar]
- Jbair, M.; Ahmad, B.; Maple, C.; Harrison, R. Threat modelling for industrial cyber physical systems in the era of smart manufacturing. Comput. Ind. 2022, 137, 103611. [Google Scholar] [CrossRef]
- Xiong, W.; Legrand, E.; Åberg, O.; Lagerström, R. Cyber security threat modeling based on the MITRE Enterprise ATT&CK Matrix. Softw. Syst. Model. 2022, 21, 157–177. [Google Scholar]
- Cao, S.; Sun, X.; Bo, L.; Wei, Y.; Li, B. Bgnn4vd: Constructing bidirectional graph neural-network for vulnerability detection. Inf. Softw. Technol. 2021, 136, 106576. [Google Scholar] [CrossRef]
- Liu, Z.; Qian, P.; Wang, X.; Zhuang, Y.; Qiu, L. Combining graph neural networks with expert knowledge for smart contract vulnerability detection. IEEE Trans. Knowl. Data Eng. 2021, 35, 1296–1310. [Google Scholar] [CrossRef]
- Zheng, Y.; Pujar, S.; Lewis, B.; Buratti, L.; Epstein, E.; Yang, B.; Su, Z. D2a: A dataset built for ai-based vulnerability detection methods using differential analysis. In Proceedings of the 2021 IEEE/ACM 43rd International Conference on Software Engineering: Software Engineering in Practice (ICSE-SEIP), Madrid, Spain, 25–28 May 2021; pp. 111–120. [Google Scholar]
- Chakraborty, S.; Krishna, R.; Ding, Y.; Ray, B. Deep learning based vulnerability detection: Are we there yet? IEEE Trans. Softw. Eng. 2021, 48, 3280–3296. [Google Scholar] [CrossRef]
- Steenhoek, B.; Rahman, M.M.; Jiles, R.; Le, W. An empirical study of deep learning models for vulnerability detection. In Proceedings of the 2023 IEEE/ACM 45th International Conference on Software Engineering (ICSE), Melbourne, Australia, 14–20 May 2023; pp. 2237–2248. [Google Scholar]
- Almazrouei, O.S.M.B.H.; Magalingam, P.; Hasan, M.K.; Hasan, M.K.; Shanmugam, M. A review on attack graph analysis for iot vulnerability assessment: Challenges, open issues, and future directions. IEEE Access 2023, 11, 44350–44376. [Google Scholar] [CrossRef]
- Zenitani, K. Attack graph analysis: An explanatory guide. Comput. Secur. 2023, 126, 103081. [Google Scholar] [CrossRef]
- Hankin, C.; Malacaria, P. Attack dynamics: An automatic attack graph generation framework based on system topology, CAPEC, CWE, and CVE databases. Comput. Secur. 2022, 123, 102938. [Google Scholar]
- Mohammadzad, M.; Karimpour, J.; Mahan, F. MAGD: Minimal Attack Graph Generation Dynamically in Cyber Security. Comput. Netw. 2023, 236, 110004. [Google Scholar] [CrossRef]
- Presekal, A.; Ştefanov, A.; Rajkumar, V.S.; Palensky, P. Attack graph model for cyber-physical power systems using hybrid deep learning. IEEE Trans. Smart Grid 2023, 14, 4007–4020. [Google Scholar] [CrossRef]
- Shin, G.Y.; Hong, S.S.; Lee, J.S.; Han, I.-S.; Kim, H.-K.; Oh, H.-R. Network security node-edge scoring system using attack graph based on vulnerability correlation. Appl. Sci. 2022, 12, 6852. [Google Scholar] [CrossRef]
- Al-Araji, Z.J.; Ahmad, S.S.S.; Abdullah, R.S. Propose vulnerability metrics to measure network secure using attack graph. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 51–58. [Google Scholar] [CrossRef]
- Al-Araji, Z.; Syed Ahmad, S.S.; Abdullah, R.S. Attack prediction to enhance attack path discovery using improved attack graph. Karbala Int. J. Mod. Sci. 2022, 8, 313–329. [Google Scholar] [CrossRef]
- Kholidy, H.A. Multi-layer attack graph analysis in the 5G edge network using a dynamic hexagonal fuzzy method. Sensors 2021, 22, 9. [Google Scholar] [CrossRef] [PubMed]
- Saravanakumar, T.; Lee, T.H. Hybrid-driven-based resilient control for networked T-S fuzzy systems with time-delay and cyber-attacks. Int. J. Robust Nonlinear Control 2023, 33, 7869–7891. [Google Scholar] [CrossRef]
- Jiang, S.; Yang, L.; Cheng, G.; Gao, X.; Feng, T.; Zhou, Y. A quantitative framework for network resilience evaluation using Dynamic Bayesian Network. Comput. Commun. 2022, 194, 387–398. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, S.; Wang, H.; Chen, M. Multiobjective network security dynamic assessment method based on Bayesian network attack graph. Int. J. Intell. Comput. Cybern. 2024, 17, 38–60. [Google Scholar] [CrossRef]
- Luo, Z.; Xu, R.; Wang, J.; Zhu, W. A Dynamic Risk Assessment Method Based on Bayesian Attack Graph. Int. J. Netw. Secur 2022, 24, 787–796. [Google Scholar]
- Hao, J.; Luo, S.; Pan, L. A novel vulnerability severity assessment method for source code based on a graph neural network. Inf. Softw. Technol. 2023, 161, 107247. [Google Scholar] [CrossRef]
- Tang, G.; Yang, L.; Zhang, L.; Cao, W.; Meng, L.; He, H.; Kuang, H.; Yang, F.; Wang, H. An attention-based automatic vulnerability detection approach with GGNN. Int. J. Mach. Learn. Cybern. 2023, 14, 3113–3127. [Google Scholar] [CrossRef]
- Li, H.J.; Wang, L.; Bu, Z.; Cao, J.; Shi, Y. Measuring the network vulnerability based on markov criticality. ACM Trans. Knowl. Discov. Data (TKDD) 2021, 16, 1–24. [Google Scholar] [CrossRef]
- Huang, B.; Liu, Y. A network vulnerability assessment method using general attack tree. In Proceedings of the 2022 5th International Conference on Data Science and Information Technology (DSIT), Shanghai, China, 22–24 July 2022; pp. 1–4. [Google Scholar]
- Yang, H.; Yuan, H.; Zhang, L. Risk assessment method of IoT host based on attack graph. Mob. Netw. Appl. 2023, 1–10. [Google Scholar] [CrossRef]
- Li, Y.; Li, X. Reseasrch on multi-target network security assessment with attack graph expert system model. Sci. Program. 2021, 2021, 9921731. [Google Scholar]
- Qian, K.; Jin, M.; Zhang, D.; Huang, H.C. Research on Evaluation Method of Network Vulnerability in Power Monitoring System. In Advances in Intelligent Information Hiding and Multimedia Signal Processing: Proceeding of the IIH-MSP 2021 & FITAT 2021; Springer: Singapore; Kaohsiung, Taiwan, 2022; Volume 2, pp. 113–123. [Google Scholar]
- Xie, J.; Keda, S.; Xubing, L. Risk assessment method of power plant industrial control information security based on Bayesian attack graph. J. Electr. Syst. 2021, 17, 529. [Google Scholar]
- Li, Z.; Liu, H.; Wu, C. Computer network security evaluation method based on improved attack graph. J. Cyber Secur. Technol. 2022, 6, 201–215. [Google Scholar] [CrossRef]
- Ying, Y. Research and Implementation of Network Security Measurement Technology Based on Attack Path Threat Analysis; Beijing University of Posts and Telecommunications: Beijing, China, 2021. [Google Scholar]
- Ma, W. Research on network vulnerability assessment based on attack graph and security metrics. J. Phys. Conf. Ser. IOP Publ. 2021, 1774, 012070. [Google Scholar] [CrossRef]
- Vasilyev, V.; Kirillova, A.; Vulfin, A.; Nikonov, A. Cybersecurity risk assessment based on cognitive attack vector modeling with CVSS Score. In Proceedings of the 2021 International Conference on Information Technology and Nanotechnology (ITNT), Samara, Russia, 20–24 September 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Kalogeraki, E.M.; Papastergiou, S.; Panayiotopoulos, T. An attack simulation and evidence chains generation model for critical information infrastructures. Electronics 2022, 11, 404. [Google Scholar] [CrossRef]
- Fan, W.; Xu, H.; Jin, W.; Liu, X.; Tang, X.; Wang, S.; Li, Q.; Tang, J.; Wang, J.; Aggarwal, C. Jointly attacking graph neural network and its explanations. In Proceedings of the 2023 IEEE 39th International Conference on Data Engineering (ICDE), Anaheim, CA, USA, 1 April 2023; pp. 654–667. [Google Scholar]
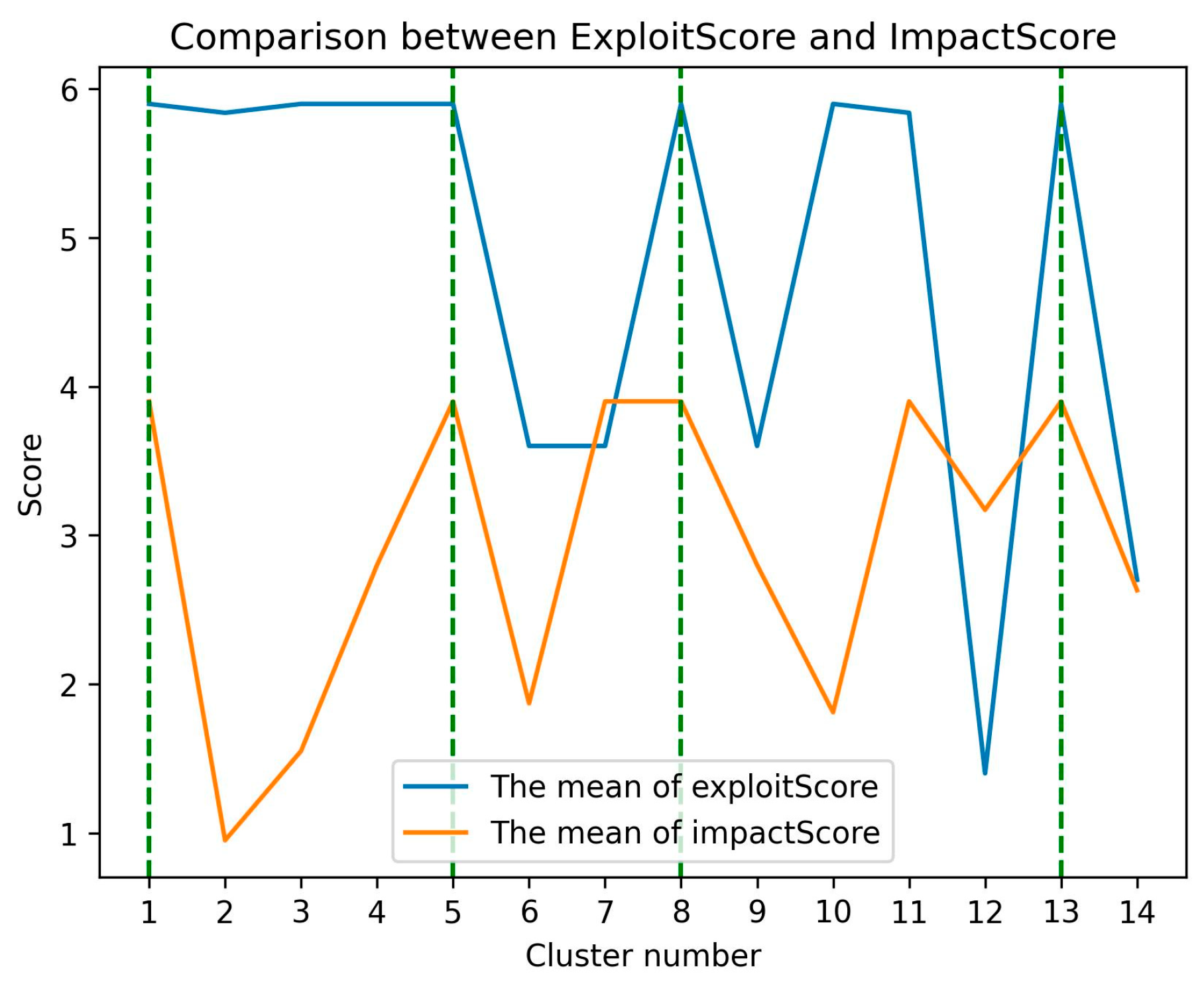
| CVEID | Base Score | Exploitability Score | Impact Score | Utilization Condition | Utilization Consequence |
|---|---|---|---|---|---|
| CVE-2022-27502 | 7.8 | 5.9 | 1.8 | LOW | user |
| CVE-2022-28704 | 7.2 | 5.9 | 1.2 | HIGH | root |
| CVE-2022-29525 | 9.8 | 5.9 | 3.9 | NONE | root |
| CVE-2022-29797 | 9.8 | 5.9 | 3.9 | NONE | user |
| CVE-2022-20148 | 6.4 | 5.9 | 0.5 | HIGH | user |
| CVE-2021-32546 | 8.8 | 5.9 | 2.8 | LOW | other |
| Community | Attack Probability | Information Group | |
|---|---|---|---|
| Attack subgraph paths | 0 | 1.91 × 10−4 | |
| 1 | 2.36 × 10−2 | ||
| 2 | 7.71 × 10−2 | ||
| Aggregated paths | - | 8.14 × 10−3 | |
| - | 3.34 × 10−4 | ||
| - | 3.94 × 10−5 |
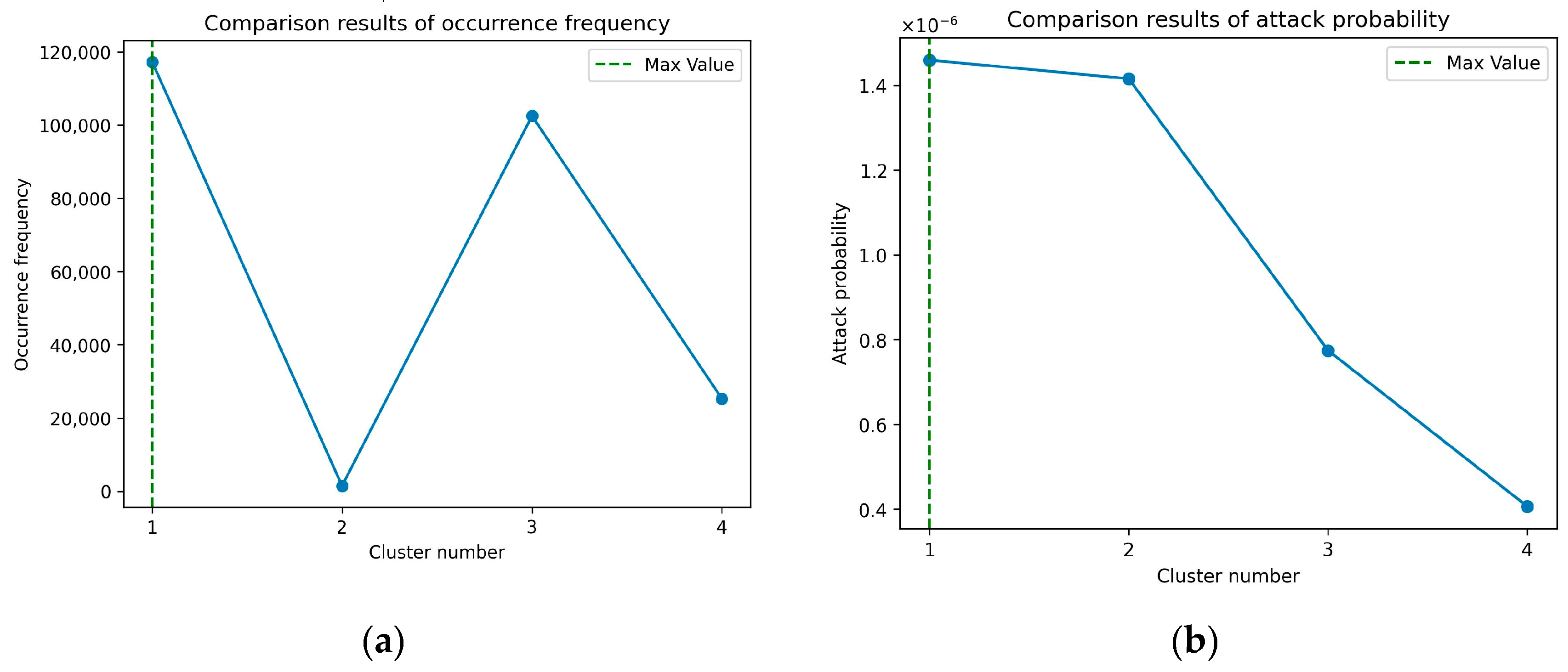
| Node Number | Exploitability Score | Impact Score | Occurrence Frequency | Attack Probability |
|---|---|---|---|---|
| 1 | 5.9 | 1.0 | 2146 | 2.43 × 10−7 |
| 18 | 2.7 | 2.8 | 27,762 | 3.39 × 10−7 |
| 49 | 3.6 | 2.8 | 15,500 | 5.39 × 10−7 |
| 160 | 3.6 | 2.8 | 15,186 | 4.46 × 10−7 |
| 215 | 5.9 | 3.9 | 118,313 | 2.51 × 10−6 |
| Class Number | Node Number Contained in This Class |
|---|---|
| 1 | (141,189,215,217) |
| 2 | (1,2,3,8,11,26,51,71,74,121,136) |
| 7 | (4,14,28,52,55,63,116,117,120,124,140,182,183,192) |
| 11 | (6,9,12,21,30,32,72,78,80,83,87,185) |
| 14 | (18,29,39,46,47,155) |
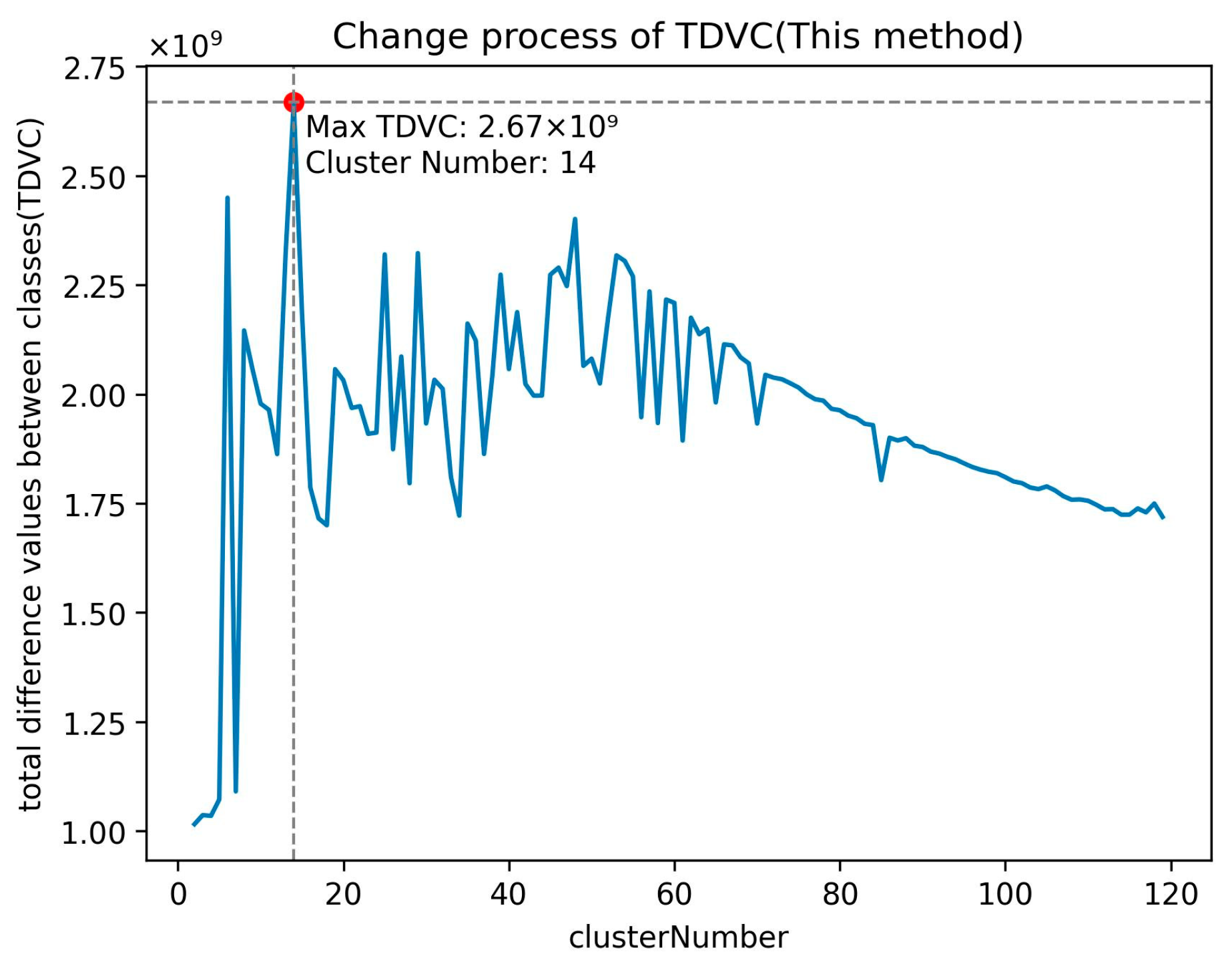
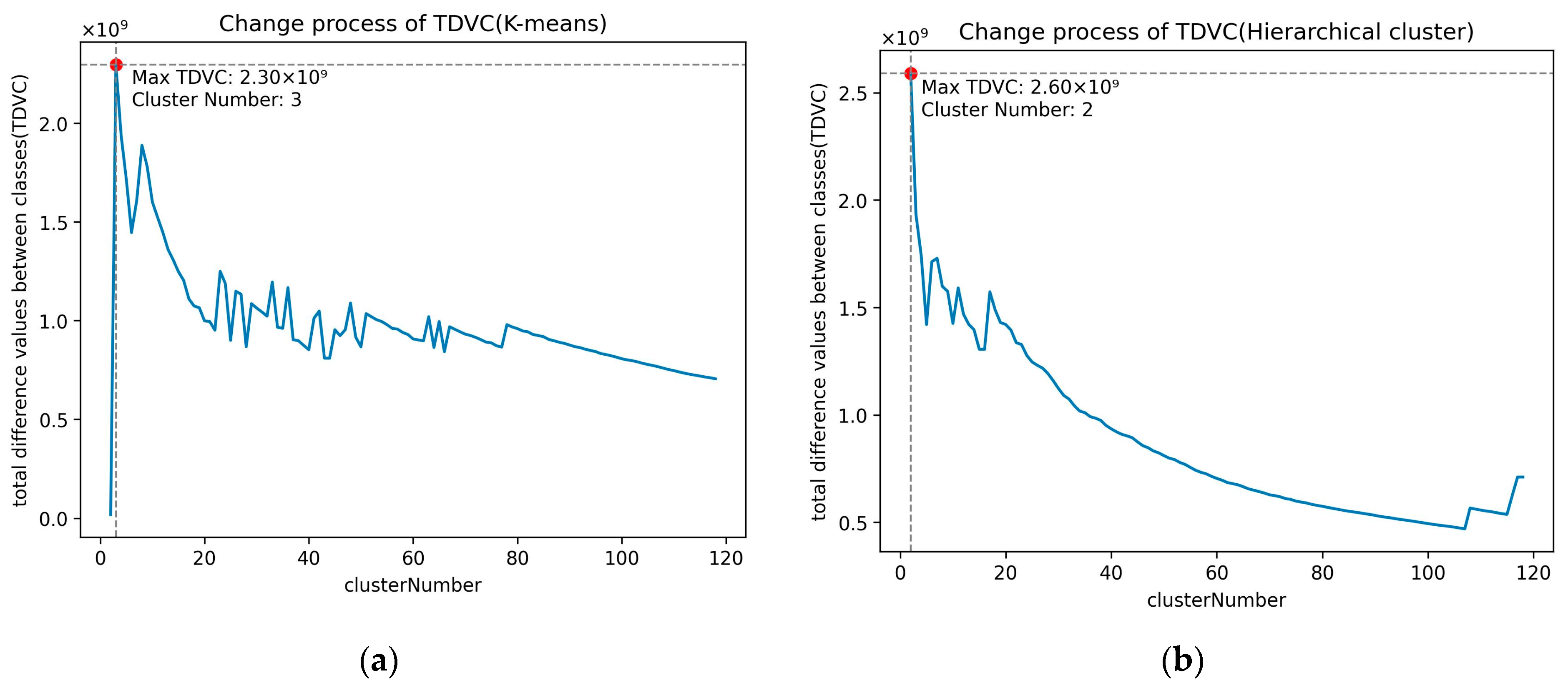
| Methods | FCM (This Method) | K-Means | Hierarchical Clustering | DBSCAN |
|---|---|---|---|---|
| Maximum TDVC | 2.6692 × 109 | 2.2973 × 109 | 2.5907 × 109 | 5.3945 × 107 |
| Corresponding cluster number | 14 | 3 | 2 | - |
| Methods | Key Vulnerability Node | Target Nodes Reachability | Number of Remaining Attack Paths |
|---|---|---|---|
| This paper | (92,141,152,189,215,217) | unreachable | 0 |
| [35] | (32,37,130,190,215) | reachable | 79,983 |
| [36] | (141,189,217) | reachable | 635 |
| [37] | (92,141,189,215,217) | reachable | 13 |
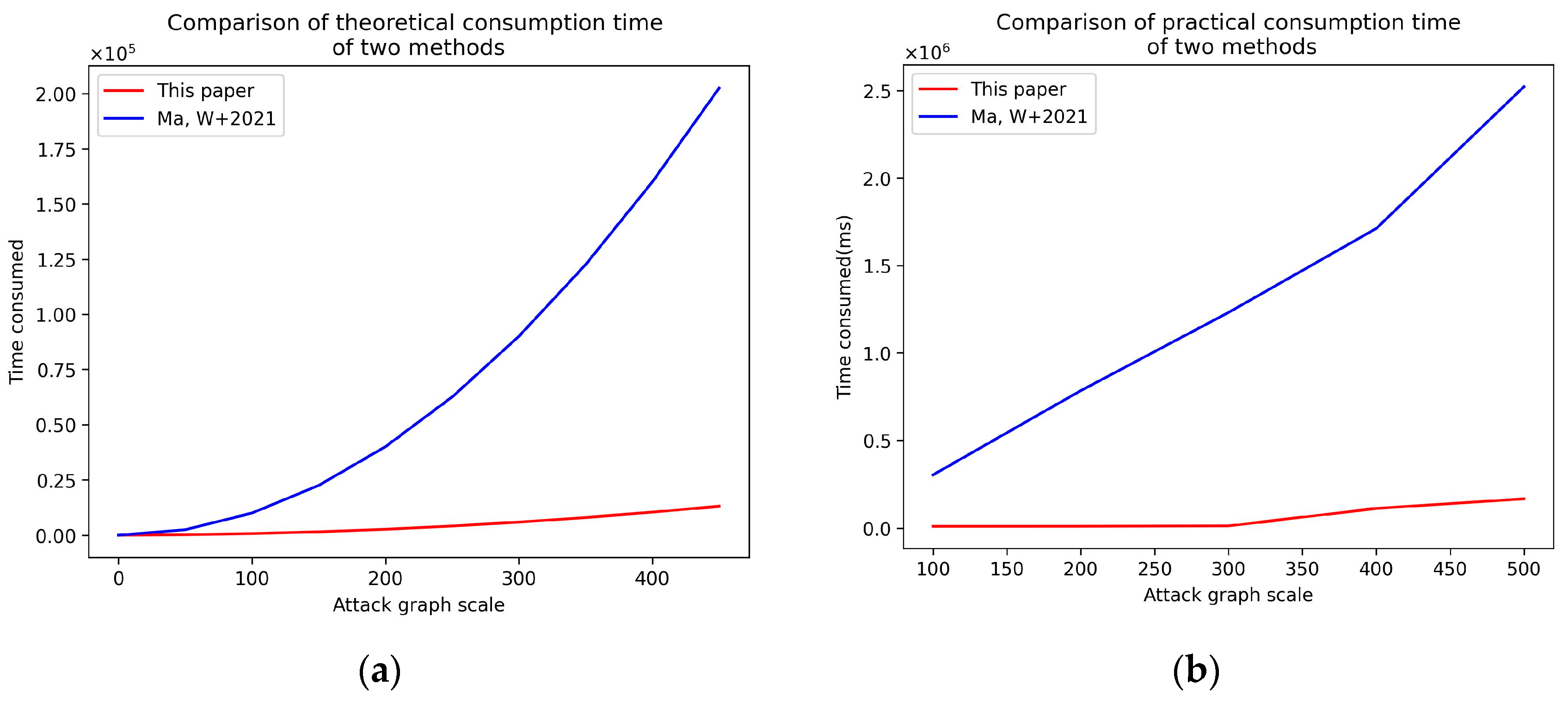
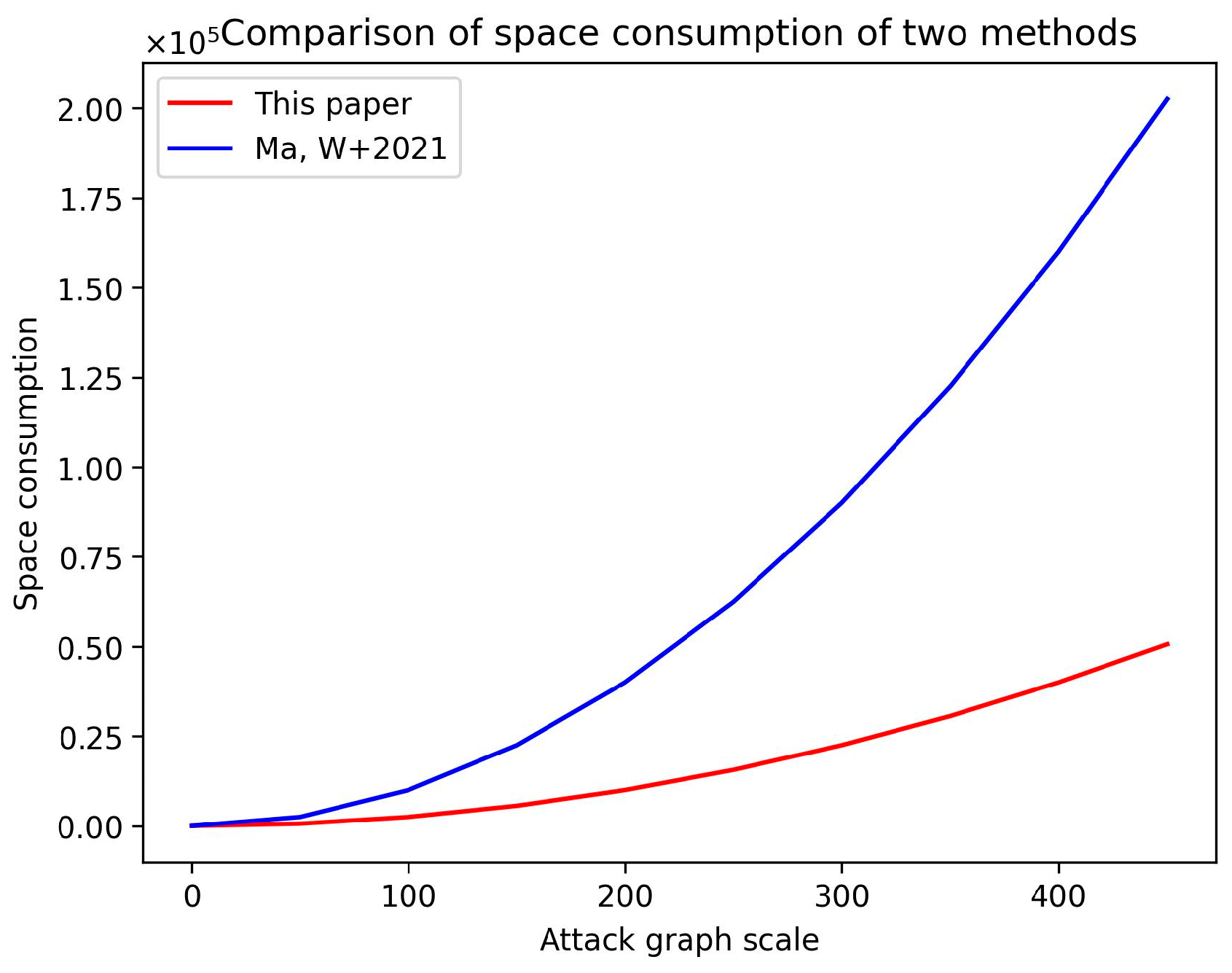
| Methods | Time Optimization | Space Optimization | Consider Vulnerability Features | Consider Actual Features | Consider All Paths | Adaptive Adjustment of Cluster Number | Get Key Vulnerabilities |
|---|---|---|---|---|---|---|---|
| [19] | Yes | No | Yes | Yes | Yes | No | No |
| [29] | Yes | No | Yes | No | No | No | Yes |
| [31] | No | No | Yes | No | Yes | No | Yes |
| [35] | No | No | Yes | No | No | No | Yes |
| [36] | Yes | No | Yes | Yes | No | No | Yes |
| This paper | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Liu, Y.; Sun, Z.; Xue, Y.; Liao, W.; Liu, C.; Sun, Z. Key Vulnerable Nodes Discovery Based on Bayesian Attack Subgraphs and Improved Fuzzy C-Means Clustering. Mathematics 2024, 12, 1447. https://doi.org/10.3390/math12101447
Xu Y, Liu Y, Sun Z, Xue Y, Liao W, Liu C, Sun Z. Key Vulnerable Nodes Discovery Based on Bayesian Attack Subgraphs and Improved Fuzzy C-Means Clustering. Mathematics. 2024; 12(10):1447. https://doi.org/10.3390/math12101447
Chicago/Turabian StyleXu, Yuhua, Yang Liu, Zhixin Sun, Yucheng Xue, Weiliang Liao, Chenlei Liu, and Zhe Sun. 2024. "Key Vulnerable Nodes Discovery Based on Bayesian Attack Subgraphs and Improved Fuzzy C-Means Clustering" Mathematics 12, no. 10: 1447. https://doi.org/10.3390/math12101447
APA StyleXu, Y., Liu, Y., Sun, Z., Xue, Y., Liao, W., Liu, C., & Sun, Z. (2024). Key Vulnerable Nodes Discovery Based on Bayesian Attack Subgraphs and Improved Fuzzy C-Means Clustering. Mathematics, 12(10), 1447. https://doi.org/10.3390/math12101447






