A New Family of Archimedean Copulas: The Half-Logistic Family of Copulas
Abstract
:1. Introduction
2. The Half-Logistic Copula
- i.
- The product copula is a limit case of the half-logistic copula when θ approaches zero.
- ii.
- The Fréchet–Hoeffding upper bound copula is a limit case of the half-logistic copula when θ tends to infinity.
3. Dependence
- i.
- Stochastically increasing, thus left-tail decreasing and right-tail increasing, hence positive quadrant-dependent;
- ii.
- is , and the survival copula is also ;
- iii.
- , where denotes Spearman’s rho correlation coefficient;
- iv.
- .
4. The Two-Parameter Half-logistic Copula
- is strictly increasing, because its first derivative is positive for all .
- is log-concave. Asis decreasing in s.
- and .
5. Applications
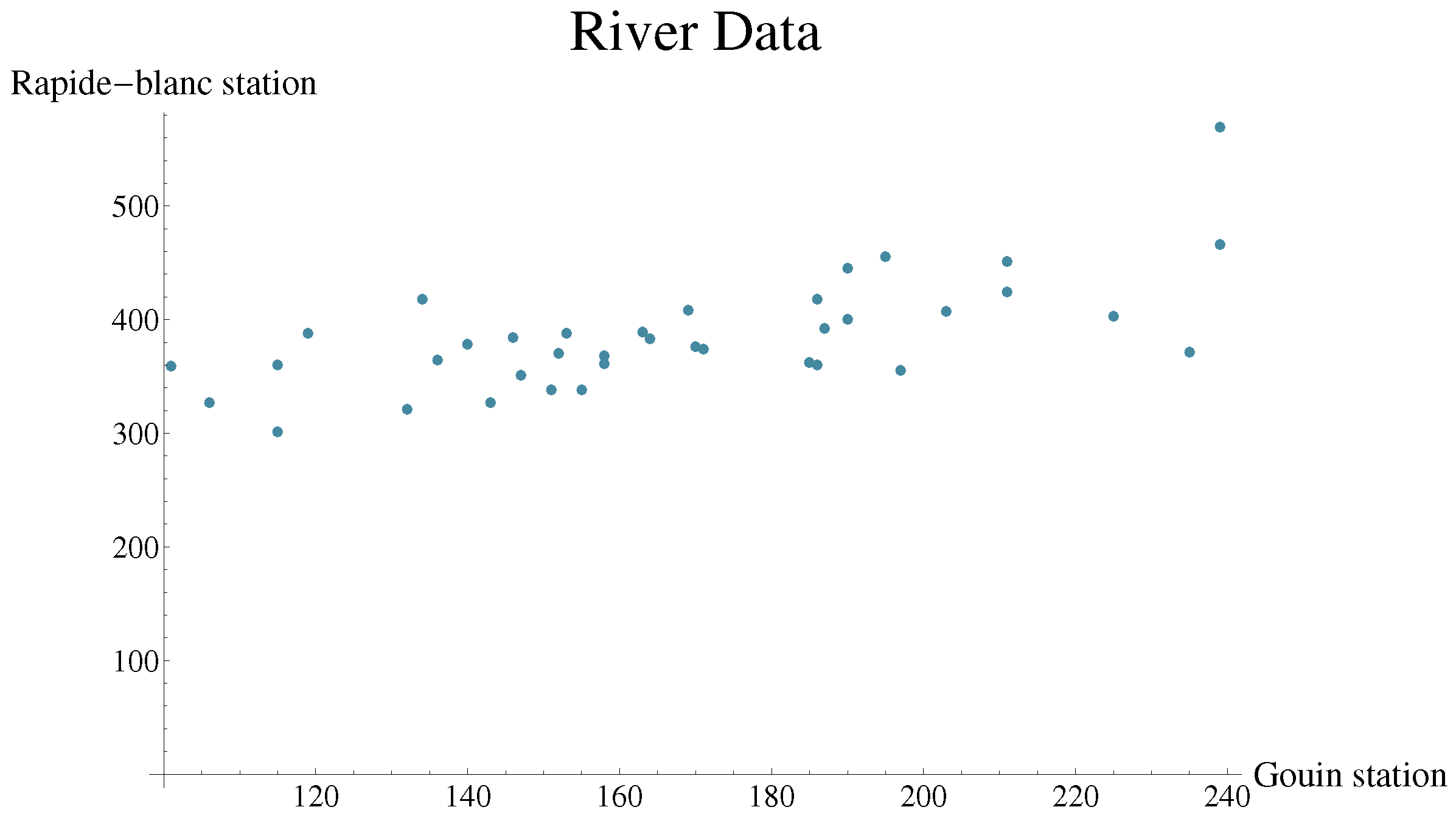
5.1. St-Maurice’s River Annual Flow Data
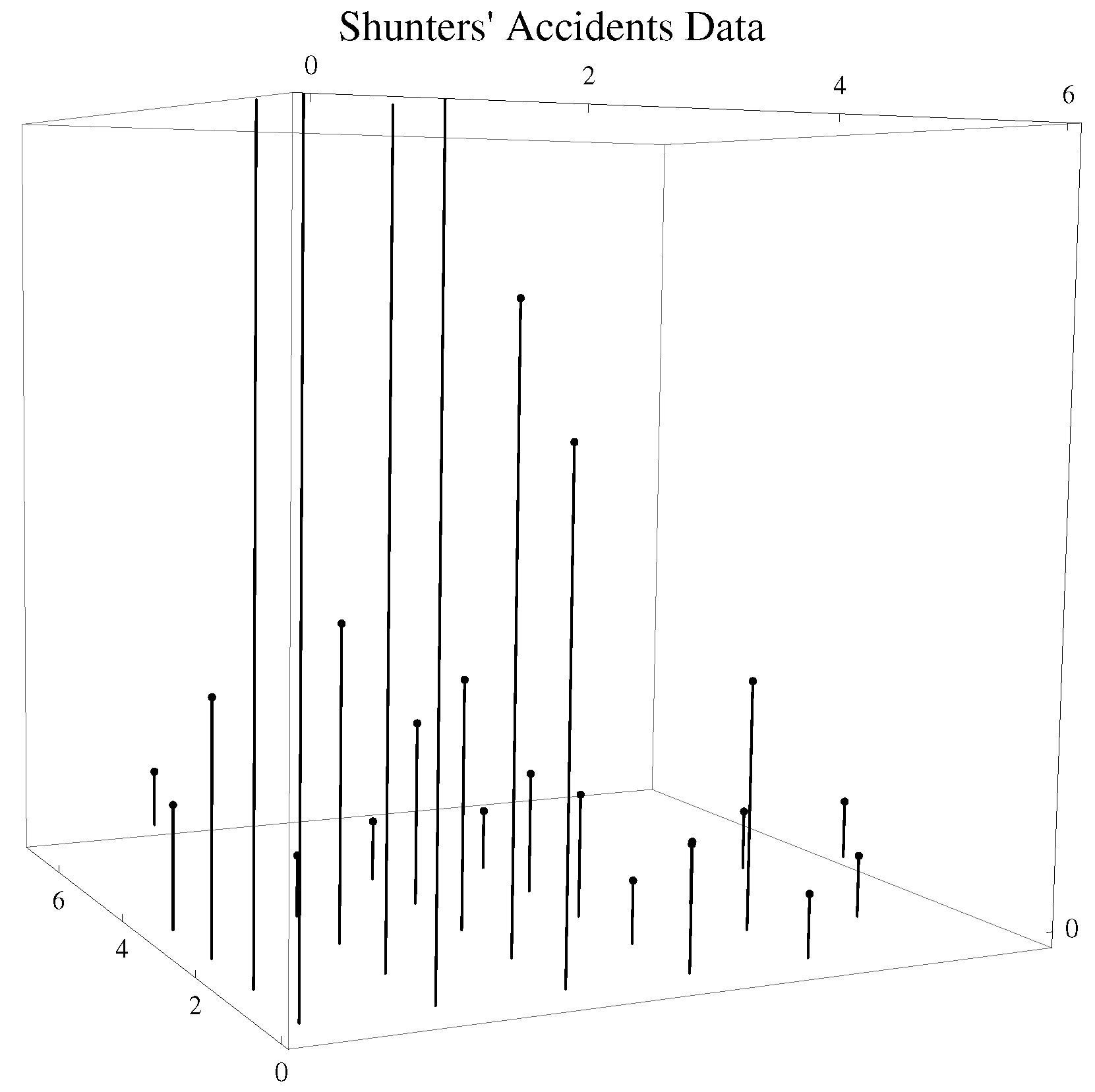
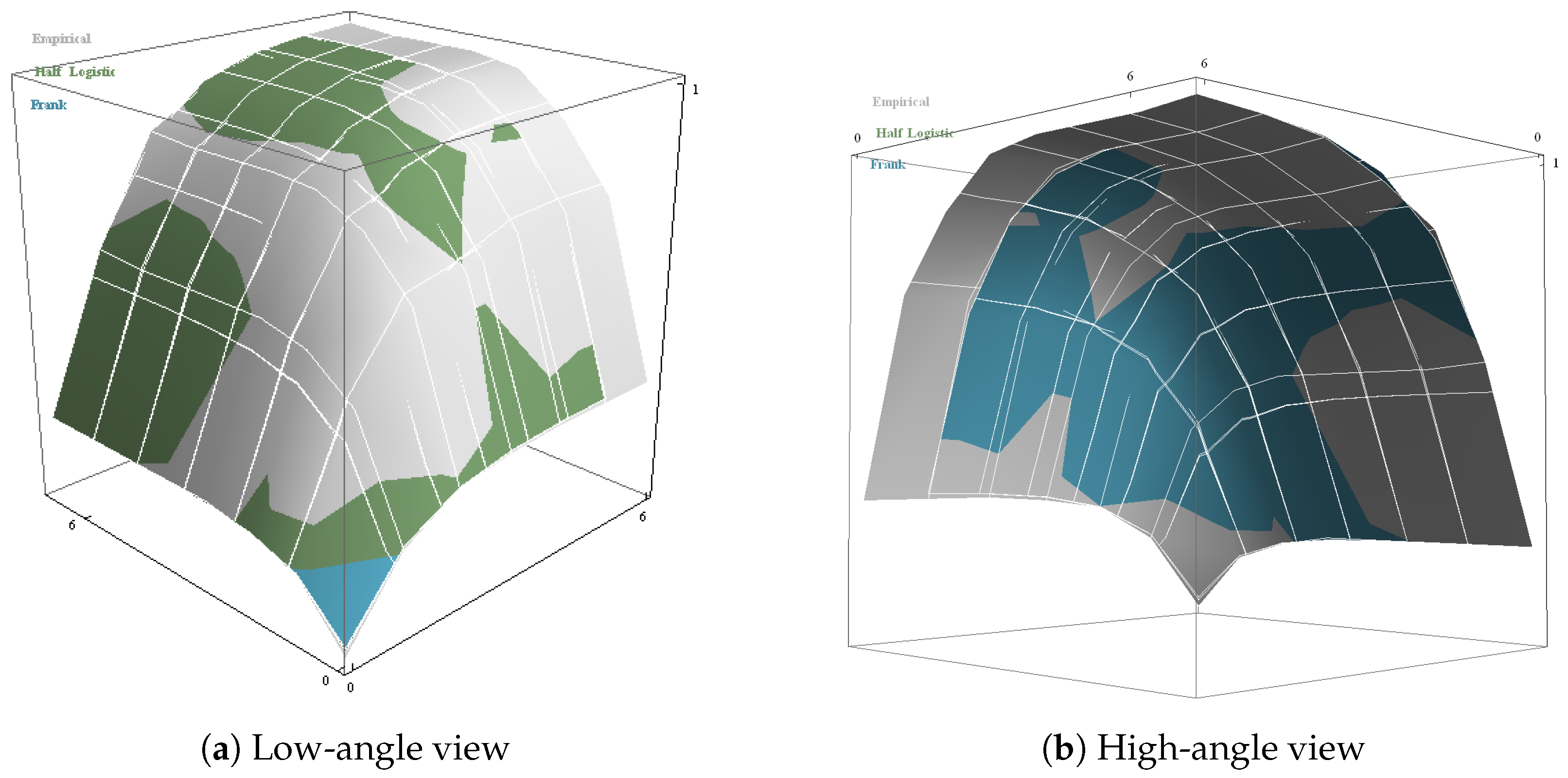
5.2. Shunters’ Accidents Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proofs
Appendix A.1. Proof of Theorem 3
- i.
- To prove this, we use (Nelsen [16], Theorem 4.4.7, p. 139). The multiplicative Archimedean generator of the product copula is ; thus, the product copula will be the limit of at if We haveTherefore,
- ii.
- To prove this, assume . Therefore, we havewhere . Hence, .
Appendix A.2. Proof of Theorem 4
Appendix A.3. Proof of Theorem 5
Appendix A.4. Proof of Theorem 6
Appendix A.5. Proof of Theorem 7
Appendix A.6. Proof of Theorem 8
References
- Émile, M.; Gumbel, J. Distributions des valeurs extrêmes en plusieurs dimensions. Ann. l’ISUP 1960, 9, 171–173. [Google Scholar]
- Hougaard, P. A class of multivanate failure time distributions. Biometrika 1986, 73, 671–678. [Google Scholar] [CrossRef]
- Clayton, D.G. A model for association in bivariate life tables and its application in epidemiological studies of familial tendency in chronic disease incidence. Biometrika 1978, 65, 141–151. [Google Scholar] [CrossRef]
- Ali, M.M.; Mikhail, N.; Haq, M.S. A class of bivariate distributions including the bivariate logistic. J. Multivar. Anal. 1978, 8, 405–412. [Google Scholar] [CrossRef]
- Frank, M.J. On the simultaneous associativity of F(x,y) and x+y-F(x,y). Aequationes Math. 1979, 19, 194–226. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. Families of multivariate distributions. J. Am. Stat. Assoc. 1988, 83, 834–841. [Google Scholar] [CrossRef]
- Genest, C.; MacKay, R.J. Copules Archimédiennes et families de lois bidimensionnelles dont les marges sont données. Can. J. Stat. 1986, 14, 145–159. [Google Scholar] [CrossRef]
- Genest, C.; Rivest, L.P. Statistical inference procedures for bivariate Archimedean copulas. J. Am. Stat. Assoc. 1993, 88, 1034–1043. [Google Scholar] [CrossRef]
- Smith, M.D. Modelling sample selection using Archimedean copulas. Econom. J. 2003, 6, 99–123. [Google Scholar] [CrossRef]
- Genest, C.; Quessy, J.F.; Rémillard, B. Goodness-of-fit procedures for copula models based on the probability integral transformation. Scand. J. Stat. 2006, 33, 337–366. [Google Scholar] [CrossRef]
- Durante, F.; Quesada-Molina, J.J.; Sempi, C. A generalization of the Archimedean class of bivariate copulas. Ann. Inst. Stat. Math. 2007, 59, 487–498. [Google Scholar] [CrossRef]
- Michiels, F.; Koch, I.; De Schepper, A. A new method for the construction of bivariate Archimedean copulas based on the λ function. Commun. Stat. Theory Methods 2011, 40, 2670–2679. [Google Scholar] [CrossRef]
- Wysocki, W. Constructing Archimedean copulas from diagonal sections. Stat. Probab. Lett. 2012, 82, 818–826. [Google Scholar] [CrossRef]
- Alhadlaq, W.; Alzaid, A. Distribution function, probability generating function and Archimedean generator. Symmetry 2020, 12, 2108. [Google Scholar] [CrossRef]
- Alzaid, A.A.; Alhadlaq, W.M. A new family of Archimedean copulas: The truncated-Poisson family of copulas. Bull. Malay. Math. Sci. Soc. 2022, 45, 477–504. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Balakrishnan, N.; Puthenpura, S. Best linear unbiased estimators of location and scale parameters of the half logistic distribution. J. Stat. Comput. Simul. 1986, 25, 193–204. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Wong, K.H.T. Approximate MLEs for the location and scale parameters of the half-logistic distribution with Type-II right-censoring. IEEE Trans. Reliab. 1991, 40, 140–145. [Google Scholar] [CrossRef]
- Torabi, H.; Bagheri, F. Estimation of parameters for an extended generalized half logistic distribution based on complete and censored data. J. Iran. Stat. Soc. 2010, 23, 1249–1257. [Google Scholar]
- Olapade, A.K. The type I generalized half logistic distribution. J. Iran. Stat. Soc. 2014, 13, 69–82. [Google Scholar]
- Samuel, A.F.; Kehinde, O.A. A study on transmuted half logistic distribution: Properties and application. Int. J. Stat. Distrib. Appl. 2019, 5, 54. [Google Scholar]
- Oluwatobi, A.P.; Portharcourt, O. Assessment of the Survival Time of Oral Cancer Patient in Nigeria Using the Beta Half Logistic Distribution; Research Proposal; Department Ofmathematics, University of Portharcourt: Portharcourt, Nigeria, 2017. [Google Scholar]
- Awodutire, P.O.; Olapade, A.K.; Kolawole, O.A.; Ilori, O.R. Assessing survival times of breast cancer patients using type I generalized half logistic survival model. J. Adv. Med. Med Res. 2018, 25, 1–7. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Asgharzadeh, A. Inference for the scaled half-logistic distribution based on progressively Type-II censored samples. Commun. Stat.-Theory Methods 2005, 34, 73–87. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Saleh, H.M. Relations for moments of progressively Type-II censored order statistics from half-logistic distribution with applications to inference. Comput. Stat. Data Anal. 2011, 55, 2775–2792. [Google Scholar] [CrossRef]
- Seo, J.I.; Kim, Y.; Kang, S.B. Estimation on the generalized half logistic distribution under Type-II hybrid censoring. Commun. Stat. Appl. Methods 2013, 20, 63–75. [Google Scholar] [CrossRef]
- Genest, C.; Rivest, L.P. On the multivariate probability integral transformation. Stat. Probab. Lett. 2001, 53, 391–399. [Google Scholar] [CrossRef]
- Nelsen, R.B.; Quesada-Molina, J.J.; Rodriguez-Lallena, J.A.; Ubeda-Flores, M. Kendall distribution functions. Stat. Probab. Lett. 2003, 65, 263–268. [Google Scholar] [CrossRef]
- Karlin, S. Total Positivity; Stanford University Press: Redwood City, CA, USA, 1968; Volume 1. [Google Scholar]
- Joe, H. Multivariate Models and Dependence Concepts; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Joe, H. Dependence Modeling with Copulas; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Chen, X.; Fan, Y. Pseudo-likelihood ratio tests for semiparametric multivariate copula model selection. Can. J. Stat. 2005, 33, 389–414. [Google Scholar] [CrossRef]
- Genest, C.; Boies, J.C. Detecting dependence with Kendall plots. Am. Stat. 2003, 57, 275–284. [Google Scholar] [CrossRef]
- Genest, C.; Rémillard, B.; Beaudoin, D. Goodness-of-fit tests for copulas: A review and a power study. Insur. Math. Econ. 2009, 44, 199–213. [Google Scholar] [CrossRef]
- Mesfioui, M.; Quessy, J.F.; Toupin, M.H. On a new goodness-of-fit process for families of copulas. Can. J. Stat. 2009, 37, 80–101. [Google Scholar] [CrossRef]
- Arbous, A.G.; Kerrich, J.E. Accident statistics and the concept of accident-proneness. Biometrics 1951, 7, 340–432. [Google Scholar] [CrossRef]
- Kocherlakota, S.; Kocherlakota, K. Bivariate Discrete Distributions; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Barbiero, A. A bivariate count model with discrete Weibull margins. Math. Comput. Simul. 2019, 156, 91–109. [Google Scholar] [CrossRef]
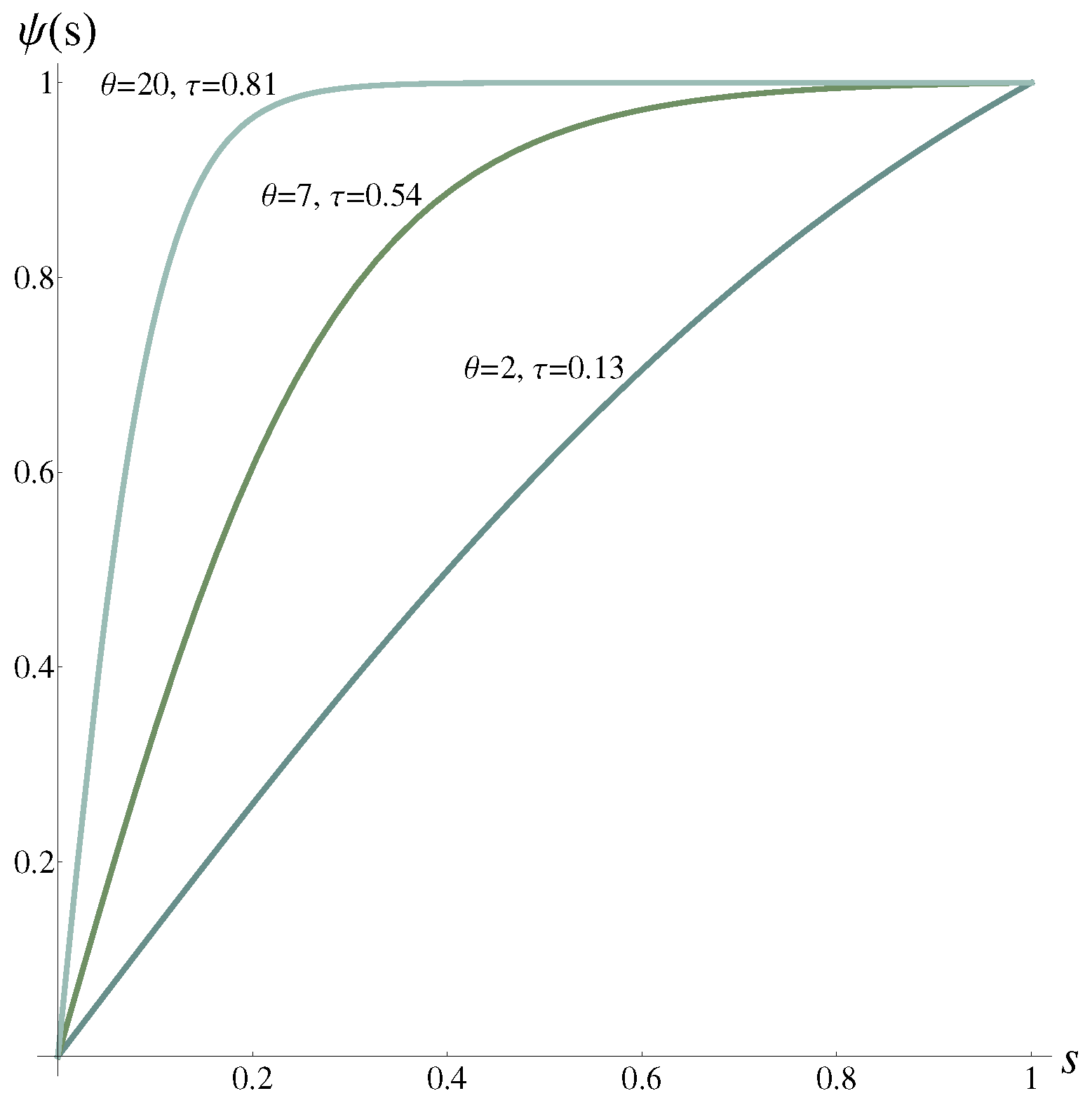




| Copula | Kendall’s Estimator | MLE | ||
|---|---|---|---|---|
| (p-Value) | (p-Value) | (p-Value) | (p-Value) | |
| Half-logistic | 0.0964 (0.21) | 0.8251 (0.03) | 0.0971 (0.19) | 0.8288 (0.52) |
| Frank | 0.0790 (0.34) | 0.7253 (0.08) | 0.0788 (0.43) | 0.7238 (0.07) |
| Clayton | 0.0879 (0.25) | 0.2494 (0.84) | 0.4488 (0.03) | 1.0006 (0.05) |
| Gumbel–Hougaard | 0.0688 (0.45) | 0.7571 (0.05) | 0.0573 (0.71) | 0.7068 (0.05) |
| Product | 0.9679 (0.00) | 1.4608 (0.00) | ||
| Copula | AIC | BIC | ||||||
|---|---|---|---|---|---|---|---|---|
| Half-logistic | 767.2 | 775.4 | 5.113 | 0.227 | 5.949 | 0.121 | 6.036 | |
| Survival half-logistic | 775.2 | 783.4 | 5.090 | 0.247 | 5.937 | 0.130 | 7.166 | |
| Frank | 767 | 775.1 | 5.116 | 0.226 | 5.952 | 0.119 | 5.515 | |
| Clayton | 773.9 | 782.1 | 5.105 | 0.235 | 5.952 | 0.119 | 1.073 | |
| Gumbel–Hougaard | 769.6 | 777.8 | 5.101 | 0.216 | 5.951 | 0.125 | 0.421 | |
| Two-parameter half-logistic | 769 | 778.8 | 5.116 | 0.226 | 5.952 | 0.120 | 5.581 | 0.101 |
| Model | AIC | BIC | ||
|---|---|---|---|---|
| FGM | 686.1 | 688.9 | 0.957 | |
| Frank | 686 | 688.8 | 2.030 | |
| Truncated Poisson | 690 | 692.8 | 5.861 | |
| Half-logistic | 685.2 | 688 | 2.703 | |
| Survival half-logistic | 736.4 | 739.2 | 4.503 | |
| Two-parameter half-logistic | 686.8 | 692.4 | 3.401 | 3.008 |
| Model | Absolute Distance | Squared Distance |
|---|---|---|
| Frank | 0.538 | 0.006 |
| Half-logistic | 0.486 | 0.005 |
| Truncated Poisson | 0.551 | 0.007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alzaid, A.A.; Alhadlaq, W.M. A New Family of Archimedean Copulas: The Half-Logistic Family of Copulas. Mathematics 2024, 12, 101. https://doi.org/10.3390/math12010101
Alzaid AA, Alhadlaq WM. A New Family of Archimedean Copulas: The Half-Logistic Family of Copulas. Mathematics. 2024; 12(1):101. https://doi.org/10.3390/math12010101
Chicago/Turabian StyleAlzaid, Abdulhamid A., and Weaam M. Alhadlaq. 2024. "A New Family of Archimedean Copulas: The Half-Logistic Family of Copulas" Mathematics 12, no. 1: 101. https://doi.org/10.3390/math12010101
APA StyleAlzaid, A. A., & Alhadlaq, W. M. (2024). A New Family of Archimedean Copulas: The Half-Logistic Family of Copulas. Mathematics, 12(1), 101. https://doi.org/10.3390/math12010101






