The Gibbons, Ross, and Shanken Test for Portfolio Efficiency: A Note Based on Its Trigonometric Properties
Abstract
1. Introduction
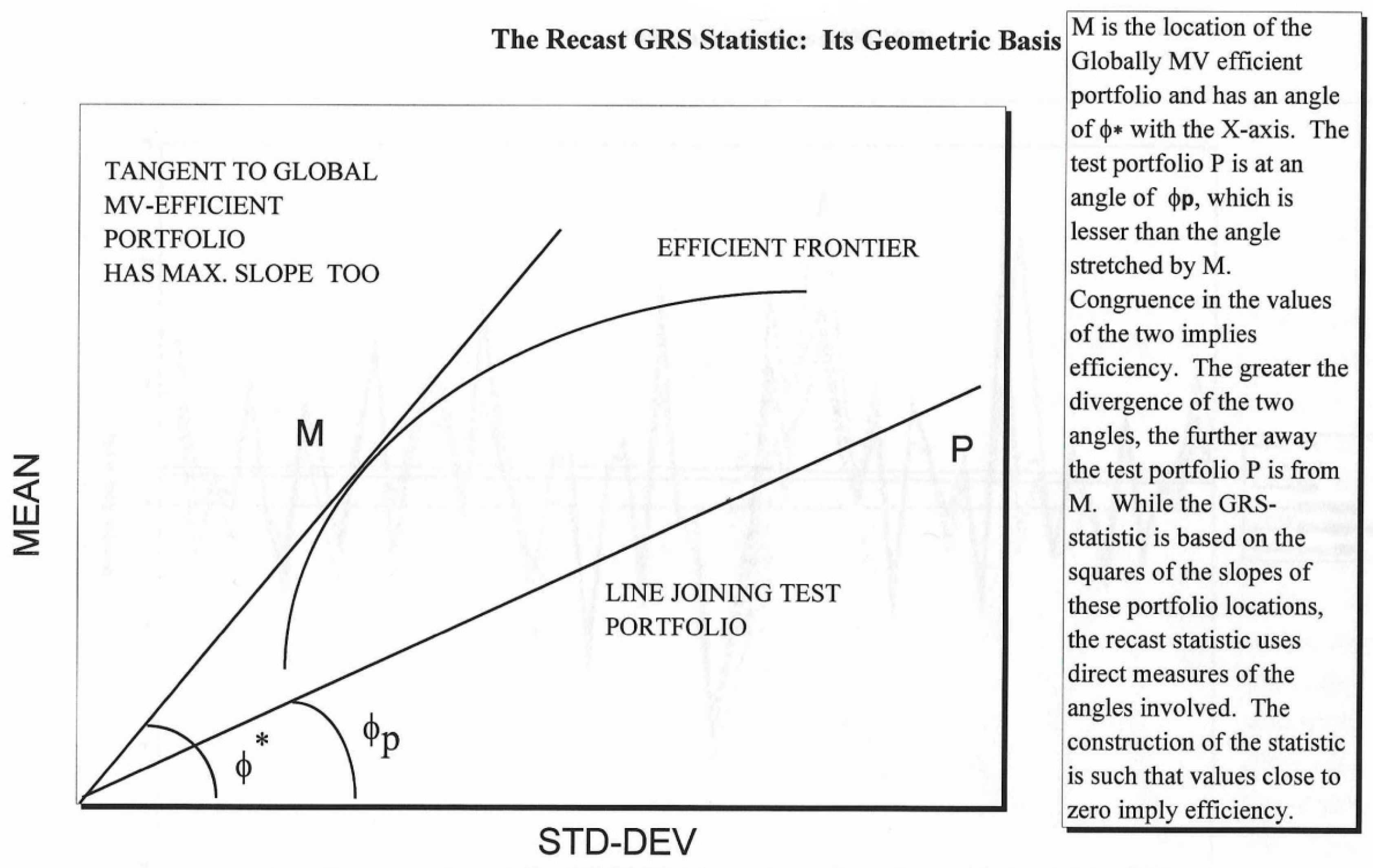
2. The Gibbons, Ross, and Shanken Test Statistic and Its Relevance
3. Suggested Recharacterization of the GRS-Statistic
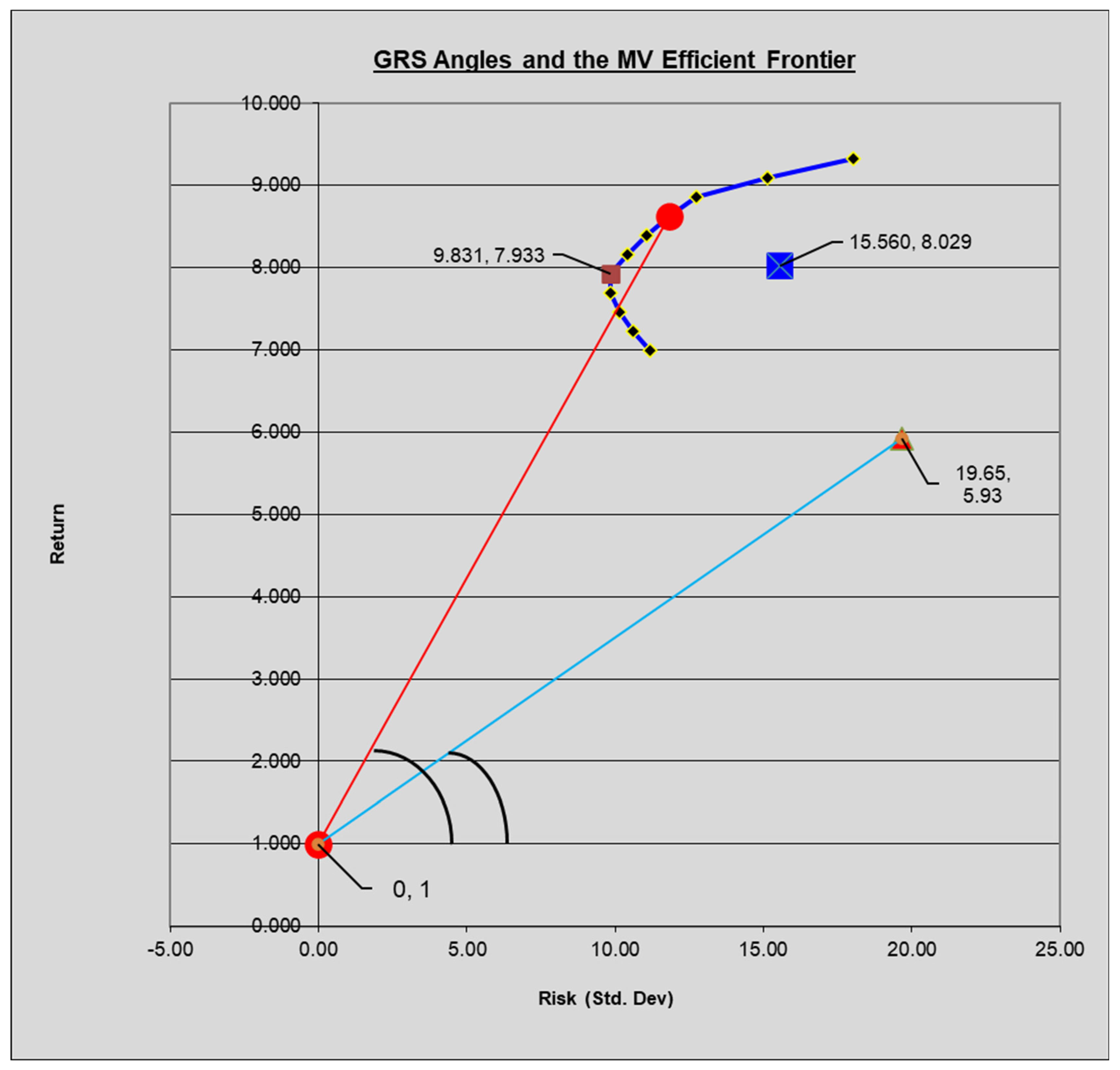
4. A Simulated Efficient Frontier and a Test of Portfolio Efficiency
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. The Kuhn-Tucker [41] Saddle Point Theorem

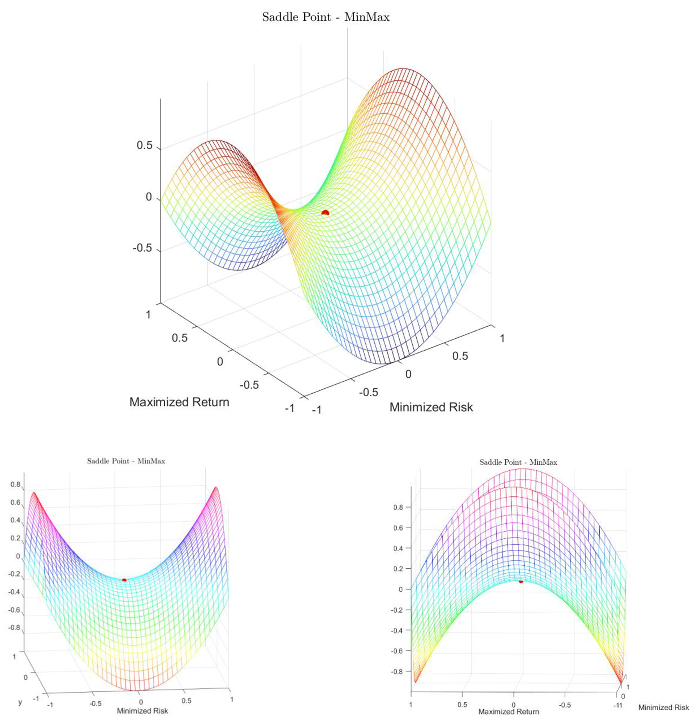
Appendix A.2. Polar Plot of the Table of Sharpe Ratios and the GRS−W Statistic
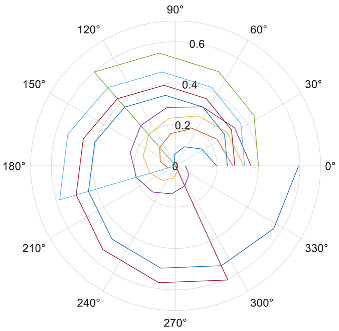
| GRS~W Stat | θ = (r − rf)/s | ||||||||
| r\s | 10 | 12 | 14 | 16 | 10 | 12 | 14 | 16 | s/r |
| 5 | 0.198 | 0.276 | 0.328 | 0.364 | 0.4 | 0.333 | 0.286 | 0.25 | 5 |
| 5.5 | 0.15 | 0.2374 | 0.297 | 0.339 | 0.45 | 0.375 | 0.321 | 0.281 | 5.5 |
| 6 | 0.101 | 0.198 | 0.265 | 0.313 | 0.5 | 0.417 | 0.357 | 0.313 | 6 |
| 6.5 | 0.053 | 0.158 | 0.232 | 0.285 | 0.55 | 0.458 | 0.393 | 0.344 | 6.5 |
| 7 | 0.005 | 0.117 | 0.198 | 0.257 | 0.6 | 0.5 | 0.429 | 0.375 | 7 |
| 7.5 | 0.077 | 0.163 | 0.228 | 0.542 | 0.464 | 0.406 | 7.5 | ||
| 8 | 0.037 | 0.129 | 0.198 | 0.583 | 0.5 | 0.438 | 8 | ||
| 8.5 | 0.094 | 0.168 | 0.536 | 0.469 | 8.5 | ||||
| 9 | 0.06 | 0.137 | 0.571 | 0.5 | 9 | ||||
| 9.5 | 0.025 | 0.107 | 0.607 | 0.531 | 9.5 | ||||
| 10 | 0.077 | 0.563 | 10 | ||||||
| 10.5 | 0.047 | 0.594 | 10.5 | ||||||
Appendix A.3. Values of the GRS-W Statistic for a Range of Angles
| Test Port | |||||||||||||
| ANGLE | 0 | 10 | 20 | 30 | 40 | 45 | 50 | 60 | 70 | 80 | 90 | ||
| mkt tangency port | cosine (xo) | 1.00 | 0.98 | 0.94 | 0.87 | 0.77 | 0.71 | 0.64 | 0.50 | 0.34 | 0.17 | 0.00 | |
| 0 | 1.00 | 0.000 | |||||||||||
| 10 | 0.98 | 0.031 | 0.000 | ||||||||||
| 20 | 0.94 | 0.132 | 0.098 | 0.000 | |||||||||
| 30 | 0.87 | 0.333 | 0.293 | 0.177 | 0.000 | ||||||||
| 40 | 0.77 | 0.704 | 0.653 | 0.505 | 0.278 | 0.000 | |||||||
| 45 | 0.71 | 1.000 | 0.940 | 0.766 | 0.500 | 0.174 | 0.000 | ||||||
| 50 | 0.64 | 1.420 | 1.347 | 1.137 | 0.815 | 0.420 | 0.210 | 0.000 | |||||
| 60 | 0.50 | 3.000 | 2.879 | 2.532 | 2.000 | 1.347 | 1.000 | 0.653 | 0.000 | ||||
| 70 | 0.34 | 7.549 | 7.291 | 6.549 | 5.411 | 4.017 | 3.274 | 2.532 | 1.137 | 0.000 | |||
| 80 | 0.17 | 32.163 | 31.163 | 28.284 | 23.873 | 18.461 | 15.582 | 12.702 | 7.291 | 2.879 | 0.000 | ||
| 90 | 0.00 | 2.6,10+32 | 2.58,10+32 | 2.35,10+32 | 1.99,10+32 | 1.56,10+32 | 1.33,10+32 | 1.10,10+32 | 6.66,10+31 | 3.12,10+31 | 8.04,10+30 | 0.000 | |
Appendix A.4. Risk Parity: Avoiding the Problem of Error Maximization in a Mean-Variance Optimization Framework
Appendix A.5. Risk Parity: Efficient Portfolio Zone as a Floating Hyperplane, the Tangency Portfolio and the GRS-W Statisctic Gradient -3D Efficient Frontier with Actual ETFs

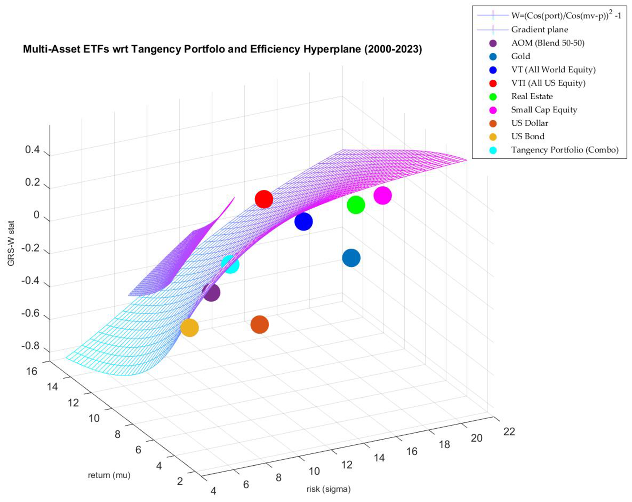
References
- Gibbons, M.R.; Ross, S.; Shanken, J. A Test of the Efficiency of the Given Portfolio. Econometrica 1989, 57, 1121–1152. [Google Scholar] [CrossRef]
- Galea, M.; Cademartori, D.; Curci, R.; Molina, A. Robust Inference in the Capital Asset Pricing Model Using the Multivariate t-distribution. J. Risk Financ. Manag. 2020, 13, 123. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. A five-factor asset pricing model. J. Financ. Econ. 2015, 116, 1–22. [Google Scholar]
- Gustafson, K. Operator Trigonometry of Multivariate Finance. J. Multivar. Anal. 2010, 101, 374–384. [Google Scholar] [CrossRef]
- Gustafson, K. A New Financial Risk Ratio. J. Stat. Comput. Simul. 2015, 85, 2682–2692. [Google Scholar] [CrossRef]
- Rodriguez, R.J. Graphical Portfolio Analysis. Financ. Rev. 1996, 31, 869–884. [Google Scholar]
- Roll, R. A critique of the asset pricing theory’s tests Part I: On past and potential testability of the theory. J. Financ. Econ. 1977, 4, 129–176. [Google Scholar] [CrossRef]
- Chen, J.M. The Capital Asset Pricing Model. Encyclopedia 2021, 1, 915–933. [Google Scholar] [CrossRef]
- Hu, S.; Li, D.; Jia, J.; Liu, Y. A Self-Learning Based Preference Model for Portfolio Optimization. Mathematics 2021, 9, 2621. [Google Scholar] [CrossRef]
- Bodnar, T.; Schmid, W. Econometrical analysis of the sample efficient frontier. Eur. J. Financ. 2009, 15, 317–335. [Google Scholar] [CrossRef]
- Cueto, J.M.; Grané, A.; Cascos, I. How to Explain the Cross-Section of Equity Returns through Common Principal Components. Mathematics 2021, 9, 1011. [Google Scholar] [CrossRef]
- Ryan, N.; Ruan, X.; Zhang, J.E.; Zhang, J.A. Choosing Factors for the Vietnamese Stock Market. J. Risk Financ. Manag. 2021, 14, 96. [Google Scholar] [CrossRef]
- Suárez, J.; Alonso-Conde, A.B. Relative Entropy and Minimum-Variance Pricing Kernel in Asset Pricing Model Evaluation. Entropy 2020, 22, 721. [Google Scholar] [CrossRef] [PubMed]
- Solórzano-Taborga, P.; Alonso-Conde, A.B.; Rojo-Suárez, J. Data Envelopment Analysis and Multifactor Asset Pricing Models. Int. J. Financ. Stud. 2020, 8, 24. [Google Scholar] [CrossRef]
- Barillas, F.; Kan, R.; Robotti, C.; Shanken, J. Model Comparison with Sharpe Ratios. J. Financ. Quant. Anal. 2020, 55, 1840–1874. [Google Scholar] [CrossRef]
- Sharpe, W.F. Mutual Fund Performance. J. Bus. 1966, 39, 119–138. Available online: http://www.jstor.org/stable/2351741 (accessed on 1 March 2023). [CrossRef]
- Kamstra, M.; Shi, R. A Note on the GRS Test; Technical Report; Department of Economics, University of California at Riverside: Riverside, CA, USA, 2021. [Google Scholar]
- Fletcher, J. An Empirical Examination of the Incremental Contribution of Stock Characteristics in UK Stock Returns. Int. J. Financ. Stud. 2017, 5, 21. [Google Scholar] [CrossRef]
- Vigo-Pereira, C.; Laurini, M. Portfolio Efficiency Tests with Conditioning Information—Comparing GMM and GEL Estimators. Entropy 2022, 24, 1705. [Google Scholar] [CrossRef]
- Basak, G.K.; Jagannathan, R.; Sun, G. A Direct Test for the Mean Variance Efficiency of a Portfolio. J. Econ. Dyn. Control 2002, 26, 1195–1215. [Google Scholar] [CrossRef]
- Kim, J.H.; Robinson, A.P. Interval-Based Hypothesis Testing and Its Applications to Economics and Finance. Econometrics 2019, 7, 21. [Google Scholar] [CrossRef]
- Shanken, J. 23 Statistical methods in tests of portfolio efficiency: A synthesis. Handb. Stat. 1996, 14, 693–711. [Google Scholar] [CrossRef]
- MacKinlay, A.C. Multifactor models do not explain deviations from the CAPM. J. Financ. Econ. 1995, 38, 3–28. [Google Scholar] [CrossRef]
- Roll, R.; Ross, S.A. On the Cross-Sectional Relation between Expected Returns and Betas. J. Financ. 1994, 49, 101. [Google Scholar] [CrossRef]
- Zhou, G. Asset-pricing Tests under Alternative Distributions. J. Financ. 1993, 48, 1927–1942. [Google Scholar] [CrossRef]
- WRDS. CRSP Pricing Data on Stocks. Wharton Research Data Services. 2023. Available online: https://wrds-www.wharton.upenn.edu/ (accessed on 1 March 2023).
- Agrrawal, P. An automation algorithm for harvesting capital market information from the web. Manag. Financ. 2009, 35, 427–438. [Google Scholar]
- Bodnar, T.; Gupta, A.K.; Vitlinskyi, V.; Zabolotskyy, T. Statistical Inference for the Beta Coefficient. Risks 2019, 7, 56. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. Common risk factors in the returns on stocks and bonds. J. Financ. Econ. 1993, 33, 3–56. [Google Scholar] [CrossRef]
- Hou, K.G.; Karolyi, G.A.; Kho, B. What Factors Drive Global Stock Returns? Rev. Financ. Stud. 2011, 24, 2527–2574. [Google Scholar] [CrossRef]
- Ehsani, S.; Linnainmaa, J.T. Factor Momentum and the Momentum Factor. J. Financ. 2022, 77, 1877–1919. [Google Scholar] [CrossRef]
- Merton, R.C. An analytical derivation of the efficient frontier. J. Financ. Quant. Anal. 1972, 7, 1851–1872. [Google Scholar] [CrossRef]
- Gómez–Déniz, E.M.E.; Ghitany, M.E.; Gupta, R.C. A bivariate generalized geometric distribution with applications. Commun. Stat. Theory Methods 2017, 46, 5453–5465. [Google Scholar] [CrossRef]
- Danko, J.; Soltés, V.; Bindzar, T. Portfolio creation using graph characteristics and testing its performance. Montenegrin J. Econ. 2022, 18, 7–17. [Google Scholar] [CrossRef]
- MacKinlay, C.A.; Richardson, M. Using Generalized Method of Moments to Test Mean-Variance Efficiency. J. Financ. 1991, 46, 511–527. [Google Scholar] [CrossRef]
- Black, F. Capital Market Equilibrium with Restricted Borrowing. J. Bus. 1972, 45, 444–454. [Google Scholar]
- Buckle, D. The Impact of Options on Investment Portfolios in the Short-Run and the Long-Run, with a Focus on Downside Protection and Call Overwriting. Mathematics 2022, 10, 1563. [Google Scholar] [CrossRef]
- Best, M.J. Equivalence of some Quadratic Programming Algorithms. Math. Program. 1984, 30, 71–87. [Google Scholar] [CrossRef]
- Best, M.J.; Grauer, R.R. On the Sensitivity of Mean-Variance-Efficient Portfolios to Changes in Asset Means: Some Analytical and Computational Results. Rev. Financ. Stud. 1991, 42, 315–342. [Google Scholar]
- Lee, W. Risk On/Risk Off. J. Portf. Manag. 2012, 38, 28–39. [Google Scholar]
- Kuhn, H.W.; Tucker, A.W. Nonlinear programming. In Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability 1950, Berkeley, CA, USA, 31 July–12 August 1950; pp. 481–492. [Google Scholar]
- Greene, W.H. Econometric Analysis; Prentice Hall: Hoboken, NJ, USA, 2002; ISBN 10: 0130661899; ISBN 13: 9780130661890. [Google Scholar]
- Shefrin, H.M.; Statman, M. Behavioral Capital Asset Pricing Theory. J. Financ. Quant. Anal. 1994, 29, 323–349. [Google Scholar] [CrossRef]
- Glabadanidis, P. Another Test of the Efficiency of a Given Portfolio. SSRN Electron. J. 2015. [Google Scholar] [CrossRef]
- Jurdi, D.J. Predicting the Australian equity risk premium. Pac. Basin Financ. J. 2022, 71, 101683. [Google Scholar] [CrossRef]
- Agrrawal, P.; Gilbert, F.W.; Harkins, J. Time Dependence of CAPM Betas on the Choice of Interval Frequency and Return Timeframes: Is There an Optimum? J. Risk Financ. Manag. 2022, 15, 520. [Google Scholar] [CrossRef]
- Bazhutov, D.; Betzer, A.; Stehle, R. Beta estimation in the European network regulation context: What matters, what doesn’t, and what is indispensable. Financ. Mark. Portf. Manag. 2023. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. The Cross-Section of Expected Stock Returns. J. Financ. 1992, 47, 427–465. [Google Scholar] [CrossRef]
- Agrrawal, P. On Certain Aspects of the Ex Ante CAPM. Ph.D. Dissertation, University of Alabama, Tuscaloosa, AL, USA, 1996. [Google Scholar]
- Markowitz, H. Portfolio Selection. J. Financ. 1952, 7, 77–91. [Google Scholar] [CrossRef]
- Balbás, A.; Balbás, B.; Balbás, R. Minimizing measures of risk by saddle point conditions. J. Comput. Appl. Math. 2010, 234, 2924–2931. [Google Scholar] [CrossRef]
- Agrrawal, P. Using Index ETFs for Multi-Asset-Class Investing: Shifting the Efficient Frontier Up. J. Beta Investig. Strateg. 2013, 4, 83–94. [Google Scholar]
- Maillard, S.; Roncalli, T.; Teïletche, J. The Properties of Equally-Weighted Risk Contributions Portfolios. J. Portf. Manag. 2010, 36, 60–70. [Google Scholar] [CrossRef]
- Qian, E. On the Financial Interpretation of Risk Contribution: Risk Budgets Do Add Up. J. Investig. Manag. 2006, 4, 41–51. [Google Scholar] [CrossRef]
- Choueifaty, Y.; Coignard, Y. Toward Maximum Diversification. J. Portf. Manag. 2008, 35, 40–51. [Google Scholar] [CrossRef]
- Yu, Z. Cross-Section of Returns, Predictors Credibility, and Method Issues. J. Risk Financial Manag. 2023, 16, 34. [Google Scholar] [CrossRef]
- de Jong, M.; diBartolomeo, D. Multiple Alpha Sources and Portfolio Design. J. Asset Manag. 2021, 22, 389–390. [Google Scholar] [CrossRef]
- Stone, A.L.; Gup, B.E.; Lee, J. New insights about the relationship between corporate cash holdings and interest rates. J. Econ. Finan. 2018, 42, 33–65. [Google Scholar] [CrossRef]

| GRS~W Stat | θ = (r − rf)/s | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| r\s | 10.00 | 12.00 | 14.00 | 16.00 | 10.00 | 12.00 | 14.00 | 16.00 | s/r |
| 5.00 | 0.198 | 0.276 | 0.328 | 0.364 | 0.400 | 0.333 | 0.286 | 0.250 | 5.00 |
| 5.50 | 0.150 | 0.2374 | 0.297 | 0.339 | 0.450 | 0.375 | 0.321 | 0.281 | 5.50 |
| 6.00 | 0.101 | 0.198 | 0.265 | 0.313 | 0.500 | 0.417 | 0.357 | 0.313 | 6.00 |
| 6.50 | 0.053 | 0.158 | 0.232 | 0.285 | 0.550 | 0.458 | 0.393 | 0.344 | 6.50 |
| 7.00 | 0.005 | 0.117 | 0.198 | 0.257 | 0.600 | 0.500 | 0.429 | 0.375 | 7.00 |
| 7.50 | 0.077 | 0.163 | 0.228 | 0.542 | 0.464 | 0.406 | 7.50 | ||
| 8.00 | 0.037 | 0.129 | 0.198 | 0.583 | 0.500 | 0.438 | 8.00 | ||
| 8.50 | 0.094 | 0.168 | 0.536 | 0.469 | 8.50 | ||||
| 9.00 | 0.060 | 0.137 | 0.571 | 0.500 | 9.00 | ||||
| 9.50 | 0.025 | 0.107 | 0.607 | 0.531 | 9.50 | ||||
| 10.00 | 0.077 | 0.563 | 10.00 | ||||||
| 10.50 | 0.047 | 0.594 | 10.50 | ||||||
| Tangency Portfolio (*) | Test Portfolio (p) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| mean, r | 7.93 | 10.50 | |||||||
| risk free, rf | 1.00 | 1.00 | |||||||
| sigma, s | 9.83 | 8.00 | |||||||
| θ = (r − rf)/s | 0.705 | 1.188 | |||||||
| GRS~W Stat | 0.046 | ||||||||
| N | No. of Assets | 30 | |||||||
| T | No. of Weekly Intervals | 520 | |||||||
| XF | 0.759 | ||||||||
| p-value | Rej. H0 (is an Efficient Port) iff p~0 | 0.8202 | |||||||
| Mean, r | Sigma, s | θ = (r − rf)/s | GRS~W Stat | N | T | XF | p-Value | ||
| Tangency Portfolio (*) | 7.93 | 9.83 | 0.705 | No. of Assets | No. of Weekly Intervals | Rej. H0 (Efficient Port) iff p~0 | |||
| Test Portfolio (p) | 10.50 | 16.00 | 0.594 | 0.047 | 30 | 520 | 0.763 | 0.81564721900 | Eff. |
| Test Portfolio (p) | 3.00 | 10.00 | 0.2 | 0.3737 | 30 | 520 | 6.115 | 0.00000000000 | Not Efficient |
| Test Portfolio (p) | 5.00 | 10.00 | 0.400 | 0.198 | 30 | 520 | 3.238 | 0.00000004498 | Not Efficient |
| Test Portfolio (p) | 5.50 | 10.00 | 0.450 | 0.150 | 30 | 520 | 2.448 | 0.00004374410 | Not Efficient |
| 6.00 | 10.00 | 0.500 | 0.101 | 30 | 520 | 1.652 | 0.01746340000 | Not Efficient | |
| 6.50 | 10.00 | 0.550 | 0.053 | 30 | 520 | 0.861 | 0.68131012700 | Eff. | |
| 7.00 | 10.00 | 0.600 | 0.005 | 30 | 520 | 0.081 | 1.00000000000 | Eff. | |
| Test Portfolio (p) | 5.00 | 12.00 | 0.333 | 0.276 | 30 | 520 | 4.513 | 0.00000000000 | Not Efficient |
| 5.50 | 12.00 | 0.375 | 0.237 | 30 | 520 | 3.884 | 0.00000000012 | Not Efficient | |
| 6.00 | 12.00 | 0.417 | 0.198 | 30 | 520 | 3.238 | 0.00000004498 | Not Efficient | |
| 6.50 | 12.00 | 0.458 | 0.158 | 30 | 520 | 2.580 | 0.00001444100 | Not Efficient | |
| 7.00 | 12.00 | 0.500 | 0.117 | 30 | 520 | 1.917 | 0.00279042500 | Not Efficient | |
| 7.50 | 12.00 | 0.542 | 0.077 | 30 | 520 | 1.256 | 0.16816038300 | Eff. | |
| 8.00 | 12.00 | 0.583 | 0.037 | 30 | 520 | 0.599 | 0.95601098600 | Eff. | |
| Test Portfolio (p) | 5.00 | 14.00 | 0.286 | 0.328 | 30 | 520 | 5.366 | 0.00000000000 | Not Efficient |
| 5.50 | 14.00 | 0.321 | 0.297 | 30 | 520 | 4.862 | 0.00000000000 | Not Efficient | |
| 6.00 | 14.00 | 0.357 | 0.265 | 30 | 520 | 4.336 | 0.00000000000 | Not Efficient | |
| 6.50 | 14.00 | 0.393 | 0.232 | 30 | 520 | 3.793 | 0.00000000028 | Not Efficient | |
| 7.00 | 14.00 | 0.429 | 0.198 | 30 | 520 | 3.238 | 0.00000004498 | Not Efficient | |
| 7.50 | 14.00 | 0.464 | 0.163 | 30 | 520 | 2.674 | 0.00000646460 | Not Efficient | |
| 8.00 | 14.00 | 0.500 | 0.129 | 30 | 520 | 2.107 | 0.00067275200 | Not Efficient | |
| 8.50 | 14.00 | 0.536 | 0.094 | 30 | 520 | 1.539 | 0.03571892400 | Not Efficient | |
| 9.00 | 14.00 | 0.571 | 0.060 | 30 | 520 | 0.973 | 0.50892160100 | Eff. | |
| 9.50 | 14.00 | 0.607 | 0.025 | 30 | 520 | 0.413 | 0.99780363100 | Eff. | |
| Test Portfolio (p) | 5.00 | 16.00 | 0.250 | 0.364 | 30 | 520 | 5.958 | 0.00000000000 | Not Efficient |
| 5.50 | 16.00 | 0.281 | 0.339 | 30 | 520 | 5.549 | 0.00000000000 | Not Efficient | |
| 6.00 | 16.00 | 0.313 | 0.313 | 30 | 520 | 5.117 | 0.00000000000 | Not Efficient | |
| 6.50 | 16.00 | 0.344 | 0.285 | 30 | 520 | 4.667 | 0.00000000000 | Not Efficient | |
| 7.00 | 16.00 | 0.375 | 0.257 | 30 | 520 | 4.202 | 0.00000000001 | Not Efficient | |
| 7.50 | 16.00 | 0.406 | 0.228 | 30 | 520 | 3.724 | 0.00000000053 | Not Efficient | |
| 8.00 | 16.00 | 0.438 | 0.198 | 30 | 520 | 3.238 | 0.00000004498 | Not Efficient | |
| 8.50 | 16.00 | 0.469 | 0.168 | 30 | 520 | 2.745 | 0.00000351764 | Not Efficient | |
| 9.00 | 16.00 | 0.500 | 0.137 | 30 | 520 | 2.249 | 0.00022052900 | Not Efficient | |
| 9.50 | 16.00 | 0.531 | 0.107 | 30 | 520 | 1.752 | 0.00899892900 | Not Efficient | |
| 10.00 | 16.00 | 0.563 | 0.077 | 30 | 520 | 1.256 | 0.16816038300 | Eff. | |
| 10.50 | 16.00 | 0.594 | 0.047 | 30 | 520 | 0.763 | 0.81564721900 | Eff. | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agrrawal, P. The Gibbons, Ross, and Shanken Test for Portfolio Efficiency: A Note Based on Its Trigonometric Properties. Mathematics 2023, 11, 2198. https://doi.org/10.3390/math11092198
Agrrawal P. The Gibbons, Ross, and Shanken Test for Portfolio Efficiency: A Note Based on Its Trigonometric Properties. Mathematics. 2023; 11(9):2198. https://doi.org/10.3390/math11092198
Chicago/Turabian StyleAgrrawal, Pankaj. 2023. "The Gibbons, Ross, and Shanken Test for Portfolio Efficiency: A Note Based on Its Trigonometric Properties" Mathematics 11, no. 9: 2198. https://doi.org/10.3390/math11092198
APA StyleAgrrawal, P. (2023). The Gibbons, Ross, and Shanken Test for Portfolio Efficiency: A Note Based on Its Trigonometric Properties. Mathematics, 11(9), 2198. https://doi.org/10.3390/math11092198






