Modified BIC Criterion for Model Selection in Linear Mixed Models

Abstract

Linear mixed-effects models are widely used in applications to analyze clustered, hierarchical, and longitudinal data. Model selection in linear mixed models is more challenging than that of linear models as the parameter vector in a linear mixed model includes both fixed effects and variance component parameters. When selecting the variance components of the random effects, the variance of the random effects must be non-negative and the parameters may lie on the boundary of the parameter space. Therefore, classical model selection methods cannot be directly used to handle this situation. In this article, we propose a modified BIC for model selection with linear mixed-effects models that can solve the case when the variance components are on the boundary of the parameter space. Through the simulation results, we found that the modified BIC performed better than the regular BIC in most cases for linear mixed models. The modified BIC was also applied to a real dataset to choose the most-appropriate model.

1. Introduction

With the development of technology in recent times, more complex and large datasets have become available. Statisticians and researchers are also developing different statistical models to extract valuable information from data to aid decision-making processes. Classical multiple linear regression models can be used to model the relationship between variables. However, one of the assumptions of linear regression is that the errors are independent. Therefore, when the observations are correlated as with longitudinal data, clustered data, and hierarchical data, linear regression models are no longer appropriate. A more powerful class of models used to model correlated data are mixed-effects models, which have been used in many fields of applications. Recently, Sheng et al. [1] compared the linear models with linear mixed-effects models and showed that estimators from the latter are more advantageous in terms of both efficiency and unbiasedness. This shows the importance of applying linear mixed-effects models in longitudinal settings.

The correlation between observations may appear when data are collected hierarchically; for example, students may be sampled from the same school, and schools may be sampled within the same district. Consequently, students in the same school have the same teachers and school environment, and therefore, the observations are not independent of one another. Observations may be taken from members of the same family, where each family is considered a group or a cluster. As the observations are dependent, we can consider this clustered data. Another type of correlated data pertains to observations from the same subjects collected over time, such as repeated blood pressure measurements over a patient’s treatment period—an example of longitudinal data. Patients (or subjects) may vary in the number and date of the collected measurements. Since observations are recorded from the same individual over time, it is reasonable to assume that subject-specific correlations exist in the trend of the response variable over time. We wish to model the pattern of the response variable over time within subjects and the variation in the time trends between subjects. Linear mixed-effects models are used to model correlated data, accounting for the variability within and between clusters in clustered data or the variability within and between repeated measurements in longitudinal data.

Model selection is an important procedure in statistical analysis, allowing the most-appropriate model to be chosen from a set of potential candidate models. A desired model is parsimonious and can adequately fit the data in order to improve two important aspects: interpretability and predictability. In linear mixed models, identifying significant random effects is a challenging step in model selection, as it involves conducting a hypothesis test for whether or not the variance components of random effects are equal to zero. For example, we want to test $H_0:{\sigma }^2=0$ against $H_1:{\sigma }^2>0$, where the parameter space of ${\sigma }^2$ is $[0,\infty )$. Under the null hypothesis, the testing value of the variance component parameter lies on the boundary of the parameter space. This violates one of the classical regularity conditions that the true value of the parameter must be an interior point of the parameter space. Therefore, classical hypothesis tests such as the likelihood ratio, score, and Wald tests are no longer appropriate. We refer to this violation as the boundary issue. (Please see a graphical example of the boundary issue in Appendix A.3). When the boundary issue occurs, the asymptotic null distribution of the likelihood ratio test statistic does not follow a chi-squared distribution. Chernoff [2], Self and Liang [3], Stram and Lee [4], Azadbakhsh et al. [5], and Baey et al. [6] pointed out that, under some conditions on the parameter space and the likelihood functions, the asymptotic null distribution of the likelihood ratio test statistic is a mixture of chi-squared distributions. For instance, the asymptotic null distribution of the likelihood ratio test statistic for testing $H_0:{\sigma }^2=0$ against $H_1:{\sigma }^2>0$ is $\frac{1}{2}{\chi }_0^2+\frac{1}{2}{\chi }_1^2$, not ${\chi }_1^2$ [4]. The distribution of a chi-bar-squared random variable depends on its mixing weights (Appendix A.2). Dykstra [7] discussed conditions on the weight distribution to ensure asymptotic normality for chi-bar-squared distributions. Shapiro [8] provided expressions to calculate the exact weights used in the mixture of chi-squared distributions for some special cases. However, in general, determining the exact weights used in the mixture of chi-squared distributions is challenging when the number of the variance components being tested under the null hypothesis is large, as the weights are not available in a tractable form (Baey et al. [6]).

There are a number of information criteria, such as the Akaike information criterion (AIC) and the Bayesian information criterion (BIC), that were developed for model selection with linear mixed models by Vaida and Blanchard [9], Pauler [10], Jones [11], and Delattre and Poursat [12]. Other methods for identifying important fixed effects and random effects variance components, including shrinkage and permutation methods, were considered in Ibrahim et al. [13], Bondell et al. [14], Peng and Lu [15], and Drikvandi et al. [16].

The BIC is susceptible to the boundary issue. If we use the regular BIC in linear mixed models, that is we treat this case as if there were no constraints on the model’s parameter vector, then the penalty term of the regular BIC would include all the components of the parameter vector. Therefore, the regular BIC would overestimate the number of degrees of freedom of the linear mixed model (which we refer to as model complexity for this article) and would not take into account the fact that variances components are constrained and bounded below by 0. Consequently, the regular BIC tends to choose under-fitted linear mixed models. Several versions of the modified BIC have been proposed for model selection in linear mixed models [10,11,17]. However, to our knowledge, none of the current BICs can directly deal with the boundary issue.

The main objective of this article was to introduce a modified BIC for model selection when the true values of the variance components’ parameters lie on the boundary of the parameter space, allowing the most-appropriate model to be chosen from a set of candidate linear mixed models. Here is the general idea on how our proposed method solves the boundary problem. From the previous literature, we know that the asymptotic null distribution of the likelihood ratio test statistic of testing the nullity of several variances is a chi-bar-squared distribution (Baey et al. [6]). Based on this theoretical result, we took the average of the chi-bar-squared distribution and included this average in the complexity of the model. When random effects are correlated, calculating the weights of the chi-bar-squared distribution is not straightforward, as the weights depend on a cone $C^{\ast }$ that contains the set of positive definite matrices. Describing the set of positive definite matrices explicitly using constraints on the components of the random effects covariance matrix is almost impossible. Thus, calculating the weights of the chi-bar-squared distribution for this case is not an easy task and has not been addressed in the literature. Our solution to this problem is to place a bound on cone $C^{\ast }$ with a bigger cone. The bigger cone has a much simpler structure and allowed us to calculate the weights of the chi-bar-squared distribution. The rest of the paper is arranged as follows. In Section 2, we develop the methodology. The simulation and application are provided in Section 3 and Section 4. We conclude with a brief discussion in Section 5.

2. Methodology

2.1. Model Setup and Definitions

Consider the linear mixed model introduced in Laird and Ware [18]:

$$\begin{array}{c}\hfill {\mathit{y}}_i={\mathit{X}}_i\mathbf{\beta }+{\mathit{Z}}_i{\mathit{b}}_i+{\mathbf{ϵ}}_i,\end{array}$$

(1)

for $i=1,\dots ,N$, where ${\mathit{y}}_i$ denotes the $n_i$-dimensional vector of response measurements for cluster i with $i=1,\dots ,N$; $\mathbf{\beta }$ is a $p\times 1$ fixed effect parameter vector; ${\mathit{X}}_i$ is an $n_i\times p$ matrix of covariates for the fixed effects; ${\mathit{Z}}_i$ is an $n_i\times q$ matrix of covariates for the random effects; ${\mathit{b}}_i$ denotes the random effects vector of the $i$-th cluster; ${\mathit{b}}_i$ is assumed to follow a multivariate normal distribution $N_q(\mathbf{0},\mathit{D})$, where $\mathit{D}$ is a $q\times q$ covariance matrix. ${\mathit{b}}_{\mathbf{1}},\cdots ,{\mathit{b}}_{\mathit{N}}$ were assumed to be independent. Fixed effects are used to model the population mean, while random effects are used to model between-cluster variation in the response. The vector of random errors ${\mathbf{ϵ}}_i$ was assumed to follow a multivariate normal distribution, $N(\mathbf{0},{\sigma }_{\mathbf{ϵ}}^2{\mathit{I}}_{n_i})$, where ${\mathit{I}}_{n_i}$ denotes the $n_i\times n_i$ identity matrix. It was assumed that ${\mathit{b}}_i$ and ${\mathbf{ϵ}}_i$ are pairwise independent for $i=1,\dots ,N$. The marginal distribution of ${\mathit{y}}_i$ is $N({\mathit{X}}_i\mathbf{\beta },{\mathit{V}}_i)$, where ${\mathit{V}}_i={\mathit{Z}}_i\mathit{D}{\mathit{Z}}_i^T+{\sigma }_{\mathbf{ϵ}}^2{\mathit{I}}_{n_i}$.

Let $\mathbf{\tau }$ denote the vector of distinct variance and covariance components in matrix $\mathit{D}$, and let $\eta ={({\mathbf{\tau }}^T,{\sigma }_{\mathbf{ϵ}}^2)}^T$. The vector of parameters for this model is $\theta ={({\mathbf{\beta }}^T,{\eta }^T)}^T$. We assumed that the response vectors ${\mathit{y}}_{\mathbf{1}},\dots ,{\mathit{y}}_{\mathit{N}}$ from N clusters are independent random observations. Given a clustered dataset, we wish to choose a linear mixed model that fits the data well and is also a parsimonious model.

Definition 1 

(Definition of an approximating cone [2]). Let $\mathsf{\Theta }\subseteq {\mathbb{R}}^p$ and ${\theta }_0\in \mathsf{\Theta }$. The set $\mathsf{\Theta }$ is said to be approximated by a cone A at ${\theta }_0$ if $d(\mathit{y},A)=o\left(\right||\mathit{y}-{\theta }_0|\left|\right)$, for all $\mathit{y}\in \mathsf{\Theta }$ and $d(\mathit{x},\mathsf{\Theta })=o\left(\right||\mathit{x}-\theta |\left|\right)$, for all $\mathit{x}\in A$, where $d(\mathit{x},\mathsf{\Omega })={inf}_{\mathit{y}\in \mathsf{\Omega }}\left|\right|\mathit{x}-\mathit{y}\left|\right|$, which is the distance between point $\mathit{x}$ and its projection onto any space $\mathsf{\Omega }$. In this case, A is called the approximating cone of $\mathsf{\Theta }$ at ${\theta }_0$ and $\mathsf{\Theta }$ is said to be Chernoff-regular at ${\theta }_0$.

Definition 2 

(Definition of a tangent cone [19]). A tangent cone $T_A\left({\theta }_0\right)$ of a set $\mathsf{\Theta }$ at a point ${\theta }_0$ in $\mathsf{\Theta }$ is the set of limits of sequences $t_n^{-1}({\theta }_n-{\theta }_0)$, where $t_n$ are positive real numbers and $t_n\to 0$ and ${\theta }_n$ in $\mathsf{\Theta }$ converge to ${\theta }_0$.

Definition 3 

(Definition of chi-bar-squared distribution [19]). Let $\mathcal{C}\subset {\mathbb{R}}^m$ be a closed convex cone, and let $\mathit{Z}\sim N_m(\mathbf{0},\mathit{V})$, where $\mathit{V}$ is a positive definite matrix. ${\overline{\chi }}^2(\mathit{V},\mathcal{C})$ is a random variable, which has the same distribution as $\left[{\mathit{Z}}^T{\mathit{V}}^{-1}\mathit{Z}-{min}_{\theta \in \mathcal{C}}{(\mathit{Z}-\theta )}^T{\mathit{V}}^{-1}(\mathit{Z}-\theta )\right]$. Therefore, we write

$$\begin{array}{cc}\hfill {\overline{\chi }}^2(\mathit{V},\mathcal{C})& ={\mathit{Z}}^T{\mathit{V}}^{-1}\mathit{Z}-\underset{\theta \in \mathcal{C}}{min}{(\mathit{Z}-\theta )}^T{\mathit{V}}^{-1}(\mathit{Z}-\mathbf{\theta })\hfill \end{array}$$

where $w_i\left(m,\mathit{V},\mathcal{C}\right),i=0,\cdots ,m$, are some non-negative numbers and ${\sum }_{i=0}^m{w}_i\left(m,\mathit{V},\mathcal{C}\right)=1$.

2.2. Proposed Methods

In this section, we introduce a modified BIC for linear mixed model selection. In linear mixed models, model selection includes the selection of the regression parameters $\mathbf{\beta }$ (fixed effects) and variance components of random effects. We first derived a modified BIC to choose random effects assuming that the random effects are independent. Then, we propose a modified BIC to choose random effects when random effects are assumed to be correlated. Lastly, we propose a modified BIC to choose both fixed effects and random effects simultaneously. We also considered two cases for when the covariance matrix for random effects $b_i$ are diagonal and full matrices.

Let $\mathcal{M}=\{M_k:k\ge 1\}$ be a countable set of possible candidate linear mixed models. Let ${\mathbf{\theta }}_k$ denote the vector of parameters of model $M_k$, and let $d_k$ be the complexity of model $M_k$. Assume that $d_k$ can be calculated and $d_k<d_l$ if $M_k\subset M_l$. Let $M_T$ be the model that generates the data (called the true model) with parameter ${\mathbf{\theta }}_T$ and the true value of ${\mathbf{\theta }}_T$ is ${\mathbf{\theta }}_{T,0}$. Any model $M_k$ that is more complex than the true model is called an over-fitting model, that is $M_T\subset M_k$ or ${\mathbf{\theta }}_T\subset {\mathbf{\theta }}_k$ and ${\mathbf{\theta }}_T\ne {\mathbf{\theta }}_k$. Let ${\mathcal{M}}^{+}$ be the set of all over-fitting models. An under-fitting model $M_k$ is a model such that ${\mathbf{\theta }}_T$’s components are not a subset of its parameter vector’s components, that is ${\mathbf{\theta }}_T⊊{\mathbf{\theta }}_k$. Let ${\mathcal{M}}^{-}$ be the set of all under-fitting models. Assume that model $M_k$ has parameter vector ${\mathbf{\theta }}_k={({{\mathbf{\beta }}_k}^T,{{\mathbf{\tau }}_k}^T,{\sigma }_{\mathbf{ϵ},k}^2)}^T$, where ${\mathbf{\beta }}_k$ is the vector of fixed effects parameters, which includes the population regression coefficients; ${\mathbf{\tau }}_k$ contains the distinct variance and covariance elements of matrix $\mathit{D}$; ${\sigma }_{\mathbf{ϵ},k}^2$ is the parameter for the variance of the random error vector ${\mathbf{ϵ}}_{\mathbf{k}}$. For a general covariance matrix, model $M_k$ is uniquely defined by its non-zero parameters in $\mathbf{\beta }$ and non-zero variance components on the diagonal of matrix $\mathit{D}$. If $d_{ii}=0$, then all elements on row i and column i of this matrix are set to 0.

2.2.1. Modified BIC for Choosing Random Effects Assuming That the Random Effects Are Independent

In this section, we considered the case where the covariance matrix of random effects, D, is a diagonal matrix. Here, $\mathbf{\tau }$ is a vector of variances on the diagonal of matrix D.

Lemma 1. 

When $\mathit{D}$ is a diagonal matrix, under assumptions $\left(C1\right)-\left(C4\right)$ (Appendix A.1), assume that we wish to test the model $M_k$ (with ${\mathbf{\tau }}_k=(d_1,\dots ,d_k)$) against model $M_1$ (with ${\mathbf{\tau }}_1=(d_1,0,\dots ,0)$) and both models have the same fixed effects part, then the null limiting distribution of the likelihood ratio test is

$$\begin{array}{ccc}\hfill {\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })& =& \sum _{i=0}^{k-1}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }){\chi }_i^2,\hfill \end{array}$$

(2)

where $C^{\ast }={\left\{0\right\}}^p\times \left\{0\right\}\times {\mathbb{R}}_{+}^{k-1}\times \left\{0\right\}$; $w_i\left(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }\right),i=0,\cdots ,k-1$, are some non-negative numbers and ${\sum }_{i=0}^{k-1}{w}_i\left(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }\right)=1$; matrix $\mathbf{\nu }\left(\mathbf{\theta }\right)$ is some positive definite matrix such that $N^{-\frac{1}{2}}{l}_N^{{}^{\prime }}\left(\mathbf{\theta }\right)\stackrel{d}{\to }{N}_m(\mathbf{0},\mathbf{\nu }\left(\mathbf{\theta }\right))$ and $N^{-1}\{-l_N^{{}^{″}}\left(\mathbf{\theta }\right)\}\stackrel{a.s.}{\to }\mathbf{\nu }\left(\mathbf{\theta }\right)$, and m is the dimension of $\mathbf{\theta }$. ${\mathbf{\theta }}^{\ast }$ denotes the true value of the parameter θ; $l_N(\mathbf{\theta };y)$ denotes the marginal log-likelihood function of the linear mixed model (1).

Proof. 

We applied the results from Baey et al. [6] on testing the nullity of r variance components of the $q\times q$ diagonal covariance matrix, $\mathit{D}$, using the likelihood ratio test statistic, assuming that the variances that are not being tested are strictly positive. Without loss of generality, assume that matrix $\mathit{D}$ can be written as $\mathit{D}=\left[\begin{array}{cc}{\mathit{D}}_{11}& \mathbf{0}\\ \mathbf{0}& {\mathit{D}}_{22}\end{array}\right]$, where ${\mathit{D}}_{11}=diag(d_1,\dots ,d_{q-r})$ and ${\mathit{D}}_{22}=diag(d_{q-r+1},\dots ,d_q)$. The parameter $\mathbf{\theta }={({\mathbf{\beta }}^T,{\mathbf{\tau }}^T,{\sigma }_{\mathbf{ϵ}})}^T\in \mathsf{\Theta }\subset {\mathbb{R}}^m$ with $\mathbf{\tau }={(d_1,\dots ,d_q)}^T$. Consider the hypothesis test, $H_0:\mathit{D}=\left[\begin{array}{cc}{\mathit{D}}_{11}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right]$ with positive definite matrix ${\mathit{D}}_{11}$ versus $H_1$: $\mathit{D}$ is positive definite.

The parameter spaces under and their corresponding tangent cones are

$$\begin{array}{ccc}\hfill {\mathsf{\Theta }}_0& =& \{\mathbf{\theta }\in {\mathbb{R}}^m/\mathbf{\beta }\in {\mathbb{R}}^p;d_1>0,\dots ,d_{q-r}>0,\hfill \\ & & d_{q-r+1}=0,\dots ,d_q=0,{\sigma }_{\mathbf{ϵ}}^2>0\}.\hfill \\ \hfill T_{{\mathsf{\Theta }}_0}\left({\mathbf{\theta }}^{\ast }\right)& =& \{{\mathbb{R}}^p\times {\mathbb{R}}^{q-r}\times {\left\{0\right\}}^r\times \mathbb{R}\}.\hfill \\ \hfill \mathsf{\Theta }& =& \{\mathbf{\theta }\in {\mathbb{R}}^m/\mathbf{\beta }\in {\mathbb{R}}^p;d_1>0,\dots ,d_{q-r}>0,\hfill \\ & & d_{q-r+1}\ge 0,\dots ,d_q\ge 0,{\sigma }_{\mathbf{ϵ}}^2>0\}.\hfill \\ \hfill T_{\mathsf{\Theta }}\left({\mathbf{\theta }}^{\ast }\right)& =& {\mathbb{R}}^p\times {\mathbb{R}}^{q-r}\times {\mathbb{R}}_{+}^r\times \mathbb{R}.\hfill \end{array}$$

In this case, $T_{{\mathsf{\Theta }}_0}\left({\mathbf{\theta }}^{\ast }\right)$ is a linear subspace in $T_{\mathsf{\Theta }}\left({\mathbf{\theta }}^{\ast }\right)$. Therefore, $C^{\ast }=T_{\mathsf{\Theta }}\left({\mathbf{\theta }}^{\ast }\right)\cap T_{{\mathsf{\Theta }}_0}{\left({\mathbf{\theta }}^{\ast }\right)}^{\perp }={\left\{0\right\}}^p\times {\left\{0\right\}}^{q-r}\times {\mathbb{R}}_{+}^r\times \left\{0\right\}$. $C^{\ast }$ is contained in a linear subspace of dimension r. Thus, $w_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })=0$ for $i=r+1,\dots ,m$. Assume that the null hypothesis holds and ${\mathbf{\theta }}^{\ast }\in {\mathsf{\Theta }}_0$,. Baey et al. [6] pointed out that the asymptotic null distribution of the log-likelihood ratio test statistic is a mixture of chi-squared distributions with the degree of freedom ranging from 0 to r, denoted by

$$\begin{array}{ccc}\hfill {\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })& =& \sum _{i=0}^r{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }){\chi }_i^2,\hfill \end{array}$$

(3)

where ${\chi }_i^2$ is a chi-squared distribution with i degrees of freedom and $\mathbf{\nu }\left(\mathbf{\theta }\right)$ is some positive definite matrix such that $N^{-\frac{1}{2}}{l}_N^{{}^{\prime }}\left(\mathbf{\theta }\right)\stackrel{d}{\to }N(0,\mathbf{\nu }\left(\mathbf{\theta }\right))$ and $N^{-1}\{-l_N^{{}^{″}}\left(\mathbf{\theta }\right)\}\stackrel{a.s.}{\to }\mathbf{\nu }\left(\mathbf{\theta }\right)$.

We applied this result to our case with $m=p+k+1$; $q=k$; and $r=k-1$. Thus, based on (3), the null limiting distribution of the likelihood ratio test statistic is

$$\begin{array}{ccc}\hfill {\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })& =& \sum _{i=0}^{k-1}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }){\chi }_i^2,\hfill \end{array}$$

(4)

where $C^{\ast }={\left\{0\right\}}^p\times \left\{0\right\}\times {\mathbb{R}}_{+}^{k-1}\times \left\{0\right\}$; $w_i\left(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }\right),i=0,\cdots ,k-1$, are some non-negative numbers and ${\sum }_{i=0}^{k-1}{w}_i\left(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }\right)=1$; matrix $\mathbf{\nu }\left(\mathbf{\theta }\right)$ is some positive definite matrix such that $N^{-\frac{1}{2}}{l}_N^{{}^{\prime }}\left(\mathbf{\theta }\right)\stackrel{d}{\to }{N}_m(\mathbf{0},\mathbf{\nu }\left(\mathbf{\theta }\right))$ and $N^{-1}\{-l_N^{{}^{″}}\left(\mathbf{\theta }\right)\}\stackrel{a.s.}{\to }\mathbf{\nu }\left(\mathbf{\theta }\right)$, and m is the dimension of $\mathbf{\theta }$. □

We now take the expectation of the chi-bar-squared distribution in Equation (2) and include it in the complexity of model $M_k$.

$$\begin{array}{c}\hfill E\left[{\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })\right]=\sum _{i=0}^{k-1}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })i.\end{array}$$

We propose the following modified BIC:

$$\begin{array}{c}\hfill BI{C}^{\ast }\left(M_k\right)=-2l({\widehat{\mathbf{\theta }}}_k;\mathit{y})+d_{k}log\left(n\right),\end{array}$$

(5)

where ${\widehat{\mathbf{\theta }}}_k$ is the maximum likelihood estimator of ${\mathbf{\theta }}_k$ in model $M_k$; $n={\sum }_{i=1}^N{n}_i$ and $d_k=p+1.5+{\sum }_{i=0}^{k-1}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })i$ for $k>1$; $d_k=p+1.5$ for $k=1$; $d_k=p+1$ for $k=0$. The first term, $-2l({\widehat{\mathbf{\theta }}}_k;y)$, measures the goodness-of-fit for model $M_k$, and the second term, $d_{k}log\left(n\right)$, is the penalty for the model complexity, which makes sure that the model selected is parsimonious.

The rationale of choosing the complexity $d_k$ for model $M_k$ when $k>1$ is as follows: p is the number of fixed effects parameters; 1 is for the ${\sigma }_{\mathbf{ϵ}}$ parameter and 0.5 for the assumed random effect in the model (such as random intercept), and the rest of $d_k$ is the expectation of the chi-bar-squared distribution in Equation (2). When $k=1$, $d_1=p+1.5$ is the complexity of model $M_1$, which is the model with fixed effects and only one random effect (such as random intercept). When $k=0$, $d_0=p+1$ is the complexity of model $M_0$, which is the model with fixed effects and no random effects. In this case, $d_0$ is exactly the regular BIC for multiple regression models. For example, $M_3$ is a model with three independent random effects. $\mathit{D}=diag({\sigma }_0^2,{\sigma }_1^2,{\sigma }_2^2)$, and $\mathbf{\tau }=({\sigma }_0^2,{\sigma }_1^2,{\sigma }_2^2)$.

We want to test $H_0:{\sigma }_0^2>0$; ${\sigma }_1^2=0$, ${\sigma }_2^2=0$, vs. $H_1:{\sigma }_0^2>0$; ${\sigma }_1^2>0$, ${\sigma }_2^2>0$. In this example, $\mathbf{\theta }={({\mathbf{\beta }}^T,{\mathbf{\tau }}^T,{\sigma }_{\mathbf{ϵ}}^2)}^T;m=p+3+1,k=3,r=2$. Therefore, the asymptotic null distribution of the log-likelihood ratio test statistic is

$$\begin{array}{ccc}\hfill {\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })& =& \sum _{i=0}^2{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }){\chi }_i^2\hfill \end{array}$$

where $C^{\ast }={\left\{0\right\}}^p\times \left\{0\right\}\times {\mathbb{R}}_{+}^2\times \left\{0\right\}$.

Cone $C^{\ast }$ can be written as $C^{\ast }=\{\mathbf{\theta }\in {\mathbb{R}}^m/\mathbf{R}\mathbf{\theta }\ge 0\}$, where $\mathbf{R}=\left({\mathbf{0}}_{p+1}\left|{\mathit{I}}_2\right|\mathbf{0}\right)$ is a $2\times m$ matrix and ${\mathit{I}}_2$ is an identity matrix of order two. The chi-bar-squared weights are $w_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })=w_i(r,\mathbf{R}\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1}{\mathbf{R}}^T,{\mathbb{R}}_{+}^2)$ under Proposition $\mathrm{3.6.1}$ of [19]. The matrix, $\mathbf{\nu }\left({\mathbf{\theta }}^{\ast }\right)$, is approximated by $\mathsf{\Gamma }=N^{-1}\left\{I_N\left({\widehat{\mathbf{\theta }}}_k\right)\right\}$, where ${\widehat{\mathbf{\theta }}}_k$ is the maximum likelihood estimator of ${\mathbf{\theta }}_k$ in model $M_k$ and ${\mathit{I}}_N\left(\mathbf{\theta }\right)$ is the Fisher information matrix. The chi-bar-squared weights, $w_i(r,\mathbf{R}{\mathsf{\Gamma }}^{-1}{\mathbf{R}}^T,{\mathbb{R}}_{+}^2)$, can be calculated using function “con-weights-boot” in the R package “restriktor” of Vanbrabant et al. [20]. In this example, we assumed that $\mathbf{R}{\mathsf{\Gamma }}^{-1}{\mathbf{R}}^T=\left[\begin{array}{cc}1& -0.5\\ -0.5& 1\end{array}\right]$. Then, we obtained the weights $w_0=0.334, w_1=0.503$, and $w_2=0.163$. Thus,

$$\begin{array}{ccc}\hfill {\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })& =& 0.334{\chi }_0^2+0.503{\chi }_1^2+0.163{\chi }_2^2,\hfill \end{array}$$

We note that, in theory, $w_1$ must be $0.5$. However, in our simulation, $w_1=0.503$. The expectation of this chi-bar-squared distribution is $0.334\left(0\right)+0.503\left(1\right)+0.163\left(2\right)=0.829$. The complexity of this model is $d_3=p+1.5+0.829$.

Theorem 1. 

Assume that Assumptions (C1)–(C4) in Appendix A.1 are satisfied, then

$$\begin{array}{cc}\hfill & \underset{n\to \infty }{lim}P(BI{C}^{\ast }\left(M_T\right)<BI{C}^{\ast }\left(M_k\right))=1\mathrm{for}\mathrm{all}{M}_k\in M^{+}\hfill \\ \hfill \mathit{and}& \underset{n\to \infty }{lim}P(BI{C}^{\ast }\left(M_T\right)<BI{C}^{\ast }\left(M_k\right))=1\mathrm{for}\mathrm{all}{M}_k\in M^{-}.\hfill \end{array}$$

Proof. 

We used $l({\widehat{\mathbf{\theta }}}_k;\mathit{y})$ instead of $l_N({\widehat{\mathbf{\theta }}}_k;\mathit{y})$ for the convenience of exposition.

Case 1: For any under-fitting model, $M_k\in M^{-}$, we want to prove that $\underset{n\to \infty }{lim}P(BI{C}^{\ast }\left(M_k\right)-BI{C}^{\ast }\left(M_T\right)>0)=1$. We have that

$$\begin{array}{cc}\hfill BI{C}^{\ast }\left(M_k\right)-BI{C}^{\ast }\left(M_T\right)& =-2\left(l({\widehat{\mathbf{\theta }}}_k;\mathit{y})-l({\widehat{\mathbf{\theta }}}_T;\mathit{y})\right)+(d_k-d_T)log\left(n\right).\hfill \\ \hfill -2\left(l({\widehat{\mathbf{\theta }}}_k;\mathit{y})-l({\widehat{\mathbf{\theta }}}_T;\mathit{y})\right)& =-2\left(l({\widehat{\mathbf{\theta }}}_k;\mathit{y})-l({\mathbf{\theta }}_{k,0};\mathit{y})\right)+2\left[l({\widehat{\mathbf{\theta }}}_T;\mathit{y})-l({\mathbf{\theta }}_{T,0};\mathit{y})\right]\hfill \\ \hfill & +2\left[l({\mathbf{\theta }}_{T,0};\mathit{y})-l({\mathbf{\theta }}_{k,0};\mathit{y})\right]-2E_{T,0}\left[l({\mathbf{\theta }}_{T,0};\mathit{Y})-l({\mathbf{\theta }}_{k,0};\mathit{Y})\right]\hfill \\ \hfill & +2E_{T,0}\left[l({\mathbf{\theta }}_{T,0};\mathit{Y})-l({\mathbf{\theta }}_{k,0};\mathit{Y})\right].\hfill \end{array}$$

We also have that $l({\widehat{\mathbf{\theta }}}_k;\mathit{y})-l({\mathbf{\theta }}_{k,0};\mathit{y})=o_p\left(1\right)$ and $l({\widehat{\mathbf{\theta }}}_T;\mathit{y})-l({\mathbf{\theta }}_{T,0};\mathit{y})=o_p\left(1\right)$ because ${\widehat{\mathbf{\theta }}}_k\stackrel{p}{\to }{\mathbf{\theta }}_{k,0}$ and ${\widehat{\mathbf{\theta }}}_T\stackrel{p}{\to }{\mathbf{\theta }}_{T,0}$ (as shown in the proof of Theorem 2 in Baey et al. [6]) and function $l(\mathbf{\theta };\mathit{y})$ is continuous with respect to $\mathbf{\theta }$. Furthermore, under Assumption $C4\left(ii\right)$, $\frac{1}{N}(l({\mathbf{\theta }}_{T,0};\mathit{y})-E_{T,0}\left[l({\mathbf{\theta }}_{T,0};\mathit{Y})\right])\stackrel{p}{\to }0$ and $\frac{1}{N}(l({\mathbf{\theta }}_{k,0};\mathit{y})-E_{T,0}\left[l({\mathbf{\theta }}_{k,0};\mathit{Y})\right])\stackrel{p}{\to }0$. Thus,

$$\begin{array}{c}\hfill \frac{1}{N}(l({\mathbf{\theta }}_{T,0};;\mathit{y})-l({\mathbf{\theta }}_{k,0};\mathit{y})-E_{T,0}[l({\mathbf{\theta }}_{T,0};\mathit{Y})-l({\mathbf{\theta }}_{k,0};\mathit{Y})])\stackrel{p}{\to }0,\end{array}$$

and therefore, $l({\mathbf{\theta }}_{T,0};\mathit{y})-l({\mathbf{\theta }}_{k,0};\mathit{y})-E_{T,0}[l({\mathbf{\theta }}_{T,0};\mathit{Y})-l({\mathbf{\theta }}_{k,0};\mathit{Y})]=o_p\left(N\right)$.

The last term can be evaluated as

$$\begin{array}{cc}\hfill E_{T,0}[l({\mathbf{\theta }}_{T,0};\mathit{Y})-l({\mathbf{\theta }}_{k,0};\mathit{Y})]& =\sum _{i=1}^N{E}_{T,0}[log{f}_i({\mathit{Y}}_i;{\mathbf{\theta }}_{T,0})-log{f}_i({\mathit{Y}}_i;{\mathbf{\theta }}_{k,0})]\hfill \\ \hfill & =\sum _{i=1}^N{E}_{T,0}\left[log{\displaystyle \frac{f_i({\mathit{Y}}_i;{\mathbf{\theta }}_{T,0})}{f_i({\mathit{Y}}_i;{\mathbf{\theta }}_{k,0})}}\right]=O_p\left(N\right).\hfill \end{array}$$

This is because $E_{T,0}\left[log{\displaystyle \frac{f_i({\mathit{Y}}_i;{\mathbf{\theta }}_{T,0})}{f_i({\mathit{Y}}_i;{\mathbf{\theta }}_{k,0})}}\right]$ is the Kullback–Leibler distance between $f_i({\mathit{Y}}_i;{\mathbf{\theta }}_{k,0})$ and $f_i({\mathit{Y}}_i;{\mathbf{\theta }}_{T,0})$; and is positive and finite by Assumption $C4\left(i\right)$.

Assume that the cluster sample sizes, $n_1,\dots ,n_N$, are uniformly bounded (Assumption $C3$), then $O_p\left(N\right)$ dominates $(d_k-d_T)log\left(n\right)$ as $N\to \infty$. Thus, $BI{C}^{\ast }\left(M_k\right)-BI{C}^{\ast }\left(M_T\right)>0$, and for all $M_k\in M^{-}$,

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}P(BI{C}^{\ast }\left(M_T\right)<BI{C}^{\ast }\left(M_k\right))=1\end{array}$$

Case 2: For any over-fitting model, $M_k\in M^{+}$, we also prove that $\underset{n\to \infty }{lim}P(BI{C}^{\ast }\left(M_k\right)-BI{C}^{\ast }\left(M_T\right)>0)=1$. Without loss of generality, assume that ${\mathbf{\theta }}_T={({{\mathbf{\beta }}_T}^T,{{\mathit{\psi }}_T}^T,\underline{0},{\sigma }_{\mathbf{ϵ},T}^2)}^T$ and ${\mathbf{\theta }}_k={({{\mathbf{\beta }}_k}^T,{{\mathit{\psi }}_{k,1}}^T,{{\mathit{\psi }}_{k,2}}^T,{\sigma }_{\mathbf{ϵ},k}^2)}^T$, where ${\mathit{\psi }}_T$ has the same dimension as ${\mathit{\psi }}_{k,1}$ and $\underline{0}$ has the same dimension as ${{\mathit{\psi }}_{k,2}}^T$. Let r be the dimension of ${\mathit{\psi }}_{k,2};dim\left({\mathit{\psi }}_{k,2}\right)=r$, and all elements of $\underline{0}$ are 0. We have that

$$BI{C}^{\ast }\left(M_k\right)-BI{C}^{\ast }\left(M_T\right)=-2\left(l({\widehat{\mathbf{\theta }}}_k;\mathit{y})-l({\widehat{\mathbf{\theta }}}_T;\mathit{y})\right)+(d_k-d_T)log\left(n\right).$$

(6)

Then, $-2(l({\widehat{\mathbf{\theta }}}_T;\mathit{y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{y}))$ is the likelihood ratio test statistic of the following hypothesis test:

$$\begin{array}{cc}\hfill & H_0:{\mathit{\psi }}_{k,1}\ge \mathbf{0},{\mathit{\psi }}_{k,2}=\mathbf{0}\hfill \\ \hfill & H_1:{\mathit{\psi }}_{k,1}\ge \mathbf{0},{\mathit{\psi }}_{k,2}>\mathbf{0}.\hfill \end{array}$$

According to Baey et al. [6], under $H_0$, the asymptotic distribution of $-2(l({\widehat{\mathbf{\theta }}}_T;\mathit{y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{y}))$ is

$$\begin{array}{c}\hfill \sum _{i=0}^r{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }){\chi }_i^2.\end{array}$$

Therefore, $-2(l({\widehat{\mathbf{\theta }}}_k;\mathit{y})-l({\widehat{\mathbf{\theta }}}_T;\mathit{y}))=O_p\left(1\right)$, according to Theorem 2.4 of [21]. We also have that

$$\begin{array}{cc}\hfill 2(l({\widehat{\mathbf{\theta }}}_T;\mathit{y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{y}))& =2\left(l({\widehat{\mathbf{\theta }}}_T;\mathit{y})-l({\widehat{\mathbf{\theta }}}_1;\mathit{y})-\left[l({\widehat{\mathbf{\theta }}}_k;\mathit{y})-l({\widehat{\mathbf{\theta }}}_1;\mathit{y})\right]\right)\hfill \\ \hfill & =-2\left(l({\widehat{\mathbf{\theta }}}_1;\mathit{y})-l({\widehat{\mathbf{\theta }}}_T;\mathit{y})\right)\hfill \\ \hfill & -\left[-2\left(l({\widehat{\mathbf{\theta }}}_1;\mathit{y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{y})\right)\right].\hfill \\ \hfill \Rightarrow E\left[2\left(l({\widehat{\mathbf{\theta }}}_T;\mathit{Y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{Y})\right)\right]& =E\left[-2\left(l({\widehat{\mathbf{\theta }}}_1;\mathit{Y})-l({\widehat{\mathbf{\theta }}}_T;\mathit{Y})\right)\right]\hfill \\ \hfill & -E\left[-2\left(l({\widehat{\mathbf{\theta }}}_1;\mathit{Y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{Y})\right)\right]=d_T-d_k,\hfill \end{array}$$

where $l({\widehat{\mathbf{\theta }}}_1;\mathit{y})$ is the maximum log-likelihood of the simplest model, that is the model with only the random intercept. Therefore,

$$\begin{array}{c}\hfill E\left[-2\left(l({\widehat{\mathbf{\theta }}}_T;\mathit{Y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{Y})\right)\right]=d_k-d_T.\end{array}$$

On the other hand, $-2\left(l({\widehat{\mathbf{\theta }}}_T;\mathit{y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{y})\right)$ asymptotically follows a mixture of the chi-squared distributions. Therefore, $E\left[-2\left(l({\widehat{\mathbf{\theta }}}_T;\mathit{Y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{Y})\right)\right]$ must be positive, and hence, $d_k-d_T>0$. Thus, $BI{C}^{\ast }\left(M_k\right)-BI{C}^{\ast }\left(M_T\right)\to \infty$ as $n\to \infty$ and

$${\displaystyle \underset{n\to \infty }{lim}P\left(BI{C}^{\ast }\left(M_k\right)-BI{C}^{\ast }\left(M_T\right)>0\right)=1}$$

for $M_k\in M^{+}$. This completes the proof of Theorem 1. □

Given a set of candidate models, we calculated the proposed BIC value for each model. Then, the selected model is the one that minimizes the proposed BIC.

2.2.2. Modified BIC for Choosing Random Effects Assuming That the Random Effects Are Correlated

In this section, we introduce a modified BIC for selecting linear mixed models with correlated random effects. We still focused on only selecting random effects. In the parameter vector $\mathbf{\theta }={({\mathbf{\beta }}^T,{\mathbf{\tau }}^T,{\sigma }_{\mathbf{ϵ}}^2)}^T$, $\mathbf{\tau }$ is the parameter of interest; $\mathbf{\beta }$ and ${\sigma }_{\mathbf{ϵ}}^2$ are considered as nuisance parameters. We now considered that the linear mixed model (1) with the covariance matrix for random effects ${\mathit{b}}_i$ is a full matrix. Therefore, vector $\mathbf{\tau }$ contains all distinct variances and covariances of matrix $\mathit{D}$.

Lemma 2. 

When $\mathit{D}$ is a full matrix and under Assumptions (C1)–(C4) in Appendix A.1, assume that we test the model $M_k$ against model $M_1$, where $M_1$ contains only one random effect, which is a random intercept, $M_k$ contains k random effects including a random intercept, and both models have the same fixed effects part, then the null limiting distribution of the likelihood ratio test is

$$\begin{array}{ccc}\hfill {\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })& =& \sum _{i=k-1}^{(k-1)(k+2)/2}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }){\chi }_i^2,\hfill \end{array}$$

(7)

where $C^{\ast }={\left\{0\right\}}^p\times \left\{0\right\}\times {\mathbb{S}}_{+}^{k-1}\times \left\{0\right\}$; m is the dimension of θ; $w_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }),i=(k-1),\cdots ,(k-1)(k+2)/2$, are some non-negative numbers; ${\sum }_{i=k-1}^{(k-1)(k+2)/2}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })=1$; ${\chi }_i^2$ is a chi-squared distribution with i degrees of freedom; $\mathbf{\nu }\left(\mathbf{\theta }\right)$ is a positive definite matrix such that $N^{-\frac{1}{2}}{l}_N^{{}^{\prime }}\left(\mathbf{\theta }\right)\stackrel{d}{\to }{N}_m(\mathbf{0},\mathbf{\nu }\left(\mathbf{\theta }\right))$ and $N^{-1}\{-l_N^{{}^{″}}\left(\mathbf{\theta }\right)\}\stackrel{a.s.}{\to }\mathbf{\nu }\left(\mathbf{\theta }\right)$. ${\mathbb{S}}_{+}^r$ denotes the set of symmetric positive semi-definite matrices of size $r\times r$.

Proof. 

When $\mathit{D}$ is a full matrix, the number of distinct variances and covariances is $q(q+1)/2$. We also applied the results from Baey et al. [6] on testing the nullity of r variance components of the $q\times q$ covariance matrix, $\mathit{D}$, when this matrix is a full matrix. Assume that matrix $\mathit{D}$ is written as $\mathit{D}=\left[\begin{array}{cc}{\mathit{D}}_{11}& {\mathit{D}}_{12}\\ {\mathit{D}}_{12}^T& {\mathit{D}}_{22}\end{array}\right]$ where the size of ${\mathit{D}}_{11}$ is $(q-r)\times (q-r)$ and the size of ${\mathit{D}}_{22}$ is $r\times r$. Consider the hypothesis test: $H_0:{\mathit{D}}_{11}>\mathbf{0},{\mathit{D}}_{12}=\mathbf{0},{\mathit{D}}_{22}=\mathbf{0}$ versus $H_1$: $\mathit{D}$ is a positive definite matrix.

The parameter space under the null hypothesis is

$$\begin{array}{ccc}\hfill {\mathsf{\Theta }}_0& =& \{\mathbf{\theta }\in {\mathbb{R}}^m/\mathbf{\beta }\in {\mathbb{R}}^p;{\mathit{D}}_{11}>\mathbf{0};{\mathit{D}}_{12}=\mathbf{0},{\mathit{D}}_{22}=\mathbf{0},{\sigma }_{\mathbf{ϵ}}^2>0\}\hfill \\ & =& \{{\mathbb{R}}^p\times {\mathbb{S}}_{+}^{q-r}\times {\left\{0\right\}}^{r(q-r)}\times {\left\{0\right\}}^{r(r+1)}\times {\mathbb{R}}_{+}\},\hfill \end{array}$$

where ${\mathbb{S}}_{+}^{q-r}$ is the set of symmetric positive semi-definite matrices of size $(q-r)\times (q-r)$.

Assume that the null hypothesis holds and ${\mathbf{\theta }}^{\ast }\in {\mathsf{\Theta }}_0$, then applying the results of Baey et al. [6], we obtain the tangent cone to ${\mathsf{\Theta }}_0$ at ${\mathbf{\theta }}^{\ast }$:

$$\begin{array}{ccc}\hfill T_{{\mathsf{\Theta }}_0}\left({\mathbf{\theta }}^{\ast }\right)& =& \{{\mathbb{R}}^p\times {\mathbb{S}}^{q-r}\times {\left\{0\right\}}^{r(q-r)}\times {\left\{0\right\}}^{r(r+1)}\times \mathbb{R}\}\hfill \\ & =& \{{\mathbb{R}}^p\times {\mathbb{R}}^{(q-r)(q-r+1)/2}\times {\left\{0\right\}}^{r(q-r)}\times {\left\{0\right\}}^{r(r+1)}\times \mathbb{R}\},\hfill \end{array}$$

where ${\mathbb{S}}^{(q-r)\times (q-r)}$ is the set of symmetric matrices of size $(q-r)\times (q-r)$. Furthermore,

$$\begin{array}{ccc}\hfill \mathsf{\Theta }& =& \{\mathbf{\theta }\in {\mathbb{R}}^m/\mathbf{\beta }\in {\mathbb{R}}^p;\mathit{D}\in {\mathbb{S}}_{+}^q,{\sigma }_{\mathbf{ϵ}}^2>0\}\hfill \\ & =& \{{\mathbb{R}}^p\times {\mathbb{S}}_{+}^q\times {\mathbb{R}}_{+}\}.\hfill \end{array}$$

According to the results of Baey et al. [6], the tangent cone to $\mathsf{\Theta }$ at ${\mathbf{\theta }}^{\ast }$ is

$$\begin{array}{ccc}\hfill T_{\mathsf{\Theta }}\left({\mathbf{\theta }}^{\ast }\right)& =& {\mathbb{R}}^p\times {\mathbb{R}}^{(q-r)(q-r+1)/2}\times {\mathbb{R}}^{r(q-r)}\times {\mathbb{S}}_{+}^r\times \mathbb{R},\hfill \end{array}$$

where ${\mathbb{S}}_{+}^r$ is the set of symmetric positive semi-definite matrices of size $r\times r$. Since $T_{{\mathsf{\Theta }}_0}\left({\mathbf{\theta }}^{\ast }\right)$ is a linear subspace in $T_{\mathsf{\Theta }}\left({\mathbf{\theta }}^{\ast }\right)$, the asymptotic null distribution of the likelihood ratio test statistic for the above hypothesis test is ${\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })$, where $C^{\ast }=T_{\mathsf{\Theta }}\left({\mathbf{\theta }}^{\ast }\right)\cap T_{{\mathsf{\Theta }}_0}{\left({\mathbf{\theta }}^{\ast }\right)}^{\perp }={\left\{0\right\}}^p\times {\left\{0\right\}}^{(q-r)(q-r+1)/2}\times {\mathbb{R}}^{r(q-r)}\times {\mathbb{S}}_{+}^r\times \left\{0\right\}$.

When $\mathit{D}$ is a full matrix, under the null hypothesis, Baey et al. [6] pointed out that the asymptotic null distribution of the log-likelihood test statistic is ${\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })$, which is a mixture of chi-squared distributions with the degree of freedom ranging from $r(q-r)$ to $r(q-r)+r(r+1)/2$.

$$\begin{array}{ccc}\hfill {\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })& =& \sum _{i=r(q-r)}^{r(q-r)+r(r+1)/2}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }){\chi }_i^2,\hfill \end{array}$$

(8)

where $w_i\left(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }\right),i=r(q-r),\cdots ,r(q-r)+r(r+1)/2$, are some non-negative numbers and ${\sum }_{i=r(q-r)}^{r(q-r)+r(r+1)/2}{w}_i\left(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }\right)=1$; ${\chi }_i^2$ is a chi-squared distribution with i degrees of freedom; $\mathbf{\nu }\left(\mathbf{\theta }\right)$ is a positive definite matrix such that $N^{-\frac{1}{2}}{l}_N^{{}^{\prime }}\left(\mathbf{\theta }\right)\stackrel{d}{\to }{N}_m(\mathbf{0},\mathbf{\nu }\left(\mathbf{\theta }\right))$ and $N^{-1}\{-l_N^{{}^{″}}\left(\mathbf{\theta }\right)\}\stackrel{a.s.}{\to }\mathbf{\nu }\left(\mathbf{\theta }\right)$.

Assume that model $M_k$ has parameter vector ${\mathbf{\theta }}_k={({{\mathbf{\beta }}_k}^T,{{\mathbf{\tau }}_k}^T,{\sigma }_{\mathbf{ϵ},k}^2)}^T$, where ${\mathbf{\beta }}_k$ represents the parameter vector of the fixed effects; ${\mathbf{\tau }}_k$ contains distinct variances and covariances of the random effect covariance matrix ${\mathit{D}}_k$, and ${\sigma }_{\mathbf{ϵ},k}^2$ is the variance of the random error term ${\mathbf{ϵ}}_{\mathbf{k}}$. Let p be the number of parameters of ${\mathbf{\beta }}_k$ and $q_k$ be the number of parameters of ${\mathbf{\tau }}_k$. Assume that we tested the model $M_k$ against model $M_1$, where $M_1$ contains only one random effect, which is a random intercept, and $M_k$ contains k random effects including a random intercept. Assume that the two models contain the same fixed effects part. In this case, $m=dim\left({\mathbf{\theta }}_k\right)=p+q_k+1$, $r=k-1$, $q=k$, and $q-r=1$. Thus, $r(q-r)=k-1$ and $r(q-r)+r(r+1)/2=(k-1)(k+2)/2$. Therefore, based on (8), the asymptotic null distribution of the log-likelihood ratio test statistic is

$$\begin{array}{ccc}\hfill {\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })& =& \sum _{i=k-1}^{(k-1)(k+2)/2}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }){\chi }_i^2,\hfill \end{array}$$

(9)

where $C^{\ast }={\left\{0\right\}}^p\times \left\{0\right\}\times {\mathbb{S}}_{+}^{k-1}\times \left\{0\right\}$; $w_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }),i=(k-1),\cdots ,(k-1)(k+2)/2$, are some non-negative numbers and ${\sum }_{i=k-1}^{(k-1)(k+2)/2}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })=1$, ${\chi }_i^2$ is a chi-squared distribution with i degrees of freedom; $\mathbf{\nu }\left(\mathbf{\theta }\right)$ is a positive definite matrix such that $N^{-\frac{1}{2}}{l}_N^{{}^{\prime }}\left(\mathbf{\theta }\right)\stackrel{d}{\to }{N}_m(\mathbf{0},\mathbf{\nu }\left(\mathbf{\theta }\right))$ and $N^{-1}\{-l_N^{{}^{″}}\left(\mathbf{\theta }\right)\}\stackrel{a.s.}{\to }\mathbf{\nu }\left(\mathbf{\theta }\right)$. □

We note that it is too complex to define ${\mathbb{S}}_{+}^{k-1}$ using equality and inequality constraints on the variance and covariance components of matrix ${\mathit{D}}_k$. Since ${\mathbb{S}}_{+}^{k-1}\subset {\mathbb{R}}^{(k-1)(k-2)/2}\times {\mathbb{R}}_{+}^{k-1}$, in our work, we approximated $C^{\ast }$ by $C={\left\{0\right\}}^p\times \left\{0\right\}\times {\mathbb{R}}^{k-1}\times {\mathbb{R}}^{(k-1)(k-2)/2}\times {\mathbb{R}}_{+}^{k-1}\times \left\{0\right\}$. Thus, ${\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })$ is approximated by

$$\begin{array}{ccc}\hfill {\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C)& =& \sum _{i=k(k-1)/2}^{(k-1)(k+2)/2}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C){\chi }_i^2,\hfill \end{array}$$

(10)

where $w_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C),i=k(k-1)/2,\cdots ,(k-1)(k+2)/2$, are some non-negative numbers and ${\sum }_{i=k(k-1)/2}^{(k-1)(k+2)/2}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C)=1$; ${\chi }_i^2$ is a chi-squared distribution with i degrees of freedom, and $\mathbf{\nu }\left(\mathbf{\theta }\right)$ is a positive definite matrix such that $N^{-\frac{1}{2}}{l}_N^{{}^{\prime }}\left(\mathbf{\theta }\right)\stackrel{d}{\to }{N}_m(\mathbf{0},\mathbf{\nu }\left(\mathbf{\theta }\right))$ and $N^{-1}\{-l_N^{{}^{″}}\left(\mathbf{\theta }\right)\}\stackrel{a.s.}{\to }\mathbf{\nu }\left(\mathbf{\theta }\right)$. This is because $C={\left\{0\right\}}^p\times \left\{0\right\}\times {\mathbb{R}}^{k-1}\times {\mathbb{R}}^{(k-1)(k-2)/2}\times {\mathbb{R}}_{+}^{k-1}\times \left\{0\right\}$ contains a linear space of dimension $(k-1)+(k-1)(k-2)/2$ and is included in a linear space of dimension $(k-1)+(k-1)(k-2))/2+(k-1)$. Therefore, the weights $w_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C)$ are zero for $i=0,\cdots ,(k-1)+(k-1)(k-2)/2-1$ and for $i=(k-1)+(k-1)(k-2))/2+(k-1)+1,\cdots ,m$ [8]. From (10), let $c_k=E({\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C)={\sum }_{i=k(k-1)/2}^{(k-1)(k+2)/2}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C)i$.

We propose the following modified BIC:

$$\begin{array}{c}\hfill BI{C}^{\ast }\left(M_k\right)=-2l({\widehat{\mathbf{\theta }}}_k;\mathit{y})+d_{k}log\left(n\right),\end{array}$$

(11)

where ${\widehat{\mathbf{\theta }}}_k$ is the maximum likelihood estimator of ${\mathbf{\theta }}_k$ in model $M_k$; $n={\sum }_{i=1}^N{n}_i$ and $d_k=p+1.5+c_k$ for $k>1$; $d_k=p+1.5$ for $k=1$; and $d_k=p+1$ for $k=0$.

2.2.3. Modified BIC for Selecting Both Fixed Effects and Random Effects in Linear Mixed Models

In this section, we propose a modified BIC to select both fixed effects and random effects for linear mixed models. We also divided the situations into two cases: when the random effects are independent, that is the covariance matrix, $\mathit{D}$, of random effects is diagonal, and when the random effects are correlated, that is the covariance matrix, $\mathit{D}$, is a full matrix.

Scenario 1: modified BIC for selecting both fixed effects and random effects when random effects are independent.

In the model selection, we assumed that the smallest model (called model $M_1$) contains only the intercept term for fixed effects and a random intercept for random effects. Model $M_k$ contains $(p_k+1)$ fixed effects, and the covariance matrix, ${\mathit{D}}_k$, of random effects is of order $k\times k$. If random effects are assumed to be independent, then the number of random effects variance components is $q_k=k$.

Lemma 3. 

When $\mathit{D}$ is a diagonal matrix, under Assumptions (C1)–(C4) in Appendix A.1, assume that we tested model $M_k$ against model $M_1$, then the asymptotic null distribution of the log-likelihood test statistic is

$$\begin{array}{ccc}\hfill {\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })& =& \sum _{i=p_k}^{p_k+k-1}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }){\chi }_i^2,\hfill \end{array}$$

(12)

where $C^{\ast }={\mathbb{R}}^{p_k}\times \left\{0\right\}\times \left\{0\right\}\times {\mathbb{R}}_{+}^{k-1}\times \left\{0\right\}$; $w_i\left(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }\right),i=p_k,\cdots ,p_k+k-1$, are some non-negative numbers and ${\sum }_{i=p_k}^{p_k+k-1}{w}_i\left(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }\right)=1$; m is the dimension of θ.

Proof. 

When $\mathit{D}$ is a diagonal matrix, $\mathit{D}=diag(d_1,\dots ,d_{q-r},d_{q-r+1},\dots ,d_q)$. The fixed effects parameter $\mathbf{\beta }=({\mathbf{\beta }}_0,{\mathbf{\beta }}_1,\cdots ,{\mathbf{\beta }}_{p-1})$. Without loss of generality, assume that we wanted to test the nullity of the s components of $\mathbf{\beta }$, which are ${\mathbf{\beta }}_1,\cdots ,{\mathbf{\beta }}_s$, and the nullity of the last r variance components of matrix $\mathit{D}$, which are $d_{q-r+1},\dots ,d_q$.

Consider the hypothesis test, $H_0:{\mathbf{\beta }}_1=0,\cdots ,{\mathbf{\beta }}_s=0;d_{q-r+1}=0,\dots ,d_q=0$ versus $H_1:{\mathbf{\beta }}_1\ne 0,\cdots ,{\mathbf{\beta }}_s\ne 0;d_{q-r+1}>0,\dots ,d_q>0$, assuming that the variances that are not tested ($d_1,\dots ,d_{q-r}$) are positive. Let ${\mathbf{\theta }}^{\ast }$ be the true value of the parameter vector. Assume that the null hypothesis holds and ${\mathbf{\theta }}^{\ast }\in {\mathsf{\Theta }}_0$, then the parameter spaces under the null and alternative hypotheses and their tangent cones at ${\mathbf{\theta }}^{\ast }$ are

$$\begin{array}{ccc}\hfill {\mathsf{\Theta }}_0& =& \{{\left\{0\right\}}^s\times {\mathbb{R}}^{p-s}\times {\left\{0\right\}}^r\times {\mathbb{R}}^{q-r}\times {\mathbb{R}}_{+}\},\hfill \\ \hfill T_{{\mathsf{\Theta }}_0}\left({\mathbf{\theta }}^{\ast }\right)& =& \{{\left\{0\right\}}^s\times {\mathbb{R}}^{p-s}\times {\mathbb{R}}^{q-r}\times {\left\{0\right\}}^r\times \mathbb{R}\},\hfill \\ \hfill \mathsf{\Theta }& =& \{{\mathbb{R}}^p\times {\mathbb{R}}_{+}^{q-r}\times {\mathbb{R}}_{+}^r\times \mathbb{R}\},\hfill \\ \hfill T_{\mathsf{\Theta }}\left({\mathbf{\theta }}^{\ast }\right)& =& {\mathbb{R}}^p\times {\mathbb{R}}^{q-r}\times {\mathbb{R}}_{+}^r\times \mathbb{R}.\hfill \end{array}$$

Since $T_{{\mathsf{\Theta }}_0}\left({\mathbf{\theta }}^{\ast }\right)$ is also a linear subspace in $T_{\mathsf{\Theta }}\left({\mathbf{\theta }}^{\ast }\right)$, Baey et al. [6] pointed out that the asymptotic null distribution of ${\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })$ is a mixture of chi-squared distributions with the degree of freedom ranging from s to $s+r$.

$$\begin{array}{ccc}\hfill {\overline{\chi }}^2\left((\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })\right)& =& \sum _{i=s}^{s+r}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }){\chi }_i^2,\hfill \end{array}$$

(13)

where $C^{\ast }=T_{\mathsf{\Theta }}\left({\mathbf{\theta }}^{\ast }\right)\cap T_{{\mathsf{\Theta }}_0}{\left({\mathbf{\theta }}^{\ast }\right)}^{\perp }={\mathbb{R}}^s\times {\left\{0\right\}}^{p-s}\times {\left\{0\right\}}^{q-r}\times {\mathbb{R}}_{+}^r\times \left\{0\right\}$; ${\chi }_i^2$ is a chi-squared distribution with i degrees of freedom and $\mathbf{\nu }\left(\mathbf{\theta }\right)$ is some positive definite matrix such that $N^{-\frac{1}{2}}{l}_N^{{}^{\prime }}\left(\mathbf{\theta }\right)\stackrel{d}{\to }N(0,\mathbf{\nu }\left(\mathbf{\theta }\right))$ and $N^{-1}\{-l_N^{{}^{″}}\left(\mathbf{\theta }\right)\}\stackrel{a.s.}{\to }\mathbf{\nu }\left(\mathbf{\theta }\right)$.

When we test model $M_k$ against model $M_1$, we are testing the nullity of the $s=p_k$ regression coefficients and $r=k-1$ random effects variance components. Therefore, based on Equation (13), the asymptotic null distribution of the log-likelihood test statistic is

$$\begin{array}{ccc}\hfill {\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })& =& \sum _{i=p_k}^{p_k+k-1}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }){\chi }_i^2,\hfill \end{array}$$

(14)

where $C^{\ast }={\mathbb{R}}^{p_k}\times \left\{0\right\}\times \left\{0\right\}\times {\mathbb{R}}_{+}^{k-1}\times \left\{0\right\}$; $w_i\left(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }\right),i=p_k,\cdots ,p_k+k-1$, are some non-negative numbers and ${\sum }_{i=p_k}^{p_k+k-1}{w}_i\left(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast }\right)=1$. □

Let $u_k$ be the expectation of ${\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })$, then $u_k={\sum }_{i=p_k}^{p_k+k-1}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })i$. We propose a modified BIC for this case as

$$\begin{array}{c}\hfill BI{C}^{\ast }\left(M_k\right)=-2l({\widehat{\mathbf{\theta }}}_k;\mathit{y})+d_{k}log\left(n\right),\end{array}$$

(15)

where ${\widehat{\mathbf{\theta }}}_k$ is the maximum likelihood estimator of ${\mathbf{\theta }}_k$ in model $M_k$; $n={\sum }_{i=1}^N{n}_i$ and $d_k=2.5+u_k$ for $k>1$; $d_k=p_k+2.5$ for $k=1$; $d_k=p_k+2$ for $k=0$. Here, in the formula $d_k=2.5+u_k$ for $k>1$, we added $2.5$ to $u_k$ to account for the degrees of freedom of a fixed effect intercept (1 degree of freedom), a random intercept (0.5 degree of freedom), and the variance component of the error term, $\mathbf{ϵ}$ (1 degree of freedom).

Scenario 2: modified BIC for selecting both fixed effects and random effects when random effects are correlated.

When random effects in the linear mixed model (1) are correlated, their covariance matrix, $\mathit{D}$, is a full matrix. Matrix $\mathit{D}$ can be written as $\mathit{D}=\left[\begin{array}{cc}{\mathit{D}}_{11}& {\mathit{D}}_{12}\\ {\mathit{D}}_{12}^T& {\mathit{D}}_{22}\end{array}\right]$, where the size of ${\mathit{D}}_{11}$ is $(q-r)\times (q-r)$ and the size of ${\mathit{D}}_{22}$ is $r\times r$. The number of distinct variance and covariance components in $\mathit{D}$ is $q(q+1)/2$.

Consider the hypothesis test, $H_0:{\mathbf{\beta }}_1=0,\cdots ,{\mathbf{\beta }}_s=0,{\mathit{D}}_{11}>\mathbf{0},{\mathit{D}}_{12}=\mathbf{0},{\mathit{D}}_{22}=\mathbf{0}$ versus $H_1:\mathbf{\beta }\in {\mathbb{R}}^p,\mathit{D}>\mathbf{0}$. That is, $\mathit{D}$ is a positive definite matrix. Let ${\mathbf{\theta }}^{\ast }$ be the true value of the parameter vector. Assume that the null hypothesis holds and ${\mathbf{\theta }}^{\ast }\in {\mathsf{\Theta }}_0$, then the parameter spaces under the null hypothesis and its tangent cone at ${\mathbf{\theta }}^{\ast }$ are:

$$\begin{array}{ccc}\hfill {\mathsf{\Theta }}_0& =& \{{\left\{0\right\}}^s\times {\mathbb{R}}^{p-s}\times {\mathbb{S}}_{+}^{q-r}\times {\left\{0\right\}}^{r(q-r)}\times {\left\{0\right\}}^{r(r+1)}\times {\mathbb{R}}_{+}\},\hfill \\ \hfill T_{{\mathsf{\Theta }}_0}\left({\mathbf{\theta }}^{\ast }\right)& =& \{{\left\{0\right\}}^s\times {\mathbb{R}}^{p-s}\times {\mathbb{S}}^{q-r}\times {\left\{0\right\}}^{r(q-r)}\times {\left\{0\right\}}^{r(r+1)}\times \mathbb{R}\},\hfill \\ & =& \{{\left\{0\right\}}^s\times {\mathbb{R}}^{p-s}\times {\mathbb{R}}^{(q-r)(q-r+1)/2}\times {\left\{0\right\}}^{r(q-r)}\times {\left\{0\right\}}^{r(r+1)}\times \mathbb{R}\},\hfill \end{array}$$

where ${\mathbb{S}}_{+}^{q-r}$ is the set of symmetric positive semi-definite matrices of size $(q-r)\times (q-r)$. Furthermore, the parameter space under the alternative hypothesis is

$$\begin{array}{ccc}\hfill \mathsf{\Theta }& =& \{\mathbf{\theta }\in {\mathbb{R}}^m/\mathbf{\beta }\in {\mathbb{R}}^p;D\in {\mathbb{S}}_{+}^q,{\sigma }_{\mathbf{ϵ}}^2>0\}\hfill \\ & =& \{{\mathbb{R}}^p\times {\mathbb{S}}_{+}^q\times {\mathbb{R}}_{+}\}.\hfill \end{array}$$

The tangent cone to $\mathsf{\Theta }$ at ${\mathbf{\theta }}^{\ast }$ is

$$\begin{array}{ccc}\hfill T_{\mathsf{\Theta }}\left({\mathbf{\theta }}^{\ast }\right)& =& {\mathbb{R}}^p\times {\mathbb{R}}^{(q-r)(q-r+1)/2}\times {\mathbb{R}}^{r(q-r)}\times {\mathbb{S}}_{+}^r\times \mathbb{R}.\hfill \end{array}$$

where ${\mathbb{S}}_{+}^r$ is the set of symmetric positive semi-definite matrices of size $r\times r$. Since $T_{{\mathsf{\Theta }}_0}\left({\mathbf{\theta }}^{\ast }\right)$ is a linear subspace in $T_{\mathsf{\Theta }}\left({\mathbf{\theta }}^{\ast }\right)$, the asymptotic null distribution of the likelihood ratio test statistic for the above hypothesis test is ${\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })$, where $C^{\ast }=T_{\mathsf{\Theta }}\left({\mathbf{\theta }}^{\ast }\right)\cap T_{{\mathsf{\Theta }}_0}{\left({\mathbf{\theta }}^{\ast }\right)}^{\perp }={\mathbb{R}}^s\times {\left\{0\right\}}^{p-s}\times {\left\{0\right\}}^{(q-r)(q-r+1)/2}\times {\mathbb{R}}^{r(q-r)}\times {\mathbb{S}}_{+}^r\times \left\{0\right\}$. As in Lemma 2, it is challenging to define ${\mathbb{S}}_{+}^r$ using equality and inequality constraints. Since ${\mathbb{S}}_{+}^r\subset {\mathbb{R}}^{r(r-1)/2}\times {\mathbb{R}}_{+}^r$, we approximated $C^{\ast }$ by $C={\mathbb{R}}^s\times {\left\{0\right\}}^{p-s}\times {\left\{0\right\}}^{(q-r)(q-r+1)/2}\times {\mathbb{R}}^{r(q-r)}\times {\mathbb{R}}^{r(r-1)/2}\times {\mathbb{R}}_{+}^r\times \left\{0\right\}$. ${\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })$ is approximated by

$$\begin{array}{ccc}\hfill {\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C)& =& \sum _{i=s+r(q-r)+r(r-1)/2}^{s+r(q-r)+r(r-1)/2+r}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C){\chi }_i^2.\hfill \end{array}$$

(16)

where $w_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C),i=s+r(q-r)+r(r-1)/2,\cdots ,s+r(q-r)+r(r-1)/2+r$, are some non-negative numbers and ${\sum }_{i=s+r(q-r)+r(r-1)/2}^{s+r(q-r)+r(r-1)/2+r}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C)=1$; ${\chi }_i^2$ is a chi-squared distribution with i degrees of freedom; $\mathbf{\nu }\left(\mathbf{\theta }\right)$ is a positive definite matrix such that $N^{-\frac{1}{2}}{l}_N^{{}^{\prime }}\left(\mathbf{\theta }\right)\stackrel{d}{\to }{N}_m(\mathbf{0},\mathbf{\nu }\left(\mathbf{\theta }\right))$ and $N^{-1}\{-l_N^{{}^{″}}\left(\mathbf{\theta }\right)\}\stackrel{a.s.}{\to }\mathbf{\nu }\left(\mathbf{\theta }\right)$.

In the model selection, we assumed that model $M_1$ contains only the intercept term for fixed effects and a random intercept for random effects. Model $M_k$ contains $(p_k+1)$ fixed effects, and the covariance matrix, ${\mathit{D}}_k$, of random effects is of order $k\times k$. When random effects are assumed to be correlated, the number of distinct random effects variance and covariance components is $q_k=k(k+1)/2$. When we tested model $M_k$ against model $M_1$, applying (16) with $s=p_k$ and $r=k-1$, then $s+r(q-r)+r(r-1)/2=p_k+k(k-1)/2$ and $s+r(q-r)+r(r-1)/2+r=p_k+(k-1)(k+2)/2$. Thus, the asymptotic null distribution of the log-likelihood ratio test statistic is approximated by

$$\begin{array}{ccc}\hfill {\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C)& =& \sum _{i=p_k+k(k-1)/2}^{p_k+(k-1)(k+2)/2}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C){\chi }_i^2,\hfill \end{array}$$

(17)

where $C={\mathbb{R}}^{p_k}\times \left\{0\right\}\times \left\{0\right\}\times {\mathbb{R}}^{k(k-1)/2}\times {\mathbb{R}}_{+}^{k-1}\times \left\{0\right\}$.

Furthermore, let $h_k$ be the expectation of ${\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C)$, then

$$\begin{array}{c}\hfill h_k=\sum _{i=p_k+k(k-1)/2}^{p_k+(k-1)(k+2)/2}{w}_i(m,\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C)i.\end{array}$$

Our proposed modified BIC for this case is

$$\begin{array}{c}\hfill BI{C}^{\ast }\left(M_k\right)=-2l({\widehat{\mathbf{\theta }}}_k;\mathit{y})+d_{k}log\left(n\right),\end{array}$$

(18)

where ${\widehat{\mathbf{\theta }}}_k$ is the maximum likelihood estimator of ${\mathbf{\theta }}_k$ in model $M_k$; $n={\sum }_{i=1}^N{n}_i$ and $d_k=2.5+h_k$ for $k>1$; $d_k=p_k+2.5$ for $k=1$; and $d_k=p_k+2$ for $k=0$.

Theorem 2. 

Assume that Assumptions $\left(C1\right)-\left(C4\right)$ Appendix A.1 are satisfied and $BI{C}^{\ast }\left(M_k\right)$ is defined as in (18), then

$$\begin{array}{cc}\hfill & \underset{n\to \infty }{lim}P(BI{C}^{\ast }\left(M_T\right)<BI{C}^{\ast }\left(M_k\right))=1\mathrm{for}\mathrm{all}{M}_k\in M^{+},\hfill \\ \hfill \mathit{and}& \underset{n\to \infty }{lim}P(BI{C}^{\ast }\left(M_T\right)<BI{C}^{\ast }\left(M_k\right))=1\mathrm{for}\mathrm{all}{M}_k\in M^{-}.\hfill \end{array}$$

Proof. 

Case 1: For any over-fitting model, $M_k\in M^{+}$, we also prove that $\underset{n\to \infty }{lim}P(BI{C}^{\ast }\left(M_k\right)-BI{C}^{\ast }\left(M_T\right)>0)=1$. Assume that model $M_k$ contains $p_k$ fixed effects and $q_k$ random effects and the true model $M_T$ contains $p_T$ fixed effects and $q_T$ random effects. Let $s=p_k-p_T$ and $r=q_k-q_T$ with $s\ge 0$, $r\ge 0$, and $s+r>0$. Without loss of generality, assume that the covariance matrix of random effects in model $M_k$ is $\mathit{D}=\left[\begin{array}{cc}{\mathit{D}}_{11}& {\mathit{D}}_{12}\\ {\mathit{D}}_{12}^T& {\mathit{D}}_{22}\end{array}\right]$, where ${\mathit{D}}_{11}$ is the covariance matrix of random effects of the true model $M_T$. The size of ${\mathit{D}}_{11}$ is $q_T\times q_T$, and the size of ${\mathit{D}}_{22}$ is $r\times r$. Let ${\mathbf{\theta }}_T={(\underline{{\mathbf{0}}_{\mathbf{\beta }}},{{\mathbf{\beta }}_T}^T,{{\mathit{\psi }}_T}^T,\underline{\mathbf{0}},{\sigma }_{\mathbf{ϵ},T}^2)}^T$ and ${\mathbf{\theta }}_k={({{\mathbf{\beta }}_{k,1}}^T,{{\mathbf{\beta }}_{k,2}}^T,{{\mathit{\psi }}_{k,1}}^T,{{\mathit{\psi }}_{k,2}}^T,{\sigma }_{\mathbf{ϵ},k}^2)}^T$, where $\underline{{\mathbf{0}}_{\mathbf{\beta }}}$ has the same dimension as ${\mathbf{\beta }}_{k,1}$; ${\mathbf{\beta }}_T$ has the same dimension as ${\mathbf{\beta }}_{k,2}$; ${\mathit{\psi }}_T$ has the same dimension as ${\mathit{\psi }}_{k,1}$; $\underline{\mathbf{0}}$ has the same dimension as ${\mathit{\psi }}_{k,2}$. All elements of $\underline{{\mathbf{0}}_{\mathbf{\beta }}}$ and $\underline{\mathbf{0}}$ are 0. We have that

$$BI{C}^{\ast }\left(M_k\right)-BI{C}^{\ast }\left(M_T\right)=-2\left(l({\widehat{\mathbf{\theta }}}_k;\mathit{y})-l({\widehat{\mathbf{\theta }}}_T;\mathit{y})\right)+(d_k-d_T)log\left(n\right).$$

(19)

Then, $-2(l({\widehat{\mathbf{\theta }}}_T;\mathit{y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{y}))$ is the likelihood ratio test statistic of the following hypothesis test:

$$\begin{array}{cc}\hfill & H_0:{{\mathbf{\beta }}_{k,1}}^T=\mathbf{0};{\mathit{D}}_{11}>\mathbf{0};{\mathit{D}}_{12}=\mathbf{0},{\mathit{D}}_{22}=\mathbf{0},\hfill \\ \hfill & H_1:{\mathbf{\beta }}_k\in {\mathbb{R}}^p,\mathit{D}>\mathbf{0}.\hfill \end{array}$$

As in Lemma 2, under $H_0$, the asymptotic distribution of $-2(l({\widehat{\mathbf{\theta }}}_T;\mathit{y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{y}))$ is ${\overline{\chi }}^2(\mathbf{\nu }{\left({\mathbf{\theta }}^{\ast }\right)}^{-1},C^{\ast })$, where $C^{\ast }=T_{\mathsf{\Theta }}\left({\mathbf{\theta }}^{\ast }\right)\cap T_{{\mathsf{\Theta }}_0}{\left({\mathbf{\theta }}^{\ast }\right)}^{\perp }={\mathbb{R}}^s\times {\left\{0\right\}}^{p-s}\times {\left\{0\right\}}^{(q-r)(q-r+1)/2}\times {\mathbb{R}}^{r(q-r)}\times {\mathbb{S}}_{+}^r\times \left\{0\right\}$ with $s=p_k-p_T$, $r=q_k-q_T$, $p=p_k+1$, and $q=q_k$; $\mathbf{\nu }\left(\mathbf{\theta }\right)$ is some positive definite matrix such that $N^{-\frac{1}{2}}{l}^{{}^{\prime }}\left(\mathbf{\theta }\right)\stackrel{d}{\to }{N}_m(\mathbf{0},\mathbf{\nu }\left(\mathbf{\theta }\right))$ and $N^{-1}\{-l^{{}^{″}}\left(\mathbf{\theta }\right)\}\stackrel{a.s.}{\to }\mathbf{\nu }\left(\mathbf{\theta }\right)$.

Therefore, $-2(l({\widehat{\mathbf{\theta }}}_T;\mathit{y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{y}))=O_p\left(1\right)$. We also have that

$$\begin{array}{cc}\hfill 2(l({\widehat{\mathbf{\theta }}}_T;\mathit{y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{y}))& =-2\left(l({\widehat{\mathbf{\theta }}}_1;\mathit{y})-l({\widehat{\mathbf{\theta }}}_T;\mathit{y})\right)\hfill \\ \hfill & -\left[-2\left(l({\widehat{\mathbf{\theta }}}_1;\mathit{y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{y})\right)\right].\hfill \\ \hfill \Rightarrow E\left[2\left(l({\widehat{\mathbf{\theta }}}_T;\mathit{Y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{Y})\right)\right]& =E\left[-2\left(l({\widehat{\mathbf{\theta }}}_1;\mathit{Y})-l({\widehat{\mathbf{\theta }}}_T;\mathit{Y})\right)\right]\hfill \\ \hfill & -E\left[-2\left(l({\widehat{\mathbf{\theta }}}_1;\mathit{Y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{Y})\right)\right]=d_T-d_k,\hfill \end{array}$$

where $l({\widehat{\mathbf{\theta }}}_1;\mathit{y})$ is the maximum log-likelihood of the simplest model, that is the model with only the intercept for fixed effects and a random intercept for random effects. Therefore,

$$\begin{array}{c}\hfill E\left[-2\left(l({\widehat{\mathbf{\theta }}}_T;\mathit{Y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{Y})\right)\right]=d_k-d_T.\end{array}$$

On the other hand, $-2\left(l({\widehat{\mathbf{\theta }}}_T;\mathit{y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{y})\right)$ asymptotically follows a mixture of the chi-squared distributions. Therefore, $E\left[-2\left(l({\widehat{\mathbf{\theta }}}_T;\mathit{Y})-l({\widehat{\mathbf{\theta }}}_k;\mathit{Y})\right)\right]$ must be positive and, therefore, $d_k-d_T>0$. Thus, $BI{C}^{\ast }\left(M_k\right)-BI{C}^{\ast }\left(M_T\right)\to \infty$ as $n\to \infty$ and ${\displaystyle \underset{n\to \infty }{lim}P(BI{C}^{\ast }\left(M_k\right)-BI{C}^{\ast }}$ $\left(M_T\right)>0)=1$ for $M_k\in M^{+}$.

Case 2: For any under-fitting model, $M_k\in M^{-}$, we want to prove that $\underset{n\to \infty }{lim}P(BI{C}^{\ast }\left(M_k\right)-BI{C}^{\ast }\left(M_T\right)>0)=1$. Using similar arguments as in the proof for Case 1 in Theorem 1, we obtain this result. □

3. Simulation

In this section, we evaluated the performance of the proposed BIC*. We compared the performance of the proposed BIC* to the regular BIC. For each candidate model, we computed the BIC* and regular BIC; then for each method, we chose the model with the minimum value of the BIC* and the regular BIC, respectively. All models were run using function “lmer” in the R package lme4 [22]. The chi-bar-squared weights were calculated using function “con-weights-boot” in the R package “restriktor” [20]. Following the methods used in Gao and Song [23] and Chen and Chen [24], the criteria we used to evaluate and compare the proposed BIC to the regular BIC were (1) positive selection rate (PSR), (2) false discovery rate (FDR), and (3) correction rate (CR). For each chosen model, the positive selection rate (PSR) is the ratio of the number of predictors that are correctly identified as significant in the chosen model to the number of predictors that are truly significant in the data-generating model. Then, we took the average of the PSR over all chosen models. The false discovery rate (FDR) is the ratio of the number of predictors that are incorrectly identified as significant in the chosen model to the number of predictors that are identified as significant in the chosen model. Then, we took the average of the FDR over all chosen models. The correction rate (CR) is the proportion of the times the true data-generating model is selected in all chosen models. For each selection criterion, we had 1001 models obtained from 1001 simulations. We then calculated the means and standard deviations of the positive selection rate and false discovery rate and the correction rate for each criterion.

3.1. Simulation Setup

Our data were generated from the linear mixed model, $\mathit{y}=\mathit{X}\mathbf{\beta }+\mathit{Z}\mathit{b}+\mathbf{ϵ}$. For all simulation, $\mathbf{ϵ}$ was generated from a multivariate normal distribution, $N(\mathbf{0},{\sigma }_{\mathbf{ϵ}}^2{\mathit{I}}_n)$ with ${\sigma }_{\mathbf{ϵ}}^2=1$.

3.1.1. Setup A: Choose Random Effects Assuming That the Random Effects Are Independent

Scenario 1: With total number of observations $n=500$ and number of clusters $N=100$, $\mathit{X}$ is an $n\times p$ matrix with $p=2$; the first column of $\mathit{X}$ includes all ones. The second column is ${\mathit{X}}_1$, which was generated from the standard normal distribution. The vector of fixed effects $\mathbf{\beta }={(1,2)}^T$. Matrix $\mathit{Z}$ contains the first two columns ${\mathit{z}}_0$, ${\mathit{z}}_1$, which are the same as two columns of matrix $\mathit{X}$, and two more columns ${\mathit{z}}_2$, ${\mathit{z}}_3$, both generated from the standard normal distributions. Random effects, ${\mathit{b}}_i$, were generated from multivariate normal distribution $N_q(\mathbf{0},\mathit{D})$ with $\mathit{D}$ a $4\times 4$ diagonal matrix and $\mathit{D}=diag({\sigma }_0^2,\dots ,{\sigma }_3^2)$. The random intercept, $b_{i0}$, had a standard deviation of ${\sigma }_0=5$. Random effects components, $b_{i1}$, $b_{i2}$, and $b_{i3}$, had standard deviations ${\sigma }_1$, ${\sigma }_2$, and ${\sigma }_3$, respectively. To measure the ability to detect the significance of the variance component parameters of the proposed $BI{C}^{\ast }$, we considered different sizes of ${\sigma }_1^2$, ${\sigma }_2^2$, and ${\sigma }_3^2$. ${\sigma }_1$ is a sequence of values from 0 to $0.5$ incrementing by $0.05$; ${\sigma }_2$ is a sequence of values from 0 to 1 incrementing by $0.1$; ${\sigma }_3$ is a sequence of values from 0 to 2 incrementing by $0.2$.

Scenario 2: With the total number of observations $n=500$ and number of clusters $N=100$, $\mathit{X}$ is an $n\times p$ matrix with $n=500$; $p=3$; the first column of $\mathit{X}$ includes all ones. The last two columns of matrix ${\mathit{X}}_1$ and ${\mathit{X}}_2$ were generated from the standard normal distributions. The vector of fixed effects $\mathbf{\beta }={(1,2,3)}^T$. Matrix $\mathit{Z}$ contains the first three columns ${\mathit{z}}_0$, ${\mathit{z}}_1$, and ${\mathit{z}}_2$, which are the same as three columns of matrix $\mathit{X}$ and three more columns ${\mathit{z}}_3$, ${\mathit{z}}_4$, and ${\mathit{z}}_5$, which were generated from the standard normal distributions. Random effects, ${\mathit{b}}_i$, were generated from multivariate normal distribution $N_q(\mathbf{0},\mathit{D})$ with $\mathit{D}$ a $6\times 6$ diagonal matrix and $\mathit{D}=diag({\sigma }_0^2,\dots ,{\sigma }_5^2)$. To measure the ability to detect the significance of the variance component parameters of the $BI{C}^{\ast }$, we also considered different sizes of ${\sigma }_1^2$, ${\sigma }_2^2$, and ${\sigma }_3^2$ as in Scenario 1 with ${\sigma }_4^2$ = 0 and ${\sigma }_5^2$ = 0. We then repeated this setup with $n=1000$ ($N=200$) and $n=250$ ($N=50$).

Scenario 3: The setup was similar to the one in Scenario 2. However, matrix $\mathit{Z}$ contains the first three columns ${\mathit{z}}_0$, ${\mathit{z}}_1$, and ${\mathit{z}}_2$, which are the same as the three columns of matrix $\mathit{X}$, and eight more columns ${\mathit{z}}_3$, …, ${\mathit{z}}_{10}$, which were generated from the standard normal distributions. Random effects, ${\mathit{b}}_i$, were generated from multivariate normal distribution $N_q(\mathbf{0},\mathit{D})$ with $\mathit{D}$ a $11\times 11$ diagonal matrix and $\mathit{D}=diag({\sigma }_0^2,\dots ,{\sigma }_{10}^2)$, where ${\sigma }_1^2=0.16$, ${\sigma }_2^2=0.64$, ${\sigma }_3^2=1$, ${\sigma }_4^2=1.44$, and ${\sigma }_5^2,\dots ,{\sigma }_{10}^2$ are all 0. We also repeated this simulation setup with $n=1000$ ($N=200$) and $n=250$ ($N=50$).

3.1.2. Setup B: Choose Random Effects Assuming That the Random Effects Are Correlated

In this set up, the total number of observations is $n=1000$ and the number of clusters is $N=100$. Matrix $\mathit{X}$ and the vector of fixed effects, $\mathbf{\beta }$, were generated the same as in Setup A Scenario 2. Matrix $\mathit{Z}$ contains the first three columns ${\mathit{z}}_0$, ${\mathit{z}}_1$, and ${\mathit{z}}_2$, which are the same as three columns of matrix $\mathit{X}$, and three more columns ${\mathit{z}}_3$, ${\mathit{z}}_4$, and ${\mathit{z}}_5$ were generated from the standard normal distributions. Random effects, ${\mathit{b}}_i$, were generated from multivariate normal distribution $N_q(\mathbf{0},\mathit{D})$ with $\mathit{D}$ a $6\times 6$ matrix. The correlation matrix between the random effects components, $b_{i0}$, $b_{i1}$, $b_{i2}$, and $b_{i3}$, in the data-generating model is

$$\begin{array}{c}\hfill R=\left[\begin{array}{cccc}1& 0.7& 0.6& 0.5\\ 0.7& 1& 0.4& 0.3\\ 0.6& 0.4& 1& 0.5\\ 0.5& 0.3& 0.5& 1\end{array}\right].\end{array}$$

To measure the ability to detect the significance of variance component parameters of the proposed $BI{C}^{\ast }$, we created different cases for different sizes of ${\sigma }_0^2$, ${\sigma }_1^2$, ${\sigma }_2^2$, and ${\sigma }_3^2$, as shown below. ${\sigma }_4^2$, ${\sigma }_5^2$, and the covariances of random effects $b_{i4}$ and $b_{i5}$ corresponding to ${\mathit{z}}_4$ and ${\mathit{z}}_5$ are all 0.

Case 1: The standard deviations of the random effects were ${\sigma }_0=5$, ${\sigma }_1=1.0$, ${\sigma }_2=0.8$, ${\sigma }_3=0.4$, ${\sigma }_4=0$, and ${\sigma }_5=0$.

Case 2: The standard deviations of the random effects were ${\sigma }_0=2$, ${\sigma }_1=0.8$, ${\sigma }_2=0.5$, ${\sigma }_3=0.3$, ${\sigma }_4=0$, and ${\sigma }_5=0$.

Case 3: The standard deviations of the random effects were ${\sigma }_0=2$, ${\sigma }_1=0.5$, ${\sigma }_2=0.4$, ${\sigma }_3=0.2$, ${\sigma }_4=0$, and ${\sigma }_5=0$.

Case 4: In this case, we kept the standard deviations of the random effects the same as the ones in Case 2. However, we increased the correlations by $0.1$ for each non-zero correlation in the correlation matrix to see how this affects the correction rates. The correlation matrix between the random effects is

$$\begin{array}{c}\hfill R_1=\left[\begin{array}{cccc}1& 0.8& 0.7& 0.6\\ 0.8& 1& 0.5& 0.4\\ 0.7& 0.5& 1& 0.6\\ 0.6& 0.4& 0.6& 1\end{array}\right].\end{array}$$

3.1.3. Setup C: Choose Both Fixed Effects and Random Effects Assuming That the Random Effects Are Correlated

With the total number of observations $n=1000$ and number of clusters $N=100$, $\mathit{X}$ is an $n\times p$ matrix with $p=6$; the first column of $\mathit{X}$ includes all ones. The last five columns, ${\mathit{X}}_1$ to ${\mathit{X}}_5$, weer generated from the standard normal distribution. The vector of fixed effects $\mathbf{\beta }={(1,2,3,1,0,0)}^T$. Matrix $\mathit{Z}$ contains the first three columns ${\mathit{z}}_0$, ${\mathit{z}}_1$, and ${\mathit{z}}_2$, which are the same as three columns of matrix $\mathit{X}$, and three more columns ${\mathit{z}}_3$, ${\mathit{z}}_4$, and ${\mathit{z}}_5$ were generated from the standard normal distributions. The correlation matrix between the random effects components, $b_{i0}$, $b_{i1}$, $b_{i2}$, and $b_{i3}$, in the data-generating model is

$$\begin{array}{c}\hfill R=\left[\begin{array}{cccc}1& 0.7& 0.6& 0.5\\ 0.7& 1& 0.4& 0.3\\ 0.6& 0.4& 1& 0.5\\ 0.5& 0.3& 0.5& 1\end{array}\right].\end{array}$$

To measure the ability to detect the significance of the fixed effects and variance component parameters of the proposed $BI{C}^{\ast }$, we explored two different cases for different sizes of ${\sigma }_0^2$, ${\sigma }_1^2$, ${\sigma }_2^2$, and ${\sigma }_3^2$, as shown below. The ${\sigma }_4^2$, ${\sigma }_5^2$, and covariances corresponding to the random effects of ${\mathit{z}}_4$ and ${\mathit{z}}_5$ are all 0.

Case 1: The standard deviations of the random effects were ${\sigma }_0=5$, ${\sigma }_1=1.5$, ${\sigma }_2=1$, ${\sigma }_3=0.5$, ${\sigma }_4=0$, and ${\sigma }_5=0$.

Case 2: The standard deviations of the random effects were ${\sigma }_0=2$, ${\sigma }_1=0.8$, ${\sigma }_2=0.5$, ${\sigma }_3=0.3$, ${\sigma }_4=0$, and ${\sigma }_5=0$.

We also ran simulations for the case when the random effects were assumed to be uncorrelated and the variances of random effects were the same as the values in Case 1 and Case 2.

3.2. Simulation Procedure

3.2.1. For Setup A

In all scenarios, for each set of values of ${\sigma }_1^2$, ${\sigma }_2^2$, and ${\sigma }_3^2$, $B=1001$ simulations were run. In each simulation, all possible candidate models were run. All these models had the same fixed effect covariates (including $X_1$ and the intercept); meanwhile, the covariates for random effects part varied in the power set of $\{1,2,3\}$. The proposed $BI{C}^{\ast }$ and regular BIC were calculated for each model. Then, one model with the minimum proposed BIC was selected and one model with the minimum regular BIC. Now, for each selection criterion, we had 1001 models obtained from 1001 simulations. We calculated the correction rate (CR) for each criterion.

In Scenario 2, for each set of values of ${\sigma }_1^2$, …, ${\sigma }_5^2$, $B=1001$ simulations were run. In each simulation, all possible candidate models were run. All these models had the same fixed effect covariates (including ${\mathit{X}}_1$, ${\mathit{X}}_2$, and the intercept); meanwhile, the covariates for random effects varied in the power set of $\{1,\dots ,5\}$. The proposed $BI{C}^{\ast }$ and regular BIC were calculated for each model. Then, one model with the minimum proposed BIC was selected, and one model with the minimum regular BIC was selected. We calculated the means and standard deviations of the positive selection rate and false discovery rate. We also calculated the correction rate for each criterion.

In Scenario 3, with the given set of values of ${\sigma }_1^2$, …, ${\sigma }_{10}^2$, $B=1001$ simulations were run. In each simulation, all possible candidate models were run. All these models had the same fixed effect covariates; meanwhile, the covariates for the random effects varied in the power set of $\{1,\dots ,10\}$. We calculated the means and standard deviations of the positive selection rate and false discovery rate and calculated the correction rate for each criterion. All simulations were performed by using R Version $4.0.2$ [25].

3.2.2. For Setup B

In each case presented above, $B=1001$ simulations were run. In each simulation, all possible candidate models were run. All these models had the same fixed effect covariates (including the intercept, ${\mathit{X}}_1$ and ${\mathit{X}}_2$); meanwhile, the covariates for the random effects part varied in the power set of $\{1,2,3,4,5\}$ and also included a random intercept. The proposed $BI{C}^{\ast }$, regular BIC, and cAIC were calculated for each model. Greven and Kneib [26] developed an analytic version of the corrected cAIC, and their method was implemented in the cAIC4 package in R [27]. Then, one model with the minimum proposed BIC was selected; one model with the minimum regular BIC was selected; one model with the minimum cAIC was selected. We calculated the means and standard deviations of the positive selection rate and false discovery rate and the correction rate for each criterion.

3.2.3. For Setup C

For each case above, we ran $B=1001$ simulations. In each simulation, all possible candidate models were run. All models contained the intercept term for the fixed effect and a random intercept for the random effects. The covariates for the fixed effects part varied in the power set of $\{1,2,3,4,5\}$ for ${\mathit{X}}_1$ to ${\mathit{X}}_5$, and the covariates for random effects part varied in the power set of $\{1,2,3,4,5\}$ for ${\mathit{z}}_1$ to ${\mathit{z}}_5$. We also included the models that included only the intercept term for the fixed effect with varying random effects and the models that included a random intercept only with varying fixed effects. The proposed $BI{C}^{\ast }$ and regular BIC were calculated for each model. Then, the model with the minimum proposed BIC was selected, and the model with the minimum regular BIC was selected.

3.3. Simulation Results

Scenario 1: Table 1 summarizes the results of Scenario 1. We observed that the correction rate for the proposed $BI{C}^{\ast }$ was greater than that of the regular BIC. Furthermore, the correction rates of the two methods were higher when the values of ${\sigma }_1^2$, ${\sigma }_2^2$, and ${\sigma }_3^2$ were bigger.

Table 1. Comparison of the proposed BIC and regular BIC methods in terms of correction rate for the simulation in Scenario 1 with $n=500$ and $N=100$.

${\mathit{\sigma }}_1$	${\mathit{\sigma }}_2$	${\mathit{\sigma }}_3$	Correction Rate
			Proposed BIC	Regular BIC
0.00	0.00	0.00	0.00	0.00
0.05	0.10	0.20	0.00	0.00
0.10	0.20	0.40	0.01	0.00
0.15	0.30	0.60	0.04	0.01
0.20	0.40	0.80	0.11	0.02
0.25	0.50	1.00	0.24	0.08
0.30	0.60	1.20	0.36	0.18
0.35	0.70	1.40	0.54	0.32
0.40	0.80	1.60	0.67	0.47
0.45	0.90	1.80	0.78	0.60
0.50	1.00	2.00	0.87	0.72

“Correction Rate” reports the proportion of times the selected model is the true data-generating model.

Scenario 2: Table 2 summarizes the results of Scenario 2. The simulation results suggested that the values of the positive selection rate (PSR) for the proposed $BI{C}^{\ast }$ were higher than the regular BIC when the values of the variance components were close to 0. That is, the ability to choose the significant variance components was higher for the proposed $BI{C}^{\ast }$ than the regular BIC. Almost all of the false discovery rate (FDR) values were within 5 percent in all cases. We also observed that the proposed BIC approach had a higher FDR and corresponding SD as compared to the regular BIC approach. For some very low values of the sigma values, the FDR values of the proposed BIC were greater than 5 percent. The possible reason behind this is because the calculation of the penalty term of the regular BIC uses an exact chi-squared distribution, meanwhile the penalty term of proposed BIC uses the approximated weights of the chi-bar-square distribution.

Table 2. Comparison of the proposed BIC and regular BIC methods in terms of the positive selection rate, the false discovery rate, and correction rate for different values of ${\sigma }_1$, ${\sigma }_2$, ${\sigma }_3$, ${\sigma }_4=0$, and ${\sigma }_5=0$ in Scenario 2 with $n=500$ and $N=100$.

			Proposed BIC			Regular BIC
${\mathit{\sigma }}_1$	${\mathit{\sigma }}_2$	${\mathit{\sigma }}_3$	PSR (SD)	FDR (SD)	Correction Rate	PSR (SD)	FDR (SD)	Correction Rate
0.00	0.00	0.00	0.029 (0.010)	0.067 (0.062)	0.00	0.004 (0.001)	0.009 (0.008)	0.00
0.05	0.10	0.20	0.118 (0.031)	0.060 (0.053)	0.00	0.037 (0.011)	0.013 (0.013)	0.00
0.10	0.20	0.40	0.392 (0.034)	0.033 (0.016)	0.01	0.292 (0.027)	0.007 (0.005)	0.00
0.15	0.30	0.60	0.537 (0.034)	0.027 (0.011)	0.03	0.429 (0.026)	0.008 (0.004)	0.01
0.20	0.40	0.80	0.657 (0.032)	0.026 (0.009)	0.12	0.568 (0.032)	0.007 (0.003)	0.04
0.25	0.50	1.00	0.734 (0.028)	0.016 (0.005)	0.23	0.660 (0.025)	0.003 (0.001)	0.10
0.30	0.60	1.20	0.796 (0.028)	0.019 (0.006)	0.37	0.719 (0.021)	0.004 (0.001)	0.18
0.35	0.70	1.40	0.854 (0.027)	0.018 (0.005)	0.53	0.777 (0.025)	0.004 (0.001)	0.33
0.40	0.80	1.60	0.902 (0.023)	0.013 (0.004)	0.67	0.830 (0.028)	0.004 (0.001)	0.48
0.45	0.90	1.80	0.945 (0.015)	0.015 (0.004)	0.80	0.888 (0.025)	0.004 (0.001)	0.66
0.50	1.00	2.00	0.960 (0.012)	0.016 (0.004)	0.83	0.916 (0.021)	0.003 (0.001)	0.74

PSR is positive selection rate, and FDR is false discovery rate; both are averaged over 1001 simulations. All values in brackets are sample standard deviations.

As the values of the variance components increased, the PSR increased. From the results obtained, we also saw that the ability to choose the true model also became larger as the values of the variance components increased. We also noted that the standard deviations were small for all cases. This means that the estimated PSR and FDR were very consistent.

Figure 1 shows the comparison of the proposed BIC and regular BIC methods in terms of the positive selection rate and correction rate for different values of ${\sigma }_1$, ${\sigma }_2$, and ${\sigma }_3$ when $n=500$ and $(N=100)$ in Scenario 2.

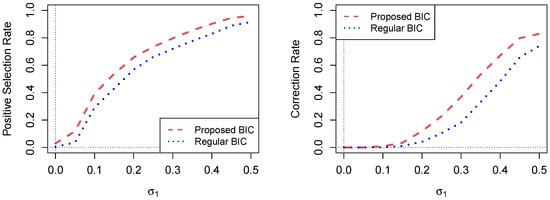
Figure 1. Comparison of the proposed BIC and regular BIC methods in terms of the positive selection rate and correction rate for different values of ${\sigma }_1$, ${\sigma }_2$, and ${\sigma }_3$, $n=500 (N=100)$. In this simulation setup, for each value of ${\sigma }_1$ on the horizontal axis, the value of ${\sigma }_2$ is $2\ast {\sigma }_1$ and the value of ${\sigma }_3$ is $4\ast {\sigma }_1$; ${\sigma }_4=0$ and ${\sigma }_5=0$.

Figure 2 shows the comparison of the positive selection rate (PSR) and correction rates for Scenario 2 when $n=250$, 500, and 1000 with $N=50$, 100, and 200, respectively. Given the same set of values of ${\sigma }_1^2$, …, ${\sigma }_5^2$, we observed that the positive sensitivity rate increased as the number of clusters N increased.

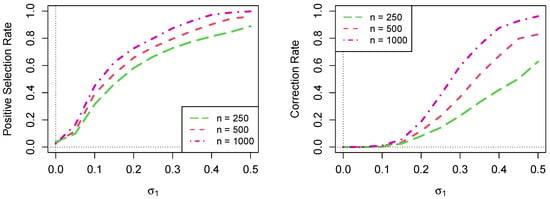
Figure 2. Comparison of the positive selection rate and correction rate for $n=250 (N=50)$, $n=500 (N=100)$, and $n=1000 (N=200)$. For each value of ${\sigma }_1$ on the horizontal axis, the value of ${\sigma }_2$ is $2\ast {\sigma }_1$ and the value of ${\sigma }_3$ is $4\ast {\sigma }_1$; ${\sigma }_4=0$ and ${\sigma }_5=0$.

We also ran 104 simulations with three more competing methods: “cAIC”, “$BI{C}_J$”, and “Splmm”, using the same setting as in Scenario 2. The cAIC is the corrected conditional AIC as implemented in the cAIC4 package in R [27]. The “$BI{C}_J$” is a modified BIC for linear mixed models as introduced in (Jones [11]). “Splmm” (simultaneous penalized linear mixed-effects models) is a method for choosing both the fixed effects and random effects for variable selection using the penalized likelihood function. This method is based on the results in (Yang and Wu [28]) and was implemented in the R-package “$Splmm$”. Figure 3 shows that the modified BIC performed better than the regular BIC, “$BI{C}_J$”, and “$Splmm$” in this scenario in terms of the positive selection rate and correction rate. The ability to choose correct variables was higher for the cAIC than the modified BIC. However, the correction rates for the cAIC were not always higher than that of the modified BIC. The “$Splmm$” method did not seem to work well in this scenario. This may be because the method works better for the case when the number of parameters is much higher than the number of observations.

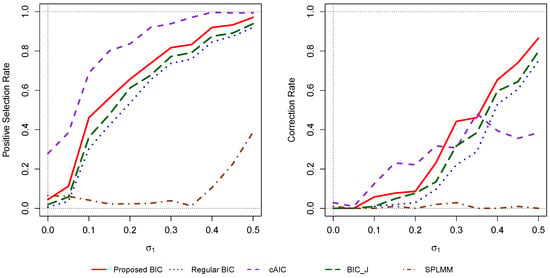
Figure 3. Comparison of the positive selection rate and correction rate for $n=500 (N=100)$ with different competing methods for different values of ${\sigma }_1$, ${\sigma }_2$, and ${\sigma }_3$. For each value of ${\sigma }_1$ on the horizontal axis, the value of ${\sigma }_2$ is $2\ast {\sigma }_1$ and the value of ${\sigma }_3$ is $4\ast {\sigma }_1$; ${\sigma }_4=0$ and ${\sigma }_5=0$.

Scenario 3: Table 3 summarizes the results of Scenario 3. We saw that, in all cases, for the sample sizes $n=250$, 500, 1000, the mean PSR and the correction rates were higher for the proposed BIC; meanwhile, the FDRs kept around $5\%$.

Table 3. Comparison of the proposed BIC and regular BIC methods in terms of the positive sensitivity rate and correction rate for $n=250$, $n=500$, and $n=1000$ in Scenario 3.

($\mathit{n},\mathit{N}$)	Method	Average PSR (SD)	Average FDR (SD)	Correction Rate
(250, 50)	Proposed BIC	0.825 (0.015)	0.063 (0.014)	0.21
	Regular BIC	0.771 (0.014)	0.017 (0.004)	0.15
(500, 100)	Proposed BIC	0.883 (0.016)	0.051 (0.010)	0.40
	Regular BIC	0.832 (0.015)	0.009 (0.002)	0.32
(1000, 200)	Proposed BIC	0.959 (0.009)	0.041 (0.008)	0.67
	Regular BIC	0.916 (0.014)	0.005 (0.001)	0.65

“Correction Rate” reports the proportion of times the selected model is the true data-generating model.

Table 4 shows the comparison of the proposed BIC, regular BIC, and cAIC methods in terms of the positive selection rate, the false discovery rate, and correction rate for Case 1 to Case 4. In all cases, the correction rate for the proposed BIC was greater than that of the regular BIC. The difference in the correction rate between these two methods was bigger when the values of ${\sigma }_1^2$, ${\sigma }_2^2$, and ${\sigma }_3^2$ were smaller. In most cases, the two methods seemed to perform better than the cAIC method.

Table 4. Comparison of the proposed BIC, regular BIC, and cAIC methods in terms of the positive selection rate, the false discovery rate, and correction rate for different values of ${\sigma }_0$, ${\sigma }_1$, ${\sigma }_2$, ${\sigma }_3$, ${\sigma }_4=0$, and ${\sigma }_5=0$ with correlated random effects.

	Proposed BIC			Regular BIC			cAIC
Case	PSR (SD)	FDR (SD)	Correction Rate	PSR (SD)	FDR (SD)	Correction Rate	PSR (SD)	FDR (SD)	Correction Rate
1	0.99 (0.0032)	0.0007 (0.0002)	0.967	0.9837 (0.0052)	0.0007 (0.0002)	0.9481	0.9950 (0.0025)	0.1110 (0.0212)	0.6054
2	0.8911 (0.0244)	0.0003 (0.0001)	0.6733	0.8541 (0.0273)	0.0 (0.000)	0.5624	0.9933 (0.0026)	0.0935 (0.0188)	0.6603
3	0.7106 (0.0132)	0.0003 (0.0001)	0.1339	0.6893 (0.0084)	0.0003 (0.0001)	0.0739	0.9314 (0.0184)	0.0940 (0.0206)	0.5355
4	0.9204 (0.0202)	0.0 (0.000)	0.7612	0.8901 (0.0246)	0.0 (0.000)	0.6703	0.995 (0.0016)	0.0904 (0.0189)	0.6763

PSR is positive selection rate, and FDR is false discovery rate; both are averaged over 1001 simulations. All values in brackets are sample standard deviations.

Table 5 shows the comparison of the proposed BIC, regular BIC, and cAIC methods in terms of fixed effects correction rate, random effects correction rate, and both effects correction rate for both Case 1 and Case 2 when random effects were assumed to be correlated.

Table 5. Comparison of the proposed BIC, regular BIC, and cAIC methods in terms of the correction rate for fixed effects, random effects, and both for different values of ${\sigma }_0$, ${\sigma }_1$, and ${\sigma }_2$ with ${\sigma }_3$, ${\sigma }_4=0$, ${\sigma }_5=0$, and correlated random effects.

	Proposed BIC			Regular BIC			cAIC
Case	FE-CR	RE-CR	Both-CR	FE-CR	RE-CR	Both-CR	FE-CR	RE-CR	Both-CR
1	0.983	0.999	0.982	0.982	0.997	0.979	0.3147	0.3177	0.1708
2	0.975	0.6673	0.6503	0.979	0.5684	0.5554	0.3377	0.3746	0.2128

FE-CR is the correction rate for fixed effects variables; RE-CR is the correction rate for random effects variables; Both-CR is the correction rate of selecting the true model. All the rates are calculated over 1001 simulations.

Based on the simulation results for the situation when random effects were assumed correlated in Table 5, we saw that the proposed BIC method performed better than the regular BIC and the cAIC methods in terms of the correction rate for selecting the fixed effects, the correction rate for selecting the random effects, and also for selecting both fixed effects and random effects simultaneously. We also saw that, when the values of the variances for random effects were smaller, the correction rates were lower for all methods. However, the performance of the proposed method was still much better than the other two methods.

When random effects were assumed uncorrelated, based on the simulation results in Table 6, we saw that the proposed BIC and regular BIC still performed well and better than the cAIC method. The proposed BIC method performed better than the regular BIC in Case 2, but did not perform better than the regular BIC in Case 1. This may be because the penalty term of the regular BIC was calculated using the exact chi-squared distribution and the calculation of the penalty term was without any error. However, for the proposed BIC, the weights of the chi-bar-squared distribution were approximated. Therefore, the penalty term was approximated only. From the simulation results, we noticed that when the values of the variances for random effects were smaller, the correction rates were lower for the proposed and regular BIC methods. However, the correction rates in Case 2 were better than Case 1 for the cAIC method.

Table 6. Comparison of the proposed BIC, regular BIC, and cAIC methods in terms of fixed effects correction rate, random effects correction rate, and both effects correction rate for different values of ${\sigma }_0$, ${\sigma }_1$, ${\sigma }_2$, and ${\sigma }_3$ with ${\sigma }_4=0$, ${\sigma }_5=0$, and independent random effects.

	Proposed BIC			Regular BIC			cAIC
Case	FE-CR	RE-CR	Both-CR	FE-CR	RE-CR	Both-CR	FE-CR	RE-CR	Both-CR
1	0.985	0.9481	0.9351	0.986	0.994	0.981	0.5105	0.4865	0.2667
2	0.980	0.8661	0.8511	0.981	0.7672	0.7532	0.5664	0.5385	0.3017

FE-CR is the correction rate for fixed effects variables; RE-CR is the correction rate for random effects variables; Both-CR is the correction rate of selecting the true model. All the rates are calculated over 1001 simulations.

Comparing the computational complexity, the proposed method requires Monte Carlo simulations to estimate the weights so that the penalty parameter can be computed. This is more computational intensive than the regular BIC. In our simulation, for one dataset with a given model, for Setup A, it took about $0.11$ to $0.42$ s for the proposed BIC method and about $0.04$ to $0.07$ s for the regular BIC. For Setup B, it took about $0.19$ s for the proposed BIC, $0.10$ s for the regular BIC, and $0.22$ s for the cAIC. For Setup C with independent random effects, it took about $0.11$ s for the proposed BIC, $0.05$ s for the regular BIC, and $0.09$ s for the cAIC. For Setup C with correlated random effects, it took about $0.19$ s for the proposed BIC, $0.10$ s for the regular BIC, and $0.21$ s for the cAIC. We noted that the model with correlated random effects took longer than the one with independent random effects. Furthermore, the computational time of the proposed method was longer than that of the regular BIC, but quite close to that of the cAIC method. The OS and CPU system specifications that we used to run our methods were Windows 10, CPU: Intel Core $i7-8550U$ with 4 cores, 8 threads. The memory requirements of our methods are 8 GB RAM.

4. Real-Data Application

In this section, we applied the proposed BIC to a real dataset. We worked with a dataset that is a subset of 120 schools of dataset “hsfull” from package “spida2” in R, which was developed by Monette et al. [29]. This dataset was originally from the 1982 “High School and Beyond” (HSB) survey dataset in Raudenbush and Bryk’s text on hierarchical linear models (Raudenbush and Bryk [30]). The data include the mathematics achievement test scores of 5307 students from 50 Catholic and 70 public high schools, with the number of students in each school ranging from 19 to 66 students.

The variables included in the analysis were school identification number, mathematics achievement score ($\mathit{Y}$), socioeconomic status (${\mathit{X}}_1$), sex (female (0) or male (1); ${\mathit{X}}_2$), visible minority status (yes (1) or no (0); ${\mathit{X}}_3$), and school sector (Catholic (0) or public (1); ${\mathit{X}}_4$). Variables ${\mathit{X}}_1$, ${\mathit{X}}_2$, and ${\mathit{X}}_3$ are group-centered. The objective was to study the relationship between students’ mathematics achievement score and socioeconomic status, sex, and visible minority status in public and Catholic schools and whether this relationship varies across schools within each sector.

The candidate variables in the fixed effects part were ${\mathit{X}}_1$, ${\mathit{X}}_2$, ${\mathit{X}}_3$, and ${\mathit{X}}_4$, which are group-centered. The candidate variables in the random effects part were ${\mathit{z}}_1$, ${\mathit{z}}_2$, and ${\mathit{z}}_3$, which are the same as ${\mathit{X}}_1$, ${\mathit{X}}_2$, and ${\mathit{X}}_3$.

We first fit a linear mixed model that included only the intercept term for fixed effects and a random intercept. Then, we fit the models with only the intercept term for fixed effects and all possible combinations of ${\mathit{z}}_1$, ${\mathit{z}}_2$, and ${\mathit{z}}_3$ with a random intercept for random effects. Next, we fit the models with all possible combinations of ${\mathit{X}}_1$, ${\mathit{X}}_2$, ${\mathit{X}}_3$, and ${\mathit{X}}_4$ for fixed effects and only a random intercept for random effects. Lastly, for each combination of ${\mathit{X}}_1$, ${\mathit{X}}_2$, ${\mathit{X}}_3$, and ${\mathit{X}}_4$ for fixed effects, we fit the models with all possible combinations of ${\mathit{z}}_1$, ${\mathit{z}}_2$, and ${\mathit{z}}_3$ with a random intercept for random effects. For each model, we recorded the values of the proposed BIC, regular BIC, and cAIC. There were 128 values for each method. Now, for each method, we chose the model with the minimum value of the corresponding criterion. We applied this procedure for both cases when random effects were assumed to be correlated and uncorrelated.

When random effects were assumed to be correlated, the optimal model we obtained using the proposed BIC was the model with all ${\mathit{X}}_1$, ${\mathit{X}}_2$, ${\mathit{X}}_3$, and ${\mathit{X}}_4$ and a random intercept; the proposed BIC was 34,379.83. The optimal model we obtained using the regular BIC was also the model with ${\mathit{X}}_1$, ${\mathit{X}}_2$, ${\mathit{X}}_3$, and ${\mathit{X}}_4$ and a random intercept only. The regular BIC of this model was also 34,379.83. The cAIC yielded the optimal model, which contained ${\mathit{X}}_1$, ${\mathit{X}}_2$, ${\mathit{X}}_3$, and ${\mathit{X}}_4$ with a random intercept and random slopes of ${\mathit{z}}_1$ and ${\mathit{z}}_3$. The cAIC of the optimal model was 34,166.25.

When random effects were assumed to be uncorrelated, the optimal model we obtained using the proposed BIC was the model with all ${\mathit{X}}_1$, ${\mathit{X}}_2$, ${\mathit{X}}_3$, and ${\mathit{X}}_4$, a random intercept, and random slopes of ${\mathit{z}}_3$; the proposed BIC value was 34,378.23. The optimal model we obtained using the regular BIC was the model with ${\mathit{X}}_1$, ${\mathit{X}}_2$, ${\mathit{X}}_3$, and ${\mathit{X}}_4$ and a random intercept only. The regular BIC of this model was 34,379.83. The cAIC yielded the optimal model, which contained ${\mathit{X}}_1$, ${\mathit{X}}_2$, ${\mathit{X}}_3$, and ${\mathit{X}}_4$ with a random intercept and random slopes of ${\mathit{z}}_1$, ${\mathit{z}}_2$, and ${\mathit{z}}_3$. The cAIC of the optimal model was 34,165.13.

Table 7 shows the proposed BIC, regular BIC, and cAIC for all models that contained ${\mathit{X}}_1$, ${\mathit{X}}_2$, ${\mathit{X}}_3$, and ${\mathit{X}}_4$ with correlated random effects considered.

Table 7. Results of the proposed BIC, regular BIC, and cAIC for all models with correlated random effects considered for the subset of the “hsfull” dataset.

Model	Proposed BIC	Regular BIC	cAIC
Random Intercept (RI)	34,379.33	34,379.83	34,176.92
RI, ${\mathit{z}}_1$	34,380.61	34,385.4	34,167.38
RI, ${\mathit{z}}_2$	34,391.38	34,396.17	34,181.23
RI, ${\mathit{z}}_1$, ${\mathit{z}}_2$	34,401.4	34,410.2	34,174.07
RI, ${\mathit{z}}_2$	34,384.58	34,389.37	34,169.18
RI, ${\mathit{z}}_1$, ${\mathit{z}}_2$	34,391.03	34,400.38	34167.38
RI, ${\mathit{z}}_2$, ${\mathit{z}}_2$	34,405.59	34,414.63	34169.18
RI, ${\mathit{z}}_1$, ${\mathit{z}}_2$, ${\mathit{z}}_2$	34,420.4	34,433.63	34,166.25

All values are rounded to two decimal places.

Table 8 shows the optimal model chosen by each method when the random effects were assumed to be independent and when the random effects were correlated. All ${\mathit{X}}_1$, ${\mathit{X}}_2$, ${\mathit{X}}_3$, and ${\mathit{X}}_4$ were included in the models.

Table 8. Comparison of the optimal model chosen by each method for correlated random effects and independent random effects.

	Proposed BIC		Regular BIC		cAIC
Case	Optimal Model	Proposed BIC	Optimal Model	Regular BIC	Optimal Model	cAIC
Correlated Random Effects	RI	34,379.33	RI	34,379.83	RI, ${\mathit{z}}_1,{\mathit{z}}_2,{\mathit{z}}_3$	34,166.25
Independent Random Effects	RI, ${\mathit{z}}_3$	34,377.73	RI	34,379.83	RI, ${\mathit{z}}_1,{\mathit{z}}_3$	34,165.13

RI means random intercept.

Based on the results presented above, we would choose the model with all ${\mathit{X}}_1$, ${\mathit{X}}_2$, ${\mathit{X}}_3$, and ${\mathit{X}}_4$ for fixed effects and a random intercept and a random slope of ${\mathit{z}}_3$ for random effects assuming that random effects are uncorrelated. There was a significant relationship between students’ math achievement score and socioeconomic status, sex, and visible minority status in public and Catholic schools, and the school mean math achievement score and minority gap effect varied across the schools within each sector.

5. Discussion

In this article, we introduced a modified BIC for linear mixed models that can directly deal with the boundary issue of variance components. First, we focused on selecting random effects variance components and proposed a model selection criterion when the random effects were assumed to be independent (the covariance matrix of random effects was a diagonal matrix). Second, we proposed a criterion for choosing random effects variance components when the random effects were assumed to be correlated. Instead of working with a complex tangent cone to the alternative parameter space, we approximated the tangent cone using a bigger, but simpler cone. This allowed us to obtain the weights of the chi-bar-squared distribution. Lastly, we presented a model selection criterion for choosing both fixed effects and random effects simultaneously in both cases: when random effects were assumed to be independent and when they were correlated. We also proved the consistency of the modified BIC.

Based on the simulation studies, the modified BIC performed quite well in terms of the correction rate. The ability to select the data-generating model of the modified BIC was better when the size of the random effects variance component or the size of correlation component was bigger. Compared to the regular BIC, the modified BIC gave higher correction rates, especially when the variances of random effects were small. Based on the correction rate, the modified BIC and performed better than the regular BIC in most cases. Furthermore, there was significant improvement in the positive selection rate in most of the simulation scenarios.

One limitation of the modified BIC is that, when choosing the optimal model, the proposed method looks at all possible models. Since the number of possible models increased exponentially as the number of fixed effects and random effects increased, the model selection process may be increasingly computationally intensive. We may combine the proposed BIC with some selection procedure such as shrinkage methods or fence methods as introduced in Müller et al. [31] to reduce the number of candidate models. Then, we can use the proposed BIC method to perform model selection.

Appendix A.1. Assumptions for Lemmas 1–3 and Theorems 1 and 2

(C1).

The observations $\mathit{y}=({\mathit{y}}_1,\dots ,{\mathit{y}}_N)$ from different clusters are independent random vectors. All the assumptions of the linear mixed model (1) are satisfied.

(C2).

Let $l_N(\mathbf{\theta };\mathit{y}$) be the log-likelihood function of the linear mixed model (1). Denote by $\mathsf{\Theta }$ the parameter space of the model parameter vector, $\mathbf{\theta }$, and let ${\mathbf{\theta }}^{\ast }$ be the true value of the parameter vector. Denote the vector of first partial derivatives of $l_N(\mathbf{\theta };\mathit{y})$ with respect to $\mathbf{\theta }$ by $l_N^{\prime }\left(\mathbf{\theta }\right)$, and denote the matrix of the second partial derivatives of $l_N(\mathbf{\theta };\mathit{y})$ with respect to $\mathbf{\theta }$ by $l_N^{″}\left(\mathbf{\theta }\right)$. Directional derivatives are used when $\mathbf{\theta }$ is on the boundary of $\mathsf{\Theta }$. (i) Assume that, for all $\mathbf{\theta }$, the first three partial derivatives of the log-likelihood function with respect to $\mathbf{\theta }$ exist almost everywhere. (ii) Furthermore, assume that $N^{-1}$ times the absolute value of the third derivative of $l_N(\mathbf{\theta };\mathit{y})$ is bounded as a function of $({\mathit{Y}}_1,\dots ,{\mathit{Y}}_N)$, whose expectation exists, and finite on the intersection of the neighborhoods of ${\mathbf{\theta }}^{\ast }$ and $\mathsf{\Theta }$.

(C3).

Assume that $n_1,\dots ,n_N$ are uniformly bounded. That is, there exists a constant $K>0$ such that $n_i\le K$ for $i=1,\dots ,N$.

(C4).

Let ${\mathbf{\theta }}_T$ be the parameter vector of the true model $M_T$, and let ${\mathbf{\theta }}_{T,0}$ denote the true value of ${\mathbf{\theta }}_T$.

(i)

For any under-fitting model, $M_k$, with model parameter ${\mathbf{\theta }}_k\in {\mathsf{\Theta }}_k$, assume that $E_{T,0}\left[log\frac{f(\mathit{y};{\mathbf{\theta }}_{T,0})}{f(\mathit{y};{\mathbf{\theta }}_k)}\right]$ exists and there exists a unique pseudo true, ${\mathbf{\theta }}_{k,0}$, such as ${\mathbf{\theta }}_{k,0}=\underset{{\mathbf{\theta }}_k\in {\mathsf{\Theta }}_k}{argmin}{E}_{T,0}\left[log\frac{f_i(\mathit{y};{\mathbf{\theta }}_{T,0})}{f_i(\mathit{y};{\mathbf{\theta }}_k)}\right]$ for all i.

(ii)

For all $\mathbf{\theta }$, $\frac{1}{N}(l(\mathbf{\theta };\mathit{y})-E_{T,0}\left[l(\mathbf{\theta };\mathit{Y})\right])\stackrel{p}{\to }0$.

(iii)

For any two nested models, $M_k\subset M_l$, $-2\left(l({\widehat{\mathbf{\theta }}}_k;\mathit{Y})-l({\widehat{\mathbf{\theta }}}_l;\mathit{Y})\right)$ is bounded by an integrable function, $M\left(\mathit{Y}\right)$, and $E\left[M\right(\mathit{Y}\left)\right]<\infty$.

Appendix A.2. Graphs of Chi-Bar-Squared Distributions

In this section, we created graphs of some density functions of different chi-bar-squared distributions.

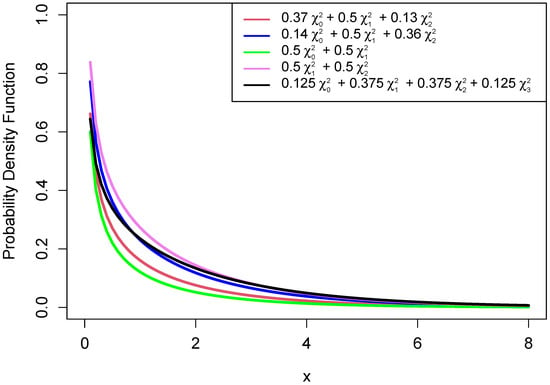
Figure A1. Chi-bar-squared distributions.

The graphs show that the distribution of a chi-bar-squared distribution depends on it mixing weights.

Appendix A.3. Graphical Example of the Boundary Issue

In this example, we tested $H_0:{\sigma }_1^2>0,{\sigma }_2^2=0$ against $H_1:{\sigma }_1^2>0,{\sigma }_2^2>0$. The parameter space under the null hypothesis was the set of all points of the form $(a,0)$ with $a>0$, illustrated by the blue interval along the axis of ${\sigma }_1^2$. Under the alternative hypothesis, the parameter space was the set of all points $(a,b)$ with $a>0$ and $b\ge 0$ and is illustrated by the shaded orange region on the graph. Under the null hypothesis, the testing value of the parameter vector lies on the boundary of the parameter space.

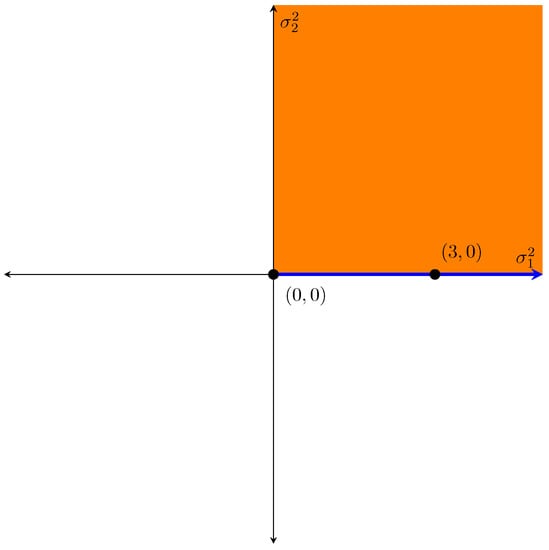
Figure A2. Graphical example of boundary issue.