Authenticating q-Gram-Based Similarity Search Results for Outsourced String Databases

Abstract

Approximate string searches have been widely applied in many fields, such as bioinformatics, text retrieval, search engines, and location-based services (LBS). However, the approximate string search results from third-party servers may be incorrect due to the possibility of malicious third parties or compromised servers. In this paper, we design an authenticated index structure (AIS) for string databases, which is based on the Merkle hash tree (MHT) method and the q-gram inverted index. Our AIS can facilitate verification object (VO) construction for approximate string searches with edit distance thresholds. We design an efficient algorithm named GS² for VO construction at the server side and search result verification at the user side. We also introduce an optimization method called GS²-opt that can reduce VO size dramatically. Finally, we conduct extensive experiments on real datasets to show that our proposed methods are efficient and promising.

1. Introduction

The advancement of big data technologies for data collection, data storage, and data analytics has led to a dramatic increase in the volume of data managed. As a result, organizations, especially small- and medium-sized enterprises, are usually overwhelmed by the maintenance and processing of huge amounts of data. To tackle these challenges, cloud computing and database outsourcing have emerged in the past decade and have become the mainstream computing paradigm today. Database outsourcing (DBO) means that the data owners (DO) delegate their data to a third-party service provider (note that we also refer to it as the server in the following), and the server takes charge of data storage for DO and query processing for users.

Although the DBO paradigm offers many benefits to companies to cope with the challenges brought by big data, it also poses threats to data privacy and security since DO is usually reluctant to reveal their data to the public and the users do not want their query results to be tampered with. A potential threat is that the server may not answer user queries honestly in order to save computational costs; for example, the server may only process query requests on a small part of the data. Another risk is that the query results may be compromised by an untrusted server. Therefore, it is essential for the user to verify or authenticate whether the query results provided by the server are correct.

Many real-world databases contain a variety of textual data, such as personal information, blogs, emails, documents, scientific reports, genome data, etc. In certain scenarios, even the entire data records in a relational database are regarded as textual data during processing [1]. Some companies may resort to the DBO paradigm by outsourcing their textual data to third parties in order to reduce the overhead of database maintenance. On the other hand, some organizations choose to maintain textual data and process user queries on their own; for example, a tool called BLAST (basic local alignment search tools) is provided to the public to search for similar nucleotide sequences. Note that in either method of database maintenance, there may exist security risks, e.g., the server might be malicious or might have been hacked; hence, the query result returned from the server may not be trusted anymore.

In this paper, we consider the problem of result authentication for approximate string searches. Currently, there exists some research work on text/string search result authentication. For example, Pang et al. designed an elegant solution for text search result verification [2]; however, the solution focuses on authenticating TF-IDF-based text search results and is not suitable for string search result authentication. Dong et al. [3] proposed an authentication mechanism for an outsourced string similarity search using the MB tree method, which integrates the B${}^{ed}$ tree [4] and MHT methods [5]. Similarly, this work cannot be applied to scenarios where strings are indexed by a q-gram inverted index.

As a general case of string matching, approximate string searches aim to find similar strings with respect to a given string. Approximate string searches have a wide range of applications, such as search engines, duplicate detection, spell checking, plagiarism checking, and genome data analysis. Various metrics are employed to measure the similarity between strings [6], with edit distance being one of the most frequently utilized metrics. However, the time complexity of directly computing edit distance between two strings is high.

Many methods have been proposed to speed up the edit-distance-based computation of approximate string searches. One widely used approach is the q-gram method, which takes q-grams as signatures to filter the candidate set of similar strings, followed by a refinement step to verify the remainder in the candidate set. The q-gram method is efficient in that it can filter candidates quickly without having to scan the entire set of strings, thus speeding up the approximate string search process.

In this paper, we first design an authenticated index structure for strings, which is based on the Merkle hash tree (MHT) method [5] and the q-gram inverted index. Then, we introduce two schemes, namely GS² and GS²-opt, for authenticating approximate string search results, with the latter being more efficient in terms of communication overhead. Both GS² and GS²-opt comprise several procedures, including approximate string search processing, verification object (VO) construction, and result verification. Our contributions in this paper are summarized as follows:

• We design an authentication structure by incorporating MHT, a popular authenticated data structure, with q-gram-based inverted index [7], an index commonly used to accelerate similar string searches.
• We design an authentication method called GS² for approximate string searches. It is a general authentication scheme suitable for several string similarity measures, such as Edit distances, Hamming distances, and Cosine similarity.
• We develop an optimal method named GS²-opt that reduces the size of VO by combining multiple filtering techniques with an optimized scheme for edit-distance-based searches.
• We complement the proposed methods and conduct extensive experiments on real datasets to verify the effectiveness of our method. According to the experimental data, the GS²-opt approach can reduce the size of VO by $96.27\%$ in comparison to the GS² scheme.

The paper is organized as follows. We introduce preliminaries and give a brief overview of related work in Section 2. In Section 3, we formally define the problem of authenticating the results of approximate string searches. In Section 4, we present our approaches, named GS² and GS²-opt, to solve the problem. Then, we analyse the security of our approach in Section 5. We present our experimental results which verify the effectiveness of our method in Section 6. Finally, we conclude the paper in Section 7.

2. Background

In this section, we will introduce the related work and preliminary knowledge relevant to the paper.

2.1. Approximate String Search

Given a query string $s_Q$, a set D of strings, and a threshold $\delta$, the problem of approximate string searches (or string similarity searches) is to retrieve all strings $s\in D$ such that the similarity score (based on some specific measure) between s and $s_Q$ is not less than $\delta$. Due to its extensive applications, approximate string searches have garnered a significant amount of attention [4,8,9].

There are several challenges in processing approximate string searches, and the most challenging one is to process approximate string searches with scalability. Many approaches have been put forward, including some that introduce novel index structures [4,10,11,12], while others concentrate on optimizing the search process [8,13,14,15,16,17].

2.2. Edit Distance

Edit distance is the most commonly used measure of string similarity, which indicates the minimum number of single-character operations that transform one string into another. Generally, the permitted edit operations are insertion, deletion, and substitution, and one can assign a specific cost or weight to each of these operations. Currently, the simplest edit distance is the Levenshtein distance [18], where the cost of each operation is 1 (except for a character substitute itself, which is 0). Note that we use the Levenshtein distance as the edit distance in this paper.

Let $ed(s_1,s_2)$ be the edit distance between two strings $s_1$ and $s_2$. Given two strings $s_1$ and $s_2$, if $ed(s_1,s_2)\le k$, where k is a pre-specified threshold, then we say that $s_1$ and $s_2$ are similar. Wagner et al. [19] presented a classical algorithm for computing edit distance with a time complexity $O\left(\right|s_1|*|s_2\left|\right)$, where $|s_i|$ is the length of $s_i$.

2.3. q-Gram-Based Inverted Index

Since the calculation of the edit distance is time-consuming, preprocessing is usually employed to speed up the calculation process, during which features of strings are generated first and then indexed subsequently. Commonly used index structures include the q-gram inverted index, trie index, suffix tree index, and BWT index.

The q-gram inverted index [20] is one of the most commonly used indexing methods for strings. Basically, q-grams of a string s are all substrings (grams) of length q, and there are $\left|s\right|-q+1$ such substrings in total. We call the set of those substrings the q-gram set, denoted by $grams(s,q)$. For instance, consider a string s = “words”; the 2-gram set of s is $\{“wo”,“or”,“rd”,“ds”\}$, i.e., $grams(s,2)=\{“wo”,“or”,“rd”,“ds”\}$. It is intuitive that similar strings share a certain number of q-grams.

The q-gram-based inverted index consists of two components, i.e., a dictionary of grams and a set of inverted lists (note that we also call it the i-list for brevity). Each entry of the dictionary includes a gram and a pointer to the corresponding i-list of the gram, and the i-list is a collection of string IDs (denoted by $Sid$), where each string contains the gram as a substring. To illustrate, an example string set is given in  

Table 1. An example string set.

Sid	String
1	$arise$
2	$braise$
3	$fraise$
4	$praise$
5	$raise$
6	$rise$

, and its corresponding 2-gram inverted index is shown in  

Table 2. 2-gram inverted index of Table 1.

Gram		Inverted List
$ai$	↦	2, 3, 4, 5
$ar$	↦	1
$br$	↦	2
$fr$	↦	3
$is$	↦	1, 2, 3, 4, 5, 6
$pr$	↦	4
$ra$	↦	2, 3, 4, 5
$ri$	↦	1, 6
$se$	↦	1, 2, 3, 4, 5, 6

.

Currently, much research effort is being put into using the q-gram based inverted index to speed up string similarity searches [9,21,22,23,24,25]. Jokinen et al. [21] quantitatively revealed the characteristics of sharing grams between query strings and candidate strings (as presented in Lemma 1), thus laying down a foundation for fast candidate string filtering without scanning the entire set of strings.

Lemma 1. 

If $ed(s_i,s_Q)\le k$, then at least $|s_Q|-q+1-kq$ grams are shared by both $s_i$ and $s_Q$ [21], i.e.,

$$\begin{array}{cc}\hfill & ed(s_i,s_Q)\le k\wedge \left|s_Q\right|-q+1-kq>0\hfill \\ \hfill \Rightarrow & |s_Q|-q+1-kq\le |grams(s_i,q)\cap grams(s_Q,q)|.\hfill \end{array}$$

(1)

2.4. Result Authentication for String Search

To solve the problem of text search result authentication, Pang et al. proposed an elegant solution for text search engines based on an inverted index [2]. Later, inspired by this work, Goodrich et al. extended Pang’s solution to support web content searches by authenticating web crawlers [26]. However, these approaches are not suitable for approximate string search authentication because they use similarity functions for documents, such as TF-IDF, which cannot be used to measure the similarity between strings.

Dong et al. presented an authentication structure that integrates the B${}^{ed}$ tree and MHT methods to prove the soundness and completeness of approximate record-joining results [1] and for outsourced string similarity searches [3]. Their approach relies on a specific data structure, i.e., the B${}^{ed}$ tree structure, and cannot be employed directly to a scenario where strings are indexed by the q-gram inverted index.

3. Problem Formulation

In this section, we describe the system model, threat model, and design goals.

3.1. System Model

Our authentication scheme for approximate string searches involves three parties, i.e., the data owner (DO), the cloud service provider (or server), and the user (or client), as shown in  Figure 1. Here, DO refers to the entity that possesses a textual dataset D and intends to outsource it to the server. To assist users to authenticate the search results from the server, the DO needs to upload additional auxiliary information along with the dataset D to the server. The server is responsible for database maintenance and query processing. When a user sends a query request with a query string $s_Q$ and a similarity threshold k to the server, the latter processes the query against D, collects the result R, generates a verification object (VO), and returns R and VO to the user. After receiving R and VO, the user can verify (1) whether the server has performed the query honestly and (2) whether the result R is correct.

3.2. Threat Model

The assumption made in this paper is that the server is not completely trustworthy, and thus, the results returned by the server may be incomplete or unsound. Therefore, the user must verify the results to guarantee both completeness and soundness. By completeness, we mean that the query result set R includes all the qualified strings from the dataset D based on the user’s query. On the other hand, by soundness, we mean that all the strings in R indeed come from D without being tampered with and meet the query criteria.

To be more specific, given a query Q issued by the user, let $R_{DO}$ and $R_S$ be the query result set obtained at the DO side (Note that DO is always honest, so $R_{DO}$ is complete and sound) and at the server side, respectively. We have the following inference:

• $R_S$ is complete, if $\forall s_i\in R_{DO}\Rightarrow s_i\in R_S$ holds.
• $R_S$ is sound, if $\forall s_i\in R_S\Rightarrow s_i\in R_{DO}$ holds.

Note that we also use correct to refer to the situation where both completeness and soundness are achieved.

We present some instances of incorrect results in  Figure 2, where the string set is D={“Alice",“Police",“Marialice"}, and the correct result for a query with $s_Q$=“Molice" and k=2 is $R_{DO}$={“Alice",“Police"}.  Figure 2a shows that an item in R_DO has been eliminated by the server.  Figure 2b shows that an additional item that does not satisfy the query requirements has been appended to the result R’ by the server.  Figure 2c shows that the server has fabricated an item and adds it to the result R’.  Figure 2d shows that the server has altered the item from “Police" to “P0lice", and, concretely, this case violates both the completeness and soundness properties.

3.3. Design Goals

There are two key goals for our solution, i.e., security and efficiency. Security means that our solution is capable of detecting incomplete or tampered query results for the user. Efficiency means that our solution should not require accessing the entire database for query result authentication. Meanwhile, our solution should also aim to minimize the size of the VO so as to cut down communication overhead between the server and user, as well as the time cost in verification at the user side.

4. Our Solutions

In this section, we first present GS², an efficient authentication method designed for approximate string searches on outsourced string databases that are indexed by a q-gram-based inverted index. Then, we introduce an optimization method called GS²-opt, which reduces VO size dramatically. Both GS² and GS²-opt can prove to the user that (1) any string in D that is similar to $s_Q$ is included in R, and there is no qualified string in D left behind, and (2) all the strings in R are indeed similar to $s_Q$ and are not tampered with.

Basically, our methods consist of three phases: (1) a preprocessing phase, during which the DO creates an authenticated data structure and signs it. Then, the DO uploads D, the root signature ($sig$) of the structure and parameter q to the server; (2) a searching phase, during which the server receives a query request from the user, performs a string search against D to find query result R, and constructs a VO with respect to R. The server then returns both R and VO to the user; and (3) an authentication phase, during which the user verifies the correctness of the query result R against VO.

4.1. GS²

We present the details of the three phases of GS² in the following.

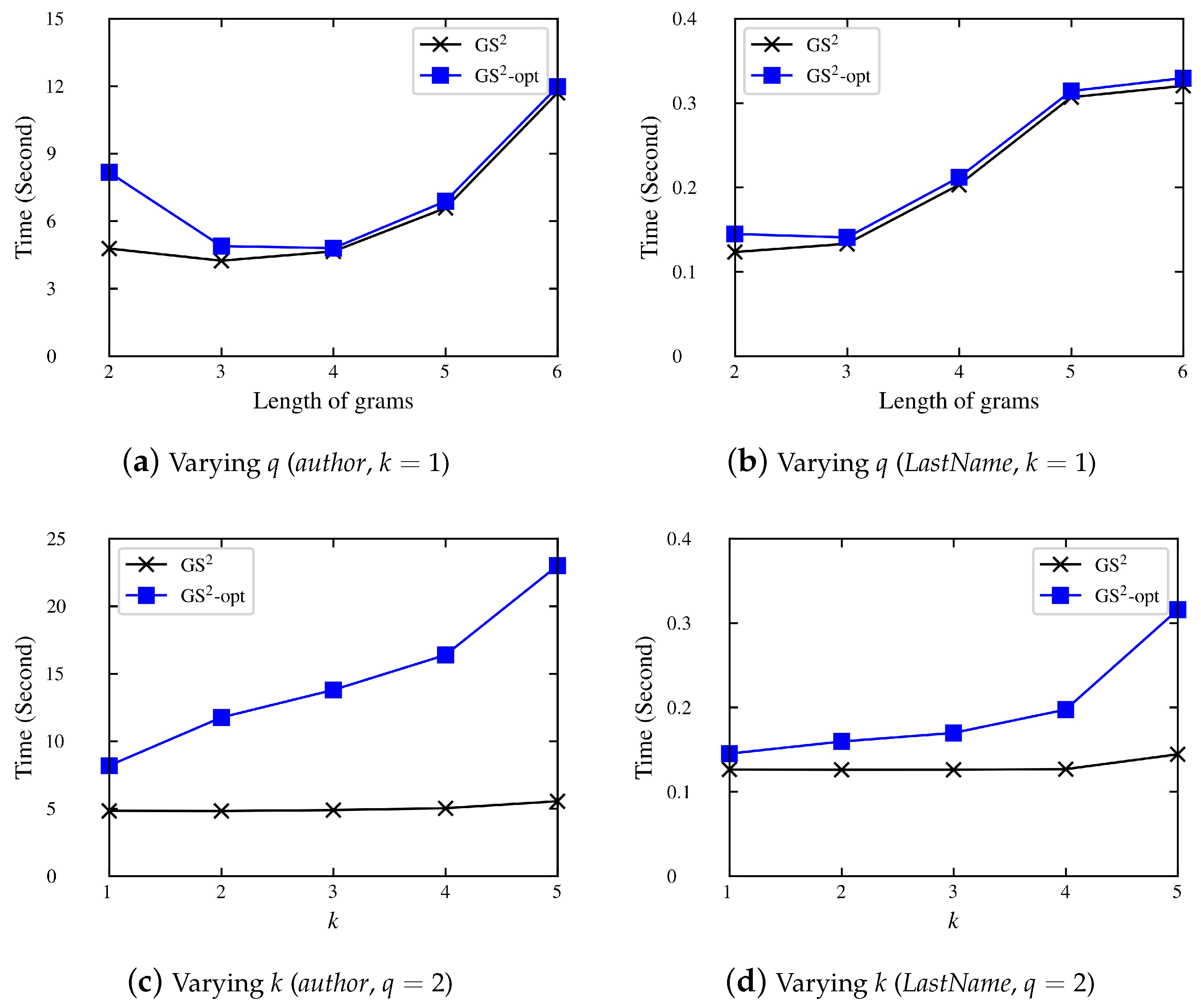
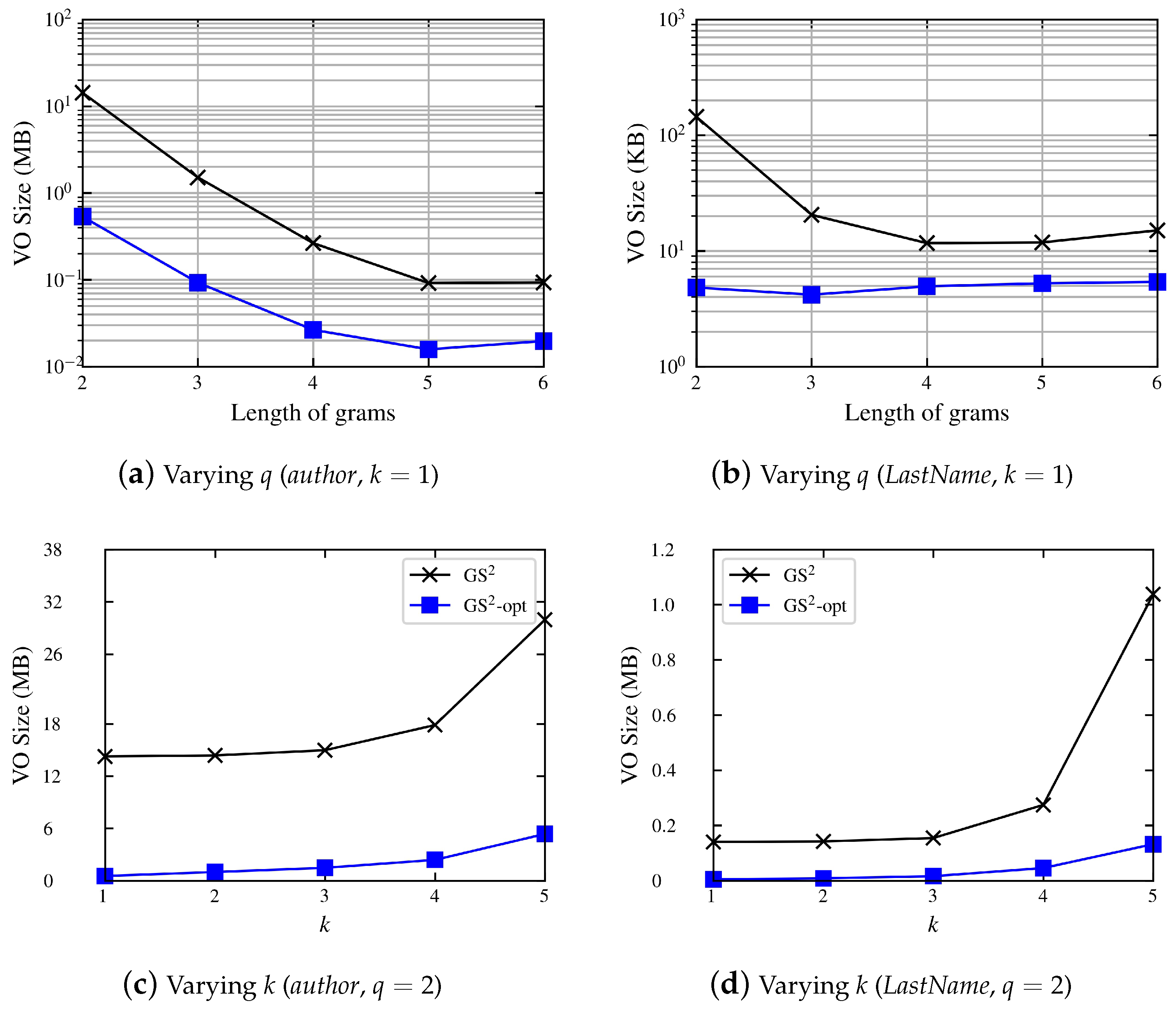
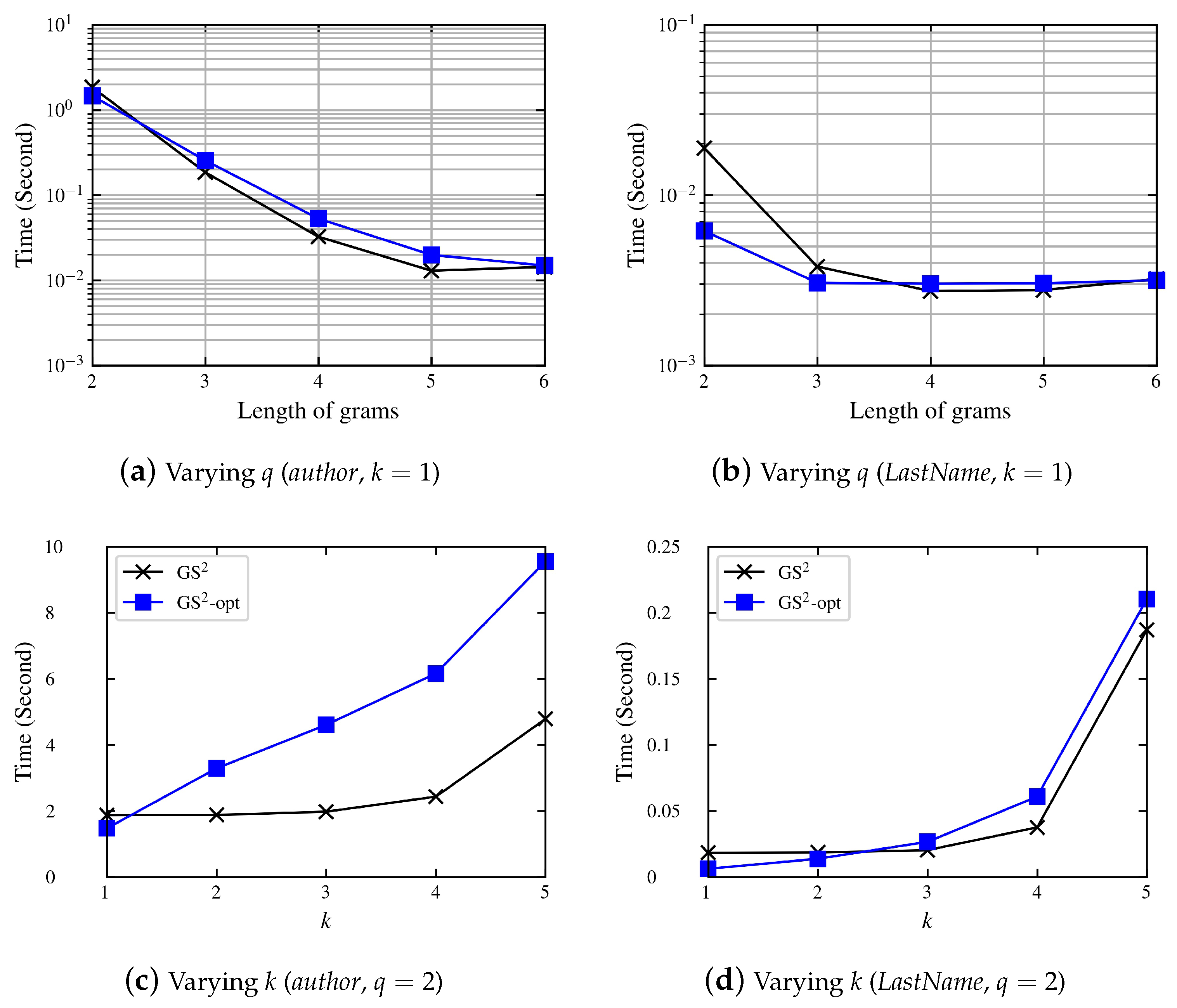
4.1.1. Preprocessing Phase

During this phase, the DO constructs and signs the authenticated index structure (AIS) for D before outsourcing D to the server. Our AIS mainly consists of two parts, namely, a dictionary and an inverted index. Thanks to its efficiency and simplicity, we use MHT for authentication of the data structure construction. We summarize the construction process in Algorithm 1.

Algorithm 1: Generate signature for dictionary.

First, we show how to generate a signature for the dictionary. As shown in line 2 of Algorithm 1, the DO sorts the strings in D in alphabetical order and assigns each string a unique ID, i.e., $Sid$, as shown in  Table 1. The reason to sort D is that the strings of a query result tend to share a common prefix; hence, sorting helps to cluster similar strings together, which can reduce VO size and thus save network costs.

The DO computes the tuple hash $h_t$ for each tuple $t(Sid,string)\in D$ as follows:

$$h_t\left(t\right)=h\left(h(t.Sid)\right|h(t.string)),$$

(2)

where ∣ stands for string concatenation, and $h(·)$ is a one-way hash function. Lines 3 to 6 of Algorithm 1 show how to compute tuple hashes. We use the tuple hash as an identifier for a tuple.

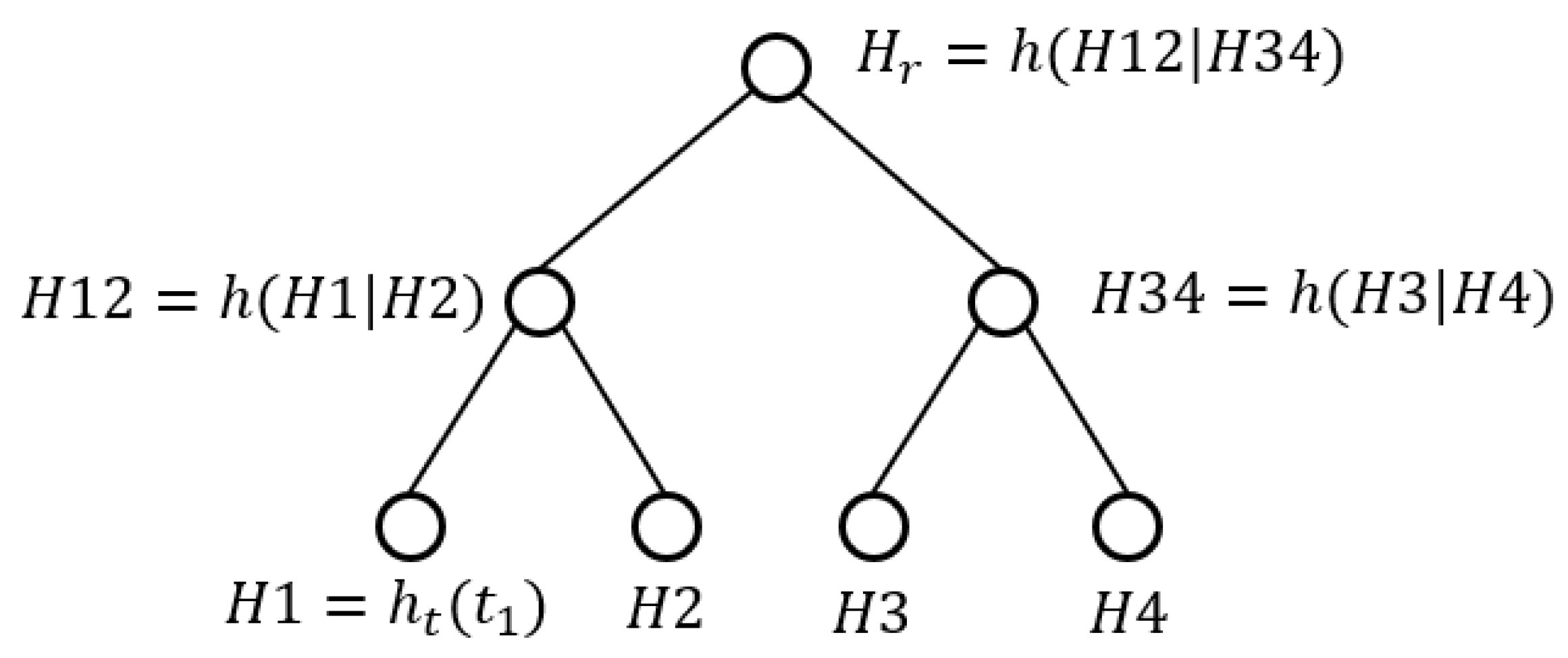
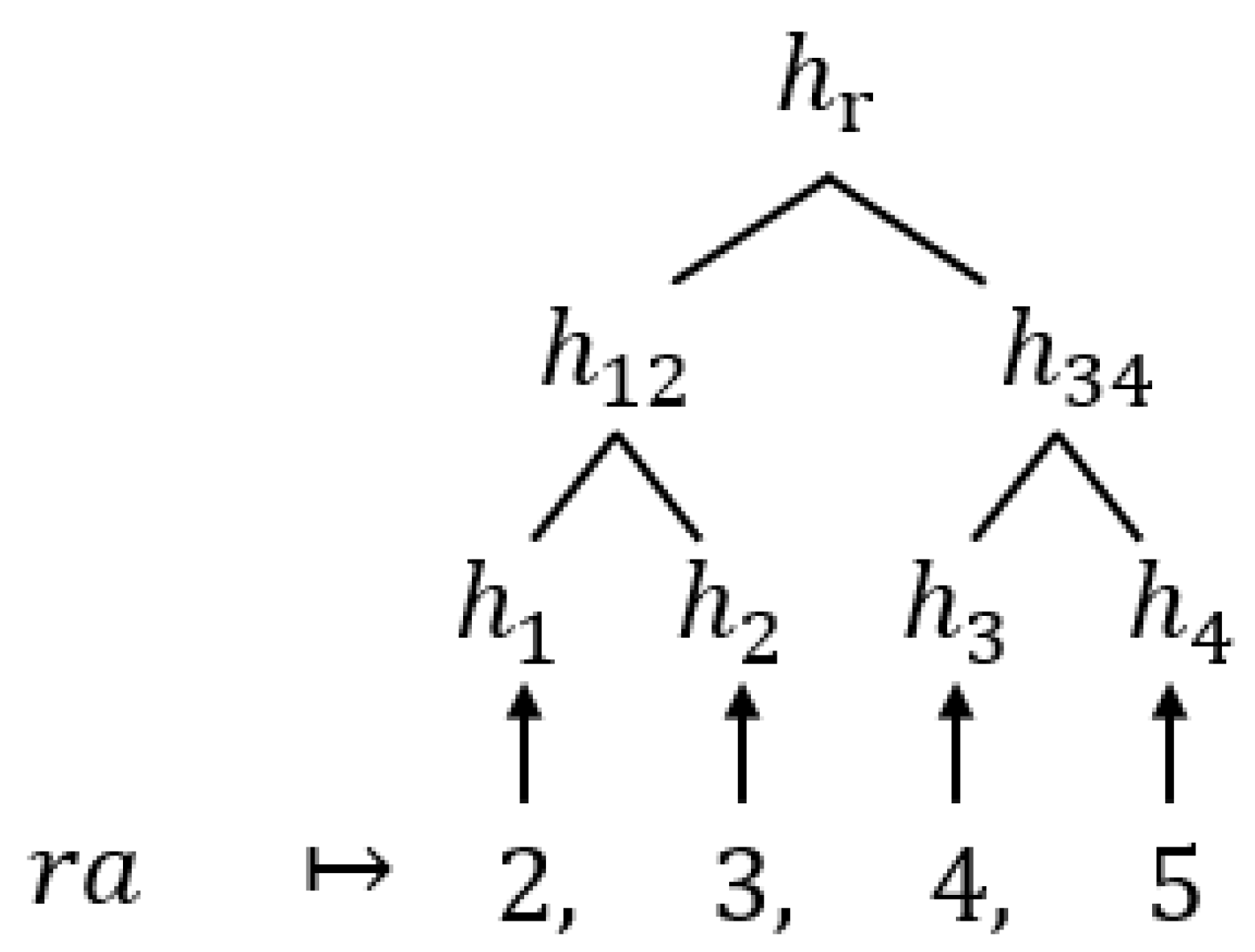
The DO builds the MHT of D in a bottom-up manner. Specifically, if node i of the MHT is a leaf node, then its hash is simply $h\left(i\right)=h_t\left(t_i\right)$, where $t_i$ is the data tuple corresponding to node i. On the other hand, if node i is an internal node, then its hash can be calculated as $h\left(i\right)=h(h_{nod{e}_l}\mid h_{nod{e}_r})$, where $h_{nod{e}_l}$ and $h_{nod{e}_r}$ are the hash values of the left and right children of node i, respectively. This process repeats until the root node of the MHT is obtained. This construction is illustrated in  Figure 3, where $Hi$ is the hash value of node i, and the “root hash” (denoted as $H_r$) is a digest of all the tuples in the Merkle hash tree. We summarize the calculation of MHT in lines 7 to 12 of Algorithm 1.

After the MHT is built, the DO generates a pair of keys $(p_k,s_k)$, where $p_k$ and $s_k$ refer to the public key and private key, respectively. Then, the DO signs the root hash $h_r$ of the MHT with the DO’s private key $s_k$, i.e., $S_{dic}=si{g}_{s_k}\left(H_r\right)$, where $sig(.)$ is a standard digital signature algorithm, such as RSA and ECDSA.

Next, we explain how to compute the signature of the inverted index, as shown in Algorithm 2. Specifically, the DO creates an inverted index for the q-grams (lines 2 to 8 of Algorithm 2), where q is a hyper-parameter that can be pre-determined based on some statistics of dataset and user queries, such as the distribution of the alphabet and the average length of the strings.

Algorithm 2: Generating a signature for inverted index.

For each i-list =$<Si{d}_1,Si{d}_2,\cdots ,Si{d}_m>$ of the inverted index (lines 9 to 12 in Algorithm 2), the DO computes the tuple hash$h_t$ for the i-list as follows:

$$h_{i-list}=h(Si{d}_1|Si{d}_2|\cdots |Si{d}_m),$$

(3)

$$h_t(gram-list)=h\left(h\left(gram\right)\right|h_{i-list}).$$

(4)

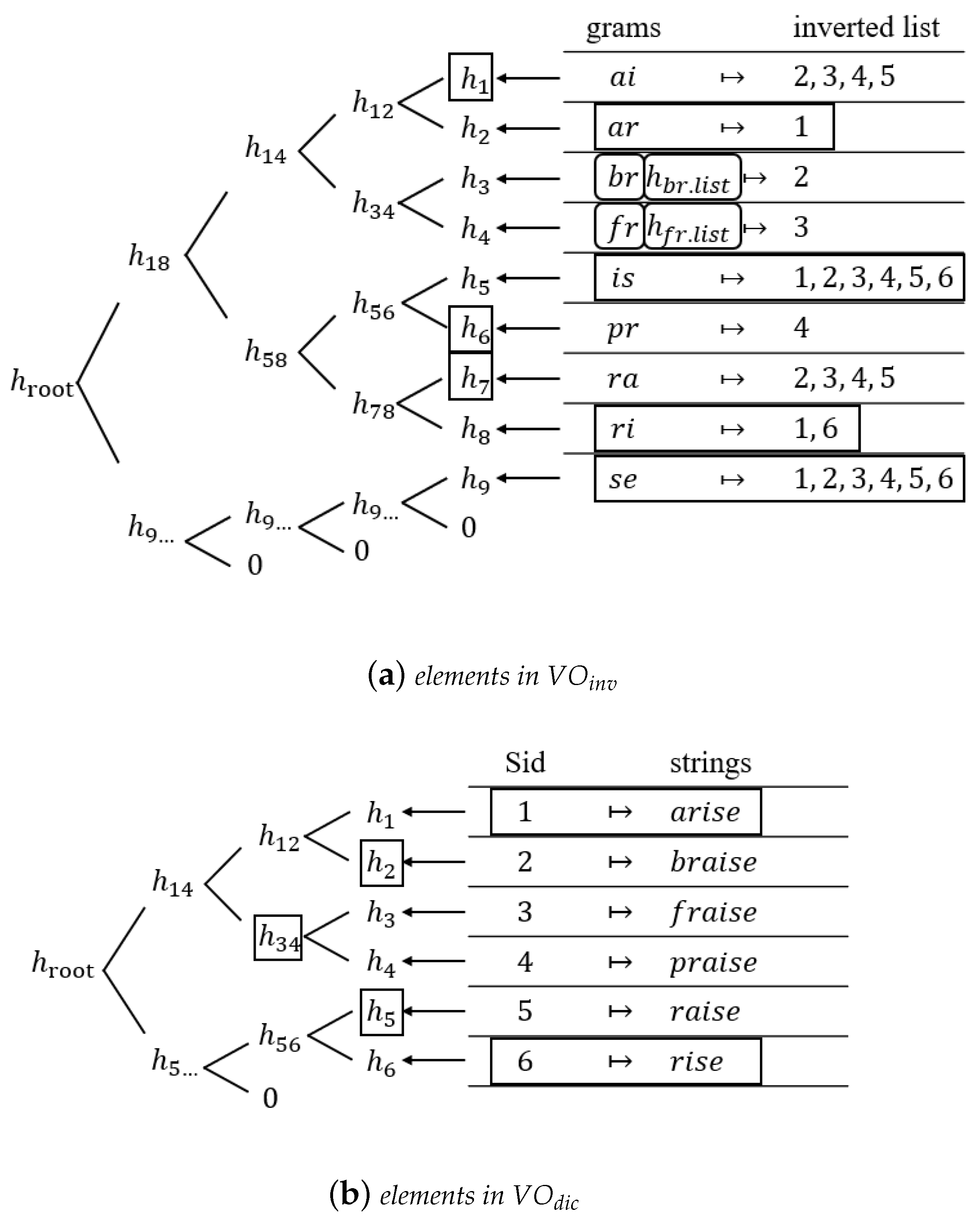
For instance, consider the gram “ai” and its corresponding list in  Table 2. We thus have $h_{“ai”.i-list}=h\left(3\right|4\left|5\right|6)$ and $h_t(“ai”)=h\left(h(“ai”)\right|h_{“ai”.i-list})$. Note that $h_t($“ai”) corresponds to $h_1$ in  Figure 4.

Then, the DO computes the MHT of the inverted index. Specifically, the gram-list of the inverted index is sorted by grams in alphabetical order, and the MHT construction process of the inverted index is the same as MHT construction for the dictionary. When the MHT is built, the DO signs the root hash to generate signature $S_{inv}$ of the inverted index (lines 13–19 of Algorithm 2). We give an example of MHT construction for the inverted index in  Figure 4.

After the AIS is constructed as described above, the DO uploads dataset D, q, and two signatures, $S_{dic}$ and $S_{inv}$, to the server. It is worth noting that in some existing outsourcing database models, the DO stores signatures locally (instead of uploading them to the server) and only sends them to users upon request. For example, [3] proposed a solution called $Auto{S}^3$, in which the DO is required to remain active to keep the system running properly. In contrast, our solution allows the DO to go offline without affecting the database outsourcing services.

4.1.2. Searching Phase

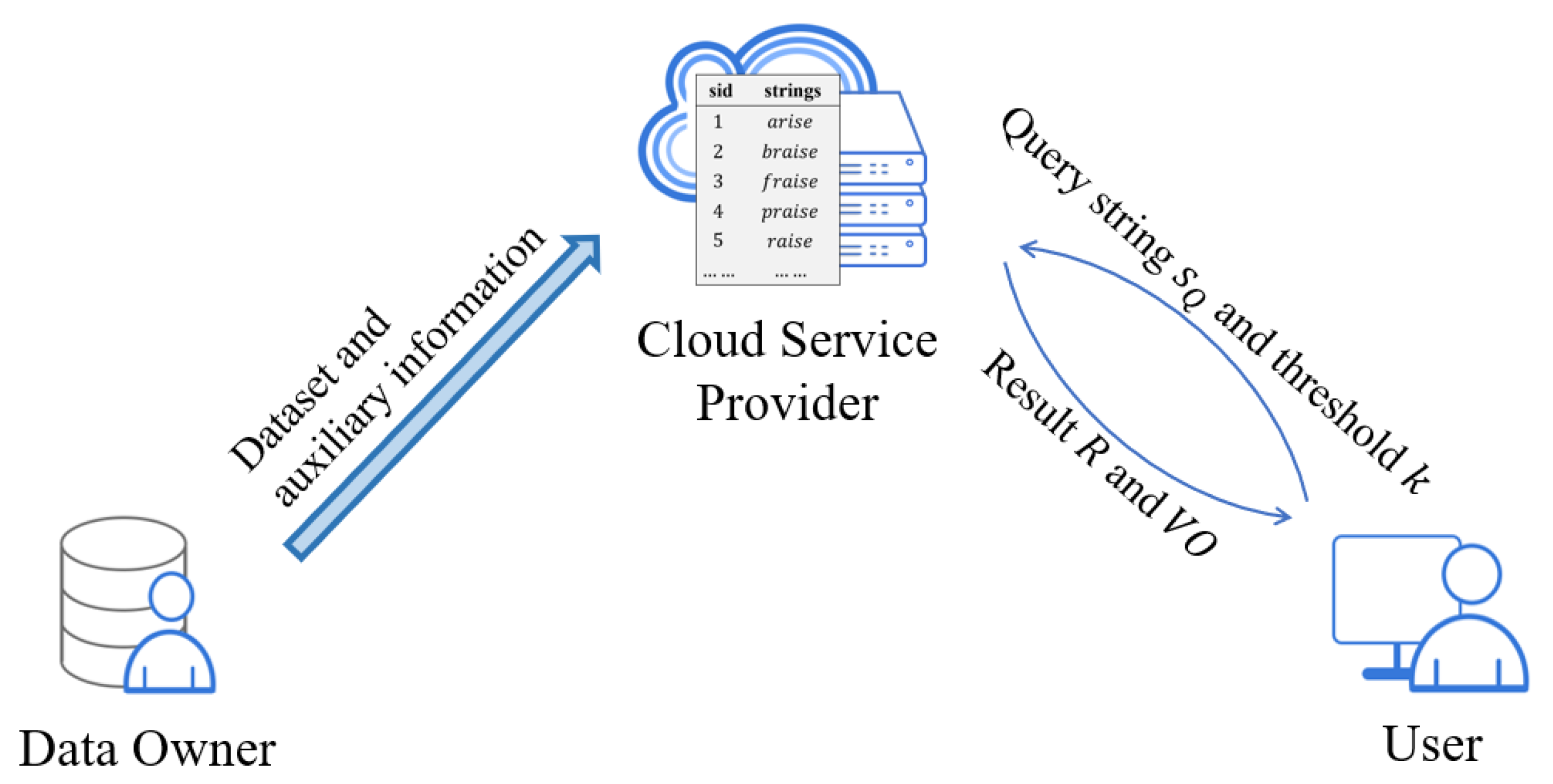
In this section, we present the process of generating the VO for user queries. In general, the VO is composed of two components, i.e., the VO of the dictionary and the VO of the inverted index. First, we provide a brief description of how the server performs approximate string searches with respect to a user query, as summarized in Algorithm 3. Then, we show how to construct VO in detail.

Upon receipt of dataset D, q, and signatures from the DO, the server builds the q-gram inverted index based on D and q. Assume the user issues a query Q with string $s_Q$ and threshold k to the server, which implies that the user wants to search for all strings whose edit distance from $s_Q$ is less than or equal to k. After receiving $s_Q$ and k from the user, the server calculates the minimum number of shared grams, denoted by $\tau$, between $s_Q$ and a string $s_i$. According to Lemma 1, we have

$$\tau =max(s_i,s_Q)-q+1-kq.$$

(5)

Without loss of generality, $\tau$ is set to the minimum value of the above equation, i.e., $\tau =|s_Q|-q+1-kq$, as shown in line 2 of Algorithm 3.

Algorithm 3: Search for similar strings in D.

The server extracts a set of $s_Q$-grams of $|s_Q|-q+1$ grams from $grams(s_Q,q)$, as shown in Line 3 of Algorithm 3. Then, all the i-lists corresponding to grams in $s_Q$-grams are fetched from the inverted index. It is possible that some gram in the $s_Q$-grams may not have a corresponding i-list in the inverted index; hence, we divide the grams in $s_Q$-grams into the following two cases (lines 4 to 6 of Algorithm 3):

• If a gram $g\in s_Q$-grams has a corresponding i-list, g is called an e-gram;
• If a gram $g\in s_Q$-grams does not have a corresponding i-list, g is called an ne-gram.

We refer to the i-lists that correspond to the e-gram as e-i-lists.

After that, the server counts the number of occurrences of $Sid$ in e-i-lists and find those that appears no less than $\tau$ times. To count the number of occurrences, there exist many efficient algorithms, e.g., the Heap algorithm, MergeOpt [7], ScanCount, MergeSkip, and DivideSkip [9]. After the counting step, we obtain a set of candidate strings, denoted by the C-string, whose Sid appears at least $\tau$ times in the e-i-lists, as shown in lines 7 to 9 in Algorithm 3.

For each string $s_c\in$C-string, the server computes the edit distance between $s_c$ and $s_Q$, and those strings whose edit distance from $s_Q$ is less than or equal to k are put into the result set R (as shown in lines 10 and 11 in Algorithm 3). Note that the server can directly use the dynamic programming technique to calculate the edit distance between two strings, or it can use the verification technique [1] or other filter-verification frameworks [27] to speed up the computation.

Example 1. 

Let us consider an example with $s_Q$=“arisen”, $k=1$, and the database D, as shown in  Table 1, and its corresponding inverted index, as shown in  Table 2. After receiving $s_Q$ and k, the server first computes $\tau =|s_Q|-q+1-kq=6-2+1-1\times 2=3$ and then extracts $s_Q$-$grams=\{$“ar”,“ri”,“is”,“se”,“en”}, from which the server obtains e-gram={“ar”,“ri”,“is”,“se”} and ne-gram={“en”}. Next, the server counts the frequency of occurrence of $Sid$ in e-i-lists, and only the strings with $Sid\in \{1,6\}$ satisfy the requirement of appearing at least τ times. Hence, we have C-string={“arise”,“rise”}. Finally, the server computes the edit distance between the strings in the C-string and $s_Q$. Among them, only the string “arise” satisfies the threshold of edit distance k. Therefore, the result $R=\{$“arise”} is returned to the user.

Next, we show how to construct VO with respect to a query result R. First, the server builds leaf nodes for all grams in the inverted index. For each e-gram, the leaf node contains the gram and its corresponding i-list. For each gram that is a neighboring list (the alphabetic predecessor and successor of a gram in the inverted index) of the ne-gram, the leaf node contains the gram and the hash value $h_{list}$ of its i-list. For each of the remaining grams, the leaf node contains its tuple hash $h_t\left(t\right)$ (lines 1 to 12 of Algorithm 4). Note that if a gram in the set of the ne-gram is out of the boundary of the inverted list, then the neighbors of that gram only contain one gram. For example, as shown in  Table 2, the neighbors of gram “aa” and “sf” are “ai” and “se”, respectively, whereas the neighbors of gram “fr” are “br” and “is”.

Similar to the process of forming VO on a traditional MHT, in our solution, the server calculates the hashes of the internal nodes (lines 13 to 18 of Algorithm 4). Similarly, the server builds the MHT for dataset D and maintains the information about the C-string, as shown in lines 19 to 25 of Algorithm 4.

The formation of VO for result set R is shown in line 26 of Algorithm 4, from which we can see that VO consists of (1) the e-grams and their corresponding e-i-lists, the neighboring grams of each ne-gram and their i-list hash values, and the hashes of other nodes; (2) C-string set along with their $Sid$ and the hashes of other nodes; and (3) the signatures of the dictionary MHT and of the inverted index MHT, respectively. The server sends R and VO to the user for verification. Note that in scenarios where the user continuously issues queries, the server only needs to send the signatures once to reduce network communication costs.

It is worth mentioning that the elements in VO are organized in such a way that the user can easily recalculate the root hash of the dictionary MHT and the root hash of the inverted index MHT. Specifically, the elements in VO are organized according to where they are located in the MHT, and a pair of parentheses is added around elements that share the same parent node in the MHT.

Algorithm 4: VO construction.

Example 2. 

Let us continue with the previous Example 1, where the result $R=\{$“arise”}. Referring to  Figure 4, it is clear that the neighbors of ne-gram=“en” are “br” and “fr”, and their corresponding i-list hashes are $h_{br.list}=h\left(2\right)$ and $h_{fr.list}=h\left(3\right)$, respectively. Similarly, after computing the other necessary hashes, i.e., $h_1$, $h_6$ and $h_7$, the server constructs the first part of VO as follows:

$$\begin{array}{cc}\hfill V{O}_{inv}=& \left\{\right((\left((h_1,(“ar”,\left(1\right)))\left((“br”,h_{br.list})(“fr”,h_{fr.list})\right)\right)\hfill \\ \hfill & \left(((“is”,(1,2,3,4,5,6)),h_6)(h_7,(“ri”,(1,6)))\right))\hfill \\ \hfill & \left(\right(\left(\right(“se”,(1,2,3,4,5,6)\left)\right)\left)\right)\left)\right\}.\hfill \end{array}$$

(6)

Recall that we have C-string={“arise”,“rise”}, and after computing $h_2$, $h_{34}$, and $h_5$, the server constructs the second part of VO as follows:

$$\begin{array}{c}\hfill V{O}_{dic}=\left\{\left((((1,“arise”),h_2),h_{34})\left((h_5,(6,“rise”))\right)\right)\right\}.\end{array}$$

(7)

 Figure 5 shows the elements that constructed $V{O}_{dic}$ and $V{O}_{inv}$. Finally, having obtained the above components, we have:

$$\begin{array}{c}\hfill VO=\{V{O}_{inv},S_{inv},V{O}_{dic},S_{dic}\}.\end{array}$$

(8)

4.1.3. Authentication Phase

Given a user query with $s_Q$ and k, the server conducts query processing and returns the query result set R, along with its corresponding VO to the user. Upon receipt of R and VO, the user verifies whether the received R is correct. Note that the user obtains the DO’s public key $p_k$ via a secure channel, such as a certificate authority (CA). We summarize the authentication procedures in Algorithm 5.

At first, based on the VO received, the user computes the root hashes for both the dictionary and the inverted index. Specifically, by using $V{O}_{inv}$ and $V{O}_{dic}$, the user can compute the hashes of internal nodes in a recursive manner until the root hashes $h_{roo{t}_i}^{\prime }$ (root hash of the inverted index) and $h_{roo{t}_d}^{\prime }$ (root hash of the dictionary) are obtained (lines 1 and 2 of Algorithm 5). Note that we assume that the DO shares with the user some necessary information, such as the hash function, the public key encryption algorithm used by the DO, and the parameter q, etc. Then, the user decrypts signatures $S_{inv}$ and $S_{dic}$ with $p_k$, as follows:

$$h_{roo{t}_i}=si{g}_{p_k}\left(S_{inv}\right),$$

(9)

$$h_{roo{t}_d}=si{g}_{p_k}\left(S_{dic}\right).$$

(10)

where $h_{roo{t}_i}$ and $h_{roo{t}_d}$ are compared against $h_{roo{t}_i}^{\prime }$ and $h_{roo{t}_d}^{\prime }$, respectively. If either $h_{roo{t}_i}^{\prime }\ne h_{roo{t}_i}$ or $h_{roo{t}_d}^{\prime }\ne h_{roo{t}_d}$, then the user concludes that the query result R returned from the server fails the correctness verification, as shown in lines 2 to 6 of Algorithm 5.

Algorithm 5: Query result authentication.

On the other hand, if VO is correct, then the user compares grams($s_Q$,q) with the gram set $G_{VO}$ that consists of all grams appearing in $V{O}_{inv}$. For each gram g, where $g\in$grams($s_Q$,q) and $g\notin$$G_{VO}$ (i.e., g is an ne-gram), the user looks for its neighbors in $G_{VO}$, and the neighbors should be adjacent to each other in VO, unless there is only one neighbor. Otherwise, the user is certain that the R fails the completeness test.

For each gram g, where $g\in$grams($s_Q$,q) and $g\in G_{VO}$ (i.e., g is an e-gram), the user counts the number of occurrences of $Sid$ in the e-i-lists. For those strings whose $Sid$ appears at least $\tau =|s_Q|-q+1-kq$ times, the user needs to check whether they appear in $V{O}_{dic}$. If any $Sid$ appears at least $\tau$ times but does not appear in $V{O}_{dic}$, then the user is certain that the R does not pass the completeness test (lines 7 and 16 in Algorithm 5).

Finally, the user extracts all strings in $V{O}_{dic}$ and computes the edit distance between each of them and $s_Q$. If the edit distance of some string is not greater than k, but the string is not included in R, then the user concludes that the result set R fails the completeness test. Conversely, if a string is in R but it is missing during the comparison, then the user is certain that R fails the soundness test (lines 17–21 in Algorithm 5).

Example 3. 

Let us recall Example 2. We have $s_Q$={“arisen”}, $k=1$, $R=\{$“arise”}, $V{O}_{inv}$, $V{O}_{dic}$, and two signatures $S_{inv}$ and $S_{dic}$. At first, the user recalculates the root hash for $V{O}_{inv}$ and $V{O}_{dic}$, respectively, as follows:

$$\begin{array}{cc}\hfill h_{roo{t}_i}^{\prime }=& h\left(h\left(h\left(h_1\right|h(“ar”|h\left(1\right)))\right|h\left(h(“br”|h_{list1})\right|h(“fr”|h_{list2})))\right|\hfill \\ \hfill & h\left(h\right(h\left(h\right(“se”\left|h\right(1,2,3,4,5,6\left)\right)\left|0\right)\left|0\right)\left|0\right));\hfill \end{array}$$

(11)

$$\begin{array}{c}\hfill h_{roo{t}_d}^{\prime }=h\left(h\left(h\left(h\left(1\right|“arise”)\right|h_2)\right|h_{34})\right|h\left(h\left(h_5\right|h\left(6\right|“rise”))\right|0)),\end{array}$$

(12)

where $h_{roo{t}_i}^{\prime }$ and $h_{roo{t}_d}^{\prime }$ are compared with the decoded signatures to verify the authenticity of VO.

Then, the user retrieves the set of e-grams and the set of neighbors of ne-gram from $V{O}_{inv}$ and compares the set of e-grams against gram(“arisen”,2) in order to obtain ne-gram={“en”}. Based on the ne-gram, the user is certain that the neighboring gram “br” lies before {“en”}, and “fr” lies after {“en”} in the inverted index. Next, the user counts the number of occurrences of $Sid$ and only strings in $\{1,6\}$ whose occurrences are greater than or equal to $\tau =3$. Finally, the user retrieves strings {“arise”,“rise”} from $V{O}_{dic}$, where $Sid=\{1,6\}$, and computes the edit distance between the string $s\in \{$“arise”,“rise”} and $s_Q$. Here, only $s=$“arise” satisfies the threshold k, which is the same as R. Hence, the user confirms that the result R sent from the server is correct.

It is worth mentioning that by modifying the computation of $\tau$ (note that an example computing method can be found in [27]), our GS² model can be applied to other threshold-based similarity measures for strings, such as Hamming distance, Edit similarity, Jaccard similarity, Cosine similarity, and Dice similarity. For example, for the Hamming distance, $\tau$ can be calculated by $\tau =\left|s_Q\right|-q+1-k*q$, and the calculation of $\tau$ values for other distance measures can be found in [27].

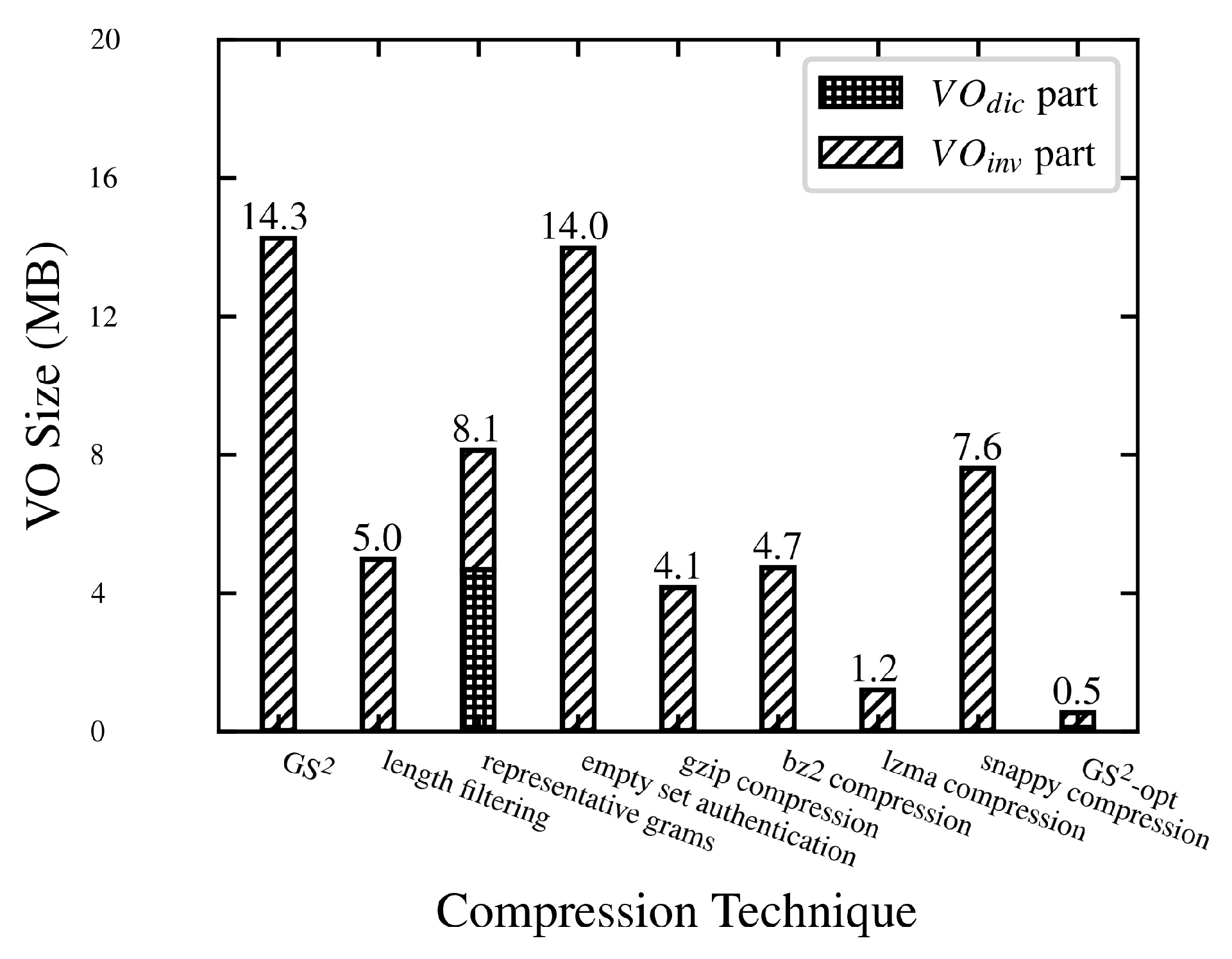
GS² is not a very cost-effective approach in terms of network communication because the size of the VO generated is large, resulting in a higher transmission cost. For most resource-constrained clients, especially mobile devices or IoT devices, the network bandwidth and battery are limited. Therefore, it is important to reduce the communication overhead between the server and the users. To address this issue, in the next section, we design an optimization scheme, which can significantly reduce the VO size.

4.2. Optimization Method for GS²

In this section, we introduce an optimization scheme named GS²-opt. In GS², $V{O}_{inv}$ and $V{O}_{dic}$ are the two components that take up the majority of the VO size, since the length of the i-list in $V{O}_{inv}$ may be excessively long, and the number of C-strings may be large for a large string dataset.

In our GS²-opt model, we reduce the size of $V{O}_{inv}$ and $V{O}_{dic}$ by using the following strategies:

• We employ a length-filtering technique to reduce the size of $V{O}_{inv}$ and $V{O}_{dic}$.
• We propose the representative grams to reduce the size of $V{O}_{inv}$ at the cost of a slight increase in the size of $V{O}_{dic}$.
• We design a solution to deal with the case where some parts of the result are empty during authentication.
• We use compression techniques to further reduce the size of VO.

Note that the goal of the above optimization strategies is to shrink the VO size, and that some of them are not suitable for similarity functions other than the edit distance. Below, we explain these strategies in detail.

4.2.1. Length Filtering

Long strings tend to cover many grams, which causes them to frequently sneak into C-strings, but they are obviously different from $s_Q$. Therefore, we use a length-filtering technique [28] to further weed out strings that do not satisfy the edit distance constraint. The application of the length-filtering technique is based on the following lemma:

Lemma 2. 

If $ed(s_i,s_Q)\le k$, then their lengths cannot differ by more than k, i.e.,

$$\begin{array}{cc}\hfill & ed(s_i,s_Q)\le k\Rightarrow ∥|s_i|-|s_Q|∥\le k.\hfill \end{array}$$

(13)

Proof of Lemma 2. 

The proof for Lemma 2 is straightforward. An insertion or deletion edit operation changes the string length by no more than 1, and the substitution operation does not change the string length at all. Therefore, within k edit operations, the string length changes by no more than k. □

To authenticate the strings pruned by length filtering, we modify some of the steps in GS². Below, we will explain the details of these changes. Specifically, during the preprocessing phase, strings are sorted by length at first and then sorted in alphabetical order. For example, given a set of strings in

Table 3. Strings sorted in alphabetical order.

Sid	String
1	$arise$
2	$braise$
3	$fraise$
4	$praise$
5	$raise$
6	$rise$

, after sorting, they are listed in

Table 4. Strings sorted by length at first, then sorted in alphabetical order.

Sid	Strings
1	$rise$
2	$arise$
3	$raise$
4	$braise$
5	$fraise$
6	$praise$

.

Additionally, before building the MHT for the inverted index, the DO sorts each of the i-list, builds an MHT for each i-list in the inverted index (as shown in Figure 6), and takes the root hash as the i-list digest:

$$h_{i-list}=h_r.$$

(14)

Figure 6 shows an example of building an MHT for an i-list of “ra", and its tuple hash is computed as follows:

$$\begin{array}{cc}\hfill h_t(“ra”)& =h\left(h(“ra”)\right|h_{i-list})\hfill \\ \hfill & =h\left(h(“ra”)\right|h_r).\hfill \end{array}$$

(15)

During the searching phase, before constructing the VO, the server calculates the desired range of length $\left[\right|s_Q|-k,|s_Q|+k]$ and filters out all the C-strings that fall outside this range. To facilitate authentication, when building the MHT for the dictionary, the strings that are immediately adjacent to the range borders are included in $V{O}_{dic}$. On the other hand, when building the MHT for the inverted index, for each gram-list, the server constructs an MHT and uses digests to represent the $Sid$ of strings whose length is not in the range (except two boundary strings that are not in the range). In this process, we also introduce the similar concept of buddy inclusion [2] to further reduce the VO size.

In the verification phase, the user verifies that the length of the first string in the C-string is not greater than $|s_Q|-k-1$ and that the length of last string in the C-string is not less than $|s_Q|+k+1$. The user also checks that the range of $Sid$ of each e-i-list covers the $Sid$ of the boundary strings and that all of the $Sid$ s in the e-i-list are continuous. With the exception of the steps described above, all other procedures are the same as those in GS².

4.2.2. Representative Grams

As discussed in [7], the frequency distribution of words in real-life datasets is often heavily skewed, with a significant portion of words appearing much more frequently than others. This phenomenon is also observed in the frequency distribution of string grams. For example, in the dataset authors obtained from DBLP ( http://dblp.uni-trier.de/xml/ (accessed on 6 July 2022)), it has been observed that nearly one-third of string grams appear much more frequently, with a frequency over ten times higher than the other one-third. Therefore, in an inverted index, some grams tend to be associated with long i-lists. On the other hand, grams with a long i-list have a higher probability of becoming an e-gram in a query than grams with a short i-list. Therefore, if a query string $s_Q$ covers some frequently occurring grams, it is likely that many strings that are very different from $s_Q$ will be included in the C-string, leading to a large VO.

To address this problem, we propose the use of representative grams. The basic idea is that instead of returning all the e-grams and the corresponding i-lists, the server only returns a few grams that represent the grams covered by $s_Q$. If a string covers grams that appear multiple times, its $Sid$ may appear several times in the same gram. To deal with this problem, we design a new format for the gram-list, i.e., a triplet ($gram$, t, $\left[list\right]$), where the element t denotes the number of times $Sid$ occurs.

An example string set is given in

Table 5. An example string set.

Sid	Strings
1	$arar$
2	$arari$
3	$rari$

, and the new format of the inverted index built on the string set can be seen in

Table 6. Example of 2-gram inverted index with occurrence time.

Grams	t		Inverted List
($ar$,	$1)$	↦	3
($ar$,	$2)$	↦	$1,2$
($ra$,	$1)$	↦	$1,2,3$
($ri$,	$1)$	↦	$2,3$

. In this example, the notation “(ar,2) $\mapsto 1,2$" means that the gram “ar" occurs twice in both strings with $Sid=1$ and $Sid=2$. Hence, the tuple hash is calculated as follows:

$$\begin{array}{c}\hfill h_t(“ar,2”)=h\left(h\left(ar\right|2)\right|h_{list}).\end{array}$$

(16)

In our previous description, if a string is considered a C-string, it must share at least $\tau =|s_Q|-q+1$ grams with $s_Q$. In GS²-opt, we change this condition so that the sum of t for a string’s grams must be greater than or equal to $\tau$. This modification allows us to more accurately evaluate the similarity of strings that may contain the same grams that appear multiple times.

For ease of discussion, we define the representative grams (i.e., those grams) to be included in $V{O}_{inv}$) as r-grams, the corresponding i-list as r-i-list, the sum of all t values for any set of grams as $st$, the sum of all t values for e-grams as $s{t}_e$, the sum of all t values for r-grams as $s{t}_r$, the subset of e-grams as sub-e-grams, and the sum of all t values for a string s in a certain sub-e-gram (i.e., how many times the $Sid$ of the string s appears in the sub-e-gram) as $s{t}_s$. Then, we have the following lemma:

Lemma 3. 

The server only needs to return those r-grams where $s{t}_r\ge$$s{t}_e-\tau +1$ and the length of i-lists is the shortest among the e-grams. All strings with $s{t}_s\ge \tau -(s{t}_e-s{t}_r)$ are included in the C-string. This allows us to reduce the number of i-lists included in $V{O}_{inv}$.

To illustrate how this method works, let us consider a string s $\in D$ that is similar to the query string $s_Q$. According to the previous similarity condition, s must share at least $\tau$ grams with $s_Q$. This indicates that for e-grams, $s{t}_s$ must be greater than or equal to $\tau$. For any subset of the e-grams with $st=s{t}_e-i$, if a string s is similar to $s_Q$, then its $s{t}_s$ must be bigger than or equal to $\tau -i$, $i\in [1,\tau -1]$. If we set $i=\tau -1$, it follows that for any subset of e-gram with the sum of t values, $st=s{t}_e-\tau +1$, and the $Sid$ of s must appear at least once in their corresponding i-list. This means that any subset of e-grams with $st\ge s{t}_e-\tau +1$ can be considered a representative gram with respect to user query Q.

Next, we provide a formal proof of the completeness of the proposed method (the soundness proof is straightforward and is omitted).

Proof of Lemma 3. 

Given a string $s\in D$, where s contains $\left|s\right|-1+q$ grams, there must be three cases, as shown below:

• Case 1: ∃gram∈r-gram. In this case, if $s{t}_s\ge \tau -(s{t}_e-s{t}_r)$, then s will appear in the C-string, and the user will check the distance between s and $s_Q$ to determine whether s should be included in R. On the other hand, if $s{t}_s<\tau -(s{t}_e-s{t}_r)$, then we can infer that for the entire e-gram, we have $s{t}_s<\tau$. Therefore, it is impossible that s is similar to $s_Q$. The VO authentication will fail if there is any violation of these inequalities.
• Case 2: (∃gram∈e-gram) ∧ (∀gram∉r-gram). In this case, we have $s{t}_e-s{t}_r\le \tau -1$, which means that for the entire e-gram, we have $s{t}_s\le \tau -1$. Therefore, it is impossible for s to be similar to $s_Q$.
• Case 3: ∀gram∉e-gram. In this case, s is not similar to $s_Q$.

□

Therefore, the server only needs to include the r-i-list, which is a subset of the e-i-list, into VO to guarantee the completeness of the results. It is worth noting that there are many possible combinations of r-grams, and the value of $s{t}_r=s{t}_e-\tau +1$ may not be the optimal value to fit all scenarios. As such, the specific number of r-grams to be included in VO should be determined according to the dataset and the user query.

4.2.3. Dealing with Empty Results

When the query result is empty, the user only needs to authenticate its completeness. Specifically, we have the following lemma:

Lemma 4. 

For a query with $s_Q$ and k, if $\alpha >k\times q$, where α is the number of ne-grams, then R is an empty set.

In this case, it is not necessary to include any i-list in VO because the result set is already known to be empty.

Proof. 

An insert or substitution operation in the edit distance creates at most q grams that contain the inserted or substituted character, while a deletion operation creates at most $q-1$ grams. Given k edit operations, at most, $kq$ grams can be created. The number of ne-gram$\alpha$ represents the number of grams that need to be created if a string $s\in$D is transformed into $s_Q$. Therefore, if $\alpha >kq$, there are no strings in D that can be transformed into $s_Q$. □

Thus, if a user query meets this condition (i.e., the number of the ne-gram is greater than $k\times q$), the server can include only the neighbours of ne-grams in $V{O}_{inv}$ with the digests that are necessary for computing the root hash, omitting all e-grams and their associated e-i-lists. The authentication phase in this case is much easier than the authentication in GS², and the size of VO is also reduced dramatically.

4.2.4. VO Compression

By analyzing the contents of VO, we found that English letters and digits, along with a few symbols such as “(“, “)” and “,”, are the most frequent characters appearing in VO, especially in $V{O}_{inv}$ (in which the e-i-list and digest of other gram-list are the main components).

To cut down the communication overhead in VO transmission, we use the Lempel–Ziv–Markov chain algorithm (LZMA) [29] to compress VO. LZMA is a dictionary-based compression method, and it uses a range encoder to compress the data. After VO construction, the server uses LZMA to compress VO and then sends it to the user. Upon receipt of the compressed VO, the user decompresses it before performing the authentication procedure.

5. Security Analysis

Given a query string $s_Q$ with threshold k, let R be the set of strings in D that are similar to $s_Q$ and let R’ be the set of similar strings returned by the server. An untrustworthy server may attempt to cheat the user by violating the soundness or completeness of the query result, as shown below.

• Violation of soundness: following the definition in Section 3.2, the server returns R’, where $\exists s\in R^{\prime }\wedge s\notin R$. This means that the server is returning some strings that do not belong D or are not similar to $s_Q$.
• Violation of completeness: the server returns R’, where $\exists s\in R\wedge s\notin R^{\prime }$. This means that the server is not returning all of the strings that are similar to $s_Q$.

Soundness. To facilitate the analysis, we divide this situation into two situations: (1) $\exists s\in R^{\prime }\wedge s\notin R\wedge s\notin D$, and (2) $\exists s\in R^{\prime }\wedge s\notin R\wedge s\in D$. For the first case, it is easy to detect this during the authentication procedures as the digest of s is different from the original strings, resulting in the root hash calculated by the user not matching the one decoded from the DO’s signature. Hence, the user is able to catch this violation during the step of comparing the root hashes.

For the second case, the server returns some strings that are not similar to $s_Q$. Apparently, this will also be identified by the user in the final step of the authentication procedure, when the user compares strings in R’ with the strings (i.e., the C-string) that meet the similarity threshold.

Completeness. When a string $s\in R$ is excluded by the server from R’, the following cheating actions may be taken by the server to convince the client to accept R’:

• Case 1: The server claims that grams shared by both $s_Q$ and s do not exist.
• Case 2: The server does not deny the existence of the grams but forges the corresponding i-list to exclude the $Sid$ of s.
• Case 3: The server returns the correct grams and their corresponding i-lists but omits s from the C-string.
• Case 4: The server only omits s from R’ but provides a correct VO.

For Case 1, the server omits the grams which it claims from $V{O}_{inv}$ to create two sibling neighbours in order to deceive the user. However, no matter how the server alters the grams in the original inverted index, it is impossible for the root hash of the inverted index MHT computed by the user to match the one decoded from the DO’s signature. The user can detect this case during the authentication phase. For Case 2, this action will also change the root hash values of the inverted index MHT and will be detected by the user, similar to Case 1. For Case 3, with the correct inverted index, the user can filter out the C-string’s $Sid$ on their own. If s does not appear in $V{O}_{dic}$, the user will conclude that R fails the completeness test. Finally, for Case 4, with the correct C-string set, the user can verify all strings in the C-string and compare them against those in R’. If a string s is similar to $s_Q$ but does not appear in R’, then the user will find that R’ is incorrect.

6. Experiment

6.1. Experiment Set-Up

Datasets and query workload. We used two real-world datasets in the experiments. The first one was the Frequently Occurring Surnames dataset (denoted by LastName) provided by the United States Census Bureau (https://www.census.gov/topics/population/genealogy/data/1990_census/1990_census_namefiles.html (accessed on 6 July 2022)), which contains 88,799 last names with an average length of 6.83 characters and a maximum length of 13 characters. The second one is the author dataset downloaded from DBLP (http://dblp.uni-trier.de/xml/ (accessed on 6 July 2022)), which includes 2,845,839 researcher names with an average length of 14.39 characters and a maximum length of 67 characters.

We built a query workload of single strings by randomly selecting 25 strings from each of the datasets, and we also artificially generated 25 strings. The reason we used synthetic strings was to ensure that the ne-gram exists. The results presented in the experiment part are the average over 10 trials.

Parameter setting. The parameters included (1) q for the q-gram inverted index and (2) the edit distance threshold k, as shown in

Table 7. Parameter setting.

Parameter	Range of Values
q	$\mathbf{2},3,4,5,6$
k	$\mathbf{1},2,3,4,5$

, where the default values are in bold.

Experimental environment. We implemented both the GS² and GS²-opt methods in Python and employed the SHA256 hash function from the Crypto Library. All the experiments were conducted on a machine with a 3.10GHz CPU and 128GB main memory, running an Ubuntu 18.04.3 LTS operating system.

To evaluate the performance of our methods, we adopted three metrics, i.e., VO construction time, VO size, and VO verification time, as described in Section 3.3. Note that the preprocessing time at the DO’s side and the network communication between the DO and the server are one-time costs that can be amortized over multiple queries and were thus not considered in our experiment. Meanwhile, we investigated the performance of each optimization technique in GS²-opt.

6.2. VO Construction Time

In this section, we measured the VO construction time at the server side. Figure 7 depicts the average VO construction time with various lengths of gram q and threshold k.

From Figure 7a, we can see that as q increases, the construction time of the GS² method first decreases slightly. The main reason is that as q increases, the length of e-i-lists in the $V{O}_{inv}$ diminishes, thus reducing the time spent in counting $Sid$. As q increases further, however, the construction time goes up steadily. This is because the number of grams in the inverted index increases, leading to (1) increases in the time spent searching for the ne-gram and (2) increases in the time for the construction of $V{O}_{inv}$. Furthermore, we can see that when q=2, the processing time of GS²-opt is significantly larger than that of GS². This is because the i-lists in the $V{O}_{inv}$ part are relatively long, and GS²-opt needs to take a long time to build MHTs for each i-list. In other cases, the performance trends of GS² and GS²-opt are basically consistent.

Figure 7b exhibits a similar trend to Figure 7a, but there are two differences. Firstly, the construction time of GS² always increases with q. The reason is that the LastName dataset is relatively small, and the time necessary to count the $Sid$ is only a small proportion of the time taken to construct the whole VO. Therefore, the reduction in the $Sid$ counting time imposes a negligible impact on the authentication time. Secondly, when q = 2, the gap between the two methods is not as significant as in Figure 7a. This is because the LastName dataset is relatively small and the i-lists in $V{O}_{inv}$ are much shorter than those in the author dataset.

Next, we investigated the impact of edit distance threshold k on VO construction time. The results are presented in Figure 7c,d. From Figure 7c, we can see that for the author dataset, the VO construction time of the GS² method increases slightly with k. The rationale is that (1) the majority of the time cost is spent on constructing $V{O}_{dic}$, and (2) the number of C-strings has little impact on the construction time of $V{O}_{dic}$. We can see that in GS²-opt, as k increases, the construction time also increases. This is due to the fact that constructing the $V{O}_{inv}$ part uses the majority of the total construction time, and as k increases, the number of $Sid$ included in the e-i-list becomes longer, leading to an increase in the construction time of $V{O}_{inv}$. Furthermore, as the volume of VO increases with k, the compression time also increases accordingly. We observe a similar performance trend on LastName dataset ( Figure 7d).

6.3. VO Size

In this section, we investigate the impact of q and k on VO size. The experimental results are shown in Figure 8.

From Figure 8a, we can see that as q increases, the VO size of the GS² method decreases dramatically at first. This is because when the length of grams grows, the number of grams will increase dramatically, and the average length of i-lists in the invert index will decrease. Therefore, the number and average length of e-i-lists will decrease accordingly, leading to a decrease in the number of C-strings and both $V{O}_{dic}$ and $V{O}_{inv}$. As q grows from 5 to 6, the VO size shows an increasing trend. The reason for this is that $\tau$ decreases as q grows, resulting in an increase in the number of C-strings and the $V{O}_{dic}$ size as well. From Figure 8a, we can also see that the performance trend of GS²-opt is similar to that of GS², but the size of VO generated by GS²-opt is much smaller than that generated by GS². The situation is similar in Figure 8b.

As shown in Figure 8a, when the length of a gram is large, e.g., q=5, the VO size will decrease drastically. However, the limitation of the threshold will be more strict with a greater gram length. If $\tau =|s_Q|-q+1-kq\le 0$, then the proposed methods will crash, and hence, the significant interval of k should be set to $[0,\frac{|s_Q|+1}{q}-1]$. Therefore, during the preprocessing phase, the length of grams should be set to a reasonable value.

Figure 8c,d depicts the impact of k on VO size. We can see that in the GS² method, as k increases, the growth rate of the VO size becomes faster. This is because (1) as k increases, the volume of $V{O}_{inv}$ remains constant, while the volume of the $V{O}_{dic}$ increases rapidly; (2) $V{O}_{dic}$ initially only accounts for a small proportion of VO, so its growth is not significant for the overall trend. However, when $V{O}_{dic}$ accounts for a larger proportion, its increase imposes a greater impact on the trend of VO size. The trend of GS²-opt is similar to that of GS² despite the fact that both $V{O}_{inv}$ size and $V{O}_{dic}$ size increase in the GS²-opt method. However, the VO volume of GS²-opt is significantly smaller than that of GS².

6.4. VO Verification Time

In this section, we study the impact of q and k on VO verification time. In general, the verification of VO involves several steps: (1) the decryption of signatures, (2) the verification of the e-gram and ne-gram, (3) the calculation of the edit distance for a C-string, (4) the verification of $V{O}_{dic}$, (5) the verification of $V{O}_{inv}$, and (6) re-counting the $Sid$. The total verification time is the sum of the time required for each of these six steps. It is worth noting that our experimental results show that time costs of the first three are negligible. Therefore, we only report the time consumed by the last three parts in our experiments.

When q increases, the verification time in the GS² method decreases at first and then increases, as shown in Figure 9a. This is because: (1) the size of $V{O}_{inv}$ part decreases, and the time needed to verify it also decreases; (2) the time needed to re-count $Sid$ decreases; (3) the time needed to verify $V{O}_{dic}$ first decreases and then increases. The change in the verification time of GS²-opt is similar, but due to a greater decrease in the time necessary for the verification of $V{O}_{inv}$, the overall verification time shows a decreasing trend. For the LastName dataset, as shown in Figure 9b, a similar trend is observed.

From Figure 9c,d we can see that when k is relatively small, the verification time of GS² on both datasets remains steady. However, when k is greater than 4, the verification time increases sharply. This is because the $V{O}_{dic}$ size increases significantly with k, resulting in a significant increase in verification time. Since the proportion of time spent on validating $V{O}_{dic}$ is very small at first, the increase in verification time has a marginal impact on the overall authentication time. On the other hand, as the proportion of $V{O}_{dic}$ increases, it incurs a greater impact on the overall authentication time. Note that in GS², $V{O}_{inv}$ does not change with k, so the time needed to verify it and recount $Sid$ remains largely unchanged.

However, for the GS²-opt method, the size of $V{O}_{inv}$ grows with an increase in k, and the time needed to verify it and recount $Sid$ increases accordingly. Therefore, the growth of GS²-opt is more significant at first.

6.5. Performance of Techniques in GS²-opt

In this section, we investigate the effect of each component in GS²-opt on VO size, and the experimental results are shown in Figure 10. It is worth noting that the VO size displayed in bars 2 to 8 in the figure were obtained by applying each optimization technique individually on the GS² approach. The last bar shows the combined effect of these four techniques, and the compression scheme used is LZMA.

The first bar depicts the VO size of GS². The second bar shows the VO size after applying the length-filtering technique on GS². The third bar is the VO size after using the representative grams technique alone, which reduces the size of $V{O}_{inv}$ and increases the size of $V{O}_{dic}$ significantly. The fourth bar presents the result of using the empty result improvement technique, the optimization effects of which seem to be ordinary, and this is because the number of strings that meet the requirement for this technique in our query set is relatively small. However, for queries that meet the criteria, the VO size can be reduced by approximately $99.96\%$ in the test. The next four bars show the VO sizes after compressing using different compression techniques, where snappy performs quite ordinarily and LZMA performs the best. The last bar gives the result of combining the previous four techniques, where the VO size is reduced to only $3.73\%$ of its original size.

7. Conclusions

In this paper, we focused on the problem of ensuring the correctness of the results of approximate string searches on outsourced text databases in the context of cloud computing. To solve this problem, we have designed an authenticating structure for a q-gram-based inverted index and proposed an efficient method named GS², with which we can efficiently build VO and verify the correctness of the query result. Furthermore, we proposed an optimal method named GS²-opt for more efficiency in terms of communication overhead. Extensive experiments on real datasets confirmed the effectiveness of our GS² and GS²-opt methods. In our future work, we will consider approximate string search result authentication with a freshness guarantee.