Adaptive Hybrid Mixed Two-Point Step Size Gradient Algorithm for Solving Non-Linear Systems

Abstract

In this paper, a two-point step-size gradient technique is proposed by which the approximate solutions of a non-linear system are found. The two-point step-size includes two types of parameters deterministic and random. A new adaptive backtracking line search is presented and combined with the two-point step-size gradient to make it globally convergent. The idea of the suggested method depends on imitating the forward difference method by using one point to estimate the values of the gradient vector per iteration where the number of the function evaluation is at most one for each iteration. The global convergence analysis of the proposed method is established under actual and limited conditions. The performance of the proposed method is examined by solving a set of non-linear systems containing high dimensions. The results of the proposed method is compared to the results of a derivative-free three-term conjugate gradient CG method that solves the same test problems. Fair, popular, and sensible evaluation criteria are used for comparisons. The numerical results show that the proposed method has merit and is competitive in all cases and superior in terms of efficiency, reliability, and effectiveness in finding the approximate solution of the non-linear systems.

1. Introduction

The computational knowledge revolution has brought many developments in different fields, such as technical sciences, industrial engineering, economics, operations research, networks, chemical engineering, etc. Therefore, many new problems are being generated continuously. These problems need to be solved. A mathematical modelling technique is a critical tool that is utilized to formulate these problems as mathematical problems [1].

The result is these problems are formulated as unconstrained (UCN), constrained (CON), multi-objective optimization problems (MOOP), and systems of non-linear equations (NE).

In recent years, there is a considerable advance in the study of non-linear equations.

Finding solutions to non-linear systems which include a large number of variables is a hard task. Hence, several derivative-free methods have been suggested to face this challenge [2]. A system of non-linear equations exists in many fields of science and technology. Non-linear equations represent various sorts of implementations [3,4].

The applications of systems of non-linear equations are arising in different fields such as compressive sensing, chemical equilibrium systems, optimal power flow equations, and financial forecasting problems [5,6].

The non-linear system of equations is defined by

$$F\left(x\right)=0,$$

(1)

where the function $F:{\mathbb{R}}^n\to {\mathbb{R}}^n$ is monotone and continuously differentiable, satisfying

$$⟨F\left(x\right)-F\left(y\right),x-y⟩\ge 0,\forall x,y\in {\mathbb{R}}^n.$$

(2)

The solution to Problem (1) can be generated by the classical methods, i.e., the new point is obtained by

$$x_{k+1}=x_{{}_k}+{\alpha }_{{}_k}{d}_{{}_k},k=0,1,2,\dots ,$$

(3)

where ${\alpha }_{{}_k}$ is the step-size obtained by an appropriate line search method with the search direction $d_{{}_k}$.

Many ideas have been implemented to obtain new proposed methods to design different formulas by which the step-size ${\alpha }_{{}_k}$ and search direction $d_{{}_k}$ are generated. For example, the Newton method [7], quasi-Newton method [8], and the conjugate gradient (CG) method [9,10,11,12].

The Newton method, the quasi-Newton method, and their related methods are widely used to solve Problem (1); due to their fast convergence speeds, see [13,14,15,16,17]. These methods require computing the Jacobian matrix or the approximate Jacobian matrix per iteration; hence, they are very expensive.

Thus, it is more useful to sidestep using these methods to deal with large-scale non-linear systems of equations.

The CG algorithm is a popular classical methods, due to its simplicity, less storage, efficiency, and good convergence properties. The CG method has become more popular in solving non-linear equations [18,19,20,21,22,23].

Currently, many derivative-free iterative methods have been proposed to deal with the large-scale Problem (1) [24].

Cruz [25] proposed a new spectral method to deal with large-scale systems of non-linear monotone equations. The core idea of the method, presented in [25], can be briefly described as follows.

$$x_{k+1}=x_{{}_k}-{\alpha }_{{}_k}{\lambda }_{{}_k}{F}_{{}_k},$$

(4)

where ${\alpha }_{{}_k}$ is the spectral parameter defined by

$${\alpha }_{{}_k}=\left\{\begin{array}{cc}\frac{\parallel y_{{}_k}{\parallel }^2}{s_{{}_k}^T{y}_{{}_k}}\hfill & \mathrm{if}\frac{F{\left(x_{k+1}\right)}^{T}F\left(x_{{}_k}\right)}{\parallel F\left(x_{{}_k}\right){\parallel }^2}\le 1-\frac{{\alpha }_{{}_k}}{{\alpha }_{{}_{max}}},\hfill \\ {\alpha }_{{}_{max}}\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(5)

where $s_{{}_k}=x_{k+1}-x_{{}_k}$ and $y_{{}_k}=F\left(x_{k+1}\right)-F\left(x_{{}_k}\right)$, with ${\alpha }_{{}_{max}}>>1$ sufficiently large, the author of [25] set ${\alpha }_{{}_{max}}=4.5\times {10}^{15}$. Furthermore, the author of [25] defined the step-size ${\lambda }_{{}_k}$ as follows ${\lambda }_{{}_k}=\lambda$, where $\lambda \in (0,1]$ is selected by a backtracking line search algorithm to make the following inequality holds:

$$\parallel F\left(x_{k+1}\right){\parallel }^2\le \parallel F\left(x_{{}_k}\right){\parallel }^2+{\zeta }_{{}_k}-\rho {\lambda }_{{}_k}{\parallel F\left(x_{{}_k}\right)\parallel }^2,$$

(6)

where ${\zeta }_{{}_k}={\left(0.999\right)}^k({10}^5+\parallel F\left(x_{{}_0}\right){\parallel }^2)$ for $k>0$.

The author of [25] used Lemma 3.3 from [26] to prove that the sequence $\{\parallel F\left(x_{{}_k}\right)\parallel \}$ converges. Furthermore, the author of [25] presented a convergence analysis for their algorithm and the numerical results show that the algorithm in is computationally efficient to solve Problem (1).

Stanimirovic et al. [27] proposed a new improved gradient descent iterations to solve Problem (1). They proposed new directions and step-size gradient methods by defining various parameters. Furthermore, they presented a theoretical convergence analysis of their methods under standard assumptions. In all four cases in [27], the direction vector is computed by using the system vector, i.e., they set $d_{{}_k}=F_{{}_k}$, with several step-size and parameters proposed by the authors.

Waziri et al. [28] proposed some hybrid derivative-free algorithms to solve Problem (1). They presented several parameters by which two methods were designed to deal with a non-linear system of equations. In both proposed methods the direction vector $d_{{}_k}$ is computed depending on the $F_{{}_k}$, i.e., the values of the non-linear system of equations (vector $F_{{}_k}$) are used to represent the search direction for some cases with several proposed parameters.

The performance of both methods was examined by solving a set of test problems of non-linear equations. These numerical experiments show the efficiency of both proposed methods.

Abubakar et al. [5] presented a new hybrid spectral-CG algorithm to find approximate solutions to Problem (1).

In all four cases used in [5], the vector $F_{{}_k}$ was utilized to compute the search direction $d_{{}_k}$.

Kumam et al. [29] proposed a new hybrid approach to deal with systems of non-linear equations applied to signal processing. The new approach suggested by the authors of [29] depends on hybridizing several parameters of the classical CG method by using a convex combination. Under sensible hypotheses, the authors of [29] proved the global convergence of their hybrid technique. Therefore, this new hybrid approach presented incredible results for solving monotone operator equations compared with other methods.

Dai and Zhu [19] proposed a modified Hestenes–Stiefel-type derivative-free (HS-CG method) to solve large-scale non-linear monotone equations. The HS-CG method was proposed by Hestenes and Stiefel [10]. The modified method presented by the authors of [19] is similar to the Dai and Wen [30] method for unconstrained optimization.

Furthermore, the authors of [19] presented a derivative-free new line search and step-size method. They established the convergence of their proposed method if the system of non-linear equations is Lipschitz, continuous and monotone. The numerical results obtained by this method demonstrate that the proposed approach in [19] is more efficient compared to other methods.

Ibrahim et al. [31] proposed a derivative-free iterative method to deal with non-linear equations with convex constraints using the projection technique. They also established a convergence analysis of the method under a few assumptions.

Thus, it can be said that there exists a consensus on estimating the value of the gradient vector in terms of the system vector, without using approximate values of the Jacobian matrix.

The hybridization of the gradient method with the random parameters (stochastic method) has been demonstrated to exhibit high efficiency in solving unconstrained and constrained optimization problems, see, for example, [32,33].

Therefore, the above briefly discusses the different ideas form previous literature by which the different formulas of step-size ${\alpha }_{{}_k}$ and search direction $d_{{}_k}$ were designed. All of these motivated and guided us in the current research.

This study aims to use numerical differentiation methods to estimate the gradient vector by which the step-size ${\alpha }_{{}_k}$ can be computed.

There are many studies which estimate the gradient vector, see, for example, [34,35,36,37]. The common approaches to the numerical differentiation methods are the forward difference and the central difference [38,39,40,41,42].

Sundry’s advanced methods provided fair results when numerically calculating the gradient vector values. See, for example, [34,35,36,37,43,44,45].

Obtaining a good estimation of the gradient vector depends on the optimal selection of the finite-difference interval h.

For example, the authors of [43,44] proposed a random mechanism for selecting the optimal finite-difference interval h and presented a good results when solving unconstrained minimization problems.

However, when solving Problem (1), using the numerical differentiation methods to compute the approximate values of the Jacobian matrix is extremely expensive.

Thus, we use the core idea of the forward difference method without computing the Jacobian matrix or the gradient vector, i.e., our suggested method will benefit from the essence of forward difference method where the function evaluation is at most one for each iteration.

Therefore, the primary aim of this article is to develop a new algorithm that solves Problem (1).

The contributions of this study are as follows:

• Suggesting a two $({\alpha }_k,{\beta }_k)$-step-size gradient method.
• Design two search directions $d_{{}_k}$ and $\overline{d_{{}_k}}$ with different trust regions that possess the sufficient descent property, i.e., $F_{{}_k}^T{d}_{{}_k}\le -C{\parallel F_{{}_k}\parallel }^2$ and $F_{{}_k}^T\overline{d_{{}_k}}\le -C{\parallel F_{{}_k}\parallel }^2$ with $0<C<1$.
• Design an iterative formula by using the ${\alpha }_k$-step-size and direction $d_{{}_k}$ by which the first candidate solution can be generated.
• Hybridization of the two-step-size gradient method, ${\alpha }_k$ and ${\beta }_k$ with the direction $\overline{d_{{}_k}}$ to generate the second candidate solution.
• A modified line search technique is presented to make the hybrid method a globally convergent method.
• A convergence analysis of the proposed algorithm is established.
• Numerical experiments including solving a set of test problems as a non-linear system.

The rest of this paper is organized as follows, in the next section, we introduce the proposed method. Section 3 presents the sufficient descent property and convergence analysis of the proposed method. Section 4 shows the numerical results, followed by the conclusion reported in the last section.

2. The Suggested Method

In this section, we propose a brand new mixed hybrid two-point step-size gradient algorithm to compute the approximate solutions to Problem (1). This proposed algorithm contains two search directions, two-point step-size, two formulas to generate the candida solutions, backtracking line search technique, and several parameters. The next section describes the proposed algorithm.

2.1. Algorithm

We generate two candidate solutions by two formulas as follows. The first one is defined by

$$x_{{}_{k+1}}=x_{{}_k}+d_{{}_k},$$

(7)

where the search direction $d_{{}_k}$ is defined as follows

$$d_{{}_k}=\left\{\begin{array}{cc}-F_{{}_0}\hfill & \mathrm{for}k=0,\hfill \\ -{\alpha }_{{}_k}{F}_{{}_k}\hfill & \mathrm{for}k\ge 1.\hfill \end{array}\right.$$

(8)

A new step-size ${\alpha }_{{}_k}$ is defined by

$${\alpha }_{{}_k}=\tau {\delta }_{{}_k}.$$

(9)

The parameter ${\delta }_{{}_k}$ is defined as follows

$${\delta }_{{}_k}=\frac{r_{{}_k}}{min\{\gamma ,max\{1,{\ell }_{{}_k}\}\}},$$

(10)

where the $\tau$ and $\gamma$ are constants with $1<\tau <\gamma <2$, and the parameter $r_{{}_k}$ is randomly generated at each iteration in the range $(0,1)$ and ${\ell }_{{}_k}=\frac{\parallel y_{{}_k}\parallel }{\parallel S_{{}_k}\parallel }$, the parameters $\parallel y_{{}_k}\parallel$ and $\parallel S_{{}_k}\parallel$ are computed in Section 2.1.1 and Section 2.1.2.

The second candidate solution is generated by the following algorithm.

Step 1: Perturb (shrink or extend) the solution obtained from Formula (7) by the following action

$$\overline{x_{{}_k}}={\alpha }_{{}_k}{x}_{{}_{k+1}}$$

(11)

where $x_{{}_{k+1}}$ is the candidate solution obtained from (7).

Step 2: Design a new research direction $\overline{d_{{}_k}}$ with a wider trust region than the trust region of the research direction $d_{{}_k}$ defined in (8). Thus, the new research direction $\overline{d_{{}_k}}$ can be defined by

$$\overline{d_{{}_k}}=-F\left(x_{{}_k}\right)+{\beta }_{{}_k}·d_{{}_k},$$

(12)

where the parameter ${\beta }_{{}_k}$ is defined by

$${\beta }_{{}_k}=\left\{\begin{array}{cc}\frac{{\ell }_{{}_k}}{\tau }\hfill & \mathrm{if}\frac{{\ell }_{{}_k}}{\tau }<\phi ,\hfill \\ {\alpha }_{{}_k}\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(13)

where $\phi$ is a constant number.

Step 3: Generate the second point by

$$\overline{x_{{}_{k+1}}}=\overline{x_{{}_k}}+{\alpha }_{{}_k}.\overline{d_{{}_k}},$$

(14)

Note 1: The perturbation (shrink or extend) in step 1 might occasionally move point (14) next to point (7).

Therefore, the second candidate solution might move far away or remain next to the first candidate solution.

Note 2: The second candidate solution obtained by (14) may give a better or worse result compared to the first candidate solution given by (7). Therefore, the best solution is picked from the two solutions obtained from (7) and (14).

Hence, the backtracking line search algorithm is applied to the best solution obtained to ensure the following inequality holds.

$$\parallel F_{{}_{k+1}}{\parallel }^2\le \parallel F_{{}_k}{\parallel }^2+{\mu }_{{}_k}-{\lambda }_{{}_k}\rho {\parallel F_{{}_k}\parallel }^2.$$

(15)

The line search in (15) imitates the line search in (6), proposed by [25] with the following changes.

The sequence ${\mu }_{{}_k}$ is defined by

$${\mu }_{{}_k}=exp(-k)·(k^2+\parallel F_{{}_k}\parallel ),$$

(16)

where k is the number of iterations at which the two candidate solutions from both Formulas (7) and (14) are generated. Furthermore, the step-size ${\lambda }_{{}_k}$ is defined by

$${\lambda }_{{}_k}=\frac{\parallel x_{{}_{k+1}}-x_{{}_k}\parallel }{\Psi (\parallel F_{{}_k}\parallel ,\epsilon )},$$

(17)

where $\Psi (\parallel F_{{}_k}\parallel ,\epsilon )=\parallel F_{{}_k}\parallel +\epsilon$, $0<\epsilon <1$.

Therefore, our step-size ${\lambda }_{{}_k}$ is designed in a different manner than the step-size proposed in [25].

We continue to reduce the step length ${\lambda }_{{}_k}$ by a dampening factor $\rho \in (0,1)$ to guarantee Inequality (15).

Note: Without the effects of the damping factor $\rho$, the step-size ${\lambda }_{{}_k}$ is bounded; therefore, it converges, as shown in Corollary 2, and it is clear that term ${\mu }_{{}_k}$ is bounded.

In the following we present two algorithms to compute the scalers $\parallel y_{{}_k}\parallel$ and $\parallel S_{{}_k}\parallel$.

The following two algorithms simulate the forward difference method, defined by

$$D_{{}_f}f\left(x_{{}_i}\right)=\frac{f\left(x_{{}_{i+1}}\right)-f\left(x_{{}_i}\right)}{x_{{}_{i+1}}-x_{{}_i}}=\frac{f(x_{{}_i}+h)-f\left(x_{{}_i}\right)}{h},$$

(18)

where $i=1,2,\dots ,n$ and n is the number of variables.

2.1.1. First Approach (App1)

Step 1: $S_{{}_k}=x_{{}_k}-x_{{}_{k+1}}$, where $|x_{{}_k}|=n$ denotes the number of components of variable $x_{{}_k}$.

Step 2: $y_{{}_k}=F\left(x_{{}_k}\right)-F\left(x_{{}_{k+1}}\right)$.

2.1.2. Second Approach (App2)

Step 1: Generate a new point next to point $x_{{}_{k+1}}$ as follows, $x_{h_{{}_k}}=x_{{}_{k+1}}+h_{{}_k}$, where $h_{{}_k}$ is a random vector generated in the range ${(0,1)}^n$ at each iteration.

Step 2: Compute $F\left(x_{h_{{}_k}}\right)$, and set $S_{{}_k}=h_{{}_k}$ and $y_{{}_k}=F\left(x_{{}_{k+1}}\right)-F\left(x_{h_{{}_k}}\right)$.

Note 1: Point $x_{{}_{k+1}}$ is the optimal solution that satisfies Inequality (15).

Note 2: From the idea presented in Algorithm 2 from [43], we randomly generate the values of $h_{{}_k}$.

The formulas and procedures mentioned above can be expressed as a set of steps to represent the proposed algorithm as follows.

Our proposed method is called the “hybrid random two-point step-size gradient method”, denoted by “HRSG”.

Therefore, two algorithms were designed to solve Problem (1), the first depends on the first approach (App1), abbreviated by “HRSG1”; while the second depends on the second approach (App2), abbreviated by “HRSG2”.

3. Convergence Analysis of the proposed algorithm

The following assumptions, lemmas and theorems are required to establish the global convergence of Algorithm 1.

Algorithm 1 New proposed algorithm “HRSG”

Input:  $F:{\mathbb{R}}^n\to {\mathbb{R}}^n$, $F\in C^1$, $0<\rho <\sigma <1$, $k=0$, a starting point $x_{{}_k}\in {\mathbb{R}}^n$ and $\epsilon >0$.   Output:  $x^{*}=x_{{}_{k+1}}$ the approximate solution of the system F, $\parallel F\left(x^{*}\right)\parallel \le \epsilon$.  1: Compute $F_{{}_k}=F\left(x_{{}_k}\right)$, and set $d_{{}_k}=-F_{{}_k}$.  2: while$\parallel F_{{}_k}\parallel >\epsilon$do  3:     Compute $x_{{}_{k+1}}=x_{{}_k}+d_{{}_k}$.                       ▹$d_{{}_k}$ defined by (8).  4:     Compute $\overline{x_{{}_{k+1}}}=\overline{x_{{}_k}}+{\alpha }_{{}_k}.\overline{d_{{}_k}}$.       ▹$\overline{x_{{}_k}}$ and $\overline{d_{{}_k}}$ defined by (11) and (12), respectively.  5:     Pick $x_{{}_{best}}$ as the best solution to $\{x_{{}_{k+1}},\overline{x_{{}_k}}\}$.  6:     Set $x_{{}_{k+1}}=x_{{}_{best}}$ and $F_{{}_{k+1}}=F\left(x_{{}_{best}}\right)$.               ▹ Accepted as the point.  7:     while $\parallel F_{{}_{k+1}}{\parallel }^2\ge \parallel F_{{}_k}{\parallel }^2+{\mu }_{{}_k}-{\lambda }_{{}_k}\rho {\parallel F_{{}_k}\parallel }^2$ do  8:         Set ${\lambda }_{{}_k}={\lambda }_{{}_k}\sigma$.                         ▹${\lambda }_{{}_k}$ computed by (17).  9:         Compute $x_{{}_{k+1}}=x_{{}_k}-{\lambda }_{{}_k}{F}_{{}_k}$. 10:         Compute $F_{{}_{k+1}}=F\left(x_{{}_{k+1}}\right)$. 11:     end while 12:     Set $F_{{}_k}=F_{{}_{k+1}}$ and $x_{{}_k}=x_{{}_{k+1}}$.                   ▹ Update the solution. 13:     Set $k=k+1$ 14: end while 15: return $x^{*}=x_{{}_{k+1}}$ and $F\left(x^{*}\right)$.

Assumption 1.  (1a) there are a set of solutions to System (1).

(1b) the set of non-linear systems F satisfies the Lipschitz condition, i.e., there exists a positive constant L such that

$$\parallel F\left(x\right)-F\left(y\right)\parallel \le L\parallel x-y\parallel ,$$

(19)

for all $x,y\in {\mathbb{R}}^n$.

The next lemma shows that the proposed method “HRSG” has the sufficient descent property and trust region feature.

  Lemma 1.

Let sequence $\left\{x_{{}_k}\right\}$ be generated by Algorithm 1. Then, we have

$$F_{{}_k}^T{d}_{{}_{{}_k}}\le -{\delta }_{{}_k}{\parallel F_{{}_k}\parallel }^2,$$

(20)

and

$$\parallel d_{{}_k}\parallel \le \tau \parallel F_{{}_k}\parallel ,$$

(21)

where $0<{\delta }_{{}_k}<1$ and $1<\tau <2$.

Proof. 

If $k=0$, $d_{{}_0}=-F_{{}_0}$, then $F_{{}_0}^T{d}_{{}_0}=-\left|\right|F_{{}_0}{\left|\right|}^2$ and $\left|\right|d_{{}_0}\left|\right|=\parallel F_{{}_0}\parallel$, implying (20) and (21).

Since $F_{{}_k}^T{d}_{{}_k}=-{\alpha }_{{}_k}{\parallel F_{{}_k}\parallel }^2$, ${\alpha }_{{}_k}=\tau .{\delta }_{{}_k}$, $0<{\delta }_{{}_k}<1$ and $\tau >1$, then

$$F_{{}_k}^T{d}_{{}_k}=-\tau .{\delta }_{{}_k}\parallel F_{{}_k}{\parallel }^2\le -{\delta }_{{}_k}{\parallel F_{{}_k}\parallel }^2.$$

Therefore, (20) is true. Since $\parallel d_{{}_k}\parallel ={\alpha }_{{}_k}\parallel F_{{}_k}\parallel$, ${\alpha }_{{}_k}=\tau .{\delta }_{{}_k}$, $\tau >1$ and $0<{\delta }_{{}_k}<1$, then $\parallel d_{{}_k}\parallel \le \tau \parallel F_{{}_k}\parallel$. Therefore, the proof is complete. □

  Lemma 2.

The sequence of the research direction $\{\overline{d_{{}_k}}$} defined by (12) satisfies the following properties.

$$F_{{}_k}^T\overline{d_{{}_{{}_k}}}\le -C{\parallel F_{{}_k}\parallel }^2,$$

(22)

and

$$\parallel \overline{d_{{}_k}}\parallel \le \overline{C}\parallel F_{{}_k}\parallel ,$$

(23)

Proof. 

Since $\overline{d_{{}_k}}=-F_{{}_k}+{\beta }_{{}_k}.d_{{}_k}$, then $F_{{}_k}^T\overline{d_{{}_k}}=-{\parallel F_{{}_k}\parallel }^2+{\beta }_{{}_k}{F}_{{}_k}^T{d}_{{}_k}$.

From (20), we obtain $F_{{}_k}^T\overline{d_{{}_k}}\le -\parallel F_{{}_k}{\parallel }^2-{\beta }_{{}_k}{\delta }_{{}_k}{\parallel F_{{}_k}\parallel }^2$.

According to (10) and (13), $0<{\delta }_{{}_k}<1$ for $k>1$, while ${\beta }_{{}_k}$ has two cases.

Case 1: If ${\beta }_{{}_k}\ge 1$, then $F_{{}_k}^T\overline{d_{{}_k}}\le -\parallel F_{{}_k}{\parallel }^2-{\beta }_{{}_k}{\delta }_{{}_k}\parallel F_{{}_k}{\parallel }^2\le -{\delta }_{{}_k}{\parallel F_{{}_k}\parallel }^2$.

We set $C=-{\delta }_{{}_k}$; hence, $F_{{}_k}^T\overline{d_{{}_k}}\le -C{\parallel F_{{}_k}\parallel }^2$, with $0<C<1$.

Case 2: If $0<{\beta }_{{}_k}<1$, then $F_{{}_k}^T\overline{d_{{}_k}}\le -\parallel F_{{}_k}{\parallel }^2-{\beta }_{{}_k}{\delta }_{{}_k}{\parallel F_{{}_k}\parallel }^2.$

In this case, since $0<{\beta }_{{}_k}<1$ and $0<{\delta }_{{}_k}<1$, then $0<{\beta }_{{}_k}{\delta }_{{}_k}<1$. Hence, we have

$$-\parallel F_{{}_k}{\parallel }^2-{\beta }_{{}_k}{\delta }_{{}_k}\parallel F_{{}_k}{\parallel }^2\le -{\beta }_{{}_k}{\delta }_{{}_k}{\parallel F_{{}_k}\parallel }^2.$$

Therefore, the following inequality is true.

$$F_{{}_k}^T\overline{d_{{}_k}}\le -\parallel F_{{}_k}{\parallel }^2-{\beta }_{{}_k}{\delta }_{{}_k}\parallel F_{{}_k}{\parallel }^2\le -{\beta }_{{}_k}{\delta }_{{}_k}{\parallel F_{{}_k}\parallel }^2.$$

(24)

Then,

$$F_{{}_k}^T\overline{d_{{}_k}}\le -{\beta }_{{}_k}{\delta }_{{}_k}{\parallel F_{{}_k}\parallel }^2.$$

We set $C={\beta }_{{}_k}{\delta }_{{}_k}$; hence, in this case, $F_{{}_k}^T\overline{d_{{}_k}}\le -C{\parallel F_{{}_k}\parallel }^2$, with $0<C<1$.

Both cases satisfy $F_{{}_k}^T\overline{d_{{}_k}}\le -C{\parallel F_{{}_k}\parallel }^2$ with $0<C<1$. Then the direction $\overline{d_{{}_k}}$ satisfies the sufficient descent condition.

Therefore, (22) is true.

Since $\parallel \overline{d_{{}_k}}\parallel =\parallel F_{{}_k}\parallel +{\beta }_{{}_k}\parallel d_{{}_k}\parallel$, by using (21), we obtain

$\parallel \overline{d_{{}_k}}\parallel \le \parallel F_{{}_k}\parallel +\tau {\beta }_{{}_k}\parallel F_{{}_k}\parallel =(1+\tau {\beta }_{{}_k})\parallel F_{{}_k}$, and set $\overline{C}=1+\tau {\beta }_{{}_k}$. Then, (23) is true, with $1<\overline{C}<\infty$.

Therefore, the proof is complete. □

We adopt the concept from [16] in the following lemmas.

  Lemma 3.

Solodov and Svaiter [16] assumed that $x^{*}\in {\mathbb{R}}^n$ satisfies $\parallel F\left(x^{*}\right)\parallel =0$. Thus, let the sequence $\left\{x_{{}_k}\right\}$ be generated by Algorithm 1. Then,

$$\parallel x_{k+1}-x^{*}{\parallel }^2\le \parallel x_{{}_k}-x^{*}{\parallel }^2-{\parallel x_{k+1}-x_{{}_k}\parallel }^2$$

(25)

  Corollary 1.

Lemma 3 implies that the sequence $\{\parallel F\left(x_{{}_k}\right)-F\left(x^{*}\right)\parallel \}$ is non-increasing, convergent and therefore bounded. Furthermore, $\left\{x_{{}_k}\right\}$ is bounded and

$$\underset{k\to \infty }{lim}{\parallel x_{k+1}-x_{{}_k}\parallel }^2=0.$$

(26)

  Corollary 2.

Form (26), it is easy to prove that the following limit is true.

$$\underset{k\to \infty }{lim}{\lambda }_{{}_k}=0,$$

(27)

where the step length ${\lambda }_{{}_k}$ is defined by (17).

Proof. 

By using the result in (26), since $\Psi (\parallel F_{{}_k}\parallel ,\epsilon )\ne 0$, then

$$\underset{k\to \infty }{lim}{\lambda }_{{}_k}=\underset{k\to \infty }{lim}\frac{\parallel x_{k+1}-x_{{}_k}{\parallel }^2}{\Psi (\parallel F_{{}_k}\parallel ,\epsilon )}=0.$$

Therefore, (27) is true. □

  Lemma 4.

Let $\left\{x_{{}_k}\right\}$ be generated by Algorithm 1, then

$$\underset{k\to \infty }{lim}\parallel d_{{}_k}\parallel =0.$$

(28)

Proof. 

By using (7)–(9), (21) and (26), since $x_{k+1}=x_{{}_k}+d_{{}_k}$, then $\parallel x_{k+1}-x_{{}_k}\parallel =\parallel d_{{}_k}\parallel$.

From (8), we have $\parallel d_{{}_k}\parallel ={\alpha }_{{}_k}\parallel F_{{}_k}\parallel$ for $k\ge 1$, where ${\alpha }_{{}_k}=\tau {\delta }_{{}_k}$. Then

$$\parallel x_{k+1}-x_{{}_k}\parallel =\tau {\delta }_{{}_k}\parallel F_{{}_k}\parallel .$$

(29)

Since $\tau >1$ and $0<{\delta }_{{}_k}<1$, then $\parallel d_{{}_k}\parallel \le \tau \parallel F_{{}_k}\parallel$.

Therefore, the following is true

$$\tau {\delta }_{{}_k}\parallel F_{{}_k}\parallel \ge {\delta }_{{}_k}\parallel d_{{}_k}\parallel .$$

(30)

From (29) and (30) we can say the following is true.

$$0\le {\delta }_{{}_k}\parallel d_{{}_k}\parallel \le \parallel x_{k+1}-x_{{}_k}\parallel .$$

(31)

By using (26), then $\underset{k\to \infty }{lim}{\delta }_{{}_k}\parallel d_{{}_k}\parallel =0$.

Since $0<{\delta }_{{}_k}<1$ for all k (where ${\delta }_{{}_k}$ is bounded), then (28) is true.

Therefore, Lemma 4 holds. □

  Theorem 1.

Let $\left\{x_{{}_k}\right\}$ be generated by Algorithm 1. Then

$$\underset{k\to \infty }{lim}\parallel F_{{}_k}\parallel =0.$$

(32)

Proof. 

By using proof contradiction, we assume that (32) does not hold true, that is, there exists a positive constant $ϵ$ such that

$$\parallel F_{{}_k}\parallel >ϵ,\forall k\ge 0.$$

(33)

By combing the sufficient descent condition (20) and the Cauchy–Schwarz inequality we obtain

$$\parallel F_{{}_k}\parallel \parallel d_{{}_k}\parallel \ge -F_{{}_k}^T{d}_{{}_k}\ge {\delta }_{{}_k}{\parallel F_{{}_k}\parallel }^2$$

(34)

Accordingly, we obtain

$$\parallel d_{{}_k}\parallel \ge {\delta }_{{}_k}\parallel F_{{}_k}\parallel >{\delta }_{{}_k}ϵ>0.$$

(35)

Then,

$$\parallel d_{{}_k}\parallel >{\delta }_{{}_k}ϵ>0.$$

(36)

By using the result in (28) with $k\to \infty$, then (36) contradicts with the facts.

Therefore, Theorem 1 holds. □

Note 1: Both search directions $d_{{}_k}$ and $\overline{d_{{}_k}}$ satisfy the sufficient descent condition, i.e., $F_{{}_k}^T{d}_{{}_k}\le -C{\parallel F_{{}_k}\parallel }^2$ and $F_{{}_k}^T\overline{d_{{}_k}}\le -C{\parallel F_{{}_k}\parallel }^2$ with $0<C<1$.

Note 2: $\parallel d_{{}_k}\parallel <\parallel \overline{d_{{}_k}}\parallel \le \overline{C}\parallel F_{{}_k}\parallel$, with $1<\overline{C}<\infty$.

Note 3: Algorithm 1 includes two different search direction $d_{{}_k}$ and $\overline{d_{{}_k}}$ and three step-sizes $\alpha {}_k$, $\beta {}_k$ and $\lambda {}_k$ with a mix of random and deterministic parameters, enabling Algorithm 1 capable of approaching an approximate solution to Problem (1). The difference between the size of the trust region of both search directions helps the proposed method search the null space (where solutions are) of the entire feasible region.

Note 4: Theorem 1 confirms that sequence $\left\{x_{{}_k}\right\}$ obtained by Algorithm 1 makes System (1) approach 0 as long as $k\to \infty$, i.e., $\underset{k\to \infty }{lim}\parallel F_{{}_k}\parallel =0.$

4. Numerical Experiments

In this section, nine test problems are considered to illustrate the convergence of the proposed Algorithm 1.

These test problems are taken from [46]. All codes were programmed in MATLAB version 8.5.0.197613 (R2015a) and ran on a PC with Intel(R) Core(TM) i5-3230M CPU@2.60GHz 2.60 GHz with RAM 4.00GB of memory on the Windows 10 operating system.

The parameters of Algorithm 1 are listed as follows.

$\rho ={10}^{-4}$, $\sigma =0.8$, $\epsilon ={10}^{-6}$, $\tau =1.001$, $\gamma =1.88$ and $\phi =3$.

Numerical Results for a Non-Linear System

The section gives the numerical results of a system of non-linear equations solved by Algorithm 1 that represents two approaches (App1 and App2).

The performance of the two approaches is tested by a set of test problems (a system of non-linear equations).

The number of dimensions of the test problems (systems of non-linear equations) are listed as follows: $n\in \{{10}^3,5\times {10}^3,{10}^4,5\times {10}^4,{10}^5\}$.

The HRSG method described by Algorithm 1 contains two algorithms (HRSG1 and HRSG2). The HRSG1 algorithm denotes the first approach (App1) described in Section 2.1.1.

While the HRSG2 algorithm indicates the second approach (App1) described in Section 2.1.2.

Therefore, the results of both algorithms listed in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14, Table 15, Table 16, Table 17 and Table 18 are obtained by running each algorithm 51 times for all the test problems with five cases of the number dimensions and seven initial points.

Table 1. Numeral results (Problem 1) for the terms BItr, BEFs and BTcpu of the three methods.

n	INP	HRSG1			HRSG2			Algo
		BItr	BEFs	BTcpu	BItr	BEFs	BTcpu	BItr	BEFs	BTcpu
1000	$x_{{}_1}$	6	12	0.002	6	18	0.002	2	7	0.015
	$x_{{}_2}$	6	12	0.002	7	21	0.003	2	7	0.009
	$x_{{}_3}$	7	14	0.002	7	21	0.004	2	7	0.021
	$x_{{}_4}$	6	12	0.002	7	21	0.003	2	7	0.009
	$x_{{}_5}$	9	18	0.003	8	24	0.003	2	7	0.013
	$x_{{}_6}$	6	12	0.002	9	27	0.004	2	7	0.007
	$x_{{}_7}$	7	14	0.002	8	24	0.003	8	32	0.010
5000	$x_{{}_1}$	5	10	0.006	7	21	0.009	2	7	0.016
	$x_{{}_2}$	6	12	0.006	7	21	0.009	2	7	0.023
	$x_{{}_3}$	5	10	0.005	8	24	0.010	2	7	0.021
	$x_{{}_4}$	7	14	0.008	8	24	0.012	2	7	0.018
	$x_{{}_5}$	8	16	0.009	9	27	0.012	2	7	0.017
	$x_{{}_6}$	8	16	0.009	9	27	0.013	2	7	0.018
	$x_{{}_7}$	7	14	0.008	6	18	0.008	8	32	0.029
10,000	$x_{{}_1}$	6	12	0.013	8	24	0.022	2	7	0.033
	$x_{{}_2}$	6	12	0.013	8	24	0.021	2	7	0.021
	$x_{{}_3}$	8	16	0.017	6	18	0.016	2	7	0.027
	$x_{{}_4}$	7	14	0.015	7	21	0.018	2	7	0.021
	$x_{{}_5}$	9	18	0.019	10	30	0.027	2	7	0.029
	$x_{{}_6}$	7	14	0.015	9	27	0.023	2	7	0.028
	$x_{{}_7}$	6	12	0.013	8	24	0.021	8	32	0.049
50,000	$x_{{}_1}$	5	10	0.059	8	24	0.116	2	7	0.083
	$x_{{}_2}$	7	14	0.082	7	21	0.104	2	7	0.082
	$x_{{}_3}$	9	18	0.105	6	18	0.086	2	7	0.134
	$x_{{}_4}$	6	12	0.072	10	30	0.142	2	7	0.096
	$x_{{}_5}$	7	14	0.085	8	24	0.113	2	7	0.108
	$x_{{}_6}$	9	18	0.107	10	30	0.142	2	7	0.097
	$x_{{}_7}$	7	14	0.083	8	24	0.128	8	32	0.218
100,000	$x_{{}_1}$	7	14	0.184	8	24	0.250	2	7	0.160
	$x_{{}_2}$	8	16	0.228	9	27	0.304	2	7	0.164
	$x_{{}_3}$	8	16	0.239	8	24	0.256	2	7	0.158
	$x_{{}_4}$	7	14	0.215	11	33	0.353	2	7	0.161
	$x_{{}_5}$	9	18	0.239	10	30	0.323	2	7	0.175
	$x_{{}_6}$	8	16	0.217	11	33	0.392	2	7	0.185
	$x_{{}_7}$	7	14	0.186	9	27	0.319	9	36	0.393

Table 2. Numeral results (Problem 2) for the terms BItr, BEFs and BTcpu for the three methods.

n	INP	HRSG1			HRSG2			Algo
		BItr	BEFs	BTcpu	BItr	BEFs	BTcpu	BItr	BEFs	BTcpu
1000	$x_{{}_1}$	4	8	0.001	4	12	0.002	6	19	0.012
	$x_{{}_2}$	4	8	0.001	4	12	0.002	6	19	0.006
	$x_{{}_3}$	5	10	0.002	3	9	0.001	6	19	0.006
	$x_{{}_4}$	6	12	0.002	5	15	0.002	7	22	0.005
	$x_{{}_5}$	5	10	0.002	4	12	0.002	6	19	0.007
	$x_{{}_6}$	6	12	0.002	3	9	0.001	8	25	0.005
	$x_{{}_7}$	4	8	0.001	5	15	0.002	15	49	0.017
5000	$x_{{}_1}$	5	10	0.006	4	12	0.006	6	20	0.015
	$x_{{}_2}$	4	8	0.004	4	12	0.006	6	20	0.021
	$x_{{}_3}$	5	10	0.005	4	12	0.006	6	19	0.014
	$x_{{}_4}$	6	12	0.007	5	15	0.007	7	23	0.021
	$x_{{}_5}$	5	10	0.006	3	9	0.006	6	19	0.016
	$x_{{}_6}$	5	10	0.006	4	12	0.007	8	25	0.019
	$x_{{}_7}$	5	10	0.005	3	9	0.007	15	50	0.042
10,000	$x_{{}_1}$	4	8	0.009	4	12	0.014	6	20	0.032
	$x_{{}_2}$	5	10	0.012	4	12	0.013	6	20	0.028
	$x_{{}_3}$	4	8	0.009	5	15	0.014	6	19	0.031
	$x_{{}_4}$	4	8	0.009	3	9	0.008	7	23	0.034
	$x_{{}_5}$	5	10	0.012	4	12	0.012	6	19	0.029
	$x_{{}_6}$	6	12	0.014	3	9	0.008	8	26	0.036
	$x_{{}_7}$	5	10	0.012	6	18	0.016	13	44	0.066
50,000	$x_{{}_1}$	5	10	0.060	4	12	0.063	6	20	0.097
	$x_{{}_2}$	4	8	0.048	4	12	0.056	6	20	0.095
	$x_{{}_3}$	5	10	0.059	4	12	0.079	7	23	0.119
	$x_{{}_4}$	5	10	0.062	4	12	0.058	7	23	0.123
	$x_{{}_5}$	5	10	0.060	4	12	0.070	7	23	0.179
	$x_{{}_6}$	6	12	0.072	5	15	0.073	8	26	0.151
	$x_{{}_7}$	5	10	0.061	4	12	0.064	15	51	0.300
100,000	$x_{{}_1}$	5	10	0.144	5	15	0.178	6	20	0.215
	$x_{{}_2}$	4	8	0.115	3	9	0.134	7	25	0.229
	$x_{{}_3}$	4	8	0.119	4	12	0.135	7	24	0.261
	$x_{{}_4}$	6	12	0.173	6	18	0.211	8	28	0.288
	$x_{{}_5}$	6	12	0.172	5	15	0.168	7	23	0.225
	$x_{{}_6}$	4	8	0.118	4	12	0.135	8	26	0.258
	$x_{{}_7}$	5	10	0.153	5	15	0.169	15	51	0.851

Table 3. Numeral results (Problem 3) for the terms BItr, BEFs and BTcpu for the three methods.

n	INP	HRSG1			HRSG2			Algo
		BItr	BEFs	BTcpu	BItr	BEFs	BTcpu	BItr	BEFs	BTcpu
1000	$x_{{}_1}$	5	10	0.002	3	9	0.002	7	27	0.006
	$x_{{}_2}$	6	12	0.002	5	15	0.002	7	28	0.007
	$x_{{}_3}$	5	10	0.002	3	9	0.002	6	24	0.007
	$x_{{}_4}$	6	12	0.002	3	9	0.001	-	-	-
	$x_{{}_5}$	6	12	0.002	6	18	0.002	-	-	-
	$x_{{}_6}$	6	12	0.002	6	18	0.002	-	-	-
	$x_{{}_7}$	5	10	0.001	5	15	0.002	-	-	-
5000	$x_{{}_1}$	5	10	0.005	5	15	0.007	7	28	0.013
	$x_{{}_2}$	4	8	0.004	4	12	0.008	8	31	0.017
	$x_{{}_3}$	5	10	0.005	5	15	0.006	7	27	0.013
	$x_{{}_4}$	6	12	0.006	6	18	0.008	-	-	-
	$x_{{}_5}$	7	14	0.007	4	12	0.005	-	-	-
	$x_{{}_6}$	5	10	0.005	6	18	0.007	8	32	0.017
	$x_{{}_7}$	5	10	0.005	6	18	0.008	-	-	-
10,000	$x_{{}_1}$	5	10	0.011	5	15	0.012	7	27	0.025
	$x_{{}_2}$	5	10	0.011	4	12	0.013	8	32	0.028
	$x_{{}_3}$	5	10	0.010	6	18	0.015	7	27	0.025
	$x_{{}_4}$	7	14	0.015	6	18	0.017	-	-	-
	$x_{{}_5}$	6	12	0.013	5	15	0.012	-	-	-
	$x_{{}_6}$	5	10	0.010	5	15	0.016	8	32	0.031
	$x_{{}_7}$	7	14	0.015	6	18	0.015	-	-	-
50,000	$x_{{}_1}$	6	12	0.068	6	18	0.089	8	32	0.117
	$x_{{}_2}$	6	12	0.066	5	15	0.061	7	27	0.094
	$x_{{}_3}$	6	12	0.067	5	15	0.062	6	23	0.080
	$x_{{}_4}$	6	12	0.066	7	21	0.087	-	-	-
	$x_{{}_5}$	5	10	0.054	7	21	0.097	-	-	-
	$x_{{}_6}$	6	12	0.075	7	21	0.103	8	31	0.112
	$x_{{}_7}$	7	14	0.077	7	21	0.118	-	-	-
100,000	$x_{{}_1}$	3	6	0.072	5	15	0.150	7	27	0.175
	$x_{{}_2}$	7	14	0.166	4	12	0.119	8	31	0.241
	$x_{{}_3}$	8	16	0.195	6	18	0.179	8	32	0.261
	$x_{{}_4}$	6	12	0.156	4	12	0.136	-	-	-
	$x_{{}_5}$	7	14	0.190	8	24	0.241	-	-	-
	$x_{{}_6}$	7	14	0.187	8	24	0.239	9	36	0.253
	$x_{{}_7}$	7	14	0.191	7	21	0.213	-	-	-

Table 4. Numeral results (Problem 4) for the terms BItr, BEFs and BTcpu for the three methods.

n	INP	HRSG1			HRSG2			Algo
		BItr	BEFs	BTcpu	BItr	BEFs	BTcpu	BItr	BEFs	BTcpu
1000	$x_{{}_1}$	2	4	0.001	3	9	0.004	2	6	0.006
	$x_{{}_2}$	3	6	0.002	2	6	0.002	2	6	0.004
	$x_{{}_3}$	3	6	0.002	4	12	0.005	2	6	0.005
	$x_{{}_4}$	3	6	0.002	5	15	0.005	2	7	0.005
	$x_{{}_5}$	2	4	0.002	1	3	0.001	2	7	0.009
	$x_{{}_6}$	4	8	0.003	5	15	0.005	2	7	0.005
	$x_{{}_7}$	5	10	0.004	4	12	0.004	25	80	0.021
5000	$x_{{}_1}$	3	6	0.007	4	12	0.011	2	6	0.019
	$x_{{}_2}$	5	10	0.011	5	15	0.015	2	6	0.017
	$x_{{}_3}$	4	8	0.009	4	12	0.011	2	6	0.019
	$x_{{}_4}$	4	8	0.009	4	12	0.011	2	7	0.020
	$x_{{}_5}$	3	6	0.007	1	3	0.004	2	7	0.019
	$x_{{}_6}$	1	2	0.002	3	9	0.009	2	7	0.016
	$x_{{}_7}$	4	8	0.009	1	3	0.003	25	79	0.103
10,000	$x_{{}_1}$	4	8	0.017	2	6	0.011	2	6	0.029
	$x_{{}_2}$	4	8	0.016	3	9	0.022	2	6	0.023
	$x_{{}_3}$	4	8	0.014	3	9	0.016	2	6	0.025
	$x_{{}_4}$	3	6	0.011	4	12	0.022	2	7	0.024
	$x_{{}_5}$	4	8	0.015	2	6	0.011	2	7	0.027
	$x_{{}_6}$	5	10	0.022	3	9	0.017	2	7	0.022
	$x_{{}_7}$	5	10	0.019	6	18	0.033	27	85	0.199
50,000	$x_{{}_1}$	5	10	0.093	3	9	0.109	2	6	0.096
	$x_{{}_2}$	5	10	0.093	4	12	0.114	2	6	0.097
	$x_{{}_3}$	2	4	0.037	4	12	0.110	2	6	0.100
	$x_{{}_4}$	6	12	0.127	2	6	0.100	2	7	0.095
	$x_{{}_5}$	1	2	0.021	1	3	0.028	2	7	0.093
	$x_{{}_6}$	5	10	0.104	3	9	0.082	2	7	0.096
	$x_{{}_7}$	5	10	0.105	5	15	0.142	29	89	0.839
100,000	$x_{{}_1}$	4	8	0.176	4	12	0.227	2	6	0.192
	$x_{{}_2}$	3	6	0.120	4	12	0.228	2	6	0.213
	$x_{{}_3}$	3	6	0.129	3	9	0.175	2	6	0.197
	$x_{{}_4}$	4	8	0.169	3	9	0.172	2	7	0.187
	$x_{{}_5}$	2	4	0.089	4	12	0.321	2	7	0.189
	$x_{{}_6}$	1	2	0.040	5	15	0.286	2	7	0.196
	$x_{{}_7}$	4	8	0.180	4	12	0.234	29	91	1.666

Table 5. Numeral results (Problem 5) for the terms BItr, BEFs and BTcpu for the three methods.

n	INP	HRSG1			HRSG2			Algo
		BItr	BEFs	BTcpu	BItr	BEFs	BTcpu	BItr	BEFs	BTcpu
1000	$x_{{}_1}$	4	8	0.001	5	15	0.002	2	7	0.004
	$x_{{}_2}$	6	12	0.002	3	9	0.001	2	7	0.004
	$x_{{}_3}$	5	10	0.002	5	15	0.002	7	28	0.005
	$x_{{}_4}$	6	12	0.002	4	12	0.002	2	7	0.006
	$x_{{}_5}$	6	12	0.002	4	12	0.002	2	7	0.004
	$x_{{}_6}$	5	10	0.002	5	15	0.002	2	7	0.004
	$x_{{}_7}$	6	12	0.002	4	12	0.002	21	84	0.024
5000	$x_{{}_1}$	4	8	0.005	3	9	0.005	2	7	0.014
	$x_{{}_2}$	3	6	0.004	5	15	0.008	2	7	0.014
	$x_{{}_3}$	5	10	0.006	5	15	0.007	8	32	0.018
	$x_{{}_4}$	6	12	0.007	6	18	0.009	2	7	0.018
	$x_{{}_5}$	4	8	0.005	5	15	0.007	2	7	0.016
	$x_{{}_6}$	5	10	0.006	4	12	0.006	2	7	0.015
	$x_{{}_7}$	5	10	0.006	3	9	0.005	41	163	0.160
10,000	$x_{{}_1}$	5	10	0.011	3	9	0.008	2	7	0.023
	$x_{{}_2}$	4	8	0.009	4	12	0.011	2	7	0.019
	$x_{{}_3}$	6	12	0.014	4	12	0.011	8	32	0.024
	$x_{{}_4}$	5	10	0.012	5	15	0.014	2	7	0.019
	$x_{{}_5}$	5	10	0.012	5	15	0.015	2	7	0.018
	$x_{{}_6}$	5	10	0.012	5	15	0.014	2	7	0.025
	$x_{{}_7}$	5	10	0.012	3	9	0.009	36	144	0.228
50,000	$x_{{}_1}$	3	6	0.036	4	12	0.057	2	7	0.069
	$x_{{}_2}$	4	8	0.052	3	9	0.043	2	7	0.069
	$x_{{}_3}$	6	12	0.071	5	15	0.068	8	32	0.092
	$x_{{}_4}$	6	12	0.072	5	15	0.068	2	7	0.095
	$x_{{}_5}$	6	12	0.073	5	15	0.068	2	7	0.079
	$x_{{}_6}$	6	12	0.073	5	15	0.067	2	7	0.083
	$x_{{}_7}$	5	10	0.061	5	15	0.068	68	271	2.160
100,000	$x_{{}_1}$	5	10	0.128	5	15	0.153	2	7	0.130
	$x_{{}_2}$	4	8	0.113	4	12	0.128	2	7	0.131
	$x_{{}_3}$	5	10	0.129	5	15	0.148	9	36	0.205
	$x_{{}_4}$	6	12	0.154	4	12	0.120	9	36	0.207
	$x_{{}_5}$	5	10	0.121	5	15	0.155	2	7	0.144
	$x_{{}_6}$	6	12	0.144	5	15	0.149	2	7	0.168
	$x_{{}_7}$	4	8	0.097	5	15	0.148	106	424	6.702

Table 6. Numeral results (Problem 6) for the terms BItr, BEFs and BTcpu for the three methods.

n	INP	HRSG1			HRSG2			Algo
		BItr	BEFs	BTcpu	BItr	BEFs	BTcpu	BItr	BEFs	BTcpu
1000	$x_{{}_1}$	7	14	0.002	6	18	0.003	17	64	0.009
	$x_{{}_2}$	8	16	0.003	5	15	0.002	18	68	0.013
	$x_{{}_3}$	7	14	0.003	10	30	0.005	26	101	0.016
	$x_{{}_4}$	9	18	0.003	6	18	0.003	27	108	0.020
	$x_{{}_5}$	8	16	0.003	8	24	0.004	31	124	0.030
	$x_{{}_6}$	9	18	0.004	6	18	0.003	75	300	0.096
	$x_{{}_7}$	3	6	0.001	8	24	0.004	58	228	0.045
5000	$x_{{}_1}$	6	12	0.007	8	24	0.012	30	115	0.098
	$x_{{}_2}$	6	12	0.007	6	18	0.010	25	96	0.064
	$x_{{}_3}$	6	12	0.007	9	27	0.013	41	159	0.140
	$x_{{}_4}$	10	20	0.012	8	24	0.012	42	167	0.158
	$x_{{}_5}$	5	10	0.006	8	24	0.012	58	230	0.247
	$x_{{}_6}$	8	16	0.009	5	15	0.011	88	352	0.595
	$x_{{}_7}$	7	14	0.009	8	24	0.014	89	355	0.425
10,000	$x_{{}_1}$	8	16	0.019	10	30	0.029	27	103	0.126
	$x_{{}_2}$	7	14	0.016	5	15	0.015	25	96	0.122
	$x_{{}_3}$	8	16	0.018	8	24	0.023	45	176	0.269
	$x_{{}_4}$	10	20	0.023	10	30	0.032	63	252	0.526
	$x_{{}_5}$	8	16	0.018	6	18	0.017	83	332	0.803
	$x_{{}_6}$	5	10	0.011	6	18	0.018	125	499	1.281
	$x_{{}_7}$	8	16	0.018	10	30	0.027	121	483	1.147
50,000	$x_{{}_1}$	5	10	0.057	9	27	0.114	35	135	0.689
	$x_{{}_2}$	5	10	0.062	8	24	0.104	34	132	0.712
	$x_{{}_3}$	11	22	0.136	9	27	0.117	80	317	2.568
	$x_{{}_4}$	8	16	0.102	9	27	0.130	112	448	4.068
	$x_{{}_5}$	7	14	0.095	11	33	0.157	120	479	4.810
	$x_{{}_6}$	10	20	0.127	9	27	0.126	205	818	10.627
	$x_{{}_7}$	7	14	0.088	11	33	0.156	198	791	8.100
100,000	$x_{{}_1}$	8	16	0.216	7	21	0.213	40	155	1.715
	$x_{{}_2}$	9	18	0.244	10	30	0.302	48	186	2.175
	$x_{{}_3}$	7	14	0.174	8	24	0.246	88	349	5.323
	$x_{{}_4}$	5	10	0.125	8	24	0.222	87	348	5.862
	$x_{{}_5}$	6	12	0.162	11	33	0.302	145	579	12.157
	$x_{{}_6}$	11	22	0.297	9	27	0.279	224	896	21.001
	$x_{{}_7}$	10	20	0.268	9	27	0.271	193	768	15.277

Table 7. Numeral results (Problem 7) for the terms BItr, BEFs and BTcpu for the three methods.

n	INP	HRSG1			HRSG2			Algo
		BItr	BEFs	BTcpu	BItr	BEFs	BTcpu	BItr	BEFs	BTcpu
1000	$x_{{}_1}$	25	50	0.014	24	72	0.016	13	52	0.019
	$x_{{}_2}$	25	50	0.013	24	77	0.017	13	52	0.011
	$x_{{}_3}$	23	46	0.012	23	72	0.016	13	52	0.014
	$x_{{}_4}$	25	50	0.014	22	68	0.016	12	48	0.013
	$x_{{}_5}$	23	46	0.012	23	69	0.015	12	48	0.015
	$x_{{}_6}$	25	51	0.014	21	65	0.015	12	48	0.013
	$x_{{}_7}$	30	60	0.016	28	86	0.019	13	52	0.014
5000	$x_{{}_1}$	26	52	0.044	22	72	0.048	13	52	0.044
	$x_{{}_2}$	24	48	0.040	25	76	0.051	13	52	0.051
	$x_{{}_3}$	22	44	0.037	23	73	0.047	13	52	0.051
	$x_{{}_4}$	23	46	0.038	22	68	0.044	13	52	0.045
	$x_{{}_5}$	24	48	0.040	23	69	0.052	13	52	0.044
	$x_{{}_6}$	26	52	0.043	22	71	0.046	13	52	0.044
	$x_{{}_7}$	29	58	0.051	30	94	0.062	13	52	0.049
10,000	$x_{{}_1}$	24	48	0.076	23	71	0.085	14	56	0.083
	$x_{{}_2}$	24	48	0.080	24	72	0.086	14	56	0.081
	$x_{{}_3}$	24	48	0.072	23	72	0.086	13	52	0.076
	$x_{{}_4}$	24	48	0.076	21	66	0.079	13	52	0.074
	$x_{{}_5}$	24	48	0.074	21	69	0.084	13	52	0.082
	$x_{{}_6}$	23	46	0.071	23	77	0.091	13	52	0.071
	$x_{{}_7}$	30	60	0.083	31	97	0.125	13	52	0.077
50,000	$x_{{}_1}$	26	52	0.348	23	71	0.414	14	56	0.332
	$x_{{}_2}$	24	48	0.323	24	75	0.433	14	56	0.340
	$x_{{}_3}$	25	50	0.364	23	71	0.407	14	56	0.413
	$x_{{}_4}$	23	47	0.344	25	77	0.438	14	56	0.312
	$x_{{}_5}$	23	46	0.340	23	72	0.414	14	56	0.327
	$x_{{}_6}$	24	48	0.370	22	69	0.394	13	52	0.314
	$x_{{}_7}$	32	64	0.442	33	106	0.611	14	56	0.361
100,000	$x_{{}_1}$	24	48	0.750	25	78	0.889	14	56	0.704
	$x_{{}_2}$	24	48	0.783	23	72	0.888	14	56	0.701
	$x_{{}_3}$	23	46	0.685	21	67	0.834	14	56	0.702
	$x_{{}_4}$	25	51	0.799	22	67	0.855	14	56	0.690
	$x_{{}_5}$	22	44	0.720	23	72	0.915	14	56	0.708
	$x_{{}_6}$	26	52	0.843	22	70	0.878	13	52	0.659
	$x_{{}_7}$	34	68	1.085	30	99	1.235	14	56	0.712

Table 8. Numeral results (Problem 8) for the terms BItr, BEFs and BTcpu for the three methods.

n	INP	HRSG1			HRSG2			Algo
		BItr	BEFs	BTcpu	BItr	BEFs	BTcpu	BItr	BEFs	BTcpu
1000	$x_{{}_1}$	10	20	0.006	13	39	0.008	7	28	0.009
	$x_{{}_2}$	10	20	0.006	12	36	0.007	7	28	0.006
	$x_{{}_3}$	7	14	0.004	10	30	0.006	6	24	0.006
	$x_{{}_4}$	10	20	0.006	10	30	0.006	7	28	0.006
	$x_{{}_5}$	10	20	0.008	12	36	0.007	7	28	0.009
	$x_{{}_6}$	9	18	0.005	12	36	0.007	8	31	0.007
	$x_{{}_7}$	10	20	0.006	10	30	0.006	11	44	0.009
5000	$x_{{}_1}$	10	20	0.017	9	27	0.017	7	28	0.018
	$x_{{}_2}$	8	16	0.013	9	27	0.017	7	28	0.017
	$x_{{}_3}$	8	16	0.013	7	21	0.014	6	24	0.017
	$x_{{}_4}$	9	18	0.016	14	42	0.025	8	32	0.022
	$x_{{}_5}$	12	24	0.022	10	30	0.019	8	32	0.023
	$x_{{}_6}$	14	28	0.025	10	30	0.019	8	31	0.033
	$x_{{}_7}$	13	26	0.023	12	36	0.027	11	44	0.030
10,000	$x_{{}_1}$	9	18	0.028	11	33	0.039	8	32	0.032
	$x_{{}_2}$	11	22	0.036	7	21	0.024	7	28	0.044
	$x_{{}_3}$	9	18	0.029	9	27	0.031	6	24	0.035
	$x_{{}_4}$	11	22	0.037	13	39	0.040	8	32	0.035
	$x_{{}_5}$	8	16	0.025	11	33	0.033	8	32	0.034
	$x_{{}_6}$	12	24	0.042	10	30	0.031	8	31	0.039
	$x_{{}_7}$	10	20	0.030	10	30	0.033	11	44	0.054
50,000	$x_{{}_1}$	13	26	0.182	13	39	0.178	8	32	0.135
	$x_{{}_2}$	13	26	0.198	12	36	0.164	8	32	0.170
	$x_{{}_3}$	11	22	0.171	10	30	0.141	7	28	0.114
	$x_{{}_4}$	11	22	0.158	10	30	0.153	8	32	0.202
	$x_{{}_5}$	12	24	0.198	11	33	0.197	8	32	0.163
	$x_{{}_6}$	11	22	0.155	12	36	0.184	9	35	0.139
	$x_{{}_7}$	14	28	0.198	12	36	0.186	12	48	0.232
100,000	$x_{{}_1}$	13	26	0.390	12	36	0.383	8	32	0.258
	$x_{{}_2}$	13	26	0.384	11	33	0.353	8	32	0.263
	$x_{{}_3}$	8	16	0.240	8	24	0.288	7	28	0.236
	$x_{{}_4}$	12	24	0.386	12	36	0.382	8	32	0.295
	$x_{{}_5}$	13	26	0.395	13	39	0.421	8	32	0.258
	$x_{{}_6}$	16	32	0.481	13	39	0.381	9	35	0.321
	$x_{{}_7}$	12	24	0.362	11	33	0.356	12	48	0.439

Table 9. Numeral results (Problem 9) for the terms BItr, BEFs and BTcpu for the three methods.

n	INP	HRSG1			HRSG2			Algo
		BItr	BEFs	BTcpu	BItr	BEFs	BTcpu	BItr	BEFs	BTcpu
1000	$x_{{}_1}$	21	52	0.037	23	80	0.043	43	172	0.213
	$x_{{}_2}$	22	56	0.039	21	76	0.044	45	180	0.251
	$x_{{}_3}$	23	58	0.040	22	80	0.046	46	184	0.232
	$x_{{}_4}$	23	59	0.041	22	78	0.044	46	184	0.241
	$x_{{}_5}$	24	57	0.041	23	86	0.046	36	144	0.205
	$x_{{}_6}$	23	56	0.047	24	88	0.047	49	196	0.274
	$x_{{}_7}$	24	63	0.045	23	84	0.046	46	184	0.252
5000	$x_{{}_1}$	23	57	0.092	22	81	0.108	45	180	1.089
	$x_{{}_2}$	23	58	0.097	23	82	0.108	45	180	1.176
	$x_{{}_3}$	22	56	0.091	22	77	0.106	42	168	1.020
	$x_{{}_4}$	22	56	0.090	23	80	0.109	41	164	0.981
	$x_{{}_5}$	23	57	0.098	21	77	0.103	43	172	1.134
	$x_{{}_6}$	24	59	0.098	23	84	0.112	46	184	1.229
	$x_{{}_7}$	23	61	0.102	22	82	0.109	44	176	1.221
10,000	$x_{{}_1}$	23	57	0.159	24	84	0.202	45	180	2.202
	$x_{{}_2}$	23	58	0.163	22	79	0.188	45	180	2.004
	$x_{{}_3}$	22	55	0.157	22	80	0.191	45	180	2.012
	$x_{{}_4}$	22	57	0.157	22	77	0.186	38	152	1.797
	$x_{{}_5}$	23	55	0.156	23	81	0.196	43	172	1.957
	$x_{{}_6}$	23	59	0.165	22	81	0.192	45	180	2.340
	$x_{{}_7}$	23	62	0.172	24	88	0.212	45	180	2.332
50,000	$x_{{}_1}$	23	58	0.741	22	80	0.898	48	192	8.885
	$x_{{}_2}$	21	56	0.707	23	83	0.958	47	188	9.060
	$x_{{}_3}$	22	58	0.704	23	82	0.914	44	176	9.092
	$x_{{}_4}$	20	51	0.630	21	75	0.856	42	168	8.086
	$x_{{}_5}$	22	55	0.683	21	75	0.925	40	160	7.622
	$x_{{}_6}$	23	59	0.719	24	86	0.983	49	196	10.299
	$x_{{}_7}$	24	57	0.764	23	86	0.983	44	176	9.279
100,000	$x_{{}_1}$	22	59	1.494	22	78	1.851	48	192	19.169
	$x_{{}_2}$	22	57	1.478	22	78	1.821	47	188	19.064
	$x_{{}_3}$	22	57	1.456	22	82	1.892	55	220	21.406
	$x_{{}_4}$	23	60	1.524	22	80	1.849	43	172	15.747
	$x_{{}_5}$	22	58	1.466	22	82	1.895	43	172	16.544
	$x_{{}_6}$	24	60	1.539	22	81	1.947	52	208	26.298
	$x_{{}_7}$	24	65	1.747	23	86	2.062	45	180	19.981

Table 10. Numeral results (Problem 1) for the terms WItr, WEFs and WTcpu for the three methods.

n	INP	HRSG1			HRSG2			HRSG1			HRSG2
		WItr	WEFs	WTcpu	WItr	WEFs	WTcpu	MEtr	MEEFs	METcpu	MEItr	MEEFs	METcpu
1000	$x_{{}_1}$	12	24	0.005	15	45	0.128	8.8	17.6	0.003	10.6	31.8	0.012
	$x_{{}_2}$	12	24	0.004	16	48	0.006	8.95	17.9	0.003	10.95	32.85	0.004
	$x_{{}_3}$	12	24	0.004	18	54	0.007	9.75	19.5	0.003	12.25	36.75	0.005
	$x_{{}_4}$	16	32	0.005	18	55	0.008	9.95	19.9	0.003	12.25	36.8	0.005
	$x_{{}_5}$	15	30	0.005	17	51	0.007	10.85	21.7	0.003	12.2	36.6	0.005
	$x_{{}_6}$	15	30	0.005	18	54	0.007	10.85	21.7	0.003	14.1	42.3	0.005
	$x_{{}_7}$	13	26	0.004	17	51	0.007	9.35	18.7	0.003	12.7	38.1	0.005
5000	$x_{{}_1}$	12	24	0.014	14	42	0.052	8.5	17	0.010	11.2	33.6	0.019
	$x_{{}_2}$	12	24	0.014	19	57	0.026	8.55	17.1	0.010	11.45	34.35	0.016
	$x_{{}_3}$	12	24	0.013	16	48	0.021	8.85	17.7	0.010	11.15	33.45	0.015
	$x_{{}_4}$	13	26	0.014	17	51	0.023	10.15	20.3	0.011	13.25	39.75	0.018
	$x_{{}_5}$	14	28	0.016	17	51	0.024	10.4	20.8	0.012	13.05	39.15	0.018
	$x_{{}_6}$	13	26	0.015	20	60	0.028	10.65	21.3	0.012	14.15	42.45	0.020
	$x_{{}_7}$	13	26	0.025	17	51	0.023	10.15	20.3	0.012	11.7	35.1	0.017
10,000	$x_{{}_1}$	12	24	0.026	18	54	0.053	8.6	17.2	0.019	11.7	35.1	0.032
	$x_{{}_2}$	13	26	0.029	18	54	0.047	9.4	18.8	0.021	12.35	37.05	0.034
	$x_{{}_3}$	13	26	0.030	19	57	0.051	10.15	20.3	0.023	11.95	35.85	0.032
	$x_{{}_4}$	14	28	0.030	21	63	0.056	10.2	20.4	0.022	12.9	38.7	0.034
	$x_{{}_5}$	14	28	0.032	20	61	0.056	11	22	0.024	13.65	41	0.037
	$x_{{}_6}$	14	28	0.031	20	60	0.053	10.15	20.3	0.023	13.7	41.1	0.037
	$x_{{}_7}$	13	26	0.035	18	54	0.048	9.45	18.9	0.021	12.55	37.65	0.034
50,000	$x_{{}_1}$	11	22	0.139	17	51	0.273	8.9	17.8	0.106	11.5	34.5	0.177
	$x_{{}_2}$	14	28	0.167	19	57	0.313	10.1	20.2	0.120	12.05	36.15	0.183
	$x_{{}_3}$	14	28	0.166	18	54	0.255	10.35	20.7	0.122	12.35	37.05	0.177
	$x_{{}_4}$	15	30	0.178	20	60	0.283	10.55	21.1	0.125	13.95	41.85	0.200
	$x_{{}_5}$	16	32	0.188	18	54	0.260	10.8	21.6	0.128	13.7	41.1	0.197
	$x_{{}_6}$	14	28	0.167	17	51	0.245	11.7	23.4	0.139	14	42	0.201
	$x_{{}_7}$	12	24	0.148	17	51	0.271	10.4	20.8	0.124	13.05	39.15	0.191
100,000	$x_{{}_1}$	12	24	0.313	16	48	0.592	9.85	19.7	0.264	11.85	35.55	0.386
	$x_{{}_2}$	12	24	0.335	19	57	0.665	10.1	20.2	0.278	13.4	40.2	0.455
	$x_{{}_3}$	12	24	0.345	19	57	0.668	10.45	20.9	0.288	14.45	43.35	0.485
	$x_{{}_4}$	15	30	0.421	20	60	0.682	11.3	22.6	0.322	15.2	45.6	0.533
	$x_{{}_5}$	16	32	0.433	18	54	0.700	11.8	23.6	0.314	14.15	42.45	0.510
	$x_{{}_6}$	14	28	0.371	19	57	0.837	11.4	22.8	0.302	15.5	46.5	0.606
	$x_{{}_7}$	12	24	0.322	15	45	0.648	10.25	20.5	0.272	12.55	37.65	0.471

Table 11. Numeral results (Problem 2) for the terms WItr, WEFs and WTcpu for the three methods.

n	INP	HRSG1			HRSG2			HRSG1			HRSG2
		WItr	WEFs	WTcpu	WItr	WEFs	WTcpu	MEtr	MEEFs	METcpu	MEItr	MEEFs	METcpu
1000	$x_{{}_1}$	8	16	0.003	8	27	0.009	6.35	12.7	0.002	6.1	18.3	0.003
	$x_{{}_2}$	8	16	0.003	9	27	0.005	6.8	13.6	0.002	6.2	18.6	0.003
	$x_{{}_3}$	10	20	0.003	9	27	0.005	7.25	14.5	0.002	6.5	19.5	0.003
	$x_{{}_4}$	9	18	0.003	9	27	0.005	6.95	13.9	0.002	6.85	20.55	0.003
	$x_{{}_5}$	10	20	0.004	9	27	0.005	7.55	15.1	0.003	7	21	0.004
	$x_{{}_6}$	11	22	0.004	9	24	0.005	7.5	15	0.003	6.15	18.45	0.003
	$x_{{}_7}$	10	20	0.003	8	24	0.004	6.8	13.6	0.002	6.45	19.35	0.003
5000	$x_{{}_1}$	10	20	0.012	8	27	0.014	7	14	0.008	6.4	19.2	0.011
	$x_{{}_2}$	9	18	0.011	9	30	0.015	6.7	13.4	0.008	6.25	18.75	0.010
	$x_{{}_3}$	10	20	0.011	10	27	0.016	7.05	14.1	0.008	7.3	21.9	0.012
	$x_{{}_4}$	11	22	0.012	9	24	0.016	8.05	16.1	0.009	6.6	19.8	0.011
	$x_{{}_5}$	11	22	0.012	8	30	0.024	7.75	15.5	0.009	6.55	19.65	0.015
	$x_{{}_6}$	12	24	0.013	10	27	0.016	7.45	14.9	0.008	7.05	21.15	0.012
	$x_{{}_7}$	10	20	0.012	9	24	0.018	7.4	14.8	0.009	6.85	20.55	0.013
10,000	$x_{{}_1}$	9	18	0.020	8	27	0.036	6.85	13.7	0.015	6.2	18.6	0.023
	$x_{{}_2}$	10	20	0.034	9	27	0.038	7.9	15.8	0.019	6.9	20.7	0.024
	$x_{{}_3}$	12	24	0.030	9	27	0.027	7.7	15.4	0.018	6.7	20.1	0.019
	$x_{{}_4}$	11	22	0.024	9	30	0.025	7.95	15.9	0.018	6.55	19.65	0.018
	$x_{{}_5}$	11	22	0.028	10	27	0.029	7.65	15.3	0.019	7.15	21.45	0.020
	$x_{{}_6}$	13	26	0.029	9	27	0.025	8.2	16.4	0.019	6.4	19.2	0.018
	$x_{{}_7}$	11	22	0.025	9	30	0.027	7.25	14.5	0.017	7.05	21.15	0.020
50,000	$x_{{}_1}$	10	20	0.126	10	30	0.141	6.95	13.9	0.094	6.5	19.5	0.100
	$x_{{}_2}$	11	22	0.166	10	27	0.142	7.2	14.4	0.092	7.1	21.3	0.103
	$x_{{}_3}$	10	20	0.121	9	30	0.169	7.1	14.2	0.088	6.8	20.4	0.106
	$x_{{}_4}$	11	22	0.135	10	27	0.185	7.9	15.8	0.096	7	21	0.115
	$x_{{}_5}$	11	22	0.133	9	27	0.214	8.5	17	0.103	6.45	19.35	0.123
	$x_{{}_6}$	10	20	0.122	9	27	0.174	8.05	16.1	0.098	7.35	22.05	0.120
	$x_{{}_7}$	11	22	0.149	9	24	0.289	7.9	15.8	0.103	6.35	19.05	0.132
100,000	$x_{{}_1}$	10	20	0.287	8	27	0.385	7.35	14.7	0.218	6.5	19.5	0.249
	$x_{{}_2}$	11	22	0.333	9	27	0.361	7.05	14.1	0.206	6.65	19.95	0.252
	$x_{{}_3}$	10	20	0.320	9	30	0.325	7.8	15.6	0.231	7.2	21.6	0.251
	$x_{{}_4}$	13	26	0.374	10	30	0.400	8.7	17.4	0.251	7.45	22.35	0.283
	$x_{{}_5}$	13	26	0.375	10	27	0.364	8.55	17.1	0.246	7.45	22.35	0.262
	$x_{{}_6}$	11	22	0.376	9	30	0.333	8.75	17.5	0.267	6.75	20.25	0.239
	$x_{{}_7}$	10	20	0.321	10		0.430	8	16	0.239	7.6	22.8	0.286

Table 12. Numeral results (Problem 3) for the terms WItr, WEFs and WTcpu for the three methods.

n	INP	HRSG1			HRSG2			HRSG1			HRSG2
		WItr	WEFs	WTcpu	WItr	WEFs	WTcpu	MEtr	MEEFs	METcpu	MEItr	MEEFs	METcpu
1000	$x_{{}_1}$	12	24	0.0054	10	30	0.0051	8.1	16.2	0.003	7.75	23.25	0.0033
	$x_{{}_2}$	11	22	0.003	11	33	0.0048	8.6	17.2	0.0026	8.1	24.3	0.003
	$x_{{}_3}$	12	24	0.004	12	36	0.007	8.65	17.3	0.003	8.5	25.5	0.004
	$x_{{}_4}$	13	26	0.004	13	39	0.006	9.4	18.8	0.003	8.35	25.05	0.004
	$x_{{}_5}$	14	28	0.004	16	48	0.007	9.05	18.1	0.003	9.75	29.25	0.004
	$x_{{}_6}$	14	28	0.004	14	42	0.008	9.75	19.5	0.003	9.75	29.25	0.004
	$x_{{}_7}$	13	26	0.004	11	33	0.005	8.9	17.8	0.003	8.3	24.9	0.004
5000	$x_{{}_1}$	12	24	0.012	11	33	0.016	8.2	16.4	0.008	8.65	25.95	0.013
	$x_{{}_2}$	11	22	0.011	12	36	0.024	8.15	16.3	0.008	8.3	24.9	0.014
	$x_{{}_3}$	13	26	0.013	13	39	0.022	9.2	18.4	0.010	8.65	25.95	0.012
	$x_{{}_4}$	12	24	0.012	14	42	0.021	9.15	18.3	0.009	9.25	27.75	0.013
	$x_{{}_5}$	14	28	0.015	13	39	0.017	9.4	18.8	0.010	10.2	30.6	0.013
	$x_{{}_6}$	14	28	0.015	13	39	0.019	9.45	18.9	0.010	9.5	28.5	0.012
	$x_{{}_7}$	13	26	0.014	13	39	0.021	9	18	0.010	9.5	28.5	0.014
10,000	$x_{{}_1}$	11	22	0.023	12	36	0.031	8.25	16.5	0.018	8.55	25.65	0.022
	$x_{{}_2}$	12	24	0.026	13	39	0.039	8.8	17.6	0.019	8.5	25.5	0.025
	$x_{{}_3}$	12	24	0.025	13	39	0.037	8.6	17.2	0.018	9.1	27.3	0.024
	$x_{{}_4}$	13	26	0.030	13	39	0.041	9.8	19.6	0.021	10	30	0.031
	$x_{{}_5}$	15	30	0.032	16	48	0.038	9.8	19.6	0.021	9.8	29.4	0.028
	$x_{{}_6}$	15	30	0.032	14	42	0.047	10.15	20.3	0.022	9.6	28.8	0.028
	$x_{{}_7}$	15	30	0.032	13	39	0.049	10.25	20.5	0.023	9.75	29.25	0.028
50,000	$x_{{}_1}$	12	24	0.140	15	45	0.205	8.85	17.7	0.099	10	30	0.136
	$x_{{}_2}$	13	26	0.146	12	36	0.171	9.1	18.2	0.101	8.35	25.05	0.111
	$x_{{}_3}$	12	24	0.151	14	42	0.176	10	20	0.113	9.35	28.05	0.119
	$x_{{}_4}$	14	28	0.153	15	45	0.187	10.15	20.3	0.115	10.5	31.5	0.133
	$x_{{}_5}$	16	32	0.176	14	42	0.218	10.9	21.8	0.122	9.7	29.1	0.143
	$x_{{}_6}$	14	28	0.157	14	42	0.196	11.1	22.2	0.122	10.6	31.8	0.149
	$x_{{}_7}$	13	26	0.143	13	39	0.224	9.75	19.5	0.108	9.75	29.25	0.157
100,000	$x_{{}_1}$	10	20	0.243	12	36	0.422	7.9	15.8	0.190	7.8	23.4	0.253
	$x_{{}_2}$	13	26	0.329	12	36	0.358	9.85	19.7	0.245	8.1	24.3	0.242
	$x_{{}_3}$	13	26	0.345	12	36	0.445	9.6	19.2	0.254	9.5	28.5	0.318
	$x_{{}_4}$	13	26	0.365	13	39	0.591	10.15	20.3	0.271	9.65	28.95	0.344
	$x_{{}_5}$	15	30	0.395	15	45	0.546	10.9	21.8	0.302	10.8	32.4	0.356
	$x_{{}_6}$	14	28	0.364	16	48	0.536	10.4	20.8	0.281	10.35	31.05	0.334
	$x_{{}_7}$	13	26	0.350	12	36	0.433	10.4	20.8	0.279	9.25	27.75	0.306

Table 13. Numeral results (Problem 4) for the terms WItr, WEFs and WTcpu for the three methods.

n	INP	HRSG1			HRSG2			HRSG1			HRSG2
		WItr	WEFs	WTcpu	WItr	WEFs	WTcpu	MEtr	MEEFs	METcpu	MEItr	MEEFs	METcpu
1000	$x_{{}_1}$	12	24	0.011	12	36	0.030	6.85	13.7	0.006	7	21	0.012
	$x_{{}_2}$	11	22	0.008	11	33	0.015	6.1	12.2	0.005	6.65	19.95	0.008
	$x_{{}_3}$	10	20	0.007	12	36	0.017	7.1	14.2	0.005	7.05	21.15	0.009
	$x_{{}_4}$	14	95	0.033	14	87	0.029	7.75	21.15	0.008	9.4	32.4	0.011
	$x_{{}_5}$	17	96	0.032	15	89	0.030	7.65	18.4	0.007	8.75	32.1	0.011
	$x_{{}_6}$	19	176	0.064	16	225	0.081	9.2	33.8	0.013	10.45	41.35	0.014
	$x_{{}_7}$	17	80	0.027	19	98	0.032	8.55	20.15	0.007	8.3	27.7	0.009
5000	$x_{{}_1}$	11	22	0.026	16	48	0.046	7.1	14.2	0.016	7.2	21.6	0.021
	$x_{{}_2}$	12	24	0.030	13	39	0.037	7.9	15.8	0.018	8.6	25.8	0.025
	$x_{{}_3}$	13	26	0.029	11	33	0.032	7.65	15.3	0.017	6.9	20.7	0.020
	$x_{{}_4}$	17	83	0.125	17	149	0.215	9.15	25.2	0.030	9.2	37.5	0.043
	$x_{{}_5}$	12	50	0.083	13	66	0.116	7.3	17.5	0.021	8.25	28.95	0.036
	$x_{{}_6}$	17	167	0.325	22	330	0.568	9.75	38.15	0.056	10.1	60.5	0.087
	$x_{{}_7}$	14	90	0.128	15	101	0.117	8.4	22.75	0.028	8	29.7	0.032
10,000	$x_{{}_1}$	12	24	0.051	11	33	0.062	7.75	15.5	0.033	6.65	19.95	0.037
	$x_{{}_2}$	15	30	0.065	13	39	0.089	7.8	15.6	0.033	7.35	22.05	0.049
	$x_{{}_3}$	10	20	0.037	13	39	0.105	6.7	13.4	0.025	8.15	24.45	0.054
	$x_{{}_4}$	15	76	0.197	17	76	0.226	8.4	19.1	0.041	9.85	31.7	0.066
	$x_{{}_5}$	17	58	0.178	18	161	0.471	9.05	21.4	0.045	9.1	32.65	0.073
	$x_{{}_6}$	19	136	0.466	15	133	0.489	10.8	45.25	0.123	9.5	34	0.076
	$x_{{}_7}$	17	134	0.319	13	128	0.438	9.65	27.85	0.059	9.25	34.25	0.082
50,000	$x_{{}_1}$	16	32	0.305	10	30	0.353	9.4	18.8	0.177	7.15	21.45	0.243
	$x_{{}_2}$	12	24	0.231	12	36	0.330	8.3	16.6	0.159	8.2	24.6	0.227
	$x_{{}_3}$	11	22	0.233	12	36	0.434	7.45	14.9	0.145	8.9	26.7	0.272
	$x_{{}_4}$	20	203	3.662	15	76	1.131	10.15	34.2	0.490	8.7	27.65	0.297
	$x_{{}_5}$	17	121	1.822	15	62	0.682	8.85	28.45	0.381	8.5	27.1	0.278
	$x_{{}_6}$	15	132	2.299	20	189	3.835	9.6	28.3	0.373	10.6	42.7	0.579
	$x_{{}_7}$	13	152	2.486	12	79	1.091	8.5	27.8	0.354	8.75	29.9	0.347
100,000	$x_{{}_1}$	18	36	0.791	14	42	0.798	8.55	17.1	0.386	8.9	26.7	0.520
	$x_{{}_2}$	11	22	0.502	11	33	0.652	8.15	16.3	0.332	8	24	0.462
	$x_{{}_3}$	12	24	0.518	13	39	0.844	7.6	15.2	0.314	7.35	22.05	0.448
	$x_{{}_4}$	22	405	17.231	14	69	1.935	10.1	46.55	1.530	8.6	27.45	0.595
	$x_{{}_5}$	17	120	5.158	14	72	2.282	9.55	34.15	1.011	9.1	29.8	0.670
	$x_{{}_6}$	13	158	5.895	17	91	3.081	8.45	26.25	0.684	10.15	35.6	0.872
	$x_{{}_7}$	16	99	3.553	14	111	3.190	9.5	25.65	0.659	8.8	30	0.665

Table 14. Numeral results (Problem 5) for the terms WItr, WEFs and WTcpu for the three methods.

n	INP	HRSG1			HRSG2			HRSG1			HRSG2
		WItr	WEFs	WTcpu	WItr	WEFs	WTcpu	MEtr	MEEFs	METcpu	MEItr	MEEFs	METcpu
1000	$x_{{}_1}$	9	18	0.0036	8	24	0.0035	6.35	12.7	0.0025	6	18	0.0028
	$x_{{}_2}$	8	16	0.0053	8	24	0.0039	7.05	14.1	0.0034	5.7	17.1	0.0027
	$x_{{}_3}$	10	20	0.0071	9	27	0.0039	7.6	15.2	0.0040	6.9	20.7	0.0032
	$x_{{}_4}$	11	22	0.0043	9	27	0.0041	7.65	15.3	0.0031	6.5	19.5	0.0030
	$x_{{}_5}$	10	20	0.0039	8	24	0.0047	7.75	15.5	0.0030	7	21	0.0034
	$x_{{}_6}$	10	20	0.0042	9	27	0.0047	7.85	15.7	0.0030	7.4	22.2	0.0035
	$x_{{}_7}$	11	22	0.0042	8	24	0.0039	8.1	16.2	0.0032	6.45	19.35	0.0030
5000	$x_{{}_1}$	10	20	0.0142	8	24	0.0130	6.45	12.9	0.0082	6.1	18.3	0.0096
	$x_{{}_2}$	8	16	0.0103	9	27	0.0133	5.95	11.9	0.0076	6.45	19.35	0.0100
	$x_{{}_3}$	12	24	0.0151	8	24	0.0120	8.35	16.7	0.0107	6.4	19.2	0.0099
	$x_{{}_4}$	10	20	0.0130	11	33	0.0171	7.65	15.3	0.0096	7.65	22.95	0.0118
	$x_{{}_5}$	9	18	0.0124	9	27	0.0156	7.1	14.2	0.0092	6.9	20.7	0.0105
	$x_{{}_6}$	11	22	0.0134	9	27	0.0139	8.05	16.1	0.0102	6.8	20.4	0.0108
	$x_{{}_7}$	12	24	0.0150	9	27	0.0133	7.85	15.7	0.0101	6.55	19.65	0.0103
10,000	$x_{{}_1}$	10	20	0.0232	8	24	0.0244	6.75	13.5	0.0158	6.25	18.75	0.0182
	$x_{{}_2}$	10	20	0.0243	9	27	0.0266	7.6	15.2	0.0180	6.2	18.6	0.0179
	$x_{{}_3}$	11	22	0.0257	10	30	0.0288	7.95	15.9	0.0186	6.9	20.7	0.0196
	$x_{{}_4}$	11	22	0.0264	10	30	0.0281	7.6	15.2	0.0181	7.7	23.1	0.0231
	$x_{{}_5}$	11	22	0.0265	10	30	0.0301	7.45	14.9	0.0177	7.45	22.35	0.0222
	$x_{{}_6}$	11	22	0.0265	9	27	0.0276	8.45	16.9	0.0203	7.4	22.2	0.0220
	$x_{{}_7}$	12	24	0.0288	9	27	0.0264	7.65	15.3	0.0195	6.6	19.8	0.0195
50,000	$x_{{}_1}$	10	20	0.1252	8	24	0.1213	7	14	0.0866	6.4	19.2	0.0929
	$x_{{}_2}$	12	24	0.1457	9	27	0.1744	7.65	15.3	0.0966	6.85	20.55	0.1046
	$x_{{}_3}$	10	20	0.1199	8	24	0.1200	7.65	15.3	0.0920	6.8	20.4	0.0949
	$x_{{}_4}$	11	22	0.1329	12	36	0.1618	8.65	17.3	0.1043	7.6	22.8	0.1040
	$x_{{}_5}$	10	20	0.1220	10	30	0.1400	7.95	15.9	0.0959	7.45	22.35	0.1025
	$x_{{}_6}$	11	22	0.1336	12	36	0.1685	8.25	16.5	0.1000	7.9	23.7	0.1101
	$x_{{}_7}$	12	24	0.1460	9	27	0.1472	7.7	15.4	0.0975	7.25	21.75	0.1023
100,000	$x_{{}_1}$	10	20	0.2923	9	27	0.2812	7.3	14.6	0.1999	6.5	19.5	0.2159
	$x_{{}_2}$	10	20	0.2678	9	27	0.3038	7.85	15.7	0.2075	6.7	20.1	0.2060
	$x_{{}_3}$	11	22	0.2867	10	30	0.2994	7.8	15.6	0.2032	7.6	22.8	0.2274
	$x_{{}_4}$	11	22	0.2638	11	33	0.3649	8.55	17.1	0.2123	7.6	22.8	0.2442
	$x_{{}_5}$	12	24	0.2887	9	27	0.2971	8.85	17.7	0.2117	7.15	21.45	0.2249
	$x_{{}_6}$	13	26	0.3088	11	33	0.3295	8.35	16.7	0.2008	8.35	25.05	0.2536
	$x_{{}_7}$	13	26	0.3360	10	30	0.3095	8.6	17.2	0.2144	7.5	22.5	0.2284

Table 15. Numeral results (Problem 6) for the terms WItr, WEFs and WTcpu for the three methods.

n	INP	HRSG1			HRSG2			HRSG1			HRSG2
		WItr	WEFs	WTcpu	WItr	WEFs	WTcpu	MEtr	MEEFs	METcpu	MEItr	MEEFs	METcpu
1000	$x_{{}_1}$	17	34	0.006	19	57	0.009	10.85	21.7	0.004	11.6	34.8	0.006
	$x_{{}_2}$	19	38	0.007	18	54	0.009	12.2	24.4	0.004	11	33	0.005
	$x_{{}_3}$	19	38	0.007	18	54	0.009	13.2	26.4	0.005	13.8	41.4	0.007
	$x_{{}_4}$	18	36	0.006	20	60	0.010	12.35	24.7	0.004	13.45	40.35	0.007
	$x_{{}_5}$	20	40	0.007	20	60	0.010	12.2	24.4	0.004	13.55	40.65	0.007
	$x_{{}_6}$	19	38	0.011	18	54	0.009	14.3	28.6	0.006	13.05	39.15	0.006
	$x_{{}_7}$	18	36	0.007	18	54	0.009	12	24	0.005	12.8	38.4	0.006
5000	$x_{{}_1}$	18	36	0.021	20	60	0.030	10.8	21.6	0.013	12.5	37.5	0.020
	$x_{{}_2}$	19	38	0.022	15	45	0.024	12.6	25.2	0.015	11.85	35.55	0.018
	$x_{{}_3}$	17	34	0.020	20	60	0.031	12.65	25.3	0.015	12.8	38.4	0.020
	$x_{{}_4}$	21	42	0.025	27	81	0.041	15	30	0.018	14.2	42.6	0.022
	$x_{{}_5}$	19	38	0.022	24	72	0.037	12.5	25	0.015	14.95	44.85	0.024
	$x_{{}_6}$	20	40	0.023	29	87	0.045	13.3	26.6	0.016	14.3	42.9	0.024
	$x_{{}_7}$	18	36	0.021	19	57	0.034	11.85	23.7	0.014	13	39	0.022
10,000	$x_{{}_1}$	19	38	0.041	17	51	0.048	13.45	26.9	0.029	13.05	39.15	0.037
	$x_{{}_2}$	19	38	0.042	20	60	0.057	12.25	24.5	0.027	12.45	37.35	0.036
	$x_{{}_3}$	21	42	0.045	22	66	0.070	13.15	26.3	0.029	13.2	39.6	0.040
	$x_{{}_4}$	19	38	0.043	20	60	0.066	14.05	28.1	0.032	15	45	0.047
	$x_{{}_5}$	18	36	0.039	24	72	0.074	13.8	27.6	0.030	13.85	41.55	0.041
	$x_{{}_6}$	20	40	0.043	22	66	0.063	12.7	25.4	0.028	14.8	44.4	0.042
	$x_{{}_7}$	19	38	0.041	21	63	0.055	13.7	27.4	0.031	14.35	43.05	0.038
50,000	$x_{{}_1}$	20	40	0.222	21	63	0.357	11.8	23.6	0.137	14	42	0.198
	$x_{{}_2}$	23	46	0.277	20	60	0.282	13.2	26.4	0.162	13.9	41.7	0.207
	$x_{{}_3}$	24	48	0.291	24	72	0.326	15.15	30.3	0.186	14.2	42.6	0.187
	$x_{{}_4}$	19	38	0.233	27	81	0.357	13.65	27.3	0.169	16.6	49.8	0.218
	$x_{{}_5}$	22	44	0.285	21	63	0.311	14.65	29.3	0.189	16.05	48.15	0.231
	$x_{{}_6}$	21	42	0.259	23	69	0.351	14.35	28.7	0.180	15.05	45.15	0.217
	$x_{{}_7}$	23	46	0.285	22	66	0.310	14.55	29.1	0.189	15.85	47.55	0.226
100,000	$x_{{}_1}$	19	38	0.508	20	60	0.627	12.85	25.7	0.350	13	39	0.414
	$x_{{}_2}$	20	40	0.566	25	75	0.739	15.7	31.4	0.433	14	42	0.428
	$x_{{}_3}$	19	38	0.504	22	66	0.658	14.05	28.1	0.363	15.4	46.2	0.475
	$x_{{}_4}$	22	44	0.548	22	66	0.608	15.35	30.7	0.388	15.95	47.85	0.442
	$x_{{}_5}$	26	52	0.649	23	69	0.618	15.4	30.8	0.402	15.7	47.1	0.434
	$x_{{}_6}$	18	36	0.519	23	69	0.683	14.35	28.7	0.398	16.5	49.5	0.496
	$x_{{}_7}$	20	40	0.524	19	57	0.566	14.55	29.1	0.388	14	42	0.424

Table 16. Numeral results (Problem 7) for the terms WItr, WEFs and WTcpu for the three methods.

n	INP	HRSG1			HRSG2			HRSG1			HRSG2
		WItr	WEFs	WTcpu	WItr	WEFs	WTcpu	MEtr	MEEFs	METcpu	MEItr	MEEFs	METcpu
1000	$x_{{}_1}$	35	70	0.030	34	105	0.028	28.3	56.6	0.017	28.3	88.15	0.021
	$x_{{}_2}$	35	70	0.019	31	101	0.032	29.05	58.1	0.016	27.6	86.45	0.022
	$x_{{}_3}$	34	68	0.018	32	96	0.026	27.5	55	0.015	27.25	84.35	0.020
	$x_{{}_4}$	34	69	0.019	36	110	0.024	28.75	57.6	0.016	28.3	87.55	0.020
	$x_{{}_5}$	33	67	0.018	31	95	0.021	28.1	56.5	0.015	27.45	85.1	0.018
	$x_{{}_6}$	35	70	0.020	34	105	0.026	28.45	56.95	0.016	27.6	86.25	0.019
	$x_{{}_7}$	40	80	0.022	38	118	0.031	34.6	69.2	0.019	32.75	102.35	0.023
5000	$x_{{}_1}$	34	68	0.062	31	96	0.071	29.5	59	0.051	27.15	84.6	0.058
	$x_{{}_2}$	34	68	0.067	34	157	0.168	29.3	58.6	0.050	28.2	90.15	0.063
	$x_{{}_3}$	36	72	0.062	32	101	0.073	28.4	56.8	0.048	27.5	86.4	0.056
	$x_{{}_4}$	33	66	0.070	31	96	0.107	27.9	55.9	0.049	26.8	83	0.061
	$x_{{}_5}$	37	74	0.069	31	97	0.134	28.4	56.9	0.051	27.2	84.55	0.070
	$x_{{}_6}$	31	63	0.068	33	101	0.106	28.5	57.15	0.051	26.9	84.5	0.070
	$x_{{}_7}$	42	84	0.073	40	121	0.082	35.85	71.7	0.062	34.65	109.3	0.073
10,000	$x_{{}_1}$	36	72	0.133	43	687	2.718	29.45	58.9	0.096	29.85	123.4	0.255
	$x_{{}_2}$	35	70	0.129	32	145	0.310	29.7	59.4	0.094	27.85	89.5	0.113
	$x_{{}_3}$	31	62	0.118	33	100	0.129	27.5	55	0.087	27.6	86.1	0.104
	$x_{{}_4}$	36	72	0.112	32	99	0.140	28.05	56.2	0.087	27.1	84.8	0.107
	$x_{{}_5}$	32	64	0.100	32	97	0.130	28.25	56.55	0.088	26.45	83.4	0.104
	$x_{{}_6}$	39	78	0.123	31	96	0.141	29.95	60.05	0.093	27.3	85.5	0.107
	$x_{{}_7}$	44	88	0.136	41	127	0.167	36.3	72.6	0.109	36.55	113.4	0.145
50,000	$x_{{}_1}$	35	70	0.474	32	99	0.593	30.3	60.6	0.407	27.75	87.45	0.513
	$x_{{}_2}$	34	68	0.492	33	148	1.488	29.7	59.4	0.406	27.55	88.85	0.563
	$x_{{}_3}$	34	68	0.522	33	108	0.615	28.9	57.8	0.436	26.45	82.8	0.479
	$x_{{}_4}$	36	72	0.531	32	99	0.581	28.4	56.9	0.427	28.2	88.15	0.521
	$x_{{}_5}$	34	68	0.503	34	107	0.611	28.1	56.3	0.416	27.25	84.85	0.492
	$x_{{}_6}$	36	72	0.556	32	98	0.602	29	58.05	0.440	26.7	84.4	0.489
	$x_{{}_7}$	41	82	0.601	41	133	0.758	36.85	73.7	0.542	37.4	117.1	0.680
100,000	$x_{{}_1}$	35	70	1.086	31	96	1.192	29.5	59	0.915	27.35	86.5	0.999
	$x_{{}_2}$	34	68	1.179	31	159	4.240	29.95	59.9	0.979	27.2	88	1.231
	$x_{{}_3}$	34	68	1.085	30	98	1.177	27.95	55.9	0.903	26.2	82.85	1.022
	$x_{{}_4}$	35	70	1.027	30	92	1.146	29.35	58.8	0.906	26.5	82.3	1.036
	$x_{{}_5}$	34	68	1.090	31	97	1.221	27.8	55.65	0.901	27.1	84.55	1.077
	$x_{{}_6}$	38	76	1.307	33	103	1.295	29.25	58.65	0.987	27.15	85.55	1.061
	$x_{{}_7}$	46	92	1.636	44	138	1.751	39.05	78.1	1.343	38.3	119.6	1.500

Table 17. Numeral results (Problem 8) for the terms WItr, WEFs and WTcpu for the three methods.

n	INP	HRSG1			HRSG2			HRSG1			HRSG2
		WItr	WEFs	WTcpu	WItr	WEFs	WTcpu	MEtr	MEEFs	METcpu	MEItr	MEEFs	METcpu
1000	$x_{{}_1}$	25	50	0.016	22	66	0.015	17.45	34.9	0.011	17.8	53.4	0.012
	$x_{{}_2}$	24	48	0.016	29	87	0.019	17.1	34.2	0.011	16.75	50.25	0.011
	$x_{{}_3}$	22	44	0.014	15	45	0.012	14.3	28.6	0.009	13.25	39.75	0.008
	$x_{{}_4}$	27	54	0.018	29	87	0.024	16.8	33.6	0.011	16.5	49.5	0.012
	$x_{{}_5}$	26	52	0.018	23	69	0.015	17.75	35.5	0.012	16.7	50.1	0.010
	$x_{{}_6}$	24	48	0.016	23	69	0.014	18.4	36.8	0.012	16.85	50.55	0.011
	$x_{{}_7}$	22	44	0.018	22	66	0.015	17.75	35.5	0.012	15.4	46.2	0.010
5000	$x_{{}_1}$	27	54	0.051	27	81	0.050	18.4	36.8	0.033	16.15	48.45	0.031
	$x_{{}_2}$	24	48	0.047	28	84	0.064	16.75	33.5	0.030	17.8	53.4	0.035
	$x_{{}_3}$	23	46	0.044	21	63	0.040	14.9	29.8	0.026	13.2	39.6	0.025
	$x_{{}_4}$	27	54	0.048	27	81	0.053	19	38	0.034	18.25	54.75	0.034
	$x_{{}_5}$	24	48	0.042	23	69	0.043	17.9	35.8	0.032	17.9	53.7	0.033
	$x_{{}_6}$	28	56	0.049	25	75	0.050	19.65	39.3	0.035	17.65	52.95	0.034
	$x_{{}_7}$	24	48	0.049	22	66	0.050	18.6	37.2	0.035	16.9	50.7	0.037
10,000	$x_{{}_1}$	28	56	0.092	24	72	0.087	18.25	36.5	0.059	18	54	0.063
	$x_{{}_2}$	26	52	0.087	23	69	0.083	18.55	37.1	0.060	16.4	49.2	0.058
	$x_{{}_3}$	26	52	0.085	24	72	0.084	15.45	30.9	0.050	15.6	46.8	0.052
	$x_{{}_4}$	24	48	0.079	26	78	0.080	18.95	37.9	0.062	18.1	54.3	0.057
	$x_{{}_5}$	29	58	0.095	25	75	0.079	19.2	38.4	0.065	18	54	0.056
	$x_{{}_6}$	25	50	0.125	26	78	0.084	19.75	39.5	0.071	18.95	56.85	0.060
	$x_{{}_7}$	25	50	0.093	25	75	0.085	17.7	35.4	0.061	18.3	54.9	0.061
50,000	$x_{{}_1}$	25	50	0.424	31	93	0.432	19.25	38.5	0.299	19.6	58.8	0.273
	$x_{{}_2}$	27	54	0.428	27	81	0.378	20.65	41.3	0.317	18.95	56.85	0.265
	$x_{{}_3}$	26	52	0.405	27	81	0.376	17.4	34.8	0.278	17.8	53.4	0.269
	$x_{{}_4}$	30	60	0.472	23	69	0.362	18.8	37.6	0.296	17.25	51.75	0.268
	$x_{{}_5}$	31	62	0.453	27	81	0.461	20.35	40.7	0.321	17.7	53.1	0.291
	$x_{{}_6}$	24	48	0.344	28	84	0.474	18.05	36.1	0.259	20.5	61.5	0.330
	$x_{{}_7}$	26	52	0.381	28	84	0.443	19.25	38.5	0.281	18.35	55.05	0.290
100,000	$x_{{}_1}$	29	58	0.937	26	78	0.859	20.85	41.7	0.644	17.45	52.35	0.563
	$x_{{}_2}$	32	64	0.965	24	72	0.764	18.95	37.9	0.579	17.4	52.2	0.561
	$x_{{}_3}$	22	44	0.669	24	72	0.772	16.4	32.8	0.496	14.6	43.8	0.476
	$x_{{}_4}$	28	56	0.847	25	75	0.809	19.55	39.1	0.607	18.6	55.8	0.599
	$x_{{}_5}$	31	62	0.942	29	87	0.954	19.9	39.8	0.632	19.45	58.35	0.625
	$x_{{}_6}$	29	58	0.870	29	87	0.853	21.45	42.9	0.651	21.8	65.4	0.647
	$x_{{}_7}$	28	56	0.846	25	75	0.810	19.3	38.6	0.584	18.35	55.05	0.585

Table 18. Numeral results (Problem 9) for the terms WItr, WEFs and WTcpu for the three methods.

n	INP	HRSG1			HRSG2			HRSG1			HRSG2
		WItr	WEFs	WTcpu	WItr	WEFs	WTcpu	MEtr	MEEFs	METcpu	MEItr	MEEFs	METcpu
1000	$x_{{}_1}$	29	76	0.052	28	108	0.056	25.05	64.55	0.044	25.8	94.95	0.051
	$x_{{}_2}$	27	70	0.049	28	105	0.065	24.1	62.25	0.043	24.85	91.8	0.056
	$x_{{}_3}$	28	74	0.050	27	97	0.073	24.65	63.1	0.043	24.65	90.5	0.056
	$x_{{}_4}$	28	68	0.050	26	96	0.058	24.8	62.2	0.045	24.3	88.05	0.052
	$x_{{}_5}$	29	75	0.062	29	108	0.058	25.2	64.35	0.046	25.15	93.15	0.050
	$x_{{}_6}$	35	93	0.077	31	120	0.064	25.7	66.85	0.057	26.15	96.8	0.053
	$x_{{}_7}$	30	81	0.059	28	106	0.058	26.65	71.6	0.050	25.7	95.35	0.052
5000	$x_{{}_1}$	27	76	0.123	31	116	0.158	25.55	67.35	0.109	25.55	95.35	0.127
	$x_{{}_2}$	29	77	0.123	32	118	0.160	25.2	65.45	0.107	25.65	94.3	0.130
	$x_{{}_3}$	27	70	0.115	28	103	0.145	24.7	63.7	0.104	24.5	89.65	0.121
	$x_{{}_4}$	28	70	0.160	27	98	0.132	24.25	61.85	0.104	24.75	89.1	0.121
	$x_{{}_5}$	28	73	0.171	30	108	0.147	25.1	63.6	0.118	24.5	89.25	0.120
	$x_{{}_6}$	30	80	0.144	33	126	0.176	26.1	68.05	0.114	26.35	97.7	0.135
	$x_{{}_7}$	29	81	0.132	31	119	0.166	26.1	69.75	0.114	26.25	98.5	0.137
10,000	$x_{{}_1}$	30	73	0.206	27	102	0.276	24.95	64.7	0.179	25.4	94.3	0.234
	$x_{{}_2}$	28	73	0.203	30	111	0.263	25.35	64.8	0.181	25.15	92.15	0.223
	$x_{{}_3}$	28	76	0.207	27	99	0.242	25.2	65.5	0.182	24.45	90	0.217
	$x_{{}_4}$	27	70	0.194	26	98	0.256	24.35	61.7	0.172	24.2	87.9	0.221
	$x_{{}_5}$	27	71	0.221	27	101	0.344	25.3	64.95	0.183	25.05	91.25	0.266
	$x_{{}_6}$	27	76	0.224	30	115	0.278	25.4	66.65	0.187	25.4	94.1	0.227
	$x_{{}_7}$	30	78	0.227	29	111	0.304	26.4	69.7	0.200	26.9	100	0.252
50,000	$x_{{}_1}$	29	78	0.984	28	105	1.224	25.3	65.8	0.840	24.9	91	1.035
	$x_{{}_2}$	28	75	1.137	29	107	1.195	24.7	64.4	0.846	26	94.9	1.066
	$x_{{}_3}$	27	71	1.023	28	100	1.183	25.25	65.3	0.840	25.25	90.85	1.036
	$x_{{}_4}$	27	71	1.005	27	96	1.127	24.8	63	0.828	24.7	89.4	1.019
	$x_{{}_5}$	27	72	0.921	30	115	1.403	25.5	65.75	0.810	25.95	95.7	1.114
	$x_{{}_6}$	32	85	1.103	34	124	1.399	25.6	67.05	0.863	25.9	95.6	1.083
	$x_{{}_7}$	29	82	1.023	31	119	1.515	26.3	70.35	0.887	26.45	99.4	1.146
100,000	$x_{{}_1}$	29	76	1.973	27	101	2.735	25.5	66.85	1.698	24.5	89.95	2.131
	$x_{{}_2}$	29	80	2.328	28	106	2.489	25.3	65.3	1.775	25.05	92.3	2.154
	$x_{{}_3}$	28	72	1.925	27	97	2.473	24.6	63.65	1.675	24.55	89.1	2.104
	$x_{{}_4}$	28	72	1.841	28	100	2.382	24.6	62.6	1.603	24.3	87.6	2.055
	$x_{{}_5}$	28	73	1.920	27	101	2.596	25.2	65.1	1.686	25	91.4	2.171
	$x_{{}_6}$	30	80	2.061	33	125	2.952	26.25	69.15	1.828	26.15	97.25	2.280
	$x_{{}_7}$	28	76	2.451	33	121	2.895	26.5	70.75	1.993	26.45	98.95	2.365

The stopping criterion and evaluation criteria of Algorithm 1 are listed as follows. The stopping criterion is $\parallel F\left(x^{*}\right)\parallel \le \epsilon$ or $Itr\ge 200$, then if the final result of a test problem is $\parallel F_{{}_k}\parallel >\epsilon$, the algorithm is incapable of solving this test problem, with setting $\epsilon ={10}^{-6}$.

Therefore, the evaluation criteria used to test the performance of our proposed method are the number of iterations (Itr), function evaluations (EFs), and time (Tcpu). Regarding these three criteria, the results obtained by 51 runs of Algorithm 1 (HRSG1 and HRSG2) are classified into three types of the results as follows.

• The best results of the number of iterations (BItr), function evaluation (BEFs), and run time (BTcpu).
• The worst results of the number of iterations (WItr), function evaluation (WEFs), and run time (WTcpu).
• The mean results of the number of iterations (MItr), function evaluation (MEFs), and run time (MTcpu).

All three types of results are listed in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14, Table 15, Table 16, Table 17 and Table 18.

Thus, we compare the performance of Algorithm 1 (HRSG1, HRSG2) with the performance of the Algo algorithm proposed by the authors of [46].

Table 1 gives the best results (BItr, BEFs, and BTcpu) of the HRSG1 algorithm versus the results of the HRSG1 and Algo algorithms. Column 1 in Table 1 contains the number dimensions of Problem 1, $n\in \{{10}^3,5\times {10}^3,{10}^4,5\times {10}^4,{10}^5\}$.

Column 1 in Table 1 presents the initial points (INP) of Problem 1. Columns 3–5 give the result of the HRSG1 algorithm according to the BItr, BEFs, and BTcpu. Columns 6–8 give the result of the HRSG2 algorithm according to the BItr, BEFs, and BTcpu. The result of the Algo algorithm according to the BItr, BEFs, and BTcpu are listed in Columns 9–12. Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9 are similar to Table 1 for Problems 2–9.

We consider the results of the Algo algorithm from [46] and present the best results (BItr, BEFs, and BTcpu), these results are taken from Columns 3–6 in Tables A1–A9 from [46]. This is because no other results of the Algo algorithm are presented in [46].

Table 10, Table 11, Table 12, Table 13, Table 14, Table 15, Table 16, Table 17 and Table 18 present the results of the HRSG1 and HRSG2 algorithms regarding the WItr, WEFs, WTcpu, MItr, MEFs, and MTcpu, respectively.

The performance profile is used to show the success of the proposed algorithm to solve the test problems [47,48,49,50,51].

Thus, the numerical results are shown in the form of performance profiles to simply display the performance of the proposed algorithms [49].

The most important characteristic of the performance profiles is that the results listed in many tables can be shown in one figure.

This is implemented by plotting the different solvers in a cumulative distribution function ${\rho }_{{}_s}\left(\tau \right)$.

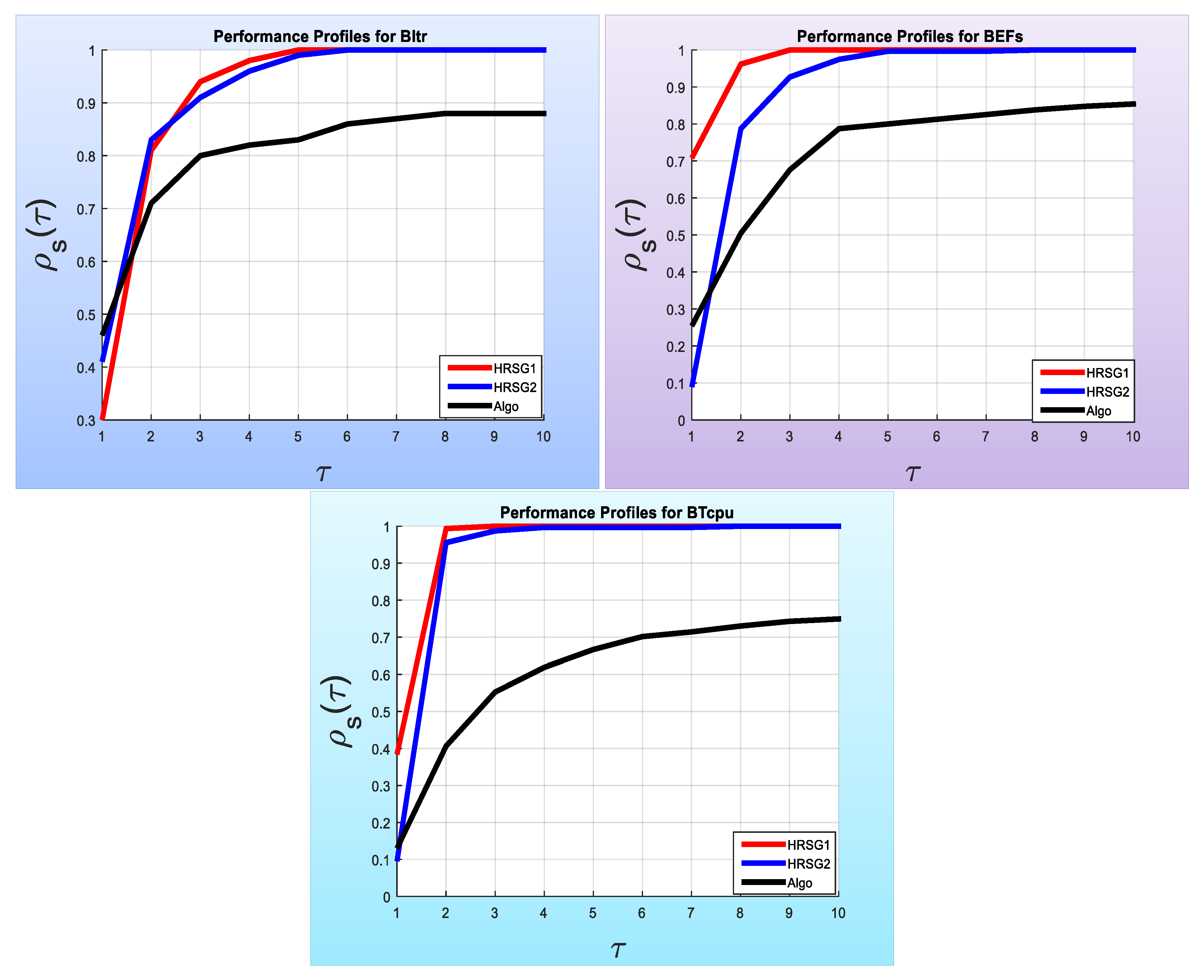
For example, the information listed in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9 are summarized in Figure 1 to give an obvious image of the performance of the three algorithms, HRSG1, HRSG2 and Algo. The first graph (left of Figure 1) gives the performance of the BItr for the three algorithms. At $\tau =1$, $46\%$ of test problems were solved by the Algo method against $41\%$ and $30\%$ of the test problems solved by the HRSG1 and HRSG2 methods, respectively. This means that the rank of the three algorithms is as follows, Algo algorithm, the HRSG2 algorithm, and HRSG1 algorithm, for the the BItr. When $\tau =2$, $83\%$ of test problems were solved by the HRSG2 method against $81\%$ and $70\%$ of the test problems solved by the HRSG1 and Algo methods, respectively. This means that the rank of the three algorithms is as follows, the HRSG2 algorithm, the HRSG1 algorithm, and the Algo algorithm, for the the BItr.

Figure 1. The BItr, BEFs, and BTcpu obtained by the HRSG1, HRSG2 and Algo methods.

If $\tau =3$, $94\%$ of the test problems were solved by the HRSG1 method against $91\%$ and $80\%$ of the test problems solved by the HRSG2 and Algo methods, respectively. This means that the rank of the three algorithms is as follows, HRSG1, HRSG2, and the Algo algorithm for the BItr.

At $\tau =5$, all the test problems were solved by the HRSG1 method against $99\%$ and $83\%$ of the test problems solved by the HRSG2 and Algo methods, respectively. This means that the rank of the three algorithms is as follows, HRSG1, HRSG2, and the Algo for the BItr.

Finally, at $\tau =10$, all the test problems were solved by the HRSG1 and HRSG2 methods against $88\%$ of the test problems solved by the Algo method. This means that the Algo method failed to solve $12\%$ of the test problems. It is worth noting that this failure is indicated by (-) in Table 3 (Table A3 of [46]).

The performance profiles for the BFEs and BTcpu are illustrated by the second and third graphs of Figure 1. Therefore, it is clear that the performance of the HRSG1 algorithm is the best.

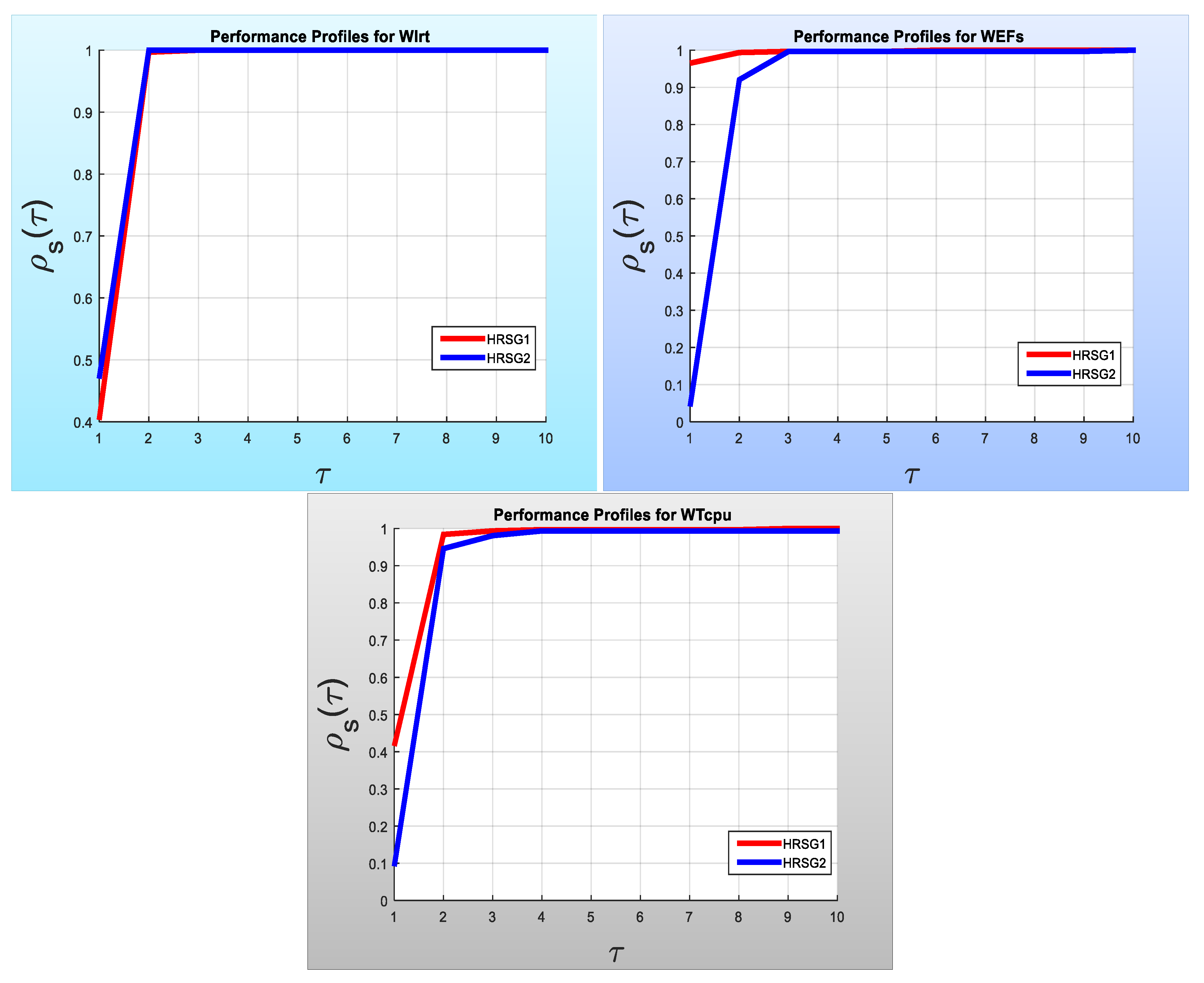
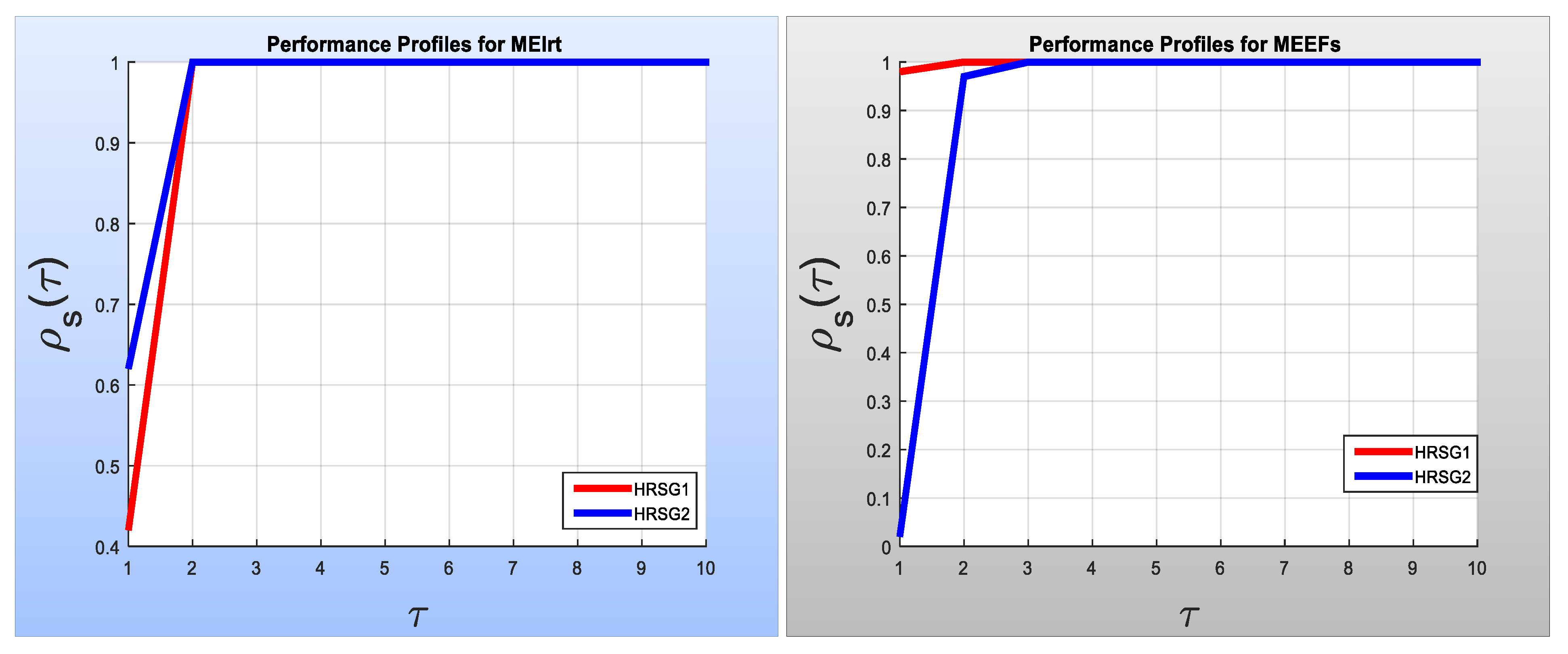
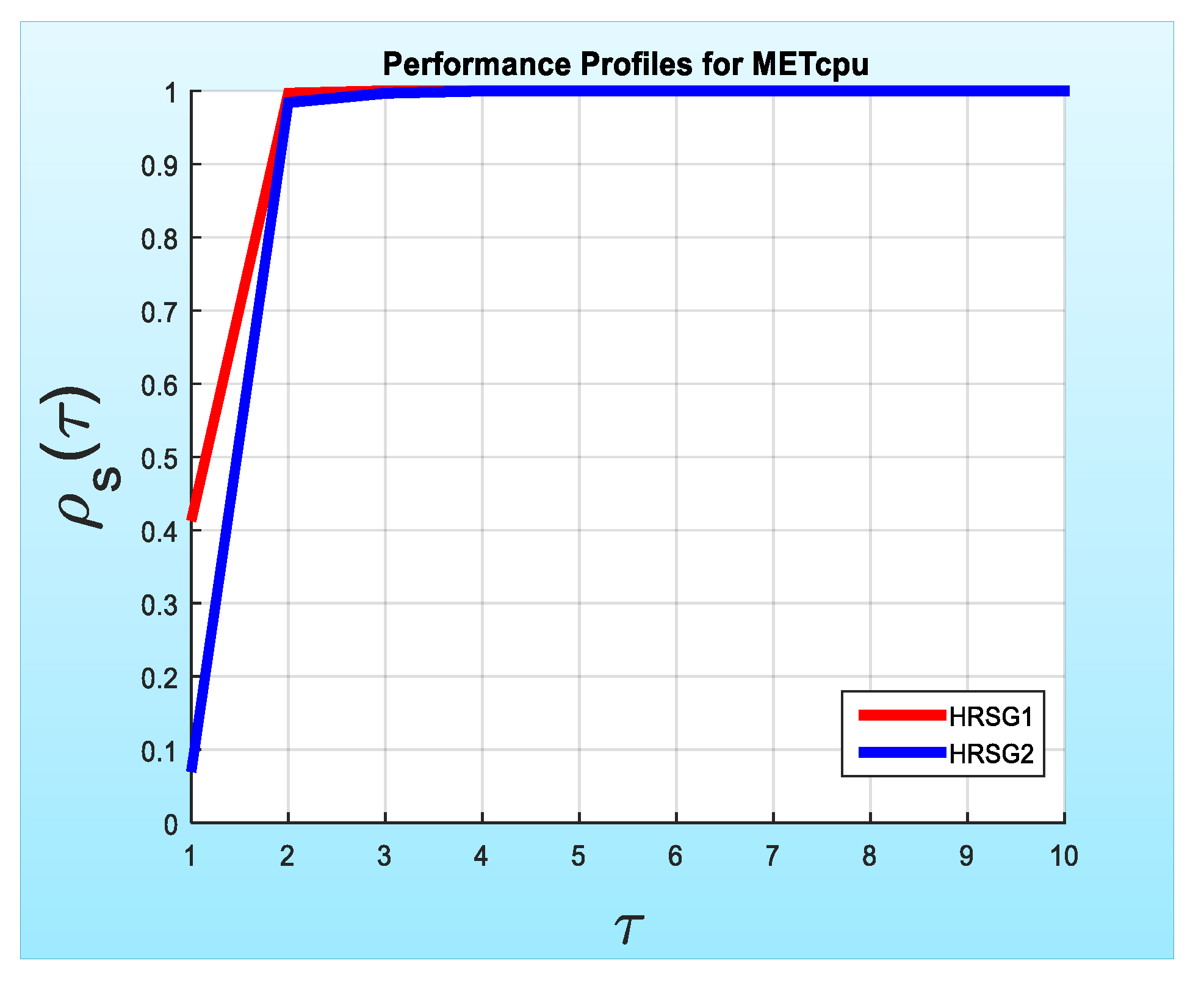
Furthermore, the results listed in Table 10, Table 11, Table 12, Table 13, Table 14, Table 15, Table 16, Table 17 and Table 18 are presented in Figure 2 and Figure 3 for the WItr, WFEs and WTcpu, and MEItr, MEFEs and METcpu, respectively.

Figure 2. The WItr, WFEs and WTcpu obtained by the HRSG1 and HRSG2 methods.

Figure 3. The MEItr, MEFEs and METcpu obtained by the HRSG1 and HRSG2 methods.

In general, the performance of the HRSG1 is better than the performance of the HRSG2.

Note: Both our proposed algorithms (HRSG1 and HRSG2) are capable of solving all the test problems at the lowest cost, where the WItr did not exceed 100, the WFEs did not exceed 1000 and the WTcpu did not exceed 10 s; while the Algo algorithm failed to solve $12\%$ of the test problems, illustrated by (-) in Table 3 (Table A3 of [46]).

Thus, in general, the proposed algorithm (HRSG) is competitive with, and in all cases superior to, the Algo algorithm in terms of efficiency, reliability and effectiveness to find the approximate solution of the test problems of the system of non-linear of equations.

5. Conclusions and Future Work

In this paper, we proposed a new adaptive hybrid two-step-size gradient method to solve large-scale systems of non-linear equations.

The proposed algorithm includes a mix of random and deterministic parameters by which two directions are designed. By simulating the forward difference method the (${\alpha }_{{}_k}$, ${\beta }_{{}_k}$) step-sizes are generated iteratively. The two search directions possess different trust regions and satisfy the sufficient descent condition. The convergence analysis of the HRSG method was established.

The diversity and multiplicity of the parameters give the proposed algorithm several opportunities to reach the feasible region. Therefore, this was a good action that made the proposed algorithm capable of rapidly approaching the approximate solution of all the test problems at each run.

In general, the numerical results demonstrated that the HRSG method is superior compared to the results obtained by the Algo method.

Several evaluation criteria were used to test the performance of the proposed algorithm, providing a fair assessment of the HRSG method.

The proposed HRSG method is represented by two algorithms, HRSG1 and HRSG2.

It is noteworthy that the performance of the HRSG1 algorithm is more efficiency and effective than the HRSG2 algorithm. This is because of the errors resulting from calculating the step-size $h\in {(0,1)}^n$ (interval).

The combination of the suggested method with the new line search approach results in a new globally convergent method. This new globally convergent method is capable of dealing with local minimization problems. Therefore, when any meta-heuristic technique as a global optimization algorithm is combined with the HRSG as a globally convergent method, the result is a new hybrid semi-gradient meta-heuristic algorithm. The idea behind this hybridization is to utilize the advantages of both techniques. Therefore, the implementation of this idea will be our interest in future work.

Furthermore, the result of this hybridization is a new hybrid semi-gradient meta-heuristic algorithm, capable of dealing with unconstrained, constrained, and multi-objective optimization problems.

It is also attractive to modify and adapt the HRSG method to make it capable of dealing with image restoration problems.

Moreover, it is possible to hybridise the HRSG method with new versions of the CG method. As a result, we could obtain a new hybrid method, capable of training deep neural networks.

The idea of the HRSG method depends on imitating the forward difference method by using one point to estimate the values of the gradient vector at each iteration, where the function evaluation is, at most, one per iteration. Therefore, the HRSG method contains two approaches used to implement this task, namely HRSG1 and HRSG2. Therefore, in future work, both approaches can be used by using the forward and central differences with more than one point.

Furthermore, the approximate values of the gradient vectors can be calculated using the forward and central differences randomly in this case, where the number of function evaluations is zero.

Hence, the proposed method obtained from the above proposals can be applied to deal with systems of non-linear equations, unconstrained, constrained, and multi-objective optimization problems, image restoration, and training deep neural networks.

List of Test Problems

Problem 1: Exponential Function [27,46].

$$F_{{}_1}=exp\left(x_{{}_1}\right)-1,$$

$$F_{{}_i}=exp\left(x_{{}_i}\right)+x_{{}_i}-1,i=2,3,\dots ,n$$

Problem 2: Exponential Function.

$$F{}_i=ln(x_{{}_i}+1)-\frac{x_{{}_i}}{n},i=1,2,3,\dots ,n.$$

Problem 3: Non-Smooth Function [27,46].

$$F_{{}_i}=2x{}_i-sin\left(\right|x{}_i\left|\right),i=1,2,3,\dots ,n.$$

Problem 4: [27,46].

$$F_{{}_i}=min\left\{min\left\{\right|x_{{}_i}|,x_{{}_i}^2\},max\{|x_{{}_i}|,x_{{}_i}^3\}\right\},i=1,2,3,\dots ,n.$$

Problem 5: Strictly Convex Function I [27,46].

$$F_{{}_i}=exp\left(x_{{}_i}\right)-1,i=1,2,3,\dots ,n.$$

Problem 6: Strictly Convex Function II [46].

$$F_{{}_i}=\frac{i}{n}exp\left(x_{{}_i}\right)-1,i=1,2,3,\dots ,n.$$

Problem 7: Tri-Diagonal Exponential Function [27,46].

$$F_{{}_1}=x_{{}_1}-exp(cos\left(h(x_{{}_1}+x_{{}_2})\right),$$

$$F_{{}_i}=x_{{}_i}-exp(cos\left(h(x_{{}_{i-1}}+x_{{}_i}+x_{{}_{i+1}})\right),i=2,3,\dots ,n-1,$$

$$F_{{}_n}=x_{{}_n}-exp(cos\left(h(x_{{}_{n-1}}+x_{{}_n})\right),$$

where $h=\frac{1}{n+1}$.

Problem 8: Non-Smooth Function [27,46].

$$F_{{}_i}=x_{{}_i}-sin\left(\right|x_{{}_i}-1\left|\right),i=1,2,3,\dots ,n.$$

Problem 9: The Trig Exponential Function [27].

$$F_{{}_1}=3x_{{}_1}^3+2x_{{}_2}-5+sin(x_{{}_1}-x_{{}_2})sin(x_{{}_1}+x_{{}_2}),$$

$$F_{{}_i}=3x_{{}_i}^3+2x_{{}_{i+1}}-5+sin(x_{{}_i}-x_{{}_{i+1}})sin(x_{{}_{{}_i}}+x_{{}_{i+1}})+4x_{{}_i}-x_{{}_{i-1}}exp(x_{{}_{i-1}}-x_{{}_i})-3,i=2,3,\dots ,n-1.$$

$$F_{{}_n}=-x_{{}_{n-1}}exp(x_{{}_{n-1}}-x_{{}_n})+4x_{{}_n}-3.$$

Initial Points (INP): $x_{{}_1}=(0.1,0.1,\dots ,0.1)$, $x_{{}_2}=(0.2,0.2,\dots ,0.2)$, $x_{{}_3}=(0.5,0.5,\dots ,0.5)$, $x_{{}_4}=(1.2,1.2,\dots ,1.2)$, $x_{{}_5}=(1.5,1.5,\dots ,1.5)$, $x_{{}_6}=(2,2,\dots ,2)$ and $x_{{}_7}=\mathrm{rand}(n,1)$.