Abstract
In this study, we contribute to the rapidly growing climate-finance literature by shedding light on the question of whether climate risks have predictive value for stock market returns. We measure climate risks in terms of both the change in the northern hemisphere temperature anomaly and its volatility and the change in the global temperature anomaly and its volatility. We study monthly data for eight advanced countries (Canada, France, Germany, Italy, Japan, Switzerland, the United Kingdom (UK), and the United States (US)). Our sample period runs from 1916 to 2021. We control for cross-market spillovers of stock market returns and volatility as well as other risks including oil-price returns and volatility, geopolitical risks, and the gold-to-silver price ratio as a measure of investor risk aversion. Given this large array of control variables, we apply the Lasso estimator to trace out the incremental predictive value of climate risks for subsequent stock market returns. We find that climate risks do not have systematic predictive value for subsequent stock market returns. We then extend our analysis in two ways. First, we show that climate risks have short-term out-of-sample predictive value for the connectedness of stock market returns. Second, we show that climate risks have predictive power for stock market returns when we study monthly historical UK data for the sample period from 1772 to 2021.
Keywords:
international stock markets; climate risks; returns forecasting; stock market connectedness MSC:
91-08
JEL Classification:
C53; G15; G17
1. Introduction
1.1. Climate Change and Finance: Theory and Evidence
Recent empirical evidence indicates that climate risks, as proxied by textual and narrative analyses of climate-change news (related to natural disasters, global warming, international summits, and climate policy) or via increased temperature as well as its volatility, contain valuable information for the in-sample predictability of stock returns (see for example, [1,2,3,4,5,6,7,8]). This evidence is not surprising insofar as climate change poses a large aggregate risk to the overall macroeconomy and the global financial system due to the occurrences of rare disasters ([9,10]). Thus, the abovementioned studies, besides proving empirical evidence, have extended the general equilibrium models of rare disaster risks (originally developed by [11,12,13]) to incorporate climate risks so as to elucidate the theoretical channels through which the economy and the stock market are impacted. In general, the results of these research efforts show that climate risks tend to reduce productivity and/or increase the stochastic depreciation rate of capital and, thereby, produce an adverse impact on macroeconomic variables and equity valuations.
1.2. Out-of-Sample Inference Is a Robust Test of Predictability
Given that in-sample tests of predictability might not translate into out-of-sample gains, we aim to extend the empirical literature on the nexus between climate risks and the stock market by analyzing the role of (the Northern Hemisphere and Global) temperature anomaly changes and their volatility for the stock returns of Canada, France, Germany, Italy, Japan, Switzerland, the United Kingdom (UK), and the United States (US) over the monthly period from February 1916 to June 2021. From a statistical perspective, such a forecasting analysis is important because it is deemed to be a more robust test of predictability compared to an in-sample analysis in terms of the predictors and econometric model specifications ([14]). Besides the statistical validation of the role of climate risks for stock returns based on a full-fledged out-of-sample forecasting experiment, the empirical results we document in this research also possess value for investors, academics, and policymakers. For instance, practitioners in finance require real-time forecasts of stock returns for asset allocation, while academics are particularly interested in stock-returns forecasts because they hold important lessons for measures of market efficiency and also help to develop more realistic asset-pricing models ([15,16]). Moreover, it is well-established that stock returns serve as a leading indicator for macroeconomic variables ([17]), and the accurate forecasting of returns would entail valuable information to policymakers in terms of designing optimal policy responses to climate risks.
1.3. Long-Span Data Guard against Sample-Selection Bias
Because we use the longest possible data sample in our empirical analysis, we avoid the issue of a possible sample-selection bias, while studying the gradual growth in the importance of climate risks over time as economies became more and more industrialized, leading to pollution and global warming, and hence, associated climate-related risks. One must also realize that because we are analyzing such a long time span, it warrants us to look at the G7 countries and Switzerland, for which data on stock markets are available over this sample period. Moreover, our decision to analyze the stock markets of these eight advanced economies is motivated by their importance in the global economy, with these eight countries representing nearly two-thirds of the global net wealth, and nearly half of the world output ([18]). Naturally, the impact of climate risks on the financial system of these economies would translate into a global effect.
1.4. Many Control Variables and a Machine-Learning Approach
In order to provide a robust forecasting exercise, i.e., prevent omitted variables-bias, driven by data availability, we also control for cross-market spillovers of stock market returns ([19,20]) and volatility, with the latter capturing financial uncertainty (with the idea dating as far back as [21,22,23] as discussed in detail by [24]), as well as other risks including risks due to fluctuations of the oil price and its volatility ([25,26]), and geopolitical risks due to adverse geopolitical acts and threats ([27]). In addition, we capture investors’ risk appetite using the gold-to-silver price ratio as a measure of investor risk aversion (motivated by [28]) based on it sharing similar properties to the gold-to-platinum ratio suggested by [29] as a metric of investors’ attitude toward risk). Given the large number of predictors, as our econometric approach, we use a machine-learning technique known as least absolute shrinkage and selection operator (Lasso), proposed by [30], which, in turn, is a regression-analysis method that performs both variable selection and regularization (i.e., the process of adding information to prevent overfitting) in order to enhance the prediction accuracy of the resulting forecasting model.
1.5. Summing Up
In light of the importance of accurate forecasting of stock returns for academics, practitioners in finance, and policymakers, the existing literature on forecasting international stock returns, based on a wide array of (linear and nonlinear) models and (macroeconomic, financial, technical, and behavioral) predictors is vast, to say the least. Hence, providing a detailed review is beyond the scope of this paper, and also not our objective, but the interested reader is referred to the recent works of [31,32,33,34,35,36,37,38] to get an idea about this ever-burgeoning area of research. Our contribution to this important and significant area of research is that our paper is the first to incorporate the role of temperature anomaly changes and its volatility in forecasting international stock returns of important advanced economies using over a century of data, based on a large number of relevant predictors incorporated into a machine-learning approach, which allows us to guard against biases due to sample-selection and omitted variables, respectively. Understandably, our results will have implications for various agents in the economy.
1.6. Organization of the Study and Its Main Findings
We organize the remainder of our paper as follows. In Section 2, we describe the data we use in our empirical analysis. In Section 3, we describe the methods we use in our empirical research. In Section 4, we report three main empirical results. First, we find that climate risks do not improve in a systematic way the accuracy of out-of-sample forecasts of stock market returns. Second, climate risks have short-term out-of-sample predictive value for the connectedness of stock market returns, an exercise we undertake by obtaining time-varying estimates of overall spillovers, as this is an important issue from the perspective of the economic significance of our results involving opportunities of equity portfolio diversification in the face of climate risks. Third, we find that climate risks have predictive power for stock market returns when we study historical UK data. In Section 5 we present our conclusions.
2. Data
2.1. Stock Market Data
The stock index data for Canada (S&P TSX 300 Composite Index), France (CAC All-Tradable Index), Germany (CDAX Composite Index), Italy (Banca Commerciale Italiana Index), Japan (Nikkei 225 Index), Switzerland (All Share Stock Index), the UK (FTSE All Share Index), and the US (S&P500 Index), are all derived from Global Financial Data. (https://globalfinancialdata.com/ accessed on 12 October 2022)—as is the West Texas Intermediate (WTI) oil-price data. We compute log-returns in percentages for the stock and oil prices. Figure 1 plots the stock market returns.
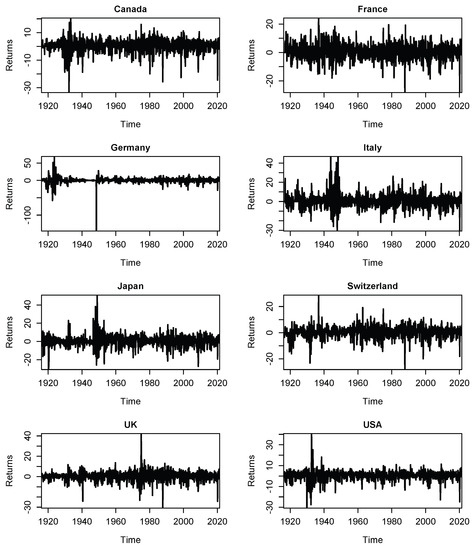
Figure 1.
Stock market returns.
2.2. Climate Data
As far as mean land and ocean temperature anomalies (given a base period of 1951–1980) of the Northern Hemisphere (as all the eight equity markets are situated in this hemisphere) and the corresponding Global values are concerned, we obtain these data from GISS Surface Temperature Analysis (GISTEMP v4), as maintained by the Goddard Institute for Space Studies of National Aeronautics and Space Administration. (https://data.giss.nasa.gov/gistemp/ accessed on 12 October 2022). We work with the first-difference of the temperature anomalies to capture its change over time. We use the standard Generalized Autoregressive Conditional Heteroskedasticity (GARCH) model to obtain the volatility of the changes in the temperature anomalies. Figure 1 plots the changes in the temperature anomalies and their volatilities. Similarly, we use a standard GARCH model to obtain the volatilities of the log-returns of stock and oil prices. The gold-to-silver price ratio is based on gold and silver prices data derived from Macrotrends. (https://www.macrotrends.net/ accessed on 12 October 2022). The usage of log-returns and the (non-logged) ratio ensure that our variables do not have issues of unit roots.
2.3. Data on Control Variables
We obtain the geopolitical risks (GPR) data from the work of [39] (https://www.matteoiacoviello.com//gpr.htm accessed on 12 October 2022), who construct measures of adverse geopolitical events based on an automated text-search analysis of newspaper articles covering geopolitical tensions in the electronic archives of 10 newspapers (Chicago Tribune, the Daily Telegraph, Financial Times, The Globe and Mail, The Guardian, the Los Angeles Times, The New York Times, USA Today, The Wall Street Journal, and The Washington Post). Ref. [39] calculate the index by counting the number of articles related to adverse geopolitical events in each newspaper for each month (as a share of the total number of news articles). They organize their search in eight categories: War Threats (Category 1), Peace Threats (Category 2), Military Buildups (Category 3), Nuclear Threats (Category 4), Terror Threats (Category 5), Beginning of War (Category 6), Escalation of War (Category 7), and Terror Acts (Category 8). Based on the search groups above, Ref. [39] also construct two subindexes: The Geopolitical Threats (GPRT) index includes words belonging to categories 1 to 5 above, and the Geopolitical Acts (GPRA) index includes words belonging to categories 6 to 8. We use these two sub-indexes rather than the overall index. The two sub-indexes are stationary, and, hence, we do not transform them further. It should be noted that, while data on the predictors are obtained from publicly-available sources, the stock market data is derived from Global Financial Data, which is the only source for reliable historical data, which, in turn, is required for our analysis spanning over a century in light of the slow evolution of climate-related risks, as economic activities in these advanced economies have grown over time.
2.4. Sample Period and Summary Statistics
Based on the availability of data at the time of writing this paper, our data period covers February 1916 to October 2020, with the start date governed by the availability of the stock price-index of Switzerland (i.e., January 1916. We lose one observation due to the computation of log-returns). We report the summary statistics of the data at the end of the paper (Appendix A; see Table A1, Table A2, Table A3 and Table A4).
3. Methods
3.1. Forecasting Model
Our general forecasting model for stock market returns (and their connectedness), at forecast horizon, h, is given by the following equation:
where c is the intercept, is an appropriately dimensioned vector of coefficients that captures how the control variables summarized in the vector, , affect subsequent stock market returns, and is a disturbance term. We use the stock market returns and their volatilities of the respective other countries in our sample, oil price returns and their volatility, the geopolitical risk variables, and the gold-to-silver price ratio as control variables. The vector, , in turn, captures the link between stock market returns and the climate predictors, . As for the forecast horizon, we set months ahead, where we forecast average returns over the relevant forecast horizon when . Moreover, we ensure that the data matrix has the same dimension for all forecast horizons. Our benchmark model is nested in our general forecasting model and is obtained upon setting .
3.2. Baseline Estimation Method
Given our large array of control variables, we use for the estimation of Equation (1) the least absolute shrinkage and selection operator (Lasso) estimator. The Lasso estimator selects the coefficients of the forecasting model so as to minimize the following expression (for an extensive discussion of the Lasso, see, e.g., the textbook by [40]):
where the index, j, denotes the elements of the coefficient vectors, N denotes the total number of observations used for estimation of the forecasting model, and denotes a shrinkage parameter. Equation (2) shows that the Lasso estimator uses the L1 norm of the coefficient vectors as a penalty function to shrink the dimension of the forecasting model. Depending on the magnitude of the shrinkage parameter, the Lasso estimator can set to zero some of the coefficients. We use 10-fold cross-validation to determine the value of the shrinkage parameter, which minimizes the mean cross-validated error.
The Lasso estimator has the advantage that it retains the basic linear structure of the type of prediction models often studied in economics and empirical finance. In theoretical terms, the Lasso model formulated in Equation (2) can be interpreted as a multi-factor asset-pricing model. The stock market returns of the respective other countries in our sample can be interpreted as proxies of the world “market portfolio”, while the volatilities of stock market returns represent conventional “GARCH-in-mean” effects. The geopolitical risk variables and the gold-to-silver price ratio are proxies for global risks. Accounting for such global risks is important because we are interested in tracing out the incremental predictive value of climate risks, that is, the potential predictive value that other popular proxies of global risks cannot capture.
3.3. Competing Estimation Methods
As a robustness check, we shall briefly discuss in Section 4 the results for two relatives of the Lasso estimator, namely the Ridge-regression estimator, which uses the L2 norm to shrink the forecasting model, and an elastic net, which, in our case, is an equally-weighted combination of the Lasso estimator and the Ridge-regression estimator. In addition, we shall present at the end of the paper (Appendix A) the results for random forests, another widely studied “off-the-shelf” machine-learning technique (which accounts for (i) potential nonlinear links between the dependent variable and its predictors, and, (ii) potential interaction effects between the predictors). The results that we summarize in Figure A1 are not fundamentally different from those we obtain based on the Lasso estimator and, hence, we shall focus on the latter in this research.
3.4. Forecast Evaluation Methods
We compare the forecasts we obtain from our benchmark model and from the forecasting model extended to include the climate predictors by means of the out-of-sample statistic defined as , where forecast error, benchmark model (without climate predictors), and rival model (potentially including climate predictors). A positive statistic indicates that the climate predictors have incremental out-of-sample predictive value for stock market returns relative to the benchmark model.
Another popular research strategy is to assess forecast accuracy in terms of absolute forecast errors, which are less prone to large influential forecast errors than squared forecast errors. In terms of absolute forecast errors, the out-of-sample statistic can be defined as . The results we report in Figure A2 at the end of the paper (Appendix A) show that the results for the out-of-sample statistic based on absolute forecast errors do not lead to fundamentally different conclusions than the results for the out-of-sample statistic based on squared forecast errors.
Another popular metric to analyze relative forecast accuracy is the root-mean-squared-forecasting error (RMSFE) statistic. As one would have expected, the results for the RMSFE statistic (rival vs. benchmark model) mirror those for the out-of-sample statistic but, as suggested by an anonymous reviewer, we report for the sake of completeness the results for the RMSFE statistic in Figure A3 at the end of the paper (Appendix A).
3.5. Implementation
We use the R language and environment for statistical computing ([41]) to estimate our forecasting model, and we use the R add-on package “glmnet” [42]) to implement the Lasso estimator.
4. Empirical Results
4.1. Full-Sample Results
Before turning to our out-of-sample forecasting results, we plot in Figure 2 on the vertical axis the estimated full-sample coefficients of the climate predictors (in this case, the northern hemisphere temperature anomaly and its volatility) as estimated by the Lasso estimator. The full-sample Lasso estimates are based on a model that features as potential predictors the control variables (that is, lagged returns, the lagged returns of all other countries, all stock market volatilities, oil returns, oil-returns volatility, and geopolitical threats, geopolitical acts, and the gold-to-silver price ratio) along with the two climate predictors. The estimated coefficients of the control variables are not plotted for better interpretability of the figure. The horizontal axis of the figure shows the shrinkage parameter. The shrinkage parameter is given in logs. The dashed vertical line indicates the optimal shrinkage parameter that minimizes the mean cross-validated error (10-fold cross-validation). As one moves from left to right, the shrinkage parameter increases, and the estimated coefficients eventually become zero.
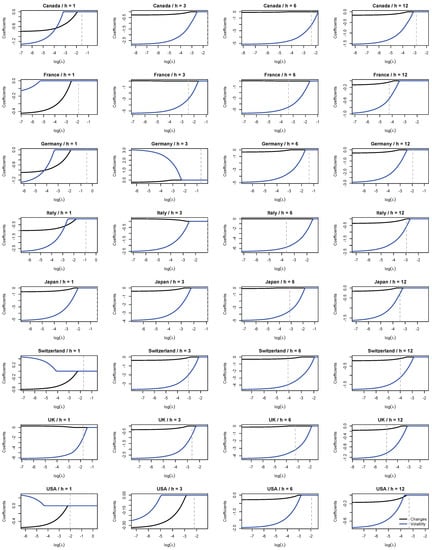
Figure 2.
Full sample Lasso coefficients. Full sample lasso coefficients as a function of the shrinkage parameter. Black line = coefficient of temperature changes. Blue line = coefficient of temperature volatility. The temperature variables are based on changes in the northern hemisphere temperature anomaly and its volatility. Dashed vertical line = shrinkage parameter that minimizes the mean cross-validated error (10-fold cross-validation). The temperature variables are based on changes in the northern hemisphere temperature anomaly and its volatility. The parameter h denotes the forecast horizon.
The full-sample results show that the estimated coefficients of the climate predictors, with only a few exceptions, are negative (or zero). Hence subsequent stock market returns tend to be negatively associated with the climate predictors. Furthermore, the estimated coefficient of temperature volatility is often larger (in absolute value) than the coefficient estimated for temperature changes. We further observe that the estimated coefficients associated with the optimal cross-validated shrinkage parameter are zero when the forecast horizon is one month, with the estimated coefficient of temperature volatility in case of the UK being the only exception. For a forecast horizon of three months, the coefficient estimated for temperature volatility is negative at the optimal shrinkage parameter when we study France, Switzerland, and the UK (but it should be noted that the exact value of the cross-validated shrinkage parameter is subject to a certain degree of random variation). The case for a negative temperature-volatility coefficient is strong for a forecast horizon of six months, where we estimate a negative coefficient at the optimal shrinkage parameter for Canada, France, Italy, Japan, Switzerland, and UK. For a forecast horizon of 12 months, we observe that the selection of the optimal shrinkage parameter leads to a negative coefficient of temperature volatility for France, Italy, Japan, Switzerland, and the UK.
4.2. Forecasting Results for Stock Market Returns
We summarize our main out-of-sample results for stock market returns in Figure 3. In order to derive our out-of-sample forecasting results, we split the sample period into a training period and an out-of-sample period. We then estimate the forecasting models on the data for the training period and use the estimated coefficients to make forecasts for the out-of-sample period. Because the choice of the training period is to some extent arbitrary, we vary the length of the training period from 50% to 75% of the sample period. Finally, we compute the out-of-sample statistic to compare the out-of-sample forecasting performance of a benchmark model and an extended model. The benchmark model includes all the control variables. The extended model includes, in addition, the climate predictors. We use changes in the northern hemisphere temperature anomaly and its volatility.
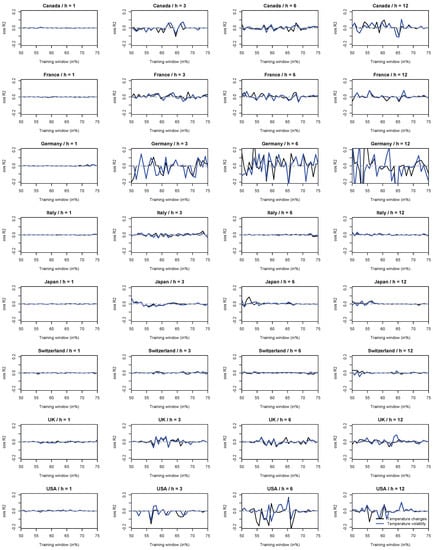
Figure 3.
Out-of-sample Statistic for stock market returns. The horizontal axis shows the length of the training window (in percent of the total sample). The vertical axis shows the out-of-sample statistic. Black line = the rival model includes temperature changes as a potential predictor. Blue line = the rival model includes temperature volatility as a potential predictor. The temperature variables are based on changes in the northern hemisphere temperature anomaly and its volatility. The parameter h denotes the forecast horizon.
While cross-validating the shrinkage parameter introduces a certain degree of random variability into the results, the results reported in Figure 3 make it clear that the evidence of in-sample predictability does not carry over to our out-of-sample forecasting exercise. The out-of-sample statistic either hovers around zero (for example, for ) or exhibits large and unsystematic fluctuations (for example, in the case of Germany), implying that it is sensitive to the choice of the out-of-sample period. Importantly, there are no signs for any country/forecast-horizon configuration that the out-of-sample statistic consistently assumes positive values. Hence, we find that the climate predictors do not systematically contain incremental predictive value for subsequent stock market returns not already contained by the predictors used by the benchmark model.
In order to assess the robustness of our results, we consider several extensions, the results of which are not reported to save journal space (the results are available from the authors upon request). First, we study the predictive value for stock market returns of changes in global temperature anomaly and its volatility as an alternative metric of climate-related anomalies (see Figure 4). Second, we use the absolute rather than the squared forecast errors to compute the out-of-sample statistic. The absolute forecast error has the advantage that it is less sensitive to very large forecast errors (which can occur, for example, in times of a stock market crash) than the squared forecast errors. Third, we apply two alternative shrinkage estimators: the Ridge-regression estimator and an elastic net. The latter is (in our parameterization) an equally weighted combination of the Lasso estimator and the Ridge-regression estimator. The results of all three robustness checks corroborate our finding that the climate predictors do not help in a systematic way to improve the accuracy of out-of-sample forecasts of stock market returns.
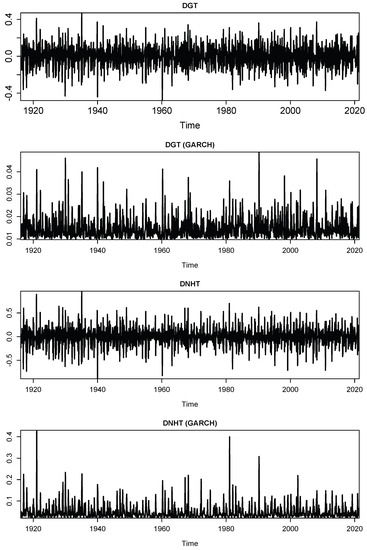
Figure 4.
Changes in temperature anomalies and volatility. DGT = change in global temperature anomaly. DNHT = change in northern hemisphere temperature anomaly. DGT (GARCH) = volatility of change in the global temperature anomaly. DNHT (GARCH) = volatility of change in the northern hemisphere temperature anomaly.
The relatively weaker performance of climate risk variables in forecasting stock returns seems to be in line with the findings of [10]. These authors surveyed 861 finance academics, professionals, and public sector regulators and policy economists about climate finance topics, and found that respondents overwhelmingly believe that asset prices underestimate climate risks rather than overestimate them.
4.3. Forecasting Results for Stock Market Connectedness
Our finding that the climate predictors do not systematically improve the out-of-sample accuracy of forecasts of stock market returns does not imply that climate anomalies do not affect stock markets per se. In order to demonstrate what we mean by this argument we next consider whether the climate predictors affect the time-varying connectedness of stock markets, by also accounting for the same across different frequencies, i.e., investment horizons. The underlying idea is that if the co-movement of the returns of these markets can be forecast out of sample by our proxies of climate risks, then such a finding has a direct bearing on the international portfolio-diversification decisions of portfolio managers.
We summarize the results of stock market connectedness in Figure 5. We report results for four different measures of connectedness of undecomposed and frequency domain-based decomposed stock returns as outlined in the recent works of [43,44,45,46,47], which can be considered as innovative extensions of the seminal contributions of [48,49,50,51], related to spillovers and connectedness in time- and frequency-domains. The technically-minded reader is referred to these two studies for the details associated with the econometric frameworks used to derive these measures of connectedness.The results demonstrate that temperature changes have a noticeable effect on the forecast accuracy of stock market connectedness at a forecast horizon of one month, with the results being generally independent of the short- or long-frequency movements of returns. Hence, diversification across the international stock markets being studied in the wake of heightened climate risks is possible in the longer-run insofar as the predictability of the connectedness of stock market returns is basically unpredictable based on the information content of temperature changes (and/or its volatility) for forecast horizons beyond one month.
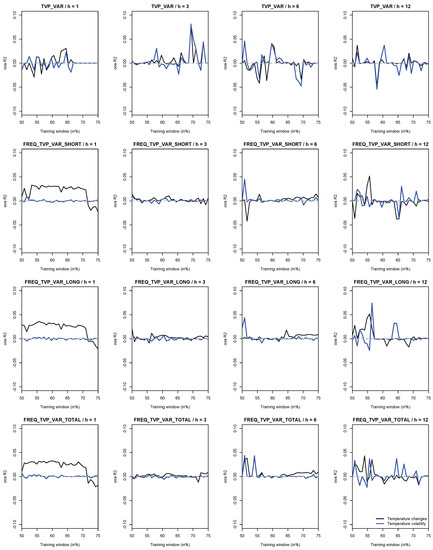
Figure 5.
Out-of-sample statistic for stock market connectedness. The horizontal axis shows the length of the training window (in percent of the total sample). The vertical axis shows the out-of-sample statistic. Black line = the rival model includes temperature changes as a potential predictor. Blue line = the rival model includes temperature volatility as a potential predictor. The temperature variables are based on changes in the northern hemisphere temperature anomaly and its volatility. The temperature variables are based on changes in the northern hemisphere temperature anomaly and its volatility. The parameter h denotes the forecast horizon.
As for the connectedness of stock markets, it is interesting to note that the so-called correlation asymmetry phenomena reported in a number of studies (see [52] for a detailed review) refers to the asymmetric pattern in which stock returns tend to be more correlated (connected) during bear market regimes (as well as during periods of extreme price fluctuations). Given that we find in Figure 2 evidence of the negative effect of the climate-risk predictors on stock returns, we test the hypothesis that stock returns are relatively more connected during relatively higher values of changes in the Northern Hemisphere temperature anomalies and due to its volatility. For this purpose, we use a smooth transition vector autoregressive (STVAR) model, developed by [53,54,55,56] (as an extension of the original works of [48,49,50] based on a linear VAR model), which produces regime-specific connectedness, with the climate-risk predictors (considered separately) being the transition variables. Due to the exogeneity of the two climate risk variables, restrictions are imposed such that lags of stock market returns do not influence temperature anomalies or its volatility. In support of the correlation asymmetry hypothesis, results show that the value of the spillover (connectedness) index is 67.66 during the upper-regime versus 60.31 in the lower regime when changes in temperature anomalies are the switch variable, while the corresponding values are 69.06 and 64.67, respectively, when the volatility of changes in temperature anomalies of the Northern Hemisphere is considered as the transition-variable. These results, complete details of which (along with the qualitatively similar ones obtained for changes in global temperature anomalies (67.42 and 59.37) and its volatility (74.01 and 64.67)) are available upon request from the authors, suggest that portfolio allocation across international stock markets would be relatively more difficult during episodes of heightened climate risks.
4.4. Lessons from Historical Data
Finally, while in our analyses we use a GARCH-based metric of conditional volatility of changes in temperature anomalies along the lines of [1,2,3,57] used the realized volatility (RV) of temperature changes to capture climate risks. Realized volatility (RV), in turn, is a model-free estimate of volatility. Given this, we analyze the role of temperature changes and its RV in forecasting the stock returns of the UK over the monthly period of 1772:01 to 2021:09. The choice of the UK is purely driven by publicly available historical data on daily temperatures, (The dataset used is the Met Office Hadley Centre Central England Temperature Data, which is available for download from: https://www.metoffice.gov.uk/hadobs/hadcet/data/download.html accessed on 12 October 2022, with stock prices again being derived from Global Financial Data), where we compute RV as the sum of squared daily changes in temperature over a month (see [58] for the RV of stock returns).
As can be seen from Table 1, temperature changes can produce forecasting gains for the stock returns of the UK not only at short, but, in the case of RV, also at a longer forecasting horizon. (We report the results for the [59] test. The results are based on a recursive estimation window, which, in our view, is an adequate approach to model a sample that spans more than two centuries of data. In addition, we estimate the forecasting models by the ordinary-least-squared technique, given that the number of predictor variables is small). This finding, although only for the UK, is quite encouraging in the sense that, unlike our observation that temperature changes and their GARCH-based measures of volatility have rather limited predictive value for stock returns when we study the data for the G8 countries (Section 4.2), the RV of temperature changes can prove to be beneficial in this regard when we study the long-range historical UK data.

Table 1.
Results for historical UK data.
5. Concluding Remarks
5.1. Findings and Implications
We have studied the implications of climate predictors for the predictability of stock market returns and the stock market connectedness of eight advanced countries (Canada, France, Germany, Italy, Japan, Switzerland, the UK, and the US) using data for an extended historical sample period ranging from 1916 to 2021. Our main empirical results show that, after controlling for a large array of other risk factors (that is, cross-market linkages of returns and volatilities, oil returns and volatility, measures of geopolitical risk, and a metric of investor risk appetite), the climate predictors that we have studied in our empirical research do not systematically improve the forecast accuracy of stock market returns. Empirical evidence for long-range historical UK data, however, show that climate predictors do have predictive value for subsequent stock market returns once we turn to a sample of data that spans more than two centuries. In addition, the climate predictors affect time-varying stock market connectedness mainly at a short (one-month) forecast horizon. Hence, international investors should keep in mind the role of climate risks in driving stock returns (and their connectedness), over and above other fundamental risks. Importantly, our results suggest that information on climate risks has the potential to be useful for designing optimal portfolio weights when investors with an intermediate forecast horizon seek to invest in the stock markets of advanced economies.
5.2. Future Research
There are at least four interesting avenues for future research. First, it would be interesting to use other machine-learning techniques than the Lasso and random forests and their relatives to study the predictive value of climate predictors. For example, the application of the techniques recently developed by [60,61,62,63,64], to name just a few recent studies in this rapidly expanding area of research, may yield interesting additional insights into how stock market returns and stock market connectedness are linked to climate predictors. Second, it is interesting to extend the type of analysis we have undertaken in this research to the stock markets of emerging market economies and to economies that are particularly vulnerable to changing climate and weather conditions such as, for example, major exporters of agricultural commodities. Third, using proprietary daily data on temperatures, one can compute the country-specific volatility of temperature changes, which, in turn, can be used to forecast stock returns, based on an alternative metric of variability of temperature capturing climate risks. Finally, another interesting avenue for future research is to switch from the kind of out-of-sample analysis that we have undertaken in this research to the type of out-of-bag analysis often used in the machine-learning literature. For a recent application of an out-of-bag analysis in empirical finance, see [65].
Another avenue for future research is to extend our analysis by combining the advanced economies we have studied in this research (and perhaps also emerging market economies) into a panel-data structure and then to use, for example, a panel Lasso approach to re-examine the predictive role of climate predictors for stock market returns. While we implement in our empirical analysis the Lasso estimator on a country-by-country basis and, thereby, account for cross-country heterogeneity, a panel Lasso approach may strengthen the statistical power of the type of forecasting experiment that we have undertaken in this research and, thereby, has the potential to shed further light on the predictive value of climate predictors for stock market returns. Preliminary fixed-effects panel regression tends to corroborate our time series results, whereby climate risks do not necessarily carry systematic predictive content for stock returns, with complete details of these results available upon request from the authors.
5.3. Limitations
It is important to point out that the risks associated with climate change can be typically categorized into physical risks and transition risks. Physical risks comprise risks arising due to, for example, rising temperatures, higher sea levels, and destructive storms. Transition risks arise due to a gradual switch over to a low-carbon economy and, thereby, reflect risks arising because of changes in the stance of climate policy, the rise of disruptive green technologies, and climate-related fluctuations in consumer preferences. Given this, a limitation of our work is that we have basically considered the physical risk components of climate change, and have completely ignored the issue of transition risks, which, in turn, can be considered as a cost of using a long-span of data. However, it must also be realized that the transition risks are likely to have become important as well in recent years, with emphasis on green technologies. However, physical risks, as captured by the first- and second-moment of temperature changes, have historically always played an important role due to their potential to cause catastrophic climate-related events.
Author Contributions
Conceptualization, R.G.; methodology, M.B., D.G. and C.P.; software, M.B., D.G. and C.P.; validation, R.G. and C.P.; formal analysis, M.B., D.G. and C.P.; investigation, M.B., D.G., R.G. and C.P.; resources, M.B., D.G., R.G. and C.P.; data curation, R.G.; writing—original draft preparation, R.G. and C.P.; writing—review and editing, M.B., D.G., R.G. and C.P.; visualization, M.B., D.G., R.G. and C.P.; project administration, R.G. All authors have read and agreed to published version of manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data will be made available upon request.
Acknowledgments
We would like to thank three anonymous referees for many helpful comments. However, any remaining errors are solely ours.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Summary statistics of stock market returns.
Table A1.
Summary statistics of stock market returns.
| Country | Obs | Max | Min | Mean | Median | Std. Dev. |
|---|---|---|---|---|---|---|
| Canada | 1265 | 20.5891 | −33.4603 | 0.4080 | 0.6870 | 4.5180 |
| France | 1265 | 24.2548 | −28.1855 | 0.6252 | 0.6739 | 5.4564 |
| Germany | 1265 | 68.8721 | −145.9963 | 0.3085 | 0.4458 | 8.2284 |
| Italy | 1265 | 46.8105 | −30.7573 | 0.5354 | 0.1368 | 7.0210 |
| Japan | 1265 | 50.8718 | −30.7862 | 0.5303 | 0.5693 | 6.1009 |
| Switzerland | 1265 | 28.7773 | −28.2157 | 0.3100 | 0.4851 | 4.3171 |
| UK | 1265 | 42.3197 | −30.9241 | 0.3963 | 0.7278 | 4.5539 |
| USA | 1265 | 40.7459 | −30.7528 | 0.4710 | 0.9369 | 4.3956 |

Table A2.
Summary statistics of stock market volatility.
Table A2.
Summary statistics of stock market volatility.
| Country | Obs | Max | Min | Mean | Median | Std. Dev. |
|---|---|---|---|---|---|---|
| Canada | 1265 | 147.0692 | 1.4390 | 20.6139 | 15.5299 | 17.4215 |
| France | 1265 | 88.9389 | 2.9790 | 29.6710 | 26.5692 | 11.4474 |
| Germany | 1265 | 3025.4947 | 19.9740 | 64.9312 | 45.1320 | 121.7298 |
| Italy | 1265 | 360.9569 | 6.0676 | 47.8981 | 35.2206 | 43.8551 |
| Japan | 1265 | 616.9305 | 7.2515 | 39.0609 | 25.2464 | 51.5448 |
| Switzerland | 1265 | 87.4715 | 2.1723 | 19.0636 | 15.5162 | 11.1824 |
| UK | 1265 | 385.7659 | 2.0532 | 22.8102 | 16.3587 | 30.0510 |
| USA | 1265 | 332.7490 | 4.6791 | 19.3910 | 12.5129 | 24.8187 |

Table A3.
Summary statistics of climate risks.
Table A3.
Summary statistics of climate risks.
| Climate Variable | Obs | Max | Min | Mean | Median | Std. Dev. |
|---|---|---|---|---|---|---|
| DGT | 1265 | 0.4700 | −0.4800 | 0.0008 | 0.0000 | 0.1216 |
| DNHT | 1265 | 0.9600 | −0.8900 | 0.0010 | 0.0000 | 0.2076 |
| DGT (GARCH) | 1265 | 0.0488 | 0.0097 | 0.0146 | 0.0132 | 0.0048 |
| DNHT (GARCH) | 1265 | 0.4303 | 0.0200 | 0.0456 | 0.0352 | 0.0333 |

Table A4.
Summary statistics of other control variables.
Table A4.
Summary statistics of other control variables.
| Control Variable | Obs | Max | Min | Mean | Median | Std. Dev. |
|---|---|---|---|---|---|---|
| Oil returns | 1265 | 54.5621 | −56.8125 | 0.2729 | 0.0000 | 6.9743 |
| Oil volatility | 1265 | 2992.3046 | 1.0831 | 73.9404 | 25.8844 | 184.8574 |
| Gold-to-silver price ratio | 1265 | 114.7485 | 15.1311 | 52.1754 | 47.3461 | 21.3582 |
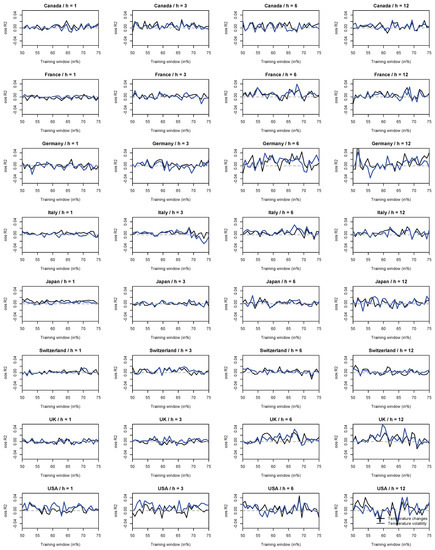
Figure A1.
Out-of-sample statistic for stock market returns (Random Forests). The horizontal axis shows the length of the training window (in percent of the total sample). The vertical axis shows the out-of-sample statistic. Black line = the rival model includes temperature changes as a potential predictor. Blue line = the rival model includes temperature volatility as a potential predictor. The temperature variables are based on changes in the northern hemisphere temperature anomaly and its volatility. The parameter h denotes the forecast horizon.
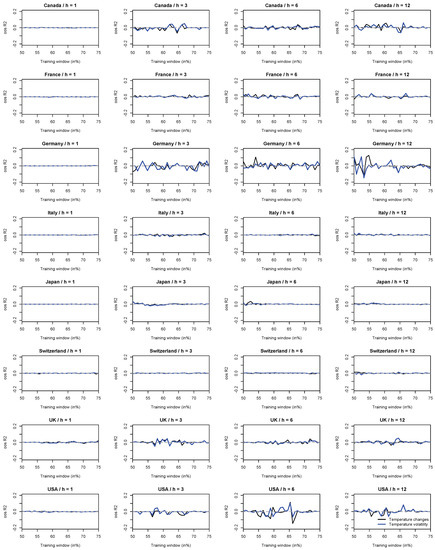
Figure A2.
Out-of-sample statistic for stock market returns (absolute forecast errors). The horizontal line shows the length of the training window (in percent of the total sample). The vertical line shows the out-of-sample statistic (based on absolute forecast errors). Black line = the rival model includes temperature changes as a potential predictor. Blue line = the rival model includes temperature volatility as a potential predictor. The temperature variables are based on changes in the northern hemisphere temperature anomaly and its volatility. The parameter h denotes the forecast horizon.
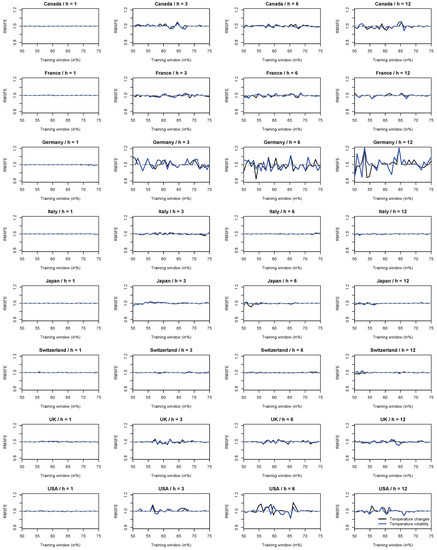
Figure A3.
Out-of-sample statistic for stock market returns. RMSFE = root-mean-squared-forecasting error. The horizontal line shows the length of the training window (in percent of the total sample). The vertical line shows the out-of-sample RMSFE statistic (rival vs. benchmark model). Black line = the rival model includes temperature changes as a potential predictor. Blue line = the rival model includes temperature volatility as a potential predictor. The temperature variables are based on changes in the northern hemisphere temperature anomaly and its volatility. The parameter h denotes the forecast horizon.
References
- Donadelli, M.; Jüppner, M.; Riedel, M.; Schlag, C. Temperature shocks and welfare costs. J. Econ. Dyn. Control. 2017, 82, 331–355. [Google Scholar] [CrossRef]
- Donadelli, M.; Jüppner, M.; Paradiso, A.; Schlag, C. Computing macro-effects and welfare costs of temperature volatility: A structural approach. Comput. Econ. 2021, 58, 347–394. [Google Scholar] [CrossRef]
- Donadelli, M.; Jüppner, M.; Vergalli, S. Temperature variability and the macroeconomy: A world tour. Environ. Resour. Econ. 2021, 83, 221–259. [Google Scholar] [CrossRef]
- Choi, D.; Gao, Z.; Jiang, W. Attention to global warming. Rev. Financ. Stud. 2020, 33, 1112–1145. [Google Scholar] [CrossRef]
- Engle, R.F.; Giglio, S.; Kelly, B.; Lee, H.; Stroebel, J. Hedging climate change news. Rev. Financ. Stud. 2020, 33, 1184–1216. [Google Scholar] [CrossRef]
- Bansal, R.; Kiku, D.; Ochoa, M. Price of Long Run Temperature Shifts in Capital Markets; NBER Working Paper No. 22529; National Bureau of Economic Research: Cambridge, MA, USA, 2021. [Google Scholar]
- Bansal, R.; Kiku, D.; Ochoa, M. Climate change and growth risks. In Climate Change Economics: The Role of Uncertainty and Risk; The Role of Uncertainty and Risk in Climate Change Economics; Chari, V.V., Litterman, R., Eds.; Wiley: Hoboken, NJ, USA, forthcoming.
- Faccini, R.; Matin, R.; Skiadopoulos, G. Dissecting Climate Risks: Are They Reflected in Stock Prices? 2021. Available online: https://ssrn.com/abstract=3795964 (accessed on 12 October 2022).
- Giglio, S.; Kelly, B.; Stroebel, J. Climate finance. Annu. Rev. Financ. Econ. 2021, 13, 15–36. [Google Scholar] [CrossRef]
- Stroebel, J.; Wurgler, J. What do you think about climate finance? J. Financ. Econ. 2021, 142, 487–498. [Google Scholar] [CrossRef]
- Rietz, T. The equity risk premium: A solution. J. Monet. Econ. 1988, 22, 117–131. [Google Scholar] [CrossRef]
- Barro, R.J. Rare disasters and asset markets in the twentieth century. Q. J. Econ. 2006, 121, 823–866. [Google Scholar] [CrossRef]
- Barro, R.J. Rare disasters, asset prices, and welfare costs. Am. Econ. Rev. 2009, 99, 243–264. [Google Scholar] [CrossRef]
- Campbell, J.Y. Viewpoint: Estimating the equity premium. Can. J. Econ. 2008, 41, 1–21. [Google Scholar] [CrossRef]
- Gupta, R.; Mwamba, J.W.M.; Wohar, M.E. The role of partisan conflict in forecasting the US equity premium: A nonparametric approach. Financ. Res. Lett. 2018, 25, 131–136. [Google Scholar] [CrossRef]
- Gupta, R.; Pierdzioch, C.; Vivian, A.J.; Wohar, M.E. The predictive value of inequality measures for stock returns: An analysis of long-span UK data using quantile random forests. Financ. Res. Lett. 2019, 29, 315–322. [Google Scholar] [CrossRef]
- Stock, J.H.; Watson, M.W. Forecasting output and inflation: The tole of asset prices. J. Econ. Lit. 2003, XLI, 788–829. [Google Scholar] [CrossRef]
- Salisu, A.A.; Lasisi, L.; Tchankam, J.P. Historical geopolitical risk and the behaviour of stock returns in advanced economies. Eur. J. Financ. 2021, 28, 889–906. [Google Scholar] [CrossRef]
- Aye, G.C.; Balcilar, M.; Gupta, R. International stock return predictability: Is the role of US time-varying? Empirica 2017, 44, 121–146. [Google Scholar] [CrossRef]
- Huber, F.; Krisztin, T.; Piribauer, P. Forecasting equity indices using large Bayesian VARs. Bull. Econ. Res. 2017, 69, 288–308. [Google Scholar] [CrossRef]
- Engle, R.F.; Lilien, D.M.; Robins, R.P. Estimating time varying risk premia in the term structure: The ARCH-M model. Econometrica 1987, 55, 391–407. [Google Scholar] [CrossRef]
- Fleming, J.; Ostdiek, B.; Whaley, R.E. Predicting stock market volatility: A new measure. J. Futur. Mark. 1995, 15, 265–302. [Google Scholar] [CrossRef]
- Guo, H.; Whitelaw, R.F. Uncovering the risk-return relation in the stock market. J. Financ. 2006, 61, 1433–1463. [Google Scholar] [CrossRef]
- Magner, N.; Lavin, J.F.; Valle, M.; Hardy, N. The predictive power of stock market’s expectations volatility: A financial synchronization phenomenon. PLoS ONE 2021, 16, e0250846. [Google Scholar] [CrossRef]
- Degiannakis, S.A.; Filis, G.; Arora, V. Oil prices and stock markets: A review of the theory and empirical evidence. Energy J. 2018, 39, 85–130. [Google Scholar] [CrossRef]
- Smyth, R.; Narayan, P.K. What do we know about oil prices and stock returns? Int. Rev. Financ. Anal. 2018, 57, 148–156. [Google Scholar] [CrossRef]
- Salisu, A.A.; Pierdzioch, C.; Gupta, R. Geopolitical risk and forecastability of tail risk in the oil market: Evidence from over a century of monthly data. Energy 2021, 235, 121333. [Google Scholar] [CrossRef]
- Gupta, R.; Pierdzioch, C.; Wong, W.-K. A note on forecasting the historical realized variance of oil-price movements: The role of gold-to-silver and gold-to-platinum price ratios. Energies 2021, 14, 6775. [Google Scholar] [CrossRef]
- Huang, D.; Kilic, M. Gold, platinum, and expected stock returns. J. Financ. Econ. 2019, 132, 50–75. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Rapach, D.E.; Zhou, G. Forecasting stock returns. In Handbook of Economic Forecasting, 2 (Part A); Elliott, G., Timmermann, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 328–383. [Google Scholar]
- Rapach, D.E.; Zhou, G. Asset pricing: Time-series predictability. Oxf. Res. Encycl. Econ. Financ. 2022. [Google Scholar] [CrossRef]
- Gupta, R.; Majumdar, A.; Wohar, M.E. The role of current account balance in forecasting the US equity premium: Evidence from a quantile predictive regression approach. Open Econ. Rev. 2017, 28, 47–59. [Google Scholar] [CrossRef]
- Gupta, R.; Huber, F.; Piribauer, P. Predicting international equity returns: Evidence from time-varying parameter vector autoregressive models. Int. Rev. Financ. Anal. 2020, 68, 101456. [Google Scholar] [CrossRef]
- Jordan, S.J.; Vivian, A.J.; Wohar, M.E. Forecasting market returns: Bagging or combining? Int. J. Forecast. 2017, 33, 102–120. [Google Scholar] [CrossRef]
- Jordan, S.J.; Vivian, A.J.; Wohar, M.E. Stock returns forecasting with metals: Sentiment vs. fundamentals. Eur. J. Financ. 2018, 24, 458–477. [Google Scholar] [CrossRef]
- Christou, C.; Gupta, R.; Jawadi, F. Does inequality help in forecasting equity premium in a panel of G7 countries? N. Am. J. Econ. Financ. 2021, 57, 101456. [Google Scholar] [CrossRef]
- Salisu, A.A.; Gupta, R. Commodity prices and forecastability of international stock returns over a century: Sentiments versus fundamentals with focus on South Africa. Emerg. Mark. Financ. Trade 2022, 58, 2620–2636. [Google Scholar] [CrossRef]
- Caldara, D.; Iacoviello, M. Measuring Geopolitical Risk. Am. Econ. Rev. 2022, 112, 1194–1225. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 10 October 2022).
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization paths for Generalized Linear Models via coordinate descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef]
- Antonakakis, N.; Gabauer, D.; Gupta, R.; Plakandaras, V. Dynamic connectedness of uncertainty across developed economies: A time-varying approach. Econ. Lett. 2018, 166, 63–75. [Google Scholar] [CrossRef]
- Antonakakis, N.; Gabauer, D.; Gupta, R. International monetary policy spillovers: Evidence from a time-varying parameter vector autoregression. Int. Rev. Financ. Anal. 2019, 65, 101382. [Google Scholar] [CrossRef]
- Antonakakis, N.; Chatziantoniou, I.; Gabauer, D. Refined measures of dynamic connectedness based on time-varying parameter vector autoregressions. J. Risk Financ. Manag. 2020, 13, 84. [Google Scholar] [CrossRef]
- Gabauer, D.; Gupta, R. On the transmission mechanism of country-specific and international economic uncertainty spillovers: A categorical TVP-VAR decomposition approach. Econ. Lett. 2018, 171, 63–71. [Google Scholar] [CrossRef]
- Chatziantoniou, I.; Gabauer, D.; Gupta, R. Integration and Risk Transmission in the Market for Crude Oil: A Time-Varying Parameter Frequency Connectednessa Approach; Working Paper No. 202147; Department of Economics, University of Pretoria: Pretoria, South Africa, 2021. [Google Scholar]
- Diebold, F.X.; Yilmaz, K. Measuring financial asset return and volatility spillovers, with application to global equity markets. Econ. J. 2009, 119, 158–171. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. Better to give than receive: Predictive directional measurement of volatility spillovers. Int. J. Forecast. 2012, 28, 57–66. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. Financial and Macroeconomic Connectedness: A Network Approach to Measurement and Monitoring, 1st ed.; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Baruník, J.; Křehlík, T. Measuring the frequency dynamics of financial connectedness and systemic risk. J. Financ. Econom. 2018, 16, 271–296. [Google Scholar] [CrossRef]
- Das, S.; Demirer, R.; Gupta, R.; Mangisa, S. The effect of global crises on stock market correlations: Evidence from scalar regressions via functional data analysis. Struct. Chang. Econ. Dyn. 2019, 50, 132–147. [Google Scholar] [CrossRef]
- Balcilar, M.; Ozdemir, A.A.; Ozdemir, H.; Wohar, M.E. Fed’s unconventional monetary policy and risk spillover in the US financial markets. Q. Rev. Econ. Financ. 2020, 78, 42–52. [Google Scholar] [CrossRef]
- Balcilar, M.; Roubaud, D.; Usman, O.; Wohar, M.E. Moving out of the linear rut: A period-specific and regime-dependent exchange rate and oil price pass-through in the BRICS countries. Energy Econ. 2021, 98, 105249. [Google Scholar] [CrossRef]
- Balcilar, M.; Roubaud, D.; Usman, O.; Wohar, M.E. Testing the asymmetric effects of exchange rate pass-through in BRICS countries: Does the state of the economy matter? World Econ. 2021, 44, 188–233. [Google Scholar] [CrossRef]
- Gupta, R.; Sheng, X.; Balcilar, M.; Ji, Q. Time-varying impact of pandemics on global output growth. Financ. Res. Lett. 2021, 41, 101823. [Google Scholar] [CrossRef]
- Alessandri, P.; Mumtaz, H. The Macroeconomic Cost of Climate Volatility; Working Paper No. 928; School of Economics and Finance, Queen Mary University of London: London, UK, 2021. [Google Scholar]
- Andersen, T.G.; Bollerslev, T. Answering the skeptics: Yes, standard volatility models do provide accurate forecasts. Int. Econ. Rev. 1998, 39, 885–905. [Google Scholar] [CrossRef]
- Clark, T.E.; West, K.D. Approximately normal tests for equal predictive accuracy in nested models. J. Econom. 2007, 138, 291–311. [Google Scholar] [CrossRef]
- Deng, C.; Huang, Y.; Hasan, N.; Bao, Y. Multi-step-ahead stock price index forecasting using long short-term memory model with multivariate empirical mode decomposition. Inf. Sci. 2022, 607, 297–321. [Google Scholar] [CrossRef]
- Liang, J.; Jia, G. China futures price forecasting based on online search and information transfer. Data Sci. Manag. 2022, 5, 187–198. [Google Scholar] [CrossRef]
- Lv, S.-X.; Peng, L.; Hu, H.; Wang, L. Effective machine learning model combination based on selective ensemble strategy for time series forecasting. Inf. Sci. 2022, 612, 994–1023. [Google Scholar] [CrossRef]
- Peng, S.; Han, W.; Jia, G. Pearson correlation and transfer entropy in the Chinese stock market with time delay. Data Sci. Manag. 2022, 5, 117–123. [Google Scholar] [CrossRef]
- Zhu, Q.; Ruan, Y.; Liu, S.; Wang, L. Novel information fusion model for simulating the effect of global public events on the Sino-US soybean futures market. Data Sci. Manag. 2021, 1, 48–59. [Google Scholar] [CrossRef]
- Bonato, M.; Çepni, O.; Gupta, R.; Pierdzioch, C. El Niño, La Niña, and forecastability of the realized variance of agricultural commodity prices: Evidence from a machine learning approach. J. Forecast. 2022. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).