Abstract
D-optimality is a well-known concept in experimental design that seeks to select an optimal set of design points to estimate the unknown parameters of a statistical model with a minimum variance. In this paper, we focus on proving a conjecture made by Ford, Torsney and Wu regarding the existence of a class of D-optimal designs for binary and weighted linear regression models. Our concentration is on models with one design variable. The conjecture states that, for any given level of precision, there exists a two-level factorial design that is D-optimal for these models. To prove this conjecture, we use an intuitive approach that explores various link functions in the generalised linear model context to establish the veracity of the conjecture. We also present explicit and clear plots of various functions wherever deemed necessary and appropriate to further strengthen the proofs. Our results establish the existence of D-optimal designs for binary and weighted linear regression models with one design variable, which have important implications for the efficient design of experiments in various fields. These findings contribute to the development of optimal experimental designs for studying binary and weighted linear regression models and provide a foundation for future research in this area.
Keywords:
D-optimal; binary response models; weighted linear regression; generalised linear model; binary weight; binary weight functions MSC:
62K05
1. Introduction
The study of D-optimality has been central to the work on optimum experimental design since the beginning, e.g., Kiefer [1]. Fedorov [2], Silvey [3] and Pazman [4], as has stress D-optimality. Farrell et al. [5] provided a summary of earlier work on D-optimality. This includes that of Kiefer and Wolfowitz [6] and Kiefer [7] which likewise concentrate on results for regression models, including extensions to -optimality.
In this paper, we focus on D-optimal designs for binary regression and weighted linear regression models that feature a single design variable. We derive minimal support D-optimal designs, which have been extensively studied in the literature for binary data. This is particularly the case for Ford Torsney and Wu [8], who considered c-optimal and D-optimal designs for generalised linear models with one design variable. Using Silvey’s [3] geometrical approach, they claimed that, in two-parameter models, many local D-optimal designs have two support points and they conjectured what these would be. Sitter and Torsney [9,10] extended this work to more than two design variables for some typical binary response models. Their results are also ‘conjecture’-based. Building on these studies, Sebastiani and Settimi [11] explored the binary logistic regression design problem, and provided an analytical proof of the conjectured designs for all design intervals. We expand on their work to encompass a class of binary regression models as well as weighted linear regression models. We expand on their work to encompass a class of binary regression models as well as weighted linear regression models. The work instrumental in the development of the research was presented in Gunduz [12], Torsney and Gunduz [13], Gunduz and Torsney [14].
Some of the later studies, especially those related to the binary regression model, include the following: Haines et al. [15] focused on locally D-optimal designs on the logistic regression model with two explanatory variables. Idais [16] studied the locally optimal designs that are derived for generalised linear models with first-order linear predictors. Amongst others, Jaffari et al. [17], Kabera et al. [18], Haines et al. [19], Gaffke et al. [20], and Zhai [21] all developed models loosely or somewhat moderately related to our present work. The main contribution of this paper is our thorough development of a rigorous proof of the conjecture made by Ford, Torsney, and Wu in 1992 regarding the existence of a class of D-optimal designs for binary and weighted linear regression models, with a concentration on models with one design variable. The paper’s approach utilises the intuitive exploration of various link functions in the generalised linear model context, along with the explicit and clear plots of various functions to strengthen the proofs. The results of this paper have important implications for the efficient design of experiments in various fields, including engineering, medicine, and social sciences. The paper’s contribution to the development of optimal experimental designs for studying binary and weighted linear regression models provides a foundation for future research in this area.
The paper is organised as follows. Section 2 provides a brief overview of the relevant literature on D-optimal designs and binary and weighted linear regression models. Section 3 introduces the notation and mathematical framework used in this paper. Section 4 presents the main result of the paper, namely the rigorous proof of the conjecture for models with one design variable. Section 5 discusses the intuition behind the approach used in the paper and provides explicit plots for various functions to support the proofs. Section 6 presents the implications of the results for the efficient design of the experiments in various fields. Finally, Section 7 concludes the paper and suggests directions for future research.
2. Models
Two-Parameter Models
We examine a binary regression model where the observed variable u is dependent on a single design variable ⊂. In this model, u can only take on two possible values: 1 if a particular event of interest takes place, and 0 otherwise. The probabilities of these outcomes can be expressed as follows:
Thus, . We assume , where is a chosen cumulative distribution function. So
For unknown parameters and , the dependence of on x only happens via a nonlinear function of the linear combination
It is a generalised linear model and the information matrix of a single replicate can be written as follows:
where . Furthermore, given , then , and
Hence, if
then
and
Non-singular linear transformations of the design space cause D-optimality to be invariant. Let us look at the D-optimal linear design problem with design vectors
where is to a weighted linear regression design problem with the weight function following Ford, Torsney and Wu [8].
Therefore, these nonlinear design problems transform into linear design problems for weighted linear regression in z with weight function , where is the density of . We now consider the implications of this. Table 1 lists examples of this kind of weight function (binary regression weight functions) in two groups: Group I and Group II. Two other groups (III and IV) are also listed. Firstly, we consider finding D-optimal designs for Group I and Group III, and then investigate Group II and Group IV separately.

Table 1.
Weight functions under consideration.
3. On the Number of Support Points
One of the main objectives of optimal experimental design is to determine the support points. A geometrical approach to the construction of D-optimal designs is sometimes useful. We therefore introduce the following set:
Box and Lucas [22] called this the design locus. The support of D-optimal designs heavily depends on the geometry of this design locus [3]. Caratheodory’s theorem guarantees that the number of support points is finite, implying the existence of a design with only two or three support points. Silvey’s geometrical characterisation, as stated in [3], can offer some insights into the nature of these points or at least their quantity. These support points refer to the points of contact between and , the smallest ellipse centred on the origin that contains . Both Silvey [23] and Sibson [24] contributed to the discussion of Wynn [25], and the idea was first conjectured by Silvey [23]. It is important to note that, for Group I weight functions, both and are bounded functions for all in the widest possible design space, , which is the sample space of . Thus, no restrictions on z exist. Furthermore, is a closed convex curve that begins and ends at the origin. This characteristic also applies to Group III weight functions of the form or where is a density function. Additionally, Group I and Group III weight functions have similar properties, which are typically unimodal with one maximal turning point (TP) at a value of (where ) and with, if and if and at the extremes of , (Table 1). Based on the plots of , it is evident that Silvey’s minimal ellipse, as stated in [3], only touches at two points for many choices of from Groups I and III. We now reveal a Theorem on this.
Theorem 1.
Assume that a weight function is continuous and differentiable and suppose , i.e., , . Let
where is the information matrix of any design ξ. Suppose that is continuous with , , differentiable with , and is first concave increasing then convex increasing. Then, the function [or the variance function] can have at most three TPs: two maximal ones and one minimal one. In consequence, a D-optimal design can have only two support points on any design interval .
Proof of Theorem 1.
Silvey’s [3] minimal ellipse argument is a geometrical characterisation of the Equivalence Theorem [6]. According to Theorem 3.9 [3], a design is D-optimal iff
This is true iff
where is a quadratic function. We would like to see to have an optimal design. To explore the shape of , we analyse its derivatives. The derivative of can be written as
where and is an increasing linear function of z because the coefficient of z is the second diagonal element of the information matrix which is positive definite. In fact, , where Z is a random variable with a probability measure of since
The intercept will be negative if is positive. The opposite is likewise true. The consequence is iff . That is, when the line crosses . Given our assumptions about , an upward sloping line can cross it, over and hence over any subset of , either one or three times. The slope of the line determines this.
Thus, the derivative of can have at most three zeros in . Additionally, such a line must initially lie above . If there is only one TP in a design interval, it must be a maximal TP. If there are three TPs, the first and third are maximal, while the second is a minimal TP. As a result, has only one minimum TP and at most two maximum TPs. When there are three solutions to , the middle one must be a minimum TP, as the line crosses the curve first from above, then from below, then from above, and then from below (Figure 1).
As a conclusion, this implies that there are only two D-optimal support points on any design interval, because three support points would need a minimum of two TPs. Hence, the lines arising under the designs must cross three times and the theorem is proven. The plots of for various weight functions exhibit similar shapes and properties, as illustrated in Figure 1. However, only a few weight functions, such as the logistic and the normal weight functions, offer an function whose change of sign can be seen analytically. □
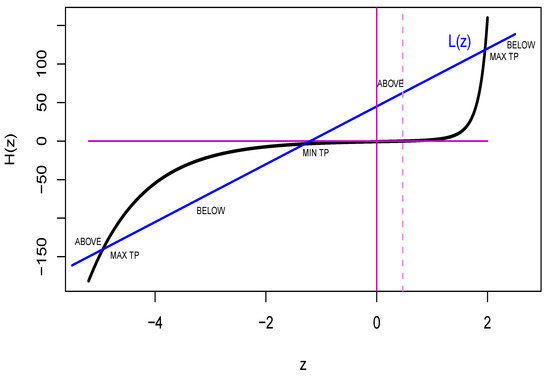
Figure 1.
A Typical Plot of and for Complementary log-log Weight Function, .
Table 2 and Table 3 list the functions for the weight functions of Group I and Group III, respectively.

Table 2.
Group I: Binary Weight Functions and functions on .

Table 3.
Group III: Density Weight Functions and functions.
4. Determination of Support Points
4.1. A Conjecture Proved under a Sufficient Condition
Let us now concentrate on identifying the two support points. Suppose that we have a two-point design on the interval . It is known that the optimal weights are always equal, regardless of the support points. Therefore, the design can be expressed as:
As the weights are optimal for and , we have (as per Equation (2) and the subsequent implications for .) For this design to be optimal on the entire space, , and must maximise the D-optimal criterion over .
Using two points of view, we show that a function with an important role in this respect is
A conjecture is given about the support points on for all and :
- Case 1: , ;
- Case 2: , , .
The D-optimal design is the same as above since contains the above support points.
- Case 3: , , , , ;
- Case 4: , , , , ;
- Case 5: , , , .
Theorem 2.
A sufficient condition for the conjecture to be true (in addition to the properties needed by ) is that is continuous, differentiable and unimodal (with a maximum at ) and that the function strictly increases over the two subsets and .
Proof of Theorem 2.
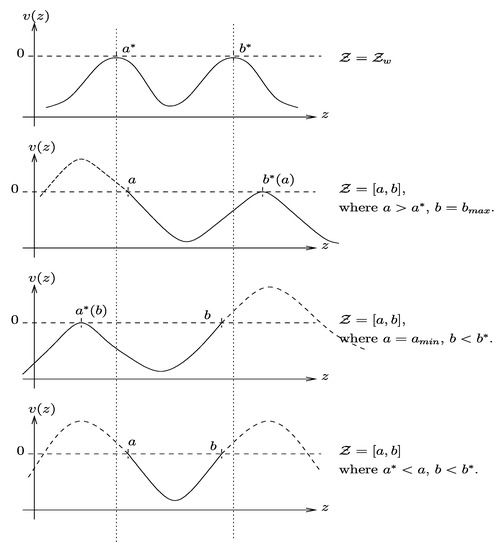
We need to check the equivalence theorem, i.e., we need . We consider various cases. We first graphically illustrate the structure if the conjecture is true, given that we know it has only 2 maximal TPs and 1 minimal one and that the D-optimum design has two support points at which must be zero (Figure 2). This illustrates when should be zero or what sign it should have at the conjectured support points if the conjecture is true. In fact, should be zero or negative, should be zero or positive depending on . □

Figure 2.
Examples of plots depicting .
These results hold if is increasing. Various cases, starting with two cases where only one support point is specified, either or , are considered. In both cases, we can show that the conjectured signs of and hold if is increasing.
- , . We show that .Since , . Moreover,The right-hand side of the equation is always positive, because and . Therefore, .
- , . We show .Since , . MoreoverThis equation is always positive on the right-hand side because and . Therefore, .
- ,Now, , is the only possible solution to Equations (10) and (11). Thus, . Thus, , identify 2 max TP’s of . Moreover, they are TP’s at which has a common value of zero since . From the property of , the only possibility is that they are the values of z say , ) at which the two maximal TP’s of , i.e., , . Hence, the Equivalence Theorem is satisfied on and on any subset which contains , . Hence, the two-point designis D-optimal for all where and .
- Because , and , and .
- Since is increasing over , and since , then . Therefore, .
- Since is increasing over , and then . Therefore, .Hence, the two-point designis D-optimal for all where .
- ,Clearly, . We want negative. First, since . Secondwhere is the inverse function of for and for . Consider and recall that . We know from Theorem (1) that is the only solution where . Thus, the functions and cross only once at . Furthermore, since , while , then at . Hence, this inequality is true for . Therefore, . Thus, the two-point designis D-optimal for all , where and . Since for , this design is also D-optimal for .
- First, . Secondly, by above. Thus, . Consider now . Because , . We assumed . If is an increasing function, . Hence, . Thus, and the two-point designis D-optimal for all where and .
- ,This is the complementary to case 4 with andThus, the two point designis D-optimal for all where and . Since for . This is also D-optimal for .
- This is the complementary of case 6 withBecause and because of andSince andThus, the two-point designis D-optimal for all where and .
4.2. Examples of
Thus, the equivalence theorem is satisfied by our conjectured optimal designs for all possible design intervals if the function
is increasing over and over . This appears to be true for a wide range of when the plots are examined. It is noteworthy that these characteristics also ensure the closed convexity of , as reported by Wu [26]. We established these properties through analytical means for a range of binary regression weight functions (Table 4 and Table 5). The plots of are given in Figure 3.

Table 4.
Group I: Binary Weight Functions and functions on . implies empirical evidence of non-decreasing property. proved these cases.

Table 5.
Group III: Density weight Functions, and functions.
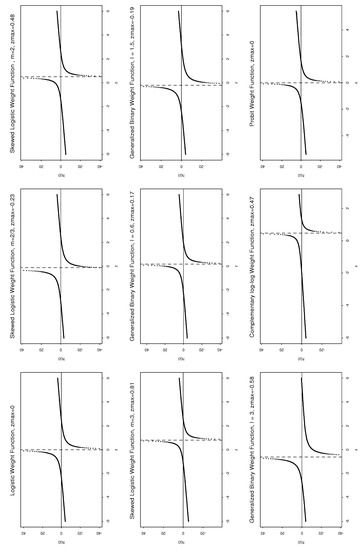
Figure 3.
Group I: Plot of for Binary Weight Functions (note: l represents ).
For some of these functions, the stronger outcome of the ratio increasing over and over has also been demonstrated (such as in the cases of the logistic, complementary log-log, and skewed logistic binary weight functions). This implies that is log-concave. On the other hand, it has been analytically proven that is an increasing function for the remaining cases (probit, double exponential, double reciprocal). Figure 4 and Figure 5 represent a typical plot of . The examination of these plots reveals a prominent feature, which is that the functions and exhibit almost identical shapes and are increasing over and with a vertical asymptote at for the listed weight functions. These findings corroborate and extend the conclusions of Wu [26].
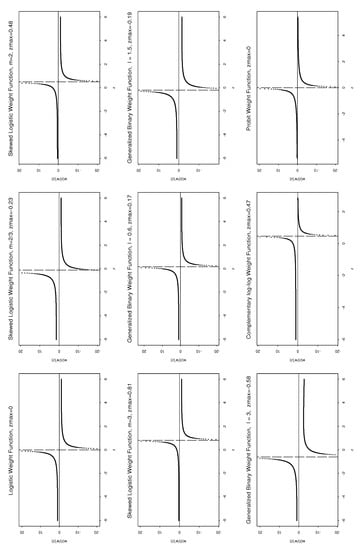
Figure 4.
Group I: Plot of for Binary Weight Functions (note: l represents ).
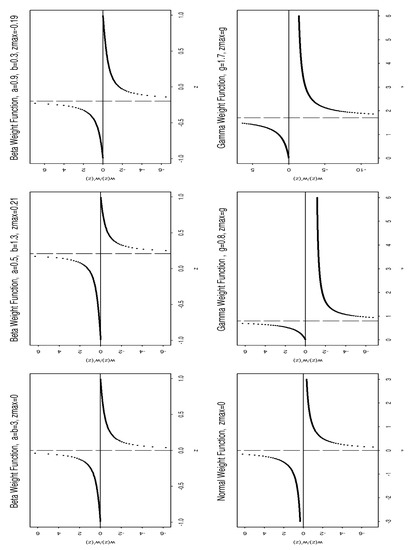
Figure 5.
Group III: Plot of for Non-Binary Weight Functions.
5. Group III and Group IV Weight Functions Results
5.1. Group III Weight Functions
The goal is to determine D-optimal designs for interval subsets of , focusing on two symmetric binary weight functions: the double reciprocal and double exponential weight functions, which are listed in Table 1. These weight functions differ from those in Group I in that they are unimodal and reach their maximum value at , but at this point, they are both non-differentiable. Therefore, these are not stationary values. For these two weight functions, the induced design space is again a closed convex curve in when , but it has a sharp vertex at (Figure 6). It is likely that the minimal central ellipsoid containing will touch more than twice in these cases, both at and at two other points symmetric with regard to zero, resulting in a D-optimal design with three support points.
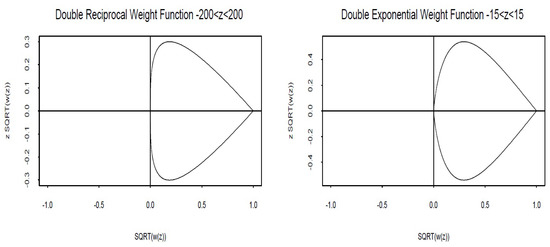
Figure 6.
Group II: Plot of for Double Reciprocal & Double Exponential Weight Functions () .
In fact, Musrati [27] and Torsney and Musrati [28] have shown that three support points may be necessary when contains 0, in which case, one of them is . They also provided an explicit solution for the optimal weights. The analysis of nicely illustrates how this can occur. It appears that is concave increasing over and convex increasing over and it is discontinuous at (Figure 7). An upward sloping line can cross up to four times which means that can have four TPs. However, such a line can only cross at most twice in and in . In these regions, the relevant parts of the conjecture are feasible. In fact, the function of is increasing in both regions for both weight functions. Interestingly, is not increasing. Since is increasing, the conjecture is satisfied if or .
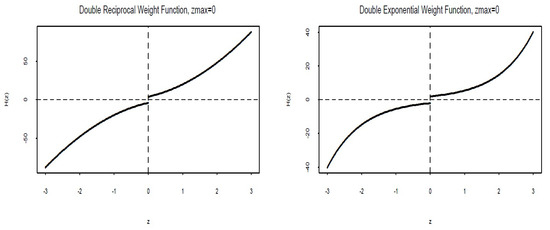
Figure 7.
Group II: Plot of for Double Reciprocal & Double Exponential Binary Weight Functions.
5.2. Group IV Other Weight Functions
D-optimal designs for the Group IV weight functions in Table 1, namely and for all were derived by Ford Torsney and Wu [8]. These weight functions arise from the transformations of D-optimal design problems for other generalised linear models such as Poisson and Inverse Regression Models. The function confirms their results. The shape of these weight functions is different from previous cases, and is no longer bounded for all . Moreover, unlike before, the components of now have a one-to-one relationship, namely and . On any this guarantees the boundedness of , and D-optimal designs have a similar structure to those of non-binary weight functions.
To start, let us look at the function : For , , (Table 6). This means that is concave increasing from up to 0 with an infinite derivative at . For , , , and . Therefore, for is concave increasing from to zero with an infinite derivative at while for , is convex increasing from zero to ∞ with a zero derivative at . For , is convex decreasing. We can then argue that an upward sloping line can cross at most twice in the cases , , ; , . As a consequence, has at most two TP’s, one a maximal TP, and one a minimal TP. Thus, only two support points are possible on any .

Table 6.
Group IV: Non-Binary Weight Functions, and .
Take the instance of , . An upward sloping line crosses only once from below. This means that has one TP, a minimal TP. This again suggests that there can be only two support points and they are the endpoints a and b. If you look at the plot of , a convex decreasing curve is seen. The minimal central ellipse containing can only touch it at its endpoints. Now, consider the function : for , which means that is an increasing linear function from to ∞; for , is linearly increasing if or ; if , is decreasing.
- Implications for support points of the D-optimal design on are
As is linear in z, explicit solutions exist for , , i.e., for the solutions to the equations
Ford, Torsney, and Wu [8] reported values of for while for , (if ) and (if ).
6. Results
D-optimal designs have been examined for models with a binary response using a single design variable, and we transformed the design problem into one for a weighted linear regression model, where the weight function is:
where is the density of , and the design interval is . Different other (non-binary) weight functions were also considered.
A two point design was settled as the optimal design for many weight functions and the support points for the z values are:
where maximise the determinant over relevant intervals. These results follow if
- The function is first concave increasing then convex increasing;
- The function is increasing (this also guarantees that is closed convex). In some cases, the ratio is also increasing. (Note: shows that induced design space and the widest possible design space.)
7. Conclusions
We presented a comprehensive study of D-optimal designs for binary and weighted linear regression models with one design variable. We specifically developed an efficient algorithmic framework for computing D-optimal designs for these models. Along with crystal clear explanations illustrated by intuitively appealing plots, we demonstrated the effectiveness of our approach through a series of numerical and thoroughly explained experiments.
Our results show that our D-optimal designs are superior to other commonly used designs in terms of precision and efficiency, and we provided a detailed analysis of the factors that affect the performance of these designs. Specifically, we showed that the choice of weight function has a significant impact on the performance of the D-optimal designs, and we provided guidance on selecting the appropriate weight function for a given problem.
In addition to the immediate practical implications of our work, there are several directions for future research. One natural extension of our study is to consider D-optimal designs for binary and weighted linear regression models with multiple design variables, which would require developing new computational techniques to handle the increased complexity of the problem. We anticipate that a large number of tools and results developed in the present manuscript will provide a solid basis to be leveraged and harnessed in multivariate settings.
Besides considering input spaces of higher dimension, our future research in this context will also seek to explore the use of D-optimal designs for other types of regression models, such as nonlinear regression models, nonparametric regression models, or even models with non-continuous response variables. It is understood that all these anticipated extensions will bring with them the need to develop new algorithms for computing D-optimal designs in these settings or investigating the theoretical properties of D-optimal designs in these models. It is also interesting to at least speculate that our present work has the potential to be applicable or at least adapted to statistical machine learning in the context of active learning.
We believe that our study has provided a valuable contribution to the field of optimal experimental design for binary and weighted linear regression models with one design variable, and we look forward to further exploring the potential applications of D-optimal designs in this context as well as others.
Author Contributions
This study is derived from N.G. doctoral thesis. The topic was suggested by B.T. B.T. is N.G.’s PhD thesis supervisor. N.G. did most of the detailed work on the problem, and B.T. reviewed it for correctness and refinements as often as the need arose. N.G. performed the literature search and worked out the derivations of the theoretical results. N.G. also performed all the analytic calculations and ran all the numerical simulations. B.T. was very helpful while N.G. was writing her doctoral thesis. Although the article was taken from N.G.’s doctoral thesis, the preparation and rewriting of the article was entirely done by N.G., including the entire revision process requested by the suggestions from the reviewers. During the whole process of this manuscript, N.G. asked for and implemented feedback from B.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Conflicts of Interest
The authors have no conflict of interest.
References
- Kiefer, J. Optimum experimental designs. J. R. Stat. Soc. Ser. B 1959, 21, 272–304. [Google Scholar] [CrossRef]
- Fedorov, V.V. Theory of Optimal Experiments; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Silvey, S. Optimal Design. An Introduction to the Theory for Parameter Estimation; Chapman and Hall: London, UK; New York, NY, USA, 1980. [Google Scholar]
- Pázman, A. Foundations of Optimum Experimental Design; Springer: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Farrell, R.H.; Kiefer, J.; Walbran, A. Optimum Multivariate Designs. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Held at the Statistical Laboratory, University of California, 21 June–18 July 1965 and 27 December 1965–7 January 1966; University of California Press: Berkeley, CA, USA, 1967; Volume 1, pp. 113–138. [Google Scholar]
- Kiefer, J.; Wolfowitz, J. The equivalence of two extremum problems. Can. J. Math. 1960, 12, 363–366. [Google Scholar] [CrossRef]
- Kiefer, J. Optimum Designs in Regression Problems, II. Ann. Math. Stat. 1961, 32, 298–325. [Google Scholar] [CrossRef]
- Ford, I.; Torsney, B.; Wu, C. The use of a canonical form in the construction of locally optimal designs for non-linear problems. J. R. Stat. Soc. Ser. B 1992, 54, 569–583. [Google Scholar] [CrossRef]
- Sitter, R.; Torsney, B. D-optimal designs for generalized linear models. MODA4-Advances in Model-Oriented Data Analysis. In Proceedings of the 4th International Workshop, Spetses, Greece, 5–9 June 1995; pp. 87–102. [Google Scholar]
- Sitter, R.R.; Torsney, B. Optimal Designs for Binary Response Experiments with Two Design Variable. Stat. Sin. 1995, 5, 405–419. [Google Scholar]
- Sebastiani, P.; Settimi, R. A note on D-optimal designs for logistic regression model. J. Stat. Plan. Inference 1997, 59, 359–368. [Google Scholar] [CrossRef]
- Gunduz, N. D-Optimal Designs for Weighted Linear Regression and Binary Regression Models. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 1999. [Google Scholar]
- Torsney, B.; Gunduz, N. On Optimal Designs for High Dimensional Binary Regression Models. In Optimum Design 2000. Nonconvex Optimization and Its Applications; Atkinson, A., Bogacka, B., Zhigljavsky, A., Eds.; Springer: Boston, MA, USA, 2001; Volume 51. [Google Scholar]
- Gunduz, N.; Torsney, B. Some advances in optimal designs in contingent valuation studies. J. Stat. Plan. Inference 2006, 136, 1153–1165. [Google Scholar] [CrossRef]
- Haines, L.H.; Kabera, G.M.; Ndlovu, P.; O’Brien, T.E. D-optimal Designs for Logistic Regression in Two Variables. Moda Adv. Model Oriented Des. Anal. 2007, 193, 136–150. [Google Scholar]
- Idais, O. On local optimality of vertex type designs in generalized linear models. Stat Pap. 2021, 62, 1871–1898. [Google Scholar] [CrossRef]
- Jafari, H.; Khazai, S.; Khaki, Y.; Jafari, T. D-Optimal Design for Logistic Regression Model with Three Independent Variables. J. Asian Sci. Res. 2014, 4, 120–124. [Google Scholar]
- Kabera, G.; Haines, L.; Ndlovu, P. The analytic construction of D-optimal designs for the two-variable binary logistic regression model without interaction. Statistics 2015, 49, 1169–1186. [Google Scholar] [CrossRef]
- Haines, L.H.; Kabera, G.M.; Ndlovu, P. D-optimal designs for the two-variable binary logistic regression model with interaction. J. Stat. Plan. Inference 2018, 193, 136–150. [Google Scholar] [CrossRef]
- Gaffke, N.; Idais, O.; Schwabe, R. Locally optimal designs for gamma models. J. Stat. Plan. Inference 2019, 203, 199–214. [Google Scholar] [CrossRef]
- Zhai, Y.; Wang, C.; Lin, H.; Fang, Z. D-optimal designs for two-variable logistic regression model with restricted design space. Commun. Stat. Theory Methods 2023, 1–18. [Google Scholar] [CrossRef]
- Box, G.E.P.; Lucas, H.L. Design of experiments in nonlinear situations. Biometrika 1959, 46, 77–90. [Google Scholar] [CrossRef]
- Silvey, S. Discussion on “Results in the theory and Construction of D-optimal experimental designs”. J. R. Stat. Soc. Ser. B 1972, 34, 174–175. [Google Scholar]
- Sibson, R. Discussion on “Results in the theory and Construction of D-optimal experimental designs”. J. R. Stat. Soc. Ser. B 1972, 34, 181–183. [Google Scholar]
- Wynn, H.P. Results in the theory and construction of D-optimal experimemtal designs. J. R. Stat. Soc. Ser. B 1972, 34, 133–147. [Google Scholar]
- Wu, C. Optimal design for percentile estimation of a quantal response curve. In Optimal Design and Analysis of Experiments; Dodge, Y., Fedorov, V.H., Eds.; Elsevier (North Holland Publishing Co.): Amsterdam, The Netherlands, 1988; pp. 213–222. [Google Scholar]
- Musrati, A.K. Locally Optimal Designs for Binary and Weighted Regression Models. Master’s Thesis, University of Glasgow, Glasgow, UK, 1992. [Google Scholar]
- Torsney, B.; Musrati, A.K. On the Construction of Optimal Designs with Applications to Binary Response and to weighted Regression Models. In Model-Oriented Data Analysis, Proceedings of the 3rd International Workshop, Petrodvorets, Russia, 25–30 May 1992 (Contributions to Statistics); Muller, W.O., Wynn, H.P., Zhigliausky, A.A., Eds.; Physica-Verlag: Heidelberg, Germany, 1993; pp. 329–341. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).