GND-PCA Method for Identification of Gene Functions Involved in Asymmetric Division of C. elegans
Abstract
1. Introduction
2. Basic Theory of GND-PCA
2.1. Background Knowledge
2.2. Definitions and Preliminaries
2.3. GND-PCA
| Algorithm 1: The training algorithm of GND-PCA |
| IN: a series of Nth-order tensors, , . OUT: N Matrices (, ) with orthogonal column vectors.
|
3. GND-PCA Procedure
3.1. Data Preprocessing
- (1)
- Embryonic image segmentation based on shape index;
- (2)
- Embryonic image registration based on AP-axes;
- (3)
- Embryonic image resampling;
- (4)
- Time registration.
3.1.1. Image Segmentation Based on Shape Index
3.1.2. Image Registration Based on AP-Axes
- (1)
- Rotate the AP-axes to the x-axis;
- (2)
- Rotate the middle point of the two nuclear centers of P1 and AB to the z-axis around the x-axis;
- (3)
- Set the middle point of the two nuclear centers of P1 and AB to [300, 300, 300] at the registered image.
3.1.3. Resampling Nuclear Images
3.1.4. Time Registration
- (1)
- is the starting time when the sphericity of both P1 and AB are larger than 0.6;
- (2)
- is the middle time of and ;
- (3)
- is the starting time when the sphericity of either P1 or AB is less than 0.6.
3.2. The Procedure of Analyzing Gene Functions Based on GND-PCA
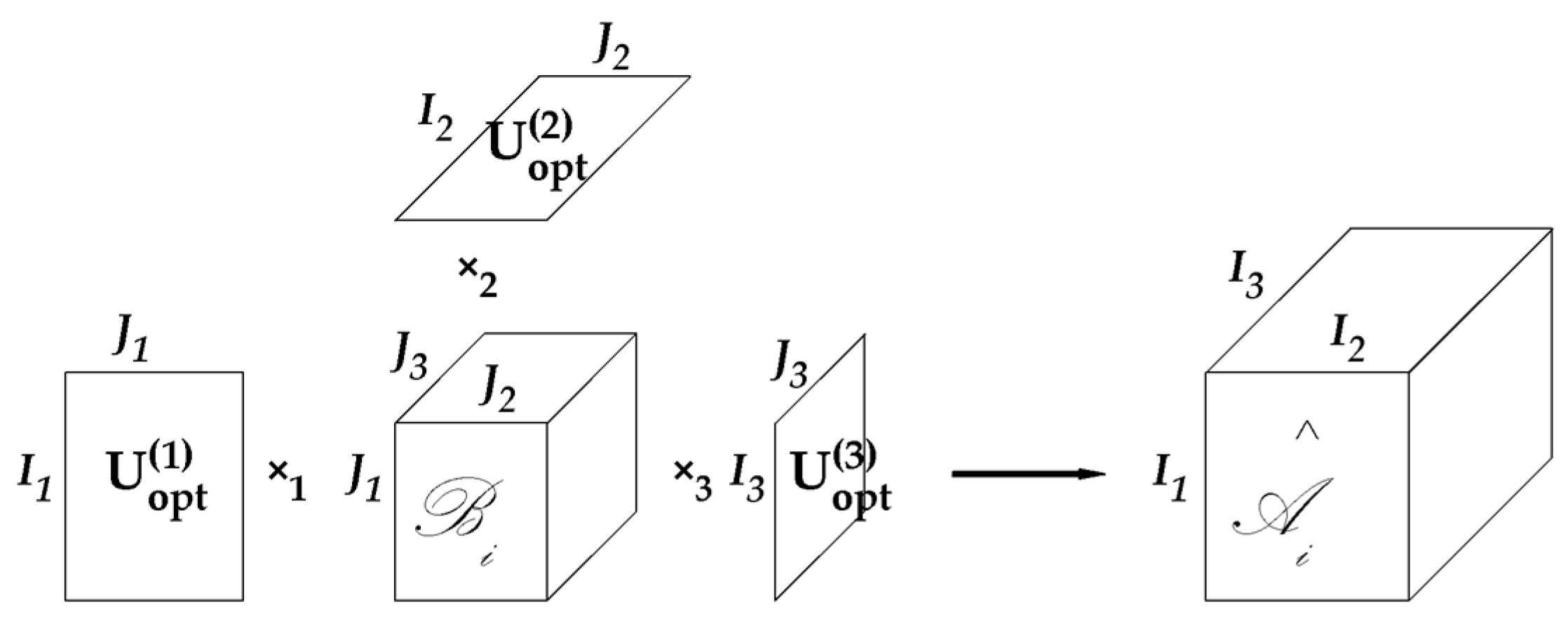
- Eigenvector Matrix: , , and are called eigenvector matrices (also called projective matrices) in Tucker decomposition. Their sizes are , , and , respectively. The calculated eigenvector matrices by GND-PCA are marked as , , and ;
- Base: The tensors built by the Kronecker product of three columns of , , and are called bases or base images: ;
- Core tensor: When using GND-PCA to project images, the built volumes are also called core tensors. It refers to in Figure 2;
- Coefficient: An entry in a core tensor is called a coefficient, and is marked by , , , and . Sometimes we need to refer to a position in the core tensor to distinguish the value (coefficient) and the location in the core tensor; we call the location the element of a core tensor.
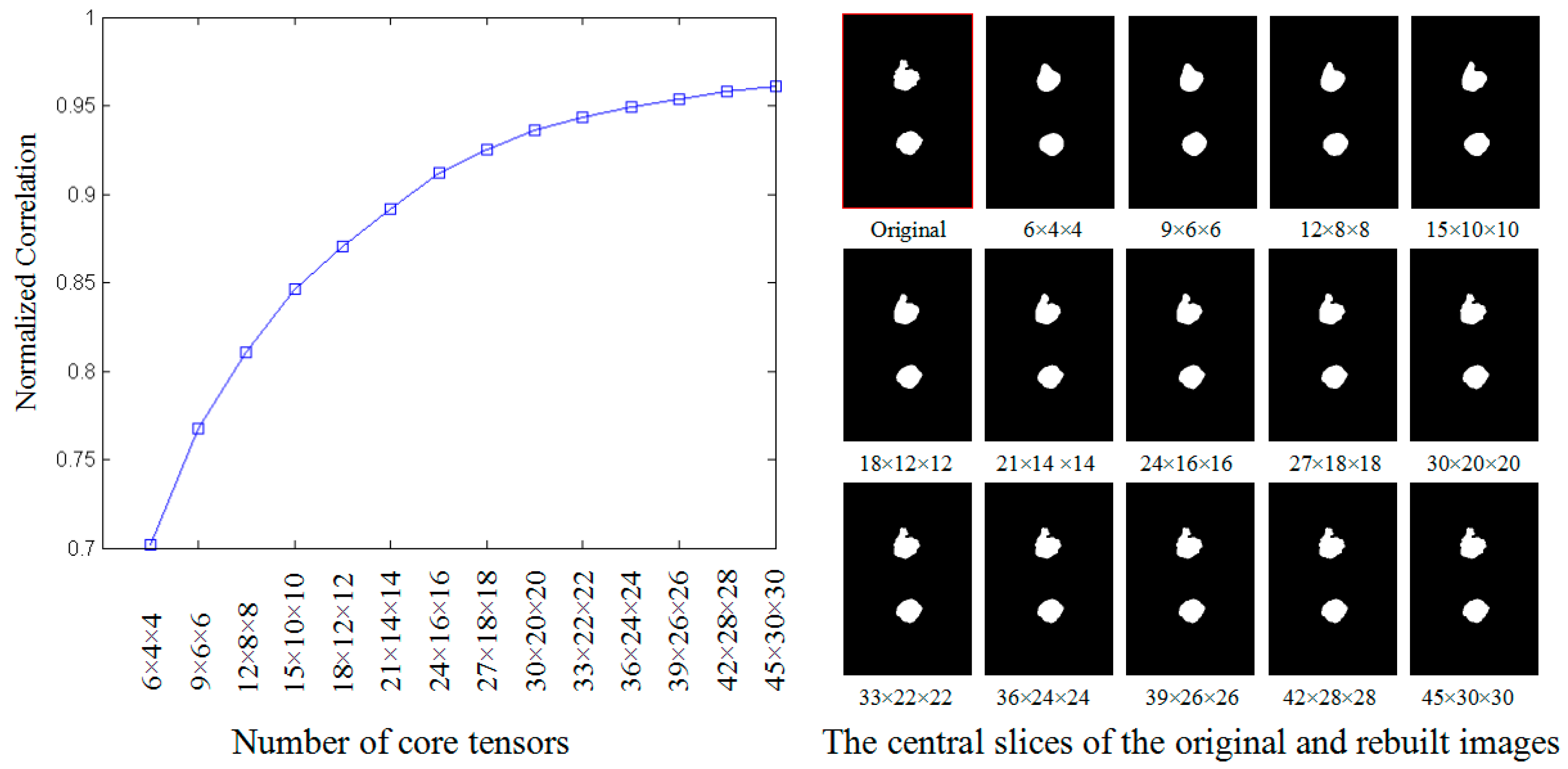
3.2.1. Determining the Size of Core Tensors
- (1)
- project all decentralized WT nuclear images , , to core tensors using GND-PCA, and save three projective matrices , , and ;
- (2)
- use the core tensors and , , and to rebuild WT nuclear images , ;
- (3)
- compare the similarity between and , .
3.2.2. Using GND-PCA Extracting Features
3.2.3. Sorting and Selecting by ‘Energy’
3.2.4. Building Base Images
3.2.5. Geometric Meaning of Selected Bases
3.3. Geometric Meaning of Bases
4. Statistical Test
4.1. Preparing RNAi Embryos
- (1)
- Use image segmentation to obtain embryonic boundaries;
- (2)
- Compute AX-axes according to the segmented boundaries;
- (3)
- Build interpolated nuclear images according to the original coordinates of nuclear image voxels;
- (4)
- Register the interpolated nuclear images based on the computed AP-axes;
- (5)
- Standardize the length of AP-axes and zoom the nuclear coordinates;
- (6)
- Resample nuclear images to 300 × 200 × 200;
- (7)
- Compute three key time points based on nuclear sphericity;
- (8)
- Decentralize these nuclear images based on computed WT mean image Nucmean.
4.2. Statistical Testing of RNAi Embryos Based on Selected Bases
- (1)
- Compute the mean value of 50 WT projective vectors , , , and ;
- (2)
- Obtain the 50 Euclidean distance between each WT projective vector to , , and build a normal model if they obey a Gaussian distribution (using ks-test to check);
- (3)
- For each projective vector of the 8 RNAi embryos, , compute the Euclidean distance between and and test its abnormality based on the built model.
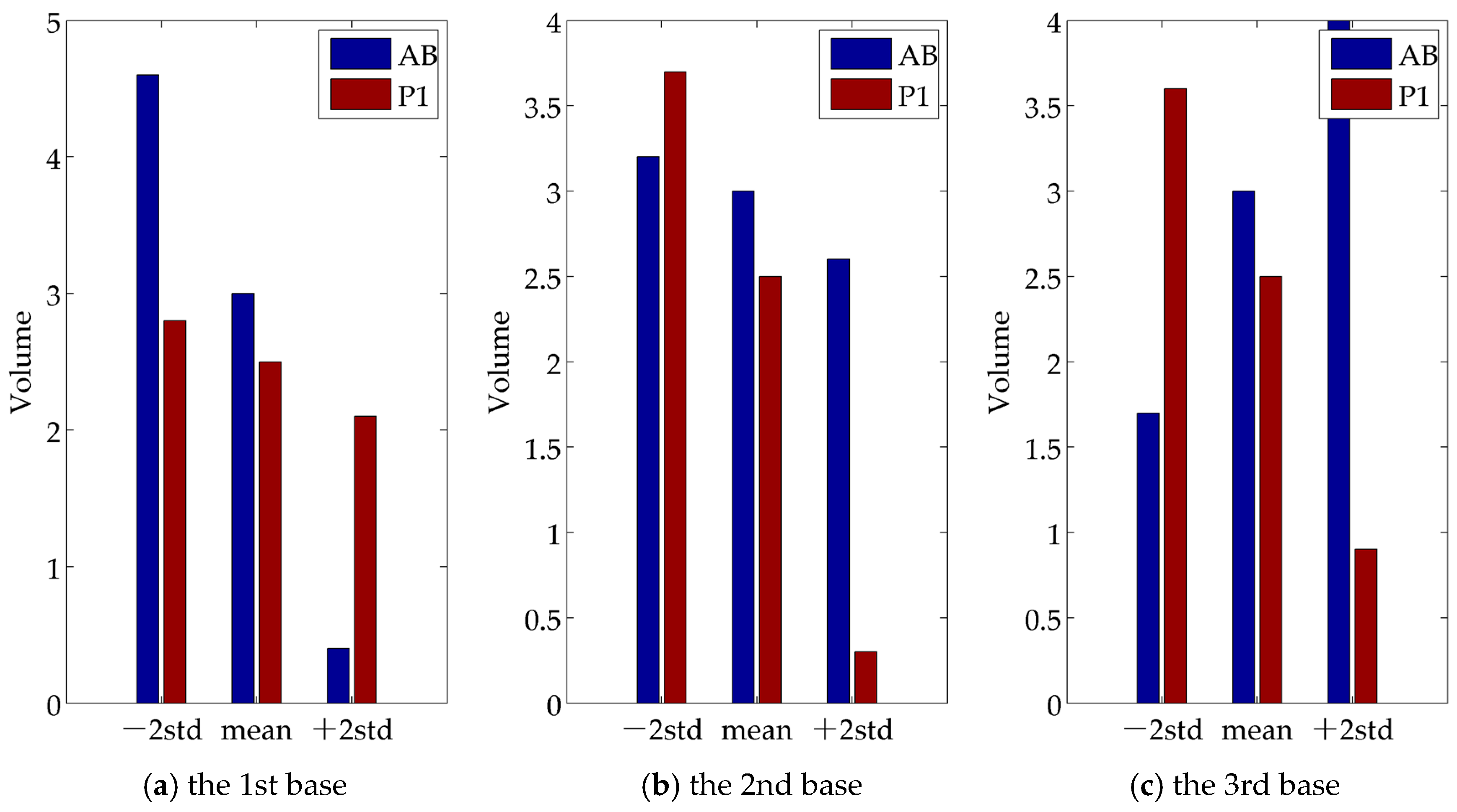
4.3. Comparative Analysis of the Test Results
- (1)
- The first component (its variance proportion is 40.0%) is mainly related to the size difference between P1 and AB. RNAi samples on lect-754, par-2, par-3, and dcn-1 are tested as abnormal;
- (2)
- The second component (its variance proportion is 20.4%) is mainly involved in the variation of the size difference. RNAi samples on dcn-1, mcm-5, and lect-754 tested abnormal;
- (3)
- The third component (its variance proportion is 11.6%) is mainly associated with the shape difference. RNAi samples on dcn-1, par-2, and par-3 tested abnormal.
- (1)
- GND-PCA correctly recognizes that the size difference between P1 and AB is an important phenomenon in the development of C. elegans. The three leading bases are all related to it. However, the selected features in [9] are based on expertise, while the computed bases here are purely learned from data;
- (2)
- In [9], lect-754, par-2, par-3, and dcn-1 have been tested to be involved in the size difference between P1 and AB by the first component. However, using the three leading bases, we can precisely point out that lect-754 is probably involved in the reverse change in size between P1 and AB; dcn-1 is mainly related to the development of AB, and par-2 may be associated with the two aspects;
- (3)
- In [9], mcm-5 has been tested to be related to the variation of the size difference between P1 and AB. In this study, it is clear that mcm-5 is vital in the beginning development of both P1 and AB, because after knocking the gene out, both of them could not change their shapes from cylinder to sphere.
5. Conclusions
- (1)
- A multidimensional image analysis system based on the GND-PCA method can effectively reduce data size and automatically extract valuable features. This process requires minimal expert knowledge, but can yield valuable results. For other image datasets with different characteristics, other more effective methods of image segmentation and registration can be chosen, which makes it feasible to use the GND-PCA method for analysis. The advantage makes this method highly practical;
- (2)
- The statistical tests in this paper are only conducted on the first three bases. By analyzing the characteristic images corresponding to the first 10 bases, it can be seen that different bases often correspond to different shape features. Therefore, using GND-PCA enables this method to automatically extract the most informative features according to the characteristics of the datasets themselves. These extracted features are powerful weapons for analyzing these datasets;
- (3)
- The illustration of this study is aimed at a specific issue. However, for a dataset with a labeled subset of samples, the dataset can be used to automatically extract effective features, whereas the labeled samples can be used to automatically screen the extracted features. After that, the selected features can be applied to unlabeled samples. In this way, the applicability of the method will be further enhanced, and this is also a valuable research topic in the future;
- (4)
- It should be pointed out that to effectively apply the method, it is not only necessary to have a certain understanding of the relevant datasets, but also to understand the relevant theories of GND-PCA. These two requirements have certain limitations on the application of this method.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aung, N.; Vargas, J.D.; Yang, C.; Cabrera, C.P.; Warren, H.R.; Fung, K.; Tzanis, E.; Barnes, M.R.; Rotter, J.I.; Taylor, K.D.; et al. Genome-wide analysis of left ventricular image-derived phenotypes identifies fourteen loci associated with cardiac morphogenesis and heart failure development. Circulation 2019, 140, 1318–1330. [Google Scholar] [CrossRef]
- Ashrafi, K.; Chang, F.Y.; Watts, J.L.; Fraser, A.G.; Kamath, R.S.; Ahringer, J.; Ruvkun, G. Genome-wide RNAi analysis of Caenorhabditis elegans fat regulatory genes. Nature 2003, 421, 268–272. [Google Scholar] [CrossRef] [PubMed]
- Bonazzola, R.; Ravikumar, N.; Attar, R.; Ferrante, E.; Syeda-Mahmood, T.; Frangi, A.F. Image-derived phenotype extraction for genetic discovery via unsupervised deep learning in CMR images. In Proceedings of the MICCAI, Strasbourg, France, 27 September–1 October 2021. [Google Scholar]
- Bai, J.; Binari, R.; Ni, J.; Vijayakanthan, M.; Li, H.-S.; Perrimon, N. RNA interference screening in Drosophila primary cells for genes involved in muscle assembly and maintenance. Development 2008, 135, 1439–1449. [Google Scholar] [CrossRef] [PubMed]
- Imakubo, M.; Takayama, J.; Okada, H.; Onami, S. Statistical image processing quantifies the changes in cytoplasmic texture associated with aging in Caenorhabditis elegans oocytes. BMC Bioinform. 2021, 22, 73. [Google Scholar] [CrossRef] [PubMed]
- Jingjie, H.; Conglie, M.; Yanhai, Y.; Fei, S. A novel method of generating RNAi libraries for high-throughputgene function analysis of creeping bentgrass. Int. Turfgrass Soc. Res. J. 2021, 14, 622–631. [Google Scholar] [CrossRef]
- Narayanaswamy, R.; Niu, W.; Scouras, A.D.; Hart, G.T.; Davies, J.; Ellington, A.D.; Iyer, V.R.; Marcotte, E.M. Systematic profiling of cellular phenotypes with spotted cell microarrays reveals mating-pheromone response genes. Genome Biol. 2006, 7, R6. [Google Scholar] [CrossRef] [PubMed]
- Hamahashi, S.; Kitano, H.; Onami, S. A system for measuring cell division patterns of early Caenorhabditis elegans embryos by using image processing and object tracking. Syst. Comput. Jpn. 2007, 38, 12–24. [Google Scholar] [CrossRef]
- Yang, S.; Han, X.; Tohsato, Y.; Kyoda, K.; Onami, S.; Nishikawa, I.; Chen, Y. Phenotype analysis method for identification of gene functions involved in asymmetric division of Caenorhabditis elegans. J. Comput. Biol. 2017, 24, 436–446. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.; Chen, Y.W. Generalized N-dimensional principal component analysis (GND-PCA) and its application on construction of statistical appearance models for medical volumes with fewer samples. Neurocomputing 2009, 72, 2276–2287. [Google Scholar] [CrossRef]
- Fraser, A.G.; Kamath, R.S.; Zipperlen, P.; Martinez-Campos, M.; Sohrmann, M.; Ahringer, J. Functional genomic analysis of C. elegans chromosome I by systematic RNA interference. Nature 2000, 408, 325–330. [Google Scholar] [CrossRef]
- Sulston, J.E.; Schierenberg, E.; White, J.G.; Thomson, J.N. The embryonic cell lineage of the nematode Caenorhabditis elegans. Dev. Biol. 1983, 100, 64–119. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.; Kemphues, K.J. Par-1, a gene required for establishing polarity in C. elegans embryos, encodes a putative Ser/Thr kinase that is asymmetrically distributed. Cell 1995, 81, 611–620. [Google Scholar] [CrossRef] [PubMed]
- Horvitz, H.R.; Herskowitz, I. Mechanisms of asymmetric cell division: Two Bs or not two Bs, that is the question. Cell 1992, 68, 237–255. [Google Scholar] [CrossRef]
- Betschinger, J.; Knoblich, J. Dare to be different: Asymmetric cell division in Drosophila, C. elegans and vertebrates. Curr. Biol. 2004, 14, R674–R685. [Google Scholar] [CrossRef]
- Gönczy, P. Mechanisms of asymmetric cell division: Flies and worms pave the way. Nat. Rev. Mol. Cell Biol. 2008, 9, 355–366. [Google Scholar] [CrossRef] [PubMed]
- Kemphues, K.J.; Priess, J.R.; Morton, D.G.; Cheng, N. Identification of genes requires for cytoplasmic localization in early C. elegans embryos. Cell 1988, 52, 311–320. [Google Scholar] [CrossRef] [PubMed]
- Cheeks, R.J.; Canman, J.C.; Gabriel, W.N.; Meyer, N.; Strome, S.; Goldstein, B.C. elegans PAR proteins function by mobilizing and stabilizing asymmetrically localized protein complexes. Curr. Biol. 2004, 14, 851–862. [Google Scholar] [CrossRef]
- Sönnichsen, B.; Koski, L.B.; Walsh, A.; Marschall, P.; Neumann, B.; Brehm, M.; Alleaume, A.-M.; Artelt, J.; Bettencourt, P.; Cassin, E.; et al. Full-genome RNAi profiling of early embryogenesis in Caenorhabditis elegans. Nature 2005, 434, 462–469. [Google Scholar] [CrossRef]
- Kyoda, K.; Adachi, E.; Masuda, E.; Nagai, Y.; Suzuki, Y.; Oguro, T.; Urai, M.; Arai, R.; Furukawa, M.; Shimada, K.; et al. WDDD: Worm Developmental Dynamics Database. Nucleic Acids Res. 2013, 41, D732–D737. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Zhang, D.; Frangi, A.F.; Yang, J.-Y. Two-dimensional PCA: A new approach to appearance-based face representation and recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 131–137. [Google Scholar] [CrossRef] [PubMed]
- Kong, H.; Wang, L.; Teoh, E.K.; Li, X.; Wang, J.-G.; Venkateswarlu, R. Generalized 2D principal component analysis for face image representation and recognition. Neural Netw. 2005, 18, 585–594. [Google Scholar] [CrossRef] [PubMed]
- Vasilescu, M.A.; Terzopoulos, D. Multilinear subspace analysis of image ensembles. In Proceedings of the IEEE CVPR, Madison, WI, USA, 16–23 June 2003. [Google Scholar] [CrossRef]
- Tan, S.; Zhang, Y.; Wang, G.; Mou, X.; Cao, G.; Wu, Z.; Yu, H. Tensor-based dictionary learning for dynamic tomographic reconstruction. Phys. Med. Biol. 2015, 60, 2803–2818. [Google Scholar] [CrossRef] [PubMed]
- Qiao, X.; Zhang, X.; Chen, W.; Xu, X.; Chen, Y.-W.; Liu, Z.-P. tensorGSEA: Detecting differential pathways in type 2 diabetes via tensor-based data reconstruction. Interdiscip. Sci. 2022, 14, 520–531. [Google Scholar] [CrossRef] [PubMed]
- Kolda, T.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Yang, S.; Han, X.; Chen, Y.W. Automatic Segmentation of Cellular/Nuclear Boundaries Based on the Shape Index of Image Intensity Surfaces. In Proceedings of the KES International Conference on Innovation in Medicine and Healthcare, Invited Session 03, Vilamoura, Portugal, 21–23 May 2017. [Google Scholar]
- Su, H.; Zhao, D.; Elmannai, H.; Heidari, A.A.; Bourouis, S.; Wu, Z.; Cai, Z.; Gui, W.; Chen, M. Multilevel threshold image segmentation for COVID-19 chest radiography: A framework using horizontal and vertical multiverse optimization. Comput. Biol. Med. 2022, 146, 105618. [Google Scholar] [CrossRef]
- Mandyartha, E.P.; Anggraeny, F.T.; Muttaqin, F.; Akbar, F.A. Global and adaptive thresholding technique for white blood cell image segmentation. J. Phys. Conf. Ser. 2020, 1569, 022054. [Google Scholar] [CrossRef]
- Kim, C.H.; Lee, Y.J. Medical image segmentation by improved 3D adaptive thresholding. In Proceedings of the ICIT, Jeju, Republic of Korea, 28–30 October 2015. [Google Scholar] [CrossRef]
- Jain, A.K.; Zhong, Y.; Dubuisson-Jolly, M. Deformable template models: A review. Signal Process. 1998, 71, 109–129. [Google Scholar] [CrossRef]
- Garrido, A.; Blanca, N.P. Applying deformable templates for cell image segmentation. Pattern Recognit. 2000, 33, 821–832. [Google Scholar] [CrossRef]
- Chowdhary, C.L.; Acharjya, D.P. Segmentation and Feature Extraction in Medical Imaging: A Systematic Review. Proc. Comput. Sci. 2020, 167, 26–36. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Niyas, S.; Pawan, S.J.; Kumar, M.A.; Rajan, J. Medical image segmentation with 3D convolutional neural networks: A survey. Neurocomputing 2022, 493, 397–413. [Google Scholar] [CrossRef]
- Jelli, E.; Ohmura, T.; Netter, N.; Abt, M.; Jiménez-Siebert, E.; Neuhaus, K.; Rode, D.K.H.; Nadell, C.D.; Drescher, K. Single-cell segmentation in bacterial biofilms with an optimized deep learning method enables tracking of cell lineages and measurements of growth rates. Mol. Microbiol. 2023; online ahead of print. [Google Scholar] [CrossRef] [PubMed]
- Greenwald, N.F.; Miller, G.; Moen, E.; Kong, A.; Kagel, A.; Dougherty, T.; Fullaway, C.C.; McIntosh, B.J.; Leow, K.X.; Schwartz, M.S.; et al. Whole-cell segmentation of tissue images with human-level performance using large-scale data annotation and deep learning. Nat. Biotechnol. 2022, 40, 555–565. [Google Scholar] [CrossRef] [PubMed]
- Koenderink, J.J.; Doom, A. Surface shape and curvature scales. Image Vis. Comput. 1992, 10, 557–564. [Google Scholar] [CrossRef]
- Li, Q.; Griffiths, J.G. Least Square Ellipsoid Specific Fitting. In Proceedings of the GMAP, Beijing, China, 13–15 April 2004. [Google Scholar] [CrossRef]
- Wikipedia. Available online: https://en.wikipedia.org/wiki/Sphericity-sphericity (accessed on 20 April 2003).


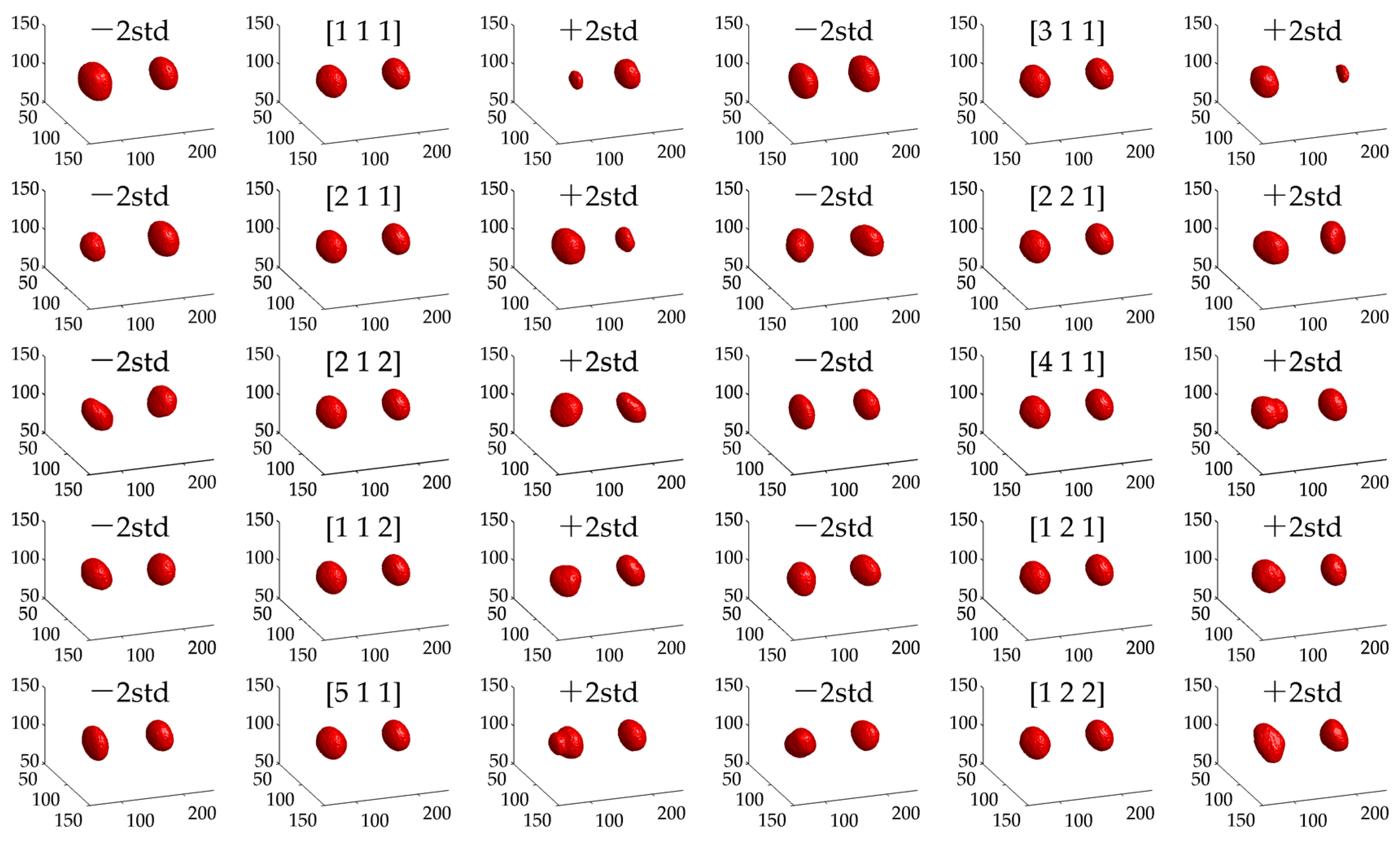
| Ord | (x,y,z) | std | Ord | (x,y,z) | std | Ord | (x,y,z) | std | Ord | (x,y,z) | std |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | (1,1,1) | 52.91 | 6 | (4,1,1) | 24.27 | 11 | (1,3,1) | 19.03 | 16 | (3,1,2) | 16.46 |
| 2 | (3,1,1) | 49.77 | 7 | (1,1,2) | 21.97 | 12 | (1,1,3) | 18.56 | 17 | (6,1,1) | 16.39 |
| 3 | (2,1,1) | 45.79 | 8 | (1,2,1) | 21.61 | 13 | (7,1,1) | 18.23 | 18 | (3,2,2) | 15.94 |
| 4 | (2,2,1) | 32.84 | 9 | (5,1,1) | 20.51 | 14 | (3,2,1) | 17.11 | 19 | (3,3,1) | 15.24 |
| 5 | (2,1,2) | 31.98 | 10 | (1,2,2) | 20.29 | 15 | (3,1,3) | 16.99 | 20 | (8,1,1) | 13.34 |
| Base | Parameters | The CDF of RNAi Embryos 1 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| μ | σ | let-754 | par-3 | par-2 | dcn-1 | ||||||||
| [1,1,1] | 58.04 | −33.13 | 15.62 | 54.68 | 29.52 | 0.609 | 0.208 | 0.255 | 0.965 | 1.000 | 1.000 | 0.982 | 1.000 |
| [3,1,1] | 29.79 | 15.55 | −21.05 | 71.51 | 40.52 | 0.568 | 0.777 | 0.886 | 0.962 | 0.490 | 0.842 | 0.774 | 0.970 |
| [2,1,1] | 48.18 | −23.10 | −27.00 | 56.00 | 28.73 | 0.497 | 0.999 | 0.781 | 0.866 | 0.995 | 0.998 | 0.907 | 0.829 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Han, X.-H.; Chen, Y.-W. GND-PCA Method for Identification of Gene Functions Involved in Asymmetric Division of C. elegans. Mathematics 2023, 11, 2039. https://doi.org/10.3390/math11092039
Yang S, Han X-H, Chen Y-W. GND-PCA Method for Identification of Gene Functions Involved in Asymmetric Division of C. elegans. Mathematics. 2023; 11(9):2039. https://doi.org/10.3390/math11092039
Chicago/Turabian StyleYang, Sihai, Xian-Hua Han, and Yen-Wei Chen. 2023. "GND-PCA Method for Identification of Gene Functions Involved in Asymmetric Division of C. elegans" Mathematics 11, no. 9: 2039. https://doi.org/10.3390/math11092039
APA StyleYang, S., Han, X.-H., & Chen, Y.-W. (2023). GND-PCA Method for Identification of Gene Functions Involved in Asymmetric Division of C. elegans. Mathematics, 11(9), 2039. https://doi.org/10.3390/math11092039






