Diffusion-Induced Instability of the Periodic Solutions in a Reaction-Diffusion Predator-Prey Model with Dormancy of Predators

Abstract

A reaction-diffusion predator-prey model with the dormancy of predators is considered in this paper. We are concerned with the long-time behaviors of the solutions of this system. We divided our investigations into two cases: for the ODEs system, we study the existence and stability of the equilibrium solutions and derive precise conditions on system parameters so that the system can undergo Hopf bifurcations around the positive equilibrium solution. Moreover, the properties of Hopf bifurcation are studied in detail. For the reaction-diffusion system, we are able to derive conditions on the diffusion coefficients so that the spatially homogeneous Hopf bifurcating periodic solutions can undergo diffusion-triggered instability. To support our theoretical analysis, we also include several numerical results.

1. Introduction

Interactions between predator and prey can generate rich dynamics and have engaged numerous investigators’ attention. In the existing literature, the following homogeneous diffusive predator-prey model has been extensively considered:

$$\left\{\begin{array}{cc}{\displaystyle \frac{\partial U}{\partial s}}=D_1\Delta U+AU\left(1-{\displaystyle \frac{U}{N}}\right)-{\displaystyle \frac{BUV}{C+U}},\hfill & x\in \Omega ,s>0,\hfill \\ {\displaystyle \frac{\partial V}{\partial s}}=D_2\Delta V+{\displaystyle \frac{EUV}{C+U}}-FV,\hfill & x\in \Omega ,s>0,\hfill \\ {\displaystyle \frac{\partial U}{\partial \nu }}={\displaystyle \frac{\partial V}{\partial \nu }}=0,\hfill & x\in \partial \Omega ,s\ge 0,\hfill \\ U(x,0)=U\left(x_0\right),V(x,0)=V\left(x_0\right),\hfill & x\in \Omega ,\hfill \end{array}\right.$$

(1)

where $\Omega$ is an open bounded domain in ${\mathbf{R}}^N$ with $N\ge 1$; $\nu$ is the outer unit normal to the boundary $\partial \Omega$, which is assumed to be sufficiently smooth; $U(s,t)$ and $V(s,t)$ are the population densities of the prey and the predator at time s and position $x\in \Omega$, respectively; $D_1$ and $D_2$ are the diffusion coefficients of U and V, respectively; $A,B,C,E,F$ are all of the positive constants; A is the intrinsic growth rate; N is the carrying capacity; B and E are the strength of the relative effect on the two species in the interaction; $U/(C+U)$ is the functional response of the predator to the prey density; C is the “saturation” effect; and F is the death rate of V.

Then, by a non-dimensionalized change of variables (see also [1]):

$$t=As,u={\displaystyle \frac{U}{C}},v={\displaystyle \frac{BV}{EC}},d_1=\frac{D_1}{A},d_2={\displaystyle \frac{D_2}{A}},k=\frac{N}{C},m={\displaystyle \frac{E}{A}},\theta ={\displaystyle \frac{F}{A}},$$

we can reduce the system (1) to the simplified dimensionless form as follows:

$$\left\{\begin{array}{cc}{\displaystyle \frac{\partial u}{\partial t}}=d_1\Delta u+u\left(1-{\displaystyle \frac{u}{k}}\right)-{\displaystyle \frac{muv}{1+u}},\hfill & x\in \Omega ,t>0,\hfill \\ {\displaystyle \frac{\partial v}{\partial t}}=d_2\Delta v+{\displaystyle \frac{muv}{1+u}}-\theta v,\hfill & x\in \Omega ,t>0,\hfill \\ {\displaystyle \frac{\partial u}{\partial \nu }}={\displaystyle \frac{\partial v}{\partial \nu }}=0,\hfill & x\in \partial \Omega ,t\ge 0,\hfill \\ u(x,0)=u\left(x_0\right),v(x,0)=v\left(x_0\right),\hfill & x\in \Omega ,\hfill \end{array}\right.$$

(2)

where u and v are the scaled densities of the prey and predator, respectively; $u(1-u/k)$ is the growth rate of u in the absence of the predator; $\theta$ is the death rate of the predator; $mu/(1+u)$ is the functional response determining the predator’s consumption of the prey’s abundance; k is the fraction of the prey’s biomass, which can be transformed into the predator’s biomass; and $d_1$ and $d_2$ are the diffusion coefficients of u and v, respectively.

System (2) and the like have been studied extensively in the existing literature. For example, for the corresponding ODE system of (2), Hsu [2] showed that the local stability of the positive equilibrium solution can also indicate its global asymptotic stability. In [3], Hsu and Shi studied the relaxation oscillations of (2), while in [4], Cheng observed that the periodic solution of the ODEs in system (2) is unique and stable. For the reaction-diffusion system of system (2), in [5], Ko and Ryu not only studied the existence of non-constant positive equilibrium solutions but also investigated the local existence of periodic solutions. In [1], Yi, Wei, and Shi performed steady-state bifurcation and Hopf bifurcation analysis of the system. In [6], Peng and Shi considered global steady-state bifurcations of the system, and their results proved that the global bifurcation of steady-state solutions comprises bounded loops.

In this paper, we mainly consider the following reaction-diffusion predator-prey system with dormancy:

$$\left\{\begin{array}{cc}{\displaystyle \frac{\partial u}{\partial t}}=d_1\Delta u+u\left(1-{\displaystyle \frac{u}{k}}\right)-{\displaystyle \frac{muv}{1+u}},\hfill & x\in \Omega ,t>0,\hfill \\ {\displaystyle \frac{\partial v}{\partial t}}=d_2\Delta v+{\displaystyle \frac{\mu muv}{1+u}}+\alpha w-\theta v,\hfill & x\in \Omega ,t>0,\hfill \\ {\displaystyle \frac{\partial w}{\partial t}}=d_3\Delta w+{\displaystyle \frac{(1-\mu )muv}{1+u}}-\alpha w,\hfill & x\in \Omega ,t>0,\hfill \\ {\displaystyle \frac{\partial u}{\partial \nu }}={\displaystyle \frac{\partial v}{\partial \nu }}={\displaystyle \frac{\partial w}{\partial \nu }}=0,\hfill & x\in \partial \Omega ,t\ge 0,\hfill \\ u(x,0)=u\left(x_0\right),v(x,0)=v\left(x_0\right),w(x,0)=w\left(x_0\right),\hfill & x\in \Omega ,\hfill \end{array}\right.$$

(3)

where $\mu \in (0,1)$, $\alpha >0$, $m>0$, $\theta >0$, $d_1>0$, $d_2>0$, and $d_3\ge 0$; w is the predator’ density with a dormant state or resting eggs; $\mu$ and $1-\mu$ denote the proportion of reproduction effects on predators between active and dormant states, respectively; and $\alpha$ stands for the hatching of dormant predators or the average dormancy period.

In [7], Kuwamura showed that the hatching of resting eggs can keep the population dynamics stable when the switching between non-resting and resting eggs is sharp. In [8], Kuwamura, Nakazawa, and Ogawa studied the stationary and oscillatory diffusion-induced instabilities of the constant equilibrium solutions.

For system (3), we are mainly interested in the influence of the dormancy of the predators on the dynamics of the system. In particular, we focus on the diffusion-induced instability of the Hopf bifurcating periodic solutions of the system, which is less understood for this particular model in the existing literature [9,10,11,12,13,14,15,16,17,18]. We shall prove that from suitable conditions on the diffusion rates $d_1,d_2,d_3$, the spatially homogeneous periodic solution can undergo diffusion-induced instability and can induce the new spatiotemporal patterns emerging consequently. We would like to remark that for the system without the dormancy of predators (e.g., system (2)), Yi, Wei, and Shi proposed that under suitable conditions, once the periodic solution is stable with respect to the ODEs, it is still stable with respect to the PDEs; thus, there is no diffusion-induced instability of the periodic solutions. Based on this, we shall present a quite interesting difference between the system with the dormancy of predators and the system without the dormancy of predators.

The rest of this paper is organized in the following way. In Section 2, we consider the dynamics of the ODEs system; in Section 3, we consider the diffusion-induced instability of the periodic solutions bifurcating from Hopf bifurcations; in Section 4, we present some numerical simulations to illustrate our theoretical analysis; and in Section 5, we draw some conclusions.

2. The Dynamical Behaviors of the Kinetic System

In this section, we consider the following kinetic system:

$$\left\{\begin{array}{cc}{\displaystyle \frac{du}{dt}}=u\left(1-{\displaystyle \frac{u}{k}}\right)-{\displaystyle \frac{muv}{1+u}},\hfill & \\ {\displaystyle \frac{dv}{dt}}={\displaystyle \frac{\mu muv}{1+u}}+\alpha w-\theta v,\hfill & \\ {\displaystyle \frac{dw}{dt}}={\displaystyle \frac{(1-\mu )muv}{1+u}}-\alpha w.\hfill & \end{array}\right.$$

(4)

2.1. The Auxiliary System: The Predator-Prey System without Dormancy of Predators

To begin with, we consider the following kinetic system of system (2):

$${\displaystyle \frac{du}{dt}}=u\left(1-{\displaystyle \frac{u}{k}}\right)-{\displaystyle \frac{muv}{1+u}},{\displaystyle \frac{dv}{dt}}={\displaystyle \frac{muv}{1+u}}-\theta v.$$

(5)

System (5) has a trivial solution $(0,0)$, a semi-trivial solution $(k,0)$, and a unique positive equilibrium solution under certain conditions stated below.

We now state the following results on system (5) due to Hsu [2] (see also [1]):

Lemma 1 

([1,2]). The following conclusions hold true:

1. 

Suppose that either $m\le \theta$ or ${\displaystyle \frac{mk}{1+k}}\le \theta <m$ holds. Then, system (5) has no positive equilibrium solutions; in this case, $(0,0)$ is unstable, while $(k,0)$ is globally asymptotically stable;

2. 

Suppose that ${\displaystyle \frac{mk}{1+k}}>\theta$ holds. Then, system (5) has a unique positive equilibrium solution $(\tau ,v_{\tau })$, where

$$\tau :={\displaystyle \frac{\theta }{m-\theta }},v_{\tau }:={\displaystyle \frac{\tau (k-\tau )}{k\theta }}.$$

(6)

In this case, both $(0,0)$ and $(k,0)$ are unstable, $(\tau ,v_{\tau })$ is globally asymptotically stable if either $0<k\le 1$ and $\tau \in (0,k)$ or $k>1$ and $\tau \in \left({\displaystyle \frac{k-1}{2}},k\right)$ holds, while $(\tau ,v_{\tau })$ is unstable if $k>1$ and $\lambda \in \left(0,{\displaystyle \frac{k-1}{2}}\right)$. In particular, the loss of the stability of $(\tau ,v_{\tau })$ leads to a Hopf bifurcation at $\tau ={\displaystyle \frac{k-1}{2}}$.

2.2. The Predator-Prey Model with Dormancy of Predators

In this subsection, we study the predator-prey system with dormancy, which is system (4). Clearly, system (4) has $(0,0,0)$ and $(k,0,0)$ as its equilibrium solutions. We have the following results:

Theorem 1. 

The following conclusions hold true:

1. 

$(0,0,0)$ is always unstable in (4).

2. 

$(k,0,0)$ is locally asymptotically stable in (4) when $\theta >{\displaystyle \frac{mk}{1+k}}$, while it is unstable when $\theta <{\displaystyle \frac{mk}{1+k}}$.

Proof. 

The Jacobian matrix of system (4) evaluated at $(0,0,0)$ is given by

$$J(0,0,0):=\left[\begin{array}{ccc}1& 0& 0\\ 0& -\theta & \alpha \\ 0& 0& -\alpha \end{array}\right],$$

which has three eigenvalues: ${\beta }_1=1>0,{\beta }_2=-\theta <0,{\beta }_3=-\alpha <0$. Thus, $(0,0,0)$ is unstable with respect to (4).

The Jacobian matrix of system (4) evaluated at $(k,0,0)$ is given by

$$J(k,0,0):=\left[\begin{array}{ccc}-1& -{\displaystyle \frac{mk}{1+k}}& 0\\ 0& {\displaystyle \frac{\mu mk}{1+k}}-\theta & \alpha \\ 0& {\displaystyle \frac{mk(1-\mu )}{1+k}}& -\alpha \end{array}\right].$$

The characteristic equation of $J_2(k,0,0)$ is given by

$$(\beta +1)\left[{\beta }^2+\left(\alpha -{\displaystyle \frac{\mu mk}{1+k}}+\theta \right)\beta +\alpha \left(\theta -{\displaystyle \frac{mk}{1+k}}\right)\right]=0.$$

(7)

If $\theta >{\displaystyle \frac{mk}{1+k}}$, for $(k,0,0)$, all of the eigenvalues of (7) have negative real parts. Thus, $(k,0,0)$ is stable.

If $\theta <{\displaystyle \frac{mk}{1+k}}<m$, then (7) has a positive eigenvalue. Thus, $(k,0,0)$ is unstable. □

Clearly, if $(\tau ,v_{\tau })$ is a positive equilibrium solution of (5), then $(\tau ,v_{\tau },w_{\tau })$ is a positive equilibrium solution of (4), where

$$\tau :={\displaystyle \frac{\theta }{m-\theta }},v_{\tau }:={\displaystyle \frac{\tau (k-\tau )}{k\theta }},w_{\tau }:={\displaystyle \frac{\tau (1-\mu )(k-\tau )}{k\alpha }}.$$

(8)

Then, by Lemma 1, we have the following results on the existence of positive equilibrium solution of system (4).

Theorem 2. 

Suppose that ${\displaystyle \frac{mk}{1+k}}>\theta$ holds. Then, system (4) has a unique positive equilibrium solution $(\tau ,v_{\tau },w_{\tau })$, which is defined by (8).

Next, we study the stability of $(\tau ,v_{\tau },w_{\tau })$ in system (4).

We choose $\alpha$ as the bifurcation parameter. Linearizing system (4) at $(\tau ,v_{\tau },w_{\tau })$, we obtain its Jacobian matrix:

$$J\left(\alpha \right):=\left[\begin{array}{ccc}-A& -\theta & 0\\ \mu B& (\mu -1)\theta & \alpha \\ (1-\mu )B& (1-\mu )\theta & -\alpha \end{array}\right],$$

(9)

where

$$A:={\displaystyle \frac{\tau (2\tau +1-k)}{k(1+\tau )}},B:={\displaystyle \frac{k-\tau }{k(1+\tau )}}.$$

(10)

The characteristic equation of $J\left(\alpha \right)$ is

$${\beta }^3+M_2\left(\alpha \right){\beta }^2+M_1\left(\alpha \right)\beta +M_0\left(\alpha \right)=0,$$

(11)

where

$$\begin{array}{cc}\hfill M_0\left(\alpha \right):=\alpha \theta B,M_1\left(\alpha \right):& =A\left(\alpha +(1-\mu )\theta \right)+\mu \theta B,M_2\left(\alpha \right):=\alpha +(1-\mu )\theta +A.\hfill \end{array}$$

(12)

To study the stability of $(\tau ,v_{\tau },w_{\tau })$, by Appendix of [19] (see also Lemma 2 below), we need to know the signs of $M_0\left(\alpha \right)$, $M_1\left(\alpha \right)$, $M_2\left(\alpha \right)$ and $M_2\left(\alpha \right)M_1\left(\alpha \right)-M_0\left(\alpha \right)$.

We make the following assumptions:

(H)

Suppose that either (1): $0<k\le 1$ and $\tau \in (0,k)$ or (2): $k>1$ and $\tau \in \left({\displaystyle \frac{k-1}{2}},k\right)$ holds so that $(\tau ,v_{\tau })$ is stable in system (5).

Under assumption (H), we have $A>0$ and $B>0$. Thus, $M_0\left(\alpha \right)>0$, $M_1\left(\alpha \right)>0$, and $M_2\left(\alpha \right)>0$ for all $\alpha >0$ and $\mu \in (0,1)$.

Thus, to study the stability of $(\tau ,v_{\tau },w_{\tau })$, it remains to study the sign of $M_2\left(\alpha \right)M_1\left(\alpha \right)-M_0\left(\alpha \right)$, which takes the following form:

$$M_2\left(\alpha \right)M_1\left(\alpha \right)-M_0\left(\alpha \right)=A{\alpha }^2+{\rho }_1\alpha +{\rho }_0,$$

(13)

where

$$\begin{array}{cc}\hfill & {\rho }_1:=A^2+\theta (1-\mu )\left[2A-B\right],{\rho }_0:=\theta \left[(1-\mu )\theta +A\right]\left[(1-\mu )A+\mu B\right].\hfill \end{array}$$

(14)

Clearly, under assumption (H), we have ${\rho }_0>0$. We now consider the sign of ${\rho }_1$.

We can check that

$$2A-B={\displaystyle \frac{4{\tau }^2+(3-2k)\tau -k}{k(1+\tau )}},$$

which has a unique positive root, denoted by $\widehat{\tau }$, which is given by

$$\widehat{\tau }:={\displaystyle \frac{2k-3+\sqrt{4k^2+4k+9}}{8}}.$$

(15)

It can be directly checked that

$$\widehat{\tau }\in \left\{\begin{array}{cc}(0,k),\hfill & \mathrm{if}0<k\le 1,\hfill \\ \left({\displaystyle \frac{k-1}{2}},k\right),\hfill & \mathrm{if}k>1.\hfill \end{array}\right.$$

(16)

Clearly, $2A-B<0$ for $\tau \in (0,\widehat{\tau })$, while $2A-B>0$ for $\tau >\widehat{\tau }$.

Then, for any $\tau \in [\widehat{\tau },k)$, $\mu \in (0,1)$ and $\theta >0$, ${\rho }_1>0$. Therefore, for any $\alpha >0$, $M_2\left(\alpha \right)M_1\left(\alpha \right)-M_0\left(\alpha \right)>0$. By Appendix of [19], $(\tau ,v_{\tau },w_{\tau })$ is locally asymptotically stable in system (4).

In what follows, we study the case when $\tau \in ({\tau }_0,\widehat{\tau })$ so that $2A-B<0$, where

$${\tau }_0:=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}0<k\le 1,\hfill \\ {\displaystyle \frac{k-1}{2}},\hfill & \mathrm{if}k>1.\hfill \end{array}\right.$$

(17)

If we regard A and B as the functions of $\tau$, we can check that $A=A\left(\tau \right)$ is increasing and $B=B\left(\tau \right)$ is decreasing in $\tau$. Moreover, $A-B<0$ for $\tau \in ({\tau }_0,\widehat{\tau })$.

One can check that for any $\tau \in ({\tau }_0,\widehat{\tau })$, ${\rho }_1=0$ (resp., ${\rho }_1<0$) is equivalent to

$$\mu =\widehat{\mu }\left(\tau \right):={\displaystyle \frac{A^2}{\theta (2A-B)}}+1,(\mathrm{resp}.,\mu <\widehat{\mu }\left(\tau \right)).$$

(18)

Then, we have

$$\begin{array}{c}\hfill {\widehat{\mu }}^{\prime }\left(\tau \right)={\displaystyle \frac{2A{A}^{\prime }(A-B)+A^2{B}^{\prime }}{\theta {(2A-B)}^2}}<0.\end{array}$$

(19)

When $\tau \to \widehat{\tau }$, $2A-B\to 0^{-}$, $A^2\to A^2\left(\widehat{\tau }\right)\ne 0$, then $\widehat{\mu }\left(\tau \right)\to -\infty$ as $\tau \to \widehat{\tau }$; When $\tau \to {\tau }_0^{+}$, since $A^2\to 0$, $2A-B\ne 0$, we have $\widehat{\mu }\left(\tau \right)\to 1$ as $\tau \to {\tau }_0^{+}$. Then, for any $\tau \in ({\tau }_0,\widehat{\tau })$, we have $\widehat{\mu }\left(\tau \right)\in (-\infty ,1)$. Since ${\widehat{\mu }}^{\prime }\left(\tau \right)<0$, a unique ${\tau }^{*}\in ({\tau }_0,\widehat{\tau })$ exists such that

$$\widehat{\mu }\left(\tau \right)\left\{\begin{array}{cc}\in (0,1),\hfill & \mathrm{if}\tau \in ({\tau }_0,{\tau }^{*}),\hfill \\ =0,\hfill & \mathrm{if}\tau ={\tau }^{*},\hfill \\ \in (-\infty ,0),\hfill & \mathrm{if}\tau \in ({\tau }^{*},\widehat{\tau }).\hfill \end{array}\right.$$

(20)

If $\tau \in [{\tau }^{*},\widehat{\tau })$, then for any $\mu \in (0,1)$, it always holds true that $\mu >\widehat{\mu }\left(\tau \right)$, which means that ${\rho }_1>0$. Thus, $M_2\left(\alpha \right)M_1\left(\alpha \right)-M_0\left(\alpha \right)>0$ for any $\alpha >0$, $(\tau ,v_{\tau },w_{\tau })$ is locally stable in system (4).

If $\tau \in ({\tau }_0,{\tau }^{*})$, then $\widehat{\mu }\left(\tau \right)\in (0,1)$. Therefore, for any $\mu \in (0,1)$, a unique ${\tau }_{\mu }\in ({\tau }_0,{\tau }^{*})$ exists, satisfying

$$\left\{\begin{array}{cc}\widehat{\mu }\left(\tau \right)>\mu ,\hfill & \mathrm{if}\tau \in ({\tau }_0,{\tau }_{\mu }),\hfill \\ \widehat{\mu }\left(\tau \right)=\mu ,\hfill & \mathrm{if}\tau ={\tau }_{\mu },\hfill \\ \widehat{\mu }\left(\tau \right)<\mu ,\hfill & \mathrm{if}\tau \in ({\tau }_{\mu },{\tau }^{*}),\hfill \end{array}\right.$$

(21)

or equivalently

$$\left\{\begin{array}{cc}{\rho }_1<0,\hfill & \mathrm{if}\tau \in ({\tau }_0,{\tau }_{\mu }),\hfill \\ {\rho }_1=0,\hfill & \mathrm{if}\tau ={\tau }_{\mu },\hfill \\ {\rho }_1>0,\hfill & \mathrm{if}\tau \in ({\tau }_{\mu },{\tau }^{*}).\hfill \end{array}\right.$$

Then, for any $\tau \in [{\tau }_{\mu },{\tau }^{*})$, $(\tau ,v_{\tau },w_{\tau })$ is locally stable in system (4).

Next, we assume the case of $\tau \in ({\tau }_0,{\tau }_{\mu })$, in which ${\rho }_1<0$. Regarding $M_2\left(\alpha \right)M_1\left(\alpha \right)-M_0\left(\alpha \right)={\alpha }^2+{\rho }_1\alpha +{\rho }_0$ as the quadratic function $\tau$, we can obtain its discriminant

$$\begin{array}{cc}\hfill {\Delta }_{\alpha }:={\theta }^2{B}^2{\mu }^2+2\theta B(2\theta A-\theta B-A^2)\mu & +A^4-2\theta A^{2}B-4{\theta }^{2}AB+{\theta }^2{B}^2.\hfill \end{array}$$

(22)

Assume that for some $\theta >0$, we have ${\Delta }_{\alpha }<0$. Then, for any $\alpha >0$, we have $M_2\left(\alpha \right)M_1\left(\alpha \right)-M_0\left(\alpha \right)={\alpha }^2+{\rho }_1\alpha +{\rho }_0>0$. Hence, for any $\alpha >0$, $(\tau ,v_{\tau },w_{\tau })$ is locally stable in system (4).

Assume that for some $\theta >0$, we have ${\Delta }_{\alpha }>0$. Then, $M_2\left(\alpha \right)M_1\left(\alpha \right)-M_0\left(\alpha \right)=A{\alpha }^2+{\rho }_1\alpha +{\rho }_0=0$ has two distinct positive solutions given by

$$\begin{array}{cc}\hfill & {\alpha }_1:={\displaystyle \frac{-{\rho }_1-\sqrt{{\Delta }_{\alpha }}}{2A}}>0,{\alpha }_2:={\displaystyle \frac{-{\rho }_1+\sqrt{{\Delta }_{\alpha }}}{2A}}>0.\hfill \end{array}$$

(23)

Thus, for any $\alpha \in (0,{\alpha }_1)\cup ({\alpha }_2,\infty )$, we have $M_2\left(\alpha \right)M_1\left(\alpha \right)-M_0\left(\alpha \right)=A{\alpha }^2+{\rho }_1\alpha +{\rho }_0>0$. Then, $(\tau ,v_{\tau },w_{\tau })$ is locally stable in system (4). While if $\alpha \in ({\alpha }_1,{\alpha }_2)$, we have $M_2\left(\alpha \right)M_1\left(\alpha \right)-M_0\left(\alpha \right)=A{\alpha }^2+{\rho }_1\alpha +{\rho }_0<0$. Then, $(\tau ,v_{\tau },w_{\tau })$ is unstable in system (4).

We are now in the position to state the stability results of $(\tau ,v_{\tau },w_{\tau })$:

Theorem 3. 

Suppose that either $0<k\le 1$ but $\tau \in (0,k)$ or $k>1$ but $\tau \in \left({\displaystyle \frac{k-1}{2}},k\right)$ holds so that $(\tau ,v_{\tau })$ is stable in system (5). Let $\widehat{\tau }$, ${\tau }_0$, ${\tau }^{*}$, and ${\tau }_{\mu }$ be defined in (16), (17), (20) and (21), respectively. Then, we have ${\tau }_0<{\tau }_{\mu }<{\tau }^{*}<\widehat{\tau }<k$. In particular,

1. 

Suppose that $\tau \in ({\tau }_0,{\tau }_{\mu })$ holds. Let ${\Delta }_{\alpha }$ be defined by (22).

(a) 

If, additionally, ${\Delta }_{\alpha }<0$, then for any $\alpha >0$, $(\tau ,v_{\tau },w_{\tau })$ is locally asymptotically stable in system (4);

(b) 

If, additionally, ${\Delta }_{\alpha }>0$, then for any $\alpha \in (0,{\alpha }_1)\cup ({\alpha }_2,+\infty )$, $(\tau ,v_{\tau },w_{\tau })$ is locally asymptotically stable in (4), while for $\alpha \in ({\alpha }_1,{\alpha }_2)$, $(\tau ,v_{\tau },w_{\tau })$ is unstable in system (4).

2. 

Suppose that $\tau \in [{\tau }_{\mu },k)$ holds. Then, for any $\alpha >0$, $(\tau ,v_{\tau },w_{\tau })$ is locally asymptotically stable in system (4).

Remark 1.

1. 

We would like to remark that it is analytically demanding to analyze the sign of ${\Delta }_{\alpha }$. Indeed, we need to resort to numerical simulations to determine when ${\Delta }_{\alpha }>0$ or ${\Delta }_{\alpha }<0$. It is found from numerical simulations that for some θ, we have ${\Delta }_{\alpha }<0$, while for the other θ, ${\Delta }_{\alpha }>0$;

2. 

We assume that either $0<k\le 1$ but $\tau \in (0,k)$ or $k>1$ but $\tau \in \left({\displaystyle \frac{k-1}{2}},k\right)$ holds so that $(\tau ,v_{\tau })$ is stable in system (5). However, for case of 2(b), when $\alpha \in ({\alpha }_1,{\alpha }_2)$, $(\tau ,v_{\tau },w_{\tau })$ is unstable. From this, we can see a difference between the system without dormancy and the system with dormancy.

Theorem 4. 

Suppose that either $0<k\le 1$ but $\tau \in (0,k)$ or $k>1$ but $\tau \in \left({\displaystyle \frac{k-1}{2}},k\right)$ holds, so that $(\tau ,v_{\tau })$ is stable in system (5). Let $\tau \in ({\tau }_0,{\tau }_{\mu })$ and ${\Delta }_{\alpha }>0$ so that ${\alpha }_1$ and ${\alpha }_2$ are well-defined. Then, at $\alpha =\overline{\alpha }$, the Hopf bifurcation around $(\tau ,v_{\tau },w_{\tau })$ occurs. Moreover, at $\alpha =\overline{\alpha }$, the Hopf bifurcating periodic solution is stable and the bifurcation direction is forward if $\mathrm{Re}\left(c_1\left(\overline{\alpha }\right)\right)<0$, while the Hopf bifurcating periodic solution is unstable and the bifurcation direction is backward if $\mathrm{Re}\left(c_1\left(\overline{\alpha }\right)\right)>0$, where $\overline{\alpha }={\alpha }_1$ or ${\alpha }_2$, and $\mathrm{Re}\left(c_1\left(\overline{\alpha }\right)\right)$ is defined by (26).

Proof. 

1. The proof of the existence of Hopf bifurcations at $\alpha ={\alpha }_1$ and ${\alpha }_2$. By the aforementioned analysis, at $\alpha ={\alpha }_1$ and ${\alpha }_2$, we have $M_2\left(\alpha \right)M_1\left(\alpha \right)-M_0\left(\alpha \right)=0$. Thus, at $\alpha ={\alpha }_1$ and ${\alpha }_2$, the eigenvalue problem has a pair of purely imaginary roots and a negative root. Furthermore, according to Theorem 3, we have

$$\begin{array}{c}\hfill M_1^{\prime }\left({\overline{\alpha }}_1\right)M_2\left({\overline{\alpha }}_1\right)+M_1\left({\overline{\alpha }}_1\right)M_2^{\prime }\left({\overline{\alpha }}_1\right)-M_0^{\prime }\left({\overline{\alpha }}_1\right)<0,\\ \hfill M_1^{\prime }\left({\overline{\alpha }}_2\right)M_2\left({\overline{\alpha }}_2\right)+M_1\left({\overline{\alpha }}_2\right)M_2^{\prime }\left({\overline{\alpha }}_2\right)-M_0^{\prime }\left({\overline{\alpha }}_2\right)>0.\end{array}$$

Therefore, by the Hopf bifurcation theorem, at $\alpha ={\alpha }_1$ and ${\alpha }_2$, the Hopf bifurcation around $(\tau ,v_{\tau },w_{\tau })$ occurs.

2. Now, we derive conditions to determine the bifurcation direction and the stability of the periodic solutions.

By Theorem A.1 of [19] (or see also Lemma 2 below), the bifurcation direction (forward or backward) and the stability/instability of the periodic solutions can be determined by the sign of $\mathrm{Re}\left(c_1\left(\overline{\alpha }\right)\right)(2\overline{\alpha }A+{\rho }_1)$, where $\overline{\alpha }={\alpha }_1$ or ${\alpha }_2$, and ${\rho }_1$ is defined in (14).

By using the framework of Theorem A.1 of [19], we need to calculate the term $\mathrm{Re}\left(c_1\left(\overline{\alpha }\right)\right)$. To that end, we define the matrix P in the following way:

$$P\left(\alpha \right)=\left(\begin{array}{ccc}1& 0& 1\\ p_{21}& p_{22}& p_{23}\\ p_{31}& p_{32}& p_{33}\end{array}\right),$$

(24)

where

$$\begin{array}{cc}\hfill p_{21}\left(\alpha \right):=& -\frac{A}{\theta },p_{22}\left(\alpha \right):=-\frac{\sqrt{M_1\left(\alpha \right)}}{\theta },p_{23}\left(\alpha \right):=\frac{\alpha +(1-\mu )\theta }{\theta },p_{31}\left(\alpha \right):=\frac{A}{\theta },\hfill \\ \hfill p_{32}\left(\alpha \right):=& \frac{\sqrt{M_1\left(\alpha \right)}(A-\theta (1-\mu ))}{\alpha \theta },p_{33}\left(\alpha \right):=-\frac{(\alpha +(1-\mu \left)\theta \right)(A+\alpha )+\mu \theta B}{\alpha \theta }.\hfill \end{array}$$

Then, we can calculate

$$\begin{array}{cc}\hfill h_1(\alpha ,y_1,y_2,y_3)=& \frac{\left(p_{22}{p}_{33}-p_{23}{p}_{32}\right)g_1+p_{32}{g}_2-p_{22}{g}_3}{det\left(P\right)},\hfill \\ \hfill h_2(\alpha ,y_1,y_2,y_3)=& \frac{\left(p_{31}{p}_{23}-p_{21}{p}_{33}\right)g_1+\left(p_{33}-p_{31}\right)g_2+\left(p_{21}-p_{23}\right)g_3}{det\left(P\right)},\hfill \\ \hfill h_3(\alpha ,y_1,y_2,y_3)=& \frac{\left(p_{21}{p}_{32}-p_{22}{p}_{31}\right)g_1-p_{32}{g}_2+p_{22}{g}_3}{det\left(P\right)},\hfill \end{array}$$

(25)

where the determinant of P denotes as $det\left(P\right)$ and

$$\begin{array}{cc}\hfill g_1:=& \frac{{(y_1+y_3)}^2}{k}-{\displaystyle \frac{m(y_1+y_3)(p_{21}{y}_1+p_{22}{y}_2+p_{23}{y}_3)}{1+y_1+y_3}},\hfill \\ \hfill g_2:=& \frac{\mu m(y_1+y_3)(p_{21}{y}_1+p_{22}{y}_2+p_{23}{y}_3)}{1+y_1+y_3},\hfill \\ \hfill g_3:=& \frac{(1-\mu )m(y_1+y_3)(p_{21}{y}_1+p_{22}{y}_2+p_{23}{y}_3)}{1+y_1+y_3},\hfill \end{array}$$

and $y_1,y_2,y_3$ denote the transformation from the variables $u,v,w$. Then, by (A.17) in Appendix of [19], we have

$$\begin{array}{cc}\hfill \mathrm{Re}\left(c_1\left(\overline{\alpha }\right)\right)& ={\displaystyle \frac{1}{16\sqrt{M_1\left(\overline{\alpha }\right)}}}\left({\left(h_1\right)}_{y_1{y}_1}{\left(h_2\right)}_{y_1{y}_1}-{\left(h_1\right)}_{y_1{y}_1}{\left(h_1\right)}_{y_1{y}_2}+{\left(h_2\right)}_{y_1{y}_1}{\left(h_2\right)}_{y_1{y}_2}\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{16}}\left({\left(h_1\right)}_{y_1{y}_1{y}_1}+{\left(h_2\right)}_{y_1{y}_1{y}_2}\right)+{\displaystyle \frac{1}{8M_2\left(\overline{\alpha }\right)}}{\left(h_3\right)}_{y_1{y}_1}\left({\left(h_1\right)}_{y_1{y}_3}+{\left(h_2\right)}_{y_2{y}_3}\right)\hfill \\ \hfill & +{\displaystyle \frac{M_2\left(\overline{\alpha }\right)}{16\left(M_2{\left(\overline{\alpha }\right)}^2+4M_1\left(\overline{\alpha }\right)\right)}}{\left(h_3\right)}_{y_1{y}_1}\left({\left(h_1\right)}_{y_1{y}_3}-{\left(h_2\right)}_{y_2{y}_3}\right)\hfill \\ \hfill & +{\displaystyle \frac{M_2\left(\overline{\alpha }\right)}{8\left(M_2{\left(\overline{\alpha }\right)}^2+4M_1\left(\overline{\alpha }\right)\right)}}{\left(h_3\right)}_{y_1{y}_2}\left({\left(h_1\right)}_{y_2{y}_3}+{\left(h_2\right)}_{y_1{y}_3}\right)\hfill \\ \hfill & +{\displaystyle \frac{\sqrt{M_1\left(\overline{\alpha }\right)}}{8\left(M_2{\left(\overline{\alpha }\right)}^2+4M_1\left(\overline{\alpha }\right)\right)}}{\left(h_3\right)}_{y_1{y}_1}\left({\left(h_2\right)}_{y_1{y}_3}+{\left(h_1\right)}_{y_2{y}_3}\right)\hfill \\ \hfill & -{\displaystyle \frac{\sqrt{M_1\left(\overline{\alpha }\right)}}{4\left(M_2{\left(\overline{\alpha }\right)}^2+4M_1\left(\overline{\alpha }\right)\right)}}{\left(h_3\right)}_{y_1{y}_2}\left({\left(h_1\right)}_{y_1{y}_3}-{\left(h_2\right)}_{y_2{y}_3}\right),\hfill \end{array}$$

(26)

where $h_1$, $h_2$, and $h_3$ are defined in (25).

By Theorem A.1 of [19] (see also Lemma 2 below), we can draw the following conclusions: at $\overline{\alpha }={\alpha }_1$, the bifurcating periodic solution is unstable and the bifurcation occurs for $\alpha \in ({\alpha }_1-ϵ,{\alpha }_1)$ for sufficiently small $ϵ>0$ if $\mathrm{Re}\left(c_1\left({\overline{\alpha }}_1\right)\right)>0$, and the bifurcating periodic solution is stable and the bifurcation occurs for $\alpha \in ({\alpha }_1,{\alpha }_1+ϵ)$ for sufficiently small $ϵ>0$ if $\mathrm{Re}\left(c_1\left({\overline{\alpha }}_1\right)\right)<0$ holds. On the other hand, at $\overline{\alpha }={\alpha }_2$, the bifurcating periodic solution is unstable and the bifurcation occurs for $\alpha \in ({\alpha }_2,{\alpha }_2+ϵ)$ for sufficiently small $ϵ>0$ if $\mathrm{Re}\left(c_1\left({\overline{\alpha }}_2\right)\right)>0$, and the bifurcating periodic solution is stable and the bifurcation occurs for $\alpha \in ({\alpha }_2-ϵ,{\alpha }_2)$ for sufficiently small $ϵ>0$ if $\mathrm{Re}\left(c_1\left({\overline{\alpha }}_2\right)\right)<0$ holds. □

Remark 2.

1. 

It is analytically demanding to obtain a explicit expression of $\mathrm{Re}\left(c_1\left(\overline{\alpha }\right)\right)$, and we shall resort to numerical tools to calculate it in the part of numerical simulations;

2. 

For simplicity, we denote $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$, and P by the Hopf bifurcating periodic solution and its minimum period.

3. Diffusion-Induced Instability of the Bifurcating Periodic Solutions

In this section, we shall consider diffusion-induced instability of the periodic solutions obtained in the last section. About diffusion-induced instability, we can see [20].

3.1. Preliminaries

We recall the following results of [19] on diffusion-induced instability of the bifurcating periodic solutions for the general reaction-diffusion system

$$\left\{\begin{array}{c}\begin{array}{c}\frac{\partial u_1}{\partial t}=d_1\Delta u_1+f_1(\alpha ,u_1,u_2,u_3),x\in \Omega ,t>0,\hfill \\ \frac{\partial u_2}{\partial t}=d_2\Delta u_2+f_2(\alpha ,u_1,u_2,u_3),x\in \Omega ,t>0,\hfill \\ \frac{\partial u_3}{\partial t}=d_3\Delta u_3+f_3(\alpha ,u_1,u_2,u_3),x\in \Omega ,t>0,\hfill \\ {\partial }_{\nu }{u}_1={\partial }_{\nu }{u}_2={\partial }_{\nu }{u}_3=0,x\in \partial \Omega ,\hfill \end{array}\hfill \end{array}\right.$$

(27)

where $f_1,f_2,f_3\in C^3$, and for any $\alpha >0$, $(0,0,0)$ is always the constant equilibrium solution; $d_1>0,d_2>0$, and $d_3>0$; $\Omega :=\{\ell y:y\in {\Omega }_{*}\}$ is star-shaped centered by the origin; $0<\ell <\infty$; and ${\Omega }_{*}$ is a bounded domain in ${\mathbf{R}}^n$ ($n\ge 1$) with sufficiently smooth boundary $\partial {\Omega }_{*}$.

The ODE system of system (27) is given by:

$$\frac{d{u}_1}{dt}=f_1(\alpha ,u_1,u_2,u_3),\frac{d{u}_2}{dt}=f_2(\alpha ,u_1,u_2,u_3),\frac{d{u}_3}{dt}=f_3(\alpha ,u_1,u_2,u_3),$$

(28)

where $f_i$$(i=1,2,3)$ are defined in (27).

The linearized operator of (28) at $(\alpha ,0,0,0)$ can be evaluated as follows:

$${\displaystyle J\left(\alpha \right):=\left(\begin{array}{ccc}{a}_{11}\left(\alpha \right)& a_{12}\left(\alpha \right)& a_{13}\left(\alpha \right)\\ a_{21}\left(\alpha \right)& a_{22}\left(\alpha \right)& a_{23}\left(\alpha \right)\\ a_{31}\left(\alpha \right)& a_{32}\left(\alpha \right)& a_{33}\left(\alpha \right)\end{array}\right),}$$

(29)

where $a_{ij}\left(\alpha \right):=\partial f_i(\alpha ,0,0,0)/\partial u_j$, for $i,j=1,2,3.$ Rewrite the system (28) in the following form:

$$\left(\begin{array}{c}{u}_1^{\prime }\\ u_2^{\prime }\\ u_3^{\prime }\end{array}\right)=J\left(\alpha \right)\left(\begin{array}{c}{u}_1\\ u_2\\ u_3\end{array}\right)+\left(\begin{array}{c}{g}_1(\alpha ,u_1,u_2,u_3)\\ g_2(\alpha ,u_1,u_2,u_3)\\ g_3(\alpha ,u_1,u_2,u_3)\end{array}\right),$$

where ${}^{\prime }:=d/dt$, and for $\delta =1,2,3$,

$$\begin{array}{cc}\hfill g_{\delta }(\alpha ,u_1,u_2,u_3)=& {\displaystyle \frac{1}{2}}\left(\sum _{k=1}^3{\displaystyle \frac{{\partial }^2{f}_{\delta }}{\partial u_k^2}}+2\sum _{1\le i<j\le 3}{\displaystyle \frac{{\partial }^2{f}_{\delta }}{\partial u_i\partial u_j}}\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{6}}\left(\sum _{k=1}^3{\displaystyle \frac{{\partial }^3{f}_{\delta }}{\partial u_k^3}}+3\sum _{1\le i<j\le 3}^3\left({\displaystyle \frac{{\partial }^2{f}_{\delta }}{\partial u_i^2\partial u_j}}+{\displaystyle \frac{{\partial }^2{f}_{\delta }}{\partial u_i\partial u_j^2}}\right)+6{\displaystyle \frac{{\partial }^3{f}_{\delta }}{\partial u_1\partial u_2\partial u_3}}\right)+o,\hfill \end{array}$$

where o is the higher order terms of $g_{\delta }(\alpha ,u_1,u_2,u_3)$.

The eigenvalue problem of $J\left(\alpha \right)$ is governed by the following equation:

$${\mu }^3+M_2\left(\alpha \right){\mu }^2+M_1\left(\alpha \right)\mu +M_0\left(\alpha \right)=0,$$

(30)

where

$$\begin{array}{cc}\hfill M_2\left(\alpha \right):=& -\sum _{i=1}^3{a}_{ii}\left(\alpha \right),M_1\left(\alpha \right):=\sum _{i=1}^3{A}_{ii}\left(\alpha \right),M_0\left(\alpha \right):=-det\left(J\left(\alpha \right)\right),\hfill \end{array}$$

(31)

where $a_{ij}\left(\alpha \right)$ is defined in (29), $A_{ij}\left(\alpha \right)$ represents the algebraic cofactor of $a_{ij}\left(\alpha \right)$, and $det(·)$ is the determinant of a matrix.

In [19], Wang and Yi obtained the following results:

Lemma 2. 

Assume that there exists a positive $\overline{\alpha }$, such that $M_0\left(\overline{\alpha }\right)>0,M_1\left(\overline{\alpha }\right)>0,M_2\left(\overline{\alpha }\right)>0$, and that

$$M_1\left(\overline{\alpha }\right)M_2\left(\overline{\alpha }\right)-M_0\left(\overline{\alpha }\right)=0,M_1\left(\overline{\alpha }\right)M_2^{\prime }\left(\overline{\alpha }\right)+M_1^{\prime }\left(\overline{\alpha }\right)M_2\left(\overline{\alpha }\right)-M_0^{\prime }\left(\overline{\alpha }\right)\ne 0.$$

(32)

Then, we have

1. 

For $\alpha \in (\overline{\alpha },\overline{\alpha }+ϵ)$, the steady state $(0,0,0)$ is locally asymptotically stable, while it is unstable for $\alpha \in (\overline{\alpha }-ϵ,\overline{\alpha })$ provided that

$$M_1\left(\overline{\alpha }\right)M_2^{\prime }\left(\overline{\alpha }\right)+M_1^{\prime }\left(\overline{\alpha }\right)M_2\left(\overline{\alpha }\right)-M_0^{\prime }\left(\overline{\alpha }\right)>0,$$

where $ϵ>0$ is the sufficiently small number.

2. 

For $\alpha \in (\overline{\alpha },\overline{\alpha }+ϵ)$, the steady state $(0,0,0)$ is unstable, while it is locally asymptotically stable for $\alpha \in (\overline{\alpha }-ϵ,\overline{\alpha })$ provided that

$$M_1\left(\overline{\alpha }\right)M_2^{\prime }\left(\overline{\alpha }\right)+M_1^{\prime }\left(\overline{\alpha }\right)M_2\left(\overline{\alpha }\right)-M_0^{\prime }\left(\overline{\alpha }\right)<0,$$

where $ϵ>0$ is the sufficiently small number.

3. 

At $\alpha =\overline{\alpha }$, near $(0,0,0)$, system (28) will experience Hopf bifurcations. The Hopf bifurcating periodic solution is stable if $\mathrm{Re}\left(c_1\left(\overline{\alpha }\right)\right)<0$, while it is unstable if $\mathrm{Re}\left(c_1\left(\overline{\alpha }\right)\right)>0$. The bifurcation direction is backward if

$$\mathrm{Re}\left(c_1\left(\overline{\alpha }\right)\right)\left(M_1\left(\overline{\alpha }\right)M_2^{\prime }\left(\overline{\alpha }\right)+M_1^{\prime }\left(\overline{\alpha }\right)M_2\left(\overline{\alpha }\right)-M_0^{\prime }\left(\overline{\alpha }\right)\right)<0,$$

while the bifurcation direction is forward if

$$\mathrm{Re}\left(c_1\left(\overline{\alpha }\right)\right)\left(M_1\left(\overline{\alpha }\right)M_2^{\prime }\left(\overline{\alpha }\right)+M_1^{\prime }\left(\overline{\alpha }\right)M_2\left(\overline{\alpha }\right)-M_0^{\prime }\left(\overline{\alpha }\right)\right)>0,$$

where $c_1\left(\overline{\alpha }\right)$ denotes the first Lyapunov coefficient and $\mathrm{Re}\left(c_1\left(\overline{\alpha }\right)\right)$ represents the real parts of $c_1\left(\overline{\alpha }\right)$.

Moreover, Wang and Yi [19] also provide conditions on $d_1,d_2,d_3$ so that diffusion-induced instability of the periodic solutions occurs, which methods and theories base on [21,22,23,24,25].

Lemma 3. 

Let α be fixed to be sufficiently close to $\overline{\alpha }$ such that $(u_1^p\left(t\right),u_2^p\left(t\right),u_3^p\left(t\right))$ is a stable bifurcating periodic solution of system (28) described in Lemma 2. Then, $(u_1^p\left(t\right),u_2^p\left(t\right),u_3^p\left(t\right))$ is unstable in system (27) if the constant ℓ is sufficiently large, and

$$\begin{array}{cc}\hfill M_1\left(\overline{\alpha }\right)& \left(\left(a_{11}\left(\overline{\alpha }\right)Q\left(\overline{\alpha }\right)-1\right)d_1+\left(a_{22}\left(\overline{\alpha }\right)Q\left(\overline{\alpha }\right)-1\right)d_2+\left(a_{33}\left(\overline{\alpha }\right)Q\left(\overline{\alpha }\right)-1\right)d_3\right)\hfill \\ \hfill & +\left(M_2\left(\overline{\alpha }\right)Q\left(\overline{\alpha }\right)+1\right)\left(A_{11}\left(\overline{\alpha }\right)d_1+A_{22}\left(\overline{\alpha }\right)d_2+A_{33}\left(\overline{\alpha }\right)d_3\right)>0,\hfill \end{array}$$

(33)

where

$$\begin{array}{cc}\hfill Q\left(\overline{\alpha }\right):=& {\displaystyle \frac{\sqrt{M_1\left(\overline{\alpha }\right)}}{M_1\left(\overline{\alpha }\right)+M_2^2\left(\overline{\alpha }\right)}}{\displaystyle \frac{\mathrm{Im}\left(c_1\left(\overline{\alpha }\right)\right)}{\mathrm{Re}\left(c_1\left(\overline{\alpha }\right)\right)}}-{\displaystyle \frac{M_2\left(\overline{\alpha }\right)}{M_1\left(\overline{\alpha }\right)+M_2^2\left(\overline{\alpha }\right)}}.\hfill \end{array}$$

(34)

3.2. Diffusion-Induced Instability of the Periodic Solutions for Predator-Prey System

In this subsection, we shall utilize the abstract contents in preliminaries to study the diffusion-induced instability of the periodic solution $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$ as defined in Section 2.

Suppose that either (1): $0<k\le 1$ and $\tau \in (0,k)$ or (2): $k>1$ and $\tau \in \left({\displaystyle \frac{k-1}{2}},k\right)$ holds so that $(\tau ,v_{\tau })$ is stable in system (5).

Let $\tau \in ({\tau }_0,{\tau }_{\mu })$ and ${\Delta }_{\alpha }>0$ so that ${\alpha }_1$ and ${\alpha }_2$ are well-defined. Then, at $\alpha ={\alpha }_1$ and $\alpha ={\alpha }_2$, the Hopf bifurcation around $(\tau ,v_{\tau },w_{\tau })$ occurs. Moreover, we assume that $\mathrm{Re}\left(c_1\left({\alpha }_1\right)\right)<0$ (resp., $\mathrm{Re}\left(c_1\left({\alpha }_2\right)\right)<0$) so that the periodic solution which bifurcating from Hopf bifurcating at $({\alpha }_1,\tau ,v_{\tau })$ (resp., $({\alpha }_2,\tau ,v_{\tau })$) is orbitally asymptotically stable.

According to Lemma 3, to study the diffusion-induced instability of the periodic solution $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$, we need to compute $\mathrm{Im}\left(c_1\left(\overline{\alpha }\right)\right)$, where $\overline{\alpha }={\alpha }_1$ or ${\alpha }_2$. Then, by using the method in Appendix of [19], we can obtain

$$\begin{array}{cc}\hfill \mathrm{Im}\left(c_1\left(\overline{\alpha }\right)\right)=& {\displaystyle \frac{1}{32\sqrt{M_1\left(\overline{\alpha }\right)}}}\left({\left(h_1\right)}_{y_1{y}_1}^2-{\left(h_2\right)}_{y_1{y}_1}^2+2{\left(h_1\right)}_{y_1{y}_2}{\left(h_2\right)}_{y_1{y}_1}\right)\hfill \\ \hfill & -{\displaystyle \frac{1}{16\sqrt{M_1\left(\overline{\alpha }\right)}}}\left({\left({\left(h_1\right)}_{y_1{y}_1}+{\left(h_1\right)}_{y_2{y}_2}\right)}^2+{\left({\left(h_2\right)}_{y_1{y}_1}+{\left(h_2\right)}_{y_2{y}_2}\right)}^2\right)\hfill \\ \hfill & -{\displaystyle \frac{1}{96\sqrt{M_1\left(\overline{\alpha }\right)}}}\left({\left({\left(h_1\right)}_{y_1{y}_1}-{\left(h_1\right)}_{y_2{y}_2}-2{\left(h_2\right)}_{y_1{y}_2}\right)}^2+{\left({\left(h_2\right)}_{y_1{y}_1}-{\left(h_2\right)}_{y_2{y}_2}+2{\left(h_1\right)}_{y_1{y}_2}\right)}^2\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{8M_2\left(\overline{\alpha }\right)}}{\left(h_3\right)}_{y_1{y}_1}\left({\left(h_2\right)}_{y_1{y}_3}-{\left(h_1\right)}_{y_2{y}_3}\right)+{\displaystyle \frac{1}{16}}\left({\left(h_2\right)}_{y_1{y}_1{y}_1}-{\left(h_1\right)}_{y_1{y}_1{y}_2}\right)\hfill \\ \hfill & +{\displaystyle \frac{M_2\left(\overline{\alpha }\right)}{16(M_2{\left(\overline{\alpha }\right)}^2+4M_1\left(\overline{\alpha }\right))}}{\left(h_3\right)}_{y_1{y}_1}\left({\left(h_2\right)}_{y_1{y}_3}+{\left(h_1\right)}_{y_2{y}_3}\right)\hfill \\ \hfill & -{\displaystyle \frac{M_2\left(\overline{\alpha }\right)}{8(M_2{\left(\overline{\alpha }\right)}^2+4M_1\left(\overline{\alpha }\right))}}{\left(h_3\right)}_{y_1{y}_2}\left({\left(h_1\right)}_{y_1{y}_3}-{\left(h_2\right)}_{y_2{y}_3}\right)\hfill \\ \hfill & -{\displaystyle \frac{\sqrt{M_1\left(\overline{\alpha }\right)}}{8(M_2{\left(\overline{\alpha }\right)}^2+4M_1\left(\overline{\alpha }\right))}}{\left(h_3\right)}_{y_1{y}_1}\left({\left(h_1\right)}_{y_1{y}_3}+{\left(h_2\right)}_{y_2{y}_3}\right)\hfill \\ \hfill & -{\displaystyle \frac{\sqrt{M_1\left(\overline{\alpha }\right)}}{4(M_2{\left(\overline{\alpha }\right)}^2+4M_1\left(\overline{\alpha }\right))}}{\left(h_3\right)}_{y_1{y}_2}\left({\left(h_2\right)}_{y_1{y}_3}+{\left(h_1\right)}_{y_2{y}_3}\right).\hfill \end{array}$$

(35)

Then, from Lemma 3, we now state our main results.

Theorem 5. 

Let α be fixed to be close to $\overline{\alpha }$, where $\overline{\alpha }={\alpha }_1$ or ${\alpha }_2$, and $\mathrm{Re}\left(c_1\left(\overline{\alpha }\right)\right)<0$ so that $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$ is stable in the kinetic system (4). Then, $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$ is able to experience diffusion-induced instability provided that the constant ℓ is large enough and

$$\begin{array}{cc}\hfill & M_1\left(\overline{\alpha }\right)\left(\left(-AQ\left(\overline{\alpha }\right)-1\right)d_1+\left((\mu -1)\theta Q\left(\overline{\alpha }\right)-1\right)d_2-\left(\overline{\alpha }Q\left(\overline{\alpha }\right)+1\right)d_3\right)\hfill \\ \hfill & +(M_2\left(\overline{\alpha }\right)Q\left(\overline{\alpha }\right)+1)\left(d_{2}A\overline{\alpha }+d_3\theta (A(1-\mu )+\mu B)\right)>0,\hfill \end{array}$$

(36)

where A, B, $M_1\left(\alpha \right)$, $M_2\left(\alpha \right)$ are set in (9) and (11); moreover,

$$\begin{array}{cc}\hfill Q\left(\overline{\alpha }\right):=& {\displaystyle \frac{\sqrt{M_1\left(\overline{\alpha }\right)}}{M_1\left(\overline{\alpha }\right)+M_2{\left(\overline{\alpha }\right)}^2}}{\displaystyle \frac{\mathrm{Im}\left(c_1\left(\overline{\alpha }\right)\right)}{\mathrm{Re}\left(c_1\left(\overline{\alpha }\right)\right)}}-{\displaystyle \frac{M_2\left(\overline{\alpha }\right)}{M_1\left(\overline{\alpha }\right)+M_2{\left(\overline{\alpha }\right)}^2}},\hfill \end{array}$$

where $\mathrm{Re}\left(c_1\left(\overline{\alpha }\right)\right)$ is described in (26).

Remark 3. 

It is analytically demanding to obtain a explicit expression of $\mathrm{Re}\left(c_1\left(\overline{\alpha }\right)\right)$, $\mathrm{Im}\left(c_1\left(\overline{\alpha }\right)\right)$ and $Q\left(\overline{\alpha }\right)$. We shall resort to numerical tools to calculate it in the part of numerical simulations.

4. Numerical Examples

In this section, we present some numerical examples. We divided our numerical simulations into two parts: “larger”$\mu$ ($\mu$ is very close to 1) and “smaller”$\mu$ ($\mu$ is very close to 0).

Case 1 (“larger”$\mu$). We set $m=100$, $\theta =10$, $k=1.1$, and $\mu =0.8$. In this case, we have

$${\overline{\alpha }}_1=8.8542,{\overline{\alpha }}_2=132.771,\mathrm{Re}\left(c_1\left({\overline{\alpha }}_1\right)\right)=-11.6638<0,\mathrm{Re}\left(c_1\left({\overline{\alpha }}_2\right)\right)=-14.3536<0.$$

By Theorem 4, at $\alpha =8.8542$ and $\alpha =132.771$, the supercritical Hopf bifurcation occurs around $(\tau ,v_{\tau },w_{\tau })=(0.1111,0.01,0.1769)$. That is, the bifurcating periodic solution, denoted by $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$, is stable in the ODEs system.

At $\alpha ={\overline{\alpha }}_1=8.8542$,

$$\mathrm{Re}\left(c_1\left({\overline{\alpha }}_1\right)\right)\left(M_1\left({\overline{\alpha }}_1\right)M_2^{\prime }\left({\overline{\alpha }}_1\right)+M_1^{\prime }\left({\overline{\alpha }}_1\right)M_2\left({\overline{\alpha }}_1\right)-M_0^{\prime }\left({\overline{\alpha }}_1\right)\right)<0,$$

which indicates that Hopf bifurcation direction is backward. Set $\alpha =8.7542$, $\Omega =(0,1000)$, $u_0\left(x\right)=\tau +0.001$, $v_0\left(x\right)=v_{\tau }+0.001$, $w_0\left(x\right)=w_{\tau }+0.0001$.

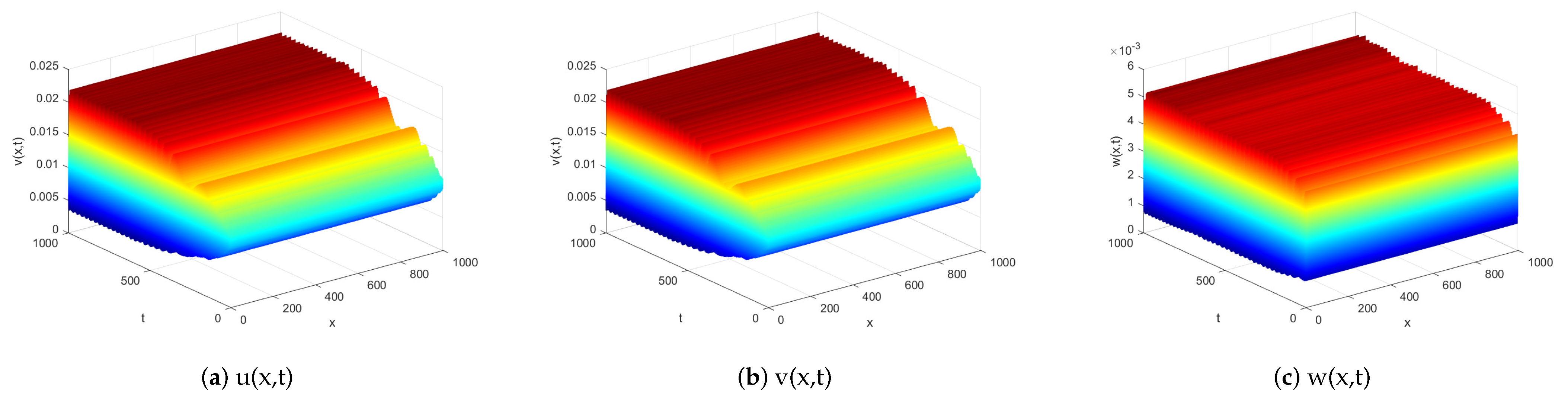
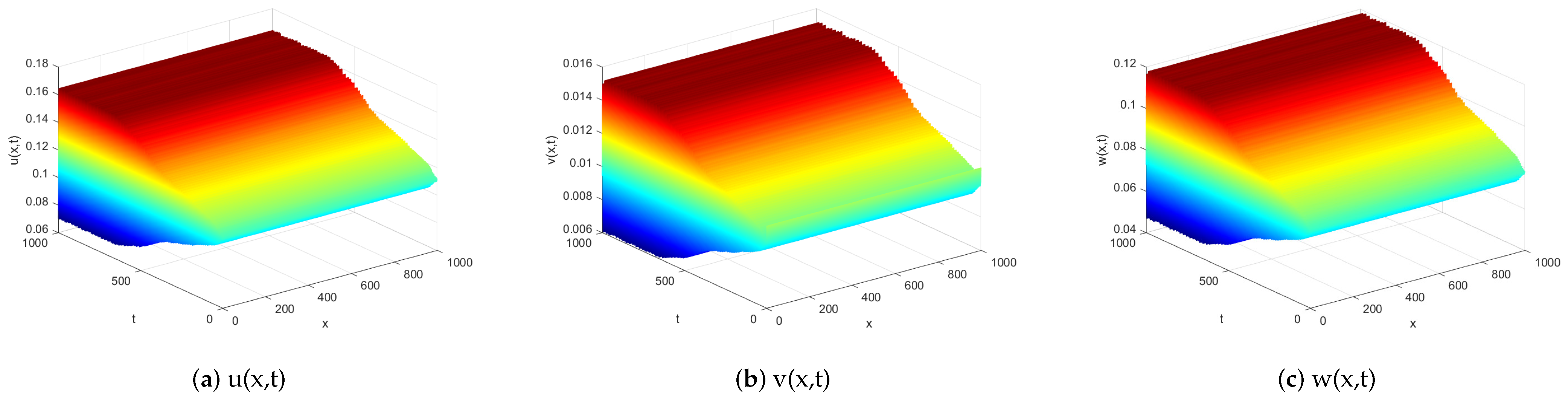
Firstly, we set $d_1=d_2=d_3=1$. Numerical simulation shows that $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$ remains stable in the diffusive system. No diffusion-induced instability of $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$ occurs (see Figure 1).

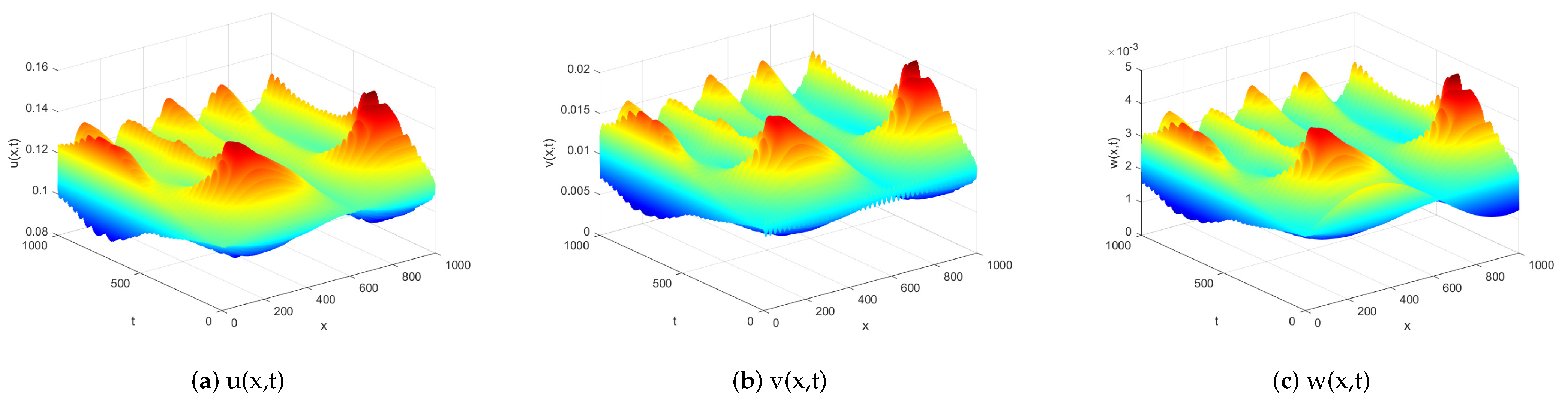
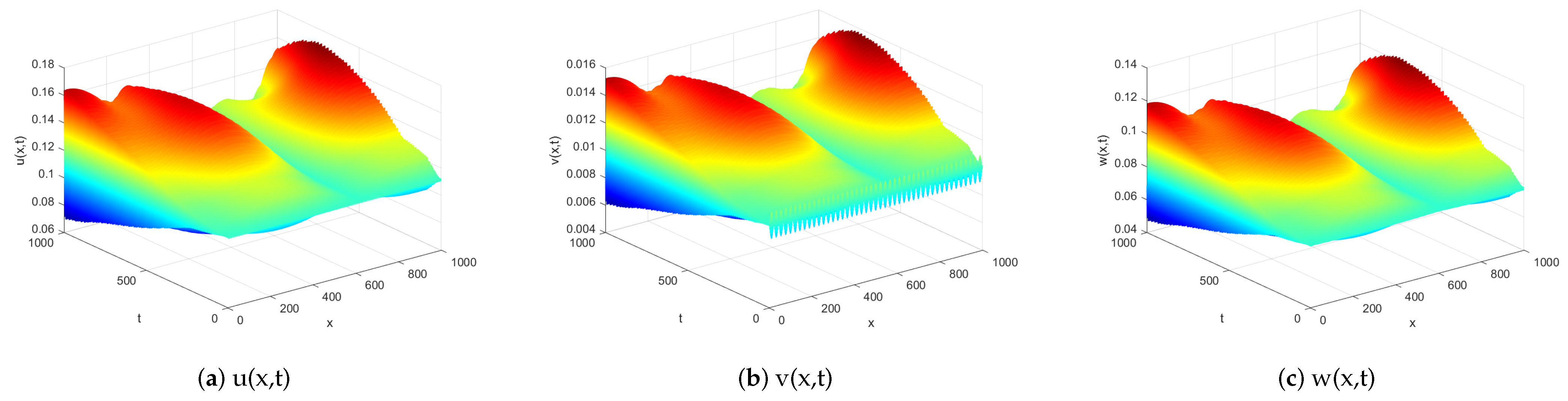
Secondly, we set $d_1=1$, $d_2=5$, $d_3=30$; $\Omega =(0,1000)$; $u_0\left(x\right)=\tau +0.001sin\left(x\right)$, $v_0\left(x\right)=v_{\tau }+0.001sin\left(3x\right)$, $w_0\left(x\right)=w_{\tau }+0.001sin\left(0.005x\right)$. By Theorem 5, $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$ becomes diffusion-induced unstable in diffusive system (3). This is demonstrated by Figure 2.

At $\alpha ={\overline{\alpha }}_2=132.771$, we have

$$\mathrm{Re}\left(c_1\left({\overline{\alpha }}_2\right)\right)\left(M_1\left({\overline{\alpha }}_2\right)M_2^{\prime }\left({\overline{\alpha }}_2\right)+M_1^{\prime }\left({\overline{\alpha }}_2\right)M_2\left({\overline{\alpha }}_2\right)-M_0^{\prime }\left({\overline{\alpha }}_2\right)\right)>0,$$

which implies that the bifurcating direction is forward. Then, we choose $\alpha =132.871$, $\Omega =(0,1000)$, $u_0\left(x\right)=\tau +0.001$, $v_0\left(x\right)=v_{\tau }+0.001$, $w_0\left(x\right)=w_{\tau }+0.0001$. In this case, there is a stable periodic solution in the system (4) and denoted by $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$.

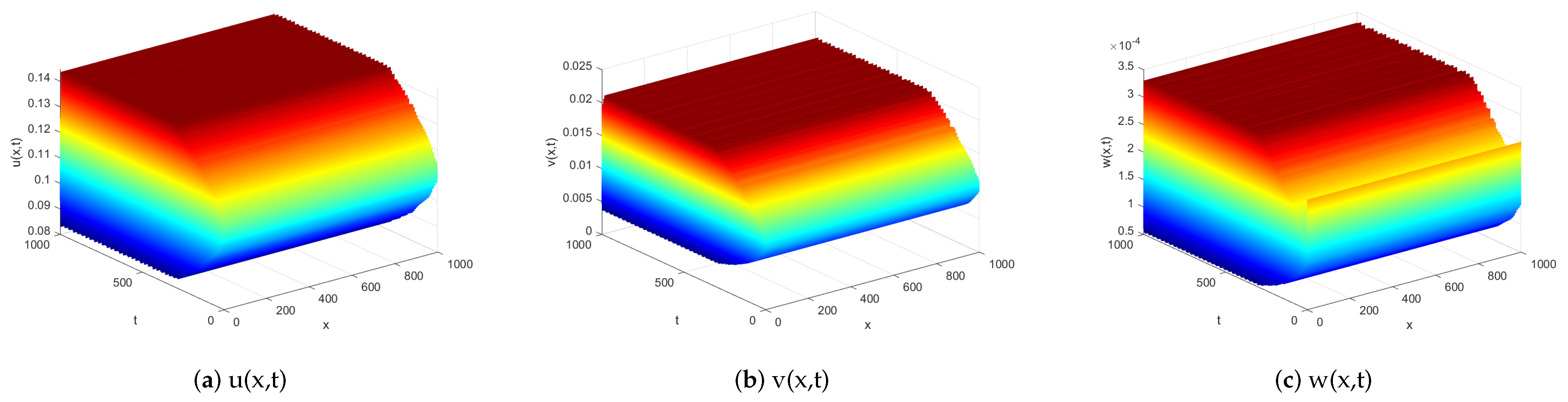
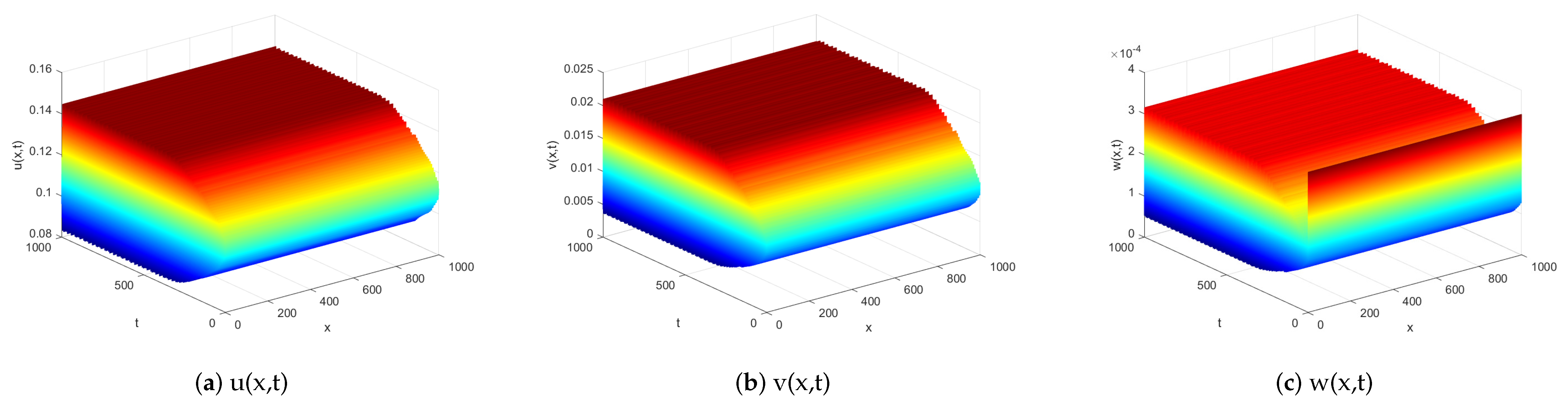
First, we set $d_1=d_2=d_3=1$. $\Omega =(0,1000)$, $u_0\left(x\right)=\tau +0.001sin\left(x\right)$, $v_0\left(x\right)=v_{\tau }+0.001sin\left(3x\right)$, $w_0\left(x\right)=w_{\tau }+0.0001sin\left(0.5x\right)$. In this case, $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$ remains stable in system (3). No diffusion-induced instability of $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$ occurs. This is demonstrated by Figure 3.

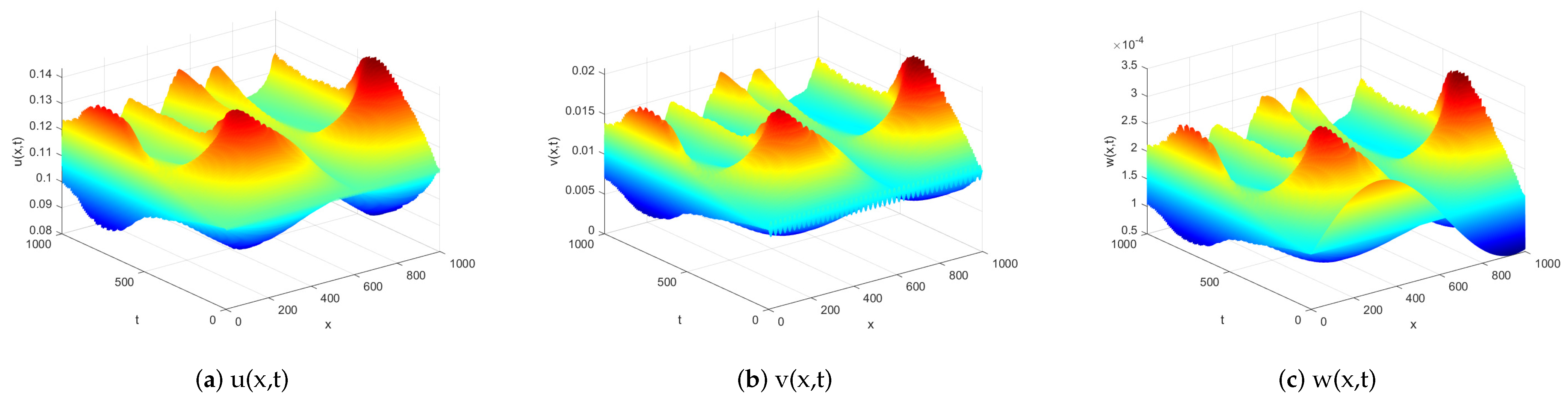
Secondly, we set $d_1=1$, $d_2=5$, $d_3=30$, $\Omega =(0,1000)$, $u_0\left(x\right)=\tau +0.001sin\left(x\right)$, $v_0\left(x\right)=v_{\tau }+0.001sin\left(3x\right)$, $w_0\left(x\right)=w_{\tau }+0.0001sin\left(0.005x\right)$. In this case, by theorem 5, $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$ becomes diffusion-induced unstable in system (3). This is demonstrated by Figure 4.

Case 2 (“smaller”$\mu$). We set $m=100$, $\theta =10$, $k=1.1$ and $\mu =0.1$. In this case, we have

$${\overline{\alpha }}_1=1.1589,{\overline{\alpha }}_2=636.1936,\mathrm{Re}\left(c_1\left({\overline{\alpha }}_1\right)\right)=-0.4907<0,\mathrm{Re}\left(c_1\left({\overline{\alpha }}_2\right)\right)=-14.3536<0.$$

According to Theorem 4, at $\alpha ={\overline{\alpha }}_1$ or $\alpha ={\overline{\alpha }}_2$, the supercritical Hopf bifurcation occurs around $(\tau ,v_{\tau },w_{\tau })=(0.1111,0.01,0.1042)$. That is, the bifurcating periodic solution, denoted by $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$, is asymptotically stable in the ODEs system.

At $\alpha ={\overline{\alpha }}_1=1.1589$,

$$\mathrm{Re}\left(c_1\left({\overline{\alpha }}_1\right)\right)\left(M_1\left({\overline{\alpha }}_1\right)M_2^{\prime }\left({\overline{\alpha }}_1\right)+M_1^{\prime }\left({\overline{\alpha }}_1\right)M_2\left({\overline{\alpha }}_1\right)-M_0^{\prime }\left({\overline{\alpha }}_1\right)\right)<0,$$

which indicates that the Hopf bifurcation direction is backward. Set $\alpha =1.0589$, $\Omega =(0,1000)$, $u_0\left(x\right)=\tau +0.001$, $v_0\left(x\right)=v_{\tau }+0.001$, and $w_0\left(x\right)=w_{\tau }+0.0001$. System (4) has a stable periodic solution, denoted by $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$.

First, we set $d_1=d_2=d_3=1$. $\Omega =(0,1000)$. No diffusion-induced instability of $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$ occurs. This is demonstrated by Figure 5.

Secondly, we set $d_1=1$, $d_2=5$, $d_3=30$. $\Omega =(0,1000)$, and $u_0\left(x\right)=\tau +0.001sin\left(x\right)$, $v_0\left(x\right)=v_{\tau }+0.001sin\left(3x\right)$, $w_0\left(x\right)=w_{\tau }+0.001sin\left(0.005x\right)$. By Theorem 5, $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$ becomes diffusion-induced unstable and the emerging spatiotemporal patterns can be found. This is demonstrated by Figure 6.

At $\alpha ={\overline{\alpha }}_2$, we have

$$\mathrm{Re}\left(c_1\left({\overline{\alpha }}_2\right)\right)\left(M_1\left({\overline{\alpha }}_2\right)M_2^{\prime }\left({\overline{\alpha }}_2\right)+M_1^{\prime }\left({\overline{\alpha }}_2\right)M_2\left({\overline{\alpha }}_2\right)-M_0^{\prime }\left({\overline{\alpha }}_2\right)\right)>0,$$

which confirms that the Hopf bifurcation is forward. We set $\alpha =636.2936$, $\Omega =(0,1000)$, $u_0\left(x\right)=\tau +0.001$, $v_0\left(x\right)=v_{\tau }+0.001$, $w_0\left(x\right)=w_{\tau }+0.0002$. Then, the kinetic system (4) possesses a periodic solution $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$, which is stable.

First, we set $d_1=d_2=d_3=1$. $\Omega =(0,1000)$. The diffusion-induced instability of $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$ cannot be found. This is demonstrated by Figure 7.

Secondly, let $d_1=1$, $d_2=5$, $d_3=30$. $\Omega =(0,1000)$, and $u_0\left(x\right)=\tau +0.001sin\left(x\right)$, $v_0\left(x\right)=v_{\tau }+0.001sin\left(3x\right)$, $w_0\left(x\right)=w_{\tau }+0.001sin\left(0.005x\right)$. By Theorem 5, $(u_p\left(t\right),v_p\left(t\right),w_p\left(t\right))$ becomes diffusion-induced unstable and the emerging spatiotemporal patterns can be observed. This is demonstrated by Figure 8.

5. Concluding Remarks

In this paper, a homogeneous diffusive predator-prey system with the dormancy of predators is mainly considered. It concentrates on the diffusion-induced instability of the Hopf bifurcating periodic solutions.

Without regard to the dormancy effect, the predator-prey system is a system with two components. Motivated by [2,3], we choose the first component $\tau$ of the positive equilibrium solution $(\tau ,v_{\tau })$ as the bifurcation parameter. We assume that the unique positive equilibrium solution of the system (the 2-component predator-prey system) is stable with respect to the corresponding ODEs system, say

$$\mathrm{either}0<k\le 1\mathrm{but}\tau \in (0,k),\mathrm{or}k>1\mathrm{but}\tau \in \left({\displaystyle \frac{k-1}{2}},k\right)$$

holds so that $(\tau ,v_{\tau })$ is stable in system (5). By [2], $(\tau ,v_{\tau })$ is globally asymptotically stable in system (5).

In the presence of the dormancy effect, the predator-prey system becomes a system with 3-components. Our results indicated that for some $\theta$, if ${\Delta }_{\alpha }>0$, then for suitable $\tau$ and $\alpha$ (say, $\tau \in ({\tau }_0,{\tau }_{\mu })$, $\alpha ={\alpha }_1$ and $\alpha ={\alpha }_2$), the ODEs predator-prey system might exhibit temporal oscillations. This suggests that the dormancy effects can favor the emergence of temporal oscillatory patterns. Precisely, the smaller $\mu$ (the modeling the strengthen of the dormancy effect) is, the larger stability range of $\tau$ is. At $\alpha ={\alpha }_1$ and $\alpha ={\alpha }_2$, Hopf bifurcations around $(\tau ,v_{\tau },w_{\tau })$ occur. By calculating the first Lyapunov coefficients, we can derive conditions to determine the stability of the periodic solutions.

When diffusions are introduced into the predator-prey system with dormancy, we can deduce the reaction-diffusion equations with the 3-components system. Referring to the abstract results in [19], we are able to expound some precise conditions on the diffusion coefficients to determine the diffusion-induced instability of the periodic solutions.