Generation and Controllability of High-Dimensional Rogue Waves in an Electromagnetically Induced Transparent Medium
Abstract
1. Introduction
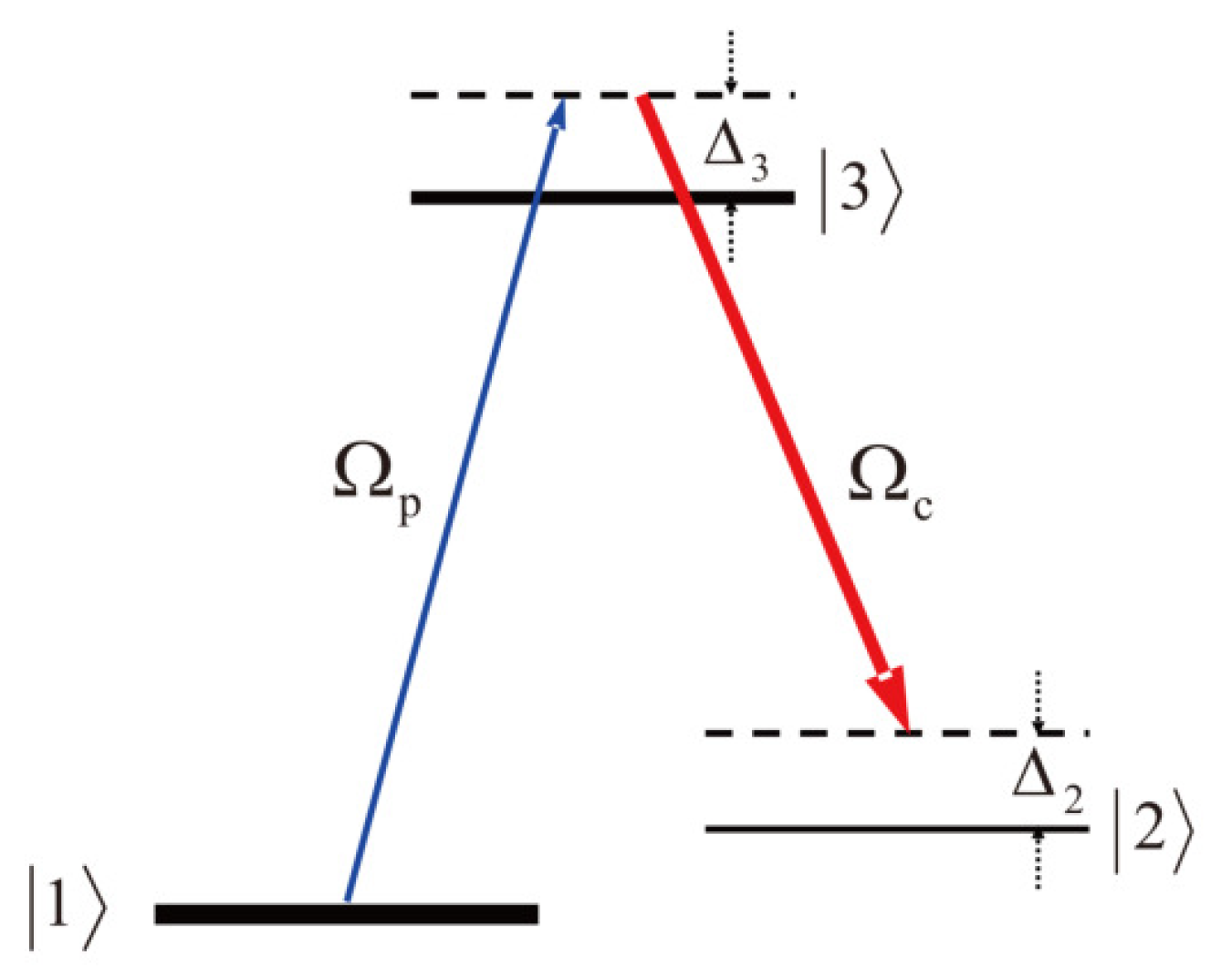
2. Model
3. High-Dimensional Rogue-Wave Solutions
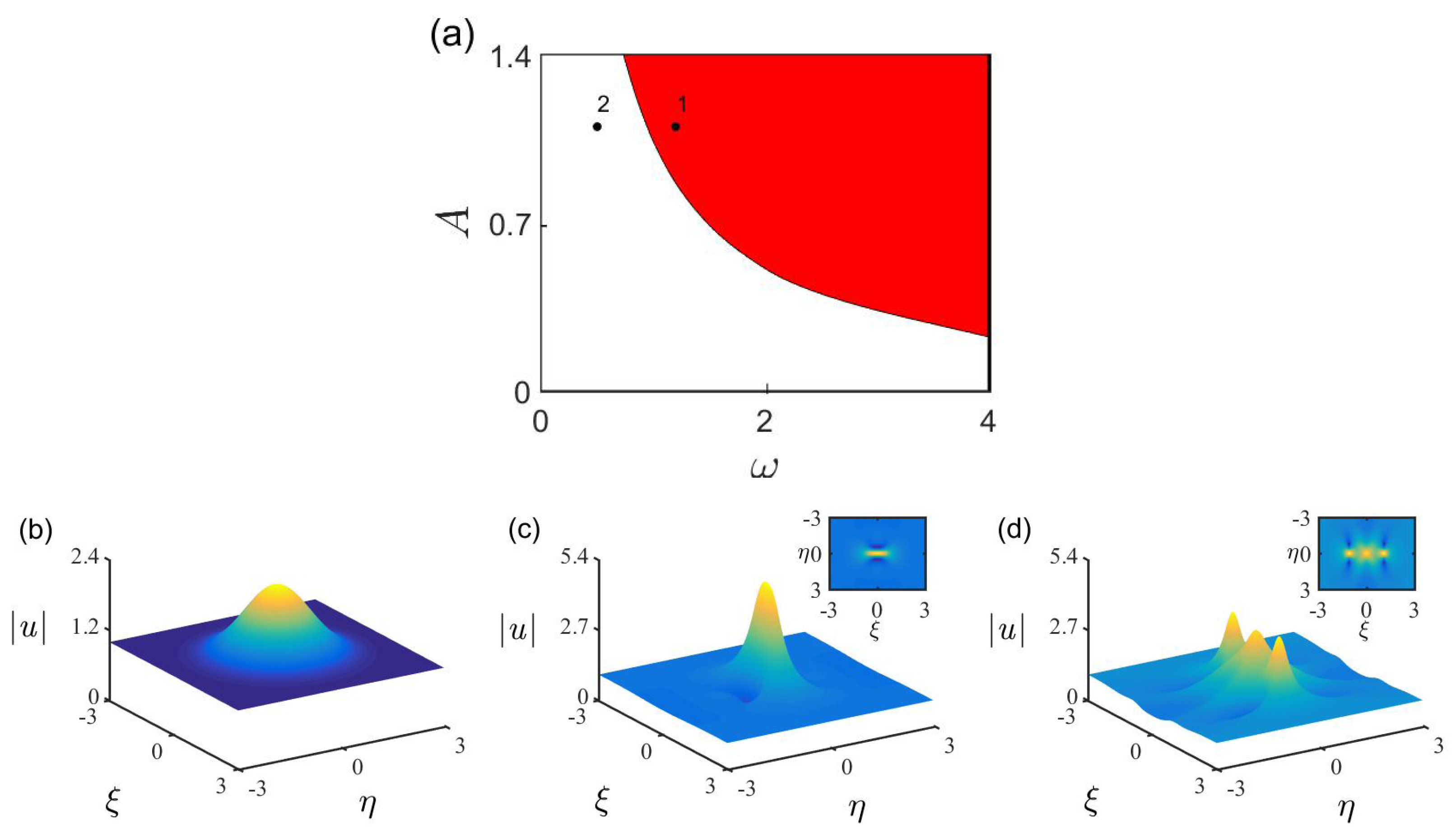
3.1. High-Dimensional Rogue Waves of the Kerr Nonlinear Schrödinger Equation
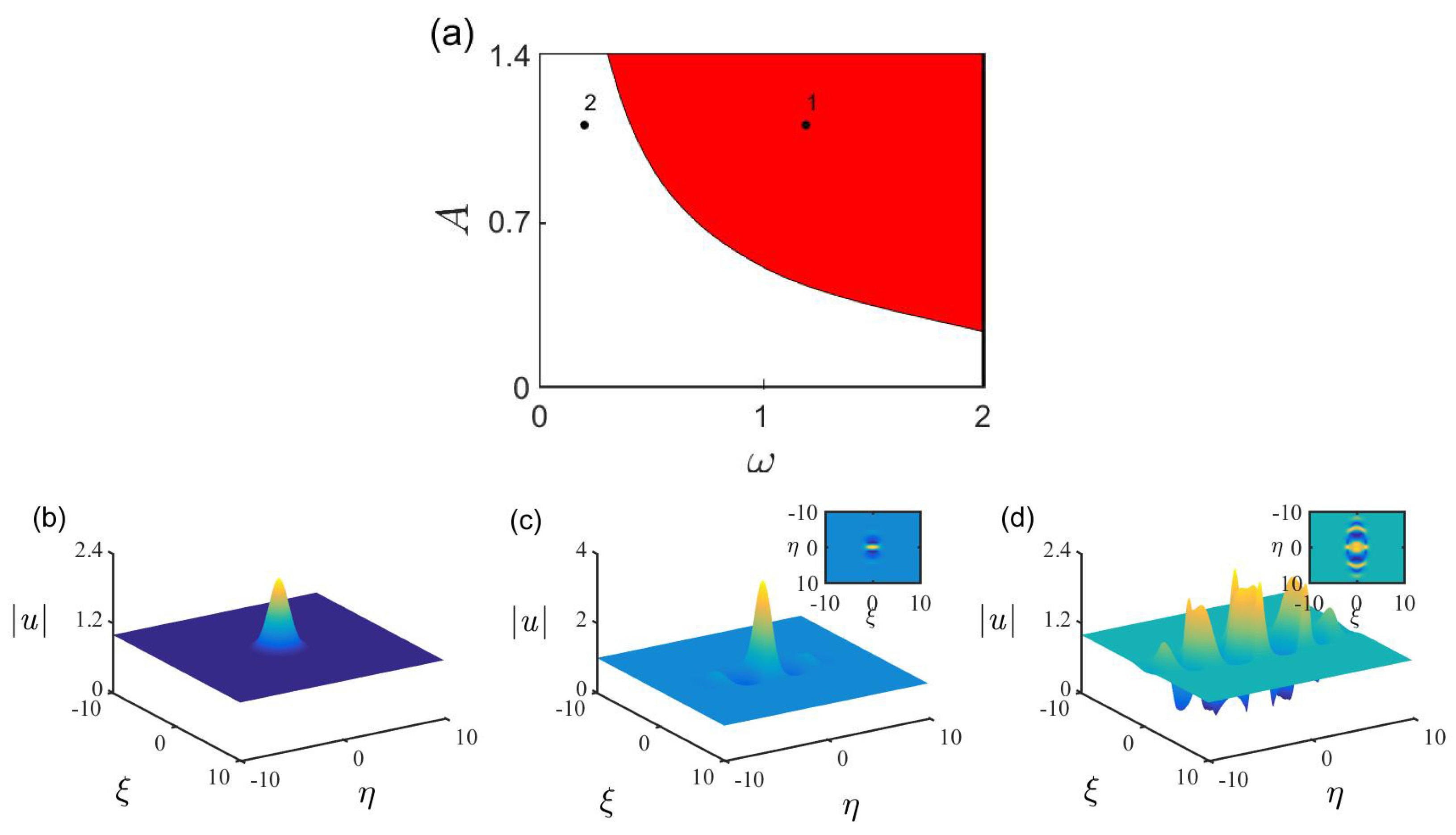
3.2. High-Dimensional Rogue Waves of the SNLSE
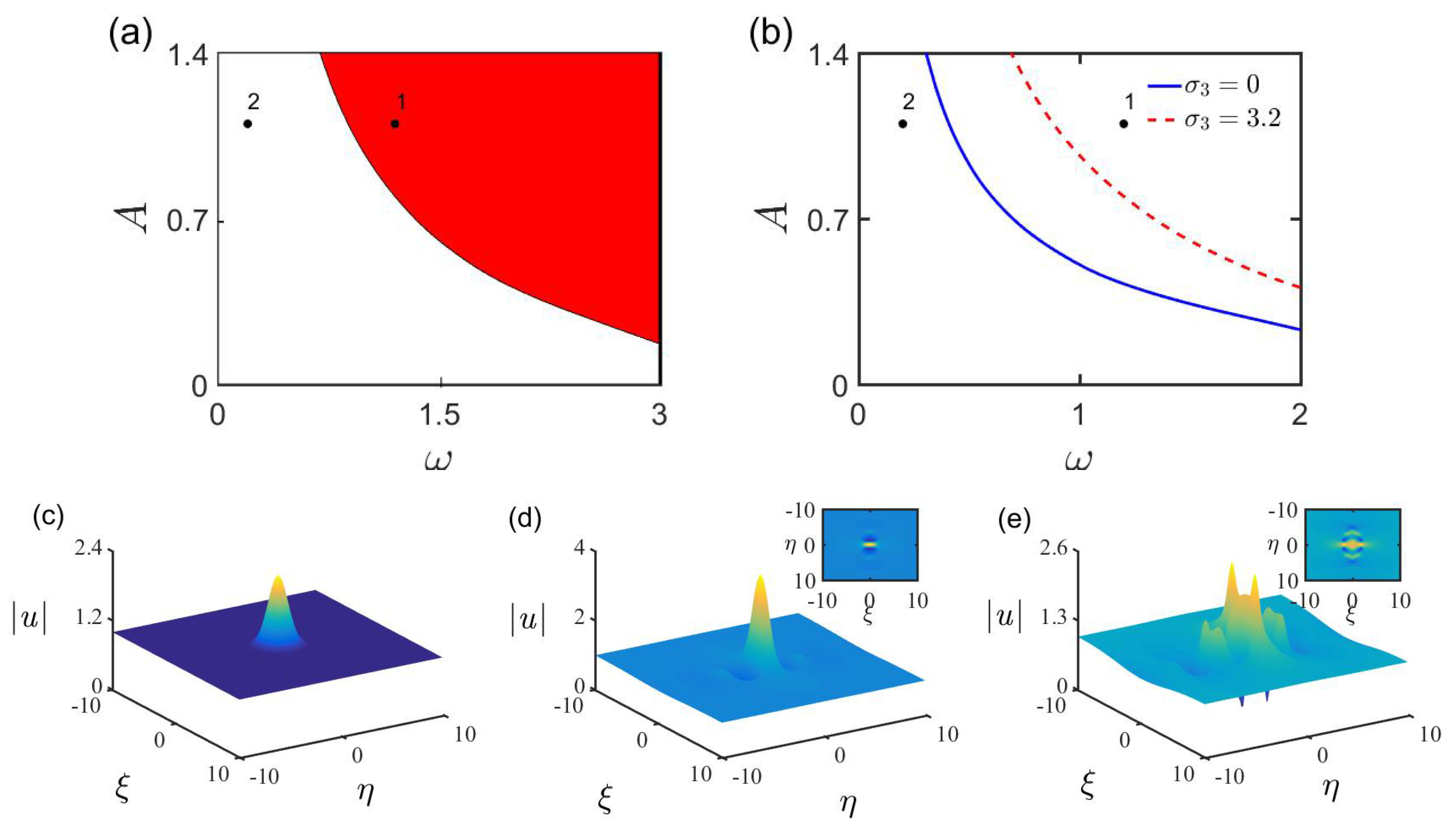
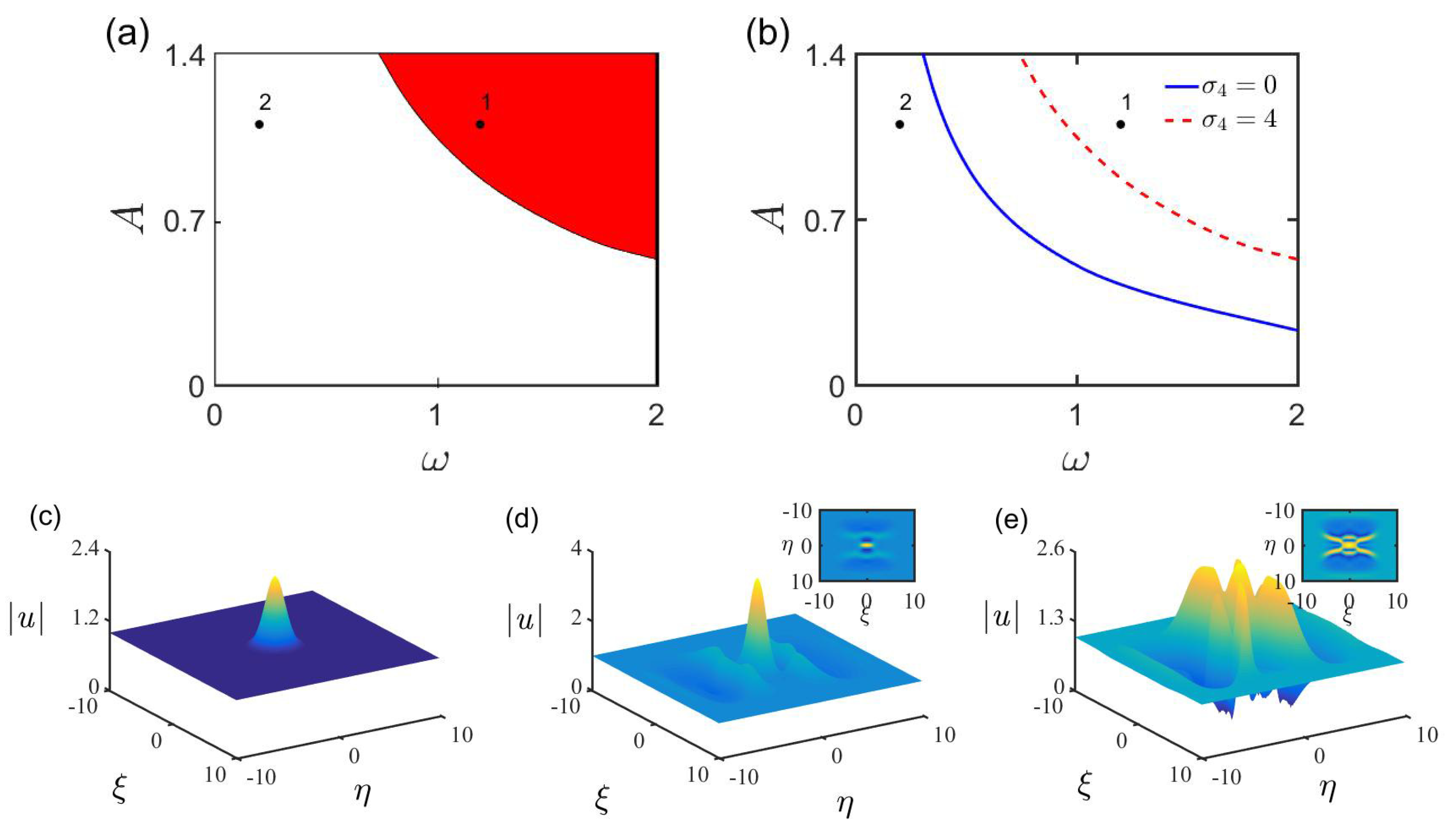
3.3. High-Dimensional Rogue Waves of the SNLSE with the Trapping Potential Contributed by a Far-Detuned (Stark) Optical Lattice Field
3.4. High-Dimensional Rogue Waves of the SNLSE with a Weak Magnetic Field
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Whitemarsh, R.P. Great sea waves. US Naval Inst. Proc. 1934, 60, 1094–1103. [Google Scholar]
- Kharif, C.; Pelinovsky, E.; Slunyaev, A. Rogue waves in the ocean. In Rogue Waves in the Ocean; Springer: Berlin/Heidelberg, Germany, 2009; p. 1. [Google Scholar]
- Kharif, C.; Pelinovsky, E.; Slunyaev, A. Rogue waves in the ocean-review and progress. EOS Trans. Am. Geophys. Union 2010, 91, 104. [Google Scholar]
- Peregrine, D.H.; Austral, J. Water waves, nonlinear Schrödinger equations and their solutions. Math. Soc. Ser. B 1983, 25, 16–43. [Google Scholar] [CrossRef]
- Akhmediev, N.; Soto Crespo, J.M.; Ankiewicz, A. Extreme waves that appear from nowhere: On the nature of rogue waves. Phys. Lett. A 2009, 373, 2137–2145. [Google Scholar] [CrossRef]
- Akhmediev, N.; Eleonskii, V.M.; Kulagin, N.E. Exact first-order solutions of the nonlinear Schrödinger equation. Theor. Math. Phys. 1987, 72, 809–818. [Google Scholar] [CrossRef]
- Kharif, C.; Pelinovshy, E. Physical mechanisms of the rogue wave phenomenon. Eur. J. Mech. B/Fluids 2003, 22, 603–634. [Google Scholar] [CrossRef]
- Onorato, M.; Residori, S.; Bortolozzo, U.; Montina, A.; Arecchi, T.F. Rogue waves and their generating mechanisms in different physical contexts. Arecchi Phys. Rep. 2013, 528, 47–89. [Google Scholar] [CrossRef]
- Akhmediev, N.; Dudley, J.M.; Solli, D.R.; Turitsyn, S.K. Recent progress in investigating optical rogue waves (Review). J. Opt. 2013, 15, 6. [Google Scholar] [CrossRef]
- Dudley, J.M.; Dias, F.; Erkintalo, M.; Genty, G. Instabilities, breathers and rogue waves in optics. Nat. Photon. 2014, 8, 755–764. [Google Scholar] [CrossRef]
- Draper, L. Freak wave. Mar. Obs. 1965, 35, 193–195. [Google Scholar]
- Kjeldsen, S.P. Dangerous wave groups. Nor. Marit. Res. 1984, 12, 4–16. [Google Scholar]
- Diekison, D. Huge waves. In Outside Magazine; W. W. Norton Company: New York, NY, USA, 1995; pp. 3–5. [Google Scholar]
- Lavernov, V. The wave energy concentration at the Agulhas current of South Affica. Nat. Hazards 1998, 17, 117–127. [Google Scholar] [CrossRef]
- Walker, D.A.G.; Taylor, P.H.; Taylor, R.E. The shape of large surface waves on the open sea and the draupner new year wave. Appl. Ocean Res. 2005, 26, 73–83. [Google Scholar] [CrossRef]
- Rosenthal, W.; Lehenr, S. Rogue waves: Results of the max wave project. J. Offshore Mech. Arct. Eng. 2008, 130, 021006. [Google Scholar] [CrossRef]
- Li, Z.Y.; Li, F.F.; Li, H.J. Exciting rogue waves, breathers, and solitons in coherent atomic media. Commun. Theor. Phys. 2020, 72, 075003. [Google Scholar] [CrossRef]
- Li, F.F.; Li, Z.Y.; Li, H.J. Manipulating rogue waves, breathers and solitons in several non-integrable nonlinear Schrödinger equations. Eur. Phys. J. D 2019, 73, 263. [Google Scholar] [CrossRef]
- Solli, D.R.; Ropers, C.; Koonath, P.; Jalali, B. Optical rogue waves. Nature 2007, 450, 1054–1057. [Google Scholar] [CrossRef]
- Kibler, B.; Fatome, J.; Finot, C.; Millot, G.; Dias, F.; Genty, G.; Akhmediev, N.; Dudley, J.M. The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 2010, 6, 790–795. [Google Scholar] [CrossRef]
- Zaviyalov, A.; Egorov, O.; Iliew, R.; Lederer, F. Rogue waves in mode-locked fiber lasers. Phys. Rev. A 2012, 85, 013828. [Google Scholar] [CrossRef]
- Manikandan, K.; Muruganandam, P.; Senthilvelan, M.; Lakshmanan, M. Manipulating matter rogue waves and breathers in Bose-Einstein condensates. Phys. Rev. E 2014, 90, 062905. [Google Scholar] [CrossRef]
- Chen, S.H.; Baronio, F.; Soto-Crespo, J.M.; Grelu, P. Chirped Peregrine solitons in a class of cubic-quintic nonlinear Schrödinger equations. Phys. Rev. E 2016, 93, 062202. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.H.; Ye, Y.L.; Soto-Crespo, J.M.; Grelu, P.; Baronio, F. Peregrine solitons beyond the threefold limit and their two-soliton interactions. Phys. Rev. Lett. 2018, 121, 104101. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Liu, C.; Wang, L. Darboux transformation and rogue wave solutions for the variable-coefficients coupled Hirota equations. J. Math. Appl. 2017, 449, 1534–1552. [Google Scholar] [CrossRef]
- Wang, X.B.; Tian, S.F.; Yan, H.; Zhang, T.T. On the solitary waves, breather waves and rogue waves to a generalized (3 + 1)-dimensional Kadomtsev-Petviashvili equation. Math. Appl. 2017, 74, 556–563. [Google Scholar] [CrossRef]
- Wang, X.B.; Tian, S.F.; Qin, C.Y.; Zhang, T.T. Characteristics of the solitary waves and rogue waves with interaction phenomena in a generalized (3 + 1)-dimensional Kadomtsev-Petviashvili equation. Appl. Math. Lett. 2017, 72, 58–64. [Google Scholar] [CrossRef]
- Li, M.; Shui, J.J.; Xu, T. Generation mechanism of rogue waves for the discrete nonlinear Schrödinger equation. Appl. Math. Lett. 2018, 83, 110–115. [Google Scholar] [CrossRef]
- Wang, X.B.; Zhang, T.T.; Dong, M.J. Dynamics of the breathers and rogue waves in the higher-order nonlinear Schrödinger equation. Appl. Math. Lett. 2018, 86, 298–304. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y.; Tang, X. Rogue wave and a pair of resonance stripe solitons to KP equation. Comput. Math. Appl. 2018, 76, 1938–1949. [Google Scholar] [CrossRef]
- Jia, R.R.; Guo, R. Breather and rogue wave solutions for the (2 + 1)-dimensional nonlinear Schrödinger-Maxwell-Bloch equation. Appl. Math. Lett. 2019, 93, 117–123. [Google Scholar] [CrossRef]
- Chen, S.; Yan, Z. The Hirota equation: Darboux transform of the Riemann-Hilbert problem and higher-order rogue waves. Appl. Math. Lett. 2019, 95, 65–71. [Google Scholar] [CrossRef]
- Yang, B.; Yang, J.K. On general rogue waves in the parity-time-symmetric nonlinear Schrödinger equation. J. Math. Anal. Appl. 2020, 487, 124023. [Google Scholar] [CrossRef]
- Banik, S.; Shikha, R.K.; Noman, A.A.; Chowdhury, N.A.; Mannan, A.; Roy, T.S.; Mamun, A.A. First and second-order dust-ion-acoustic rogue waves in non-thermal plasma. Eur. Phys. J. D 2021, 75, 43. [Google Scholar] [CrossRef]
- Mohammadnejad, M.; Akbari-Moghanjughi, M. Formation of ion acoustic rogue waves in warm dense matter. Eur. Phys. J. D 2021, 75, 307. [Google Scholar] [CrossRef]
- Talouneh, K.; Kheradmand, R.; Tissoni, G.; Eslami, M. Influence of transverse carrier diffusion on two-dimensional optical rogue waves in broad-area semiconductor lasers with a saturable absorber. Phys. Rev. A 2022, 105, 013501. [Google Scholar] [CrossRef]
- Cheng, D.; Wang, W.W.; Pan, C.C.; Hou, C.; Chen, S.H.; Mihalache, D.; Baronio, F. Photonic rogue waves in a strongly dispersive coupled-cavity array involving self-attractive Kerr nonlinearity. Phys. Rev. A 2022, 105, 013717. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Davide, T.C. Transverse instability of rogue waves. Phys, Rev. Lett. 2021, 127, 104101. [Google Scholar] [CrossRef]
- Marcucci, G.; Kheradmand, P.; Claudio, C. Theory of neuromorphic computing by waves: Machine learning by rogue waves, dispersive shocks, and solitons. Phys. Rev. A 2020, 125, 093901. [Google Scholar] [CrossRef]
- Asgarnezhad-Zorgabad, S.; Sadighi-Bonabi, R.; Kibler, B.; Ozdemir, S.K.; Sanders, B.C. Surface-polaritonic phase singularities and multimode polaritonic frequency combs via dark rogue-wave excitation in hybrid plasmonic waveguide. New J. Phys. 2020, 22, 033008. [Google Scholar] [CrossRef]
- Tan, Y.C.; Bai, X.D.; Li, T.T. Super rogue waves: Collision of rogue waves in Bose-Einstein condensate. Phys. Rev. E 2022, 106, 014208. [Google Scholar] [CrossRef]
- Tlidi, M.; Taki, M. Rogue waves in nonlinear optics. Adv. Opt. Photonics 2022, 14, 87–147. [Google Scholar] [CrossRef]
- Copus, M.G.; Camley, R.E. Creation of magnetic rogue waves. Phys. Rev. B 2020, 102, 220410. [Google Scholar] [CrossRef]
- Ankiewicz, A.; Chowdury, A. Analysis of characteristics of rogue waves for higher-order equations. Nonlinear Dyn. 2022, 22, 07497. [Google Scholar] [CrossRef]
- Sgrignuoli, F.; Chen, Y.; Gorsky, S.; Britton, W.A.; Negro, L.D. Optical rogue waves in multifractal photonic arrays. Phys. Rev. B 2021, 103, 195403. [Google Scholar] [CrossRef]
- Gatz, S.; Herrmann, J. Soliton propagation in materials with saturable nonlinearity. J. Opt. Soc. Am. B 1991, 8, 2296. [Google Scholar] [CrossRef]
- Gatz, S.; Herrmann, J. Soliton propagation and soliton collision in double-doped fibers with a non-Kerr-like nonlinear refractive-index change. Opt. Lett. 1992, 17, 484. [Google Scholar] [CrossRef]
- Herrmann, J. Propagation of ultrashort light pulses in fibers with saturable nonlinearity in the normal-dispersion region. J. Opt. Soc. Am. B 1991, 8, 1507–1511. [Google Scholar] [CrossRef]
- Krolikowski, W.; Luther-Davies, B. Analytic solution for soliton propagation in a nonlinear saturable medium. Opt. Lett. 1992, 17, 1414. [Google Scholar] [CrossRef]
- Jakubowski, M.H.; Steiglitz, K.; Squier, R. Information transfer between solitary waves in the saturable Schrödinger equation. Phys. Rev. E 1997, 56, 7267. [Google Scholar] [CrossRef]
- Melvin, T.R.; Champneys, A.R.; Kevrekidis, P.G.; Cuevas, J. Radiationless traveling waves in saturable nonlinear Schrödinger lattices. Phys. Rev. Lett. 2006, 97, 124101. [Google Scholar] [CrossRef]
- Chen, G.; Ma, S. Ground state and geometrically distinct solitons of discrete nonlinear Schrödinger equations with saturable nonlinearities. Stud. Appl. Math. 2013, 131, 389. [Google Scholar] [CrossRef]
- Krolikowski, W.; Luther-Davies, B. Dark optical solitons in saturable nonlinear media. Opt. Lett. 1993, 18, 188. [Google Scholar] [CrossRef]
- Zhang, K.; Liang, Y.Z.; Lin, J.; Li, H.J. Controlling the stability of nonlinear optical modes via electromagnetically induced transparency. Phys. Rev. A 2018, 97, 023844. [Google Scholar] [CrossRef]
- Li, H.J.; Dong, L.W.; Hang, C.; Huang, G.X. Gain-assisted high-dimensional self-trapped laser beams at very low light levels. Phys. Rev. A 2011, 83, 023816. [Google Scholar] [CrossRef]
- Schmidt, H.; Imamoglu, A. Giant Kerr nonlinearities obtained by electromagnetically induced transparency. Opt. Lett. 1996, 21, 1936–1938. [Google Scholar] [CrossRef]
- Harris, S.E. Electromagnetically induced transparency. Phys. Today 1997, 50, 36–42. [Google Scholar] [CrossRef]
- Hau, L.V.; Harris, S.E.; Dutton, Z.; Behroozi, C.H. Light speed reduction to 17 metres per second in an ultracold atomic gas. Nature 1999, 397, 594–598. [Google Scholar] [CrossRef]
- Li, H.J.; Wu, Y.P.; Hang, C.; Huang, G.X. (3 + 1)-dimensional superluminal spatiotemporal optical solitons and vortices at weak light level. Phys. Rev. A 2012, 86, 25181–25194. [Google Scholar] [CrossRef]
- Liu, J.Y.; Hang, C.; Huang, G.X. Weak-light rogue waves, breathers, and their active control in a cold atomic gas via electromagnetically induced transparency. Phys. Rev. A 2016, 93, 063836. [Google Scholar] [CrossRef]
- Liu, J.Y.; Hang, C.; Huang, G.X. Weak-light vector rogue waves, breathers, and their Stern-Gerlach deflection via electromagnetically induced transparency. Opt. Express 2017, 25, 23408–23423. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Lin, J.; Li, H. Generation and Controllability of High-Dimensional Rogue Waves in an Electromagnetically Induced Transparent Medium. Mathematics 2023, 11, 1829. https://doi.org/10.3390/math11081829
Li Z, Lin J, Li H. Generation and Controllability of High-Dimensional Rogue Waves in an Electromagnetically Induced Transparent Medium. Mathematics. 2023; 11(8):1829. https://doi.org/10.3390/math11081829
Chicago/Turabian StyleLi, Zhongyin, Ji Lin, and Huijun Li. 2023. "Generation and Controllability of High-Dimensional Rogue Waves in an Electromagnetically Induced Transparent Medium" Mathematics 11, no. 8: 1829. https://doi.org/10.3390/math11081829
APA StyleLi, Z., Lin, J., & Li, H. (2023). Generation and Controllability of High-Dimensional Rogue Waves in an Electromagnetically Induced Transparent Medium. Mathematics, 11(8), 1829. https://doi.org/10.3390/math11081829




