About Oscillations in Nonlinear Systems with Elastic Bonds
Abstract
1. Introduction
- -
- design a mathematical model of the system in the absence of friction;
- -
- analyze the conditions for the occurrence of oscillations in a frictionless system and determine the critical value of the coefficient of elasticity;
- -
- design a mathematical model of the system in the presence of friction;
- -
- study the behavior of the system under various initial conditions and values of the friction coefficient.
2. Materials and Methods
3. Results and Discussion
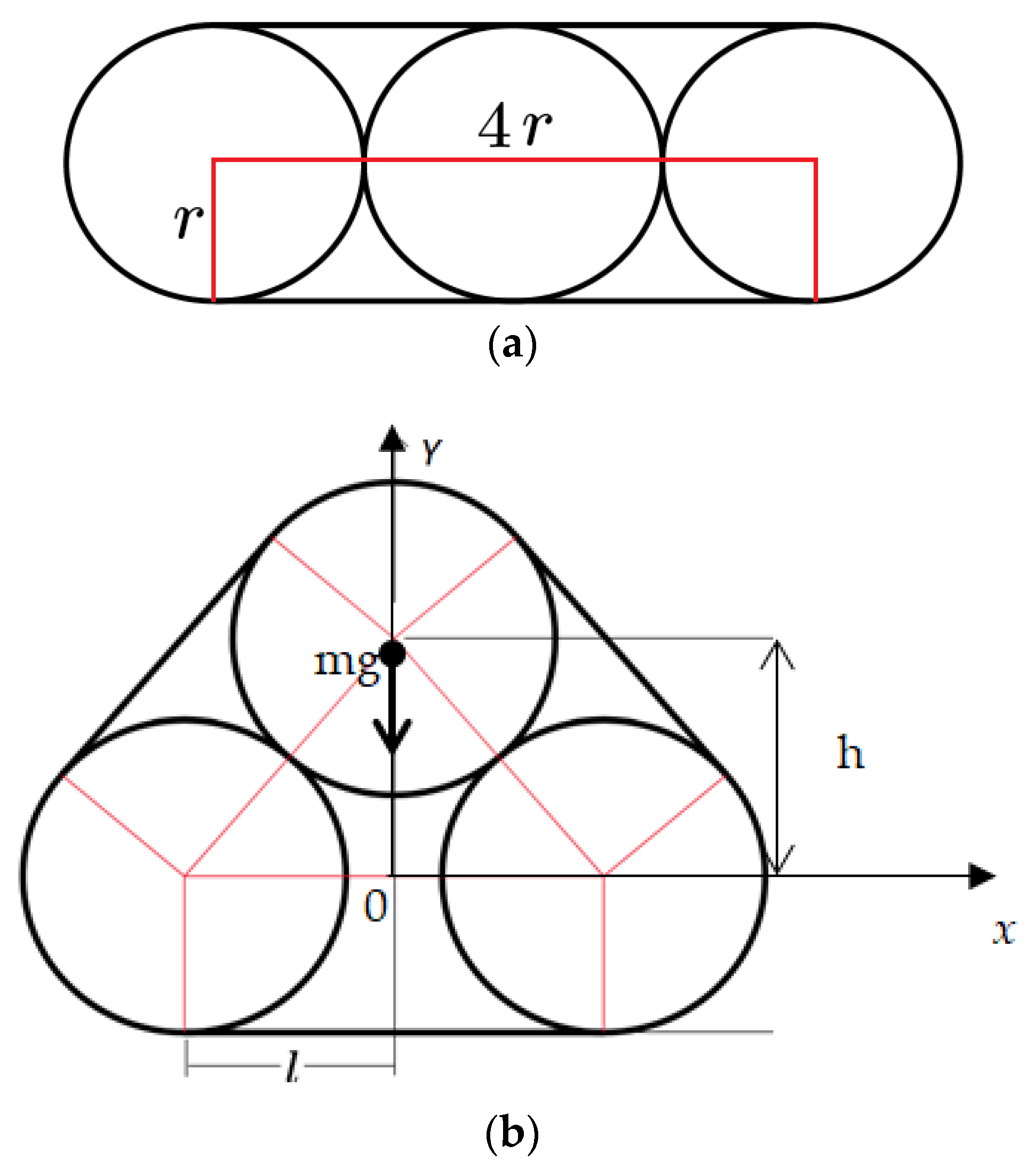
3.1. Mathematical Model of a Pendulum without Friction Forces
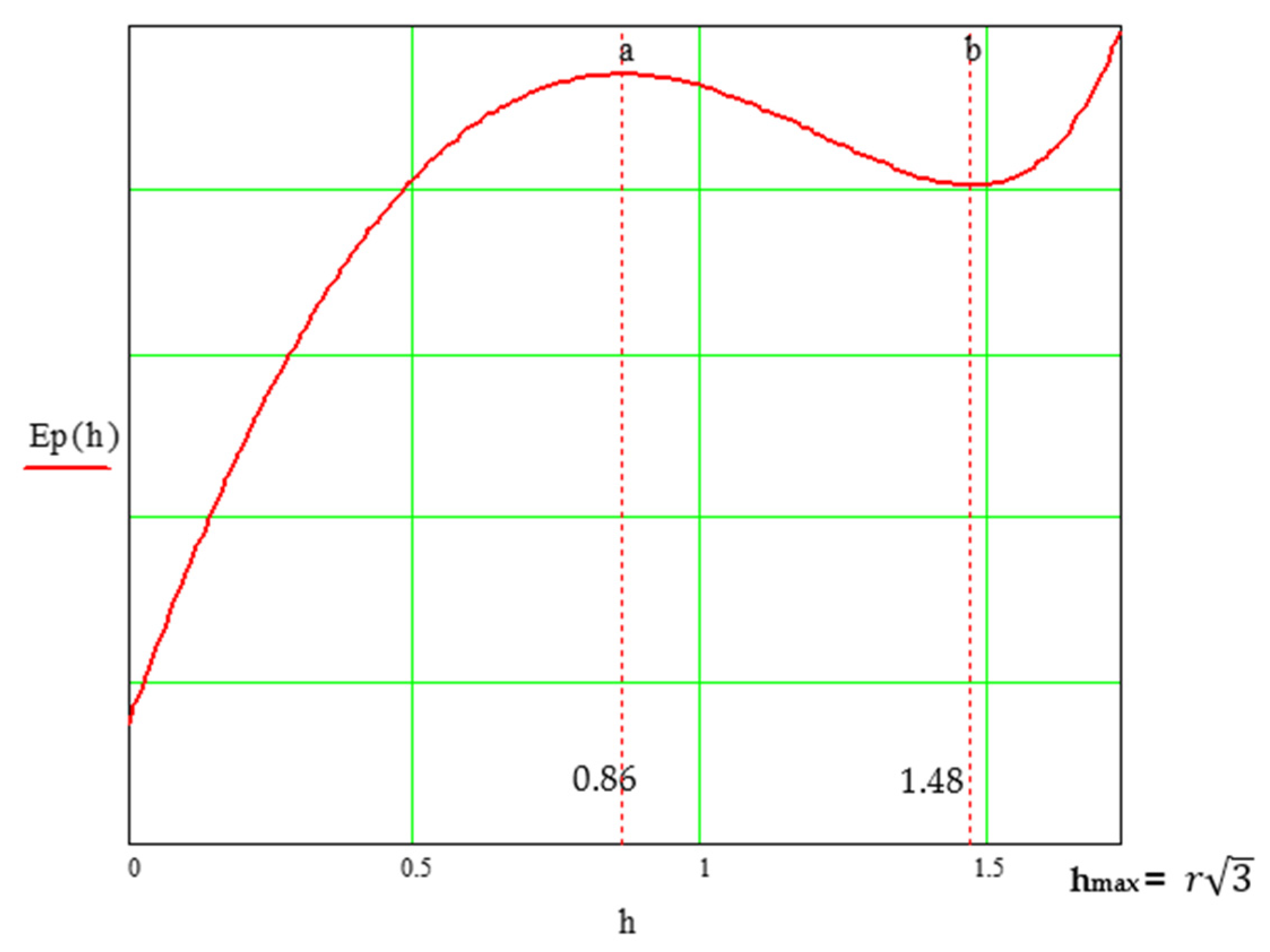
3.2. Analysis of the Conditions for the Occurrence of Periodic Oscillations
3.3. Mathematical Model of a Pendulum Taking into Account Friction Forces
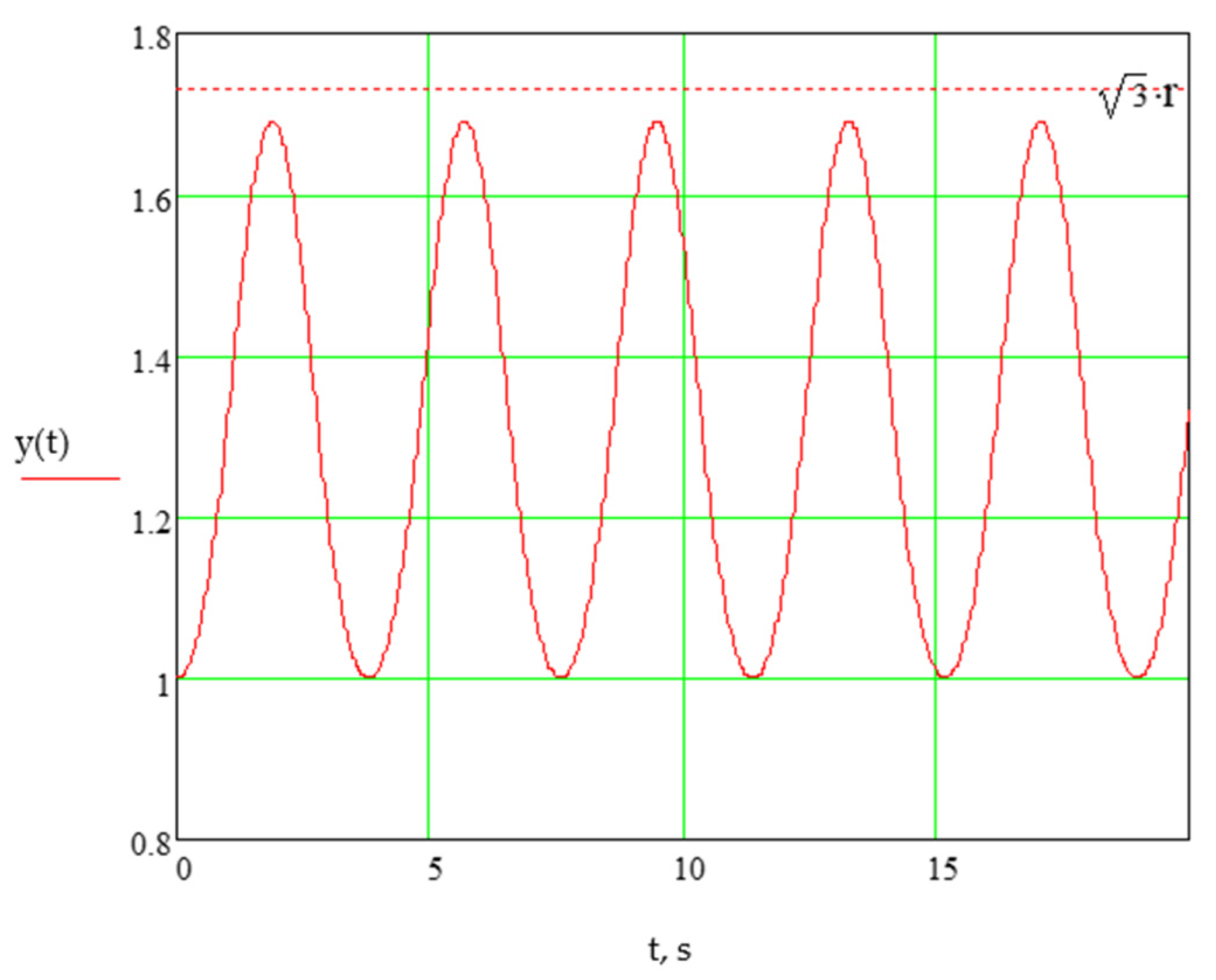
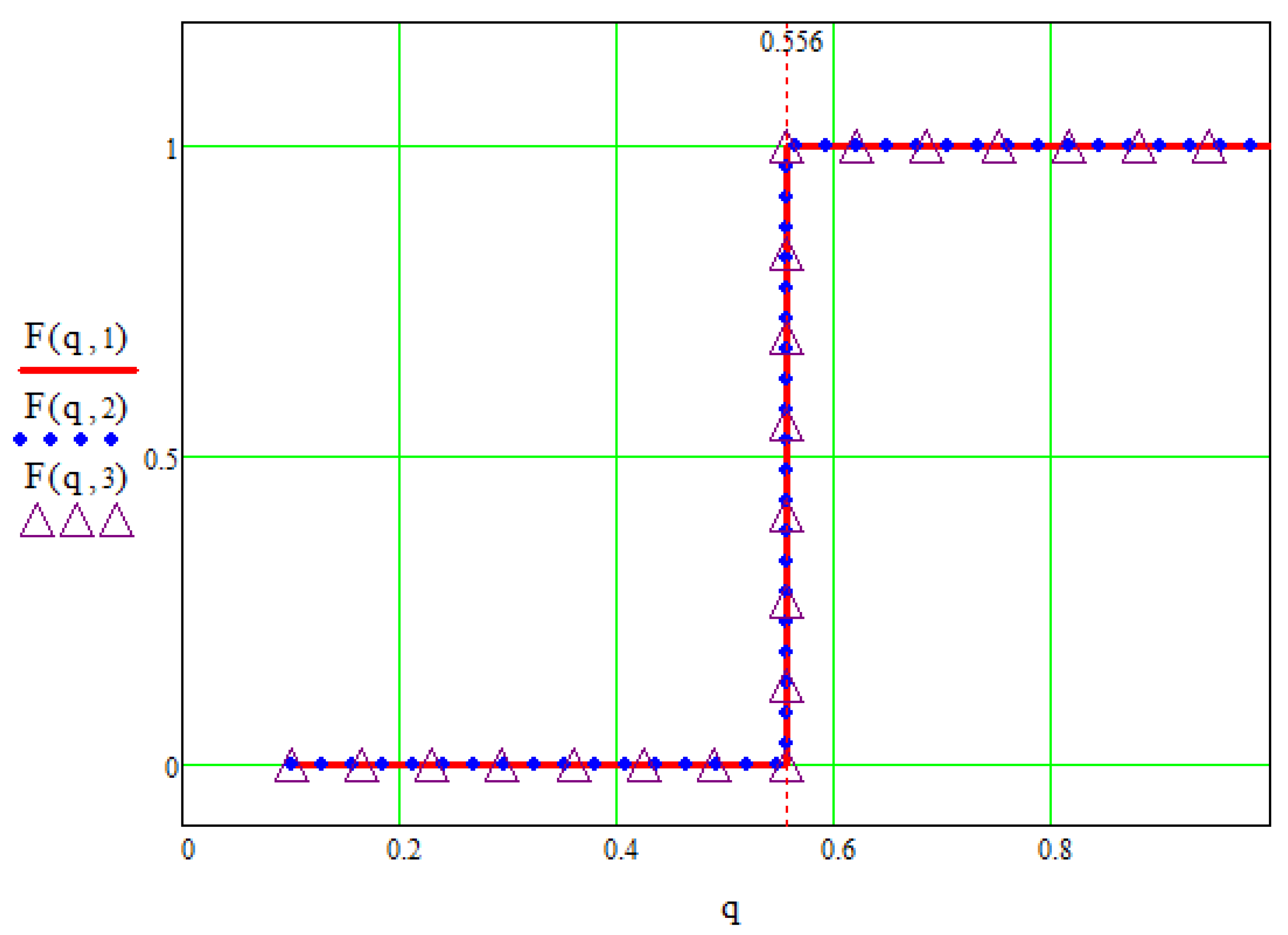
3.4. System Motion Study
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Atluri, S. Computational methods for nonlinear dynamical systems. Mech. Eng. Rev. 2017, 4, 17-00040. [Google Scholar] [CrossRef]
- Fuchs, A. Nonlinear Dynamics in Complex Systems. In Theory and Applications for the Life-, Neuro- and Natural Sciences; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Chernousko, F.; Ananievski, I.; Reshmin, S. Control of Nonlinear Dynamical Systems. In Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Aghagholizadeh, M. Study on Dynamics of an Elastic Oscillator Coupled with a Rocking Wall. arXiv 2018, arXiv:1803.02669v4. [Google Scholar]
- Mogilevich, L.; Popov, V.; Kondratov, D.; Rabinskiy, L. Bending oscillations of a cylinder, surrounded by an elastic medium and containing a viscous liquid and an oscillator. J. Vibroeng. 2017, 19, 5758–5766. [Google Scholar] [CrossRef]
- Tan, X.; Hua, L.; Lu, C.; Yang, C.; Wang, Y. Study of the optimization of matching between torsional vibration damper and elastic coupling based on energy method. J. Vibroeng. 2017, 19, 769–782. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, H.; Xing, Y. New Insights into a Three-Sub-Step Composite Method and Its Performance on Multibody Systems. Mathematics 2022, 10, 2375. [Google Scholar] [CrossRef]
- El-Latif, A.A.A.; Ramadoss, J.; Abd-El-Atty, B.; Khalifa, H.S.; Nazarimehr, F. A Novel Chaos-Based Cryptography Algorithm and Its Performance Analysis. Mathematics 2022, 10, 2434. [Google Scholar] [CrossRef]
- Hosen, M.A.; Chowdhury, M.; Ali, M.Y.; Ismail, A.F. An analytical approximation technique for the duffing oscillator based on the energy balance method. Ital. J. Pur. Appl. Math. 2017, 37, 455–466. [Google Scholar]
- Koochi, A.; Goharimanesh, M. Nonlinear Oscillations of CNT Nano-resonator Based on Nonlocal Elasticity: The Energy Balance Method. Rep. Mech. Eng. 2021, 2, 41–50. [Google Scholar]
- Big-Alabo, A.; Ossia, C.V. Periodic oscillation and bifurcation analysis of pendulum with spinning support using a modified continuous piecewise linearization method. Int. J. Appl. Comput. Math. 2019, 5, 114. [Google Scholar] [CrossRef]
- Khan, N.A.; Alshammari, F.S.; Romero, C.A.T.; Sulaiman, M. Study of Nonlinear Models of Oscillatory Systems by Applying an Intelligent Computational Technique. Entropy 2021, 23, 1685. [Google Scholar] [CrossRef]
- Bataineh, A.S. Application of adaptation HAM for nonlinear oscillator typified as a mass attached to a stretched elastic wire. Commun. Math. Appl. 2017, 8, 157–165. [Google Scholar]
- Kimura, M.; Hikihara, T. Nonlinear oscillations in two coupled elastic beams with tunable nonlinear potentials. In Proceedings of the International Symposium on Nonlinear Theory and its Applications, Kobe, Japan, 4–7 September 2011. [Google Scholar]
- Parovik, R. Mathematical Modeling of Linear Fractional Oscillators. Mathematics 2020, 8, 1879. [Google Scholar] [CrossRef]
- Rill, G. Multibody Systems and Simulation Techniques. In Vehicle Dynamics of Modern Passenger Cars; Lugner, P., Ed.; CISM International Centre for Mechanical Sciences: Udine, Italy; Springer: Cham, Switzerland, 2019; Volume 582. [Google Scholar] [CrossRef]
- Petcu, M.A.; Ionescu-Feleaga, L.; Ionescu, B.-Ș.; Moise, D.-F. A Decade for the Mathematics: Bibliometric Analysis of Mathematical Modeling in Economics, Ecology, and Environment. Mathematics 2023, 11, 365. [Google Scholar] [CrossRef]
- Kuzkin, V.; Asonov, I. Vector-based model of elastic bonds for DEM simulation of solids. arXiv 2012, arXiv:1202.0001v2. [Google Scholar]
- Kuzkin, V.; Krivtsov, A. Enhanced vector-based model for elastic bonds in solids. Lett. Mater. 2017, 7, 455–458. [Google Scholar] [CrossRef]
- Ochkov, V.; Vasileva, I.; Orlov, K.; Chudova, J.; Tikhonov, A. Visualization in Mathematical Packages When Teaching with Information Technologies. Mathematics 2022, 10, 3413. [Google Scholar] [CrossRef]
- Mala, F.A. Book Review: Stacy A. Costa, Marcel Danesi, Dragana Martinovic (Eds.) (2020) Mathematics (education) in the information age. Educ. Stud. Math. 2022, 112, 199–205. [Google Scholar] [CrossRef]
- Brenner, A.; Shacham, M.; Cutlip, B. Applications of mathematical software packages for modeling and simulations in environmental engineering education. Environ. Model. Softw. 2005, 20, 1307–1313. [Google Scholar] [CrossRef]
- Ochkov, V.; Vasileva, I. Application of difference schemes to decision the pursuit problem. SPIIRAS Proc. 2019, 18, 1406–1433. [Google Scholar] [CrossRef]
- Bauchau, O.; Hodges, D. Analysis of Nonlinear Multibody Systems with Elastic Couplings. Multibody Syst. Dyn. 1999, 3, 163–188. [Google Scholar] [CrossRef]
- Fonkou, R.; Louodop, P.; Talla, P.; Woafo, P. Analysis of the dynamics of new models of nonlinear systems with state variable damping and elastic coefficients. Heliyon 2022, 8, e10112. [Google Scholar] [CrossRef] [PubMed]
- Forni, F.; Sepulchre, R. Differential analysis of nonlinear systems: Revisiting the pendulum example. arXiv 2014, arXiv:1409.4712v1. [Google Scholar]
- Bratu, P. Multibody System with Elastic Connections for Dynamic Modeling of Compactor Vibratory Rollers. Symmetry 2020, 12, 1617. [Google Scholar] [CrossRef]
- Rose, G.K.; Newman, B.A.; Nguyen, D.T. A path following method for identifying static equilibrium in multi-body-dynamic systems. Multibody Syst. Dyn. 2019, 45, 315–359. [Google Scholar] [CrossRef]
- Ochkov, V.; Vasileva, I.; Nori, M.; Orlov, K.; Nikulchev, E. Symbolic computation to solving an irrational equation on based symmetric polynomials method. Computation 2020, 8, 40. [Google Scholar] [CrossRef]
- Thorne, K.S.; Blandford, R.D. Modern Classical Physics: Optics, Fluids, Plasmas, Elasticity, Relativity, and Statistical Physics; Princeton University Press: Princeton, NY, USA, 2017. [Google Scholar]
- Temur, R.; Bekdas, G.; Toklu, Y. Total potential energy minimization method in structural analysis considering material nonlinearity. Chall. J. Struct. Mech. 2017, 3, 129. [Google Scholar] [CrossRef]
- Sadd, M.H. Elasticity: Theory, Applications, and Numerics, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Fu, Y.; Ogden, R. (Eds.) Nonlinear Elasticity; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar] [CrossRef]
- Morin, D. Introduction to Classical Mechanics with Problems and Solutions; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Berger, E. Friction modeling for dynamic system simulation. Appl. Mech. Rev. 2002, 55, 535–577. [Google Scholar] [CrossRef]
- Plaçais, P.-Y.; Balland, M.; Guérin, T.; Joanny, J.-F.; Martin, P. Spontaneous Oscillations of a Minimal Acto-Myosin System Under Elastic Loading. Biophys. J. 2010, 98, 561a. [Google Scholar] [CrossRef]
- Lei, H.; Zhang, Z.; Han, F.; Liu, B.; Zhang, Y.-W.; Gao, H. Elastic Bounds of Bioinspired Nanocomposites. J. Appl. Mech. 2013, 80, 061017. [Google Scholar] [CrossRef]
- Zhu, M.; Feilong, Z.; Chen, X. Bioinspired Mechanically Interlocking Structures. Small Struct. 2020, 1, 2000045. [Google Scholar] [CrossRef]
- Arena, P.; Bucolo, M.; Buscarino, A.; Fortuna, L.; Frasca, M. Reviewing Bioinspired Technologies for Future Trends: A Complex Systems Point of View. Front. Phys. 2021, 9, 750090. [Google Scholar] [CrossRef]




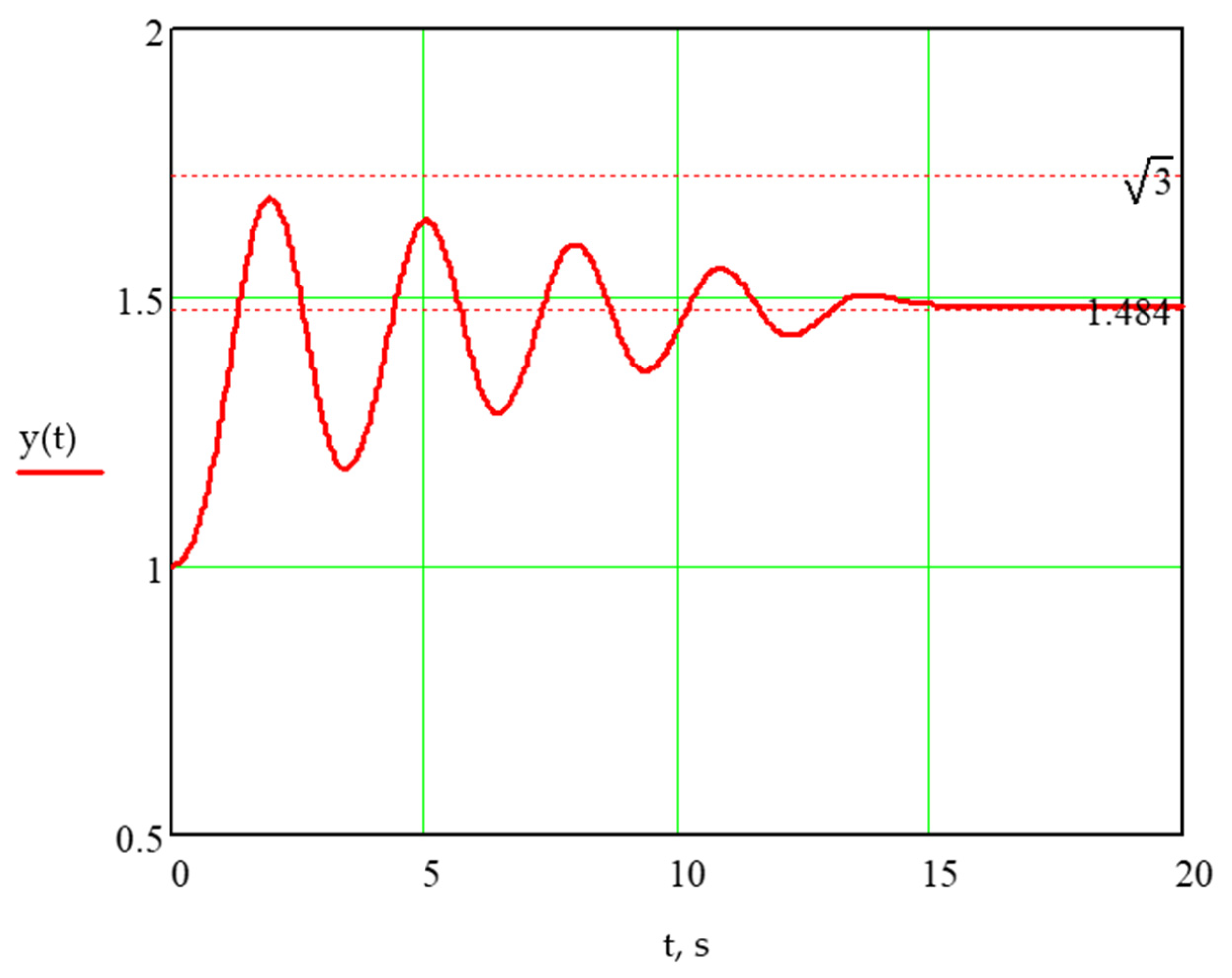
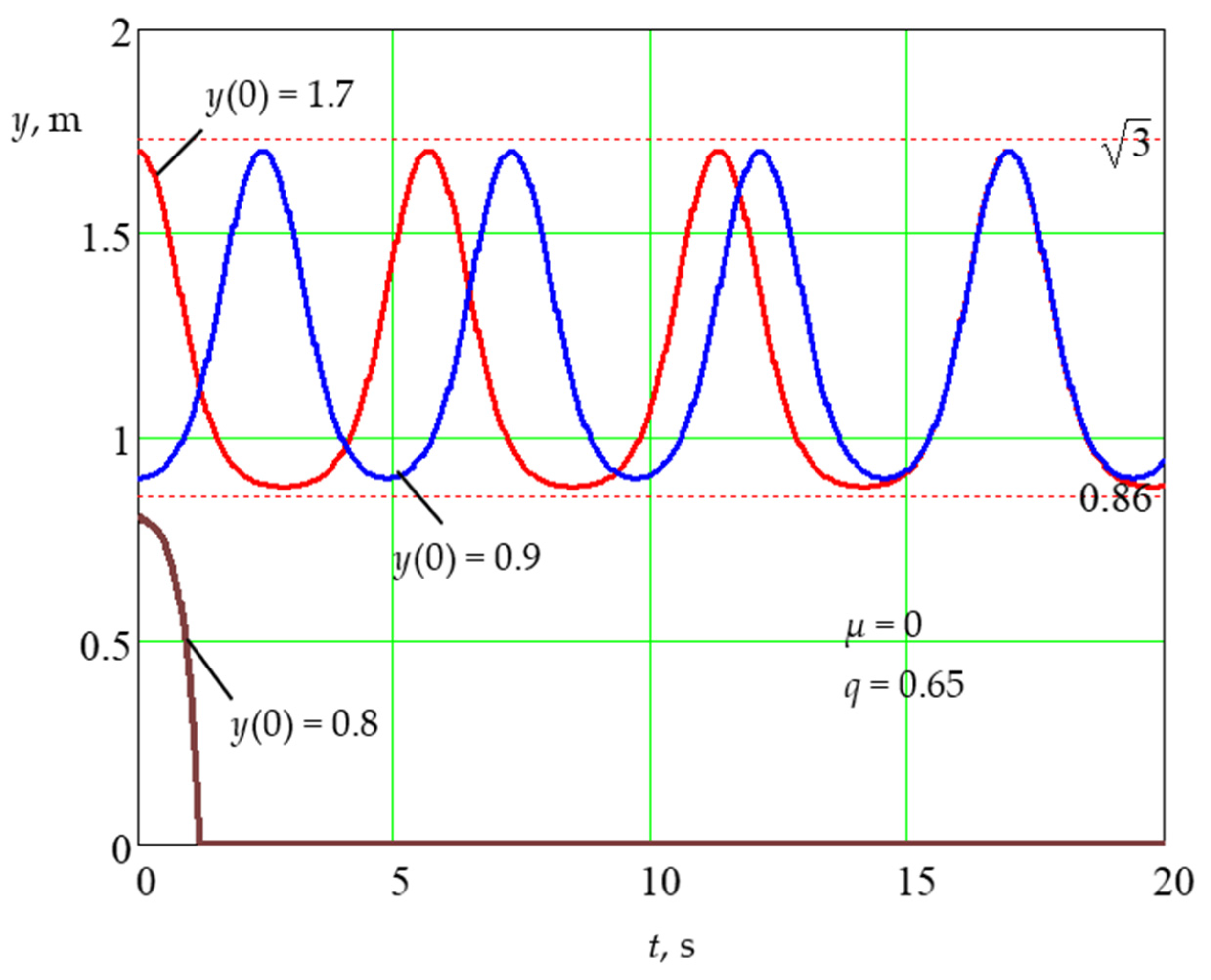
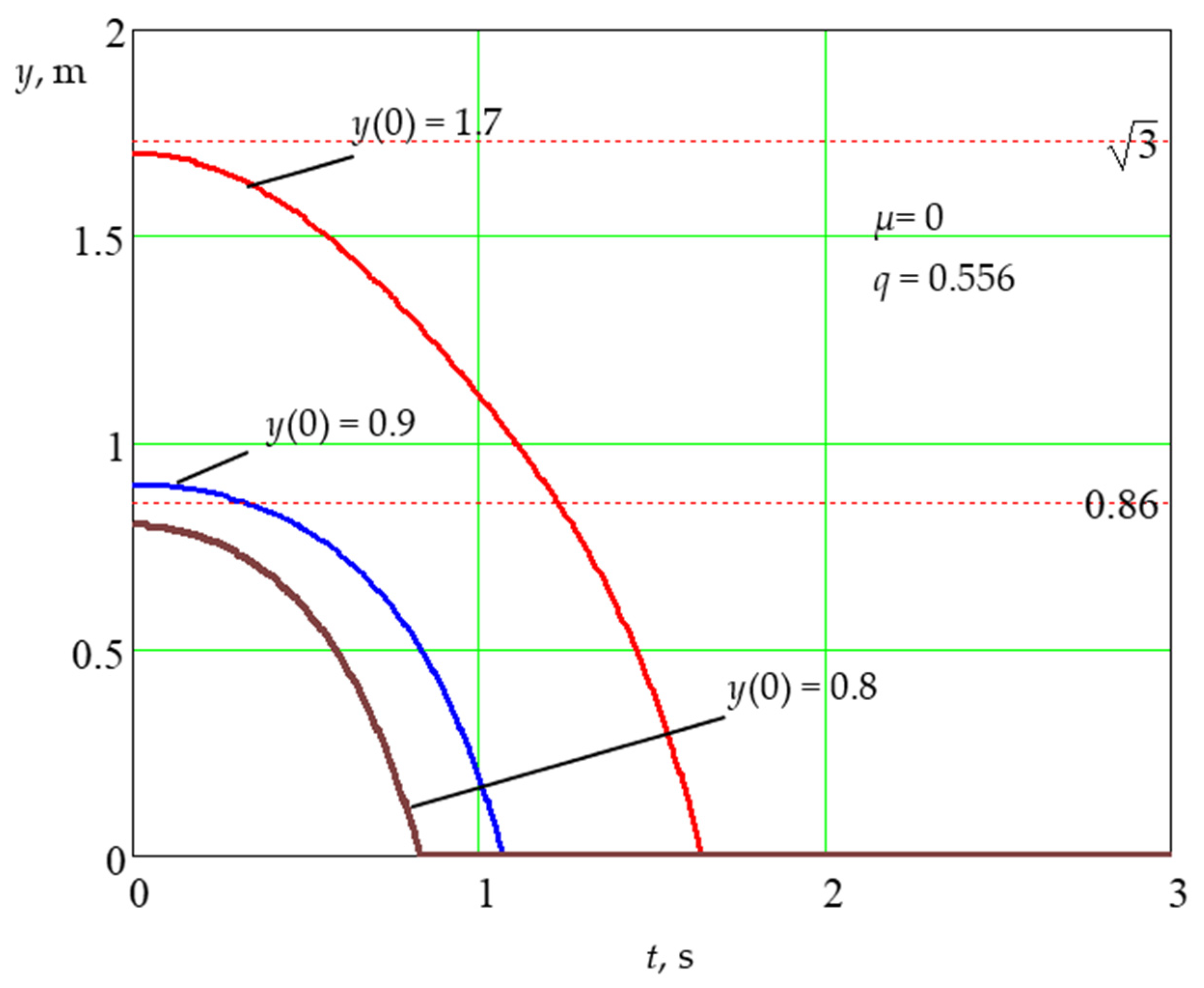

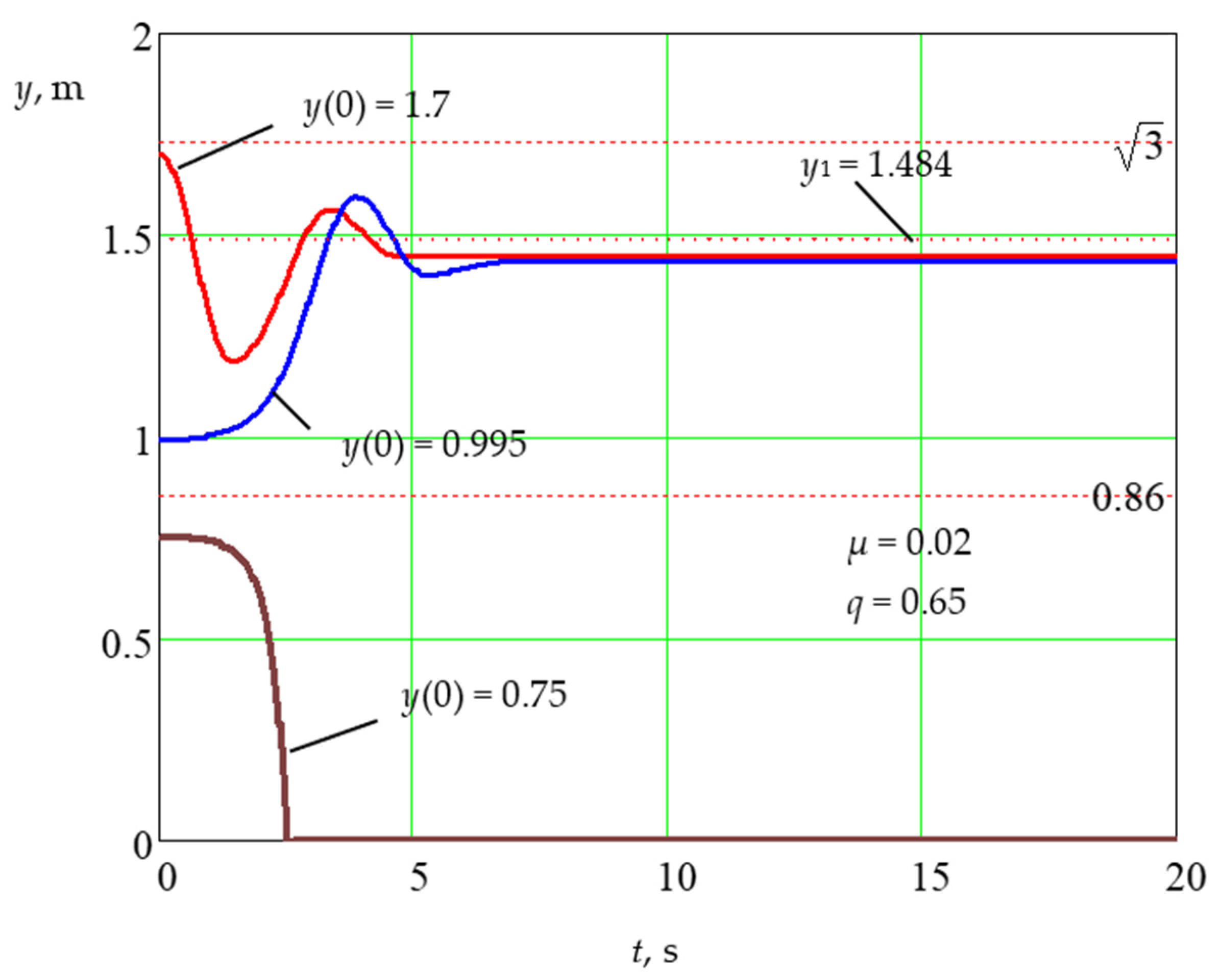

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ochkov, V.; Vasileva, I.; Chudova, Y.; Tikhonov, A. About Oscillations in Nonlinear Systems with Elastic Bonds. Mathematics 2023, 11, 1765. https://doi.org/10.3390/math11081765
Ochkov V, Vasileva I, Chudova Y, Tikhonov A. About Oscillations in Nonlinear Systems with Elastic Bonds. Mathematics. 2023; 11(8):1765. https://doi.org/10.3390/math11081765
Chicago/Turabian StyleOchkov, Valery, Inna Vasileva, Yulia Chudova, and Anton Tikhonov. 2023. "About Oscillations in Nonlinear Systems with Elastic Bonds" Mathematics 11, no. 8: 1765. https://doi.org/10.3390/math11081765
APA StyleOchkov, V., Vasileva, I., Chudova, Y., & Tikhonov, A. (2023). About Oscillations in Nonlinear Systems with Elastic Bonds. Mathematics, 11(8), 1765. https://doi.org/10.3390/math11081765






