Abstract
The theory of functional connections, an analytical framework generalizing interpolation, was extended and applied in the context of fractional-order operators (integrals and derivatives). The extension was performed and presented for univariate functions, with the aim of determining the whole set of functions satisfying some constraints expressed in terms of integrals and derivatives of non-integer order. The objective of these expressions was to solve fractional differential equations or other problems subject to fractional constraints. Although this work focused on the Riemann–Liouville definitions, the method is, however, more general, and it can be applied with different definitions of fractional operators just by changing the way they are computed. Three examples are provided showing, step by step, how to apply this extension for: (1) one constraint in terms of a fractional derivative, (2) three constraints (a function, a fractional derivative, and an integral), and (3) two constraints expressed in terms of linear combinations of fractional derivatives and integrals.
Keywords:
functional interpolation; fractional derivatives and integrals; Riemann–Liouville derivative; shifted Chebyshev polynomials MSC:
41A05; 26A33; 65D05
1. Introduction
During the past few decades, fractional calculus has been applied in different fields of science. Introductory surveys can be found in [1,2]. In engineering, it finds applications in fields such as control theory [3], the mechanics’ theory of viscoelasticity [4,5], in sedimentology with diffusion and transport in porous rocks (using fractional derivatives with the theory of fractals) [6], in (bio)chemistry with the modeling of polymers and proteins [7], in finance on stochastic computation with respect to fractional Brownian motion [8], and in medicine on the modeling of human tissue under mechanical loads [9], as well as in many other fields such as anomalous diffusion [10], anomalous convection [11], power laws [12], probability [13], optimal control [14], allometric scaling laws [15], long-range interactions [16], the description of galaxy rotation [17], market price dynamics [18], and so on.
The use of fractional derivatives and integrals (the term “fractional” must be actually intended as an extension to real values, rather than limited to integer values) in applied science and engineering has been dormant for a long time. There is no reason why the laws of the natural phenomena must be restricted to integer-order derivatives and integrals, and the idea to extend these operators to real orders is actually quite old, dating back to 1695 [19]. The reason for this delay is perhaps due to the fact that the various different approaches/definitions (with respect to the “boundary” constraints being coincident, in some specific domains, with the classical integer-order definitions) provide different results.
In addition, solving fractional-order problems turns out to be much more difficult than in the integer-order case, and sophisticated (analytical and numerical) methods are necessary; indeed, they are the subject of more and more ongoing investigations.
In this study, the theory of functional connections (TFC), a new mathematical framework generalizing interpolation using functionals [20], is extended for the first time to fractional derivatives and integrals. The capability to derive expressions representing all functions subject to fractional constraints (the main objective of this article) has a direct impact on solving fractional differential equations [21] and, in general, in any other problem subject to fractional constraints. In fact, this capability allows transforming these constrained optimization problems to unconstrained problems, which can then be solved using simpler, more robust, more accurate, faster, and more reliable methods. Therefore, the main aim of this article was to pave the way for devising advanced mathematical tools to solve fractional differential equations (FDEs) using the TFC.
In previous TFC applications, functional interpolation problems were solved by expanding the TFC free function in terms of orthogonal polynomials (Chebyshev, Legendre, etc.). Since fractional derivatives and integrals involve the computation of negative powers of the independent variable (a complex value for ), shifted Chebyshev polynomials (SCPs), defined in the range, were adopted, and a brief description of SCPs and how to evaluate the derivatives is provided.
To achieve these goals, we first provide, in Section 2, a brief survey of the background materials on fractional calculus. Hence, Section 3 summarizes what the TFC is, where it has already be applied, and how it derives functionals representing all functions always satisfying a set of linear constraints. Shifted Chebyshev polynomials and their applications to represent derivatives of fractional order are discussed in Section 4. Finally, some numerical experiments to show the applications of the TFC with different constraints involving fractional integrals and fractional derivatives are presented. The Appendices at the end of the paper collect more technical details.
2. Background on Fractional Calculus
To allow the use of the TFC with fractional-order operators, it is necessary to preliminarily provide some basic material on fractional calculus.
2.1. The Gamma Function
The introduction of fractional-order operators requires recalling the Gamma function, , and some of its main properties. The Gamma function is defined as
and it is analytically continuable in .
The extension of the factorial definition using the Gamma function is supported by the Bohr–Mollerup theorem [22]: the Gamma function is indeed the unique function defined on satisfying the following properties:
- ;
- , for ;
- is logarithmically convex (or superconvex).
Property 2 implicitly states that when , and the similarity to the analogous property of the factorial, , is evident.
Along with the definition given in (1), the Gamma function allows expressing factorials in terms of the Gamma function, namely when , and extending the factorial operator to non-integer values. For instance,
This is also true for functions derived from the factorial, as for instance the binomial coefficient , which can be, therefore, defined also for non-integer values as
2.2. Riemann–Liouville Fractional Integral
Cauchy’s formula allows representing the n-times repeated integration on in terms of just one integral:
an expression valid for . By replacing , this formula holds for any , . What is obtained is the Riemann–Liouville (RL) fractional integral:
which coincides with the usual definition of the integral operator when is an integer. This RL fractional operator satisfies the following semigroup properties:
for real and .
As in the integer-order case, RL fractional integration improves the smoothness properties of functions (see Appendix A for an explanation).
2.3. Riemann–Liouville Fractional Derivative
Different kinds of operators inverting the RL integral are possible. For a sufficiently smooth function f, the RL fractional derivative of order is defined as
where . In view of the mentioned semigroup properties of , one can immediately check that .
The reverse composition of the RL derivative and integral instead involves initial conditions at , namely [23] (Theorem 2.23)
provided that possesses a sufficient regularity.
There is a substantial difference with integer-order differential operators: the operator thus-obtained has a non-local character. This is known as the “memory effect”, and this property is more deeply explained in Appendix B.
The fractional derivative is a linear operator:
and the RL derivative of power functions is given by
thus showing that the RL derivative of a constant c is not 0, but . By setting , we readily obtain the RL fractional derivative of monomials as
which is known as the fractional power rule. This expression is useful when expanding a function in Taylor series or in terms of orthogonal polynomials as, for instance, the shifted Chebyshev polynomials.
In some cases (see [23] (Theorem 2.3)), the RL derivative may satisfy a subsequent derivation property such as
which allows re-conducting fractional derivatives in the restricted range ; indeed, when , , one can find such that and write
as for instance in
(the use of (4) must be done, however, with caution since it does not hold for any function f and for any pair of orders and ). On the basis of this observation, we restricted our investigation to the range .
2.4. Caputo Fractional Derivative
The RL derivative is not the only operator performing the inversion of the RL integral . A further definition is known as the Caputo fractional derivative:
and also in this case, it is easy to check that .
The Caputo derivative requires a stronger regularity of the function f, but its left inversion by means of the RL integral involves initial conditions expressed in terms of integer-order derivatives since [23] (Theorem 2.3)
This property is of importance in fractional differential equations since it implies that initial-value problems with the Caputo fractional derivative are initialized by values of the integer-order derivative of the solution (which are standard in physical problems) and not by the limits of fractional-order integrals as with the RL derivative. However, the two derivatives are strictly connected since
and therefore, focusing on just one of them does not appear too restrictive. In this preliminary work, our attention was mainly devoted to the RL definition.
2.5. Grünwald–Letnikov Definitions
It is worthwhile to mention the Grünwald–Letnikov (GL) definition of fractional derivatives [24], which provides discrete access to the fractional calculus, and it is particularly suitable for numerical treatment. Indeed, the GL derivative is defined as
where the binomial coefficient must be intended as in (2). It is immediate to see that allows a numerical approximation once a constant (possibly small) step , rather than the limit as , is selected. Reference [24] analyzed the numerical stability, convergence, and error of FDEs using the GL derivative, where the asymptotic and the absolute stability of these methods were proven.
The GL definition is obtained from a generalization of the definition of the integer-order derivative expressed as the limit of the difference quotient and after imposing, in order to ensure the convergence of the series, that the function has a value of 0 before the initial point a (see, for instance, [25]). Under the necessary assumptions on the smoothness of f, it is possible to prove an equivalence between the GL and RL definitions.
A integral of the GL type can be defined as well after considering a negative-order in , i.e.,
which instead corresponds to the RL integral initialized at a.
3. Background on the Theory of Functional Connections
The theory of functional connections (TFC) performs linear functional interpolation, and functional interpolation is a generalization of interpolation. Instead of selecting a function (or a class of functions) satisfying a set of constraints, functional interpolation derives functionals (called constrained expressions) representing the whole set of functions satisfying the constraints; stated in a different way, TFC derives functionals that always satisfy the whole set of constraints (the constraints are embedded in the functional). In this way, functional interpolation identifies the subset of the function space that fully satisfies the constraints.
These functionals contain a free function, , and by spanning all possible expressions of the free function, the whole space of functions satisfying the constraints is covered. In particular, the free function always appears linear in the TFC, thus simplifying optimization processes. This approach was introduced in [26], and then, immediate applications appeared for solving differential equations [27,28,29,30] and for other mathematical problems [31,32,33,34].
To give a simple example of what functional interpolation is, consider the functional:
where denotes the derivative of g. This equation always satisfies the two constraints, and , regardless of the function . The function is a free function subject to being defined, where the constraints are specified, only. Functionals such as (5) represent the whole set of functions satisfying the set of constraints they are derived for. These functionals project the whole space of functions to just the subspace fully satisfying the constraints. This way, constrained optimization problems, such as differential equations, can be transformed to unconstrained problems and, consequently, be solved using simpler, faster, more robust, and more accurate methods. Univariate functionals such as (5) can be generated by either one of these two formal expressions, called constrained expressions (CEs):
where n is the number of linear constraints, is the free function, is a set of n user-defined linearly independent support functions, are coefficient functionals, are switching functions (they are 1 when evaluated at the constraint they reference and 0 when evaluated at all other constraints), and are projection functionals representing the constraints written in terms of the free function.
Numerically efficient applications of the TFC have already been implemented in optimization problems, outperforming the current methods, especially in solving differential equations. In this area, the TFC has unified initial, boundary, and multi-value problems by usually providing fast solutions with high accuracy.
A Simple Explanatory Example
Let us consider the problem of determining functions f satisfying the initial condition:
where, to adopt a more concise notation, from now on, will denote the fractional RL derivative of order , previously identified as , and its value at . Using the “” formulation (6), the constrained expression is
After imposing (8) at , the coefficient can be derived as
and the constrained expression becomes
This constrained expression represents the whole set of functions satisfying the given constraint (8). It can be used, for instance, in a constrained optimization process, subject to satisfying (8). By means of (10), an initial constrained optimization problem can be transformed to the unconstrained problem of finding the expression of the free function, namely , generating the optimal [20].
The most-simple function satisfying the constraint (8) is obtained from (10) after setting :
and indeed, it is easy to check that
In Figure 1, we show, for three different choices of the free function g, namely , , and , the plots of (left plot) and of its RL derivative (right plot). We imposed the constraint (8) with , , and , and we considered the constrained expression (9) with . Although we obtained three different functionals , all their RL satisfy the constraint (8): indeed, in the right plot, we observe that . For the evaluation of the RL derivatives, we used the formulas in Appendix A.
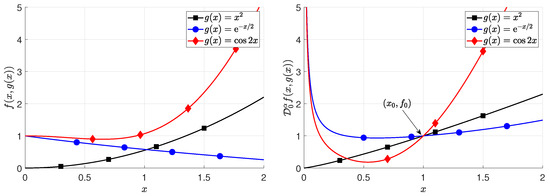
Figure 1.
Functional (left plot) and its RL derivative (right plot) for some choices of . Here, , , and .
4. Shifted Chebyshev Polynomials
Chebyshev polynomials of the first kind are orthogonal polynomials defined for as , . They can be built in different ways, such as, for instance, by means of the three-term recurrence relation:
To operate with fractional-order operators initialized at some points , it is convenient to use shifted Chebyshev polynomials (SCPs) preserving orthogonality on the shifted interval. Appendix C provides a summary of various approaches to perform the least squares. They can be adopted in optimization to estimate the coefficients of the free function, which is expanded in terms of shifted Chebyshev polynomials.
To simplify the notation, we considered the fractional integral and the fractional RL derivative initialized at , and we assumed we are interested in approximating functions on the interval . The generalization to different intervals is always possible without particular difficulties.
SCPs on are connected to Chebyshev polynomials by the relationship:
and the corresponding three-term recurrence relation is
In order to expand free functions in the TFC, it is convenient to express SCPs in terms of monomials:
where coefficients , , mapping SCPs to monomials, are obtained from the recursive form (11) of SCPs; a closed form can be obtained, for instance, from [35] as
Therefore, it is possible to represent the SCPs up to degree m as
and the first few coefficients (for ) can be easily evaluated as
The matrix expression of the SCPs allows us to provide the RL fractional derivatives of the SCPs after using (3) for the RL derivatives of monomials:
where is a diagonal matrix made of functions ratio terms
It is well known that integer-order derivatives of SCPs can expressed in terms of SCPs themselves according to
and
where matrices B and C can be easily built in a recursive way. Indeed, by using the expression of their first column:
one can build the following columns according to
For instance, for , the B and C lower-triangular matrices are
To obtain a similar relationship with RL derivatives, we first observe that the inverse mapping of (12) is also available, namely
where coefficients , are given (after simple manipulations) by [35]
Thus, we write
We note that , and therefore, thanks to (13) one obtains
Example
Let us consider, on the interval , the following function:
and its approximation obtained by the first terms in the shifted Chebyshev expansion, namely
where coefficients can be easily evaluated after computing (by some accurate quadrature rule) the integrals:
with and for any . By using (14), we are, hence, able to evaluate
which provides an approximation to in terms of shifted Chebyshev polynomials.
In the left plot of Figure 2, we show the function and the error for some values of m. The RL derivative of , where , is instead presented in the right plot of Figure 2 for .
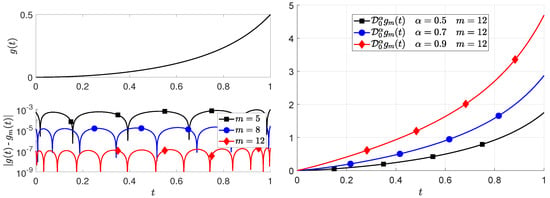
Figure 2.
Function and errors of truncated approximations (left plot). RL derivatives for (right plot).
5. Numerical Examples
This section shows, by three distinct examples, how to apply the TFC to obtain functionals, called constrained expressions, with embedded fractional constraints. The first example involves, again, a single fractional derivative constraint that is solved using the switching projection TFC formulation, while the second examples shows how to derive, via the TFC formulation [20], the constrained expression subject to three constraints specified by the values of the function, of its fractional derivative, and of its fractional integral. The third example is devoted to presenting the use of the switching-projection formulation [20] to derive the constrained expression for two constraints defined as a linear combination of fractional constraints specified in distinct locations.
5.1. Single Fractional Constraint
Let us derive, by the switching-projection TFC formulation (7), the functional representing all functions satisfying the single fractional derivative constraint:
The number of constraints is . Therefore, just one support function and one switching function are needed. Let be the support function. The switching function is , and it is subject to
from which the unknown coefficient is computed. Therefore, the expressions of the switching function and of the projection functional are
and the constrained expression, , representing the whole set of functions satisfying (15), is
Note that, by setting , the simplest interpolation result is obtained, i.e.,
Equation (16) can also be validated using any expression of the free function. For example, by setting , thanks to (A2) and (A8), we obtain
and hence,
5.2. Three Mixed Constraints
This example includes constraints, the function value, fractional derivative, and fractional integral constraints:
For these constraints, the constrained expression is derived using the formulation (6). Let the support functions be . Then, the constraints imply
By inverting the matrix, the coefficients can be computed in terms of the free functions:
whose approximated solution is
Then, all functions simultaneously satisfying the constraints given in (17) can be represented by the constrained expression:
5.3. Two Linear Combinations of Fractional Constraints
This example is provided to show how to proceed with a multiple linear combination of constraints. Let the constraints be
The constrained expression of these two constraints is derived using the TFC switching-projection formulation given in (7). Using the support functions , the switching functions are expressed in terms of the coefficients:
To better clarify, let us write the constraints (18) as
and express the switching conditions as
Therefore, in view of the linearity of and , the switching conditions are given by
After evaluating constraints and at the support functions and :
coefficients are computed by the simple matrix inversion [20]:
and the switching functions can be approximated as
The projection functionals are [20]
and by using the expressions provided by (19) and (20), the constrained expression representing all functions satisfying the constraints given in (18) is
The constrained expressions must be validated by showing that they satisfy all constraints, no matter what the free function is. In particular, by selecting , the functional interpolation problem is transformed into a simple interpolation problem that uses the support functions selected.
Equation (21) satisfies the constraints given in (18) for any free function. Let us prove it by selecting (for simplicity) , where c is an unknown constant. Using this free function, the projection functionals become
and using the approximated expression of the switching functions and the projection functionals, the constrained expression becomes
Thus, by replacing this expression in the constraints, we obtain the residuals:
which have values at the machine error level, as we show in Figure 3, where and are plotted as a function of (note that all available digits provided by Matlab were used for the coefficients and not just the few digits displayed in (19) and (22)).
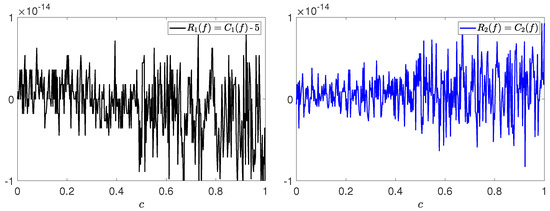
Figure 3.
Residual of the constraints (left plot) and (right plot) when applied to the functional given by (22).
6. Discussion
This work extended the application of the theory of functional connections (TFC), an analytical framework to derive functionals representing all functions interpolating a set of constraints, to constraints made of fractional-order operators (derivatives and integrals). The TFC has been developed for constraints defined by points, integer derivatives and integrals, limits, components, and any linear combination of them for the univariate and the multivariate case [20]. In this article, constraints made of fractional derivatives and fractional integrals for the univariate case were included in the TFC framework. Although the extension was presented for the Riemann–Liouville definition of the fractional derivative and integral, this choice is actually not restrictive, since the method presented can be used, as it is, for other definitions; the only difference is in the corresponding way to compute the fractional operators.
The representation of all functions’ interpolating set by the TFC for some linear constraints was obtained by deriving analytical functionals, called constrained expressions, containing a free function, . No matter what is, the constrained expression analytically satisfies the constraints, and in addition, by spanning all possible expressions of , the whole set of functions interpolating the constraints was obtained.
The extension was validated by three illustrative examples.
Author Contributions
Conceptualization, formal analysis, methodology, software, writing: D.M., R.G., and L.N.; supervision, D.M. and R.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| TFC | Theory of functional connections |
| SCP | Shifted Chebyshev polynomials |
Appendix A. Some Fractional Integrals and Derivatives with Closed-Form Expressions
Here, we provide closed-form expressions for fractional integrals and derivatives of some elementary functions. We refer to [25,36] for further results on this subject. Note that all operators are initialized at . Moreover, is any real number (possibly an integer) and .
with and denoting, respectively, the lower incomplete gamma function:
and the Mittag–Leffler function:
The fractional derivatives of trigonometric functions are useful when representing a function by Fourier series.
Appendix B. Non-Locality of Fractional Operators (Memory Effect)
This Appendix explains the smoothness properties and the “memory effect” of the fractional integral. Let us recall the definition of the Holder space, , with order :
The condition, which can also be defined for functions between metric spaces, generalizes the Lipschitzianity (if ) that characterizes a function that has limited growth, in the sense that the ratio between the variation of the ordinate and the variation of the abscissa can never exceed a fixed value, called the Lipschitz constant. It is a stronger condition than continuity. If , this condition reduces to the boundedness of the function.
Theorem A1.
Let for some and . Therefore [23],
for some Φ. This function Φ satisfies
for , where indicates that is the same order of the infinitesimal of for . Furthermore,
Theorem A2.
Let . Then,
for , where indicates that is an infinitesimal of higher order of for . If also , so and .
Memory effect property: Be and calculate the difference between two valuations in such that :
If , the second integral is canceled:
Therefore, H depends only on what happens in , and no information about is needed for . This property expresses the locality of the integer-order differential operator.
For the fractional case, the situation is different. In general, the first integral is not zero, and therefore, to evaluate H, it is necessary to know the history of from the initial point 0 to the point of interest; this is to underline the non-locality of fractional differential and integral operators, which characterizes the memory effect in the process.
Interesting applications of the memory effect of the fractional integrals are the description of the behavior of a crowd of pedestrians, especially to characterize the competitive and cooperative interactions between pedestrians [37], and the generalization of the dynamical model of love/hate [38].
Appendix C. Least-Squares Approaches
There are several different approaches to solve by least squares the over-determined linear system , where :
- The common solution: ;
- The QR decomposition: , then , where and R an upper-triangular matrix;
- The SVD decompositions: , then where and and where is the pseudo-inverse of , which is formed by replacing every non-zero diagonal entry by its reciprocal and transposing the resulting matrix;
- The Cholesky decomposition: , then , where U is an upper-triangular matrix.
To reduce the condition number of the matrix to invert, scaling the columns of matrix A:
is highly suggested. In (A9), S is the scaling diagonal matrix, whose elements are the inverse of the norms of the corresponding A matrix columns, , or the maximum absolute value, .
The least-squares approach adopted in this article is the scaled QR:
References
- Hilfer, R.; Butzer, P.; Westphal, U. An introduction to fractional calculus. In Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2010; pp. 1–85. [Google Scholar]
- Gorenflo, R.; Mainardi, F. Fractional calculus: Integral and differential equations of fractional order. arXiv 2008, arXiv:0805.3823. [Google Scholar]
- Caponetto, R.; Dongola, G.; Fortuna, L.; Petráš, I. Fractional Order Systems: Modeling and Control Applications; World Scientific: Singapore, 2010; pp. 1–178. [Google Scholar]
- Sasso, M.; Palmieri, G.; Amodio, D. Application of fractional derivative models in linear viscoelastic problems. Mech. Time-Depend. Mater. 2011, 15, 367–387. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 2022; pp. 37+587. [Google Scholar]
- Fomin, S.; Chugunov, V.; Hashida, T. Application of fractional differential equations for modeling the anomalous diffusion of contaminant from fracture into porous rock matrix with bordering alteration zone. Transp. Porous Media 2010, 81, 187–205. [Google Scholar] [CrossRef]
- Pritz, T. Five-parameter fractional derivative model for polymeric damping materials. J. Sound Vib. 2003, 265, 935–952. [Google Scholar] [CrossRef]
- Nualart, D. Stochastic calculus with respect to fractional Brownian motion. Ann. Fac. Sci. Toulouse Math. 2006, 15, 63–78. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional calculus in bioengineering: A tool to model complex dynamics. In Proceedings of the 13th International Carpathian Control Conference (ICCC), High Tatras, Slovakia, 28–31 May 2012; pp. 464–469. [Google Scholar] [CrossRef]
- Meerschaert, M.M. Fractional calculus, anomalous diffusion, and probability. In Fractional Dynamics: Recent Advances; World Scientific: Singapore, 2012; pp. 265–284. [Google Scholar]
- Liu, L.; Zheng, L.; Liu, F.; Zhang, X. Anomalous convection diffusion and wave coupling transport of cells on comb frame with fractional Cattaneo–Christov flux. Commun. Nonlinear Sci. Numer. Simul. 2016, 38, 45–58. [Google Scholar] [CrossRef]
- Bagley, R.L. Power law and fractional calculus model of viscoelasticity. AIAA J. 1989, 27, 1412–1417. [Google Scholar] [CrossRef]
- Beghin, L.; Garra, R.; Macci, C. Correlated fractional counting processes on a finite-time interval. J. Appl. Probab. 2015, 52, 1045–1061. [Google Scholar] [CrossRef]
- Antil, H.; Warma, M. Optimal control of fractional semilinear PDEs. ESAIM Control Optim. Calc. Var. 2020, 26, 30. [Google Scholar] [CrossRef]
- Zhao, Z.; Guo, Q.; Li, C. A fractional model for the allometric scaling laws. Open Appl. Math. J. 2008, 2, 26–30. [Google Scholar] [CrossRef]
- West, B.J. Fractal physiology and the fractional calculus: A perspective. Front. Physiol. 2010, 1, 12. [Google Scholar] [CrossRef]
- Giusti, A. MOND-like fractional Laplacian theory. Phys. Rev. D 2020, 101, 124029. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional econophysics: Market price dynamics with memory effects. Phys. A: Stat. Mech. Its Appl. 2020, 557, 124865. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. Theory and applications of differentiation and integration to arbitrary order, With an annotated chronological bibliography by Bertram Ross. In The Fractional Calculus; Academic Press: New York, NY, USA, 1974; Volume 111, p. 13+234. [Google Scholar]
- Leake, C.; Johnston, H.; Mortari, D. The Theory of Functional Connections: A Functional Interpolation. Framework with Applications; Lulu: Morrisville, NC, USA, 2022. [Google Scholar]
- Garrappa, R. Numerical solution of fractional differential equations: A survey and a software tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef]
- Artin, E. The Gamma Function; Courier Dover Publications: Miniola, NY, USA, 2015. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Scherer, R.; Kalla, S.L.; Tang, Y.; Huang, J. The Grünwald–Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef]
- Garrappa, R.; Kaslik, E.; Popolizio, M. Evaluation of Fractional Integrals and Derivatives of Elementary Functions: Overview and Tutorial. Mathematics 2019, 7, 407. [Google Scholar] [CrossRef]
- Mortari, D. The Theory of Connections: Connecting Points. Mathematics 2017, 5, 57. [Google Scholar] [CrossRef]
- Mortari, D. Least-Squares Solution of Linear Differential Equations. Mathematics 2017, 5, 48. [Google Scholar] [CrossRef]
- Mortari, D.; Johnston, H.R.; Smith, L. High accuracy least-squares solutions of nonlinear differential equations. J. Comput. Appl. Math. 2019, 352, 293–307. [Google Scholar] [CrossRef] [PubMed]
- Leake, C.D. The Multivariate Theory of Functional Connections: An n-Dimensional Constraint Embedding Technique Applied to Partial Differential Equations. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2021. [Google Scholar]
- Johnston, H.R. The Theory of Functional Connections: A Journey from Theory to Application. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2021. [Google Scholar]
- Schiassi, E.; Furfaro, R.; Leake, C.D.; Florio, M.D.; Johnston, H.R.; Mortari, D. Extreme theory of functional connections: A fast physics-informed neural network method for solving ordinary and partial differential equations. Neurocomputing 2021, 457, 334–356. [Google Scholar] [CrossRef]
- Wang, Y.; Topputo, F. A TFC-based homotopy continuation algorithm with application to dynamics and control problems. J. Comput. Appl. Math. 2022, 401, 113777. [Google Scholar] [CrossRef]
- Yassopoulos, C.; Leake, C.D.; Reddy, J.; Mortari, D. Analysis of Timoshenko–Ehrenfest beam problems using the Theory of Functional Connections. Eng. Anal. Bound. Elem. 2021, 132, 271–280. [Google Scholar] [CrossRef]
- Johnston, H.R.; Schiassi, E.; Furfaro, R.; Mortari, D. Fuel-Efficient Powered Descent Guidance on Large Planetary Bodies via Theory of Functional Connections. J. Astronaut. Sci. 2020, 67, 1521–1552. [Google Scholar] [CrossRef]
- Wolfram, D.A. Change of Basis between Classical Orthogonal Polynomials. arXiv 2021, arXiv:2108.13631. [Google Scholar]
- Dorrah, A.; Sutrisno, A.; Desfan Hafifullah, D.; Saidi, S. The Use of Fractional Integral and Fractional Derivative “α=5/2” in the 5-th Order Function and Exponential Function using the Riemann–Liouville Method. Appl. Math. 2021, 11, 23–27. [Google Scholar]
- Cao, K.; Chen, Y.; Stuart, D. A fractional micro-macro model for crowds of pedestrians based on fractional mean field games. IEEE/CAA J. Autom. Sin. 2016, 3, 261–270. [Google Scholar] [CrossRef]
- Ahmad, W.M.; El-Khazali, R. Fractional-order dynamical models of love. Chaos Solitons Fractals 2007, 33, 1367–1375. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).