A Co-Optimization Algorithm Utilizing Particle Swarm Optimization for Linguistic Time Series

Abstract

The linguistic time-series forecasting model (LTS-FM), which has been recently proposed, uses linguistic words of linguistic variable domains generated by hedge algebras (HAs) to describe historical numeric time-series data. Then, the LTS-FM was established by utilizing real numeric semantics of words induced by the fuzziness parameter values (FPVs) of HAs. In the existing LTS-FMs, just the FPVs of HAs are optimized, while the used word set is still chosen by human experts. This paper proposes a co-optimization method of selecting the optimal used word set that best describes numeric time-series data in parallel with choosing the best FPVs of HAs to improve the accuracy of LTS-FMs by utilizing particle swarm optimization (PSO). In this co-optimization method, the outer loop optimizes the FPVs of HAs, while the inner loop optimizes the used word set. The experimental results on three datasets, i.e., the “enrollments of the University of Alabama” (EUA), the “killed in car road accidents in Belgium” (CAB), and the “spot gold in Turkey” (SGT), showed that our proposed forecasting model outperformed the existing forecasting models in terms of forecast accuracy.

1. Introduction

The human ability to predict future events and phenomena has attracted the interest of the scientific community for many years, with many forecasting methodologies proposed based on observed historical data. In particular, the forecasting method based on time-series analysis has been investigated by numerous researchers using various models, such as ARMA, ARIMA, and so on. In time-series forecasting models, future values can be forecasted based on only past data. The characteristics of time-series data, such as trends, seasonality, stability, outliers, etc., have been considered to establish forecasting models for future values.

The fuzzy time series proposed by Q. Song and B. S. Chissom [1,2,3] is a forecasting method of time-series analysis that combines the principles of the fuzzy set theory proposed by L. A. Zadeh [4] with traditional time-series techniques. The fuzzy time series is particularly useful in handling the uncertainty, vagueness, and imprecision of data, which is often encountered in real-world applications. The approach allows for modeling the uncertainty and vagueness of the data by representing the relationships between linguistic variables as fuzzy sets rather than crisp sets. In a fuzzy time series, the forecasted values are not simply single-point estimates, but rather a range of values that reflect the uncertainty in the data. This provides a more realistic and robust representation of future trends in the time series, especially when dealing with non-linear and complex data. Fuzzy time series have been applied in a variety of domains, including finance, economics, environmental science, and engineering, where traditional time-series methods may not be adequate. Recently, many proposed models use optimization algorithms, such as genetic algorithm [5,6], particle swarm optimization (PSO) [7,8], etc., to optimize forecasting model parameter values to improve the forecasting accuracy.

People often use natural language as a tool to communicate effectively with each other. They also store and process recorded information through linguistic variables with their values. Linguistic values are also used by humans to forecast events occurring in nature and society so that they can better prepare for future planning. In addition to the fuzzy set theory for handling linguistic variables, hedge algebras (HAs), proposed by N. C. Ho and W. Wechler [9,10], exploit the order-based semantics structure of the word domains of linguistic variables, which provides a mathematical formalism for generating the computational semantics of words that can be applied to solve real-life application problems in various domains, such as image processing [11], fuzzy control [12], data mining [13,14,15,16,17], etc. HAs are qualitative models; therefore, they need to be quantified by measurable quantities based on qualitative semantics. The words of linguistic variables convey their qualitative semantics in relation to the other words in the whole variable domain. Because the linguistic words of a variable are interdependent, they only disclose their full qualitative semantics in the comparative context of the whole variable domain. The fuzziness measure of linguistic words [18] is the crucial concept of fuzzy information and plays an important role in quantification by hedge algebras. The quantitative or numerical semantics of a word induced by its fuzziness measure is the semantically quantifying mapping (SQM) value that is the basis for generating computational semantics for solving real-world application problems. Recently, hedge algebras have been applied to solve time-series forecasting problems in such a way that historical numeric time-series data are transformed into linguistic data by using the real numeric semantics of words defined based on their corresponding SQM values. Then, the LTS-FMs were established [19,20,21,22].

In LTS-FMs, instead of partitioning historical data into intervals, a datum of the historical data is assigned a linguistic word based on the nearest real numeric semantic. By doing so for all historical data, the numeric time series is transformed into an LTS. The linguistic words used to describe historical data are used to define the logical relationship between the data of the current year and those of the next year. Then, the linguistic logical relationships (LLRs) and linguistic logical relationship groups (LLRGs) are established. The fuzzy forecasted values are induced and, finally, based on them, the corresponding crisp forecasted values are computed. It can be seen that the SQM values of words determined by the FPVs of HAs are crucial in establishing LTS-FMs. Obtaining an optimal set of FPVs is not a trivial task, so an optimization algorithm should be applied to obtain it automatically. Among the optimization algorithms, PSO is efficient and is applied to solving many real-world problems [7,8,14,16,21]. It needs few algorithm parameters, so it is easy to implement. In [21], the FPVs of HAs were automatically optimized for LTS-FMs by applying PSO. However, the word set used to describe numeric time-series data was chosen by human experts, so the selected words may not have reflected the nature of the historical data. To overcome this drawback, this paper presents a method of selecting an optimal word set that best describes numeric time-series data in parallel with optimizing the FPVs of HAs by applying a co-optimization algorithm of particle swarm optimization (Co-PSO). In Co-PSO, the outer loop optimizes the FPVs of HAs, while the inner loop optimizes the used word set. The experimental results for three datasets, i.e., the “enrollments of the University of Alabama” (EUA), the “killed in car road accidents in Belgium” (CAB), and the “spot gold in Turkey” (SGT), showed that our proposed forecasting model had better forecasting accuracy than the existing models.

The remainder of this paper is organized as follows. Section 2 briefly restates the theory of hedge algebras and some concepts related to LTS-FM and PSO. The proposed forecasting model, called COLTS, is introduced in Section 3. In Section 4, some experiments with three datasets and discussions about the forecasted results are addressed. Finally, the summary of this work and some suggestions for future work are provided in Section 5.

2. Background

2.1. A Brief Introduction of Hedge Algebras

Each linguistic domain of variable $𝒳$, denoted by Dom($𝒳$), consists of a word set that can be generated from two generator words, e.g., “cold” and “hot”, by the action of linguistic hedges on them. For example, with two hedges of “very” and “rather”, the words generated by the action of two those hedges on the two generator words of “cold” and “hot” can be “very cold”, “rather cold”, “very hot”, “very very hot”, and so on. It can be observed that they are linearly ordered and are comparable, e.g., “very cold” ≤ “cold” ≤ “rather cold” ≤ “hot” ≤ “very hot” ≤ “very very hot”.

From the above intuitive observation, Ho et al. introduced hedge algebras (HAs) in 1990 [9,10], a mathematical structure that can directly manipulate the word domain of $𝒳$. An HA of $𝒳$, denoted by $\mathcal{AX}$$,$ is an order-based structure $\mathcal{AX}$ = (X, G, C, H, ≤), where X ⊆ Dom($𝒳$) is a word set of $𝒳$; G = {c⁻, c⁺} is a set of two generators, where c⁻ ≤ c⁺; C = {0, W, 1} is a set of three constants satisfying the order relationship 0 ≤ c⁻ ≤ W ≤ c⁺ ≤ 1, where 0, 1, and W are the lowest, highest, and neutral constants, respectively; a set of hedges of H = H⁻ ∪ H⁺, where H⁻ and H⁺ are the negative and positive hedges, respectively; and ≤ is an operator that indicates the order relation between the inherent word semantics of $𝒳$.

String representation can be used to represent the words in X, so a word x ∈ X is either c or ωc, where c ∈ {c⁻, c⁺}, ω = h_n…h₁, h_i ∈ H, i = 1, …, n. H(x) denotes all words generated from x, so H(x) = {ωx, ω ∈ H}. If all hedges in H are linearly ordered, all words in X are also linearly ordered. In this case, linear HA is achieved. Hereafter, some main properties of the linear Has are presented:

• The signs of the negative generator c⁻ and the positive generator word c⁺ are sign(c⁻ = −1 and sign(c⁺) = +1, respectively;
• Every h ∈ H⁺ increases the semantic of c⁺ and has sign(h) = +1, whereas, every h ∈ H^- decreases the semantic of c⁻ and has sign(h) = −1;
• If hedge h strengthens the of hedge k, the relative sign between h and k is sign(h, k) = +1. On other hand, if the hedge h weakens the semantic of the hedge k, sign(h, k) = −1. Thus, the sign of a word x = h_nh_n−1…h₂h₁c is specified as follows:

sign(x) = sign(h_n, h_n−1) × … × sign(h₂, h₁) × sign(h₁) × sign(c).

Based on the word sign, if sign(hx) = +1, x ≤ hx, and if sign(hx) = −1, hx ≤ x.

Based on the syntactical semantics of words generated by HAs, the words in H(x), x ∈ X, induced from x, have had their semantics changed by the hedges in H, but they still convey the original semantics of x. Therefore, H(x) can be considered as the fuzziness of x and the diameter of H(x) is considered as the fuzziness measure of x, denoted by fm(x).

Assume that AX is a linear HA. The function fm: X → [0, 1] is the fuzziness measure of the words in X, provided that the following properties are satisfied [13]:

(F1): fm(c⁻) + fm(c⁺) = 1 and ${\displaystyle \sum }_{h\in H}fm\left(hu\right)=fm\left(u\right)$, for $\forall u\in X$;

(F2): fm(x) = 0 for all H(x) = x, especially, fm(0) = fm(W) = fm(1) = 0;

(F3): $\forall x,y\in X,\forall h\in H$, the proportion $\frac{fm\left(hx\right)}{fm\left(x\right)}=\frac{fm\left(hy\right)}{fm\left(y\right)}$ is called the fuzziness measure of hedge h, denoted by μ(h).

From the properties of (F1) and (F3), fm(x), where x = h_n…h₁c and c ∈ {c⁻, c⁺}, is computed as fm(x) = μ(h_n)… μ(h₁)fm(c), where ${\displaystyle \sum }_{h\in H}\mu \left(h\right)=1$. For a given word in X, its fuzziness measure can be computed when the values of fm(c) and μ(h_j) ∈ H are specified.

Semantically quantifying mapping (SQM) [13] of AX is a mapping of $v:X\to \left[0,1\right]$, provided that the following conditions are satisfied:

(SQM1): It preserves the order-based structure of X, i.e., $x\le y\to v\left(x\right)\le v\left(y\right),\forall x\in X$;

(SQM2): It is one-to-one mapping and $v\left(x\right)$ is dense in [0, 1].

Let fm be a fuzziness measure on X, ${\displaystyle \sum }_{i=-q}^{-1}\mu \left(h_i\right)=\alpha$, ${\displaystyle \sum }_{i=1}^p\mu \left(h_i\right)=\beta$, $\alpha ,\beta >0$, and $\alpha +\beta =1$. $v\left(x\right)$ is computed recursively based on fm as follows:

(1)

$v\left(W\right)=\theta =fm\left(c^{-}\right),v\left(c^{-}\right)=\theta -\alpha fm\left(c^{-}\right)=\beta fm\left(c^{-}\right),v\left(c^{+}\right)=\theta +\alpha fm\left(c^{+}\right)$;

(2)

$v\left(h_{j}x\right)=v\left(x\right)+sign\left(h_{j}x\right)\left({\displaystyle \sum }_{i=sign\left(j\right)}^{j}fm(h_{i}x)-\omega \left(h_{j}x\right)fm\left(h_{j}x\right)\right)$, where j ∈ [−q^p] = {j: −q ≤ j ≤ p & j ≠ 0} and

$$\omega (h_{j}x)=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.[1+sign(h_{j}x)sign(h_p{h}_{j}x)(\beta -\alpha )]\in \{\alpha ,\beta \}.$$

The SQM values of words are the basis of computing the real numerical semantics of words, and then a time series is transformed into LTS.

2.2. Linguistic Time Series-Forecasting Model

Based on the theory of hedge algebras, Hieu et al. [19] introduced the concept of LTS and its application to the enrollment forecasting problem. The quantitative (numerical) semantics, known as SQM values, of linguistic words were directly used to establish the LTS-FM. Specifically, the numerical semantics of words were linearly transformed to the real numerical semantic domain of the universe of discourse (UD) of the linguistic variable. Thus, each datum of a time series, whether recorded in numerical or linguistic values, could be naturally associated with the corresponding real numerical semantics of the used linguistic words of the LTS. These are also the distinguishing and outstanding properties of LTS compared with fuzzy time series.

In order to have a theoretical basis for proposing a forecasting model, in this subsection, some concepts of LTS proposed by Hieu et al. [19] are presented.

Definition 1

([19]). (LTS) Let 𝕏 be a set of natural linguistic words of variable $𝒳$ defined on the UD to describe its numeric values. Then, any chronological series L(t), t = 0, 1, 2, …, where L(t) is a finite subset of 𝕏, is called a linguistic time series.

Definition 2

([19]). (LLR) Suppose X_i and X_j are the linguistic words representing the data at time t and t + 1, respectively. Then, there exists a relationship between X_i and X_j called a linguistic logical relationship (LLR), denoted by

X_i → X_j

Definition 3

([19]). (LLRG) Assume that there are LLRs, such as

X_i → X_j1,

X_i → X_j2,

…

X_i → X_jn.

Then, they can be grouped into a linguistic logical relationship group (LLRG) and are denoted by

X_i → X_j1, X_j2, …, X_jn.

In [19], Hieu et al. also presented a forecasting model called LTS-FM. The procedure of an LTS-FM is depicted in Figure 1.

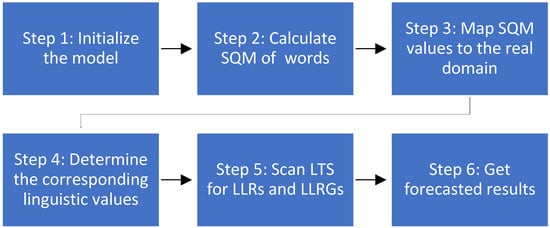
Figure 1. The procedure of an LTS-FM.

In Figure 1, the LTS-FM procedure includes six steps, which can be briefly described as follows (for more detail, please see [19,22]):

Step 1. Determine the UD of the linguistic variable, the syntactical semantics, and the FPVs of the associated Has, and choose the used linguistic words to describe the designated time series;

Step 2. Calculate the quantitative semantics of the used words;

Step 3. Map the quantitative semantics of the used words to the real domain of the UD to obtain the real numerical semantics;

Step 4. Transform the designated time series into LTS. For each specified datum, its semantics are specified based on the nearest real semantic;

Step 5. Establish the LLRs of words, then group them into the LLRGs;

Step 6. Forecast based on LLRGs, then compute the crisp forecasted values.

The evaluation measures of the forecasting models are the mean-square error (MSE), the root-mean-square error (RMSE), and the mean-absolute-percentage error (MAPE) which are calculated as follows:

$$MSE=\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n{\left(F_i-R_i\right)}^2,$$

(1)

$$RMSE=\sqrt{MSE},$$

(2)

$$MAPE=\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n\left|\frac{F_i-R_i}{F_i}\right|\times 100\%.$$

(3)

where n denotes the number of forecasted data, and F_i and R_i are the forecasted and real data at the time i, respectively.

2.3. Standard PSO

In 1995, Kennedy and Eberhart introduced an optimization method, so-called particle swarm optimization (PSO) [22,23]. This is a swarm intelligence-based optimization method that has been applied to solve a lot of real-world problems. It mimics the way the birds fly to find food sources. The birds in the swarm will follow the leader who is the nearest to the food source. Suppose that a swarm S = {x₁, x₂, …, x_N} with N particles, with each particle’s position being $X_i^t$ at generation t computed as follows:

$$X_i^{t+1}=X_i^t+V_i^{t+1},$$

(4)

where $V_i^{t+1}$ is x_i’s velocity at generation t + 1, computed as follows:

$$V_i^{t+1}=\omega \times V_i^t+c_1\times r_1\times (P_i^t-X_i^t)+c_2\times r_2\times (P_g^t-X_i^t),$$

(5)

where $P_g^t$ and $P_i^t$ are the best global and local solutions found so far, respectively; r₁ and r₂ are two random numbers uniformly distributed in [0, 1]; and c₁, c₂, and ω are self-cognitive coefficient, social cognitive coefficient, and inertia weight, respectively. The standard PSO is described in brief as follows:

Step 1: Initialize a swarm S with two random vectors, the position vector X and velocity vector V. Initialize the number of cycle constants N and the cycle variable t;

Step 2: Calculate each particle’s objective value f($X_i^t$);

Step 3: Check each particle’s objective. If the current position $X_i^t$ is better than the personal best $P_i^t$ then update $P_i^t$ with $X_i^t$;

Step 4: Check if there exists the best particle position in the current cycle whose objective value is better than the objective value of the global best $P_g^t$, then update $P_g^t$ with the best particle position;

Step 5: Update each particle’s velocity $V_i^t$ by Equation (4) and move to its new position $X_i^t$ by Equation (5);

Step 6: Terminate if variable t reaches the maximum number of cycles; otherwise, let t = t + 1 and go to Step 2.

3. Improve the LTS-FM by the Co-Optimization of PSO

In this subsection, a hybrid LTS-FM integrated with particle swarm co-optimization (COLTS) is presented. In the LTS-FMs, the word set in the domain of a linguistic variable is generated automatically by hedge algebras associated with a linguistic variable. Therefore, the cardinality of the generated word set is unlimited. However, in a specific period, a given number of words are selected to describe the numeric time series. The number of automatically generated words depends on the max specificity level k of the words specified by human experts, and the maximum word length in the word domain is equal to k.

In the proposed optimization model of LTS presented in [21], the word set used to describe the historical numeric time-series data (so-called used word set) should be selected intuitively by human experts before the fuzziness parameter value optimization processes. Hence, the used word set depends on the human expert’s intuition and may not be optimal. To select the optimal used word set to best describe historical numeric time-series data from the linguistic variable domain, an optimization process should be executed. The FPVs should be optimized in parallel with the word set’s selection to select the best numerical semantics of used words. Therefore, a co-optimization process for concurrently selecting the optimal used word set and FPVs is applied by utilizing PSO. Specifically, the co-optimization process includes inner and outer loops. The inner loop (inner PSO) optimizes the used word set, while the outer loop (outer PSO) optimizes the FPVs. Real encoding is used for both the outer and inner loops. Specifically, as in other applications of hedge algebras [11,12,13,14,15,16,17], in our experiments, only two linguistic hedges (Little and Very) are used to generate the word set of the linguistic variable domain, so the number of optimized FPVs is only 2. They are the fuzziness measure of one of two generator words (e.g., fm(c⁻)) and the fuzziness measure of one of two hedges (e.g., $\mu \left(Little\right)$). From the constraints of fm(c⁻) + fm(c⁺) = 1 and $\mu \left(Little\right)+\mu \left(Very\right)=1$, it can be inferred that fm(c⁺) = 1 − fm(c⁻) and $\mu \left(Very\right)=1-\mu \left(Little\right)$. Each particle of the outer loop $Y_i^t$ = {fm(c⁻), $\mu \left(Little\right)$}, i = 1, …, N, in the swarm represents those two FPVs. For the inner loop, each particle corresponds to a solution represented as an array of real numbers $p_i=\left(w_1,\dots ,w_{d_w},w_j\in \left[0,1\right]\right)$. Each word x_l of the used word set X_i is selected from word set W_set of ${\mathcal{X}}_L$ by the zero-based index, as follows:

$$X_i^t=\{x_l\in W_{set}|l=\lfloor w_j\times \left|W_{set}\right|\rfloor ,0\le l<\left|W_{set}\right|\}$$

(6)

where $\lfloor \cdot \rfloor$ denotes the integer part of a real number.

The details of all steps of the proposed co-optimization algorithm are as follows (Algorithms 1 and 2):

Algorithm 1. UWO (Gwmax, Wset, dw, δ)//Used word set-optimization procedure

Input:    Parameters: Gwmax, Wset, dw, δ;    // Gwmax is the number of generations, Wset is the word set of ${\mathcal{X}}_L$, dw is the cardinality of the used word set selected from Wset, δ is a set of FPVs. Output: The optimal word set $S_g^{G_{wmax}-1}$ and the associated best MSE value; Begin   Randomly initialize a swarm W0 = {$Y_i^0;V_i^0$ | i = 1, …, M, |$Y_i^0$|= dw};   //$Y_i^t$ is a subset of index values in interval [0, |Wset|], where |Wset| is the cardinality of Wset, |$Y_i^t$| is the number of elements of $Y_i^t$.   Sort the elements of $Y_i^0$;   For each particle xi in swarm do begin     Implement the LTS forecasting procedure from Step 2 to Step 6 based on δ and $Y_i^0$;     Evaluate the value of the MSE of xi by Equation (1);     Assign the personal best position $S_i^0$ of xi to the current position;   End;   Assign the global best position $S_g^0$ to the best position in current swarm;    t = 1;   Repeat     For each particle xi in swarm do begin       Compute new velocity $V_i^t$ of xi by Equation (5);       Compute new position $Y_i^t$ of xi by Equation (4);       Sort the elements of $Y_i^t$;       Implement the LTS forecasting procedure from Step 2 to Step 6 based on δ and $Y_i^t$;       Evaluate the value of the MSE of xi by Equation (1);       If $Y_i^t$ is better than $Y_i^{t-1}$ then        Update $S_i^t$ of xi based on the value of MSE;       End;      End;      Update $S_g^t$ based on the values of MSE;      t = t + 1;   Until t = Gwmax;   Return the best position $S_g^{G_{wmax}-1}$ and its best MSE value; End.

Algorithm 2. PSCO_FPVO//Fuzziness parameter value optimization

Input: The designated time-series dataset D;    Parameters: N, Gmax, Gwmax, the syntactical semantics of HAs, kmax, dw;    //Gmax and Gwmax are the number of generations of outer and inner PSO, respectively; kmax is the maximum word length; dw is the used word set’s cardinality. Output: The optimal FPVs $P_g^{G_{max}-1}$ and the best-used word set W*set; Begin   Generate the word set Wset of ${\mathcal{X}}_L$ with the maximum word length kmax utilizing HA;   Randomly initialize a swarm S0 = {$X_i^0;V_i^0$ | i = 1, …, N}, where $X_i^0=\left\{fm\left(c^{-}\right),\mu \left(Little\right)\right\}$;   //$X_i^t$ is a set of FPVs   //The best used word set W*set and the best MSE value MSE*   (W*set, MSE*) = (∅, +∞);   For each particle xi do begin    (W*set, MSE*) = UWO(Gwmax, Wset, dw, δ = $X_i^0$); //call the inner PSO    $F_i^0$ = MSE*; //Fitness value associated with particle xi    Assign the personal best position $P_i^0$ of xi to the current position;   End;   Assign the global best position $P_g^0$ the best position in current swarm;   t = 1;   Repeat    For each particle xi do begin      Compute new velocity $V_i^t$ of xi by Equation (5);      Compute new position $X_i^t$ of xi by Equation (4);      (Wtmp_set, MSE) = UWO(Gwmax, Wset, dw, δ = $X_i^t$); //call the inner PSO      $F_i^t$ = MSE; //Fitness value associated with particle i      If $F_i^t$ is better than $F_i^{t-1}$ then begin        Update the personal best $P_i^t$ of xi based on $F_i^t$’s value;        If MSE is better than MSE* then begin          (W*set, MSE*) = (Wtmp_set, MSE);          Update the global best position $P_g^t$;        End;      End;    End;    t = t + 1;  Until t = Gmax;  Return the best position $P_g^{G_{max}-1}$ and W*set; End.

As shown in the UWO and PSCO_FPVO algorithms, the PSCO_FPVO algorithm optimizes the FPVs and runs as an outer iteration of COLTS. Each particle of PSCO_FPVO represents a given FPV set $X_i^t=\left\{fm\left(c^{-}\right),\mu \left(Little\right)\right\}$, which is the input of UWO. In turn, UWO finds the optimally used word set from word set W_set of ${\mathcal{X}}_L$ based on the given FPV set as its input. Each particle of UWO represents a given used word set. The output of UWO includes the local best used word set contained in $S_g^{G_{wmax}-1}$ corresponding to the input FPV set and the associated local best MSE value. The output of PSCO_FPVO includes the best FPV set contained in $P_g^{G_{max}-1}$ and the global best used word set W^*_set, which is the best found solution so far.

4. Experimental Studies and Discussion

The experiments aim to show the necessity of optimizing the used linguistic word set to describe a numeric time series in parallel with optimizing FPVs, and our proposed forecasting models outperformed the models used for comparison. To show the efficiency of our proposed models, their experimental results on the three forecasting problems of the EUA, CAB, and GT were evaluated and compared with those proposed by Uslu et al. [6], Chen et al. [8], and Phong et al. [21]. The objective function of the optimization problem is the MSE. The values of MSE, RMSE, and MAPE were used to evaluate the forecasting models used for comparison.

In the experiments, our proposed forecasting models were implemented using the C# programming language running on Microsoft Windows 10 64 bit with the hardware configuration of an Intel Core i5-8250U 1.6 GHz CPU integrated with 8 GB of RAM. Each experiment was attempted five times. Then, the smallest obtained MSE values were chosen as the forecasting accuracy.

To limit the running time, the parameter values of the optimization algorithm were set as in the existing forecasting models; for the inner iteration, the number of cycles was 100 and the number of particles was 30, and for the outer iteration, the number of cycles was 30 and the number of particles was 20. By trial and error and our experience in applying PSO in our previous studies, for both inner and outer iterations, the Inertia weight ω was 0.4, and both the self-cognitive factor c₁ and the social cognitive factor c₂ were 2.0.

4.1. Forecast the “Enrollments of the University of Alabama”

To show the efficiency of the proposed LTS-FM described above, it was applied to forecast the EUA, as shown in Table 1. As in the counterparts, the UD of the EUA was U = [13,000, 20,000] and the number of linguistics used to describe the numeric time series was 16. Instead of partitioning U into the intervals in the existing methods, it was transformed into linguistic words to form an LTS in our proposed forecasting methods. The linguistic word set was generated by the associated hedge algebras, so its cardinality was not limited. In fact, in a specific period, the number of words used to describe the numeric time series was limited. Therefore, PSO was applied to select the best used word set to improve the accuracy of the forecasting model.

Table 1. Comparative simulation of the enrollments forecast in the case of 16 used words and a maximum word length of 5.

Year	Enrollments	CCO6 [5]	HPSO [7]	Uslu et al. [6]	Chen et al. [8]	Phong et al. [21]	COLTS3	COLTS4	COLTS5
1971	13,055
1972	13,563	13,714	13,555	13,650	13,469	13,515	13,515	13,562	13,598
1973	13,867	13,714	13,994	13,650	13,952	14,001	14,001	13,759	13,900
1974	14,696	14,880	14,711	14,836	14,596	14,800	14,800	14,722	14,817
1975	15,460	15,467	15,344	15,332	15,439	15,509	15,509	15,412	15,445
1976	15,311	15,172	15,411	15,447	15,241	15,509	15,509	15,464	15,487
1977	15,603	15,467	15,411	15,447	15,925	15,509	15,509	15,464	15,487
1978	15,861	15,861	15,411	15,447	15,880	15,752	15,752	15,798	15,877
1979	16,807	15,831	16,816	16,746	16,801	16,693	16,693	16,799	16,805
1980	16,919	17,106	17,140	17,075	17,009	16,949	16,949	16,975	16,995
1981	16,388	16,380	16,464	16,380	16,260	16,779	16,779	16,431	16,323
1982	15,433	15,464	15,457	15,504	15,435	15,553	15,553	15,412	15,445
1983	15,497	15,172	15,447	15,431	15,212	15,509	15,509	15,464	15,487
1984	15,145	15,172	15,447	15,077	15,282	15,132	15,132	15,286	15,221
1985	15,163	15,467	15,332	15,297	15,344	15,132	15,132	15,312	15,241
1986	15,984	15,467	16,027	15,848	15,714	15,752	15,752	15,824	15,898
1987	16,859	16,831	16,746	16,835	16,833	16,693	16,693	16,833	16,825
1988	18,150	18,055	18,211	18,145	18,016	17,888	17,888	18,193	18,205
1989	18,970	18,998	19,059	18,880	18,937	18,911	18,911	18,833	18,845
1990	19,328	19,300	19,059	19,418	19,345	19,439	19,439	19,246	19,389
1991	19,337	19,149	19,059	19,260	19,147	19,307	19,307	19,143	19,253
1992	18,876	19,149	19,059	19,031	19,152	19,043	19,043	18,936	18,981
MSE		35,324	31,722	31,684	23,710	22,403	22,403	9755	6332
RMSE		187.95	178.11	178.00	153.98	149.68	149.68	98.77	79.57
MAPE		1.13%	0.84%	0.90%	0.73%	0.72%	0.72%	0.49%	0.40%

To facilitate a significant comparison with the existing methods, seven, fourteen, and sixteen linguistic words were, in turn, used to describe U, and to show the significance of the word length; the maximum word length was, in turn, limited to 3, 4, and 5. The best MSE and MAPE values in accordance with the best word set selected by the inner iteration of the linguistic word optimization process and the best FPVs optimized by the outer iteration are shown in Table 2. It can be seen that, with the same number of used words, the higher the maximum word length was, the better the MSE value we obtained. However, this was not absolutely true when slightly increasing the number of used words. In the case of a maximum word length of 3, the LTS-FMs with 14 used words were better than that with 16 used words when compared by both the MSE and MAPE values. The cause of this situation will be analyzed more deeply in a future study. It may be attributed to the limitation of the cardinality of the word domain of the linguistic variable. According to the theory of HAs [9,10], when limiting the maximum word length to 3 and 2 linguistic hedges, the number of words in the word domain generated by the associated HAs is only 17. In the case of 16 used words, to choose 16 words out of 17, PSO does not have much choice, and among them, at least one word has semantics that are suitable for the natural distribution of time-series data, leading to worse forecasted results than those obtained in the case of 14 used words. In the case of maximum word lengths of 4 and 5, the higher the number of used words was, the better the MSE value we obtained. Therefore, the best MSE was reached in the case of 16 used words and a maximum word length of 5.

Table 2. The MSE values of the first-order LTS-FMs with different numbers of words and different maximum word lengths.

Maximum Word Length	Evaluation Method	Number of Used Words	Number of Used Words	Number of Used Words
		7	14	16
3	MSE	24,111	19,989	22,415
	MAPE	0.80%	0.63%	0.72%
4	MSE	21,284	10,853	9758
	MAPE	0.74%	0.50%	0.49%
5	MSE	19,795	9639	6332
	MAPE	0.72%	0.44%	0.40%

To show the efficiency of our proposed LTS-FMs with co-optimization PSO in comparison with other forecasting models, the best experimental results of the proposed LTS-FMs with maximum word lengths of 3, 4, and 5, denoted by COLTS3, COLTS4, and COLTS5, respectively, were compared with the state-of-the-art LTS-FM of Phong et al. [21] and the existing FTS-FMs, such as the CCO6 model of Chen and Chung, applying a genetic algorithm [5], HPSO [7], applying a PSO algorithm, Uslu et al. [6], considering the number of iterations of a fuzzy logical relationship, and Chen et al. [8], applying PSO and a new defuzzification technique. The experimental results and their comparative presentation are shown in Table 1 and visualized in Figure 2. By analyzing the experimental results shown in Table 1, it can be recognized that our proposed LTS-FM with a word length of 3 (COLTS3) had the same MSE and MAPE values as the LTS-FM proposed by Phong et al. [21] and had better MSE and MAPE values than those of FTS-FMs CCO6 [5], HPSO [7], Uslu et al. [6], and Chen et al. [8]. Meanwhile, both COLTS4 and COLTS5 had better MSE and MAPE values than those of the compared forecasting models. Recall that the word set used to describe the numeric time-series data in the LTS-FM proposed in [21] was chosen by human experts. Therefore, it depended on their cognitive recognition. To achieve a better result, they could also perform some trial and error to obtain the best word set. The number of cycles and the number of particles of the PSO in [21] were too large, at 1000 and 300, respectively. Based on the comparison results described above, it can be stated that the proposed LTS-FMs were better than the FTS-FMs and the COLTS5 was the best.

Figure 2. Comparison chart of the forecasted values of the EUA of the compared forecasting models.

4.2. Forecast the “Killed in Car Road Accidents in Belgium”

The proposed LTS-FMs were also applied to the CAB’s problem to evaluate them again. The minimum and maximum values of the historical data of CAB observed from 1974 to 2004 were 953 and 1644, respectively. Thus, the UD was defined as U = [900, 1700]. The number of used words was set to 17, which was equal to the number of intervals in [6,8].

It is easy to see from the comparison results in Table 3 that the MSE values of COLTS3, COLTS4, and COLTS5 were, in turn, 794, 444, and 421, which were much better than those of the compared forecasting methods of Uslu et al. [6] and Chen et al. [8], which were 1731 and 1024, respectively. When comparing by the MAPE values, we can also see that all three of our LTS-FMs, COLTS3, COLTS4, and COLTS5, had better MAPE values than those of Uslu et al. and Chen et al. [6,8], respectively. Therefore, our proposed LTS-FMs outperformed the FTS-FMs presented in [6,8] in forecasting the problem of CAB. In addition, among our three LTS-FMs, COLTS5 was better than COLTS4 and, in turn, COLTS4 was better than COLTS3. Therefore, the statement “with the same number of used words, the longer the maximum word length is, the better MSE value we obtain” presented above is also true for the CAB problem.

Table 3. Comparative simulation of CAB forecast in the case of 16 used words and a maximum word length of 5.

Year	Actual Data	Uslu et al. [6]	Chen et al. [8]	COLTS3	COLTS4	COLTS5
1974	1574
1975	1460	1506	1451	1498	1495	1464
1976	1536	1453	1490	1500	1502	1515
1977	1597	1598	1622	1555	1592	1610
1978	1644	1584	1575	1593	1638	1623
1979	1572	1584	1593	1579	1568	1568
1980	1616	1506	1585	1593	1582	1610
1981	1564	1584	1582	1557	1560	1583
1982	1464	1506	1513	1485	1464	1462
1983	1479	1453	1494	1474	1471	1474
1984	1369	1375	1393	1423	1367	1381
1985	1308	1383	1336	1352	1333	1315
1986	1456	1454	1419	1450	1440	1462
1987	1390	1453	1485	1411	1417	1428
1988	1432	1383	1384	1419	1399	1391
1989	1488	1509	1459	1474	1479	1483
1990	1574	1598	1585	1534	1572	1580
1991	1471	1506	1451	1498	1500	1468
1992	1380	1375	1369	1411	1367	1381
1993	1346	1383	1361	1377	1333	1323
1994	1415	1383	1437	1400	1392	1381
1995	1228	1231	1217	1213	1276	1250
1996	1122	1135	1152	1136	1139	1156
1997	1150	1180	1172	1134	1122	1131
1998	1224	1245	1211	1225	1225	1187
1999	1173	1135	1147	1160	1158	1187
2000	1253	1245	1245	1249	1244	1246
2001	1288	1284	1280	1227	1281	1253
2002	1145	1143	1148	1158	1130	1163
2003	1035	970	1028	1058	1032	1032
2004	953	970	953	964	987	982
MSE		1731	1024	794	444	421
RMSE		41.61	32.00	28.18	21.07	20.52
MAPE		2.29%	1.77%	1.68%	1.253%	1.250%

4.3. Forecast the “Spot Gold in Turkey”

The proposed LTS-FMs were applied once again to a more complex forecasting problem of SGT. The minimum and maximum of the historical data of SGT observed from December 7th to November 10th were 30,503 and 62,450, respectively, so the UD was set to [30,000, 63,000]. The number of used words was 16, which was equal to the number of intervals in [6,8].

The experimental results of our proposed LTS-FMs shown in Table 4 were compared with those of Uslu et al. and Chen et al. [6,8], respectively. It can be seen in Table 4 that, when compared by both the MSE and MAPE values, all three of our proposed LTS-FMs, COLTS3, COLTS4, and COLTS5, outperformed the FTS-FMs of Uslu et al. and Chen et al. [6,8], respectively, in forecasting the problem of SGT. When compared by the MSE or RMSE values, COLTS5 was better than COLTS4, and COLTS3 was worse than COLTS4. However, when compared by the MAPE value, COLTS5 was slightly worse than COLTS4. In general, once again, we can state that, with the same number of used words, the longer the maximum word length, the better the MSE value obtained.

Table 4. The forecasted values of the SGT of our proposed FTS-FMs compared with those of existing forecasting models.

Date	Actual Spot Gold	Uslu et al. [6]	Chen et al. [8]	COLTS3	COLTS4	COLTS5
7 December	30,503
8 January	33,132	32,740.18	32,341.38	32,023.45	33,145.28	33,317.23
8 February	35,201	34,882.78	34,479.36	34,437.4	34,368.77	34,748.84
8 March	38,529	37,409.66	38,605.47	38,926.53	37,751.7	38,047.16
8 April	38,300	39,894.23	38,203.34	39,174.45	38,551.01	38,697.57
8 May	36,142	37,023.88	37,406.67	36,597.27	36,770.38	37,115.76
8 June	35,837	37,409.66	36,749.36	35,157.36	35,971.07	36,465.34
8 July	37,074	37,409.66	36,452.85	37,719.55	37,151.04	37,608.49
8 August	32,955	32,740.18	31,805.51	33,950.38	32,537.23	32,693.81
8 September	33,277	34,882.78	34,335.42	34,437.4	33,745.95	33,755.9
8 October	38,295	37,409.66	38,120.71	37,719.55	38,545.47	38,720.65
8 November	38,677	37,023.88	37,402.31	37,804.25	38,551.01	38,697.57
8 December	40,724	39,894.23	40,726.33	40,381.42	40,353.8	40,187.07
9 January	43,985	43,666.21	44,515.67	43,539.13	44,427.03	43,640.45
9 February	49,931	49,662.4	49,800.77	47,966.48	50,125.47	49,223.14
9 March	50,823	51,971.99	50,962.66	51,420.1	50,985.28	51,307.51
9 April	46,167	45,938.07	45,869.8	46,046.6	46,786.96	46,273.1
9 May	46,716	46,435.4	46,548.24	46,526.57	47,031.66	46,568.11
9 June	47,337	46,435.4	47,067.02	46,526.57	47,031.66	46,568.11
9 July	46,088	46,435.4	47,653.83	46,526.57	47,031.66	46,568.11
9 August	45,839	46,435.4	46,473.59	46,526.57	47,031.66	46,568.11
9 September	48,053	46,435.4	46,238.3	47,966.48	48,255.15	48,043.13
9 October	49,592	49,662.4	48,330.41	50,213.13	50,501.27	50,458.94
9 November	53,693	51,971.99	54,338.06	52,866.27	53,035.95	53,317.76
9 December	54,553	54,188.41	54,509.96	54,270.66	54,472.2	54,596.41
10 January	53,022	54,188.41	53,663.01	53,483.95	54,472.2	53,323.23
10 February	53,613	54,188.41	54,183.79	54,232.71	54,472.2	53,031.02
10 March	55,031	54,188.41	54,471.07	54,270.66	54,472.2	54,304.20
10 April	55,181	54,188.41	55,887.68	55,209.21	55,316.72	54,836.46
10 May	60,300	60,069.32	60,030.78	60,575.56	61,184.06	60,631.89
10 June	62,100	60,069.32	59,888.46	61,171.38	62,123.95	60,829.09
10 July	60,500	59,849.5	61,610.89	61,181.67	61,184.06	60,914.75
10 August	59,200	60,069.32	60,079.84	59,725.21	59,495.78	59,526.34
10 September	61,250	60,069.32	61,520.74	61,894.46	61,184.06	61,480.46
10 October	62,450	62,437.15	60,797.52	62,393.89	62,123.95	61,339.03
10 November	61,600	59,849.5	61,945.8	61,894.46	61,184.06	61,339.03
MSE		1,030,692	805,291	504,909	332,503	302,749
RMSE		1015.23	897.38	710.57	576.63	550.23
MAPE		1.80%	1.55%	1.38%	0.98%	1.00%

5. Conclusions

In this study, we proposed a hybrid LTS-FM with a co-optimization procedure using PSO to determine applicable fuzziness parameter values and the best word set describing the observed data. When compared with the former studies, our proposed model achieved better forecasting accuracies. Based on this research, we can continue studying to improve the forecasted accuracy of the forecasting model and apply it to different forecasting application problems with various datasets. In addition, research on better data representation methods using LTS to improve the accuracy and the performance of the forecasting model is a good idea for future work.