Three-Species Predator–Prey Stochastic Delayed Model Driven by Lévy Jumps and with Cooperation among Prey Species
Abstract
1. Introduction
2. Properties of the Solution
2.1. Existence and Uniqueness of a Global Positive Solution
2.2. Stochastic Boundedness
3. Stochastic Extinction of the Prey and Predator
4. Stochastic Extinction of Predator
5. Stochastic Persistence
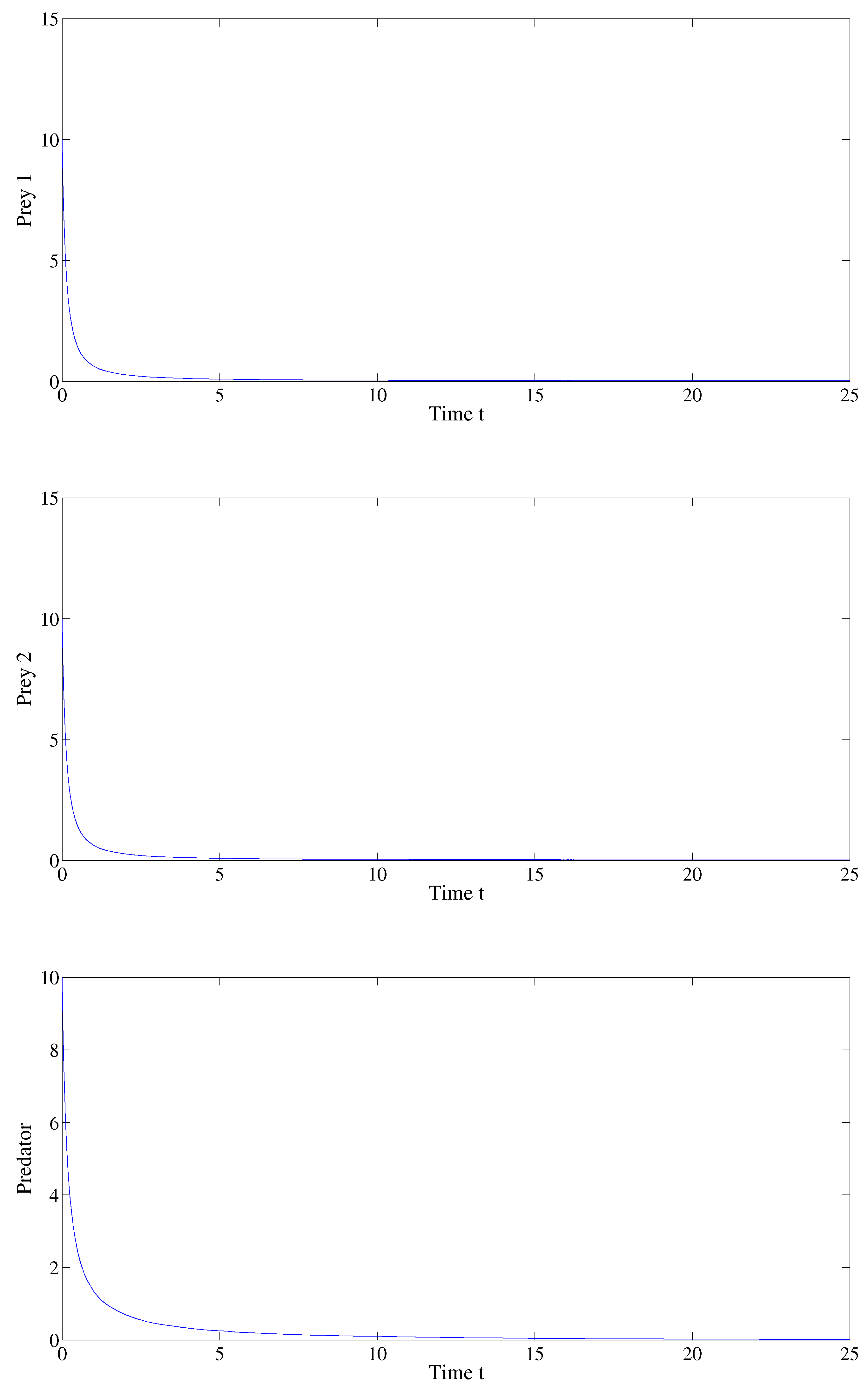
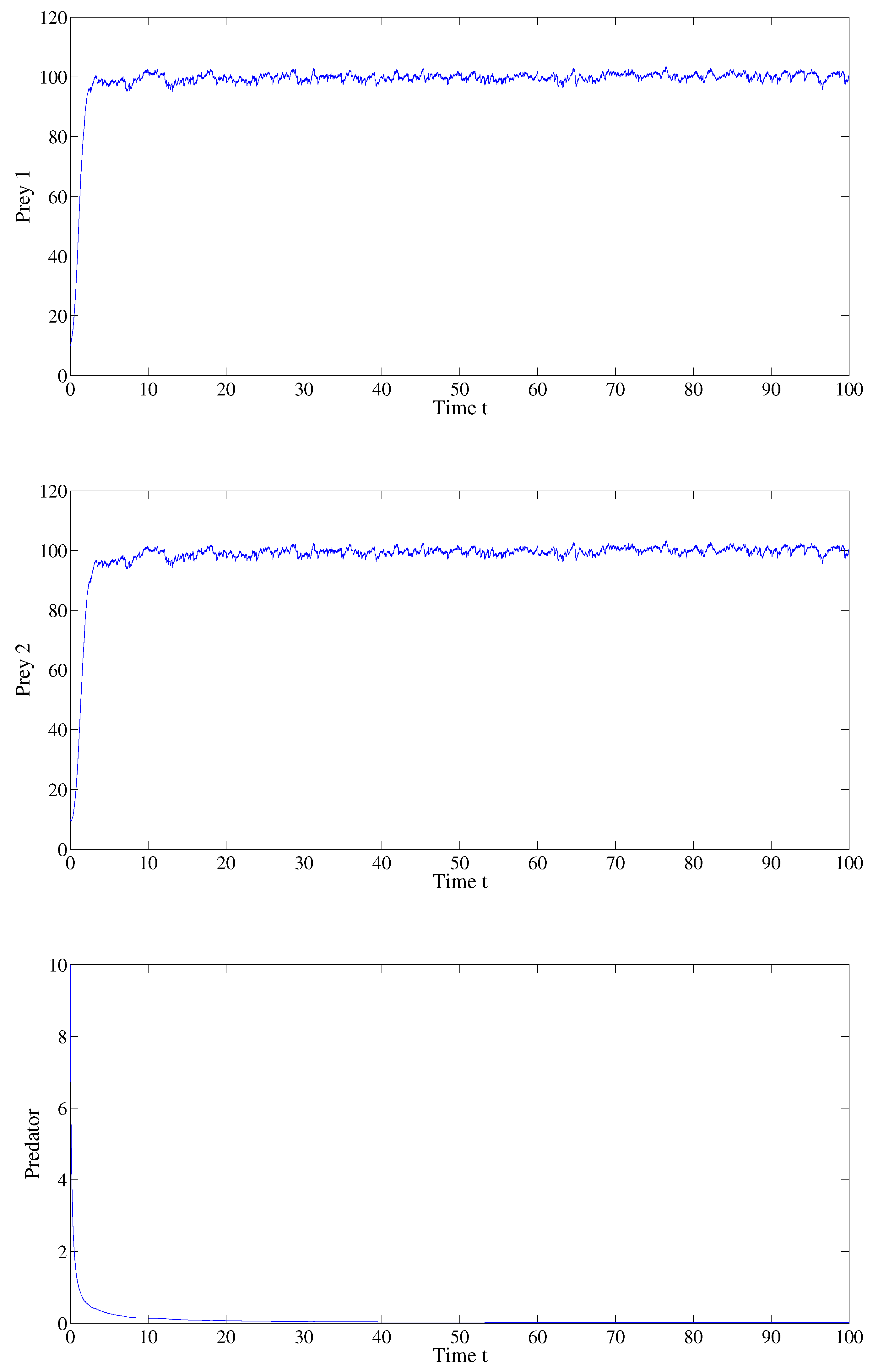
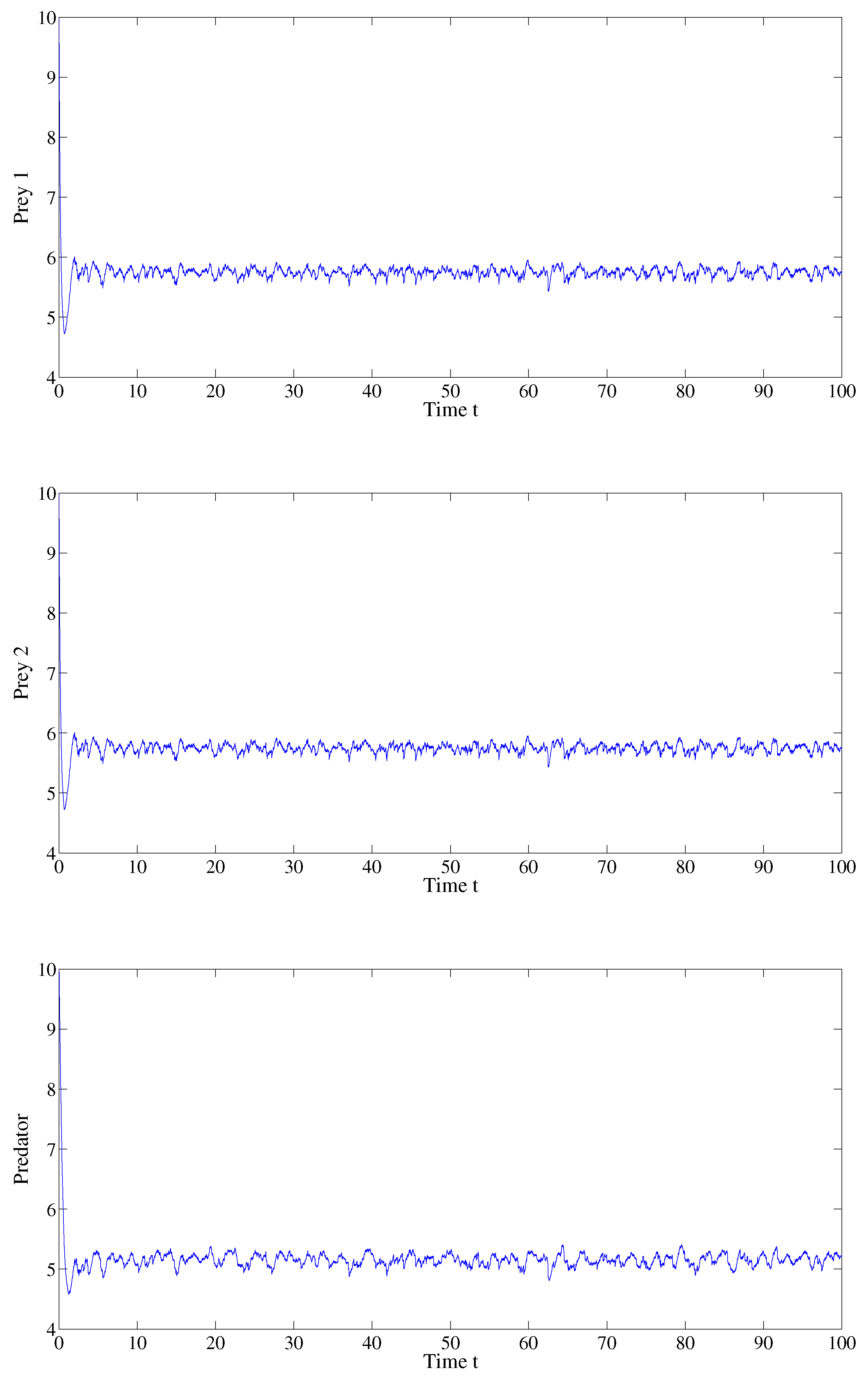
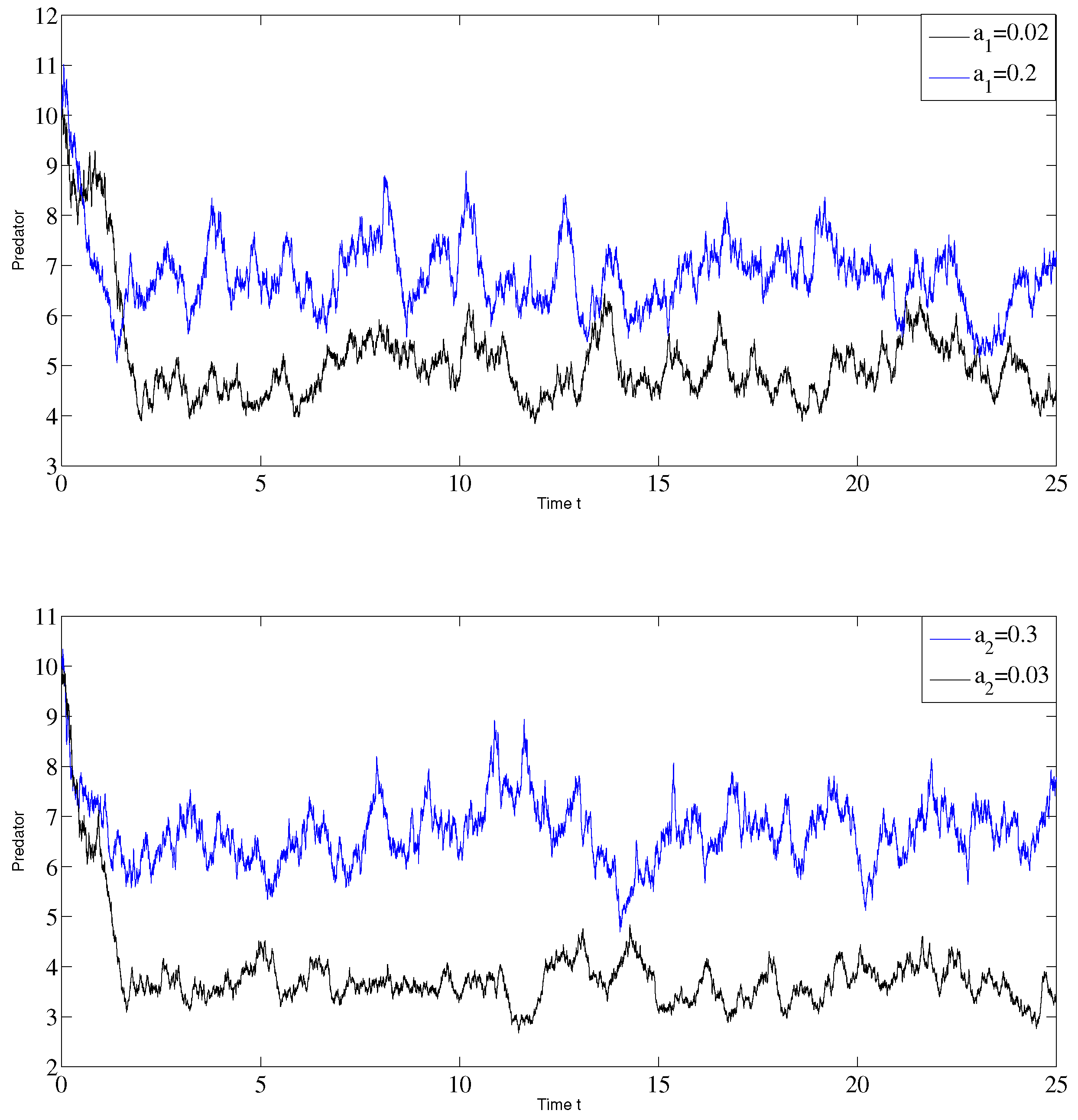
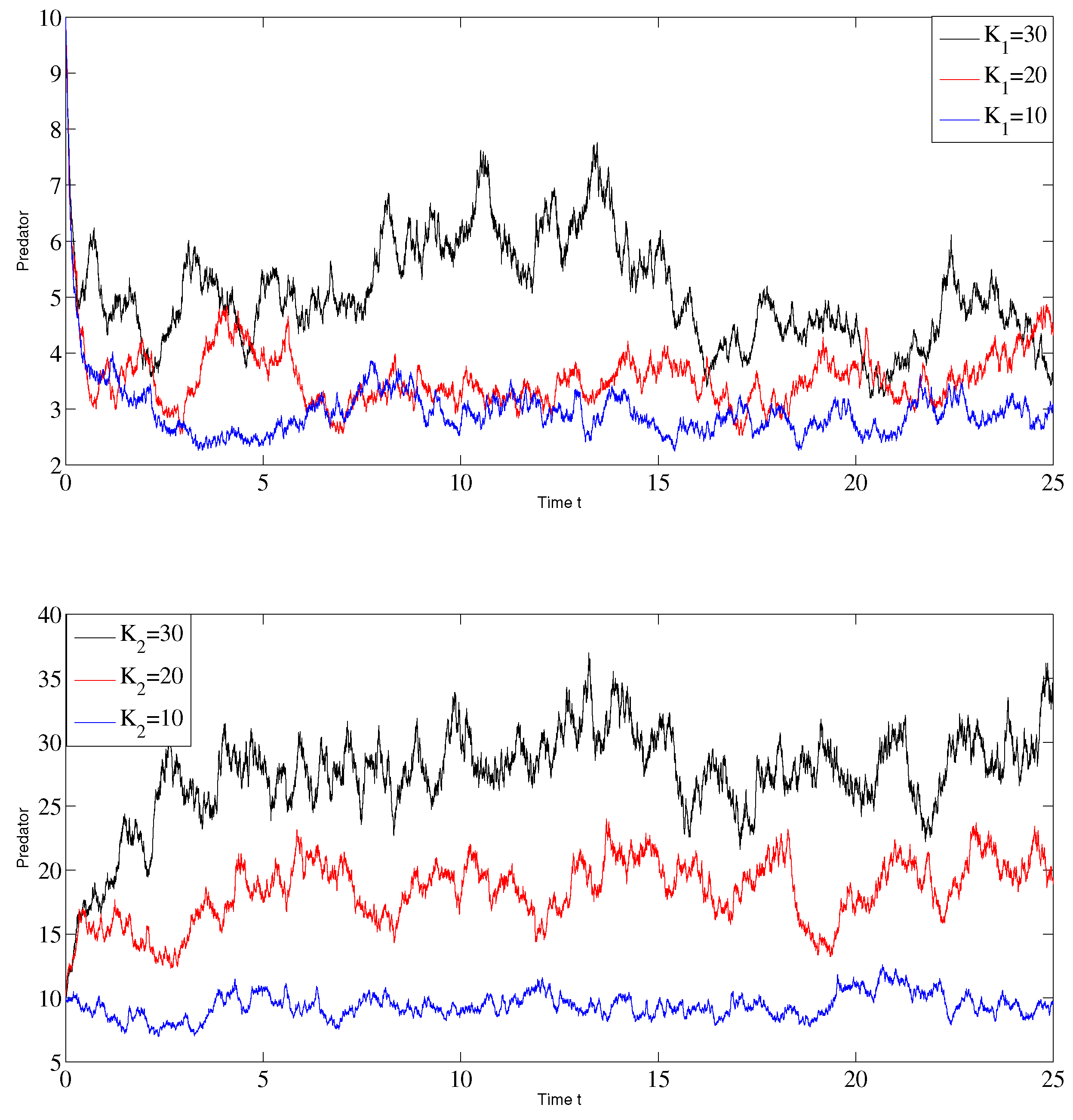
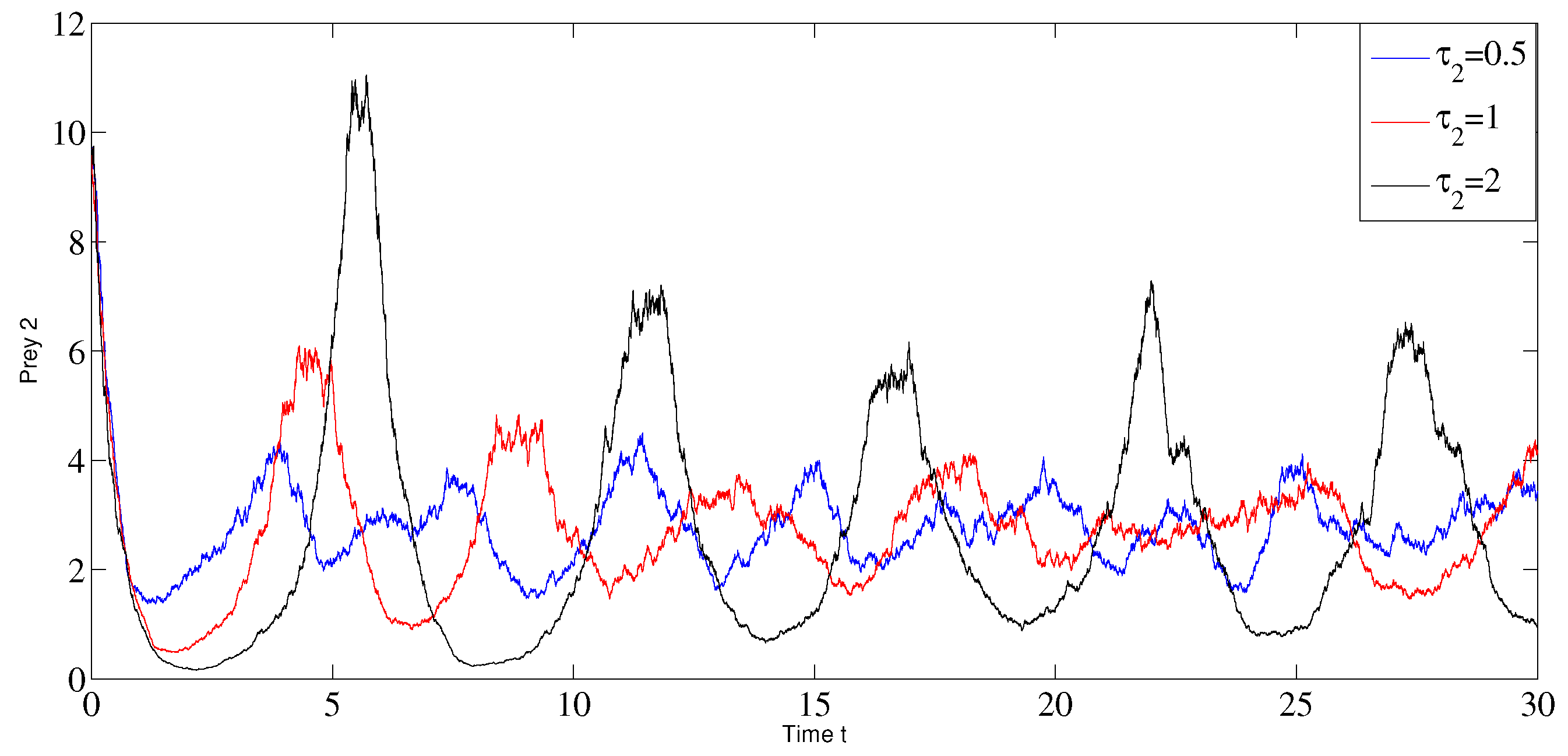
6. Numerical Simulations
7. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tripathi, J.P.; Tyagi, S.; Abbas, Ṡ. Global analysis of a delayed density dependent predator-prey model with Crowley-Martin functional response. Commun. Nonlinear Sci. Numer. Simul. 2016, 30, 45–69. [Google Scholar] [CrossRef]
- Meng, X.-Y.; Huo, H.-F.; Xiang, H.; Yin, Q.-Y. Stability in a predator-prey model with Crowley-Martin function and stage structure for prey. Appl. Math. Comput. 2014, 232, 810–819. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.; Hayat, T.; Alsaedi, Ȧ. Dynamics of a stochastic predator-prey model with stage structure for predator and Holling type II functional response. J. Nonlinear Sci. 2018, 28, 1151–1187. [Google Scholar] [CrossRef]
- Lotka, A.J. Elements of Physical Biology; Dover: New York, NY, USA, 1956. [Google Scholar]
- Fay, T.H.; Greeff, J.C. Lion, wildebeest and zebra: A predator-prey model. Ecol. Model. 2006, 196, 237–244. [Google Scholar] [CrossRef]
- Spencer, P.D.; Collie, J.S. A simple predator-prey model of exploited marine fish populations incorporating alternative prey. Ices J. Mar. Sci. 1996, 53, 615–628. [Google Scholar] [CrossRef]
- Verhulst, P.-F. Notice sur la loi que la population suit dans son accroissement. Corresp. Math. Phys. 1838, 10, 113–121. [Google Scholar] [CrossRef]
- Edelstein-Keshet, L. Mathematical Models in Biology; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2005. [Google Scholar] [CrossRef]
- Kingsland, S. The refractory model: The logistic curve and the history of population ecology. Q. Rev. Biol. 1982, 57, 29–52. [Google Scholar] [CrossRef]
- Kot, M. Elements of Mathematical Ecology; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar] [CrossRef]
- MacLean, M.C.; Turner, Ȧ.W. The logistic curve applied to Canada’s population. Can. J. Econ. Polit. Sci. 1937, 3, 241–248. [Google Scholar] [CrossRef]
- Pearl, R.; Reed, Ŀ.J. The logistic curve and the census count of i930. Science 1930, 72, 399–401. [Google Scholar] [CrossRef]
- Abraha, T.; Basir, F.A.; Obsu, L.L.; Torres, D.F.M. Pest control using farming awareness: Impact of time delays and optimal use of biopesticides. Chaos Solitons Fractals 2021, 146, 11. [Google Scholar] [CrossRef]
- Arino, J.; Wang, L.; Wolkowicz, G.S.K. An alternative formulation for a delayed logistic equation. J. Theor. Biol. 2006, 241, 109–119. [Google Scholar] [CrossRef] [PubMed]
- Hutchinson, G.E. Circular causal systems in ecology. Ann. N. Y. Acad. Sci. 1948, 50, 221–246. [Google Scholar] [CrossRef] [PubMed]
- Kundu, S.; Maitra, S. Dynamical behaviour of a delayed three species predator-prey model with cooperation among the prey species. Nonlinear Dyn. 2018, 92, 627–643. [Google Scholar] [CrossRef]
- Rihan, F.A.; Alsakaji, H.J. Stochastic delay differential equations of three-species prey-predator system with cooperation among prey species. Discrete Contin. Dyn. Syst. Ser. S 2022, 15, 245–263. [Google Scholar] [CrossRef]
- Choo, S.; Kim, Y.-H. Global stability in stochastic difference equations for predator-prey models. J. Comput. Anal. Appl. 2017, 23, 462–486. [Google Scholar]
- Yang, L.; Zhong, S. Global stability of a stage-structured predator-prey model with stochastic perturbation. Discrete Dyn. Nat. Soc. 2014, 2014, 8. [Google Scholar] [CrossRef]
- Zhao, S.; Song, M. A stochastic predator-prey system with stage structure for predator. Abstr. Appl. Anal. 2014, 2014, 7. [Google Scholar] [CrossRef]
- Danane, J.; Allali, K.; Hammouch, Z.; Nisar, K.S. Mathematical analysis and simulation of a stochastic COVID-19 Lévy jump model with isolation strategy. Results Phys. 2021, 23, 12. [Google Scholar] [CrossRef]
- Akdim, K.; Ez-zetouni, A.; Danane, J.; Allali, K. Stochastic viral infection model with lytic and nonlytic immune responses driven by Lévy noise. Phys. A 2020, 549, 11. [Google Scholar] [CrossRef]
- Danane, J. Stochastic predator-prey Lévy jump model with Crowley-Martin functional response and stage structure. J. Appl. Math. Comput. 2021, 67, 41–67. [Google Scholar] [CrossRef]
- Zhang, X.; Li, W.; Liu, M.; Wang, K. Dynamics of a stochastic Holling II one-predator two-prey system with jumps. Phys. A 2015, 421, 571–582. [Google Scholar] [CrossRef]
- Liu, Q.; Chen, Q. Analysis of a stochastic delay predator-prey system with jumps in a polluted environment. Appl. Math. Comput. 2014, 242, 90–100. [Google Scholar] [CrossRef]
- Liu, M.; Bai, C.; Deng, M.; Du, B. Analysis of stochastic two-prey one-predator model with Lévy jumps. Phys. A 2016, 445, 176–188. [Google Scholar] [CrossRef]
- Zhao, Y.; Yuan, S. Stability in distribution of a stochastic hybrid competitive Lotka-Volterra model with Lévy jumps. Chaos Solitons Fractals 2016, 85, 98–109. [Google Scholar] [CrossRef]
- Wu, J. Stability of a three-species stochastic delay predator-prey system with Lévy noise. Phys. A 2018, 502, 492–505. [Google Scholar] [CrossRef]
- Øksendal, B.K.; Sulem, A. Applied Stochastic Control of Jump Diffusions, 3rd ed.; Universitext Series; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Zou, X.; Wang, K. Numerical simulations and modeling for stochastic biological systems with jumps. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 1557–1568. [Google Scholar] [CrossRef]
- Shao, Y.; Kong, W. A predator-prey model with Beddington-DeAngelis functional response and multiple delays in deterministic and stochastic environments. Mathematics 2022, 10, 3378. [Google Scholar] [CrossRef]
- Shao, Y. Dynamics of an impulsive stochastic predator-prey system with the Beddington-DeAngelis functional response. Axioms 2021, 10, 323. [Google Scholar] [CrossRef]
- Gholami, M.; Ghaziani, R.K.; Eskandari, Z. Three-dimensional fractional system with the stability condition and chaos control. Math. Model. Numer. Simul. Appl. 2022, 2, 41–47. [Google Scholar] [CrossRef]
- Yavuz, M.; Sene, N. Stability analysis and numerical computation of the fractional predator-prey model with the harvesting rate. Fractal Fract. 2020, 4, 35. [Google Scholar] [CrossRef]
- Naim, M.; Sabbar, Y.; Zeb, A. Stability characterization of a fractional-order viral system with the non-cytolytic immune assumption. Math. Model. Numer. Simul. Appl. 2022, 2, 164–176. [Google Scholar] [CrossRef]



| Parameters | Description |
|---|---|
| The intrinsic growth rate for prey x | |
| The intrinsic growth rate for prey y | |
| The carrying capacity for x | |
| The carrying capacity for y | |
| The predation rate of prey x | |
| The predation rate of prey y | |
| The rate of cooperation of preys x and y against predator z | |
| The predator death rate | |
| The rate of intra-species competition within the predators | |
| The transformation rate of predator to preys x | |
| The transformation rate of predator to preys y |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danane, J.; Torres, D.F.M. Three-Species Predator–Prey Stochastic Delayed Model Driven by Lévy Jumps and with Cooperation among Prey Species. Mathematics 2023, 11, 1595. https://doi.org/10.3390/math11071595
Danane J, Torres DFM. Three-Species Predator–Prey Stochastic Delayed Model Driven by Lévy Jumps and with Cooperation among Prey Species. Mathematics. 2023; 11(7):1595. https://doi.org/10.3390/math11071595
Chicago/Turabian StyleDanane, Jaouad, and Delfim F. M. Torres. 2023. "Three-Species Predator–Prey Stochastic Delayed Model Driven by Lévy Jumps and with Cooperation among Prey Species" Mathematics 11, no. 7: 1595. https://doi.org/10.3390/math11071595
APA StyleDanane, J., & Torres, D. F. M. (2023). Three-Species Predator–Prey Stochastic Delayed Model Driven by Lévy Jumps and with Cooperation among Prey Species. Mathematics, 11(7), 1595. https://doi.org/10.3390/math11071595









