Distributed Moving Horizon Fusion Estimation for Nonlinear Constrained Uncertain Systems

Abstract

This paper studies the state estimation of a class of distributed nonlinear systems. A new robust distributed moving horizon fusion estimation (DMHFE) method is proposed to deal with the norm-bounded uncertainties and guarantee the estimation performance. Based on the given relationship between a state covariance matrix and an error covariance matrix, estimated values of the unknown parameters in the system model can be obtained. Then, a local moving horizon estimation optimization algorithm is constructed by using the measured values of sensor nodes themselves, the measured information of adjacent nodes and the prior state estimates. By solving the above nonlinear optimization problem, a local optimal state estimation is obtained. Next, based on covariance intersection (CI) fusion strategy, the local optimal state estimates sent to the fusion center are fused to derive optimal state estimates. Furthermore, the sufficient conditions for the square convergence of the fusion estimation error norm are given. Finally, a simulation example is employed to demonstrate the effectiveness of the proposed algorithm.

1. Introduction

In recent years, multi-sensor fusion estimation problems were the focus of intense research. In traditional estimation problems information was always obtained from a single sensor [1], which had limitations. With the development of science and technology, higher precision requirements are put forward for various industrial control processes. Multi-sensor fusion estimation technology has been widely used in various real environments, including intelligent robot systems and driverless cars, target tracking, signal processing, etc. [2,3,4,5,6]. In addition, multi-sensor systems are easily affected by external disturbances during operation, which causes certain uncertainties to appear in the system model parameters [7,8]. Therefore, it is of great theoretical significance and engineering application value to study the distributed state fusion estimation of uncertain systems.

At present, there are three basic methods for state estimation of multi-sensor information fusion: centralized fusion, distributed fusion and sequential fusion. Although centralized fusion can obtain global optimal fusion estimation, it involves a heavy computational burden and has poor fault tolerance. Sequential fusion is more convenient for handling asynchronous sampling systems [9]. Distributed fusion has attracted wide attention because of its parallel structure and easy fault detection and isolation. In [10], a signal selection method based on event trigger is proposed to deal with packet loss caused by network and packet confusion which is caused by random transmission delay. Reference [11] put forward an algorithm that can get consistent output local estimation when the basic model was unknown but fixed. The authors of reference [12] proposed a distributed fusion Kalman filter (DFKF) algorithm based on an optimal weighted fusion criterion. In [13], a cross covariance matrix of estimation error between any two local prediction variables was deduced, and the authors successfully analyzed the steady-state characteristics of these variables. In [14], a distributed extended Kalman filter algorithm based on sensor networks is proposed to solve norm-bounded uncertain parameters in nonlinear systems. Unfortunately, the algorithms used in the above-mentioned studies are all based on Kalman or extended Kalman filters, which are characterized by high statistical noise and cannot consider the constraints of the system. Therefore, in this study we adopt a moving horizon estimation method, which can deal with system constraints and has high estimation accuracy for complex nonlinear systems.

Moving horizon estimation (MHE) is a finite horizon estimation method which has developed rapidly in recent years. By introducing a performance index, the solution for optimization problems is limited to a fixed horizon window. It is characterized by moving optimization, explicit processing constraints, and does not have special requirements for statistical characteristics of noise [15,16]. At present, moving horizon estimation has been widely used in chemical process state estimation [17], fault detection [18], system identification [19], exchange systems [20,21], large-scale systems [22,23,24], networked systems [25], uncertain systems and distributed systems [25,26,27,28,29,30,31,32,33,34]. In [22], two distributed moving horizon estimation algorithms were proposed, which can deal with interference and noise constraints. In [23], an event-triggered mechanism was introduced to govern the evaluation of given estimators and the network information exchange between the device and the estimators, which can provide good estimation performance while reducing the processor usage and network communication frequency. In [30], a distributed moving horizon estimation method is proposed for nonlinear constrained systems. The dynamic characteristics of state variables that cannot be observed by each sensor are described, and the conditions of local information exchange are provided. In [34], a robust estimation problem of linear multi-sensor system constrained by additive and multiplicative uncertainties is studied, and a moving horizon $H_{\infty }$ fusion-estimation algorithm is proposed. However, none of the above studies consider the uncertain parameters in distributed systems: when there are uncertain parameters in the system, the traditional moving horizon estimation algorithm cannot satisfy the stability requirements of the system, which reduces its estimation efficiency. Therefore, there is a need to improve the original algorithm.

Based on the above analysis, this paper presents a distributed moving horizon fusion estimation (DMHFE) for nonlinear constrained uncertain systems. The main innovations are as follows:

(1)

By constructing an augmented system, the relationship between the estimation error covariance and the state covariance of the augmented system is established, and the estimated values of the uncertain parameters are obtained by optimizing the upper bound of the error covariance matrix.

(2)

By introducing a covariance intersection fusion estimation strategy and considering the fusion estimation error of the system, a sufficient condition for the square convergence of local estimation error norm is given. Moreover, the relationship between fusion estimation error and local estimation error is derived.

The structure of this article is as follows. The distributed moving horizon estimation problem of the desired solution is introduced, and the expression of local performance index is given in Section 2. Estimated values of the system uncertainty parameters are given in Section 3. The fusion estimation criterion and the calculation method of weighted coefficient are given in Section 4. A stability analysis is given in Section 5. Numerical simulation examples are given in Section 6. The conclusions are summarized in Section 7.

Notation: For a column vector $\nu$, the notation ${∥\nu ∥}_Y^2$ stands for ${\nu }^{T}Y\nu$, where Y is a symmetric positive–semidefinite matrix and ${\nu }^T$ represents the transpose of $\nu$. ${\Re }^m$ represents m-dimensional Euclidean space. The matrix diag $\left\{m_1,\cdots ,m_n\right\}$ is a block diagonal with blocks $m_n$, I represents identity matrix, and $∥·∥$ stands for the Euclidean norm. $E\left(·\right)$ represents the expectation of the random variable. For any matrix $S,S>0\left(S\ge 0\right)$ means that S is a positive definite (semi-positive definite) matrix and ${\lambda }_{max}\left(M\right),{\lambda }_{min}\left(M\right)$ represent the maximum and minimum singular values of matrix M, respectively.

2. Problem Description

Consider the following distributed nonlinear system model with uncertain parameters:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_{t+1}=f\left(x_t\right)+{\omega }_t\hfill \\ y_t^i=h^i\left(x_t\right)+v_t^i,i\in {\Im }_i,i=1,2\cdots L\hfill \end{array}\right.\end{array}$$

(1)

where $x_t\in {\Re }^n$ is the system state and $y_t^i\in {\Re }^m$ is the measured value of sensor i. $\Delta f_t^i=M_1^i{\mathsf{{\rm Y}}}_{1,t}^i{S}_1^i$, ${\mathsf{{\rm Y}}}_{1,t}^i$ is a Lebesgue measurable unknown function matrix, satisfying ${\mathsf{{\rm Y}}}_{1,t}^i{\left({\mathsf{{\rm Y}}}_{1,t}^i\right)}^T\le I$. I is the identity matrix with appropriate dimensions; $M_1^i$ and $S_1^i$ are the matrices with known appropriate dimensions. ${\omega }_t$ and $v_t^i$ represent the process noise and measurement noise of the system, respectively, with the following statistical characteristics:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}E\left\{{\omega }_t\right\}=0,\hfill \\ E\left\{v_t^i\right\}=0,\hfill \\ E\left\{{\omega }_t{\left(v_t^i\right)}^T\right\}=0,\hfill \\ E\left\{{\omega }_i{\left({\omega }_t\right)}^T\right\}=Q{\delta }_{it},\hfill \\ E\left\{v_t^i{\left(v_t^i\right)}^T\right\}=R^i{\delta }_{it},\hfill \\ t=0,1,2,\cdots \hfill \end{array}\right.\end{array}$$

where, ${\delta }_{it}$ is a sign function, and Q and $R^i$ represent the covariance matrices of process noise and measurement noise, respectively, satisfying $Q>0,R^i>0$. Next, we will discuss the proposed distributed moving horizon fusion estimator design which includes L sensors for the distributed nonlinear system of (1). A schematic of this algorithm is shown in Figure 1.

Table 1 shows the meaning of each item in Equation (1). It can be seen from Figure 1 that sensor $i\left(i=1,2\cdots L\right)$ sends the measured value $y_t^i\left(i=1,2\cdots L\right)$ to the local estimator $i\left(i=1,2\cdots L\right)$, and the local optimal estimator ${\widehat{x}}_t^{i*}$ is solved by solving the nonlinear optimization problem. Then ${\widehat{x}}_t^{i*}\left(i=1,2\cdots L\right)$ is sent to the fusion center through the communication network, and the fusion estimate ${\widehat{x}}_t^{*}$ is obtained using the covariance intersection fusion estimation strategy. In order to realize the above distributed fusion estimation, the following optimization problem of local moving horizon estimation is presented:

 Problem 1. 

$$\begin{array}{c}\hfill \underset{{\widehat{x}}_{t-N|t}^{i*}}{min}{J}_t^i\left({\widehat{x}}_{t-N|t}^{i*}\right)\end{array}$$

$$\begin{array}{cc}\hfill J_t^i\left({\widehat{x}}_{t-N|t}^{i*}\right)=& {\mu }_i{∥{\widehat{x}}_{t-N|t}^i-{\tilde{x}}_{t-N}^i∥}_{{\left({\tilde{P}}_{t-N}^i\right)}^{-1}}^2+{\displaystyle \sum _{j(j\ne i)\in {\Im }_i}}{\mu }_j{∥{\widehat{x}}_{t-N|t}^i-{\tilde{x}}_{t-N}^j∥}_{{\left({\tilde{P}}_{t-N}^j\right)}^{-1}}^2\hfill \\ \hfill & +{\displaystyle \sum _{k=t-N}^t}{∥y_k^i-{\widehat{h}}^i\left({\widehat{x}}_{k|t}^i\right)∥}_{{\left(R^i\right)}^{-1}}^2+{\displaystyle \sum _{k=t-N}^t}{\displaystyle \sum _{j\in {\Im }_i}}{∥y_k^j-{\widehat{h}}^j\left({\widehat{x}}_{k|t}^i\right)∥}_{{\left(R^j\right)}^{-1}}^2\hfill \end{array}$$

(2)

with the following constraints:

$$\begin{array}{c}\hfill \begin{array}{c}X=\left\{x:∥x∥\le {\theta }_x\right\}\hfill \\ V^i=\left\{v:∥v∥\le {\theta }_{v^i}\right\}\hfill \\ W=\left\{\omega :∥\omega ∥\le {\theta }_{\omega }\right\}\hfill \end{array}\end{array}$$

where $X,V^i,W$ is the set of convex polyhedra satisfying the corresponding constraints.

Table 1. The symbolic nomenclature of Formula (1).

i	The local sensor
L	The number of sensors
${\Im }_i$	The set of sensors adjacent to sensor i
$f\left(x_t\right)={\widehat{f}}^i\left(x_t\right)+\Delta f_t^i{x}_t$	The unknown nonlinear function
${\widehat{f}}^i\left(·\right)$	The known nominal nonlinear dynamic function
$h^i\left(·\right)$	The known nominal nonlinear observation function
$\Delta f_t^i$	The system model error

Table 1. The symbolic nomenclature of Formula (1).

i	The local sensor
L	The number of sensors
${\Im }_i$	The set of sensors adjacent to sensor i
$f\left(x_t\right)={\widehat{f}}^i\left(x_t\right)+\Delta f_t^i{x}_t$	The unknown nonlinear function
${\widehat{f}}^i\left(·\right)$	The known nominal nonlinear dynamic function
$h^i\left(·\right)$	The known nominal nonlinear observation function
$\Delta f_t^i$	The system model error

In Equation (2), considering a moving window of fixed length $N+1$, ${\Omega }_t=\{t-N,t-N+1,\dots ,t\}$, $J_t^i\left({\widehat{x}}_{t-N|t}^{i*}\right)$ represents the performance index of a local optimization problem. $\mu$ is the weight coefficient, satisfying ${\mu }_i+{\displaystyle \sum _{j(j\ne i)\in {\Im }_i}}{\mu }_j=1$. The first two terms represent the arrival cost, which summarizes the impact of the data before the time $t-N$ on the current data; ${\tilde{P}}_{t-N}^i$ is a symmetric positive definite weight matrix quantifying the confidence of the prior state estimate ${\tilde{x}}_{t-N}^i$, which penalizes the distance between the initial state estimate in the moving window ${\Omega }_t$ and the prior state estimate ${\tilde{x}}_{t-N}^i$. It is noted that in traditional moving horizon estimation algorithms, the arrival cost usually takes the following form:

$$\begin{array}{c}\hfill {∥{\widehat{x}}_{t-N|t}^i-{\overline{x}}_{t-N}^i∥}_{{\left(P_{t-N}^i\right)}^{-1}}^2\end{array}$$

However, in the distributed system, in order to ensure the observability of the entire state vector, we reconstruct the arrival cost into the fusion arrival cost obtained by the weighted average of the local arrival cost of node i and the local arrival cost of node i’s in-neighbors j, corresponding to the first two terms in (2), respectively. For the third term, the distance between the expected output based on the state estimate and the actual measurement are weighted using $R^i$. Finally, the fourth term, represents the case that, at time t, sensor i may receive measurement information $y_t^j$ from the in-neighbors node $j\in {\Im }_i$.

By solving optimization Problem 1, the optimal state estimation value ${\widehat{x}}_{t-N|t}^{i*}$ is obtained. It is worth noting that the estimated state at other times in optimization Problem 1 can be calculated using the following formula:

$$\begin{array}{cc}\hfill {\widehat{x}}_{g+1|t}^{i*}=& f\left({\widehat{x}}_{g|t}^{i*}\right)+\Delta {\widehat{f}}_t^i{\widehat{x}}_{g|t}^{i*}+{\widehat{K}}_t^i(y_t^i-{\widehat{h}}^i\left({\widehat{x}}_{g|t}^{i*}\right))+{\widehat{Z}}_t^i{\displaystyle \sum _{j\in {\Im }_i}}{\left({\tilde{P}}_t^j\right)}^{-1}{\mu }_j({\widehat{x}}_{g|t}^{i*}-{\tilde{x}}_{g|t}^{j*})\hfill \\ \hfill & g=t-N,\cdots t-1\hfill \end{array}$$

(3)

where $\Delta {\widehat{f}}_t^i,{\widehat{K}}_t^i,{\widehat{Z}}_t^i$ and ${\tilde{P}}_t^j$ are matrices with appropriate dimensions. Similarly, the prior estimated state at time $t-N$ can also be calculated using (3). Before solving the above local optimization problem, unknown parameters in (3) must be solved.

 Remark 1. 

From (3), one can find that the window estimation model consists of four components. Therein, the last three terms are designed to improve estimation performance [14]. So the key of this paper is to find the optimal gain matrices $\Delta {\widehat{f}}_t^{i*},{\widehat{K}}_t^{i*},{\widehat{Z}}_t^{i*}$ and the upper bound of error covariance ${\tilde{P}}_t^j$.

3. The Method of Solving the Estimated Value of Uncertain Parameter in System

This section, considering the system model (1), proves that the estimation error covariance matrix is bounded even if uncertain parameters exist in the system models, and the estimated values of the uncertain parameters are given.

At time t, to facilitate the addressing of linearization errors and norm-bounded uncertainties in Taylor series expansions, ${\widehat{f}}^i\left(x_t\right)$ and $h^i\left(x_t\right)$ at ${\widehat{x}}_t^i$, using Taylor expansion, can be written into the following formulas:

$$\begin{array}{c}{\widehat{f}}^i\left(x_t\right)={\widehat{f}}^i\left({\widehat{x}}_t^i\right)+B_t^i(x_t-{\widehat{x}}_t^i)+{\tilde{B}}_t^i(x_t-{\widehat{x}}_t^i)\hfill \\ h^i\left(x_t\right)={\widehat{h}}^i\left({\widehat{x}}_t^i\right)+C_t^i(x_t-{\widehat{x}}_t^i)+{\tilde{C}}_t^i(x_t-{\widehat{x}}_t^i)\hfill \end{array}$$

(4)

where $B_t^i=\frac{\partial {\widehat{f}}^i\left(x_t\right)}{\partial x_t|x_t={\widehat{x}}_t^i},C_t^i=\frac{\partial h^i\left(x_t\right)}{\partial x_t|x_t={\widehat{x}}_t^i},{\tilde{B}}_t^i=M_2^i{\mathsf{{\rm Y}}}_{2,t}^i{S}_2^i,{\tilde{C}}_t^i=M_3^i{\mathsf{{\rm Y}}}_{3,t}^i{S}_3^i$; the Lebesgue measurable unknown function matrices ${\mathsf{{\rm Y}}}_{2,t}^i$, ${\mathsf{{\rm Y}}}_{3,t}^i$ satisfy ${\mathsf{{\rm Y}}}_{2,t}^i{\left({\mathsf{{\rm Y}}}_{2,t}^i\right)}^T\le I$, ${\mathsf{{\rm Y}}}_{3,t}^i{\left({\mathsf{{\rm Y}}}_{3,t}^i\right)}^T\le I$; and $M_2^i,S_2^i,M_3^i,S_3^i$ are known matrices with appropriate dimensions.

Following [14], the gain matrices $\Delta {\widehat{f}}_t^i,{\widehat{K}}_t^i,{\widehat{Z}}_t^i$ from (3) and ${\tilde{P}}_t^j$ in the perfomance index (2) should be solved. Therefore, we construct an augmented system and derive the upper bound of the estimation error covariance matrix in system (1) by finding the upper bound of the state covariance matrix of the augmented system. Letting ${\overline{x}}_{t+1}^i={\left[{\left(x_{t+1}\right)}^T({\widehat{x}}_{t+1}^i{)}^T\right]}^T$, the augmented system is written as:

$${\overline{x}}_{t+1}^i=({\overline{A}}_t^i+\Delta {\overline{A}}_t^i){\overline{x}}_t^i+{\overline{f}}_t^i+{\overline{\omega }}_t^i+{\overline{Z}}_t^i$$

(5)

with

$$\begin{array}{c}{\overline{A}}_t^i=\left[\begin{array}{cc}{B}_t^i& -B_t^i\\ {\widehat{K}}_t^i{C}_t^i& \Delta {\widehat{f}}_t^i-{\widehat{K}}_t^i{C}_t^i\end{array}\right]\hfill \\ \Delta {\overline{A}}_t^i=\left[\begin{array}{cc}\Delta f_t^i+{\tilde{B}}_t^i& -{\tilde{B}}_t^i\\ {\widehat{K}}_t^i{\tilde{C}}_t^i& -{\widehat{K}}_t^i{\tilde{C}}_t^i\end{array}\right]\hfill \\ {\overline{f}}_t^i=\left[\begin{array}{c}{\widehat{f}}^i\left({\widehat{x}}_t^i\right)\\ {\widehat{f}}^i\left({\widehat{x}}_t^i\right)\end{array}\right],{\overline{\omega }}_t^i=\left[\begin{array}{c}{\omega }_t\\ {\widehat{K}}_t^i{v}_t^i\end{array}\right]\hfill \\ {\overline{Z}}_t^i=\left[\begin{array}{c}0\\ {\widehat{Z}}_t^i{\displaystyle \sum _{j\in {\Im }_i}}{\left({\tilde{P}}_t^j\right)}^{-1}{\mu }_j({\widehat{x}}_t^i-{\tilde{x}}_t^j)\end{array}\right]\hfill \end{array}$$

(6)

The state covariance matrix of the augmented system is defined as ${\overline{P}}_{t+1}^i=E\left\{{\overline{x}}_{t+1}^i{\left({\overline{x}}_{t+1}^i\right)}^T\right\}$ and the estimation error covariance matrix for sensor i at time $t+1$ is defined as $P_{t+1}^i=E\left\{(x_{t+1}-{\widehat{x}}_{t+1}^i){(x_{t+1}-{\widehat{x}}_{t+1}^i)}^T\right\}$. It is noted that the error covariance matrix and the augmented system state covariance matrix should satisfy the following lemma:

 Lemma 1. 

Given error covariance matrix $P_{t+1}^i$ and augmented system state covariance matrix ${\overline{P}}_{t+1}^i$, the estimated value of uncertain parameters are

$$\begin{array}{c}\hfill \Delta {\widehat{f}}_t^{i*}=U_{3,t,i}^{-1}\left[\left({\left(B_t^i\right)}^{\mathrm{T}}-{\left(C_t^i\right)}^{\mathrm{T}}{\left({\widehat{K}}_t^i\right)}^{\mathrm{T}}\right)\left(U_{2,t,i}-U_{3,t,i}\right)\right]\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{c}{\widehat{K}}_t^{i*}=\left(2{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}^{\mathrm{T}}{U}_{2,t,i}{B}_t^i{U}_{3,t,i}^{-1}-2B_t^i{C}_t^i{U}_{1,t,i}\right)\times \hfill \\ {\left\{\begin{array}{c}(1+{\beta }_{1,i}+{\beta }_{2,i})\left(\begin{array}{c}2{\left(C_t^i\right)}^{\mathrm{T}}{U}_{1,t,i}{C}_t^i-{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}{C}_t^i-2{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}^{\mathrm{T}}\hfill \\ \times U_{3,t,i}^{-1}{U}_{2,t,i}{C}_t^i+{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}\hfill \end{array}\right)\hfill \\ +2\left((1+{\beta }_{1,i}+{\beta }_{2,i}){\rho }_{3,i}^{-1}{M}_3^i{\left(M_3^i\right)}^{\mathrm{T}}+R^i\right)\hfill \end{array}\right\}}^{-1}\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{c}{\widehat{Z}}_t^{i*}=\left(2{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}^{\mathrm{T}}{U}_{2,t,i}{B}_t^i{U}_{3,t,i}^{-1}-2B_t^i{C}_t^i{U}_{1,t,i}\right)\times \hfill \\ {\left\{\begin{array}{c}(1+{\beta }_{1,i}+{\beta }_{2,i})\left(\begin{array}{c}2{\left(C_t^i\right)}^{\mathrm{T}}{U}_{1,t,i}{C}_t^i-{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}{C}_t^i-2{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}^{\mathrm{T}}\hfill \\ \times U_{3,t,i}^{-1}{U}_{2,t,i}{C}_t^i+{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}\hfill \end{array}\right)\hfill \\ +2\left((2+{\beta }_{1,i}^{-1}){\Psi }_t^i\right)\hfill \end{array}\right\}}^{-1}\hfill \end{array}\end{array}$$

which means the following inequality

$$\begin{array}{c}\hfill P_{t+1}^i=\left[\begin{array}{cc}I& -I\end{array}\right]{\overline{P}}_{t+1}^i{\left[\begin{array}{cc}I& -I\end{array}\right]}^T\le {\tilde{P}}_{t+1}^i\end{array}$$

holds. Here, ${\Psi }_t^i={\overline{c}}_i{\displaystyle \sum _{j\in {\Im }_i}}{\left({\tilde{P}}_t^j\right)}^{-1}$, and ${\overline{c}}_i$ is the number of sensors adjacent to sensor i.

 Proof. 

By applying ([14], Lemma 1),  the state covariance matrix of the augmented system can be transformed into the following form:

$$\begin{array}{cc}\hfill {\overline{P}}_{t+1}^i=& E\left\{{\overline{x}}_{t+1}^i{\left({\overline{x}}_{t+1}^i\right)}^T\right\}\le (1+{\beta }_{1,i}+{\beta }_{2,i})({\overline{A}}_t^i+\Delta {\overline{A}}_t^i)E\left\{{\overline{x}}_t^i{\left({\overline{x}}_t^i\right)}^T\right\}{({\overline{A}}_t^i+\Delta {\overline{A}}_t^i)}^T\hfill \\ \hfill & +(2+{\beta }_{2,i}^{-1}){\overline{f}}_t^i{\left({\overline{f}}_t^i\right)}^T+(2+{\beta }_{1,i}^{-1})E\left\{{\overline{Z}}_t^i{\left({\overline{Z}}_t^i\right)}^T\right\}+E\left\{{\overline{\omega }}_t^i{\left({\overline{\omega }}_t^i\right)}^T\right\}\hfill \end{array}$$

(7)

where ${\beta }_{1,i},{\beta }_{2,i}$ are appropriate positive constants. It is noted that there are four terms on the right side of inequality (7); every term will be analyzed separately.

For the sake of analysis, $\Delta {\overline{A}}_t^i$ can be written as follows:

$$\begin{array}{c}\Delta {\overline{A}}_t^i=\left[\begin{array}{cc}{M}_1^i{\mathsf{{\rm Y}}}_{1,t}^i{S}_1^i+M_2^i{\mathsf{{\rm Y}}}_{2,t}^i{S}_2^i& -M_2^i{\mathsf{{\rm Y}}}_{2,t}^i{S}_2^i\\ {\widehat{K}}_t^i{M}_3^i{\mathsf{{\rm Y}}}_{3,t}^i{S}_3^i& -{\widehat{K}}_t^i{M}_3^i{\mathsf{{\rm Y}}}_{3,t}^i{S}_3^i\end{array}\right]\hfill \\ =\left[\begin{array}{c}{M}_1^i\\ 0\end{array}\right]{\mathsf{{\rm Y}}}_{1,t}^i\left[\begin{array}{cc}{S}_1^i& 0\end{array}\right]+\left[\begin{array}{c}{M}_2^i\\ 0\end{array}\right]{\mathsf{{\rm Y}}}_{2,t}^i\left[\begin{array}{cc}{S}_2^i& 0\end{array}\right]+\left[\begin{array}{c}-M_2^i\\ 0\end{array}\right]{\mathsf{{\rm Y}}}_{2,t}^i\left[\begin{array}{cc}0& S_2^i\end{array}\right]\hfill \\ +\left[\begin{array}{c}{\widehat{K}}_t^i{M}_3^i\\ -{\widehat{K}}_t^i{M}_3^i\end{array}\right]{\mathsf{{\rm Y}}}_{3,t}^i\left[\begin{array}{cc}0& S_3^i\end{array}\right]\hfill \end{array}$$

(8)

where $S_1^i,S_2^i,S_3^i$ be the unit matrices of proper dimensions. Then, the following formula is satisfied by applying ([14], Lemma 2):

$$\begin{array}{c}\hfill \begin{array}{c}({\overline{A}}_t^i+\Delta {\overline{A}}_t^i)E\left\{{\overline{x}}_t^i{\left({\overline{x}}_t^i\right)}^T\right\}{({\overline{A}}_t^i+\Delta {\overline{A}}_t^i)}^T\hfill \\ ={\overline{A}}_t^i\left[\begin{array}{cc}{\overline{U}}_{1,t,i}^{}& {\overline{U}}_{2,t,i}\\ {\overline{U}}_{2,t,i}^T& {\overline{U}}_{3,t,i}\end{array}\right]{\left({\overline{A}}_t^i\right)}^T+{\rho }_{1,i}^{-1}\left[\begin{array}{cc}{M}_1^i{\left(M_1^i\right)}^T& 0\\ 0& 0\end{array}\right]\hfill \\ +2{\rho }_{2,i}^{-1}\left[\begin{array}{cc}{M}_2^i{\left(M_2^i\right)}^T& 0\\ 0& 0\end{array}\right]+{\rho }_{3,i}^{-1}\left[\begin{array}{cc}I& -I\\ -I& I\end{array}\right]{\widehat{K}}_t^i{M}_3^i{\left(M_3^i\right)}^T{\left({\widehat{K}}_t^i\right)}^T\hfill \end{array}\end{array}$$

(9)

with the appropriate positive constants ${\rho }_{1,i}^{},{\rho }_{2,i}^{},{\rho }_{3,i}^{}$, and

$$\begin{array}{c}\hfill \left[\begin{array}{cc}{\overline{U}}_{1,t,i}^{}& {\overline{U}}_{2,t,i}\\ {\overline{U}}_{2,t,i}^T& {\overline{U}}_{3,t,i}\end{array}\right]={\left({\overline{P}}_t^i-\left[\begin{array}{cc}{\rho }_{1,i}I& {\rho }_{1,i}I\\ {\rho }_{1,i}I& ({\rho }_{1,i}+2{\rho }_{2,i}+{\rho }_{3,i})I\end{array}\right]\right)}^{-1}.\end{array}$$

For the fourth term on the right-hand side of inequality (7), the equation is

$$\begin{array}{c}\hfill E\left\{{\overline{\omega }}_t^i{\left({\overline{\omega }}_t^i\right)}^T\right\}=\left[\begin{array}{cc}Q& 0\\ 0& {\widehat{K}}_t^i{R}^i{\left({\widehat{K}}_t^i\right)}^T\end{array}\right].\end{array}$$

For the third term on the right of inequality (7), based on the basic knowledge of graph theory, we obtain

$$\begin{array}{c}\hfill \begin{array}{c}E\left\{{\overline{Z}}_t^i{\left({\overline{Z}}_t^i\right)}^T\right\}\hfill \\ \le \left[\begin{array}{cc}0& 0\\ 0& {\widehat{Z}}_t^{i}E\left\{\begin{array}{c}\left({\displaystyle \sum _{j\in {\Im }_i}}{\left({\tilde{P}}_t^j\right)}^{-1}{\mu }_j({\widehat{x}}_t^i-{\tilde{x}}_t^j)\right)\times \hfill \\ {\left({\displaystyle \sum _{j\in {\Im }_i}}{\left({\tilde{P}}_t^j\right)}^{-1}{\mu }_j({\widehat{x}}_t^i-{\tilde{x}}_t^j)\right)}^T\hfill \end{array}\right\}{\left({\widehat{Z}}_t^i\right)}^T\end{array}\right]\hfill \\ \\ \le \left[\begin{array}{cc}0& 0\\ 0& {\widehat{Z}}_t^i{\overline{\Psi }}_t^i{\left({\widehat{Z}}_t^i\right)}^T\end{array}\right]\hfill \end{array}\end{array}$$

where ${\overline{\Psi }}_t^i={\overline{c}}_i{\displaystyle \sum _{j\in {\Im }_i}}{\left({\tilde{P}}_t^j\right)}^{-1}{P}_t^j{\left({\left({\tilde{P}}_t^j\right)}^{-1}\right)}^T$.

To sum up, (7) can be written as:

$$\begin{array}{c}\hfill \begin{array}{cc}{\overline{P}}_{t+1}^i\hfill & \le (1+{\beta }_{1,i}+{\beta }_{2,i}){\overline{A}}_t^i\left[\begin{array}{cc}{\overline{U}}_{1,t,i}^{}& {\overline{U}}_{2,t,i}\\ {\overline{U}}_{2,t,i}^T& {\overline{U}}_{3,t,i}\end{array}\right]{\left({\overline{A}}_t^i\right)}^T\hfill \\ \hfill & +(2+{\beta }_{1,i}^{-1})\left[\begin{array}{cc}0& 0\\ 0& {\widehat{Z}}_t^i{\overline{\Psi }}_t^i{\left({\widehat{Z}}_t^i\right)}^T\end{array}\right]+O_t^i+\left[\begin{array}{cc}0& 0\\ 0& I\end{array}\right]{\widehat{K}}_t^i\left((1+{\beta }_{1,i}+{\beta }_{2,i}){\rho }_{3,i}^{-1}{M}_3^i{\left(M_3^i\right)}^T+R^i\right){\left({\widehat{K}}_t^i\right)}^T\hfill \end{array}\end{array}$$

(10)

where

$$\begin{array}{c}\hfill \begin{array}{cc}{O}_t^i\hfill & =(2+{\beta }_{2,i}^{-1}){\overline{f}}_t^i{\left({\overline{f}}_t^i\right)}^{\mathrm{T}}+\left[\begin{array}{cc}Q& 0\\ 0& 0\end{array}\right]+(1+{\beta }_{1,i}+{\beta }_{2,i}){\rho }_{1,i}^{-1}\left[\begin{array}{cc}{M}_1^i{\left(M_1^i\right)}^{\mathrm{T}}& 0\\ 0& 0\end{array}\right]\hfill \\ \hfill & +2(1+{\beta }_{1,i}+{\beta }_{2,i}){\rho }_{2,i}^{-1}\left[\begin{array}{cc}{M}_2^i{\left(M_2^i\right)}^{\mathrm{T}}& 0\\ 0& 0\end{array}\right]\hfill \end{array}\end{array}$$

(11)

It is noted from (10) that:

$$\begin{array}{c}\hfill \begin{array}{cc}{\widehat{P}}_{t+1}^i\hfill & =(1+{\beta }_{1,i}+{\beta }_{2,i}){\overline{A}}_t^i\left[\begin{array}{cc}{U}_{1,t,i}^{}& U_{2,t,i}\\ U_{2,t,i}^T& U_{3,t,i}\end{array}\right]{\left({\overline{A}}_t^i\right)}^{\mathrm{T}}\hfill \\ \hfill & +(2+{\beta }_{1,i}^{-1})\left[\begin{array}{cc}0& 0\\ 0& {\widehat{Z}}_t^i{\Psi }_t^i{\left({\widehat{Z}}_t^i\right)}^{\mathrm{T}}\end{array}\right]+\left[\begin{array}{cc}0& 0\\ 0& I\end{array}\right]{\widehat{K}}_t^i\left((1+{\beta }_{1,i}+{\beta }_{2,i}){\rho }_{3,i}^{-1}{M}_3^i{\left(M_3^i\right)}^{\mathrm{T}}+R^i\right){\left({\widehat{K}}_t^i\right)}^{\mathrm{T}}\hfill \\ \hfill & +O_t^i\hfill \end{array}\end{array}$$

(12)

and

$$\begin{array}{c}\hfill \left[\begin{array}{cc}{U}_{1,t,i}^{}& U_{2,t,i}\\ U_{2,t,i}^T& U_{3,t,i}\end{array}\right]={\left({\left({\tilde{P}}_t^i\right)}^{-1}-\left[\begin{array}{cc}{\rho }_{1,i}I& {\rho }_{1,i}I\\ {\rho }_{1,i}I& ({\rho }_{1,i}+2{\rho }_{2,i}+{\rho }_{3,i})I\end{array}\right]\right)}^{-1}.\end{array}$$

(13)

By applying ([14], Lemma 3), if the initial conditions of the state covariance matrix ${\overline{P}}_0^i\le {\widehat{P}}_0^i$ are satisfiedwith the positive definite matrices $U_{1,t,i},U_{2,t,i},U_{3,t,i}$, then, in turn, the following inequalities are satisfied:

$$\begin{array}{c}\hfill {\overline{P}}_t^i\le {\widehat{P}}_t^i\end{array}$$

(14)

Considering the relationship between the error covariance matrix and the augmented system state covariance matrix, it follows that

$$\begin{array}{c}\hfill \begin{array}{cc}{P}_{t+1}^i\hfill & =\left[\begin{array}{cc}I& -I\end{array}\right]{\overline{P}}_{t+1}^i{\left[\begin{array}{cc}I& -I\end{array}\right]}^T\le \left[\begin{array}{cc}I& -I\end{array}\right]{\widehat{P}}_{t+1}^i{\left[\begin{array}{cc}I& -I\end{array}\right]}^T={\tilde{P}}_{t+1}^i\hfill \\ \hfill & =(1+{\beta }_{1,i}+{\beta }_{2,i})\left\{\begin{array}{c}{\left(B_t^i\right)}^T\left(\Pi U_{1,t,i}+\Xi U_{2,t,i}^T-\Pi U_{2,t,i}+\Xi U_{3,t,i}^T\right)\hfill \\ -{\left(C_t^i\right)}^T{\left({\widehat{K}}_t^i\right)}^T\left(\Pi U_{1,t,i}-\Xi U_{2,t,i}^T\right)-\Lambda \left(\Pi U_{2,t,i}-\Xi U_{3,t,i}^T\right)\hfill \end{array}\right\}\hfill \\ \hfill & +(2+{\beta }_{1,i}^{-1}){\widehat{Z}}_t^i{\Psi }_t^i{\left({\widehat{Z}}_t^i\right)}^T+{\Gamma }_t^i\hfill \end{array}\end{array}$$

(15)

where

$$\begin{array}{c}\hfill \begin{array}{cc}\Pi =\hfill & B_t^i-{\widehat{K}}_t^i{C}_t^i\hfill \\ \Xi =\hfill & {\widehat{K}}_t^i{C}_t^i-B_t^i-\Delta {\widehat{f}}_t^i\hfill \\ \Lambda =\hfill & {(\Delta {\widehat{f}}_t^i)}^T-{\left(C_t^i\right)}^T{\left({\widehat{K}}_t^i\right)}^T\hfill \\ {\Gamma }_t^i=\hfill & 2(2+{\beta }_{2,i}^{-1}){\overline{f}}_t^i{\left({\overline{f}}_t^i\right)}^T+Q+(1+{\beta }_{1,i}+{\beta }_{2,i}){\rho }_{1,i}^{-1}{M}_1^i{\left(M_1^i\right)}^T+2(1+{\beta }_{1,i}+{\beta }_{2,i}){\rho }_{1,i}^{-1}{M}_2^i{\left(M_2^i\right)}^T\hfill \\ \hfill & +{\widehat{K}}_t^i\left((1+{\beta }_{1,i}+{\beta }_{2,i}){\rho }_{3,i}^{-1}{M}_3^i{\left(M_3^i\right)}^T+R^i\right){\left({\widehat{K}}_t^i\right)}^T.\hfill \end{array}\end{array}$$

(16)

Then, by calculating the partial derivative of the trace of (15) with respect to $\Delta {\widehat{f}}_t^i$, we obtain

$$\begin{array}{c}\hfill \frac{\partial {\tilde{P}}_{t+1}^i}{\partial \Delta {\widehat{f}}_t^i}=2B_t^i{U}_{2,t,i}-2B_t^i{U}_{3,t,i}-2{\left(C_t^i\right)}^T{\left({\widehat{K}}_t^i\right)}^T{U}_{2,t,i}+2{\left(C_t^i\right)}^T{\left({\widehat{K}}_t^i\right)}^T{U}_{2,t,i}=0.\end{array}$$

Similarly, by calculating the partial derivative of the trace of ${\tilde{P}}_{t+1}^i$ with respect to ${\widehat{K}}_t^i,{\widehat{Z}}_t^i$, it follows that

$$\begin{array}{c}\hfill \begin{array}{c}\frac{\partial {\tilde{P}}_{t+1}^i}{\partial {\widehat{K}}_t^i}={\widehat{K}}_t^i\left\{\begin{array}{c}(1+{\beta }_{1,i}+{\beta }_{2,i})\times \left(\begin{array}{c}2{\left(C_t^i\right)}^T{U}_{1,t,i}{C}_t^i-{\left(C_t^i\right)}^T{U}_{2,t,i}{C}_t^i-\hfill \\ 2{\left(C_t^i\right)}^T{U}_{2,t,i}^T{U}_{3,t,i}^{-1}{U}_{2,t,i}\times C_t^i+{\left(C_t^i\right)}^T{U}_{2,t,i}\hfill \end{array}\right)\hfill \\ +2\left((1+{\beta }_{1,i}+{\beta }_{2,i}){\rho }_{3,i}^{-1}{M}_3^i{\left(M_3^i\right)}^T+R^i\right)-2B_t^i{C}_t^i{U}_{1,t,i}+2{\left(C_t^i\right)}^T{U}_{2,t,i}^T{U}_{2,t,i}{B}_t^i{U}_{3,t,i}^{-1}\hfill \end{array}\right\}\hfill \\ =0\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{c}\frac{\partial {\tilde{P}}_{t+1}^i}{\partial {\widehat{Z}}_t^i}={\widehat{Z}}_t^i\left\{\begin{array}{c}(1+{\beta }_{1,i}+{\beta }_{2,i})\times \left(\begin{array}{c}2{\left(C_t^i\right)}^{\mathrm{T}}{U}_{1,t,i}{C}_t^i-{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}{C}_t^i-\hfill \\ 2{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}^{\mathrm{T}}{U}_{3,t,i}^{-1}{U}_{2,t,i}{C}_t^i+{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}\hfill \end{array}\right)\hfill \\ +2\left((2+{\beta }_{1,i}^{-1}){\Psi }_t^i\right)-2B_t^i{C}_t^i{U}_{1,t,i}+2{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}^{\mathrm{T}}{U}_{2,t,i}{B}_t^i{U}_{3,t,i}^{-1}\hfill \end{array}\right\}\hfill \\ =0\hfill \end{array}\end{array}$$

Through calculation, the estimated values of the gain matrix are derived by

$$\begin{array}{c}\hfill \Delta {\widehat{f}}_t^{i*}=U_{3,t,i}^{-1}\left[\left({\left(B_t^i\right)}^{\mathrm{T}}-{\left(C_t^i\right)}^{\mathrm{T}}{\left({\widehat{K}}_t^i\right)}^{\mathrm{T}}\right)\left(U_{2,t,i}-U_{3,t,i}\right)\right]\end{array}$$

(17)

$$\begin{array}{c}\hfill \begin{array}{c}{\widehat{K}}_t^{i*}=\left(2{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}^{\mathrm{T}}{U}_{2,t,i}{B}_t^i{U}_{3,t,i}^{-1}-2B_t^i{C}_t^i{U}_{1,t,i}\right)\times \hfill \\ {\left\{\begin{array}{c}(1+{\beta }_{1,i}+{\beta }_{2,i})\left(\begin{array}{c}2{\left(C_t^i\right)}^{\mathrm{T}}{U}_{1,t,i}{C}_t^i-{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}{C}_t^i-2{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}^{\mathrm{T}}\hfill \\ \times U_{3,t,i}^{-1}{U}_{2,t,i}{C}_t^i+{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}\hfill \end{array}\right)\hfill \\ +2\left((1+{\beta }_{1,i}+{\beta }_{2,i}){\rho }_{3,i}^{-1}{M}_3^i{\left(M_3^i\right)}^{\mathrm{T}}+R^i\right)\hfill \end{array}\right\}}^{-1}\hfill \end{array}\end{array}$$

(18)

$$\begin{array}{c}\hfill \begin{array}{c}{\widehat{Z}}_t^{i*}=\left(2{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}^{\mathrm{T}}{U}_{2,t,i}{B}_t^i{U}_{3,t,i}^{-1}-2B_t^i{C}_t^i{U}_{1,t,i}\right)\times \hfill \\ {\left\{\begin{array}{c}(1+{\beta }_{1,i}+{\beta }_{2,i})\left(\begin{array}{c}2{\left(C_t^i\right)}^{\mathrm{T}}{U}_{1,t,i}{C}_t^i-{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}{C}_t^i-2{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}^{\mathrm{T}}\hfill \\ \times U_{3,t,i}^{-1}{U}_{2,t,i}{C}_t^i+{\left(C_t^i\right)}^{\mathrm{T}}{U}_{2,t,i}\hfill \end{array}\right)\hfill \\ +2\left((2+{\beta }_{1,i}^{-1}){\Psi }_t^i\right)\hfill \end{array}\right\}}^{-1}\hfill \end{array}\end{array}$$

(19)

Based on the above analysis, we obtained the upper bound of the estimated error covariance matrix by deriving the relationship between the error covariance matrix and the augmented system state covariance matrix. Through optimizing the upper bound, estimates of unknown parameters were obtained, thus ensuring the feasibility of optimization Problem 1. In the following section, a fusion estimation criterion will be designed to compensate for the uncertainty of single sensor measurement.   □

 Remark 2. 

It is noted that in (4), the same idea as the extended Kalman filter is used to carry out Taylor expansion of the nonlinear function, and linearization error is introduced. However, different from the conventional extended Kalman filter, here a time-varying matrix ${\mathsf{{\rm Y}}}_{2,t}^i,{\mathsf{{\rm Y}}}_{3,t}^i$ considering linearization error and norm-bounded uncertainty is introduced, and then the uncertainty problem is embedded into the solution of nonlinear optimization Problem 1 to compensate for the linearization error.

4. Covariance Intersection Fusion Estimator

In distributed linear systems, considering the real-time requirements of estimation, we often adopt the scalar weighted linear minimum variance fusion estimation criterion, which needs to calculate the mutual covariance matrix between two adjacent nodes. However, for distributed nonlinear systems, it is very difficult to solve the mutual covariance matrices of fusion estimation algorithms. Therefore, based on the algorithm in [35], a covariance intersection (CI) fusion estimation algorithm is proposed. Furthermore, the following lemma is given:

 Lemma 2 

([35]). Given an n-dimensional random vector $x_{t-N}\in {\Re }^n$ and an unbiased estimate ${\widehat{x}}_{t-N|t}^{i*}(i=1,2,\cdots L)$, and given ${\tilde{P}}_{t-N}^i$ can be calculated using (15), then a covariance intersection (CI) fusion estimation algorithm is given by:

$${\widehat{x}}_{t-N|t}^{*}={\tilde{P}}_{t-N}\sum _{i=1}^L{\mu }_i{\left({\tilde{P}}_{t-N}^i\right)}^{-1}{\widehat{x}}_{t-N|t}^{i*}$$

(20)

$${\tilde{P}}_{t-N}^{-1}=\sum _{i=1}^L{\mu }_i{\left({\tilde{P}}_{t-N}^i\right)}^{-1}$$

(21)

$$0\le {\mu }_i\le 1,\sum _{i=1}^L{\mu }_i=1$$

where the scalar ${\mu }_i$ can be obtained from the following formula:

$$\begin{array}{c}\hfill \underset{{\mu }_i\in [0,1],{\displaystyle \sum _{i=1}^L}{\mu }_i=1}{min}tr\left({\tilde{P}}_{t-N}\right)\end{array}$$

(22)

Based on the above analysis, the above distributed moving horizon fusion estimation method can be summarized in Algorithm 1.   

Algorithm 1: Distributed moving horizon fusion estimation

1: When $t>N$, ${\tilde{x}}_0^i,{\widehat{P}}_0^i,Q,R^i,N$ can be initialized; 2: At time $t-N$, $\Delta {\widehat{f}}_t^i,{\widehat{K}}_t^i,{\widehat{Z}}_t^i$ are calculated using (4), (13), and (17)–(19); 3: The prior estimation state ${\tilde{x}}_{t-N}^i$ is calculated using (3), and ${\widehat{P}}_{t-N}^i$ is calculated using (12). 4: By solving the optimization Problem 1, get the optimal state estimation value ${\widehat{x}}_{t-N|t}^{i*}$; 5: Calculate the state estimate at the current moment using (3); 6: The fusion estimation value ${\widehat{x}}_{t-N|t}^{*}$ is calculated using (20)–(22). 7: At time $t-N+1$, by repeating calculation based on the new measurements, return to step 2.

 Remark 3. 

When $t\le N$, the full information moving horizon estimation problem should be solved to obtain the local optimal state estimate. The specific solution process can be referred to in [31].

 Remark 4. 

The method presented in this paper is different from the traditional moving horizon estimation; the error covariance matrix is not fixed, but changes with time. Therefore, it is a fault tolerant state estimation algorithm. For the sake of stability analysis in the next section, the calculation of the state estimate in the window should be consistent with the recursive formula of the prior state estimation model, i.e., (3) can be used to calculate both the state estimation at the current time and the prior state estimation at initial time.

In this section, a fusion estimation criterion was introduced and gave the calculation method of the weighting coefficient $\mu$. For convenience of application, the above distributed moving horizon fusion estimation was summarized as Algorithm 1. In the next section, the stability of the proposed algorithm will be proven, and a sufficient condition for the square convergence of the fusion estimation error norm will be given.

5. Algorithm Stability Analysis

The stability analysis is divided into two parts: firstly, the boundedness of the error covariance matrix is proven, and then the convergence of the error square of the fusion estimation is proven. Before proving the stability, we first define the following variables:

$$\begin{array}{c}\hfill M_N\left(x_{t-N}\right)\stackrel{\Delta }{=}\left[\begin{array}{c}{h}^i\left(x_{t-N}\right)\hfill \\ h^i\circ f\left(x_{t-N}\right)\hfill \\ ⋮\hfill \\ h^i\circ \underset{N}{\underbrace{f\circ \cdots \circ f}}\left(x_{t-N}\right)\hfill \end{array}\right]\end{array}$$

where the symbol “∘” represents the composition of functions, and

$$\begin{array}{c}\hfill \begin{array}{c}{\Phi }_{\omega }\left(x_{t-N}\right)=\hfill \\ {\left.\left[\begin{array}{cccc}0& 0& \cdots & 0\\ \frac{\partial h^i\circ f_{\left(1\right)}^{{\omega }_{t-N}}}{\partial {\omega }_{t-N}}& 0& \cdots & 0\\ \frac{\partial h^i\circ f_{\left(2\right)}^{{\omega }_{t-N}^{t-N+1}}}{\partial {\omega }_{t-N}}& \frac{\partial h^i\circ f_{\left(2\right)}^{{\omega }_{t-N}^{t-N+1}}}{\partial {\omega }_{t-N+1}}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial h^i\circ f_{\left(N\right)}^{{\omega }_{t-N}^{t-1}}}{\partial {\omega }_{t-N}}& \frac{\partial h^i\circ f_{\left(N\right)}^{{\omega }_{t-N}^{t-1}}}{\partial {\omega }_{t-N+1}}& \cdots & \frac{\partial h^i\circ f_{\left(N\right)}^{{\omega }_{t-N}^{t-1}}}{\partial {\omega }_{t-1}}\end{array}\right]\right|}_{{\omega }_{t-N}^{t-1}=0}\hfill \end{array}\end{array}$$

where

$$\begin{array}{c}\hfill \begin{array}{c}{f}_{\left(n\right)}^{}=\underset{\left(n\right)times}{\underbrace{f\circ \cdots \circ f}}\hfill \\ f_{\left(n\right)}^{{\omega }_{t-N}^{t-N+n-1}}\left(x\right)=f(\cdots f(f\left(x\right)+\omega {}_{t-N})+{\omega }_{t-N+1}\cdots )+{\omega }_{t-N+n-1}\hfill \\ \\ {\gamma }_{\omega }=max∥{\Phi }_{\omega }\left(x_{t-N}\right)∥,d_x=max∥x-\widehat{x}∥,{\lambda }_{\max }{\left({\tilde{P}}_{t-N}^i\right)}^{-1}={\theta }_{p^i}∥{\left(R^i\right)}^{-1}∥={\theta }_{r^i},\hfill \\ \\ R=diag\underset{(N+1)times}{\underbrace{(R^i,\cdots R^i)}},\overline{f}=max{∥\Delta f_t^i∥}^2,\overline{K}=max{∥{\widehat{K}}_t^i∥}^2,\overline{Z}=max{∥{\widehat{Z}}_t^i∥}^2\hfill \end{array}\end{array}$$

(23)

Furthermore

$$\begin{array}{c}\hfill {\epsilon }^i=\underset{n=1,\cdots N}{\underbrace{max{\epsilon }_n^i}}\end{array}$$

which satisfies

$$\begin{array}{c}\hfill \begin{array}{c}∥\begin{array}{c}{\left.\frac{\partial h^i\circ f_{\left(1\right)}^{{\omega }_{t-N}^{}}\left(x_{t-N}\right)}{\partial {\omega }_{t-N}}\right|}_{{\omega }_{t-N}={\tilde{\omega }}_{t-N}}\hfill \\ -{\left.\frac{\partial h^i\circ f_{\left(1\right)}^{{\omega }_{t-N}^{}}\left(x_{t-N}\right)}{\partial {\omega }_{t-N}}\right|}_{{\omega }_{t-N}=0}\hfill \end{array}∥\le {\epsilon }_1^i∥{\tilde{\omega }}_{t-N}∥\hfill \\ ⋮\hfill \\ ∥\begin{array}{c}{\left.\frac{\partial h^i\circ f_{\left(N\right)}^{{\omega }_{t-N}^{t-1}}\left(x_{t-N}\right)}{\partial {\omega }_{t-N}^{t-1}}\right|}_{{\omega }_{t-N}^{t-1}={\tilde{\omega }}_{t-N}^{t-1}}\hfill \\ -{\left.\frac{\partial h^i\circ f_{\left(1\right)}^{{\omega }_{t-N}^{t-1}}\left(x_{t-N}\right)}{\partial {\omega }_{t-N}^{t-1}}\right|}_{{\omega }_{t-N}^{t-1}=0}\hfill \end{array}∥\le {\epsilon }_N^i∥{\tilde{\omega }}_{t-N}^{t-1}∥\hfill \end{array}\end{array}$$

(24)

obtained from the classical mean value theorem [36].

Before proving the stability of the system, we first introduce the following definitions and assumptions:

 Definition 1. 

A continuous function $\xi :\left[0,x\right)\to \left[0,\infty \right)$ is a K-function if it is strictly monotonically increasing, $\xi \left(x\right)>0$ for $x\ne 0,\xi \left(0\right)=0$, and $\underset{x\to \infty }{lim}\xi \left(x\right)=\infty$.

 Definition 2. 

If feasible solutions to Problem 1 exists, then ${\widehat{P}}_k^i={\left({\widehat{P}}_k^i\right)}^T\ge 0\left(0\le k\le t\right)$ exists, such that (12) holds.

 Definition 3. 

If a K-function $\xi \left(·\right)$ exists, such that$\xi \left({∥x_1-x_2∥}^2\right)\le {∥M_N\left(x_1\right)-M_N\left(x_2\right)∥}^2$holds, then the system (1) is a fully observable system in $N+1$ steps.

 Assumption 1. 

System (1) is fully observable in $N+1$ steps with a K-function $\xi \left(·\right)$ defined by Definition 3.

 Assumption 2. 

Functions $f\left(·\right),h^i\left(·\right)$ satisfy Lipschitz continuity, i.e., scalars $m_1,m_2>0$ exist, such that the following inequalities hold:

$$\begin{array}{c}\hfill \begin{array}{c}{∥f\left(x_1\right)-f\left(x_2\right)∥}^2\le m_1{∥x_1-x_2∥}^2\hfill \\ {∥h^i\left(x_1\right)-h^i\left(x_2\right)∥}^2\le m_2{∥x_1-x_2∥}^2\hfill \end{array}\end{array}$$

Based on the assumptions and definitions above, the following theorem is given

 Theorem 1. 

If the estimation error covariance matrix can be calculated by (12) and the solution of Problem 1 exists, then the estimation error covariance is bounded for system (1).

 Proof. 

It can be seen from Definition 2 that the recursive window estimation model given in (3) is feasible, i.e., when $T\to \infty$, the error covariance matrix ${\widehat{P}}_t^i$ obtained from (12) tends to the unique positive semidefinite matrix. If the solution of Problem 1 exists, i.e., the performance index $J_t^{i*}$ is bounded, it is expressed as follows:

$$\begin{array}{c}\hfill J_t^{i*}=\underset{{\widehat{x}}_{t-N|t}^{i*}}{min}{J}_t^i\left({\widehat{x}}_{t-N|t}^{i*}\right)<\Theta ,\Theta >0\end{array}$$

Then it can be inferred that

$$\begin{array}{c}\hfill {\left(v_t^i\right)}^T{\left(R^i\right)}^{-1}{v}_t^i<J_t^{i*}=\underset{{\widehat{x}}_{t-N|t}^{i*}}{min}{J}_t^i\left({\widehat{x}}_{t-N|t}^{i*}\right)<\Theta \end{array}$$

Let $v_t^i=y_t^i-{\widehat{y}}_t^i$; combining it with Assumption 2, we get:

$$\begin{array}{c}\hfill \begin{array}{c}E\left[{\lambda }_{min}{\left(R^i\right)}^{-1}tr\left(v_t^i{\left(v_t^i\right)}^T\right)I\right]\ge {\lambda }_{min}{\left(R^i\right)}^{-1}E\left(v_t^i{\left(v_t^i\right)}^T\right)\hfill \\ ={\lambda }_{min}{\left(R^i\right)}^{-1}\left\{m_{2}E\left[\begin{array}{c}(x_t-{\widehat{x}}_t^i){(x_t-{\widehat{x}}_t^i)}^T\hfill \end{array}\right]+R^i\right\}\hfill \end{array}\end{array}$$

According to $P_t^i=E\left\{\left(x_t-{\widehat{x}}_t^i\right){\left(x_t-{\widehat{x}}_t^i\right)}^T\right\}$, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\lambda }_{min}{\left(R^i\right)}^{-1}(m_2{P}_t^i+R^i)& \le E\left[\begin{array}{c}{\lambda }_{min}{\left(R^i\right)}^{-1}tr\left(v_t^i{\left(v_t^i\right)}^T\right)I\hfill \end{array}\right]\le {\left(v_t^i\right)}^T{\left(R^i\right)}^{-1}{v}_t^i<J_t^{i*}\hfill \\ \hfill & =\underset{{\widehat{x}}_{t-N|t}^{i*}}{min}{J}_t^i\left({\widehat{x}}_{t-N|t}^{i*}\right)<\Theta \hfill \end{array}\end{array}$$

So the upper bound of estimation error covariance is $\Theta$. Next, we substitute the upper bound value into (20) and rewrite (20) into the following form:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\widehat{x}}_{t-N|t}^{*}& ={\left({\displaystyle \sum _{i=1}^L}{\mu }_i{\Theta }^{-1}\right)}^{-1}{\displaystyle \sum _{i=1}^L}{\mu }_i{\Theta }^{-1}{\widehat{x}}_{t-N|t}^{i*}\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^L}{\mu }_i{\widehat{x}}_{t-N|t}^{i*}\hfill \end{array}\end{array}$$

(25)

Then the proof is complete. Next we prove the boundedness of the norm square of the fusion estimation error and define the local estimation error at time $t-N$ as

$$\begin{array}{c}\hfill \begin{array}{c}{e}_{t-N}^i=x_{t-N}-{\widehat{x}}_{t-N|t}^{i*}\hfill \end{array}\end{array}$$

(26)

Similarly, the fusion estimation error at time $t-N$ is defined as

$$\begin{array}{c}\hfill \begin{array}{c}{e}_{t-N}=x_{t-N}-{\widehat{x}}_{t-N|t}^{*}.\hfill \end{array}\end{array}$$

□

Then, the necessary theorem should be introduced:

 Theorem 2. 

Supposing that Assumptions 1 and 2 hold, a K-function $\xi \left(·\right)$ defined in Assumption 1 exists and satisfies the following conditions:

$$\begin{array}{c}\hfill \varphi =inf\frac{\xi \left({∥x_1-x_2∥}^2\right)}{{∥x_1-x_2∥}^2}\ge 0\end{array}$$

(27)

If the error covariance matrix corresponding to ${\tilde{x}}_{t-N}^i$ in (3) and weight matrix ${\tilde{P}}_{t-N}^i,R^i$ in (2) cause the following inequality

$$\begin{array}{c}\hfill \frac{20{\mu }_i{\theta }_{p^i}L(m_1^2+\overline{Z}{\mu }_i{\theta }_{p^i}L\ell )}{{\mu }_i{\theta }_{p^i}+\varphi {\theta }_{r^i}}<1\end{array}$$

(28)

to hold, then

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}{∥e_{t-N}^i∥}^2\le \frac{{\vartheta }^i}{1-{\delta }^i}\end{array}$$

(29)

Furthermore, the norm square of the fusion estimation error satisfies the following form:

$$\begin{array}{c}\hfill {∥e_{t-N}∥}^2\le {∥e_{t-N}^i∥}^2\le {\chi }_{t-N}^i\end{array}$$

(30)

where ${\chi }_{t-N}^i$ has the following form:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\chi }_0^i={\vartheta }_0^i\hfill \\ {\chi }_t^i={\delta }^i{\chi }_{t-1}^i+{\vartheta }^i,t=1,2\cdots \hfill \end{array}\right.\end{array}$$

(31)

with

$$\begin{array}{c}\hfill \begin{array}{c}{\delta }^i=\frac{20{\mu }_i{\theta }_{p^i}L(m_1^2+\overline{Z}{\mu }_i{\theta }_{p^i}L\ell )}{{\mu }_i{\theta }_{p^i}+\varphi {\theta }_{r^i}}\hfill \\ \\ {\vartheta }^i=\frac{4}{{\mu }_i{\theta }_{p^i}+\varphi {\theta }_{r^i}}\left\{\begin{array}{c}2{\mu }_i{\theta }_{p^i}{\theta }_{\omega }^2+{\theta }_{r^i}({\gamma }_{\omega }\sqrt{N}{\theta }_{\omega }+\sqrt{N+1}{\theta }_{v^i}\frac{{\epsilon }^i}{2}\sqrt{\frac{N(N+1)(2N+1)}{6}}{\theta }_{\omega }^2{)}^2\hfill \end{array}\right\}\hfill \\ \\ {\vartheta }_0^i=\frac{4}{{\mu }_i{\theta }_{p^i}+\varphi {\theta }_{r^i}}\left\{\begin{array}{c}{\mu }_i{\theta }_{p^i}{d}_x^2+{\theta }_{r^i}({\gamma }_{\omega }\sqrt{N}{\theta }_{\omega }+\sqrt{N+1}{\theta }_{v^i}\frac{{\epsilon }^i}{2}\sqrt{\frac{N(N+1)(2N+1)}{6}}{\theta }_{\omega }^2{)}^2\hfill \end{array}\right\}.\hfill \end{array}\end{array}$$

 Proof. 

The performance index can be rewritten as the following form:

$$\begin{array}{c}\hfill J_t^i\left({\widehat{x}}_{t-N|t}^{i*}\right)=\sum _{j(j\ne i)\in {\Im }_i}{\mu }_j{∥{\widehat{x}}_{t-N|t}^i-{\tilde{x}}_{t-N}^j∥}_{{\left({\tilde{P}}_{t-N}^j\right)}^{-1}}^2+\sum _{k=t-N}^t{∥y_k^i-{\widehat{h}}^i\left({\widehat{x}}_{k|t}^i\right)∥}_{{\left(R^i\right)}^{-1}}^2\end{array}$$

According to ${\widehat{x}}_{t-N|t}^{i*}$ being optimal, the upper bound of the optimal performance index $J_t^{i*}$ is given by

$$\begin{array}{c}\hfill J_t^{i*}\le \sum _{j(j\ne i)\in {\Im }_i}{\mu }_j{∥x_{t-N}^{}-{\tilde{x}}_{t-N}^j∥}_{{\left(P_{t-N}^j\right)}^{-1}}^2+\sum _{k=t-N}^t{∥y_k^i-h^i\left(x_k\right)∥}_{{\left(R^i\right)}^{-1}}^2\end{array}$$

Each of the terms in the second term of the right-hand side of the above inequality can be written as:

$$\begin{array}{c}\hfill \begin{array}{c}k=0:{∥v_{t-N}^i∥}^2\hfill \\ k=1:{∥h\left[f_{\left(1\right)}^{{\omega }_{t-N}}\left(x_{t-N}^{}\right)\right]-h\left[f_{\left(1\right)}^{}\left(x_{t-N}^{}\right)\right]+v_{t-N+1}^i∥}^2\hfill \\ =∥{\left.\frac{\partial h^i\circ f_{\left(1\right)}^{{\omega }_{t-N}^{}}\left(x_{t-N}\right)}{\partial {\omega }_{t-N}^{}}\right|}_{{\omega }_{t-N}^{}=0}{\omega }_{t-N}+{\varpi }^{\left(1\right)}+v_{t-N+1}^i∥\hfill \\ ⋮\hfill \\ k=N:{∥h\left[f_{\left(N\right)}^{{\omega }_{t-N}^{t-1}}\left(x_{t-N}^{}\right)\right]-h\left[f_{\left(N\right)}^{}\left(x_{t-N}^{}\right)\right]+v_t^i∥}^2\hfill \\ =∥{\left.\frac{\partial h^i\circ f_{\left(1\right)}^{{\omega }_{t-N}^{t-1}}\left(x_{t-N}\right)}{\partial {\omega }_{t-N}^{t-1}}\right|}_{{\omega }_{t-N}^{t-1}=0}{\omega }_{t-N}^{t-1}+{\varpi }^{\left(N\right)}+v_t^i∥\hfill \end{array}\end{array}$$

${\varpi }^{\left(k\right)}$ is a function of $x_{t-N},{\omega }_{t-N}^{}$, and $\Xi =col(0,{\varpi }^{\left(1\right)},{\varpi }^{\left(2\right)},\cdots {\varpi }^{\left(N\right)})$, so the upper bound of the performance index is changed to

$$\begin{array}{c}\hfill J_t^{i*}\le \sum _{j(j\ne i)\in {\Im }_i}{\mu }_j{∥x_{t-N}^{}-{\tilde{x}}_{t-N}^j∥}_{{\left({\tilde{P}}_{t-N}^j\right)}^{-1}}^2+{\theta }_{r^i}{({\gamma }_{\omega }\sqrt{N}{\theta }_{\omega }+\sqrt{N+1}{\theta }_{v^i}+∥\Xi ∥)}^2\end{array}$$

(32)

After a little bit of algebra, we obtain:

$$\begin{array}{c}\hfill \begin{array}{c}∥{\varpi }^{\left(1\right)}∥\le \frac{1}{2}{\epsilon }_1^i{∥{\omega }_{t-N}∥}^2\hfill \\ ⋮\hfill \\ ∥{\varpi }^{\left(N\right)}∥\le \frac{1}{2}{\epsilon }_N^i{∥{\omega }_{t-N}^{t-1}∥}^2=\frac{1}{2}{\epsilon }_N^i{\displaystyle \sum _{s=0}^{N-1}}{∥{\omega }_{t-N+s}∥}^2\hfill \\ {∥\Xi ∥}^2\le {\left(\frac{1}{2}{\epsilon }_1^i{∥{\omega }_{t-N}∥}^2\right)}^2+\cdots {\left(\frac{1}{2}{\epsilon }_n^i{\displaystyle \sum _{s=0}^{N-1}}{∥{\omega }_{t-N+s}∥}^2\right)}^2\hfill \end{array}\end{array}$$

According to the formula of inequality of the sum of squares and the relevant definitions in (23), we obtain:

$$\begin{array}{c}\hfill \begin{array}{c}{∥\Xi ∥}^2\le \frac{{\left({\epsilon }^i\right)}^2}{4}({\theta }_{\omega }^4+\cdots +N^2{\theta }_{\omega }^4)=\frac{{\left({\epsilon }^i\right)}^2}{4}{\theta }_{\omega }^4{\displaystyle \sum _{k=1}^N}{k}^2=\frac{{\left({\epsilon }^i\right)}^2}{4}\frac{N(N+1)(2N+1)}{6}{\theta }_{\omega }^4\hfill \end{array}\end{array}$$

Then (32) is rewritten as

$$\begin{array}{c}\hfill \begin{array}{c}{J}_t^{i*}\le {\displaystyle \sum _{j(j\ne i)\in \Im {}_i}}{\mu }_j{∥x_{t-N}^{}-{\tilde{x}}_{t-N}^i∥}_{{\left({\tilde{P}}_{t-N}^j\right)}^{-1}}^2+{\theta }_{r^i}({\gamma }_{\omega }\sqrt{N}{\theta }_{\omega }+\sqrt{N+1}{\theta }_{v^i}+\frac{{\epsilon }^i}{2}\sqrt{\frac{N(N+1)(2N+1)}{6}}{\theta }_{\omega }^2{)}^2\hfill \end{array}\end{array}$$

For simplicity of expression, let

$$\begin{array}{c}\hfill \begin{array}{c}q={\theta }_{r^i}({\gamma }_{\omega }\sqrt{N}{\theta }_{\omega }+\sqrt{N+1}{\theta }_{v^i}+\frac{{\epsilon }^i}{2}\sqrt{\frac{N(N+1)(2N+1)}{6}}{\theta }_{\omega }^2{)}^2\hfill \end{array}\end{array}$$

So we get the upper bound of the optimal performance index as

$$\begin{array}{c}\hfill J_t^{i*}\le {\displaystyle \sum _{j(j\ne i)\in \Im {}_i}}{\mu }_j{∥x_{t-N}^{}-{\tilde{x}}_{t-N}^i∥}_{{\left({\tilde{P}}_{t-N}^j\right)}^{-1}}^2+q\end{array}$$

(33)

Similarly, we give the derivation process of the lower bound of the optimal performance index. The second term on the right of the inequality can be rewritten as

$$\begin{array}{c}\hfill {\displaystyle \sum _{k=t-N}^t}{∥y_k^i-h^i\left({\widehat{x}}_{k|t}^i\right)∥}_{{\left(R^i\right)}^{-1}}^2={∥Y_{t-N}^t-M_N\left({\widehat{x}}_{t-N|t}^{i*}\right)∥}_{{\left(R\right)}^{-1}}^2\end{array}$$

Because

$$\begin{array}{c}\hfill \begin{array}{c}{∥M_N\left(x_{t-N}\right)-M_N\left({\widehat{x}}_{t-N|t}^{i*}\right)∥}_{{\left(R\right)}^{-1}}^2={∥\left[Y_{t-N}^t-M_N\left({\widehat{x}}_{t-N|t}^{i*}\right)\right]-\left[Y_{t-N}^t-M_N\left(x_{t-N}\right)\right]∥}_{{\left(R\right)}^{-1}}^2\hfill \end{array}\end{array}$$

where, $Y_{t-N}^t=col(y_{t-N}^i,\cdots y_t^i)$.

Further, using Assumption 1, we obtain

$$\begin{array}{c}\hfill \begin{array}{c}{∥Y_{t-N}^t-M_N\left({\widehat{x}}_{t-N|t}^{i*}\right)∥}_{R^{-1}}^2\ge \frac{1}{2}\xi \left({∥x_{t-N}-{\widehat{x}}_{t-N|t}^{i*}∥}_{{\left({\tilde{P}}_{t-N}^i\right)}^{-1}}^2\right)-q\hfill \end{array}\end{array}$$

(34)

For the first term in inequality (32), it is shown that

$$\begin{array}{c}\hfill \begin{array}{c}{∥x_{t-N}-{\widehat{x}}_{t-N|t}^{i*}∥}_{{\left({\tilde{P}}_{t-N}^j\right)}^{-1}}^2\le 2{∥x_{t-N}-{\tilde{x}}_{t-N}^i∥}_{{\left({\tilde{P}}_{t-N}^j\right)}^{-1}}^2+2{∥{\tilde{x}}_{t-N}^i-{\widehat{x}}_{t-N|t}^{i*}∥}_{{\left({\tilde{P}}_{t-N}^j\right)}^{-1}}^2\hfill \end{array}\end{array}$$

(35)

By combining (26) and (34), the lower bound of the optimal value of the performance index is

$$\begin{array}{c}\hfill \begin{array}{c}{J}_t^{i*}\ge \frac{1}{2}{\mu }_i{\theta }_{p^i}{∥e_{t-N}^i∥}^2+\frac{1}{2}\xi \left[{\theta }_{r^i}{∥e_{t-N}^i∥}^2\right]-{\mu }_i{\theta }_{p^i}{\displaystyle \sum _{j(j\ne i)\in {\Im }_i}}{\mu }_j{∥x_{t-N}-{\tilde{x}}_{t-N}^i∥}^2-q\hfill \end{array}\end{array}$$

(36)

Combining (33) and (36), we obtain

$$\begin{array}{c}\hfill \begin{array}{c}\frac{1}{2}{\mu }_i{\theta }_{p^i}{∥e_{t-N}^i∥}^2+\frac{1}{2}\xi \left[{\theta }_{r^i}{∥e_{t-N}^i∥}^2\right]\le 2{\theta }_{p^i}{\displaystyle \sum _{j(j\ne i)\in {\Im }_i}}{\mu }_j{∥x_{t-N}-{\tilde{x}}_{t-N}^i∥}^2+2q\hfill \end{array}\end{array}$$

(37)

According to Theorem 2, we obtain

$$\begin{array}{c}\hfill \varphi \left({∥e_{t-N}^i∥}_{{\left({\tilde{P}}_{t-N}^i\right)}^{-1}}^2\right)\le \xi \left({∥e_{t-N}^i∥}_{{\left({\tilde{P}}_{t-N}^i\right)}^{-1}}^2\right)\end{array}$$

After sorting out, we obtain

$$\begin{array}{c}\hfill {∥e_{t-N}^i∥}^2\le \frac{4{\mu }_i{\theta }_{p^i}L}{{\mu }_i{\theta }_{p^i}+\varphi {\theta }_{r^i}}{∥x_{t-N}-{\tilde{x}}_{t-N}^i∥}^2+\frac{4}{{\mu }_i{\theta }_{p^i}+\varphi {\theta }_{r^i}}q\end{array}$$

(38)

Based on (38) and (23), we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {∥x_{t-N}-{\tilde{x}}_{t-N}^i∥}^2& ={∥\begin{array}{c}f\left(x_{t-N-1}\right)+{\omega }_{t-N-1}-f\left({\widehat{x}}_{t-N-1|t-1}^{i*}\right)-\Delta {\widehat{f}}_{t-N-1}^i{\widehat{x}}_{t-N-1|t-1}^{i*}\hfill \\ -{\widehat{K}}_{t-N-1}^i(y_{t-N-1}^i-{\widehat{h}}^i\left({\widehat{x}}_{t-N-1|t-1}^{i*}\right))-{\widehat{Z}}_{t-N-1}^i\times \hfill \\ {\displaystyle \sum _{j\in {\Im }_i}}{\left({\tilde{P}}_{t-N-1}^j\right)}^{-1}{\mu }_j({\widehat{x}}_{t-N-1|t-1}^{i*}-{\tilde{x}}_{t-N-1}^j)\hfill \end{array}∥}^2\hfill \\ \hfill & \le 5{∥f\left(x_{t-N-1}\right)-f\left({\widehat{x}}_{t-N-1|t-1}^{i*}\right)∥}^2+5{∥{\omega }_{t-N-1}∥}^2+5{\overline{f}}^2{\theta }_x^2+5\overline{K}{q}^2\hfill \\ \hfill & +10\overline{Z}L{\mu }_i{\theta }_{p^i}(\ell {∥e_{t-N-1}^i∥}^2-\eta )\hfill \\ \hfill & \le 5m_1^2{∥x_{t-N-1}-{\widehat{x}}_{t-N-1|t-1}^{i*}∥}^2+5{\theta }_{\omega }^2+5{\overline{f}}^2{\theta }_x^2+5\overline{K}{q}^2\hfill \\ \hfill & +10\overline{Z}L{\mu }_i{\theta }_{p^i}(\ell {∥e_{t-N-1}^i∥}^2-\eta )\hfill \\ \hfill & =(5m_1^2+5\overline{Z}L{\mu }_i{\theta }_{p^i}\ell ){∥e_{t-N-1}^i∥}^2+5{\theta }_{\omega }^2+5{\overline{f}}^2{\theta }_x^2+5\overline{K}{q}^2-5\overline{Z}L{\mu }_i{\theta }_{p^i}\eta \hfill \end{array}\end{array}$$

(39)

where,

$$\begin{array}{c}\hfill \ell =\frac{\left(4L+1\right){\mu }_i{\theta }_{p^i}+\varphi {\theta }_{r^i}}{2{\mu }_i{\theta }_{p^i}L},\eta =\frac{2q}{{\mu }_i{\theta }_{p^i}L}\end{array}$$

Substituting (39) into (38) obtains

$$\begin{array}{c}\hfill \begin{array}{c}{∥e_{t-N}^i∥}^2\le \hfill \\ \\ \frac{4{\mu }_i{\theta }_{p^i}L}{{\mu }_i{\theta }_{p^i}+\varphi {\theta }_{r^i}}\left\{\begin{array}{c}(5m_1^2+5\overline{Z}L{\mu }_i{\theta }_{p^i}\ell ){∥e_{t-N-1}^i∥}^2+5{\theta }_{\omega }^2+5{\overline{f}}^2{\theta }_x^2+5\overline{K}{q}^2-5\overline{Z}L{\mu }_i{\theta }_{p^i}\eta \hfill \end{array}\right\}\hfill \\ \\ +\frac{4}{{\mu }_i{\theta }_{p^i}+\varphi {\theta }_{r^i}}q\hfill \\ \\ =\frac{20{\mu }_i{\theta }_{p^i}L(m_1^2+\overline{Z}{\mu }_i{\theta }_{p^i}L\ell ){∥e_{t-N-1}^i∥}^2}{{\mu }_i{\theta }_{p^i}+\varphi {\theta }_{r^i}}+\frac{20{\mu }_i{\theta }_{p^i}L\left({\theta }_{\omega }^2+{\overline{f}}^2{\theta }_x^2+\overline{K}{q}^2-\overline{Z}L{\mu }_i{\theta }_{p^i}\eta \right)+4q}{{\mu }_i{\theta }_{p^i}+\varphi {\theta }_{r^i}}\hfill \end{array}\end{array}$$

(40)

If inequality (28) holds, it is easy to obtain the upper bound ${\vartheta }^i/(1-{\delta }^i)$ of the square of the local estimation error norm, because ${\chi }_t^i={\left({\delta }^i\right)}^t{\chi }_0^i+{\vartheta }^i{\displaystyle \sum _{s=0}^{t-1}}{\left({\chi }^i\right)}^s$. Then the boundedness proof of local estimation error is completed. □

Here, the stability of the local estimation error is analyzed. Next, we will prove the stability of the fusion estimation error by introducing Definition 4.

 Definition 4. 

For any point set $\left\{x_i\right\}$, if ${\sigma }_i\ge 0,{\displaystyle \sum _i}{\sigma }_i=1$, the convex function $g\left(x\right)$ satisfies the following inequality:

$$\begin{array}{c}\hfill g\left({\displaystyle \sum _{i=1}^M}{\sigma }_i{x}_i\right)\le {\displaystyle \sum _{i=1}^M}{\sigma }_{i}g\left(x_i\right).\end{array}$$

 Proof. 

The fusion estimation error can be rewritten as

$$\begin{array}{c}\hfill e_{t-N}^{}=x_{t-N}-{\displaystyle \sum _{i=1}^L}{\mu }_i{\widehat{x}}_{t-N|t}^{i*}.\end{array}$$

(41)

According to Definition 4, we obtain

$$\begin{array}{c}\hfill g\left({\displaystyle \sum _{i=1}^L}{\mu }_i{\widehat{x}}_{t-N|t}^{i*}\right)\le {\displaystyle \sum _{i=1}^L}{\mu }_{i}g\left({\widehat{x}}_{t-N|t}^{i*}\right)\end{array}$$

(42)

Let $g\left({\widehat{x}}_{t-N|t}^{i*}\right)={∥{\widehat{x}}_{t-N|t}^{i*}-{\tilde{x}}_{t-N}^j∥}_{{\left(P_{t-N}^j\right)}^{-1}}^2$. It is easy to prove that $g\left({\widehat{x}}_{t-N|t}^{i*}\right)$ is a convex function. We record the upper bound of $g\left({\widehat{x}}_{t-N|t}^{i*}\right)\left(i=1,2\cdots L\right)$ as D. Then (42) is converted into

$$\begin{array}{c}\hfill g\left({\displaystyle \sum _{i=1}^L}{\mu }_i{\widehat{x}}_{t-N|t}^{i*}\right)\le {\displaystyle \sum _{i=1}^L}{\mu }_{i}g\left({\widehat{x}}_{t-N|t}^{i*}\right)\le D{\displaystyle \sum _{i=1}^L}{\mu }_i\end{array}$$

(43)

By combining (36), (38) and (40), we get

$$\begin{array}{c}\hfill {∥{\widehat{x}}_{t-N|t}^{i*}-{\tilde{x}}_{t-N}^j∥}_{{\left(P_{t-N}^j\right)}^{-1}}^2\le \ell {∥e_{t-N}^i∥}^2-\eta \end{array}$$

(44)

Similarly, substituting ${\widehat{x}}_{t-N|t}^{*}$ as a feasible solution into $g\left({\widehat{x}}_{t-N|t}^{i*}\right)\left(i=1,2\cdots L\right)$ obtains

$$\begin{array}{c}\hfill {∥{\widehat{x}}_{t-N|t}^{*}-{\tilde{x}}_{t-N}^j∥}_{{\left(P_{t-N}^j\right)}^{-1}}^2\le \ell {∥e_{t-N}^{}∥}^2-\eta \end{array}$$

(45)

Combining (42), (44) and (45), we obtain

$$\begin{array}{c}\hfill {∥e_{t-N}^{}∥}^2\le {∥e_{t-N}^i∥}^2\end{array}$$

(46)

When $t=N$, (47) can be obtained from (37):

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {∥e_0∥}^2& \le {∥e_0^i∥}^2\le \frac{4}{{\mu }_i{\theta }_{p^i}+\varphi {\theta }_{r^i}}\left\{\begin{array}{c}{\mu }_i{\theta }_{p^i}{d}_x^2+{\theta }_{r^i}({\gamma }_{\omega }\sqrt{N}{\theta }_{\omega }+\sqrt{N+1}{\theta }_{v^i}\frac{{\epsilon }^i}{2}\sqrt{\frac{N(N+1)(2N+1)}{6}}{\theta }_{\omega }^2{)}^2\hfill \end{array}\right\}\hfill \\ \hfill & ={\vartheta }_0^i\hfill \end{array}\end{array}$$

(47)

It can be seen from (40), (46) and (47) that (30) and (31) are proven. It is the same as the previous stability analysis of the local estimation error, if (28) is established, then (29) and (30) are established, because ${\chi }_t^i={\left({\delta }^i\right)}^t{\chi }_0^i+{\vartheta }^i{\displaystyle \sum _{s=0}^{t-1}}{\left({\chi }^i\right)}^s$. Then the proof is complete. □

6. Numerical Simulation

To verify the effectiveness of the proposed distributed moving horizon fusion estimation algorithm, we consider the following unstable state space model with two sensors:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_{t+1}^1=x_t^1+\Delta f_t^1{x}_t^2+{\omega }_t\hfill \\ x_{t+1}^2=-0.5x_t^1+5cos{x}_t^2+\Delta f_t^2{x}_t^2+{\omega }_t\hfill \\ y_t^1=5sin{x}_t^1+v_t^1\hfill \\ y_t^2=5cos{x}_t^2+v_t^2\hfill \end{array}\right.\end{array}$$

(48)

We let $\Delta f_t^i=M_1^i{\mathsf{{\rm Y}}}_{1,t}^i{S}_1^i,M_1^i=M_2^i=M_3^i=0.005,S_1^i=S_2^i=S_3^i=I,{\mathsf{{\rm Y}}}_{j,t}^i{\left({\mathsf{{\rm Y}}}_{j,t}^i\right)}^T\le I\left(j=1,2,3\right),P_0^i=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],{\widehat{x}}_0^i={\left[\begin{array}{cc}0& 0\end{array}\right]}^T$; similar to [14] the uncertain parameters are chosen as ${\beta }_{1,i}=0.2,{\beta }_{2,i}=1,{\rho }_{1,i}={\rho }_{2,i}=0.001,{\rho }_{3,i}=0.01$ and the variances are chosen as $Q=15,R^i=10$. It is noted that the $U_{1,t,i},U_{2,t,i},U_{3,t,i}$ matrix can be calculated using (13), and the Jacobian matrix $B_t^i$ calculated according to model (48) is

$$\begin{array}{c}\hfill \left[\begin{array}{cc}1& \Delta f_t^1\\ -0.5& -5sin{x}_t^2+\Delta f_t^2\end{array}\right]\end{array}$$

and

$$\begin{array}{c}\hfill C_t^i=\left[\begin{array}{cc}5cos{x}_t^1& 0\\ -5sin{x}_t^2& 0\end{array}\right]\end{array}$$

Additionally, the constraints of the system noise are set as ${\omega }_t>0$, the simulation number n is set to 100 and the moving horizon window length N is set to 4. The performance of the proposed algorithm is evaluated using root mean square error (RMSE), which is written as

$$\begin{array}{c}\hfill RMSE=\sqrt{\frac{1}{n+1}{\displaystyle \sum _{k=t-n}^t}{∥{\widehat{x}}_{k|t}^{i*}-{\tilde{x}}_k^j∥}^2}\end{array}$$

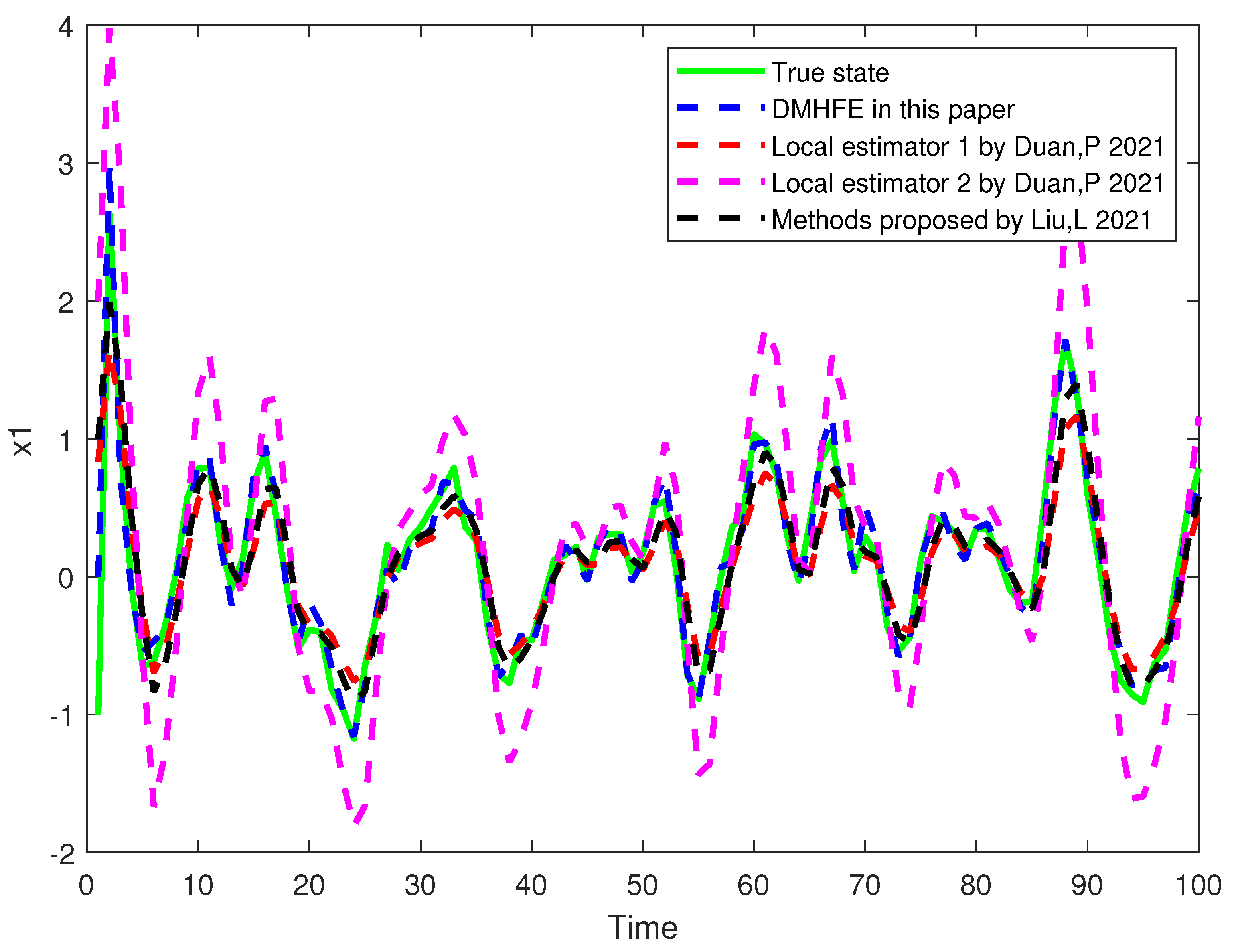
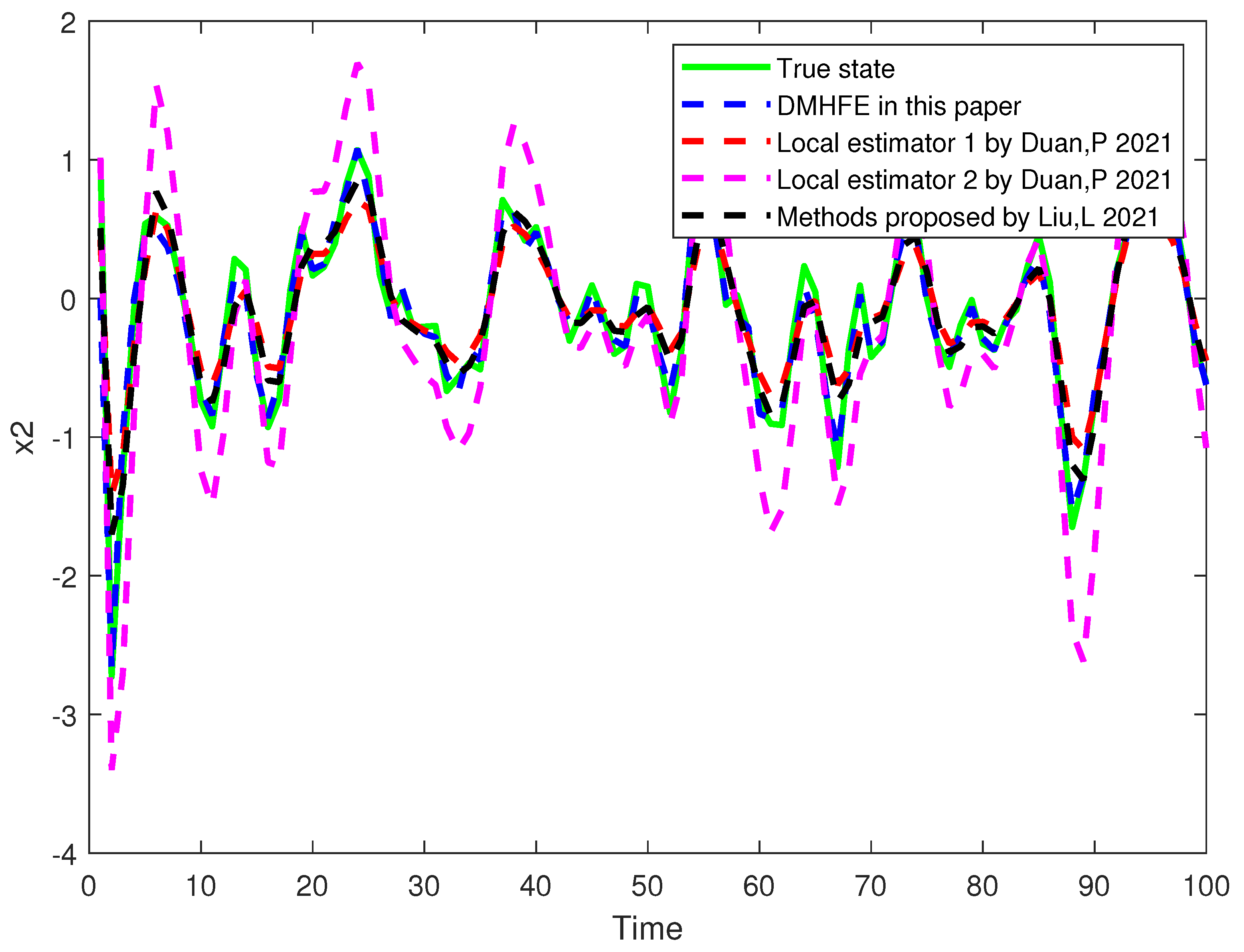
We compared the methods in [10,14] respectively. In [10], the matrix-weighted fusion estimation algorithm is used, which is complex and takes a long time to calculate. In [14], a distributed robust extended Kalman filter algorithm is proposed, but fusion estimation is not carried out. Figure 2 and Figure 3 show the state trajectory of the system, and Figure 4 shows the comparison of root mean square error. It can be seen from the figure that the state trajectory after fusion estimation has a better tracking effect and lower root mean square error than that of local state estimation in [14] and fusion estimation in [10].

Table 2. The mean root mean square error (RMSE) of different window lengths N.

Window Length	2	4	8	16
DMHFE in this paper	0.0398	0.0369	0.0226	0.0106
Methods proposed in [10]	0.0445	0.0423	0.0254	0.0156
Local estimator 1 in [14]	0.0798	0.0722	0.0301	0.0214
Local estimator 2 in [14]	0.1108	0.1030	0.0515	0.0321

shows the mean root mean square error under different moving horizon window lengths. It can be seen from the table that the system error decreases with an increase in window length, but the amount of computation also increases with the increase in the window length. Therefore, a larger N is not better, and N is generally selected as twice the system order. We fully balance the two factors of computation and root mean square error, and choose N as 4. The results show that the accuracy of distributed moving horizon fusion estimation is higher than that of both the local estimation in [14] and the matrix-weighted fusion estimation method in [10]. Meanwhile, Figure 4 also shows that the estimation errors of each local estimator and fusion estimator are bounded. Finally,

Table 3. Run time (s) under different simulation times m.

m	50	100	200	400
DMHFE in this paper	0.7483	0.9380	1.9846	4.0806
Methods proposed in [10]	1.1205	1.4049	2.3869	4.1246
Methods proposed in [14]	0.9758	1.3229	2.2768	4.0969

shows the running time of different algorithms. In 100 simulations, the calculation time of the proposed method is increased by 33.23% and 29.1%, respectively, compared to [10,14]. The results show that the proposed method not only achieves a high estimation accuracy, but also improves computation efficiency.

7. Conclusions

In this paper, the problem of estimating the state was solved by following the MHE paradigm for a class of distributed nonlinear systems in the presence of norm-bounded uncertainty. By constructing an augmented system, the upper bound of the estimation error covariance was derived, and the upper bound was optimized to obtain estimated values of the uncertain parameters in the system. In addition, the proposed method fully considered the system constraints: by constructing performance indicators, the state estimation problem was transformed into a nonlinear optimization problem, which avoided the fussy recursive solution of the traditional Kalman filter. Then a fusion estimation method based on covariance intersection (CI) strategy was proposed, which compensated for the difficulty in solving the cross-covariance matrix in the fusion estimation of nonlinear systems, reduced the computational burden of the estimation problem and improved the computational efficiency. More importantly, the sufficient conditions for the convergence of the norm square of the fusion estimation error were given. Finally, a numerical simulation example was given to verify the effectiveness of the algorithm. In future work, the correlation of noise should be fully considered, and the proposed algorithm should be applied to distributed nonlinear systems with correlated noises.