An Iterated Population-Based Metaheuristic for Order Acceptance and Scheduling in Unrelated Parallel Machines with Several Practical Constraints

Abstract

This study considers order acceptance and scheduling problems in unrelated parallel machines with several practical constraints, including order release times, sequence-dependent setup times, machines’ unequal ready times, and preventive maintenance. In a make-to-order production environment, issues with order acceptance and scheduling are mainly caused by the limited production capacity of a factory, which makes it impossible to accept all orders. Consequently, some orders must be rejected in order to maximize profits and the accepted orders must be completed by the due date or no later than the deadline. An iterated population-based metaheuristic is proposed to solve the problems. The algorithm begins with an efficient initial solution generator to generate an initial solution, and then uses the destruction and construction procedure to generate a population with multiple solutions. Then, a solution is selected from the population, and a variable neighborhood descent search algorithm with several new reduced-size neighborhood structures is applied to improve the selected solution. Following the completion of the local search, a method for updating the members of the population was devised to enhance its diversity. Finally, the metaheuristic allows the populations to evolve for several generations until the termination condition is satisfied. To evaluate the performance of the proposed metaheuristic, a heuristic rule and an iterated local search algorithm are examined and compared. The computational experimental results indicate that the presented metaheuristic outperforms the other heuristics.

1. Introduction

Most of the previously conducted studies have investigated the scheduling problem of processing and completing all jobs. In the make-to-order production environment, production capacity is limited, making it impossible to accept all orders and fulfill them within the required delivery time. This has led to the need to decline some orders to meet customer requirements. This scenario creates order acceptance and scheduling (OAS) issues. The OAS problem simultaneously involves determining two decision problems for maximum profit. The first is to select the orders to be accepted and the second is to schedule the accepted orders [1].

In this study, we consider order acceptance and scheduling problems in an unrelated parallel-machine production system. The scheduling problem of parallel machines may not only be considered in single-stage manufacturing environments but may also be a critical stage in complex manufacturing environments. Unrelated parallel machines often appear in real manufacturing environments, such as customized heating, ventilation and air conditioning (HVAC) equipment [2], ceramic plants [3], packaging industry [4], electronic assembly industry [5], additive manufacturing [6], and printed circuit board assembly [7]. In addition, we consider several practical constraints in the problems, including job release times, sequence-dependent setup times, machines’ unequal ready times, and preventive maintenance. The objective is to maximize profits.

Over the years, considerable attention has been paid to the OAS problem associated with parallel machines. Studies have focused on a variety of objectives, such as measures related to monetary and multiple objectives. For monetary-related measures, Wang et al. [8] addressed the OAS problem in the context of monetary measures by developing two heuristics and an exact algorithm to maximize profit on two identical parallel machines. Emami et al. [9] developed a Lagrangian relaxation algorithm to solve the OAS on nonidentical parallel machines with sequence-dependent setup times. Wu et al. [10] proposed a modified water flow-like algorithm to solve the OAS problem for identical parallel machine scheduling with sequence-dependent setup times. Naderi and Roshanaei [11] proposed a mixed-integer programming model and a branch-relax-and-check algorithm to solve the OAS problem on identical parallel machines. Erişgin Barak and Koyuncu [12] presented a fuzzy mathematical model and genetic algorithm to solve the problem on identical parallel machines.

Zhong and Lu [13] considered the parallel-machine scheduling problem for multi-objective-related measures with release dates and rejection. The objective is to minimize the makespan of the accepted job in addition to the total penalty of all rejected jobs. They provided a two-approximation algorithm for the problem and a fully polynomial time approximation scheme for the unique case when the number of machines was fixed. Zhong and Ou [14] considered the same problem and presented an improved two-approximation and a polynomial time-approximation scheme for the problem. Ou and Zhong [15] presented heuristics to solve the OAS problem on parallel machines, and the number of rejected orders was limited to be no greater than a given service-level value k. The objective was to minimize the completion time of the last accepted order and the total penalty for all rejected orders. Bartal et al. [16] addressed the scenario where jobs may be rejected at a certain penalty on identical parallel machines. They developed two heuristics and an exact algorithm to minimize the makespan of the schedule for accepted jobs and the penalties of rejected jobs. Krim et al. [17] proposed a mixed-integer linear program model and two generalizable tabu-search metaheuristics to solve the bi-objective, that is, job rejection costs and weighted sum of completion times, for two different parallel machines with a periodic preventive maintenance policy.

Most of the previous studies have made several assumptions, such as equal release times for orders, equal machine ready times, absence of setup times, and no preventive maintenance. However, in real-world cases, these constraints often occur in manufacturing environments. A review of the available literature leads us to conclude that the candidate problem in this study has not been studied. The unrelated parallel machines total tardiness problem with sequence-dependent setup times is a special case of the OAS problem. This case only focuses on scheduling a given set of orders and does not involve acceptance/rejection decisions. It is widely acknowledged to be strongly NP-hard. This implies that the OAS problem considered in the study is also strongly NP-hard and, therefore, exact solution methods are impractical and heuristic algorithms should be used instead. In this study, an iterated population-based metaheuristic (IPBM) is proposed for cases involving scheduling with unrelated parallel machines with order release times, sequence-dependent setup times, machines unequal ready times, and preventive maintenance. Various key components of the metaheuristic were also considered and examined. These include initial population solution generators, several reduced-size neighborhoods, and updated methods for population members. A heuristic rule, an iterated local search, and several test instances were used to evaluate the performance of the iterated population-based metaheuristic.

The remainder of this paper is organized as follows. Section 2 introduces the problem considered in this study. Section 3 describes the proposed algorithm. Section 4 describes the generation of the test data and analyzes the computational results. Finally, Section 5 presents conclusions and recommendations for future research.

2. Description of the Problem

This study addresses the issue of order acceptance and scheduling in unrelated parallel machines while considering practical constraints such as varying order release times, sequence-dependent setup times, unequal machine ready times, and preventive maintenance. The objective is to maximize profits. The following assumptions were used in this study: the number of machines is at least two and the number of orders is at least equal to the number of machines, there are no machine breakdowns, and each machine is limited to processing one order at a time and cannot be preempted. The candidates consider a set of n orders that need to be processed on m unrelated machines. Each machine $k$ has an individual non-negative ready time $b_k$ and the time for each machine k to start production must be after $b_k$. In order to maintain the desired operating level of the manufacturing system, preventive maintenance (PM) operation is considered. A machine undergoes at least one maintenance activity during its production period, and it cannot be engaged in manufacturing production during that time. PM activities are performed on a machine at predefined intervals regardless of the length of time the machine has been in operation.

For each machine k, each order $i$ has a positive processing time $p_{ik}$. Every order $i$ has a positive sequence-dependent setup time $s_{jik}$ that is influenced by both the order in which the orders are processed and the machine that is being used. This implies that if order i is scheduled to execute directly after order j on machine k in any possible valid schedule, then the associated setup time will be incurred. The $s_{0ik}$ represent initial setup times to process order i first on machine k.

In addition, each order $i$ has an individual non-negative release time $r_i$, a due date $d_i$, a deadline $e_i$, and a maximum revenue $u_i$. The time for each order i to begin manufacturing must exceed its release time $r_i$. The manufacturer has the option to finish the order i within the specified deadline $e_i$. However, for every unit of time that exceeds the due date $d_i$, a penalty cost of $w_i$ will be imposed as a tardiness penalty cost. We set $w_i$ to $u_i/\left(e_i-d_i\right)$ for each order i. Let $c_i$ denote the completion time of order i. If $c_i>e_i$, the order i is rejected. Otherwise, if $c_i\le e_i$, the order i is accepted. If $c_i\le d_i$, the maximum revenue $u_i$ of order i is obtained. If $c_i\le e_i$ and $c_i>d_i$, the delay penalty is calculated as follows: $\left(e_i-d_i\right)\times w_i$.

The following notations are used to describe the considered OAS problem and the proposed algorithm in the next section:

• i = order index, i = 1,2, 3, …, n
• k = machine index, k = 1, 2, 3, …, m
• $p_{ik}$= processing time of order i on machine k
• $s_{jik}$ = sequence-dependent setup time of order i is processed immediately after order j on machine k
• $s_{0ik}$ = initial sequence-dependent setup time of order i is processed first on machine k
• $r_i$ = release time of order i
• $b_k$ = ready time of machine k
• $d_i$ = due date of order i
• $e_i$ = deadline of order i
• $c_i$ = completion time of order i
• $D_{PM}$ = completion time of order i
• $u_i$ = maximum revenue of order i
• $w_i$ = a penalty weight of tardiness of order i
• ${\overline{p}}_i$ = average processing time of order i
• ${\overline{s}}_i$ = average setup time of order i
• $MAXOPT$ = maximum processing time
• d = the number of orders to be removed used in the DC procedure
• ns_size = the number of neighborhood structures
• ns = neighborhood structure index, ns = 1, 2, 3,…, ns_size
• ${\Pi }^{gbest}$ = the global best solution
• $V^{gbest}$ = the value of the global best solution
• ${\Pi }_p$ = the solution of member p
• $V_p$ = the value of the member p
• ${\Pi }_{p^{\prime }}$ = the solution of member p′ generated by exploring neighborhood structure ns
• $V_{p^{\prime }}$ = the value of the member p′
• ${\Pi }^{VND}$ = the solution generated by variable neighborhood descent (VND) algorithm
• $V^{VND}$ = the value of the solution generated by VND algorithm
• AO = the set of accepted orders
• RO = the set of rejected orders
• $I_i=\left\{\begin{array}{ll}1& \mathrm{i}\mathrm{f} \mathrm{o}\mathrm{r}\mathrm{d}\mathrm{e}\mathrm{r} i \mathrm{i}\mathrm{s} \mathrm{a}\mathrm{c}\mathrm{c}\mathrm{e}\mathrm{p}\mathrm{t}\mathrm{e}\mathrm{d},\\ 0& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\end{array}\right.$
• $T_i=\left\{\begin{array}{ll}(c_i-{\mathrm{d}}_i)& \mathrm{i}\mathrm{f} (c_i-{\mathrm{d}}_i)>0,\\ 0& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\end{array}\right.$

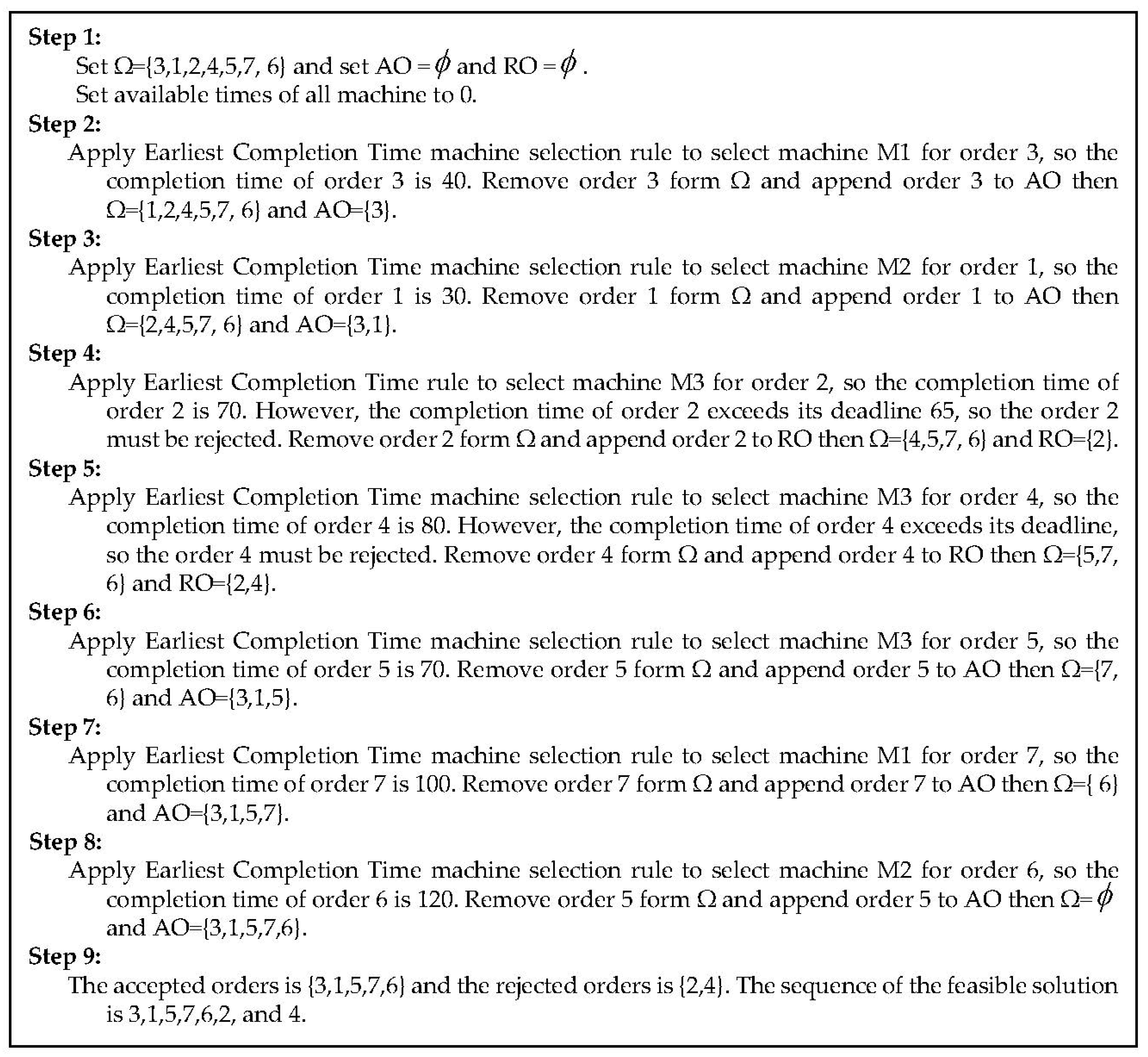
The schedule decides which orders should be accepted, and the accepted orders should be scheduled on unrelated parallel machines. The objective is to determine a schedule such that profit is maximized, which can be defined as follows: Objective = Maximize ${\sum }_{i=1}^n{I}_i{(u}_i-{w_{i}T}_i).$

3. Proposed Iterated Population-Based Metaheuristic

The proposed iterated population-based metaheuristic is a modification of the IPBVND algorithm proposed by Chen [18] to solve the OAS problem considered in this study. For convenience, the proposed algorithm is referred to as the IPBM. The main components of the IPBM include initialization of the population, a variable neighborhood descent (VND) search for improving the solution quality, and a member-updated method for increasing population diversity. Figure 1 shows the functionality of the IPBM. As shown in Figure 1, the IPBM first applies a heuristic rule to generate an initial solution, and based on the initial solution, the destruction and construction (DC) procedure [19] is subsequently used to construct the initial population with m members. Thereafter, a good solution is selected from the population, and the VND algorithm with several reduced-size neighborhoods is implemented to improve the selected solution. A block-based crossover operator (BCO) and DC procedure are used in the member update method to update the solution of each member at each iteration after the VND search. The search process continues until the termination criterion is satisfied. The main difference between the proposed IPBM and IPBVND is that a new population member-generated method, several new reduced-size neighborhood structures, and a member-updated method are constructed in the IPBM for the considered problems. The main components of the proposed IPBM are as follows.

3.1. Solution Encoding

The linear permutation of all n orders was used as the solution-encoding scheme. A feasible solution to the OAS problem consists of two parts. The first part is the sequence of accepted orders and the other is the sequence of rejected orders. An order at a particular position in a member is accepted for processing only when its deadline constraint is not violated, considering all accepted orders preceding it in the member and its release date.

Figure 2 and Figure 3 are used to illustrate the transformation of feasible solutions. The processing times of the orders on each machine, the due dates of the orders, the deadline of the orders, and completion time of orders are shown in Figure 2. Suppose there are seven orders, 1, 2, …, 7. Solution sequences 3, 1, 2, 4, 5, 7, and 6 were generated using the earliest due date (EDD) rule. The machine selection rule uses the earliest completion time when the order is assigned to all the machines, including available and unavailable machines. The result of this sequence after scheduling is 3, 1, 5, 7, 6, 2, and 4. Orders 2 and 4 violate their respective deadlines when we try to schedule them according to their position in the solution; then, these orders will not be accepted. The remaining orders will be accepted and scheduled according to their position in the solution; that is, orders will be executed in the order 3, 1, 4, 5, and 7. Sequences 3, 1, 5, 7, 6, 2, and 4 are stored in a member.

3.2. Initial Population Generators

Two heuristics, a dispatching rule and the DC procedure, were constructed as the initial population generators to generate the initial population for the proposed algorithm. The proposed initial population generator works as follows: a rule is applied to generate a solution; subsequently, based on the generated solution, the DC procedure is used to regenerate m different solutions, where m is the population size.

Two rules are constructed to generate the initial solutions for the proposed initial population generator. The first rule is the earliest deadline rule (EDL): it states that the sequence of orders is determined by the order deadlines. The second rule utilizes the characteristics of deadline, release time, revenue, total average processing time, and setup time. For convenience, the proposed rule is referred to as DRRT and can be expressed as follows: $e_i\times r_i/(u_i/({\overline{p}}_i+{\overline{s}}_i))$ where $e_i$ is the deadline of order i, $r_i$ is the release time of order i, $u_i$ is the revenue of order i, and $\overline{p}$ and $\overline{s}$ represent the average processing time of order i and average setup time of order i, respectively.

The DC procedure presented by Ruiz and Stutzle [19] was applied to generate members of the population. Two functions were implemented in the DC procedure. The first function, the destruction operation, randomly chooses and removes d orders from the incumbent solution and results in two partial permutations. The first permutation contains the removed jobs, while the second permutation contains the remaining jobs from the original permutation. The second function, also known as the construction function, sequentially inserts the removed orders back into the partial sequence. This process is repeated until all d orders are inserted back into the partial sequence, resulting in a new complete solution. Figure 4 is used to illustrate the DC procedure. Suppose the value d is equal to two and the incumbent solution is 3, 1, 2, 4, 5, 7, and 6. The destruction function randomly chooses and removes two orders from the solution; the removed orders are 2 and 4. The partial sequence of the remaining jobs is 3, 1, 5, 7, and 6. After the operations of the destruction function, the construction function sequentially inserts the removed orders (2 and 4) back into the partial sequence. Suppose the first selected order, 2, is inserted into position 1 of the partial sequence, which results in the best new partial sequence of 2, 3, 1, 5, 7, and 6. Then, the last removed order, 4, is inserted into position 5 of the new partial sequence, generating the complete solution 3, 1, 2, 5, 4, 7, and 6.

3.3. Proposed VND

The VND was developed by Hansen and Mladenović [20], and its main procedure is shown in Figure 5. This search algorithm first defines a set of neighborhood structures and explores each neighborhood individually. A characteristic of VND is that each search starts from the best solution of the previous iteration.

Five reduced-size neighborhood structures were constructed in this study to enhance both the efficiency and effectiveness of the proposed VND. Because the objective of the candidate problem is to decide which orders should be accepted and which should be calculated, the first neighborhood structure (NS₁) is proposed, in which only the accepted orders can be exchanged with other orders. In the second neighborhood structure (NS₂), only the accepted orders can be inserted into all possible positions of the accepted and rejected orders. Moreover, rejected orders may produce better results if the rejected order can be inserted into other positions. In the third neighborhood structure (NS₃), all rejected orders can be inserted into all possible positions of the accepted and rejected orders. According to NS₂ and NS₃, two consecutive orders can be inserted at other positions. In the fourth neighborhood structure (NS₄), only two consecutive orders in the accepted orders can be inserted into all possible positions on the accepted and rejected orders. In the last neighborhood structure (NS₅), only two consecutive orders in the rejected orders can be inserted into all possible positions on the accepted and rejected orders.

3.4. Member-Updated Method

The population members are updated at each iteration. Two member-updated methods, a block-based crossover operator (BCO), and the DC procedure are built to update the solution. These two functions were also used by Chen [18] to update the members. The BCO exchanges information between a member and the global best solution. BCO first selects a block of consecutive orders from the best global solution. The second step is to construct a new solution by assigning this block to the same position in the new solution as it occupies in the global best solution. The final step is to sequentially assign orders that are not in the block to empty positions in the new solution. Based on these two functions, four methods were developed to update the population members. The first method is to apply BCO and the second is to apply the DC procedure to update the members. The third and fourth methods combine the BCO and DC procedure. The third method is to execute the BCO first, and then execute the DC procedure. In contrast, the fourth function is to execute the DC procedure first, and then execute the BCO.

4. Computational Experiments

Two experiments were conducted and analyzed to evaluate the performance of the proposed heuristics. The first part evaluates the parameters of the proposed IPBM, including the initial population member generation methods, neighborhood structures, and member update methods. The second part compares the performance of the best IPBM algorithm found in the first part with the best initial solution generator heuristic rule and iterated local search metaheuristic.

For the first part, the number of orders was set to 40 and the number of machines was set to 3. The processing time of each order has 2 levels, with values set to a discrete uniform integer distribution at $U(10,30)$ (low) and $U(10,100)$ (high). The setup times were uniformly distributed and ranged from 20% to 40% of the mean processing time. The release times of orders were generated from a discrete uniform integer distribution $U(0,\alpha t_{max}$), and the due dates of the orders were generated from a discrete uniform integer distribution $r_i+U\left(1,1+\beta \right)\times \left({\overline{p}}_i+{\overline{s}}_i\right),$ $t_{max}=\raisebox{1ex}{${\sum }_{i=1}^n{(\overline{p}}_i+{\overline{s}}_i)$}\!\left/ \!\raisebox{-1ex}{$m$}\right.$, where α and β have 2 levels, with values set to 0.25 (Low) and 0.75 (High). A deadline was generated as $d_i+R\times \left({\overline{p}}_i+{\overline{s}}_i\right),\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} R \mathrm{h}\mathrm{a}\mathrm{s} 2 \mathrm{l}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{l}\mathrm{s}, \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} \mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}\mathrm{s} \mathrm{s}\mathrm{e}\mathrm{t} \mathrm{t}\mathrm{o} 0.25 \left(\mathrm{L}\mathrm{o}\mathrm{w}\right) \mathrm{a}\mathrm{n}\mathrm{d} 1.0 \left(\mathrm{H}\mathrm{i}\mathrm{g}\mathrm{h}\right)$. The ready time for some machines or machines is a nonzero unit of time. The ready time of the machines is uniformly distributed, ranging from $U(0,1)\times MAXOPT$, where $MAXOPT$ is the maximum processing time. The machine has a preventive maintenance schedule, with each maintenance service taking $U\left(0.5,0.5+\gamma \right)\times MAXOPT$ time units, where $\gamma$ has 2 levels, with values set to 0.5 (Low) and 1.5 (High). The number of maintenance sessions was set to one. The revenue $u_i$ for each order i was generated randomly from $U(100,500)$. Hence, 32 test scenarios exist with 5 different test problems for each scenario. Three parameters used in the IPBM—population member-generated methods, forms of neighborhood structures, and member-updated methods—were examined. There are two types of initial solution generators: the EDL and DRRT. Two search strategies, namely, full and partial, were examined. For a full search, three neighborhoods were defined: SWAP, INSERT, and INSERT-2O. The neighborhood size of the general SWAP in a searching iteration will search $n(n-1)/2$ neighbors, and the neighborhood size of the general INSERT in a searching iteration will search $n(n-1)$ neighbors. INSERT-2O implies that two consecutive orders can be inserted into all possible positions. Based on the three neighborhood structures, two forms of neighborhood structures were developed: SWAP + INSERT and SWAP + INSERT + INSERT-2O. For partial search, five neighborhoods were defined: NS₁, NS₂, NS₃, NS₄, and NS₅. Based on the five neighborhood structures, two forms of neighborhood structures were developed: NS₁ + NS₂ + NS₃ and NS₁ + NS₂ + NS₃ + NS₄ + NS₅. Therefore, there are a total of four forms of neighborhood structures examined in the study. There are four member-updated methods in this study: BCO, DC, BCO + DC, and DC + BCO. The value d = 4 was used in this study. Therefore, 32 IPBM algorithms were constructed in the first part. Additionally, the number of population members was set to 40. The termination condition of the proposed IPBM was set to 5 s of maximum CPU time.

A series of computational experiments is presented to compare the results provided by all algorithms for randomly generated problems. All algorithms were implemented in the C++ language, and all experiments were performed on a PC with an i7-4790 3.4 GHz CPU and 8 GB of RAM.

Table 1. Performance comparisons of the parameters in IPBM (in terms of average RPD and ATP).

Population Member-Generated Methods	Forms of Neighborhood Structures	Average RPD				ATP
		Member-Updated Methods				Member-Updated Methods
		BCO	DC	BCO + DC	DC + BCO	BCO	DC	BCO + C	DC + BCO
EDL	SWAP + INSERT	16.95	9.26	18.93	19.02	10,702.9	10,140.7	10,846.1	10,848.2
	NS1 + NS2 + NS3	16.78	8.97	18.94	19.25	10,689.0	10,129.5	10,848.3	10,867.9
	SWAP + INSERT + INSERT-2O	17.09	10.17	18.74	19.22	10,708.5	10,189.6	10,828.2	10,860.8
	NS1 + NS2 + NS3 + NS4 + NS5	17.24	11.24	18.88	19.20	10,720.1	10,288.9	10,843.0	10,864.5
DRRT	SWAP + INSERT	16.75	11.68	19.05	19.12	10,670.3	10,256.8	10,853.8	10,854.1
	NS1 + NS2 + NS3	16.93	10.74	18.81	19.46	10,687.6	10,175.8	10,835.5	10,879.6
	SWAP + INSERT + INSERT-2O	16.86	11.35	18.86	19.11	10,681.4	10,253.8	10,835.6	10,853.1
	NS1 + NS2 + NS3 + NS4 + NS5	17.14	12.09	18.88	19.33	10,701.3	10,292.9	10,838.8	10,872.9

Bold means best result.

presents the computational results of the 2 population member generation methods and the 4 forms of neighborhood structures for the 160 test problems, with each of the 4 member-updated methods. Relative percentage deviation (RPD) and average total profit (ATP) are used to evaluate the IPBM performance. The RPD is defined as follows:

$RPD=\frac{S_a-S_w}{S_w}\times 100$. S_a is the solution value obtained by method a and S_w is the worst solution value among those obtained by the methods included in the comparison.

The results for the average RPD and ATP in Table 1 show several noteworthy points. First, the member update methods significantly affect the performance of IPBMs. When the EDL population member generation method and forms of neighborhood structures are used, the average of the RPD produced by BCO is 17.01; the numbers of DC, BCO + DC, and DC + BCO are 9.91, 18.87, and 19.17, respectively. These numbers indicate that DC + BCO dominates BCO, DC, and BCO + DC by 11.3%, 48.3%, and 1.6%, respectively. A similar result can be obtained for the DRRT population member generation method; DC + BCO dominates BCO, DC, and BCO + DC by 12.1%, 40.5%, and 1.8%, respectively. Therefore, we conclude that DC + BCO is an updated member method that should be considered for the candidate problem. Second, within each of the member-updated methods, the average RPD produced by the population member-generated methods is very close, and the DRRT population member generation method performed better than the EDL population member-generated method. When DC + BCO was used, the average RPD produced by the EDL population member generation method was 19.17, and that produced by the DRRT population member generation method was 19.25. In addition, within each of the DC + BCO member-updated methods, the average RPD produced by the forms of neighborhood structures is very close, and NS₁ + NS₂ + NS₃ is the best form of the neighborhood structures.

The ATP results in Table 1 strongly support the previous conclusions. When the EDL population member generation method is used, the ATP produced by BCO is 10,705.1 for the member-updated methods; the numbers of DC, BCO + DC, and DC + BCO are 10,187.1, 10,841.4, and 10,860.4, respectively. These numbers indicate that DC + BCO dominates BCO, DC, and BCO + DC by 1.4%, 6.2%, and 0.2%, respectively. A similar result can be obtained for the DRRT population member generation method; DC + BCO dominates BCO, DC, and BCO + DC by 1.7%, 5.7%, and 0.2%, respectively. When DC + BCO is used, the ATP produced by the EDL population member-generated method is 10,860.4, and that produced by the DRRT population member-generated method is 10,864.9. The DRRT population member generation method performed better than the EDL. In addition, when DC + BCO and DRRT were used, the ATP produced by the NS₁ + NS₂ + NS₃ form of neighborhood structures was 10,879.6, and NS₁ + NS₂ + NS₃ was the best form of neighborhood structures. These results indicate that the DRRT population member generation method, NS₁ + NS₂ + NS₃ form of neighborhood structures, and DC + BCO member-updated method are the best parameters of the IPBM. The performances of the initial rules were compared at the end of the first part of the experiment. Based on the above analysis, we can observe that the performance produced by the population member-generated methods is very close. As a result, the proposed algorithm performs equally well regardless of which population member-generated method is employed. However, the ATP produced by EDL and DRRT were 9039.7 and 9228.8, respectively. These numbers show that DRRT dominated EDL by 2%. This indicates that the DRRT rule is effective for candidate problems. It was used as the basis for the comparison of IPBM algorithms in the second part of the experiment.

For the second part of the experiment, the performance of the proposed algorithms that combined the best set of parameters from the first part of the experiment was investigated. These parameters are as follows: DRRT population member-generated method, NS₁ + NS₂ + NS₃ form of neighborhood structures, and DC + BCO member-updated method. In addition, the parameter of termination conditions for IPBM was examined to verify the performance of the IPBM under varying computational times. To equitably compare the proposed algorithm with other methods, the maximum computational time was used as the termination condition for the algorithms. This parameter has 2 levels, with values set to 0.125 $\times$ n and 0.25 $\times$ n seconds, where n is the number of orders.

In addition to the factors of the first part, additional levels for the number of orders, machines, and preventive maintenance activities are considered. The number of orders had 2 levels, with values set to 50 (low) and 100 (high). The number of machines had two levels, with values set to two (low) and five (high). The number of PM activities had two levels, with values set to two (low) and four (high). Hence, 256 test scenarios were considered and 10 datasets were generated for each scenario.

To evaluate the performance of the IPBM, the DRRT rule and iterated local search (ILS) metaheuristic were used for comparison. The ILS metaheuristic is a variant of the IPBM that uses only one member. The IPBM and ILS with two termination conditions resulted in four algorithms. Hence, five algorithms are constructed in this part of the experiment. The algorithm is denoted by an algorithm/termination condition: all the algorithms were evaluated on 2560 testing problems.

Analysis of variance and Duncan’s multiple range test were applied to determine the RPD of the 2560 test problems and evaluate the performance of the IPBM. The ANOVA table (

Table 2. ANOVA table for testing the significance of all algorithms and factors (α = 0.01).

Source	Sum of Squared Error	Degree of Freedom	Mean Squared Error	F **
Algorithms	553,463.876	4	138,365.969	2003.605 **
Number of orders	46,591.712	1	46,591.712	674.670 **
Number of machines	27,922.411	1	27,922.411	404.330 **
Processing times	4616.050	1	4616.050	66.843 **
Releasing times	77,386.278	1	77,386.278	1120.590 **
Due date tightness	558,204.485	1	558,204.485	8083.066 **
Deadline	69,677.639	1	69,677.639	1008.965 **
Number of PM	2.468	1	2.468	0.036
PM duration times	0.460	1	0.460	0.007
Error	88,3051.194	12,787	69.059
Total	4,401,614.271	12,800
Corrected total	2,220,916.572	12,799

** Difference in the effects at significance level 0.01.

) shows that, except for the number of PM and PM duration times, several factors such as algorithms, processing times, number of orders, number of machines, releasing times, due date tightness, and deadline significantly affect the output (RPD) of the test problems.

Table 3. Results of Duncan’s multiple range test for initial solution generator and algorithms with different termination conditions (α = 0.01).

Algorithms	Results (Groups)	Average RPD
IPBM/0.25 × n	A	17.4800
IPBM/0.125 × n	A	16.9500
ILS/0.25 × n	B	15.5308
ILS/0.125 × n	B	15.2964
DRRT	C	0.0053

presents the results of Duncan’s multiple range test for the algorithms. Note that the algorithms are sequenced in descending order based on the average RPD. If two algorithms have the same letter in the column of results (groups), it is considered that no significant difference exists between the performance of the two algorithms. The results of Duncan’s multiple range test (Table 3) showed that IPBM/0.125 × n and IPBM/0.25 $\times$ n significantly outperformed all other algorithms. The average RPDs of DRRT, ILS/0.125 × n, ILS/0.25 × n, IPBM/0.125 × n, and IPBM/0.25 × n were 0.0053, 15.2965, 15.5308, 16.9500, and 17.4800, respectively. These results highlight two important observations. First, the termination conditions did not significantly affect the performances of the IPBM and ILS algorithms. This implies that the IPBM and ILS algorithms only need to use 0.125 × n seconds of computing time to achieve the same results as those obtained in 0.25 × n seconds. Second, within each termination condition, the IPBM algorithm outperformed ILS. In particular, the IPBM, with 0.125 × n, outperforms the ILS, with 0.25 × n. This demonstrates that the IPBM is both effective and efficient.

The effects of each experimental factor on the five algorithms were investigated.

Table 4. Results for different number of orders and number of machines (in RPD).

Algorithms	Number of Orders		Number of Machines
	Low	High	Low	High
DRRT	0.0086	0.0021	0.0059	0.0048
ILS/0.125 × n	17.4821	13.1108	13.6465	16.9464
IPBM/0.125 × n	19.5756	14.3244	14.9858	18.9142
ILS/0.25 × n	17.7835	13.2782	13.8431	17.2186
IPBM/0.25 × n	19.9520	15.0075	15.3962	19.5633

Bold means best result.

presents the average RPD produced by each algorithm at each level of the number of orders and machines.

Table 5. Results for different processing times, releasing times, due-date tightness, and deadline (in RPD).

Algorithms	Processing Times		Releasing Times		Due-Date Tightness		Deadline
	Low	High	Low	High	Low	High	Low	High
DRRT	0.0007	0.0100	0.0052	0.0055	0.0000	0.0107	0.0081	0.0026
ILS/0.125 × n	15.9772	14.6158	17.9678	12.6251	22.8366	7.7563	12.4694	18.1235
IPBM/0.125 × n	17.7398	16.1602	20.3696	13.5303	25.6325	8.2675	14.0545	19.8455
ILS/0.25 × n	16.2829	14.7788	18.2451	12.8166	23.2388	7.8229	12.5669	18.4948
IPBM/0.25 × n	18.2644	16.6951	20.9688	13.9907	26.5733	8.3861	14.4977	20.4618

Bold means best result.

presents the average RPD produced by each algorithm at each level of processing time, release time, due date tightness, and deadline.

Table 6. Results for different number of orders and number of machines (in RPD).

Algorithms	Number of PM		PM Duration Time
	Low	High	Low	High
DRRT	0.0047	0.0060	0.0031	0.0075
ILS/0.125 × n	15.3461	15.2468	15.2941	15.2988
IPBM/0.125 × n	16.9459	16.9541	16.9072	16.9928
ILS/0.25 × n	15.5310	15.5307	15.5649	15.4967
IPBM/0.25 × n	17.5041	17.4554	17.4630	17.4965

Bold means best result.

presents the average RPD produced by each of the algorithms at each level of PM and PM duration. These results show that within each termination condition, the IPBM outperforms the ILS at every level of experimental factors.

Finally, the efficiency of the IPBM was evaluated. Because the IPBM and ILS use the same termination conditions, the CPU times of the two algorithms are equal. The average CPU time for IPBM/0.125 × n to solve a 100-order problem is 12.5 s, making it sufficiently fast to be used in practical applications.

5. Conclusions

This paper studied the order acceptance and scheduling problem (OAS) in an unrelated parallel machines environment with several practical constraints, including order release times, sequence-dependent setup times, machines’ unequal ready times, and preventive maintenance. The objective was to maximize total profit. To the best of our knowledge, this issue remains unresolved in the existing literature. The OAS problem is strongly NP-hard. It is practical to develop heuristics to solve OAS problems. Therefore, an iterated population-based metaheuristic (IPBM) was proposed to solve the candidate problems.

Considering the characteristics of the considered problems, several new mechanisms are developed in the IPBM to achieve better performance. These mechanisms include one effective population member generation method, several reduced-size neighborhood structures, and one member update method. Numerous computational experiments are performed on randomly generated test problems. For various test problems, the proposed IPBM, which uses the DRRT population member-generated method, the NS₁ + NS₂ + NS₃ neighborhood structure, and the DC + BCO member-updated method, emerged as the most effective algorithm. To evaluate the performance of the proposed algorithm, the DRRT rule and iterated local search (ILS) were examined for comparison. On randomly generated test problems, a large number of computational experiments were conducted. The results were promising and indicated that the proposed IPBM performs better than the other algorithms for various test problems. Future research should explore how various stop conditions and perturbations influence the IPBM. In addition, the proposed IPBM can be applied to other manufacturing environments such as hybrid flow shops or open shops.