Quantum Advantages of Teleportation and Dense Coding Protocols in an Open System
Abstract
1. Introduction
2. The Model and Its Solution
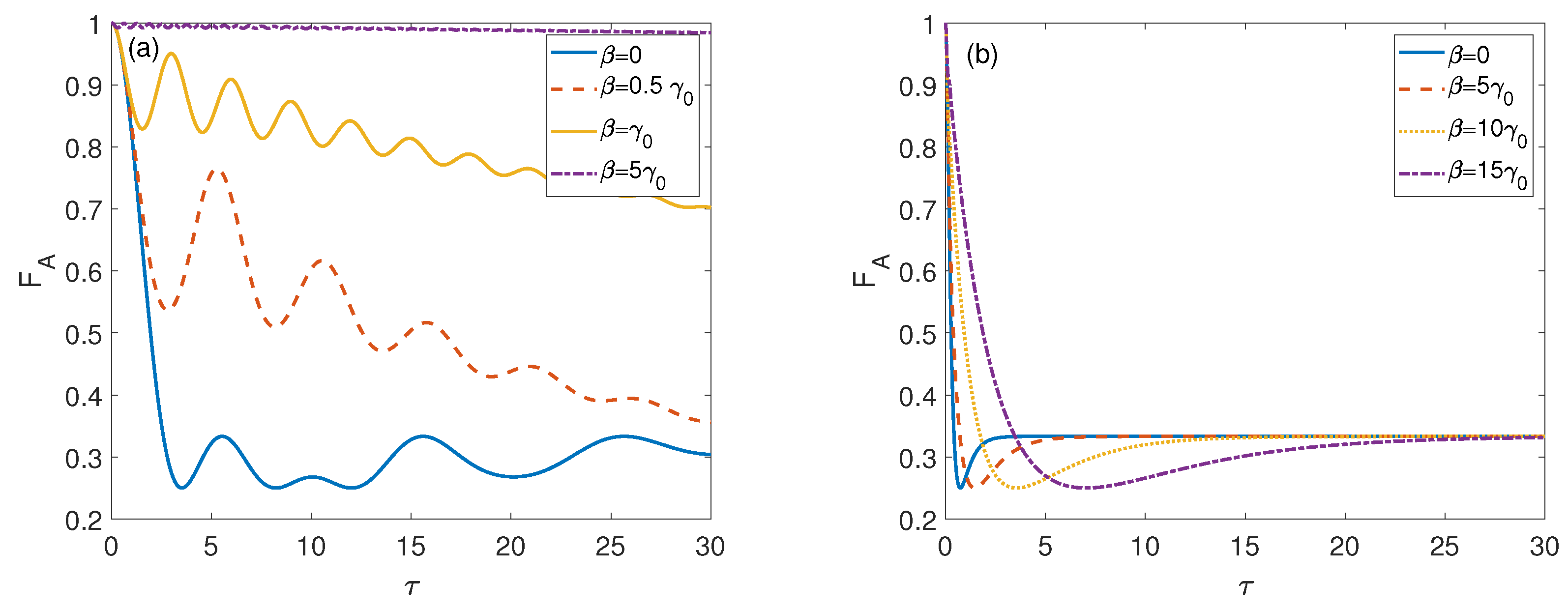
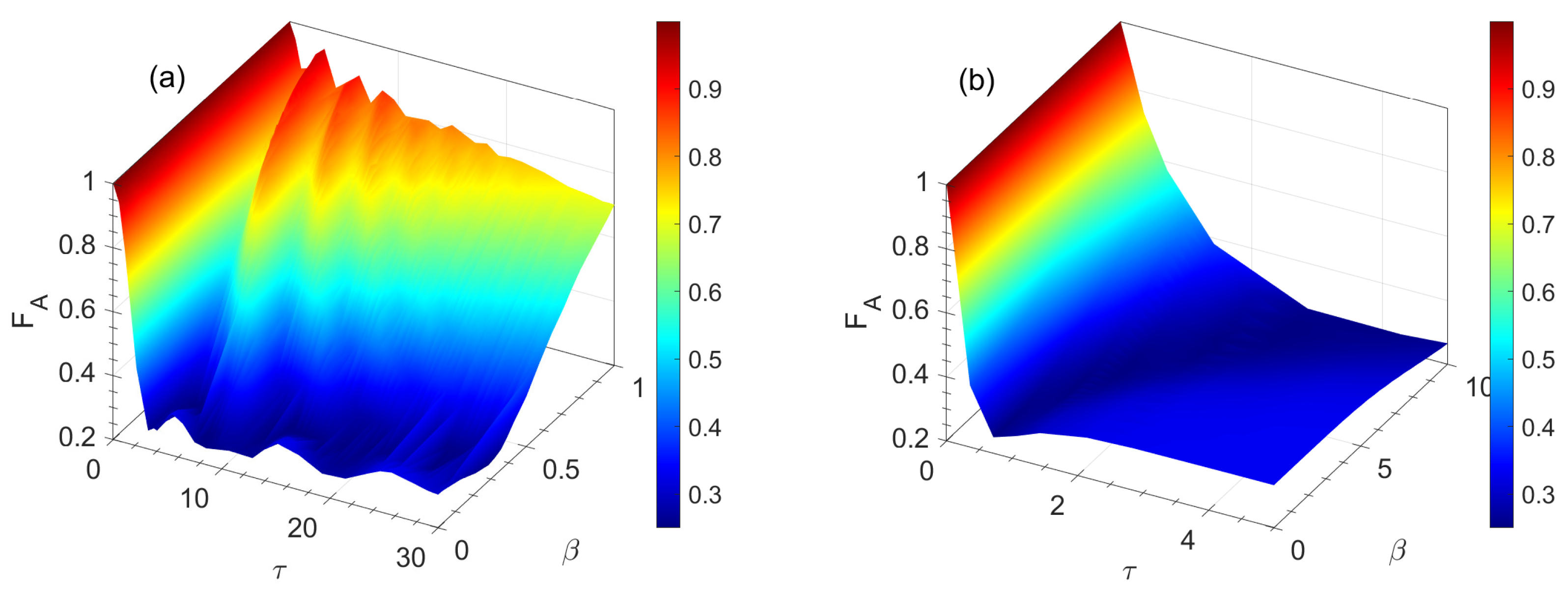
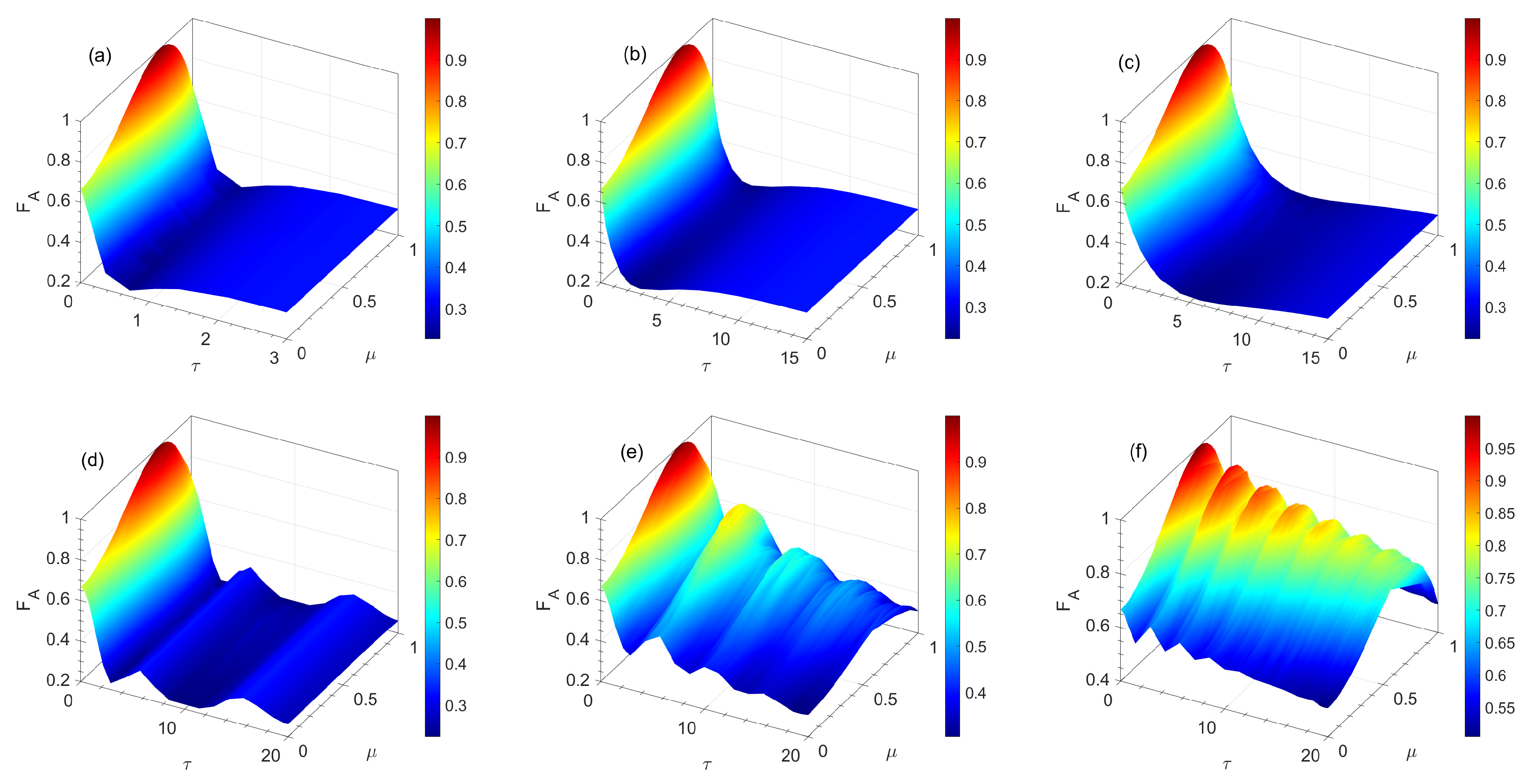
3. Quantum Teleportation
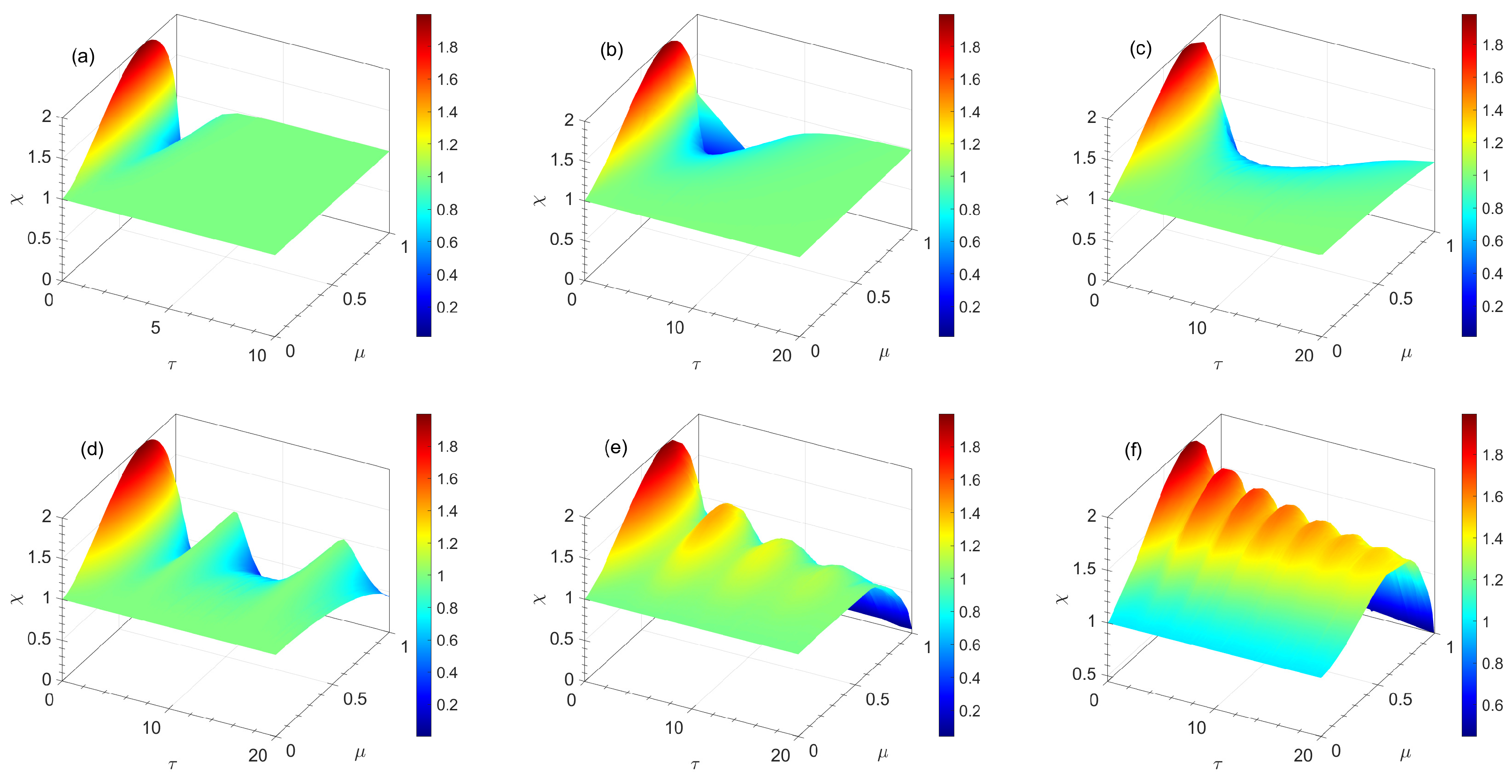
4. Quantum Dense Coding
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Pirandola, S.; Andersen, U.L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; et al. Advances in quantum cryptography. Adv. Opt. Photon. 2020, 12, 1012. [Google Scholar] [CrossRef]
- Wang, H.-W.; Tsai, C.-W.; Lin, J.; Huang, Y.-Y.; Yang, C.-W. Efficient and secure measure-resend authenticated semi-quantum key distribution protocol against reflecting attack. Mathematics 2022, 10, 1241. [Google Scholar] [CrossRef]
- Zhu, Y.; Mao, L.; Hu, H.; Wang, Y.; Guo, Y. Adaptive continuous-variable quantum key distribution with discrete modulation regulative in free space. Mathematics 2022, 10, 4450. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, M.; Horodecki, P. Teleportation, Bell’s inequalities and inseparability. Phys. Lett. A 1996, 222, 21. [Google Scholar] [CrossRef]
- Popescu, S. Bell’s inequalities versus teleportation: What is nonlocality. Phys. Rev. Lett. 1994, 72, 797. [Google Scholar] [CrossRef] [PubMed]
- Horodecki, M.; Horodecki, P.; Horodecki, R. General teleportation channel, singlet fraction, and quasidistillation. Phys. Rev. A 1999, 60, 1888. [Google Scholar] [CrossRef]
- Verstraete, F.; Verschelde, H. Optimal teleportation with a mixed state of two qubits. Phys. Rev. Lett. 2003, 90, 097901. [Google Scholar] [CrossRef]
- Bennett, C.H.; Wiesner, S.J. Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 1992, 69, 2881. [Google Scholar] [CrossRef]
- Bareno, A.; Ekert, A. Dense coding based on quantum entanglement. J. Mod. Opt. 1995, 42, 1253. [Google Scholar] [CrossRef]
- Mattle, K.; Weinfurter, H.; Kwiat, P.G.; Zeilinger, A. Dense coding in experimental quantum communication. Phys. Rev. Lett. 1996, 76, 4656. [Google Scholar] [CrossRef] [PubMed]
- Hiroshima, T. Optimal dense coding with mixed state entanglement. J. Phys. A Math. Gen. 2001, 34, 6907. [Google Scholar] [CrossRef]
- Bowen, G.; Bose, S. Teleportation as a depolarizing quantum channel, relative entropy, and classical capacity. Phys. Rev. Lett. 2001, 87, 267901. [Google Scholar] [CrossRef] [PubMed]
- Albeverio, S.; Fei, S.M.; Yang, W.L. Optimal teleportation based on Bell measurements. Phys. Rev. A 2002, 66, 012301. [Google Scholar] [CrossRef]
- Hu, M.L. Relations between entanglement, Bell-inequality violation and teleportation fidelity for the two-qubit X states. Quantum Inf. Process. 2013, 12, 229. [Google Scholar] [CrossRef]
- Horodecki, M.; Piani, M. On quantum advantage in dense coding. J. Phys. A Math. Theor. 2012, 45, 105306. [Google Scholar] [CrossRef]
- Hu, M.L.; Hu, X.; Wang, J.C.; Peng, Y.; Zhang, Y.R.; Fan, H. Quantum coherence and geometric quantum discord. Phys. Rep. 2018, 762–764, 1–100. [Google Scholar] [CrossRef]
- Lee, J.; Kim, M.S. Entanglement teleportation via Werner states. Phys. Rev. Lett. 2000, 84, 4236. [Google Scholar] [CrossRef]
- Oh, S.; Lee, S.; Lee, H.W. Fidelity of quantum teleportation through noisy channels. Phys. Rev. A 2002, 66, 022316. [Google Scholar] [CrossRef]
- Jung, E.; Hwang, M.R.; Ju, Y.H.; Kim, M.S.; Yoo, S.K.; Kim, H.; Park, D.; Son, J.W.; Tamaryan, S.; Cha, S.K. Greenberger–Horne–Zeilinger versus W states: Quantum teleportation through noisy channels. Phys. Rev. A 2008, 78, 012312. [Google Scholar] [CrossRef]
- Bhaktavatsala Rao, D.D.; Panigrahi, P.K.; Mitra, C. Teleportation in the presence of common bath decoherence at the transmitting station. Phys. Rev. A 2008, 78, 022336. [Google Scholar]
- Yeo, Y.; Kho, Z.W.; Wang, L. Effects of Pauli channels and noisy quantum operations on standard teleportation. EPL 2009, 86, 40009. [Google Scholar] [CrossRef]
- Shadman, Z.; Kampermann, H.; Macchiavello, C.; Bruß, D. Optimal super dense coding over noisy quantum channels. New J. Phys. 2010, 12, 073042. [Google Scholar] [CrossRef]
- Quek, S.; Li, Z. Effects of quantum noises and noisy quantum operations on entanglement and special dense coding. Phys. Rev. A 2010, 81, 024302. [Google Scholar] [CrossRef]
- Li, J.K.; Xu, K.; Zhang, G.F. Dense coding capacity in correlated noisy channels with weak measurement. Chin. Phys. B 2021, 30, 110302. [Google Scholar] [CrossRef]
- Haddadi, S.; Hu, M.L.; Knedif, Y.; Dolatkhah, H.; Pourkarimi, M.R.; Daoud, M. Measurement uncertainty and dense coding in a two-qubit system: Combined effects of bosonic reservoir and dipole–dipole interaction. Results Phys. 2022, 32, 105041. [Google Scholar] [CrossRef]
- Sun, Y.H.; Xie, Y.X. Memory effect of a dephasing channel on measurement uncertainty, dense coding, teleportation, and quantum Fisher information. Results Phys. 2022, 37, 105526. [Google Scholar] [CrossRef]
- Yeo, Y. Teleportation with a mixed state of four qubits and the generalized singlet fraction. Phys. Rev. A 2006, 74, 052305. [Google Scholar] [CrossRef]
- Yeo, Y. Local noise can enhance two-qubit teleportation. Phys. Rev. A 2008, 78, 022334. [Google Scholar] [CrossRef]
- Laine, E.M.; Breuer, H.P.; Piilo, J. Nonlocal memory effects allow perfect teleportation with mixed states. Sci. Rep. 2014, 4, 4620. [Google Scholar] [CrossRef]
- Guo, Y.N.; Tian, Q.L.; Zeng, K.; Chen, P.X. Fidelity of quantum teleportation in correlated quantum channels. Quantum Inf. Process. 2020, 19, 182. [Google Scholar] [CrossRef]
- Hu, M.L.; Zhang, Y.H.; Fan, H. Nonlocal advantage of quantum coherence in a dephasing channel with memory. Chin. Phys. B 2021, 30, 030308. [Google Scholar] [CrossRef]
- Li, Y.L.; Zu, C.J.; Wei, D.M. Enhance quantum teleportation under correlated amplitude damping decoherence by weak measurement and quantum measurement reversal. Quantum Inf. Process. 2019, 18, 2. [Google Scholar] [CrossRef]
- Tian, M.B.; Zhang, G.F. Improving the capacity of quantum dense coding by weak measurement and reversal measurement. Quantum Inf. Process. 2018, 17, 19. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Rivas, Á.; Huelga, S.F. Open Quantum Systems. An Introduction; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Cai, X.; Zheng, Y. Quantum dynamical speedup in a nonequilibrium environment. Phys. Rev. A 2017, 95, 052104. [Google Scholar] [CrossRef]
- Cai, X.; Zheng, Y. Non-Markovian decoherence dynamics in nonequilibrium environments. J. Chem. Phys. 2018, 149, 094107. [Google Scholar]
- Cai, X. Quantum dephasing induced by non-Markovian random telegraph noise. Sci. Rep. 2020, 10, 88. [Google Scholar] [CrossRef]
- Czerwinski, A. Quantum communication with polarization-encoded qubits under majorization monotone dynamics. Mathematics 2022, 10, 3932. [Google Scholar] [CrossRef]
- Breuer, H.P.; Laine, E.M.; Piilo, J. Measure for the degree of non-Markovian behavior of quantum processes in open systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef]
- Breuer, H.P.; Laine, E.M.; Piilo, J.; Vacchini, B. Colloquium: Non-Markovian dynamics in open quantum systems. Rev. Mod. Phys. 2016, 88, 021002. [Google Scholar] [CrossRef]
- Chen, H.; Han, T.; Chen, M.; Ren, J.; Cai, X.; Meng, X.; Peng, Y. Quantum state tomography in nonequilibrium environments. Photonics 2023, 10, 134. [Google Scholar] [CrossRef]
- Werlang, T.; Souza, S.; Fanchini, F.F.; Villas Boas, C.J. Robustness of quantum discord to sudden death. Phys Rev. A 2009, 80, 024103. [Google Scholar] [CrossRef]
- Xu, J.S.; Li, C.F.; Zhang, C.J.; Xu, X.Y.; Zhang, Y.S.; Guo, G.C. Experimental investigation of the non-Markovian dynamics of classical and quantum correlations. Phys Rev. A 2010, 82, 042328. [Google Scholar] [CrossRef]
- Altintas, F.; Eryigit, R. Dissipative dynamics of quantum correlations in the strong-coupling regime. Phys. Rev. A 2013, 87, 022124. [Google Scholar] [CrossRef]
- Czerwinski, A. Dynamics of open quantum systems–Markovian semigroups and beyond. Symmetry 2022, 14, 1752. [Google Scholar] [CrossRef]
- Haddadi, S.; Pourkarimi, M.R.; Wang, D. Tripartite entropic uncertainty in an open system under classical environmental noise. J. Opt. Soc. Am. B 2021, 38, 2620. [Google Scholar] [CrossRef]
- Pourkarimi, M.R.; Haseli, S.; Haddadi, S.; Hadipour, M. Scrutinizing entropic uncertainty and quantum discord in an open system under quantum critical environment. Laser Phys. Lett. 2022, 19, 065201. [Google Scholar] [CrossRef]
- Rahman, A.U.; Haddadi, S.; Javed, M.; Kenfack, L.T.; Ullah, A. Entanglement witness and linear entropy in an open system influenced by FG noise. Quantum Inf. Process. 2022, 21, 368. [Google Scholar] [CrossRef]
- Rahman, A.U.; Ali, H.; Haddadi, S.; Zangi, S.M. Generating non-classical correlations in two-level atoms. Alex. Eng. J. 2023, 67, 425. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J.H. Finite-time disentanglement via spontaneous emission. Phys. Rev. Lett. 2004, 93, 140404. [Google Scholar] [CrossRef]
- Almeida, M.P.; de Melo, F.; Hor-Meyll, M.; Salles, A.; Walborn, S.P.; Souto Ribeiro, P.H.; Davidovich, L. Environment-induced sudden death of entanglement. Science 2007, 316, 579. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J.H. Sudden death of entanglement. Science 2009, 323, 5914. [Google Scholar] [CrossRef] [PubMed]
- Bellomo, B.; Lo Franco, R.; Compagno, G. Non-Markovian effects on the dynamics of entanglement. Phys. Rev. Lett. 2007, 99, 160502. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Chen, H.; Han, T.; Cai, X. Disentanglement Dynamics in Nonequilibrium Environments. Entropy 2022, 24, 1330. [Google Scholar] [CrossRef]
- Czerwinski, A. Entanglement dynamics governed by time-dependent quantum generators. Axioms 2022, 11, 589. [Google Scholar] [CrossRef]
- Kim, Y.S.; Lee, J.C.; Kwon, O.; Kim, Y.H. Protecting entanglement from decoherence using weak measurement and quantum measurement reversal. Nat. Phys. 2012, 8, 117. [Google Scholar] [CrossRef]
- Lidar, D.A.; Birgitta Whaley, K. Decoherence-Free Subspaces and Subsystems. Irreversible Quantum Dynamics; Benatti, F., Floreanini, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Flores, M.M.; Galapon, E.A. Two qubit entanglement preservation through the addition of qubits. Ann. Phys. 2015, 354, 21. [Google Scholar] [CrossRef]
- Mortezapour, A.; Ahmadi Borji, M.; Lo Franco, R. Protecting entanglement by adjusting the velocities of moving qubits inside non-Markovian environments. Laser Phys. Lett. 2017, 14, 055201. [Google Scholar] [CrossRef]
- Haas, M.; Jentschura, U.D.; Keitel, C.H.; Kolachevsky, N.; Herrmann, M.; Fendel, P.; Fischer, M.; Udem, T.; Holzwarth, R.; Hänsch, T.W.; et al. Two-photon excitation dynamics in bound two-body Coulomb systems including ac Stark shift and ionization. Phys. Rev. A 2006, 73, 052501. [Google Scholar] [CrossRef]
- Agarwal, G.S.; Pathak, P.K. dc-field-induced enhancement and inhibition of spontaneous emission in a cavity. Phys. Rev. A 2004, 70, 025802. [Google Scholar] [CrossRef]
- Ghosh, B.; Majumdar, A.S.; Nayak, N. Control of atomic entanglement by the dynamic Stark effect. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 065503. [Google Scholar] [CrossRef]
- Baghshahi, H.R.; Tavassoly, M.K.; Faghihi, M.J. Entanglement analysis of a two-atom nonlinear Jaynes–Cummings model with nondegenerate two-photon transition, Kerr nonlinearity, and two-mode Stark shift. Laser Phys. 2014, 24, 125203. [Google Scholar] [CrossRef]
- Golkar, S.; Tavassoly, M.K. Dynamics and maintenance of bipartite entanglement via the Stark shift effect inside dissipative reservoirs. Laser Phys. Lett. 2018, 15, 035205. [Google Scholar] [CrossRef]
- Puri, R.R.; Bullough, R.K. Quantum electrodynamics of an atom making two-photon transitions in an ideal cavity. J. Opt. Soc. Am. B 1988, 5, 2021. [Google Scholar] [CrossRef]
- Spohn, H. Kinetic equations from Hamiltonian dynamics: Markovian limits. Rev. Mod. Phys. 1980, 52, 569. [Google Scholar] [CrossRef]
- Dalton, B.J.; Barnett, S.M.; Garraway, B.M. Theory of pseudomodes in quantum optical processes. Phys. Rev. A 2001, 64, 053813. [Google Scholar] [CrossRef]
- Yeo, Y. Teleportation via thermally entangled states of a two-qubit Heisenberg XX chain. Phys. Rev. A 2002, 66, 062312. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, G.F. Quantum teleportation via a two-qubit Heisenberg XXZ chain–effects of anisotropy and magnetic field. Eur. Phys. J. D 2008, 47, 227. [Google Scholar] [CrossRef]
- Benabdallah, F.; Haddadi, S.; Arian Zad, H.; Pourkarimi, M.R.; Daoud, M.; Ananikian, N. Pairwise quantum criteria and teleportation in a spin square complex. Sci. Rep. 2022, 12, 6406. [Google Scholar] [CrossRef]
- Liang, Y.C.; Yeh, Y.H.; Mendonça, P.E.M.F.; Teh, R.Y.; Reid, M.D.; Drummond, P.D. Quantum fidelity measures for mixed states. Rep. Prog. Phys. 2019, 82, 076001. [Google Scholar] [CrossRef]
- Rahman, A.U.; Haddadi, S.; Pourkarimi, M.R.; Ghominejad, M. Fidelity of quantum states in a correlated dephasing channel. Laser Phys. Lett. 2022, 19, 035204. [Google Scholar] [CrossRef]
- Zidan, N.; Rahman, A.U.; Haddadi, S. Quantum teleportation in a two-superconducting qubit system under dephasing noisy channel: Role of Josephson and mutual coupling energies. Laser Phys. Lett. 2023, 20, 025204. [Google Scholar] [CrossRef]
- Pourkarimi, M.R.; Haddadi, S. Quantum-memory-assisted entropic uncertainty, teleportation, and quantum discord under decohering environments. Laser Phys. Lett. 2020, 17, 025206. [Google Scholar] [CrossRef]
- Schumacher, B.; Westmoreland, M.D. Sending classical information via noisy quantum channels. Phys. Rev. A 1997, 56, 131. [Google Scholar] [CrossRef]
- Holevo, A.S. The capacity of the quantum channel with general signal states. IEEE Trans. Inf. Theory 1998, 44, 269. [Google Scholar] [CrossRef]
- Haddadi, S.; Ghominejad, M.; Akhound, A.; Pourkarimi, M.R. Exploring entropic uncertainty relation and dense coding capacity in a two-qubit X-state. Laser Phys. Lett. 2020, 17, 095205. [Google Scholar] [CrossRef]
- Abd-Rabbou, M.Y.; Khalil, E.M. Dense coding and quantum memory assisted entropic uncertainty relations in a two-qubit state influenced by dipole and symmetric cross interactions. Ann. Phys. 2022, 534, 2200204. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haddadi, S.; Hadipour, M.; Haseli, S.; Rahman, A.U.; Czerwinski, A. Quantum Advantages of Teleportation and Dense Coding Protocols in an Open System. Mathematics 2023, 11, 1407. https://doi.org/10.3390/math11061407
Haddadi S, Hadipour M, Haseli S, Rahman AU, Czerwinski A. Quantum Advantages of Teleportation and Dense Coding Protocols in an Open System. Mathematics. 2023; 11(6):1407. https://doi.org/10.3390/math11061407
Chicago/Turabian StyleHaddadi, Saeed, Maryam Hadipour, Soroush Haseli, Atta Ur Rahman, and Artur Czerwinski. 2023. "Quantum Advantages of Teleportation and Dense Coding Protocols in an Open System" Mathematics 11, no. 6: 1407. https://doi.org/10.3390/math11061407
APA StyleHaddadi, S., Hadipour, M., Haseli, S., Rahman, A. U., & Czerwinski, A. (2023). Quantum Advantages of Teleportation and Dense Coding Protocols in an Open System. Mathematics, 11(6), 1407. https://doi.org/10.3390/math11061407







