Building Fixed Point-Free Maps with Memristor

Abstract

A memristor is a two-terminal passive electronic device that exhibits memory of resistance. It is essentially a resistor with memory, hence the name “memristor”. The unique property of memristors makes them useful in a wide range of applications, such as memory storage, neuromorphic computing, reconfigurable logic circuits, and especially chaotic systems. Fixed point-free maps or maps without fixed points, which are different from normal maps due to the absence of fixed points, have been explored recently. This work proposes an approach to build fixed point-free maps by connecting a cosine term and a memristor. Four new fixed point-free maps displaying chaos are reported to illustrate this approach. The dynamics of the proposed maps are verified by iterative plots, bifurcation diagram, and Lyapunov exponents. Because such chaotic maps are highly sensitive to the initial conditions and parameter variations, they are suitable for developing novel lightweight random number generators.

1. Introduction

Chaos is a fascinating phenomenon that occurs in many natural systems, from weather patterns to the motion of planets and stars [1]. One of the key tools used to study chaos is the chaotic map, which is a mathematical function that describes the evolution of a system over time [2,3,4,5,6]. Chaotic map is a discrete-time dynamic system, meaning that the state of the system at a given time step is determined by the state at the previous time step. Chaotic maps are non-linear, meaning that small changes in the initial conditions of the system can lead to vastly different outcomes. This sensitivity to initial conditions is known as the butterfly effect and is a hallmark of chaotic systems.

Chaotic maps have a wide range of applications in different fields such as physics, engineering, and computer science [7,8,9,10]. In physics, chaotic maps can be used to model the dynamics of complex systems, such as the motion of particles in a fluid or the behavior of electronic circuits. In engineering, chaotic maps can be used to design secure communication systems and pseudo-random number generators [11,12,13]. In computer science, chaotic maps are used for tasks such as image compression, encryption, and signal processing [14,15]. One popular application of chaotic maps is in the development of random number generators [16,17,18]. A random number generator is a system that produces a sequence of numbers that appear to be random, but are actually determined by a deterministic algorithm. Chaotic maps can be used to generate pseudo-random numbers by iterating the map with a seed value and using the output as the input for the next iteration. The resulting sequence of numbers appears random but can be reproduced if the seed value and the map are known. Chaotic maps are a powerful tool for understanding and controlling complex systems. With the continued development of new techniques and technologies, the potential applications of chaotic maps are likely to continue to expand in the future.

Recent research in chaotic maps has focused on new trends such as the use of memristors, fractional calculus, hidden attractors, multistability, and fixed point-free maps (FPFMs) [19,20,21,22,23]. Memristors are a new type of electronic component that can change their resistance based on the history of current flowing through them. Memristor was first theorized by Professor Leon Chua in 1971 and later physically realized by Hewlett-Packard in 2008. Memristor was applied in simple memristive hyperchaotic systems, multi-scroll memristive Hopfield neural network, image encryption application, medical data privacy protection, generation of chaotic attractors [24,25,26,27,28,29,30]. The discrete memristor was proposed and related works were published [31,32]. Researchers have been exploring the use of memristors in chaotic maps to create new types of dynamic systems with unique properties [33,34,35]. Fractional calculus is a generalization of the standard calculus that allows for the use of non-integer order derivatives. Researchers have been using fractional calculus to develop new types of chaotic maps with different properties [36,37]. Hidden attractors in chaotic maps are attractors that are not easily visible in traditional plots of the map’s phase space. Multistability in chaotic maps refers to the ability of the map to have multiple attractors [38]. Fixed point-free maps are rare chaotic maps that do not have any fixed points, which can lead to new types of dynamic behavior. From the viewpoint of maps with hidden chaotic dynamics, Jiang et al. first introduced 2D and 3D maps without fixed points [39,40]. While searching simple maps, the simplest fixed point-free maps with quadratic nonlinearities were found by Panahi et al. [41]. Different discrete maps without fixed points were listed in [20]. Shatnawi et al. explored a fractional discrete map without equilibrium [42]. Fixed point-free maps are different from conventional chaotic maps, which often have unstable fixed points. The stability of fixed point plays a vital role while discovering conventional chaotic maps.

Following such recent trends, this work introduces a new approach to building a fixed point-free map (FPFM). Figure 1 illustrates the relationship of this work with other discrete maps. Our work focuses only on special memristive maps without fixed points. The general model of fixed point-free maps is proposed in Section 2. Section 3 presents a typically built fixed point-free map. Further discussions and conclusions are reported in Section 4 and Section 5.

2. General Model of Fixed Point-Free Maps

Recent research in chaotic maps has focused on developing new types of chaotic maps, such as memristor chaotic maps and fractional chaotic maps. Memristor chaotic maps use a type of circuit element called a memristor, which can remember its previous state. This allows for the creation of more complex and dynamic chaotic systems. We build a map as shown in Figure 2 by using a cosine function $cos(.)$ and a memristor with discrete memristance $M\left(y\left(n\right)\right)$. Two amplifiers $a_1$ and $a_2$ are used to change the effect of the cosine function and the memristor.

From Figure 2, we have the mathematical model

$$\left\{\begin{array}{c}x\left(n+1\right)=a_{1}cos\left(x\left(n\right)\right)+a_{2}M\left(y\left(n\right)\right)x\left(n\right)\hfill \\ y\left(n+1\right)=y\left(n\right)+x\left(n\right)\hfill \end{array}\right.$$

(1)

with parameters $a_1$, $a_2$. In Figure 2, the cosine term and the memristor are connected parallel. As a result, the location of the discrete memristance $M\left(y\right(n\left)\right)$ can be changed in Equation (1).

If $P\left(x^{*},y^{*}\right)$ is the fixed point [1] of model (1), we have

$$\left\{\begin{array}{c}{x}^{*}=a_{1}cos\left(x^{*}\right)+a_{2}M\left(y^{*}\right)x^{*}\hfill \\ y^{*}=y^{*}+x^{*}\hfill \end{array}\right.$$

(2)

Thus, it becomes

$$\left\{\begin{array}{c}{a}_{1}cos\left(x^{*}\right)=0\hfill \\ x^{*}=0\hfill \end{array}\right.$$

(3)

From Equation (3), the map (1) is fixed point-free map when $a_1\ne 0$. A fixed point-free chaotic map is a special chaotic map without a fixed point. The absence of fixed points makes it different from conventional chaotic maps, which often have unstable fixed points [1,43]. It is noted that there are some pros and cons of using fixed point-free maps. Chaotic fixed point-free maps have a high degree of randomness because there are no fixed points. This can make them more difficult to predict. The complexity of chaotic fixed point-free maps makes them difficult to analyze and utilize common reverse engineering. However, chaotic fixed point-free maps may have limited output ranges, which can limit their usefulness for certain types of real applications. In addition, chaotic fixed point-free maps can take longer to converge to a steady state than common chaotic maps.

By selecting

$$M\left(y\left(n\right)\right)={\left(y\left(n\right)\right)}^2-1$$

(4)

the fixed point-free map (named FPFM${}_1$ map) is built

$$\left\{\begin{array}{c}x\left(n+1\right)=a_{1}cos\left(x\left(n\right)\right)+a_2\left({\left(y\left(n\right)\right)}^2-1\right)x\left(n\right)\hfill \\ y\left(n+1\right)=y\left(n\right)+x\left(n\right)\hfill \end{array}\right.$$

(5)

For $a_1=0.1$, $a_2=1.7$, the FPFM${}_1$ map exhibits chaos (see Figure 3). The FPFM${}_1$ map’s maximum Lyapunov exponent is 0.2188, which is calculated by using the algorithm of Wolf et al. [44].

3. FPFM${}_{\mathbf{1}}$ Map

The map (5) is studied to understand its dynamics. Although the map (5) is a fixed point-free one, it has attractive behavior. The initial conditions are fixed $x\left(0\right)=1$, $y\left(0\right)=-0.5$. Figure 4 summarizes the FPFM${}_1$ map’s dynamics in the range $a_2\in \left[1.35,1.85\right]$. In Figure 4b, the red and blue curves present the first and second Lyapunov exponents, respectively. Chaos can be observed for $a_2>1.6$. Especially, the map displays hyperchaos indicated by two positive Lyapunov exponents. It is noted that the minimum dimension for a continuous hyperchaotic system is four. However, 1D discrete maps can exhibit chaos and 2D discrete maps can display hyperchaos [43,45]. The FPFM${}_1$ map is also sensitive to the parameter $a_1$. The FPFM${}_1$ map’s dynamics is reported in Figure 5 for the range $a_1\in \left[0,0.25\right]$. We can see the chaotic and hyperchaotic behaviors of the FPFM${}_1$ map when changing $a_1$.

A controller k can be added as

$$\left\{\begin{array}{c}x\left(n+1\right)=a_{1}cos\left(x\left(n\right)\right)+a_2\left({\left(y\left(n\right)+k\right)}^2-1\right)x\left(n\right)\hfill \\ y\left(n+1\right)=y\left(n\right)+x\left(n\right)\hfill \end{array}\right.$$

(6)

for modifying y. Value of y is modified conveniently with k as illustrated in Figure 6.

4. Discussion

The general model in Section 2 is also applied to build different fixed point-free maps. For example, with the discrete memristance

$$M\left(y\left(n\right)\right)=\left|y\left(n\right)\right|-1$$

(7)

we get the FPFM${}_2$ map

$$\left\{\begin{array}{c}x\left(n+1\right)=a_{1}cos\left(x\left(n\right)\right)+a_2\left(\left|y\left(n\right)\right|-1\right)x\left(n\right)\hfill \\ y\left(n+1\right)=y\left(n\right)+x\left(n\right)\hfill \end{array}\right.$$

(8)

Other found fixed point-free maps are summarized in

Table 1. Fixed point-free maps derived from the general model.

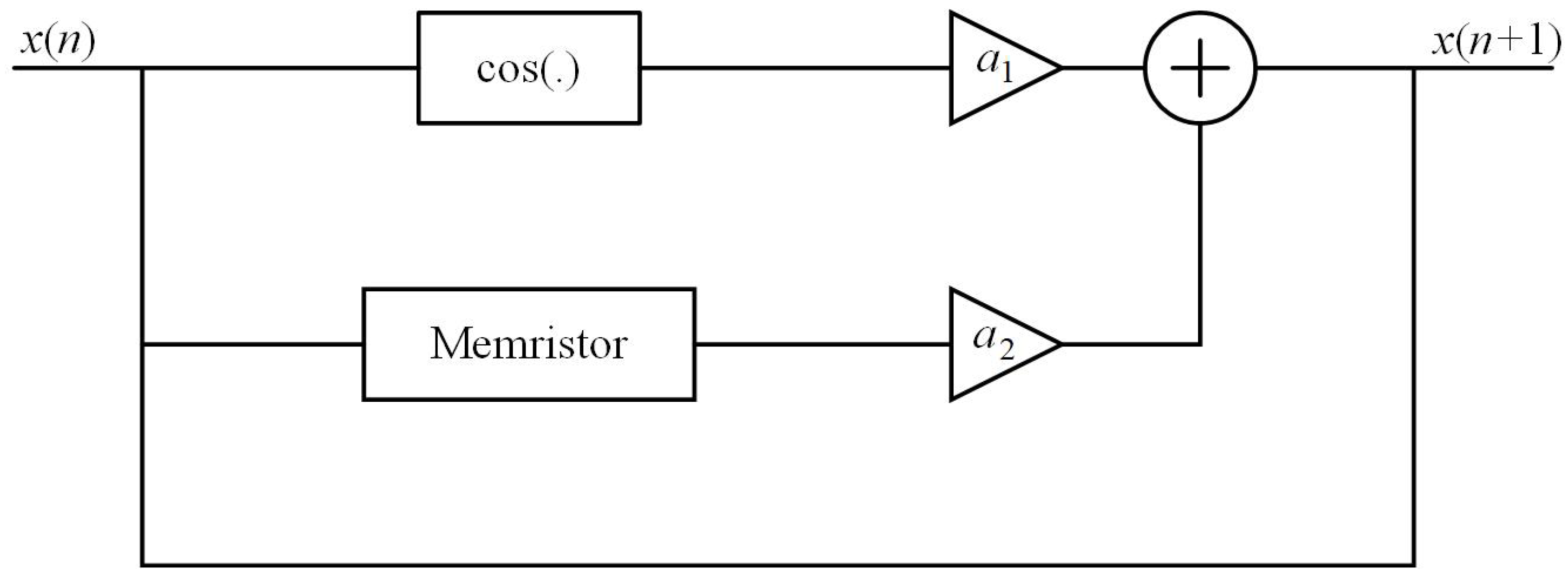
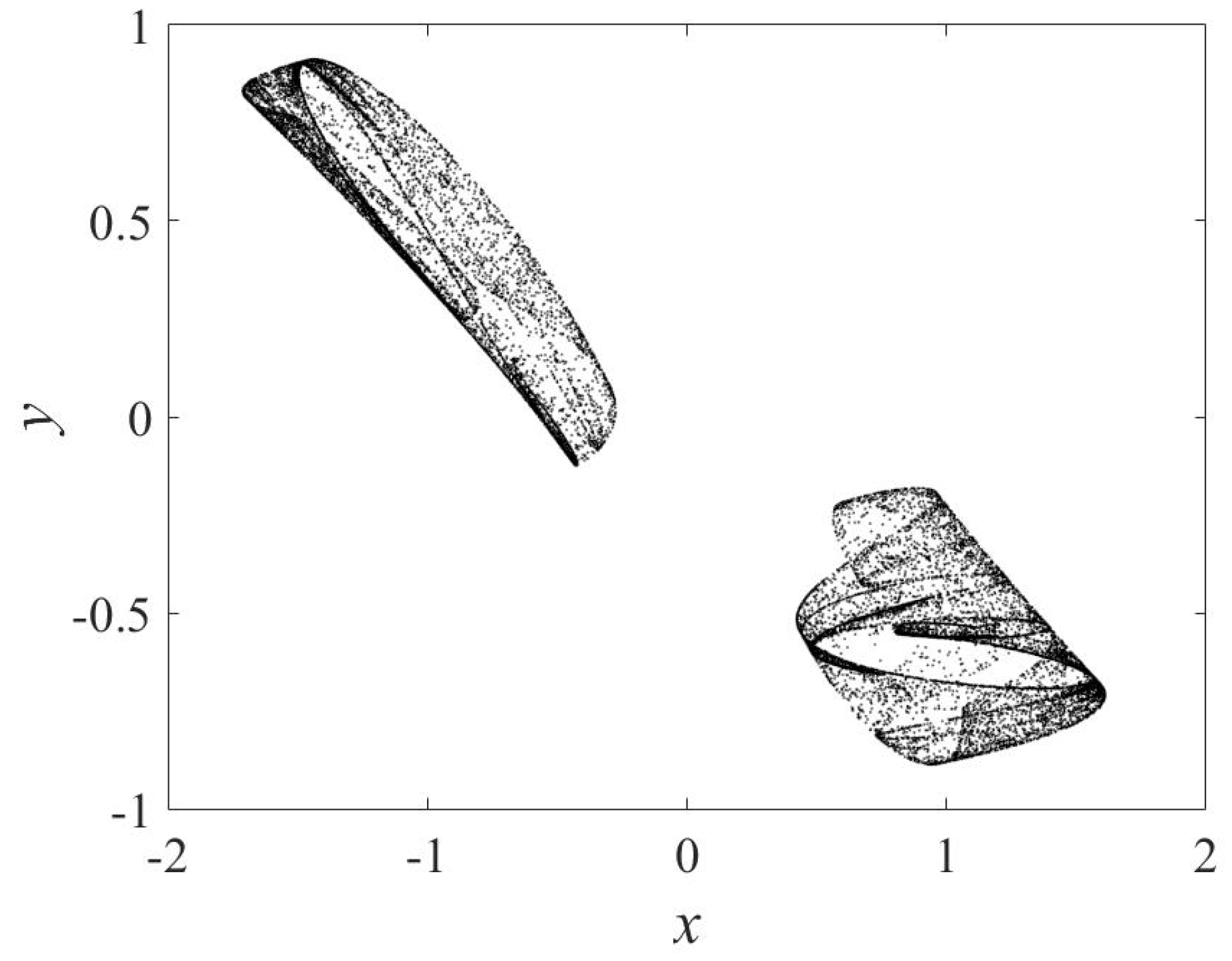
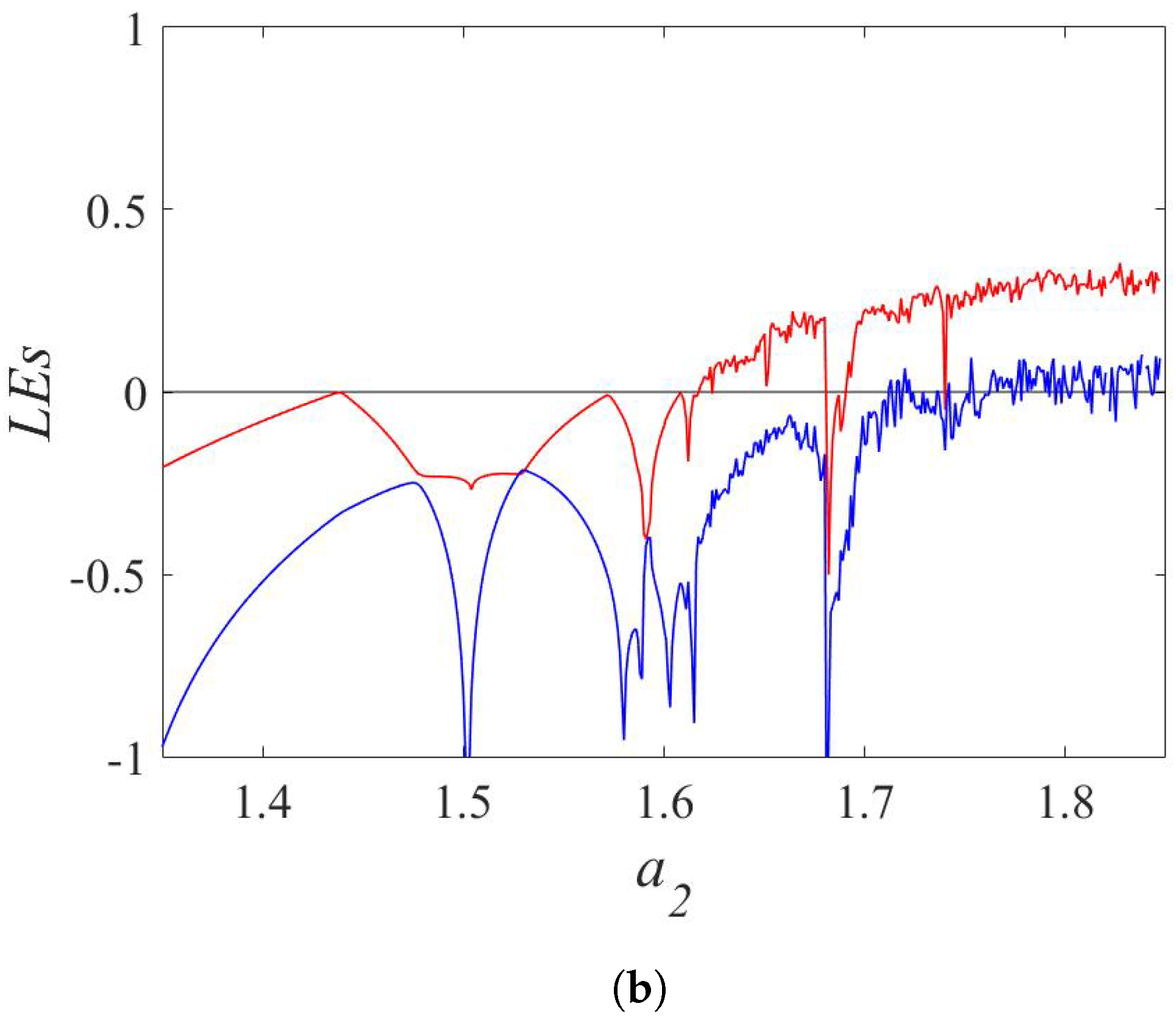
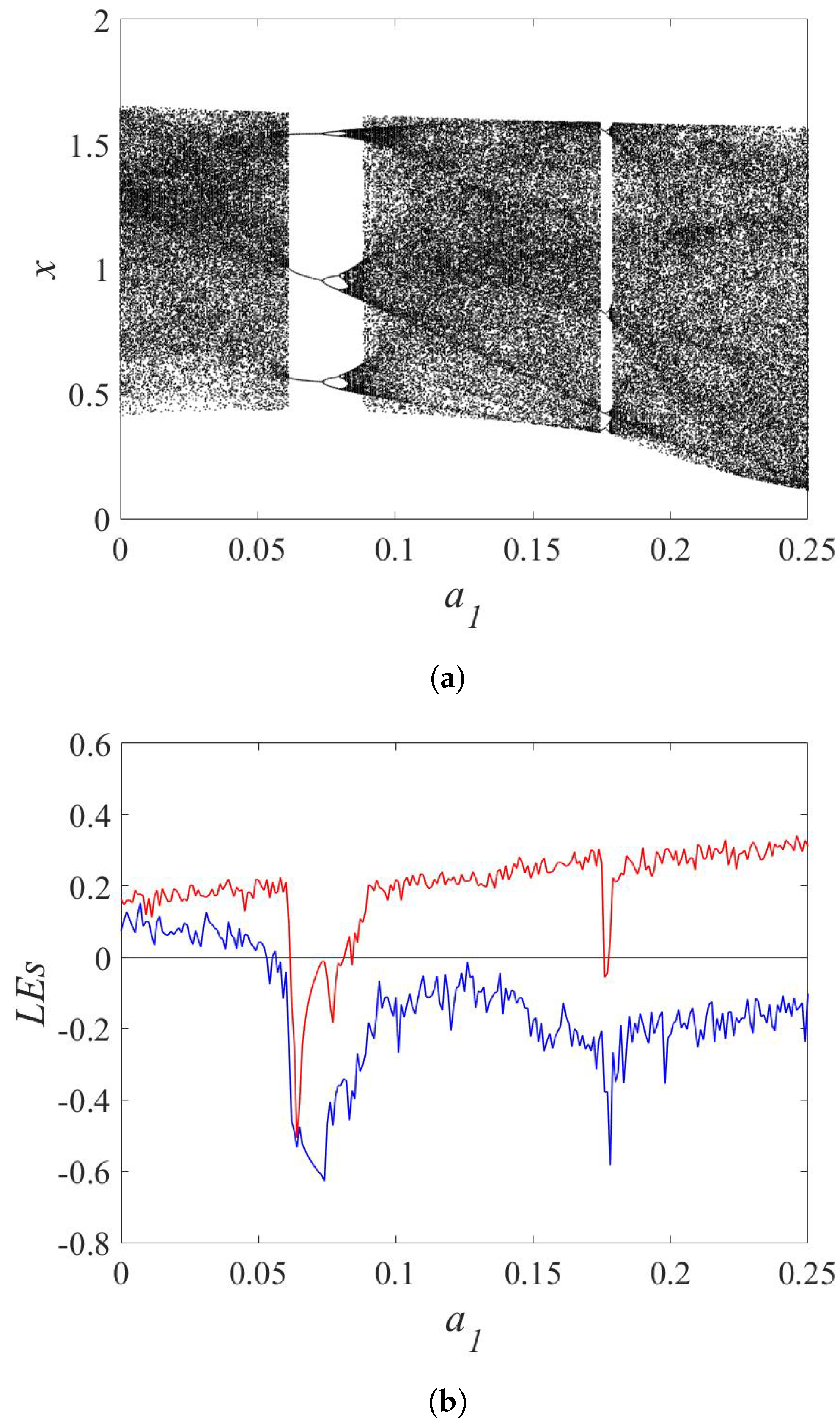
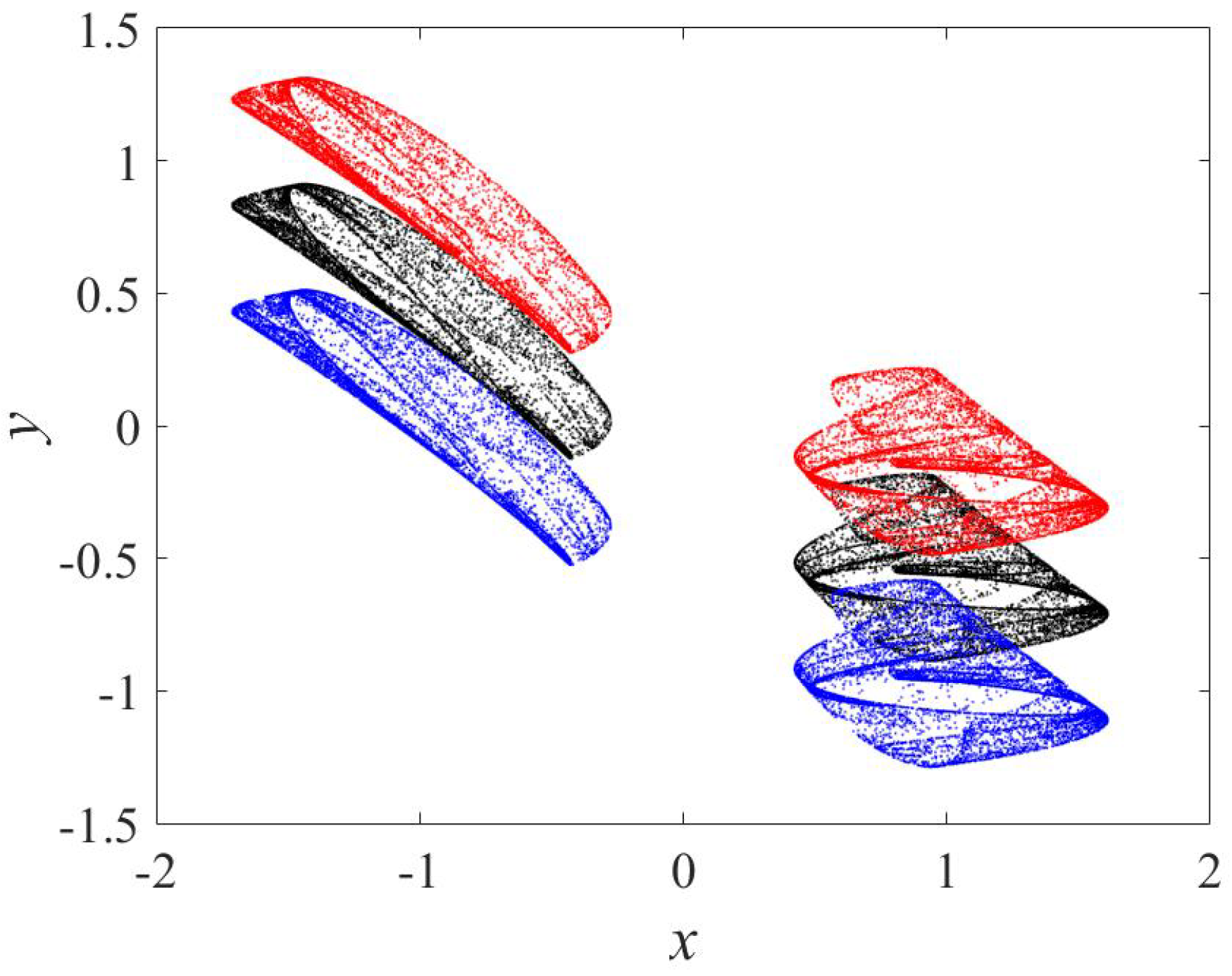
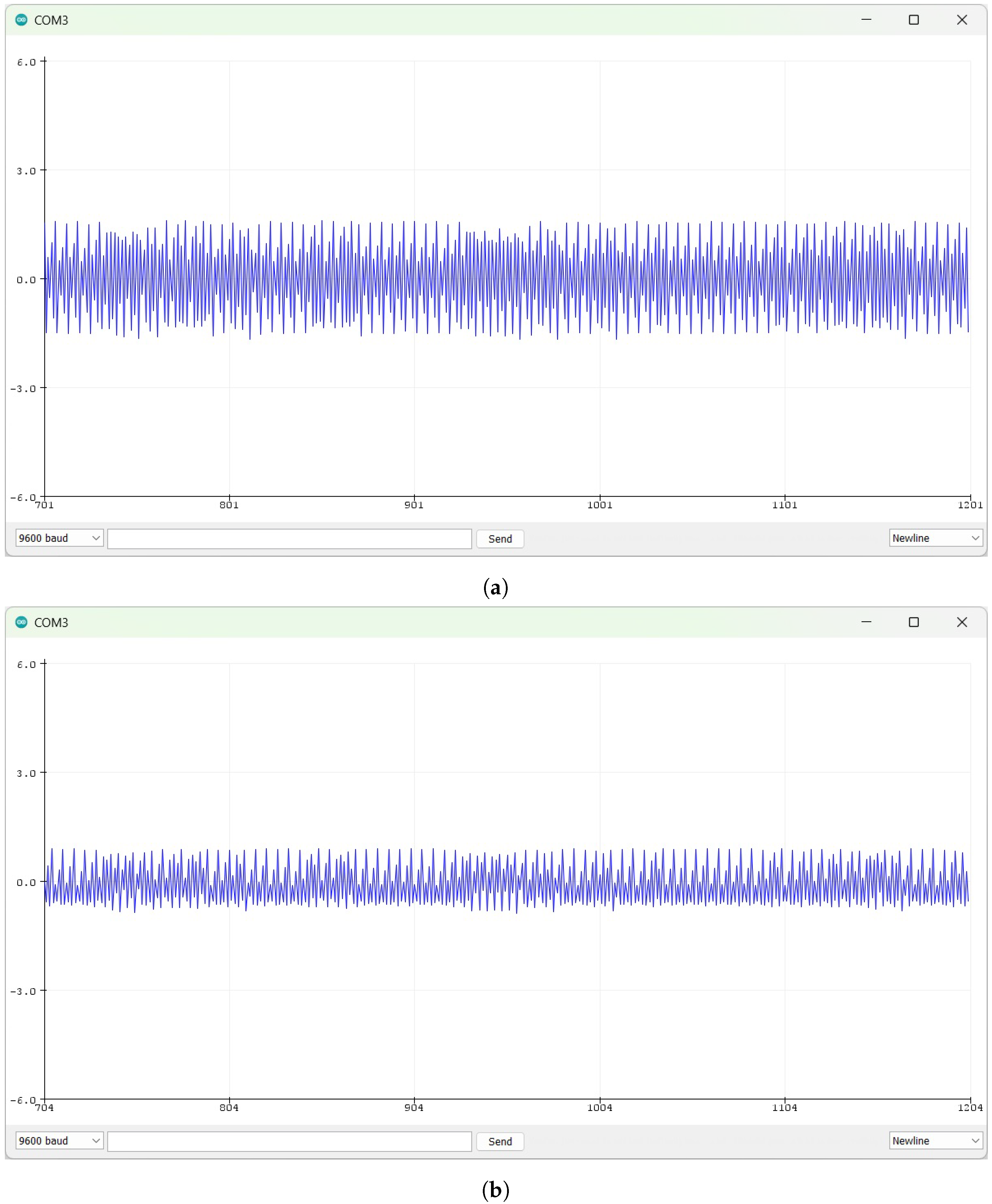
Map	Equations	Parameters	$\left(\mathit{x}\right(0),\mathit{y}(0\left)\right)$
FPFM${}_1$	$x\left(n+1\right)=a_{1}cos\left(x\left(n\right)\right)+a_2\left({\left(y\left(n\right)\right)}^2-1\right)x\left(n\right)$	$a_1=0.1$	$x\left(0\right)=1$
	$y\left(n+1\right)=y\left(n\right)+x\left(n\right)$	$a_2=1.7$	$y\left(0\right)=-0.5$
FPFM${}_2$	$x\left(n+1\right)=a_{1}cos\left(x\left(n\right)\right)+a_2\left(\left|y\left(n\right)\right|-1\right)x\left(n\right)$	$a_1=0.05$	$x\left(0\right)=1$
	$y\left(n+1\right)=y\left(n\right)+x\left(n\right)$	$a_2=2.3$	$y\left(0\right)=-0.5$
FPFM${}_3$	$x\left(n+1\right)=a_{1}cos\left(x\left(n\right)\right)+a_{2}sin\left(\pi y\left(n\right)\right)x\left(n\right)$	$a_1=0.05$	$x\left(0\right)=0.5$
	$y\left(n+1\right)=y\left(n\right)+x\left(n\right)$	$a_2=1.82$	$y\left(0\right)=-0.8$
FPFM${}_4$	$x\left(n+1\right)=a_{1}cos\left(x\left(n\right)\right)+a_2\left(e^{-cos\left(\pi y\left(n\right)\right)}-1\right)x\left(n\right)$	$a_1=0.05$	$x\left(0\right)=-0.5$
	$y\left(n+1\right)=y\left(n\right)+x\left(n\right)$	$a_2=2.6$	$y\left(0\right)=0.4$

. The initial conditions are provided in Table 1 because chaotic systems are sensitive to initial conditions. A small change in the initial conditions of the chaotic system can lead to vastly different outcomes [1,43]. The chaos of such maps is presented in iterative plots in Figure 7. Moreover, considering other memristors, such as an HP memristor, should be investigated in future works.

The feasibility of a chaotic map is essential because it determines whether the map can be effectively used to achieve the desired results in practical applications. In addition, the feasibility of the map must be experimentally validated, to ensure that it works as expected in a real-world scenario. The fixed point-free map can be realized with a cheap hardware board. We have used an Arduino Uno board to realize the FPFM${}_1$ map. The board is connected to a laptop using a USB cable (see Figure 8). Obtained signals from the micro-controller are reported in Figure 9 to show the map’s feasibility.

There is a rapid development of information and communication technologies in recent years. Especially, the quick growth of the Internet and telecommunications requires different security approaches. Security features play an important role in information and communication systems and attract significant attention. When considering the security issues in the field of information, encryption algorithms, key generation, and key management are vital factors. In such factors, one of the most important components is the random number generator. The design and implementation of effective random number generators are still attractive research topics. This work is the first step in our project for designing a random number generator. We have concentrated on chaotic maps without a fixed point because they are rare maps, which belong to a special class of systems with “hidden attractors” [46,47]. We believe that some properties of fixed point-free maps make them attractive for use in random number generators. However, the pros and cons of using fixed point-free maps should be investigated carefully. We would like to develop a lightweight random number generator. We will focus on the design and implementation of lightweight random number generators based on such fixed point-free maps in the next study.

5. Conclusions

This work proposed a general model to build new fixed point-free maps. The general model was constructed with a cosine function and memristor. The dynamics of the proposed maps were verified via iterative plots, bifurcation diagram, and Lyapunov exponents. Chaotic fixed point-free maps play a crucial role in various fields including cryptography, image processing, and data compression. These maps are important because of their complex, dynamic behavior that results in seemingly random output, making them useful for applications that require unpredictable and unique sequences. These proposed maps can be used for developing novel lightweight random number generators. However, fixed point-free maps have both advantages and disadvantages compared to other types of chaotic maps. Therefore, practical applications of chaotic maps without fixed points must be studied further. It is noted that stabilization and synchronization are vital aspects when investigating chaotic maps. Control schemes for stabilizing and synchronizing the proposed fixed point-free maps will be considered in our next works.