Abstract
The immense application of mathematical modeling for the improvement of bioprocesses determines model development as a topical field. Metaheuristic techniques, especially hybrid algorithms, have become a preferred tool in model parameter identification. In this study, two efficient algorithms, the ant lion optimizer (ALO), inspired by the interaction between antlions and ants in a trap, and the genetic algorithm (GA), influenced by evolution and the process of natural selection, have been hybridized for the first time. The novel ALO-GA hybrid aims to balance exploration and exploitation and significantly improve its global optimization ability. Firstly, to verify the effectiveness and superiority of the proposed work, the ALO-GA is compared with several state-of-the-art hybrid algorithms on a set of classical benchmark functions. Further, the efficiency of the ALO-GA is proved in the parameter identification of a model of an Escherichia coli MC4110 fed-batch cultivation process. The obtained results have been studied in contrast to the results of various metaheuristics employed for the same problem. Hybrids between the GA, the artificial bee colony (ABC) algorithm, the ant colony optimization (ACO) algorithm, and the firefly algorithm (FA) are considered. A series of statistical tests, parametric and nonparametric, are performed. Both numerical and statistical results clearly show that ALO-GA outperforms the other competing algorithms. The ALO-GA hybrid algorithm proposed here has achieved an improvement of 6.5% compared to the GA-ACO model, 7% compared to the ACO-FA model, and 7.8% compared to the ABC-GA model.
Keywords:
ant lion optimizer; genetic algorithm; parameter identification; Escherichia coli; cultivation process MSC:
68W01; 78M50; 90C27; 93B30; 93B40
1. Introduction
Due to an insufficient understanding of the underlying phenomena, there are no available detailed models for many industrially relevant processes. Mathematical models, which could be incomplete and inaccurate to a certain degree, can still be very useful and effective in describing the processes that are essentials for control, optimization, or understanding. Modeling cultivation processes are a difficult and challenging task, due to their characteristics such as nonlinearity, time-varying parameters, and interdependent process variables, etc., [1,2,3]. Microorganisms have been highly regarded as biotechnological tools. Many valuable bacteria, yeasts, and fungi are widely spread in nature. However, the optimal conditions for their formation and growth in a natural environment are rarely found. Different models have been developed [4,5,6,7] due to their importance for process control, reduction in production costs, and improvement of product quality in cultivation. In [8], the authors concluded that the flexibility of the model allows optimizations of the bioreactor performance and further development of the process by adjusting its conditions and configurations. In their work, Du et al. [9] stated that, “…after collaborating with a range of disciplines to develop new mathematical and computational tools while enhancing our knowledge of biology, the evolution of fermentation process modeling could be limitless”. The authors of [10] performed process optimization by mathematical modeling. It was proved that the usage of co-cultures of different bacteria could enhance the process performance. In [11], a model for syngas fermentation was developed and the simulations indicated more than a 50% increase in bioethanol productivity. In [12], the developed model was employed in finding the best experimental conditions for achieving the maximum bioethanol concentration. The proposed model could be used to predict the bioethanol concentration under various conditions without performing real experimental measurements. The novel model proposed in [13] is particularly suitable to assist the rational design of cultivation processes because it can represent complex biochemistry in more detail. The generated model is robust and can be considered for control and optimization purposes. The above-mentioned works constitute a very small part of the existing investigations in the past two years.
This paper considers the modeling of a fed-batch cultivation process of the bacteria Escherichia coli—a host organism with great significance for recombinant protein production [14]. Often, the cultivation of such recombinant microorganisms is a means to produce pharmaceutical biochemicals such as interleukins, insulin, interferons, enzymes, and growth factors at a reasonable price. Some of the most recent works featuring mathematical models of E. coli are as follows: two E. coli outer membrane models were investigated using molecular dynamics simulations [15]; two E. coli strains with modified tryptophan models were reported [16]; the cytokine response of the cells of the biomimetic porcine urothelial model to different E. coli strains was studied [17]; an enhanced segment particle swarm optimization algorithm that can estimate the values of small-scale kinetic parameters was described and applied as a model system to the main metabolic network of E. coli [18]; and the kinetics of wild-type and recombinant broccoli myrosinases produced in E. coli were characterized in terms of the reaction conditions [19].
The choice of an appropriate optimization method for model parameter identification is of utmost importance when dealing with a complex model structure. Over the years, researchers have shown interest in finding optimal model parameter values aimed at the global optimization conditions. Mathematical models of various natural phenomena, the theory of physics and biology, animal and human nature, and even the rules of some games have inspired a great variety of metaheuristic algorithms [20,21]. Metaheuristic techniques, especially hybrid metaheuristic algorithms that show better computational efficiency in avoiding local optima, have become a preferred tool in the parameter identification of models of cultivation processes [1,18,22,23,24,25,26,27]. Hybrid metaheuristic algorithms are widely accepted and well-employed in real-life challenging problems. This is the primary motivation for applying a hybrid metaheuristic to the parameter identification problem considered here.
In this work, a hybrid between the ant lion optimizer (ALO) [28] and the genetic algorithm (GA) [29,30] is developed to improve the classic ALO performance and engage in the parameter identification of an E. coli cultivation process. Since the ALO suffers from local optima stagnation [31], this study intends to propose a new ALO hybrid that will lead to an enhanced efficiency and accuracy of the algorithm. A hybridization with the GA, which is well-established with its global optimum performance [32,33], is considered to overcome the local optima stagnation. Contrariwise, the GA drawback, which is that there is a lot of computational effort to converge to the optimum when the randomly generated GA initial population is quite distant from it, will be overcome by the hybridization with the ALO. The authors expect that the combination of these techniques will lead either to a better performance concerning the computational resources or, which is of greater interest to the authors, to a better model of the bacteria cultivation processes considered here in terms of lower objective function values, and correspondingly higher model accuracy.
According to the two comprehensive surveys [34,35] and to our best knowledge, the ALO has been successfully modified using a differential mutation operator [36] and an arithmetic crossover operation of the GA [37,38]. Our understanding is that this is the first comprehensive hybrid between the ALO and GA. Moreover, the ALO, classic or hybridized, has not been applied so far for the parameter identification of cultivation process models. These facts are the secondary motivation to present a hybrid ALO-GA metaheuristic.
The performance of the proposed ALO-GA has been compared with other existing hybrid techniques discussed in the Literature Review, using a classical set of benchmark functions. The ALO-GA has been applied for the parameter identification of a nonlinear mathematical model of a cultivation process. The optimization problem has been solved by utilizing real experimental data from an E. coli fed-batch cultivation. The ALO-GA results have been compared with already published results of different hybrid metaheuristic algorithms employed for the same model parameter identification problem.
An experimental analysis is usually used to assess whether an algorithm is regarded as better than other methods. This may not be a trivial task as it includes confirming whether this algorithm achieves a meaningful improvement in the objective of a given problem over the others. Statistical tests are widely adopted to evaluate the performance of a given method [39,40]. Therefore, the obtained numerical results in this research were analyzed by applying nonparametric tests, namely, the Friedman test [41,42,43], the Wilcoxon test [44], and its parametric equivalent, the paired t-test, the Kruskal–Wallis test [45], and its parametric equivalent, the one-way analysis of variance (ANOVA) test [46].
The main contributions of this work include the following:
- This work intends to propose a novel hybrid ALO-GA that can fully balance exploration and exploitation, and significantly improve the global optimization ability. The algorithm performance is validated on a set of classical benchmark functions.
- The ALO-GA hybrid has been applied for the first time for the parameter identification of a nonlinear mathematical model of an E. coli cultivation process. The outperformance of the ALO-GA has been confirmed. The algorithm provides better results than the recent hybrid metaheuristics applied to an E. coli model parameter identification.
- The better ALO-GA performance is further confirmed by applying two parametric and three nonparametric statistical tests. The results show that the ALO-GA statistically outperforms the other algorithms considered in the comparison.
- A new improved model of the fed-batch cultivation process of the strain E. coli MC4110 has been obtained. It is 6.5% better than the best model known so far. The developed mathematical model could be further used for process investigation and optimization based on process monitoring and control.
The rest of the paper is organized in the following order. A brief review of some of the recent hybrid metaheuristic algorithms is presented in Section 2. The considered E. coli fed-batch cultivation process and its mathematical model are given in Section 3. The proposed hybrid technique ALO-GA is described in Section 4. The obtained numerical results and the provided statistical analysis are presented and discussed in Section 5. Concluding remarks and some future research directions are presented in Section 6.
2. Literature Review
The ALO is a novel metaheuristic swarm-based approach [28] designed to emulate the hunting behavior of antlions in nature. Recent investigations show that various modifications and hybridizations of ALO have improved its exploration, exploitation, convergence, and ability to avoid local optima. An ALO algorithm with an adaptive boundary and optimal guidance was proposed in [47] to enhance the ALO convergence speed and global search ability. The ABLALO algorithm exhibited improved convergence speed, search accuracy, and robustness through the simulation results of the six benchmark functions’ optimizations. A novel opposition-based ALO (OB-L-ALO) was introduced in [48] to improve the performance of the original ALO by enhancing the exploration of the algorithm. The results of the OB-L-ALO application on a set of 27 benchmark problems confirmed the progress in the performance. In [36], an approach based on ALO and a differential mutation operator called ALO-DM was proposed. A differential mutation operator and a greedy strategy enhanced the population’s diversity. The simulation results demonstrated that ALO-DM is a feasible and effective hybrid algorithm. A novel ALO hybrid, namely HALO, was discussed in [37]. The ALO was hybridized with the arithmetic crossover operation of the GA to improve the exploration of the search space. The proposed algorithm provided effective and robust high-quality solutions. In [38], the HALO algorithm was compared to the spotted hyena algorithm. The authors confirmed that the hybridization had enhanced the convergence rate. A modified ALO (MALO) was considered in [49] and proved superior in instance reduction problems. The ALO performance was improved by adding a new parameter that was dependent on the step length of each ant while revising the antlion’s position. The results obtained by applying the algorithm to 23 benchmark functions for 500 iterations and 13 benchmark functions for 1000 iterations demonstrated that the proposed MALO algorithm could escape the local optima and provide a better convergence rate as compared to the basic ALO algorithm and state-of-the-art optimizers [49]. The authors point out the need to determine the best values of the algorithm parameters as a possible limitation of the method. The K-means algorithm was integrated with the ALO in [50] for optimal clustering. The results showed that the K-means-ALO performed better than the K-means and K-means-PSO algorithms. An improved ALO combined with a support vector regression (IALO-SVR) was introduced in [51]. The method exhibited a high prediction accuracy in battery health prognosis. In [31], the ALO was hybridized with a sine cosine algorithm approach. The EALO-SCA algorithm revealed a better tracking performance, especially for abrupt motion.
Other recently published hybrid metaheuristics are discussed next. All of them were tested on a set of classical benchmark functions. The obtained results have been further used in comparison with the results of the ALO-GA hybrid proposed here. To be easily identified, all discussed algorithms are summarized in Table 1.
In [21], a novel chaotic opposition-based learning-driven hybrid aquila optimizer (AO) and artificial rabbits optimization (ARO) algorithm called CHAOARO was introduced. To verify the superiority of the algorithm, CHAOARO was compared with the original AO and ARO on 23 classical benchmark functions and the IEEE CEC2019 test suite. CHAOARO demonstrated significantly better results than the other competitor methods in terms of solution accuracy, convergence speed, and robustness. The IHAOAVOA hybrid algorithm between AO and the African vultures optimization algorithm was proposed in [52]. The performance of IHAOAVOA was analyzed on 23 classical benchmark functions and the IEEE CEC2019 test suite. The numerical and statistical results showed that IHAOAVOA outperformed the competing algorithms. The algorithm’s computational cost was pointed out as a potential limitation. In [53], a chaotic salp swarm algorithm based on opposition-based learning (OCSSA) was presented. The algorithm performed better when tested on 28 benchmark functions with unimodal or multimodal characteristics. The grey wolf optimizer (GWO) was modified in [54] to improve the exploration and exploitation ability of the algorithm. The COGWO2D algorithm is a combination of the chaotic logistic map, the opposition-based learning, the differential evolution (DE), and the disruption operator. The comparison with other competing algorithms, based on the classical CEC2005 and the CEC2014 benchmark functions, showed the higher accuracy obtained by COGWO2D. The limitation of the algorithm pointed out by the authors was the time complexity, which should be reduced. A hybrid HGGWA embedding three genetic operators into the standard GWO was presented in [55]. The effectiveness of HGGWA was proved by the simulation results. In [56], a hybrid LGWO, an enhanced version of the GWO with Lévy flight, was introduced. The Lévy flight was employed as a special navigation solution for alpha, beta, and delta wolves. The performance of the LGWO appeared to be substantially increased. A new variant of PSO, namely APSO-PDC, was proposed in [57] based on an adaptive selection of particle roles, population diversity control, and an adaptive control of parameters. A More preferable searching accuracy and searching reliability of the algorithm were shown by comparison with other well-established PSO variants on 21 unimodal and multimodal functions. A modified marine predators algorithm, MMPA, was considered in [58]. A logistic opposition-based learning mechanism and effective self-adaptive updating methods (new position-updating rule, inertia weight coefficient, and nonlinear step size control parameter strategy) were introduced into the original algorithm. The algorithm performance was tested on 23 classical benchmark functions and the CEC 2020 test suite. The results demonstrated that the MMPA exhibited a superior performance. The authors of [59] suggested a framework for using an orthogonal crossover (OX) in DE variants. The numerical results demonstrated that the performance of the DE variants could be refined through OXDE hybrids. An improved version of the arithmetic optimization algorithm (AOA), called nAOA, was proposed in [60]. The exploratory ability of the AOA was enhanced with high-density values generated by the natural logarithm and exponential operators. The efficient performance of nAOA was studied on thirty benchmark functions and three engineering design benchmarks.
There are a few applications of hybrid metaheuristics for the parameter identification of cultivation process models. In [22], a hybrid between the ant colony optimization (ACO) and the firefly algorithm (ACO-FA) was proposed. The ACO-FA was applied for model identification of an E. coli fed-batch cultivation process. For the same identification problem, a hybrid between the GA and ACO was considered in [26]. The comparison results showed that the hybrid GA-ACO outperformed ACO-FA. Recently published research on a hybrid between the artificial bee colony (ABC) and GA [24] showed a better quality performance of the algorithm when it was compared to both the GA-ACO and ACO-FA. The model of the E. coli fed-batch cultivation obtained by the ABC-GA was of the highest quality.
According to the literature review, a comprehensive hybridization between the ALO and GA has not yet been applied. Moreover, the ALO, neither modified nor hybridized, has been implemented for the parameter identification of cultivation process models.

Table 1.
Recently proposed hybrid approaches used as competing algorithms.
Table 1.
Recently proposed hybrid approaches used as competing algorithms.
| Hybrid Algorithm | Year | Used Approach |
|---|---|---|
| ABLALO [47] | 2019 | ALO with adaptive boundary and optimal guidance |
| OB-L-ALO [48] | 2017 | A novel opposition-based ALO |
| ALO-DM [36] | 2018 | ALO with differential mutation operator |
| HALO [37,38] | 2019 and 2021 | ALO with arithmetic crossover operation |
| MALO [49] | 2022 | ALO with a new algorithm parameter |
| K-means-ALO [50] | 2019 | ALO with integrated K-means clustering |
| IALO-SVR [51] | 2019 | ALO with support vector regression |
| EALO-SCA [31] | 2020 | ALO with a sine cosine algorithm approach |
| CHAOARO [21] | 2022 | Aquila optimizer and artificial rabbits optimization algorithm |
| IHAOAVOA [52] | 2022 | Aquila optimizer and African vultures optimization algorithm |
| ABC-GA [24] | 2021 | Artificial bee colony with genetic algorithm |
| ACO-FA [22] | 2014 | Ant colony optimization with firefly algorithm |
| GA-ACO [26] | 2016 | Ant colony optimization with genetic algorithm |
| OCSSA [53] | 2020 | Chaotic salp swarm algorithm based on opposition-based learning |
| COGWO2D [54] | 2018 | Grey wolf optimizer combined with a chaotic logistic map, opposition-based learning, differential evolution, and a disruption operator |
| HGGWA [55] | 2019 | Grey wolf optimizer with genetic operators |
| LGWO [56] | 2022 | Grey wolf optimizer with Lévy flight |
| APSO-PDC [57] | 2019 | Particle swarm optimization based on an adaptive selection of particle roles, population diversity control, and adaptive control of parameters |
| MMPA [58] | 2021 | Marine predators algorithm and logistic opposition-based learning mechanism and effective self-adaptive updating methods |
| OXDE [59] | 2012 | Orthogonal crossover and differential evolution variants |
| nAOA [60] | 2021 | Arithmetic optimization algorithm with the use of natural logarithm and exponential operators |
3. Escherichia coli Fed-Batch Cultivation Process
The experimental data sets of E. coli MC4110 were obtained by a fed-batch cultivation process carried out at the Institute of Technical Chemistry, University of Hannover, Germany [61]. A full description of the cultivation process conditions and experimental data is given in [22].
A system of nonlinear differential equations was introduced following the application of the general state space dynamical model to the fed-batch cultivation process of E. coli: [22]:
where X is the concentration of the biomass measured in [g·L−1]; S denotes the substrate concentration (glucose), [g·L−1]; F denotes the feeding rate, [h−1]; V is the volume of the bioreactor, [l]; is designated for the initial glucose concentration in the feeding solution, [g·L−1]; marks the maximum growth rate, [h−1]; is the saturation constant, [g·L−1]; and the mass of cells formed per unit mass of consumed substrate is expressed by the yield coefficient , [g·g−1].
The model is based on the following a priori assumptions [22]: (1) the bioreactor is completely mixed; (2) the main product is the biomass; (3) the oxidative consumption of glucose is expressed by the Monod kinetics; (4) the growth conditions are considered balanced, since there is no significant diversity in the elemental composition of biomass when the growth rate and substrate consumption are changed; (5) and the parameters (e.g., temperature, pH, and pO2) are controlled at their constant set points.
According to [22], the initial conditions of the process are as follows:
t0 = 6.68 h, X(t0) = 1.25 g·L−1, S(t0) = 0.8 g·L−1, and = 100 g·L−1.
4. Hybrid Ant Lion Optimizer-Genetic Algorithm (ALO-GA)
The ALO is a novel swarm-based metaheuristic approach [28] that mimics the hunting behavior of antlions in nature. The hunting process is carried out in five important phases: a random walk, building a trap, trapping ants, sliding the ants toward the antlion, catching the prey, and rebuilding the trap. The ALOs phases are repeated for a certain number of iterations T. The algorithm presented in detail in [28] is adopted here.
Ants search through the parameter space using a random walk. They are guided to promising regions by the antlions. The initial populations of ants and antlions are generated randomly based on the following equation:
where and signify, respectively, the lower and upper bounds of the problem parameters. The location of each ant and antlion in a D-dimensional search space is represented as a vector of size D.
The building of the trap is simulated with the choice of an antlion by the roulette wheel selection (RWS). Antlions with better fitness evaluations are more likely to be selected and to catch ants.
The random walk of each ant at each iteration of the algorithm is modelled as follows:
where is the cumulative sum; T is the maximum number of iterations; and r(t) is 0 if a generated , and 1, if not. To guarantee that the position of the ants will remain inside the search space, it is normalized using the upper and lower bounds of the search space:
where and are, respectively, the minimum and maximum of the random walk of the ith variable; and denote the minimum and maximum of the ith variable at the tth iteration.
Trapping the ants in the antlions’ pits is modelled by the influence of the antlions on the ants’ movement:
Two antlions have an impact on the random walk of each ant. The first one is selected by the RWS. The second is the elite antlion with the best fitness evaluation.
On each iteration, the positions of the ants are changed in the following manner [28]:
is the position of the ith ant at the tth iteration. The random walk around a selected antlion at the tth iteration is denoted as . is the random walk around the elite at the tth iteration.
Sliding the ants toward the trap, or converging to an antlion, is represented by decreasing the boundaries of the following variables:
where is the shrinking factor. For the first 10% of all iterations, . For the rest of the iterations, . The constant depends on the number of the current iteration, t, according to Table 2:

Table 2.
Dependence of the constant k on the current iteration.
The final phase at each iteration is catching the prey and rebuilding the trap. When an ant becomes fitter than an antlion, the antlion takes the position of the ant.
The ALO produces the initial population of the GA for n executions. The GA improves the population over several generations. Parents are selected using the RWS based on the evaluations of the individuals. The new generation is formed by applying two genetic operators to the parents.
The new individual is a result of the recombination of two parents x and y:
where is selected with uniform probability.
Each element of the individual mutates with a probability inversely proportional to D:
where ; ; is the mutation range; and , is from a Bernoulli probability distribution, and k ∈ [4; 20] is the mutation precision related to the minimum step size and the distribution of mutation steps in the mutation range.
The next generation includes offspring with a better fitness evaluation. A new generation is produced until the maximum number of generations specified as MaxGen is reached. The best individual in the last generation of the GA is the solution of the ALO-GA hybrid to the problem. According to [31], there is a higher probability for the RWS method to choose the elite. This can lead to falling into a local optimum. A hybridization with the GA [29,30] is proposed to avoid this limitation of the ALO algorithm. On the other hand, one drawback of the GA is that convergence to the optimum may take a lot of computational effort when the randomly generated initial population is quite distant from it. The collaborative combination of the two algorithms has a positive effect on this constraint as well. The ALO runs for a few iterations. As a result, the population gradually converges toward the optimum. The final population of the ALO is a much better starting point for the GA than any random one. Subsequently, the computational resources required by the GA to obtain the final solution are reduced. The genetic evolution of the ALO aims to provide a good balance between exploration and exploitation.
The ALO-GA pseudo-code is presented below (Algorithm 1). The hybrid ALO-GA is developed based on the ALO algorithm presented in [28] and the GA implemented in [24].
| Algorithm 1: Pseudo-code of ALO-GA |
| 1: begin 2: Define the input parameters for both ALO and GA 3: Define the parameters of the problem under consideration 4: % Start ALO 5: Generate randomly the initial populations of ants and antlions 6: Calculate the corresponding fitness estimations 7: Find the best antlion and adopt it as the elite (determined optimum) 8: for j:= 1 to the size of initial population Pop0 9: while the end criterion is not satisfied 10: for each ant 11: Select an antlion using the roulette wheel selection 12: Update the parameters of the random walk 13: Create a random walk and normalize it 14: Update the position of the ant 15: end for 16: Evaluate all ants 17: Replace an antlion with its corresponding ant if it becomes fitter 18: Update the elite if an antlion becomes fitter 19: end while 20: Memorize the best solution for the current iteration in Pop0 21: end for 22: % Start GA 23: Set the initial population Pop0 to the set of best solutions generated by ALO 24: Calculate the value of the fitness function for each individual in Pop0 25: for j:= 1 to MaxGeneration 26: Select individuals Popi from the current population Popi−1 in a way that gives an advantage to better individuals 27: Perform crossover with probability pc 28: Perform mutation with probability pm 29: Calculate the value of the fitness function for each individual in Popi 30: end for 31: Rank the solutions, find the current best, and memorize it 32: end begin |
The flowchart of the ALO-GA hybrid algorithm, according to the presented pseudo-code (Algorithm 1), is given in Figure 1.
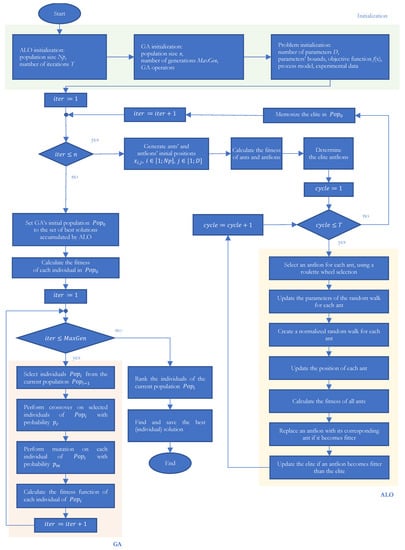
Figure 1.
Flowchart of the ALO-GA hybrid algorithm.
The two algorithms ALO and GA are applied consequently in the ALO-GA hybrid. Therefore, the computational complexity of the hybrid can be estimated in the following way.
Let O(f) be the computational complexity of the assessment of the fitness function.
The computational complexity of the ALO depends on the number of iterations T, the size of the population Np, and the complexity of the fitness function.
The generation of a random population of ants and antlions has a computational complexity of O(Np × D). The evaluation of the population is estimated as O(Np × f). Sorting the search agents according to their fitness evaluations and selecting the elite antlion has a complexity of O(Np × log Np).
The ALO algorithm runs for T iterations. The selection of an antlion at each iteration is estimated as O(Np). The computational complexity of the random walk around an antlion is O(Np × D). Updating the positions of the ants is executed with a complexity of O(Np). The evaluation of these new positions is O(Np × f).
The computational complexity of the ALO can be assessed finally as O(T × Np × (D + f)).
The ALO is required to generate the initial population of GA. Therefore, the ALO is executed n times, where n is the number of individuals in the GA. The computational complexity of the GA can be estimated as O(MaxGen × n × f).
The overall computational complexity of the ALO-GA hybrid is O((MaxGen × f + Np × T × (D + f)) × n). The computational complexity of the method is sacrificed for the sake of its computational precision. This can be regarded as a limitation of the ALO-GA hybrid. The MaxGen, n, Np, and T used in the hybrid, however, are significantly smaller than those usually exploited in standard ALO and GA algorithms. Since the initial position of the GA is not random but rather directed to the optimum, the GA requires far fewer generations to come to a final solution.
5. Results and Discussion
5.1. ALO-GA Hybrid Algorithm Performance on Test Functions
The proposed algorithm ALO-GA has been tested on several well-known benchmark functions listed in Table 3. These optimization problems fell into two groups: unimodal (UM) (F1, F2, F4, F5, and F7) and multimodal (MM) (F9–F11). All benchmark functions are considered with a dimension of 30.

Table 3.
Benchmark optimization problems.
The exploitation properties of an algorithm can be evaluated through the unimodal functions (F1, F2, F4, F5, and F7), which have only one global optimum. The exploration properties of an algorithm as well as its ability to avoid local optima are tested on multimodal functions (F9–F11).
The qualitative analysis results (search history metric) of the proposed ALO-GA approach in solving the considered benchmark functions are presented in Figure 2. The purpose of this metric is to display the position of the solutions in the search space during the iterations of the algorithm, thus tracking the exploration of the parameter space.
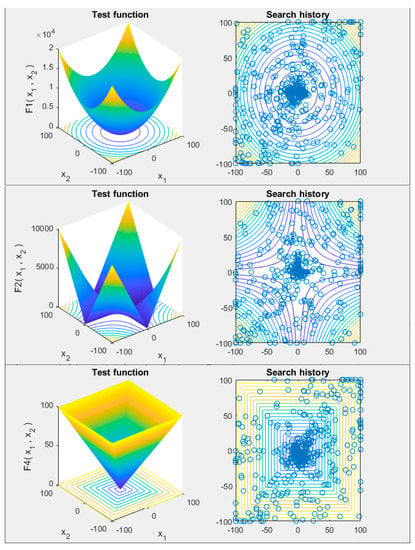
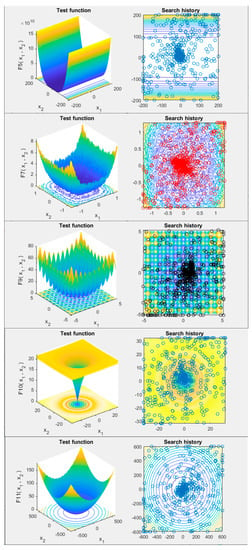
Figure 2.
Search history diagrams of the ALO-GA hybrid algorithm.
The search history diagrams show that ALO-GA has scanned the search space well, both globally and locally, and after identifying the main optimal area, the method converges toward the optimal solution with a high convergence rate.
To verify the performance of the ALO-GA, the obtained results are compared with some hybrid metaheuristic algorithms proposed in the literature, which are as follows:
- (i)
- Evolution-based algorithms (COGWO2D [54], HGGWA [55], and OXDE [59]);
- (ii)
- Physics-based algorithms (nAOA [60]);
- (iii)
- Swarm-based algorithms (CHAOARO [21], OCSSA [53], IHAOAVOA [52], APSO-PDC [57], MMPA [58], ABLALO [47], MALO [49], and OB-L-ALO [48]).
The obtained results (the mean value and the standard deviation (SD)) are presented in Table 4. The performance of the compared hybrid algorithms is ranked for each benchmark function. The final ranking based on the results of all benchmark functions is also calculated.

Table 4.
Results for the benchmark functions for different hybrid algorithms.
According to Table 4, ALO-GA produced the best mean value for five of the eight benchmark functions: three best results of the five considered UM functions and the two best results of the three considered MM functions, respectively. For the unimodal functions F5 (Rosenbrock) and F7 (Quartic), the best mean values were obtained by the hybrids IHAOAVOA [52] and APSO-PDC [57], respectively. APSO-PDC obtained the best mean value in the case of the multimodal function F10, too. The hybrids IHAOAVOA and APSO-PDC are ranked in second and third place, respectively. The fourth place is for the CHAOARO hybrid, followed by the MALO algorithm.
The results show that the ALO-GA hybrid exhibits a better performance compared to some existing ALO hybrid algorithms [47,48,49], as well as compared to the other nine hybrid techniques [21,52,53,54,55,57,58,59,60]. The presented search history diagrams (Figure 2) and the performance comparison (Table 4) demonstrate that ABC-GA achieved a good balance between the algorithm’s exploration and exploitation.
5.2. Parameter Identification of E. coli MC4110 Fed-Batch Cultivation Process
The parameter identification of the nonlinear mathematical model (Equations (1)–(3)) of the E. coli MC4110 fed-batch cultivation process performed using the ALO-GA hybrid algorithm is described below.
5.2.1. Simulation Setup
The proposed mathematical model consists of a set of three ODEs (Equations (1)–(3)) with two dependent state variables x = [] and three unknown parameters .
The population of the ALO-GA hybrid consists of a set of individuals that are possible solutions to the considered problem. The solutions are represented as vectors with elements corresponding to the unknown model parameters. Based on the authors’ expertise [23,62,63], the ranges of these parameters are estimated as the following:
The initial set of solutions is generated based on Equation (4). The solutions are later improved according to the specifics of the nature-inspired algorithms involved in the ALO-GA hybrid while observing the limitations in the values of the model parameters (Equation (14)). If necessary, the new solutions are additionally pushed back within the defined bounds.
The calculations are performed on Intel® Core™i7-8700 CPU @ 3.20 GHz, 3192 MHz, 32 GB Memory (RAM), with a Windows 10 pro (64 bit) operating system. The considered competing algorithms are implemented in Matlab R2019a, based on [22,24,26]. The implementation of the ALO-GA hybrid technique follows the above-presented pseudo-code and flowchart in Figure 1. The mathematical model of E. coli is created in the Simulink R2019a environment. The solver options are the fixed-step size of 0.01 and ode4 (Runge–Kutta) with TIMESPAN = [6.68 11.57].
ALO has only two main parameters, namely the population size Np and the number of iterations T [28,31]. The values of these input parameters were determined with several preliminary tests. The characteristics of the specific identification problem solved here were also taken into consideration while defining the ALO-GA parameters. Finally, the parameter values were set as Np = 50 and T = 50. The constant depended on the number of the current iteration t according to Table 2. A small population (Np = 50) was engaged in the beginning. The set of initial solutions for the GA was generated by the ALO for only 50 iterations. The main GA parameters were set as follows: number of generations—100; population size—50 individuals; crossover rate—0.7; mutation rate—0.1; generation gap—0.97. The following GA operators were chosen: RWS as a selection function; recombination extended intermediate as a recombination function; and a real-value mutation like the breeder genetic algorithm [64] as a mutation function.
A series of parameter identification procedures of the model Equations (1)–(3) using ALO-GA were performed. Due to the stochastic characteristics of the applied algorithms, 30 runs were conducted. The model parameter’s vector, namely , was estimated based on the objective function J:
where n is the length of the data vector for the state variables and ; the existing experimental data are denoted as and ; and the model predictions for a given set of parameters are marked as and .
5.2.2. Numerical Results
The results of the application of the novel ALO-GA hybrid algorithm to the parameter identification of an E. coli MC4110 cultivation process model are presented in Table 5 and Table 6. The mean, the best, and the worst results for the criteria value J of the performed 30 runs and the obtained SD are summarized in Table 5. The estimated model parameters with their SD are listed in Table 6. The algorithm convergence curves of the 30 runs and 150 total iterations are shown in Figure 3.

Table 5.
Comparison of the objective function values obtained by ALO with published results.

Table 6.
Comparison of the parameter estimates obtained by ALO with the published results.
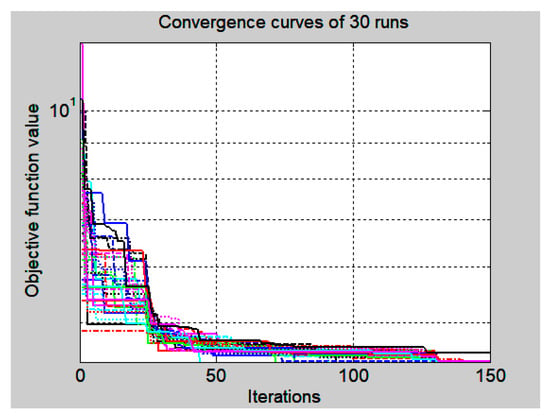
Figure 3.
Semi-log scale plot of the ALO-GA convergence curves for the 30 runs (each run is shown with a different line or color).
To show the superiority of the ALO-GA hybrid metaheuristic algorithm proposed here, the obtained results are compared to already-known outcomes for the same problem. The following published hybrid algorithms are considered: ABC-GA [24], GA-ACO [26], and ACO-FA [22]. The most accurate mathematical model of the cultivation process of E. coli MC4110 so far was obtained by GA-ACO with Jbest = 4.3803.
Semi-log scale plot of convergence curves shows that the hybrid converges for the 150 iterations very well.
All results presented in Table 5 show that the ALO-GA hybrid algorithm finds the highest quality solution, e.g., the solution with the smallest objective function value (J = 4.1128), and improves the accuracy of the model presented in [22]. According to the mean J values, the ALO-GA model is 4.7% better than ACO-FA, 5.3% better than the ABC-GA model, and 5.9% better than the GA-ACO model. Considering the best-obtained J value, the GA-ACO model is improved by 6.5%. The improvement of the ACO-FA model is 7% and 7.8% when the ALO-GA model is compared to the ABC-GA model. Despite these good results, the observed SD of ALO-GA has the largest value compared to the SD values of other hybrid metaheuristics. Different possibilities for improving this performance of the algorithm can be investigated in future research.
The model parameter estimates summarized in Table 6 are adequate and correspond to their physical meaning [65,66,67]. The obtained SD values indicate the good performance of the applied algorithms. The results show that the model estimates are very close. However, there is a statistically significant difference between them, which will be shown below. It can be concluded that the best model is obtained by ALO-GA.
The predictions for the E. coli fed-batch cultivation process variables (biomass and substrate) acquired by exploiting the estimated model parameters in Table 6 are represented graphically in Figure 4. They are examined in contrast to the measured real experimental data. The obtained results are compared to the results of ABC-GA, GA-ACO, and ACO-FA.
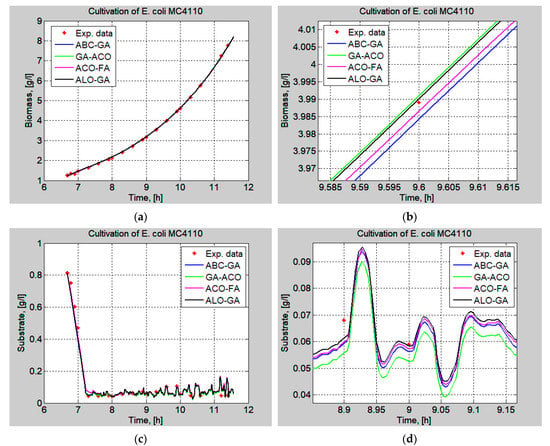
Figure 4.
Time profiles of the process variables: real experimental data and model predicted data: (a) biomass; (b) zoomed result; (c) substrate; and (d) zoomed result.
To show the superior performance of the ALO-GA hybrid, a zoomed perspective of the graphical results is also presented. The graphical comparisons show that the ALO-GA model describes the experimental data superbly, following the trend of the process dynamics. The ALO-GA model dynamics are the closest to the dynamics of the experimental data.
5.2.3. Statistical Analysis
Two classes of statistical procedures are employed in the statistical analysis: parametric and nonparametric. Experiments are usually analyzed with parametric tests. Generally, they have more statistical power than their nonparametric equivalents [68] and are more likely to detect significant differences when such do exist. When it comes to analyzing the performance of stochastic algorithms, the assumptions of parametric tests are most probably violated [43]. Nonparametric statistical procedures are a practical tool when previous assumptions cannot be satisfied [39]. Nonparametric tests, namely, the Friedman test, the Wilcoxon test, and its parametric equivalent, the paired t-test, the Kruskal–Wallis test, and its parametric equivalent, the one-way analysis of variance (ANOVA) test, are applied here to obtain numerical data and to compare the performance of the algorithms. The tests are performed in Matlab, using the following functions: Friedman test—‘friedman’; Wilcoxon test—‘ranksum’; Paired t-test—‘ttest2′; Kruskal–Wallis test—‘kruskalwallis’; ANOVA—‘anova1′. The tests are applied to the results of the objective function J obtained by the 30 runs of each algorithm. The results are summarized in Table 7.

Table 7.
Results from statistical tests.
The statistical results presented in Table 7 reveal that there are statistical differences between the ALO-GA hybrid and the competing hybrid algorithms—GA-ACO, ACO-FA, and ABC-GA. All tests show significantly lower p-values than 0.05. Thus, the null hypothesis that the mean of the objective function is the same for all four algorithms can be rejected. This is sufficient evidence to conclude that the results obtained by GA-ACO, ACO-FA, ABC-GA, and ALO-GA are statistically significant. Since the mean J value of ALO-GA is the lowest compared to the other observed mean values, it may be concluded that the proposed hybrid metaheuristic outperforms all considered algorithms in the case of parameter identification of an E. coli cultivation model (Equations (1)–(3)).
The performance of the investigated hybrid algorithms is statistically evaluated by a comparison of the acquired mean values, SD, and the median of the estimated model parameters and the obtained objective function value J. To visualize the summary statistics, box plot diagrams are presented in Figure 5.
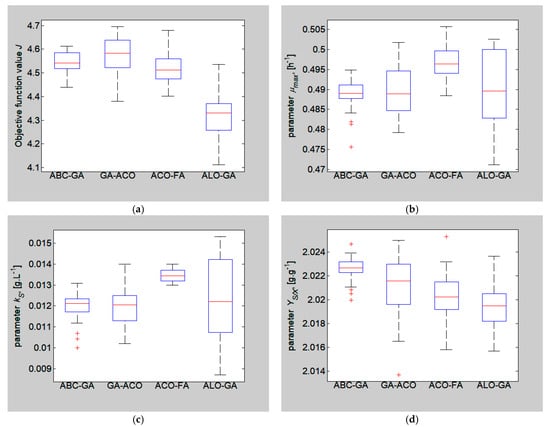
Figure 5.
Box plot for the results from the parameter identification of an E. coli cultivation model: (a) objective function J; (b) parameter ; (c) parameter ; and (d) parameter .
The proposed hybrid algorithm evidently outperforms the ABC-GA, GA-ACO, and ACO-FA metaheuristics. The collaborative combination between the ALO and GA improves the ALOs performance. Its source of exploitation is the selection according to the fitness of the solutions, while the mutation and crossover operators are the sources of exploration [69,70]. According to [71], recombination is quite useful in exploitation when the necessary diversity of the population is somehow ensured. Such diversity in the GA is achieved through higher mutation rates as in the proposed hybrid in the case of E. coli modeling.
6. Conclusions and Future Research Directions
A novel ALO-GA hybrid metaheuristic algorithm is proposed for parameter identification of a nonlinear mathematical model of the E. coli MC4110 fed-batch cultivation process. The collaboration between the ALO algorithm and GA in the proposed hybrid aims to balance exploration and exploitation properly.
The proposed hybrid is examined in comparison to a set of classical benchmark functions (unimodal and multimodal) and other hybrids of population-based metaheuristic algorithms inspired by nature. The ABC-GA, GA-ACO, and ACO-FA algorithms were chosen as they had been previously applied to the same parameter identification problem. The ALO-GA hybrid shows the best performance based on the final ranking in comparison to the 12 hybrid algorithms applied for the considered benchmark function. The numerical simulation results for the parameter identification of an E. coli MC4110 cultivation process model show that the ALO-GA hybrid algorithm surpasses the other competing algorithms. The statistical analysis based on the Friedman test, Wilcoxon test, Kruskal–Wallis test, paired t-test, and ANOVA confirms the obtained results. The results observed for the best objective function J value reveal an improvement of 6.5% compared to the GA-ACO model, 7% compared to the ACO-FA model, and 7.8% compared to the ABC-GA model. The outcomes are encouraging, and they demonstrate the high performance of the novel ACO-GA hybrid metaheuristic algorithm in the model identification problem of an E. coli MC4110 fed-batch cultivation process. In the future, the algorithm can be applied to designing more complex nonlinear mathematical models of cultivation processes.
Various new hybrid algorithms can be further developed for this topical field. The coyote optimization algorithm [72], the water cycle algorithm [73], the grey wolf optimization [74], etc., can be hybridized to enhance the ALO performance and propose a powerful technique for the nonlinear model parameter identification problem.
Author Contributions
Conceptualization, O.R. and V.L.; methodology, O.R.; software, D.Z. and G.R.; validation, O.R., D.Z. and V.L.; formal analysis, O.R. and V.L.; investigation, O.R., D.Z., G.R. and V.L.; writing—original draft preparation, O.R. and D.Z.; writing—review and editing, O.R., D.Z. and V.L.; visualization, O.R., D.Z. and G.R.; supervision, O.R. and V.L.; project administration, V.L.; funding acquisition, V.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Bulgarian National Science Fund Project KП-06-H32/3 “Interactive System for Education in Modelling and Control of Bioprocesses (InSEMCoBio)”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- de Menezes, L.H.S.; Carneiro, L.L.; de Carvalho Tavares, I.M.; Santos, P.H.; das Chagas, T.P.; Mendes, A.A.; da Silva, E.G.P.; Franco, M.; de Oliveira, J.R. Artificial Neural Network Hybridized with a Genetic Algorithm for Optimization of Lipase Production from Penicillium roqueforti ATCC 10110 in Solid-State Fermentation. Biocatal. Agric. Biotechnol. 2021, 31, 101885. [Google Scholar] [CrossRef]
- Pan, N.; Wang, H.; Tian, Y.; Chorukova, E.; Simeonov, I.; Christov, N. Comparison Study of Dynamic Models for One-stage and Two-stage Anaerobic Digestion Processes. IFAC-PapersOnLine 2022, 55, 667–672. [Google Scholar] [CrossRef]
- Chorukova, E.; Hubenov, V.; Gocheva, Y.; Simeonov, I. Two-Phase Anaerobic Digestion of Corn Steep Liquor in Pilot Scale Biogas Plant with Automatic Control System with Simultaneous Hydrogen and Methane Production. Appl. Sci. 2022, 12, 6274. [Google Scholar] [CrossRef]
- Brou, P.; Patricia, T.; Beaufort, S.; Brandam, C. Modelling of S. cerevisiae and T. delbrueckii pure culture fermentation in synthetic media using a compartmental nitrogen model. OENO One 2020, 54, 299–311. [Google Scholar] [CrossRef]
- Zentou, H.; Zainal Abidin, Z.; Yunus, R.; Awang Biak, D.R.; Abdullah Issa, M.; Yahaya Pudza, M. A new model of alcoholic fermentation under a byproduct inhibitory effect. ACS Omega 2021, 6, 4137–4146. [Google Scholar] [CrossRef]
- Ma, X.; Wu, Y.; Shen, J.; Duan, L.; Liu, Y. ML-LME: A Plant Growth Situation Analysis Model Using the Hierarchical Effect of Fractal Dimension. Mathematics 2021, 9, 1322. [Google Scholar] [CrossRef]
- Guzmán-Palomino, A.; Aguilera-Vázquez, L.; Hernández-Escoto, H.; García-Vite, P.M. Sensitivity, Equilibria, and Lyapunov Stability Analysis in Droop’s Nonlinear Differential Equation System for Batch Operation Mode of Microalgae Culture Systems. Mathematics 2021, 9, 2192. [Google Scholar] [CrossRef]
- Benalcázar, E.A.; Noorman, H.; Filho, R.M.; Posada, J.A. Modeling ethanol production through gas fermentation: A biothermodynamics and mass transfer-based hybrid model for microbial growth in a large-scale bubble column bioreactor. Biotechnol. Biofuels 2020, 13, 59. [Google Scholar] [CrossRef]
- Du, Y.H.; Wang, M.Y.; Yang, L.H.; Tong, L.L.; Guo, D.S.; Ji, X.J. Optimization and Scale-Up of Fermentation Processes Driven by Models. Bioengineering 2022, 9, 473. [Google Scholar] [CrossRef]
- Dulf, E.H.; Vodnar, D.C.; Danku, A.; Martău, A.G.; Teleky, B.E.; Dulf, F.V.; Ramadan, M.F.; Crisan, O. Mathematical Modeling and Optimization of Lactobacillus Species Single and Co-Culture Fermentation Processes in Wheat and Soy Dough Mixtures. Front. Bioeng. Biotechnol. 2022, 10, 888827. [Google Scholar] [CrossRef] [PubMed]
- Krista, G.M.; Kresnowati, M.T.A.P. Modeling the synthetic gas fermentation for bioethanol production. IOP Conf. Ser. Earth Environ. Sci. 2022, 963, 012013. [Google Scholar] [CrossRef]
- Ezzatzadegan, L.; Yusof, R.; Morad, N.A.; Shabanzadeh, P.; Muda, N.S.; Borhani, T.N. Experimental and artificial intelligence modelling study of oil palm trunk sap fermentation. Energies 2021, 14, 2137. [Google Scholar] [CrossRef]
- Alvarado-Santos, E.; Aguilar-López, R.; Neria-González, M.I.; Romero-Cortés, T.; Robles-Olvera, V.J.; López-Pérez, P.A. A novel kinetic model for a cocoa waste fermentation to ethanol reaction and its experimental validation. Prep. Biochem. 2022, 53, 167–182. [Google Scholar] [CrossRef]
- Mori, H.; Kataoka, M.; Yang, X. Past, Present, and Future of Genome Modification in Escherichia coli. Microorganisms 2022, 10, 1835. [Google Scholar] [CrossRef]
- Necula, G.; Bacalum, M.; Radu, M. Interaction of Tryptophan- and Arginine-Rich Antimicrobial Peptide with E. coli Outer Membrane—A Molecular Simulation Approach. Int. J. Mol. Sci. 2023, 24, 2005. [Google Scholar] [CrossRef]
- Castro-López, D.A.; González de la Vara, L.E.; Santillán, M.; Martínez-Antonio, A. A Molecular Dynamic Model of Tryptophan Overproduction in Escherichia coli. Fermentation 2022, 8, 560. [Google Scholar] [CrossRef]
- Predojević, L.; Keše, D.; Bertok, D.Ž.; Korva, M.; Kreft, M.E.; Erjavec, M.S. Cytokine Response of the Biomimetic Porcine Urothelial Model to Different Escherichia coli Strains. Appl. Sci. 2022, 12, 8567. [Google Scholar] [CrossRef]
- Azrag, M.A.K.; Zain, J.M.; Kadir, T.A.A.; Yusoff, M.; Jaber, A.S.; Abdlrhman, H.S.M.; Ahmed, Y.H.Z.; Husain, M.S.B. Estimation of Small-Scale Kinetic Parameters of Escherichia coli (E. coli) Model by Enhanced Segment Particle Swarm Optimization Algorithm ESe-PSO. Processes 2023, 11, 126. [Google Scholar] [CrossRef]
- Jiménez, A.; Castillo, A.; Mahn, A. Kinetic Study and Modeling of Wild-Type and Recombinant Broccoli Myrosinase Produced in E. coli and S. cerevisiae as a Function of Substrate Concentration, Temperature, and pH. Catalysts 2022, 12, 683. [Google Scholar] [CrossRef]
- Dehghani, M.; Trojovská, E.; Zuščák, T. A new human-inspired metaheuristic algorithm for solving optimization problems based on mimicking sewing training. Sci. Rep. 2022, 12, 17387. [Google Scholar] [CrossRef]
- Wang, Y.; Xiao, Y.; Guo, Y.; Li, J. Dynamic Chaotic Opposition-Based Learning-Driven Hybrid Aquila Optimizer and Artificial Rabbits Optimization Algorithm: Framework and Applications. Processes 2022, 10, 2703. [Google Scholar] [CrossRef]
- Roeva, O.; Fidanova, S. Parameter Identification of an E. coli cultivation process model using hybrid metaheuristics. Int. J. Metaheuristics 2014, 3, 133–148. [Google Scholar] [CrossRef]
- Roeva, O.; Atanassova, V. Cuckoo search algorithm for model parameter identification. Int. J. Bioautom. 2016, 20, 483–492. [Google Scholar]
- Roeva, O.; Zoteva, D.; Lyubenova, V. Escherichia coli Cultivation Process Modelling Using ABC-GA Hybrid Algorithm. Processes 2021, 9, 1418. [Google Scholar] [CrossRef]
- Angelova, M.; Vassilev, P.; Pencheva, T. Genetic Algorithm and Cuckoo Search Hybrid Technique for Parameter Identification of Fermentation Process Model. Int. J. Bioautom. 2020, 24, 277–288. [Google Scholar] [CrossRef]
- Roeva, O.; Fidanova, S.; Paprzycki, M. InterCriteria analysis of ACO and GA hybrid algorithms. Stud. Comput. Intell. 2016, 610, 107–126. [Google Scholar]
- Khoja, I.; Ladhari, T.; M’sahli, F.; Sakly, A. Cuckoo search approach for parameter identification of an activated sludge process. Comput. Int. Neurosci. 2018, 2018, 3476851. [Google Scholar] [CrossRef]
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Goldberg, D. Genetic Algorithms in Search, Optimization and Machine Learning, 1st ed.; Addison-Wesley Professional: Boston, MA, USA, 1989. [Google Scholar]
- Zhang, H.; Gao, Z.; Zhang, J.; Liu, J.; Nie, Z.; Zhang, J. Hybridizing extended ant lion optimizer with sine cosine algorithm approach for abrupt motion tracking. EURASIP J. Image Video Process. 2020, 2020, 1–18. [Google Scholar] [CrossRef]
- Velasco, L.; Guerrero, H.; Hospitaler, A. Can the global optimum of a combinatorial optimization problem be reliably estimated through extreme value theory? Swarm Evol. Comput. 2022, 75, 101172. [Google Scholar] [CrossRef]
- Pandey, H.M. 3—State of the Art: Genetic Algorithms and Premature Convergence; Hari, M.P., Ed.; State of the Art on Grammatical Inference Using Evolutionary Method; Academic Press: Cambridge, MA, USA, 2022; pp. 35–124. [Google Scholar] [CrossRef]
- Assiri, A.S.; Hussien, A.G.; Amin, M. Ant lion optimization: Variants, hybrids, and applications. IEEE Access 2020, 8, 77746–77764. [Google Scholar] [CrossRef]
- Abualigah, L.; Shehab, M.; Alshinwan, M.; Mirjalili, S.; Elaziz, M.A. Ant lion optimizer: A comprehensive survey of its variants and applications. Arch. Comput. Methods Eng. 2021, 28, 1397–1416. [Google Scholar] [CrossRef]
- Hu, P.; Wang, Y.; Wang, H.; Zhao, R.; Yuan, C.; Zheng, Y.; Lu, Q.; Li, Y.; Masood, I. ALO-DM: A Smart Approach Based on Ant lion Optimizer with Differential Mutation Operator in Big Data Analytics. In Database Systems for Advanced Applications. DASFAA 2018; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 10829, pp. 64–73. [Google Scholar] [CrossRef]
- Dwivedi, D.; Balasubbareddy, M. Optimal power flow using hybrid ant lion optimization algorithm. Pramana Res. J. 2019, 9, 368–380. [Google Scholar]
- Singh, D.K.; Srivastava, S.; Khanna, R.K. Optimal Power Flow using Hybrid Ant Lion Optimization and Spotted Hyena Optimization Algorithm: Comparison and Analysis. Elem. Educ. Online 2021, 19, 3055. [Google Scholar]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Sheskin, D.J. Handbook of Parametric and Nonparametric Statistical Procedures, 4th ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar]
- Friedman, M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J. Am. Stat. Assoc. 1937, 32, 674–701. [Google Scholar] [CrossRef]
- Friedman, M. A comparison of alternative tests of significance for the problem of m rankings. Ann. Math. Stat. 1940, 11, 86–92. [Google Scholar] [CrossRef]
- García, S.; Molina, D.; Lozano, M.; Herrera, F. A study on the use of nonparametric tests for analyzing the evolutionary algorithms’ behaviour: A case study on the CEC’2005 special session on real parameter optimization. J. Heuristics 2009, 15, 617–644. [Google Scholar] [CrossRef]
- García, S.; Fernández, A.; Luengo, J.; Herrera, F. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Inf. Sci. 2010, 180, 2044–2064. [Google Scholar] [CrossRef]
- Kruskal, W.; Wallis, W. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Fisher, R.A. Statistical Methods and Scientific Inference, 2nd ed.; Oliver and Boyd: Edinburgh, UK, 1959. [Google Scholar]
- Wang, R.A.; Zhou, Y.W.; Zheng, Y.Y. Ant lion optimizer with adaptive boundary and optimal guidance. In Proceedings of the Recent Developments in Mechatronics and Intelligent Robotics: Proceedings of International Conference on Mechatronics and Intelligent Robotics (ICMIR2018), Kunming, China, 19–20 May 2018; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 379–386. [Google Scholar]
- Dinkar, S.K.; Deep, K. Opposition based Laplacian Ant Lion Optimizer. J. Comput. Sci. 2017, 23, 71–90. [Google Scholar] [CrossRef]
- El Bakrawy, L.M.; Cifci, M.A.; Kausar, S.; Hussain, S.; Islam, M.A.; Alatas, B.; Desuky, A.S. A Modified Ant Lion Optimization Method and Its Application for Instance Reduction Problem in Balanced and Imbalanced Data. Axioms 2022, 11, 95. [Google Scholar] [CrossRef]
- Majhi, S.K.; Biswal, S. A hybrid clustering algorithm based on Kmeans and ant lion optimization. In Emerging Technologies in Data Mining and Information Security; Springer: Berlin/Heidelberg, Germany, 2019; pp. 639–650. [Google Scholar]
- Wang, Y.; Ni, Y.; Li, N.; Lu, S.; Zhang, S.; Feng, Z.; Wang, J. A method based on improved ant lion optimization and support vector regression for remaining useful life estimation of lithium-ion batteries. Energy Sci. Eng. 2019, 7, 2797–2813. [Google Scholar] [CrossRef]
- Xiao, Y.; Guo, Y.; Cui, H.; Wang, Y.; Li, J.; Zhang, Y. IHAOAVOA: An improved hybrid aquila optimizer and African vultures optimization algorithm for global optimization problems. Math. Biosci. Eng. 2022, 19, 10963–11017. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, F.; Han, Y.; Cui, Y. An opposition-based chaotic salp swarm algorithm for global optimization. IEEE Access 2020, 8, 36485–36501. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Abd Elaziz, M.; Lu, S. Chaotic opposition-based grey-wolf optimization algorithm based on differential evolution and disruption operator for global optimization. Expert Syst. Appl. 2018, 108, 1–27. [Google Scholar] [CrossRef]
- Gu, Q.; Li, X.; Jiang, S. Hybrid genetic grey wolf algorithm for large-scale global optimization. Complexity 2019, 2019, 2653512. [Google Scholar] [CrossRef]
- Sang-To, T.; Le-Minh, H.; Mirjalili, S.; Wahab, M.A.; Cuong-Le, T. A new movement strategy of grey wolf optimizer for optimization problems and structural damage identification. Adv. Eng. Softw. 2022, 173, 103276. [Google Scholar] [CrossRef]
- Song, Z.; Liu, B.; Cheng, H. Adaptive particle swarm optimization with population diversity control and its application in tandem blade optimization. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 1859–1875. [Google Scholar] [CrossRef]
- Fan, Q.; Huang, H.; Chen, Q.; Yao, L.; Yang, K.; Huang, D. A modified self-adaptive marine predators algorithm: Framework and engineering applications. Eng. Comput. 2021, 38, 3269–3294. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Z.; Zhang, Q. Enhancing the search ability of differential evolution through orthogonal crossover. Inf. Sci. 2012, 185, 153–177. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E. Advanced arithmetic optimization algorithm for solving mechanical engineering design problems. PLoS ONE 2021, 16, e0255703. [Google Scholar] [CrossRef] [PubMed]
- Pencheva, T.; Roeva, O.; Hristozov, I. Functional State Approach to Fermentation Processes Modelling; Prof. Marin Drinov Academic Publishing House: Sofia, Bulgaria, 2006. [Google Scholar]
- Slavov, T.; Roeva, O. Genetic Algorithm Tuning of PID Controller in Smith Predictor for Glucose Concentration Control. Int. J. Bioautom. 2011, 15, 101–114. [Google Scholar]
- Roeva, O. Application of Artificial Bee Colony Algorithm for Model Parameter Identification. In Innovative Computing, Optimization and Its Applications; Zelinka, I., Vasant, P., Duy, V., Dao, T., Eds.; Studies in Computational Intelligence; Springer: Cham, Switzerland, 2018; Volume 741, pp. 285–303. [Google Scholar] [CrossRef]
- Mühlenbein, H.; Schlierkamp-Voosen, D. Predictive models for the breeder genetic algorithm I. Continuous parameter optimization. Evol. Comput. 1993, 1, 25–49. [Google Scholar] [CrossRef]
- Anane, E.; Neubauer, P.; Bournazou, M.N.C. Modelling Overflow Metabolism in Escherichia coli by Acetate Cycling. Biochem. Eng. J. 2017, 125, 23–30. [Google Scholar] [CrossRef]
- Chen, R.; John, J.; Rode, B.; Hitzmann, B.; Gerardy-Schahn, R.; Kasper, C.; Scheper, T. Comparison of Polysialic Acid Production in Escherichia coli K1 During Batch Cultivation and Fed-batch Cultivation Applying Two Different Control Strategies. J. Biotechnol. 2011, 154, 222–229. [Google Scholar] [CrossRef]
- Vital, M.; Hammes, F.; Egli, T. Competition of Escherichia coli O157 with a Drinking Water Bacterial Community at low Nutrient Concentrations. Water Res. 2012, 46, 6279–6290. [Google Scholar] [CrossRef]
- Campbell, M.J.; Swinscow, T.D.V. Statistics at Square One, 11th ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2009. [Google Scholar]
- Črepinšek, M.; Liu, S.H.; Mernik, M. Exploration and exploitation in evolutionary algorithms: A survey. ACM Comput. Surv. 2013, 45, 1–33. [Google Scholar] [CrossRef]
- Hussain, A.; Muhammad, Y.S. Trade-off between exploration and exploitation with genetic algorithm using a novel selection operator. Complex Intell. Syst. 2020, 6, 1–14. [Google Scholar] [CrossRef]
- Corus, D.; Oliveto, P.S. On the benefits of populations for the exploitation speed of standard steady-state genetic algorithms. In Proceedings of the Genetic and Evolutionary Computation Conference, Prague, Czech Republic, 13–17 July 2019; pp. 1452–1460. [Google Scholar]
- Pierezan, J.; Dos Santos Coelho, L. Coyote Optimization Algorithm: A New Metaheuristic for Global Optimization Problems. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Eskandar, H.; Sadollah, A.; Bahreinineja, A.; Shukor, M. Water cycle algorithm—A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110, 151–166. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).